- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive

Null Hypothesis: Definition, Rejecting & Examples
By Jim Frost 6 Comments
What is a Null Hypothesis?
The null hypothesis in statistics states that there is no difference between groups or no relationship between variables. It is one of two mutually exclusive hypotheses about a population in a hypothesis test.

- Null Hypothesis H 0 : No effect exists in the population.
- Alternative Hypothesis H A : The effect exists in the population.
In every study or experiment, researchers assess an effect or relationship. This effect can be the effectiveness of a new drug, building material, or other intervention that has benefits. There is a benefit or connection that the researchers hope to identify. Unfortunately, no effect may exist. In statistics, we call this lack of an effect the null hypothesis. Researchers assume that this notion of no effect is correct until they have enough evidence to suggest otherwise, similar to how a trial presumes innocence.
In this context, the analysts don’t necessarily believe the null hypothesis is correct. In fact, they typically want to reject it because that leads to more exciting finds about an effect or relationship. The new vaccine works!
You can think of it as the default theory that requires sufficiently strong evidence to reject. Like a prosecutor, researchers must collect sufficient evidence to overturn the presumption of no effect. Investigators must work hard to set up a study and a data collection system to obtain evidence that can reject the null hypothesis.
Related post : What is an Effect in Statistics?
Null Hypothesis Examples
Null hypotheses start as research questions that the investigator rephrases as a statement indicating there is no effect or relationship.
| Does the vaccine prevent infections? | The vaccine does not affect the infection rate. |
| Does the new additive increase product strength? | The additive does not affect mean product strength. |
| Does the exercise intervention increase bone mineral density? | The intervention does not affect bone mineral density. |
| As screen time increases, does test performance decrease? | There is no relationship between screen time and test performance. |
After reading these examples, you might think they’re a bit boring and pointless. However, the key is to remember that the null hypothesis defines the condition that the researchers need to discredit before suggesting an effect exists.
Let’s see how you reject the null hypothesis and get to those more exciting findings!
When to Reject the Null Hypothesis
So, you want to reject the null hypothesis, but how and when can you do that? To start, you’ll need to perform a statistical test on your data. The following is an overview of performing a study that uses a hypothesis test.
The first step is to devise a research question and the appropriate null hypothesis. After that, the investigators need to formulate an experimental design and data collection procedures that will allow them to gather data that can answer the research question. Then they collect the data. For more information about designing a scientific study that uses statistics, read my post 5 Steps for Conducting Studies with Statistics .
After data collection is complete, statistics and hypothesis testing enter the picture. Hypothesis testing takes your sample data and evaluates how consistent they are with the null hypothesis. The p-value is a crucial part of the statistical results because it quantifies how strongly the sample data contradict the null hypothesis.
When the sample data provide sufficient evidence, you can reject the null hypothesis. In a hypothesis test, this process involves comparing the p-value to your significance level .
Rejecting the Null Hypothesis
Reject the null hypothesis when the p-value is less than or equal to your significance level. Your sample data favor the alternative hypothesis, which suggests that the effect exists in the population. For a mnemonic device, remember—when the p-value is low, the null must go!
When you can reject the null hypothesis, your results are statistically significant. Learn more about Statistical Significance: Definition & Meaning .
Failing to Reject the Null Hypothesis
Conversely, when the p-value is greater than your significance level, you fail to reject the null hypothesis. The sample data provides insufficient data to conclude that the effect exists in the population. When the p-value is high, the null must fly!
Note that failing to reject the null is not the same as proving it. For more information about the difference, read my post about Failing to Reject the Null .
That’s a very general look at the process. But I hope you can see how the path to more exciting findings depends on being able to rule out the less exciting null hypothesis that states there’s nothing to see here!
Let’s move on to learning how to write the null hypothesis for different types of effects, relationships, and tests.
Related posts : How Hypothesis Tests Work and Interpreting P-values
How to Write a Null Hypothesis
The null hypothesis varies by the type of statistic and hypothesis test. Remember that inferential statistics use samples to draw conclusions about populations. Consequently, when you write a null hypothesis, it must make a claim about the relevant population parameter . Further, that claim usually indicates that the effect does not exist in the population. Below are typical examples of writing a null hypothesis for various parameters and hypothesis tests.
Related posts : Descriptive vs. Inferential Statistics and Populations, Parameters, and Samples in Inferential Statistics
Group Means
T-tests and ANOVA assess the differences between group means. For these tests, the null hypothesis states that there is no difference between group means in the population. In other words, the experimental conditions that define the groups do not affect the mean outcome. Mu (µ) is the population parameter for the mean, and you’ll need to include it in the statement for this type of study.
For example, an experiment compares the mean bone density changes for a new osteoporosis medication. The control group does not receive the medicine, while the treatment group does. The null states that the mean bone density changes for the control and treatment groups are equal.
- Null Hypothesis H 0 : Group means are equal in the population: µ 1 = µ 2 , or µ 1 – µ 2 = 0
- Alternative Hypothesis H A : Group means are not equal in the population: µ 1 ≠ µ 2 , or µ 1 – µ 2 ≠ 0.
Group Proportions
Proportions tests assess the differences between group proportions. For these tests, the null hypothesis states that there is no difference between group proportions. Again, the experimental conditions did not affect the proportion of events in the groups. P is the population proportion parameter that you’ll need to include.
For example, a vaccine experiment compares the infection rate in the treatment group to the control group. The treatment group receives the vaccine, while the control group does not. The null states that the infection rates for the control and treatment groups are equal.
- Null Hypothesis H 0 : Group proportions are equal in the population: p 1 = p 2 .
- Alternative Hypothesis H A : Group proportions are not equal in the population: p 1 ≠ p 2 .
Correlation and Regression Coefficients
Some studies assess the relationship between two continuous variables rather than differences between groups.
In these studies, analysts often use either correlation or regression analysis . For these tests, the null states that there is no relationship between the variables. Specifically, it says that the correlation or regression coefficient is zero. As one variable increases, there is no tendency for the other variable to increase or decrease. Rho (ρ) is the population correlation parameter and beta (β) is the regression coefficient parameter.
For example, a study assesses the relationship between screen time and test performance. The null states that there is no correlation between this pair of variables. As screen time increases, test performance does not tend to increase or decrease.
- Null Hypothesis H 0 : The correlation in the population is zero: ρ = 0.
- Alternative Hypothesis H A : The correlation in the population is not zero: ρ ≠ 0.
For all these cases, the analysts define the hypotheses before the study. After collecting the data, they perform a hypothesis test to determine whether they can reject the null hypothesis.
The preceding examples are all for two-tailed hypothesis tests. To learn about one-tailed tests and how to write a null hypothesis for them, read my post One-Tailed vs. Two-Tailed Tests .
Related post : Understanding Correlation
Neyman, J; Pearson, E. S. (January 1, 1933). On the Problem of the most Efficient Tests of Statistical Hypotheses . Philosophical Transactions of the Royal Society A . 231 (694–706): 289–337.
Share this:

Reader Interactions
January 11, 2024 at 2:57 pm
Thanks for the reply.
January 10, 2024 at 1:23 pm
Hi Jim, In your comment you state that equivalence test null and alternate hypotheses are reversed. For hypothesis tests of data fits to a probability distribution, the null hypothesis is that the probability distribution fits the data. Is this correct?
January 10, 2024 at 2:15 pm
Those two separate things, equivalence testing and normality tests. But, yes, you’re correct for both.
Hypotheses are switched for equivalence testing. You need to “work” (i.e., collect a large sample of good quality data) to be able to reject the null that the groups are different to be able to conclude they’re the same.
With typical hypothesis tests, if you have low quality data and a low sample size, you’ll fail to reject the null that they’re the same, concluding they’re equivalent. But that’s more a statement about the low quality and small sample size than anything to do with the groups being equal.
So, equivalence testing make you work to obtain a finding that the groups are the same (at least within some amount you define as a trivial difference).
For normality testing, and other distribution tests, the null states that the data follow the distribution (normal or whatever). If you reject the null, you have sufficient evidence to conclude that your sample data don’t follow the probability distribution. That’s a rare case where you hope to fail to reject the null. And it suffers from the problem I describe above where you might fail to reject the null simply because you have a small sample size. In that case, you’d conclude the data follow the probability distribution but it’s more that you don’t have enough data for the test to register the deviation. In this scenario, if you had a larger sample size, you’d reject the null and conclude it doesn’t follow that distribution.
I don’t know of any equivalence testing type approach for distribution fit tests where you’d need to work to show the data follow a distribution, although I haven’t looked for one either!
February 20, 2022 at 9:26 pm
Is a null hypothesis regularly (always) stated in the negative? “there is no” or “does not”
February 23, 2022 at 9:21 pm
Typically, the null hypothesis includes an equal sign. The null hypothesis states that the population parameter equals a particular value. That value is usually one that represents no effect. In the case of a one-sided hypothesis test, the null still contains an equal sign but it’s “greater than or equal to” or “less than or equal to.” If you wanted to translate the null hypothesis from its native mathematical expression, you could use the expression “there is no effect.” But the mathematical form more specifically states what it’s testing.
It’s the alternative hypothesis that typically contains does not equal.
There are some exceptions. For example, in an equivalence test where the researchers want to show that two things are equal, the null hypothesis states that they’re not equal.
In short, the null hypothesis states the condition that the researchers hope to reject. They need to work hard to set up an experiment and data collection that’ll gather enough evidence to be able to reject the null condition.
February 15, 2022 at 9:32 am
Dear sir I always read your notes on Research methods.. Kindly tell is there any available Book on all these..wonderfull Urgent
Comments and Questions Cancel reply
Understanding the Null Hypothesis for Linear Regression
Linear regression is a technique we can use to understand the relationship between one or more predictor variables and a response variable .
If we only have one predictor variable and one response variable, we can use simple linear regression , which uses the following formula to estimate the relationship between the variables:
ŷ = β 0 + β 1 x
- ŷ: The estimated response value.
- β 0 : The average value of y when x is zero.
- β 1 : The average change in y associated with a one unit increase in x.
- x: The value of the predictor variable.
Simple linear regression uses the following null and alternative hypotheses:
- H 0 : β 1 = 0
- H A : β 1 ≠ 0
The null hypothesis states that the coefficient β 1 is equal to zero. In other words, there is no statistically significant relationship between the predictor variable, x, and the response variable, y.
The alternative hypothesis states that β 1 is not equal to zero. In other words, there is a statistically significant relationship between x and y.
If we have multiple predictor variables and one response variable, we can use multiple linear regression , which uses the following formula to estimate the relationship between the variables:
ŷ = β 0 + β 1 x 1 + β 2 x 2 + … + β k x k
- β 0 : The average value of y when all predictor variables are equal to zero.
- β i : The average change in y associated with a one unit increase in x i .
- x i : The value of the predictor variable x i .
Multiple linear regression uses the following null and alternative hypotheses:
- H 0 : β 1 = β 2 = … = β k = 0
- H A : β 1 = β 2 = … = β k ≠ 0
The null hypothesis states that all coefficients in the model are equal to zero. In other words, none of the predictor variables have a statistically significant relationship with the response variable, y.
The alternative hypothesis states that not every coefficient is simultaneously equal to zero.
The following examples show how to decide to reject or fail to reject the null hypothesis in both simple linear regression and multiple linear regression models.
Example 1: Simple Linear Regression
Suppose a professor would like to use the number of hours studied to predict the exam score that students will receive in his class. He collects data for 20 students and fits a simple linear regression model.
The following screenshot shows the output of the regression model:

The fitted simple linear regression model is:
Exam Score = 67.1617 + 5.2503*(hours studied)
To determine if there is a statistically significant relationship between hours studied and exam score, we need to analyze the overall F value of the model and the corresponding p-value:
- Overall F-Value: 47.9952
- P-value: 0.000
Since this p-value is less than .05, we can reject the null hypothesis. In other words, there is a statistically significant relationship between hours studied and exam score received.
Example 2: Multiple Linear Regression
Suppose a professor would like to use the number of hours studied and the number of prep exams taken to predict the exam score that students will receive in his class. He collects data for 20 students and fits a multiple linear regression model.

The fitted multiple linear regression model is:
Exam Score = 67.67 + 5.56*(hours studied) – 0.60*(prep exams taken)
To determine if there is a jointly statistically significant relationship between the two predictor variables and the response variable, we need to analyze the overall F value of the model and the corresponding p-value:
- Overall F-Value: 23.46
- P-value: 0.00
Since this p-value is less than .05, we can reject the null hypothesis. In other words, hours studied and prep exams taken have a jointly statistically significant relationship with exam score.
Note: Although the p-value for prep exams taken (p = 0.52) is not significant, prep exams combined with hours studied has a significant relationship with exam score.
Additional Resources
Understanding the F-Test of Overall Significance in Regression How to Read and Interpret a Regression Table How to Report Regression Results How to Perform Simple Linear Regression in Excel How to Perform Multiple Linear Regression in Excel
The Complete Guide: How to Report Regression Results
R vs. r-squared: what’s the difference, related posts, how to normalize data between -1 and 1, vba: how to check if string contains another..., how to interpret f-values in a two-way anova, how to create a vector of ones in..., how to determine if a probability distribution is..., what is a symmetric histogram (definition & examples), how to find the mode of a histogram..., how to find quartiles in even and odd..., how to calculate sxy in statistics (with example), how to calculate sxx in statistics (with example).

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
13.6 Testing the Regression Coefficients
Learning objectives.
- Conduct and interpret a hypothesis test on individual regression coefficients.
Previously, we learned that the population model for the multiple regression equation is
[latex]\begin{eqnarray*} y & = & \beta_0+\beta_1x_1+\beta_2x_2+\cdots+\beta_kx_k +\epsilon \end{eqnarray*}[/latex]
where [latex]x_1,x_2,\ldots,x_k[/latex] are the independent variables, [latex]\beta_0,\beta_1,\ldots,\beta_k[/latex] are the population parameters of the regression coefficients, and [latex]\epsilon[/latex] is the error variable. In multiple regression, we estimate each population regression coefficient [latex]\beta_i[/latex] with the sample regression coefficient [latex]b_i[/latex].
In the previous section, we learned how to conduct an overall model test to determine if the regression model is valid. If the outcome of the overall model test is that the model is valid, then at least one of the independent variables is related to the dependent variable—in other words, at least one of the regression coefficients [latex]\beta_i[/latex] is not zero. However, the overall model test does not tell us which independent variables are related to the dependent variable. To determine which independent variables are related to the dependent variable, we must test each of the regression coefficients.
Testing the Regression Coefficients
For an individual regression coefficient, we want to test if there is a relationship between the dependent variable [latex]y[/latex] and the independent variable [latex]x_i[/latex].
- No Relationship . There is no relationship between the dependent variable [latex]y[/latex] and the independent variable [latex]x_i[/latex]. In this case, the regression coefficient [latex]\beta_i[/latex] is zero. This is the claim for the null hypothesis in an individual regression coefficient test: [latex]H_0: \beta_i=0[/latex].
- Relationship. There is a relationship between the dependent variable [latex]y[/latex] and the independent variable [latex]x_i[/latex]. In this case, the regression coefficients [latex]\beta_i[/latex] is not zero. This is the claim for the alternative hypothesis in an individual regression coefficient test: [latex]H_a: \beta_i \neq 0[/latex]. We are not interested if the regression coefficient [latex]\beta_i[/latex] is positive or negative, only that it is not zero. We only need to find out if the regression coefficient is not zero to demonstrate that there is a relationship between the dependent variable and the independent variable. This makes the test on a regression coefficient a two-tailed test.
In order to conduct a hypothesis test on an individual regression coefficient [latex]\beta_i[/latex], we need to use the distribution of the sample regression coefficient [latex]b_i[/latex]:
- The mean of the distribution of the sample regression coefficient is the population regression coefficient [latex]\beta_i[/latex].
- The standard deviation of the distribution of the sample regression coefficient is [latex]\sigma_{b_i}[/latex]. Because we do not know the population standard deviation we must estimate [latex]\sigma_{b_i}[/latex] with the sample standard deviation [latex]s_{b_i}[/latex].
- The distribution of the sample regression coefficient follows a normal distribution.
Steps to Conduct a Hypothesis Test on a Regression Coefficient
[latex]\begin{eqnarray*} H_0: & & \beta_i=0 \\ \\ \end{eqnarray*}[/latex]
[latex]\begin{eqnarray*} H_a: & & \beta_i \neq 0 \\ \\ \end{eqnarray*}[/latex]
- Collect the sample information for the test and identify the significance level [latex]\alpha[/latex].
[latex]\begin{eqnarray*}t & = & \frac{b_i-\beta_i}{s_{b_i}} \\ \\ df & = & n-k-1 \\ \\ \end{eqnarray*}[/latex]
- The results of the sample data are significant. There is sufficient evidence to conclude that the null hypothesis [latex]H_0[/latex] is an incorrect belief and that the alternative hypothesis [latex]H_a[/latex] is most likely correct.
- The results of the sample data are not significant. There is not sufficient evidence to conclude that the alternative hypothesis [latex]H_a[/latex] may be correct.
- Write down a concluding sentence specific to the context of the question.
The required [latex]t[/latex]-score and p -value for the test can be found on the regression summary table, which we learned how to generate in Excel in a previous section.
The human resources department at a large company wants to develop a model to predict an employee’s job satisfaction from the number of hours of unpaid work per week the employee does, the employee’s age, and the employee’s income. A sample of 25 employees at the company is taken and the data is recorded in the table below. The employee’s income is recorded in $1000s and the job satisfaction score is out of 10, with higher values indicating greater job satisfaction.
| 4 | 3 | 23 | 60 |
| 5 | 8 | 32 | 114 |
| 2 | 9 | 28 | 45 |
| 6 | 4 | 60 | 187 |
| 7 | 3 | 62 | 175 |
| 8 | 1 | 43 | 125 |
| 7 | 6 | 60 | 93 |
| 3 | 3 | 37 | 57 |
| 5 | 2 | 24 | 47 |
| 5 | 5 | 64 | 128 |
| 7 | 2 | 28 | 66 |
| 8 | 1 | 66 | 146 |
| 5 | 7 | 35 | 89 |
| 2 | 5 | 37 | 56 |
| 4 | 0 | 59 | 65 |
| 6 | 2 | 32 | 95 |
| 5 | 6 | 76 | 82 |
| 7 | 5 | 25 | 90 |
| 9 | 0 | 55 | 137 |
| 8 | 3 | 34 | 91 |
| 7 | 5 | 54 | 184 |
| 9 | 1 | 57 | 60 |
| 7 | 0 | 68 | 39 |
| 10 | 2 | 66 | 187 |
| 5 | 0 | 50 | 49 |
Previously, we found the multiple regression equation to predict the job satisfaction score from the other variables:
[latex]\begin{eqnarray*} \hat{y} & = & 4.7993-0.3818x_1+0.0046x_2+0.0233x_3 \\ \\ \hat{y} & = & \mbox{predicted job satisfaction score} \\ x_1 & = & \mbox{hours of unpaid work per week} \\ x_2 & = & \mbox{age} \\ x_3 & = & \mbox{income (\$1000s)}\end{eqnarray*}[/latex]
At the 5% significance level, test the relationship between the dependent variable “job satisfaction” and the independent variable “hours of unpaid work per week”.
Hypotheses:
[latex]\begin{eqnarray*} H_0: & & \beta_1=0 \\ H_a: & & \beta_1 \neq 0 \end{eqnarray*}[/latex]
The regression summary table generated by Excel is shown below:
| Multiple R | 0.711779225 | |||||
| R Square | 0.506629665 | |||||
| Adjusted R Square | 0.436148189 | |||||
| Standard Error | 1.585212784 | |||||
| Observations | 25 | |||||
| Regression | 3 | 54.189109 | 18.06303633 | 7.18812504 | 0.001683189 | |
| Residual | 21 | 52.770891 | 2.512899571 | |||
| Total | 24 | 106.96 | ||||
| Intercept | 4.799258185 | 1.197185164 | 4.008785216 | 0.00063622 | 2.309575344 | 7.288941027 |
| Hours of Unpaid Work per Week | -0.38184722 | 0.130750479 | -2.9204269 | 0.008177146 | -0.65375772 | -0.10993671 |
| Age | 0.004555815 | 0.022855709 | 0.199329423 | 0.843922453 | -0.04297523 | 0.052086864 |
| Income ($1000s) | 0.023250418 | 0.007610353 | 3.055103771 | 0.006012895 | 0.007423823 | 0.039077013 |
The p -value for the test on the hours of unpaid work per week regression coefficient is in the bottom part of the table under the P-value column of the Hours of Unpaid Work per Week row . So the p -value=[latex]0.0082[/latex].
Conclusion:
Because p -value[latex]=0.0082 \lt 0.05=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis. At the 5% significance level there is enough evidence to suggest that there is a relationship between the dependent variable “job satisfaction” and the independent variable “hours of unpaid work per week.”
- The null hypothesis [latex]\beta_1=0[/latex] is the claim that the regression coefficient for the independent variable [latex]x_1[/latex] is zero. That is, the null hypothesis is the claim that there is no relationship between the dependent variable and the independent variable “hours of unpaid work per week.”
- The alternative hypothesis is the claim that the regression coefficient for the independent variable [latex]x_1[/latex] is not zero. The alternative hypothesis is the claim that there is a relationship between the dependent variable and the independent variable “hours of unpaid work per week.”
- When conducting a test on a regression coefficient, make sure to use the correct subscript on [latex]\beta[/latex] to correspond to how the independent variables were defined in the regression model and which independent variable is being tested. Here the subscript on [latex]\beta[/latex] is 1 because the “hours of unpaid work per week” is defined as [latex]x_1[/latex] in the regression model.
- The p -value for the tests on the regression coefficients are located in the bottom part of the table under the P-value column heading in the corresponding independent variable row.
- Because the alternative hypothesis is a [latex]\neq[/latex], the p -value is the sum of the area in the tails of the [latex]t[/latex]-distribution. This is the value calculated out by Excel in the regression summary table.
- The p -value of 0.0082 is a small probability compared to the significance level, and so is unlikely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis. In other words, the regression coefficient [latex]\beta_1[/latex] is not zero, and so there is a relationship between the dependent variable “job satisfaction” and the independent variable “hours of unpaid work per week.” This means that the independent variable “hours of unpaid work per week” is useful in predicting the dependent variable.
At the 5% significance level, test the relationship between the dependent variable “job satisfaction” and the independent variable “age”.
[latex]\begin{eqnarray*} H_0: & & \beta_2=0 \\ H_a: & & \beta_2 \neq 0 \end{eqnarray*}[/latex]
The p -value for the test on the age regression coefficient is in the bottom part of the table under the P-value column of the Age row . So the p -value=[latex]0.8439[/latex].
Because p -value[latex]=0.8439 \gt 0.05=\alpha[/latex], we do not reject the null hypothesis. At the 5% significance level there is not enough evidence to suggest that there is a relationship between the dependent variable “job satisfaction” and the independent variable “age.”
- The null hypothesis [latex]\beta_2=0[/latex] is the claim that the regression coefficient for the independent variable [latex]x_2[/latex] is zero. That is, the null hypothesis is the claim that there is no relationship between the dependent variable and the independent variable “age.”
- The alternative hypothesis is the claim that the regression coefficient for the independent variable [latex]x_2[/latex] is not zero. The alternative hypothesis is the claim that there is a relationship between the dependent variable and the independent variable “age.”
- When conducting a test on a regression coefficient, make sure to use the correct subscript on [latex]\beta[/latex] to correspond to how the independent variables were defined in the regression model and which independent variable is being tested. Here the subscript on [latex]\beta[/latex] is 2 because “age” is defined as [latex]x_2[/latex] in the regression model.
- The p -value of 0.8439 is a large probability compared to the significance level, and so is likely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis. In other words, the regression coefficient [latex]\beta_2[/latex] is zero, and so there is no relationship between the dependent variable “job satisfaction” and the independent variable “age.” This means that the independent variable “age” is not particularly useful in predicting the dependent variable.
At the 5% significance level, test the relationship between the dependent variable “job satisfaction” and the independent variable “income”.
[latex]\begin{eqnarray*} H_0: & & \beta_3=0 \\ H_a: & & \beta_3 \neq 0 \end{eqnarray*}[/latex]
The p -value for the test on the income regression coefficient is in the bottom part of the table under the P-value column of the Income row . So the p -value=[latex]0.0060[/latex].
Because p -value[latex]=0.0060 \lt 0.05=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis. At the 5% significance level there is enough evidence to suggest that there is a relationship between the dependent variable “job satisfaction” and the independent variable “income.”
- The null hypothesis [latex]\beta_3=0[/latex] is the claim that the regression coefficient for the independent variable [latex]x_3[/latex] is zero. That is, the null hypothesis is the claim that there is no relationship between the dependent variable and the independent variable “income.”
- The alternative hypothesis is the claim that the regression coefficient for the independent variable [latex]x_3[/latex] is not zero. The alternative hypothesis is the claim that there is a relationship between the dependent variable and the independent variable “income.”
- When conducting a test on a regression coefficient, make sure to use the correct subscript on [latex]\beta[/latex] to correspond to how the independent variables were defined in the regression model and which independent variable is being tested. Here the subscript on [latex]\beta[/latex] is 3 because “income” is defined as [latex]x_3[/latex] in the regression model.
- The p -value of 0.0060 is a small probability compared to the significance level, and so is unlikely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis. In other words, the regression coefficient [latex]\beta_3[/latex] is not zero, and so there is a relationship between the dependent variable “job satisfaction” and the independent variable “income.” This means that the independent variable “income” is useful in predicting the dependent variable.
Concept Review
The test on a regression coefficient determines if there is a relationship between the dependent variable and the corresponding independent variable. The p -value for the test is the sum of the area in tails of the [latex]t[/latex]-distribution. The p -value can be found on the regression summary table generated by Excel.
The hypothesis test for a regression coefficient is a well established process:
- Write down the null and alternative hypotheses in terms of the regression coefficient being tested. The null hypothesis is the claim that there is no relationship between the dependent variable and independent variable. The alternative hypothesis is the claim that there is a relationship between the dependent variable and independent variable.
- Collect the sample information for the test and identify the significance level.
- The p -value is the sum of the area in the tails of the [latex]t[/latex]-distribution. Use the regression summary table generated by Excel to find the p -value.
- Compare the p -value to the significance level and state the outcome of the test.
Introduction to Statistics Copyright © 2022 by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Simple linear regression
Simple linear regression #.
Fig. 9 Simple linear regression #
Errors: \(\varepsilon_i \sim N(0,\sigma^2)\quad \text{i.i.d.}\)
Fit: the estimates \(\hat\beta_0\) and \(\hat\beta_1\) are chosen to minimize the (training) residual sum of squares (RSS):
Sample code: advertising data #
Estimates \(\hat\beta_0\) and \(\hat\beta_1\) #.
A little calculus shows that the minimizers of the RSS are:
Assessing the accuracy of \(\hat \beta_0\) and \(\hat\beta_1\) #
Fig. 10 How variable is the regression line? #
Based on our model #
The Standard Errors for the parameters are:
95% confidence intervals:
Hypothesis test #
Null hypothesis \(H_0\) : There is no relationship between \(X\) and \(Y\) .
Alternative hypothesis \(H_a\) : There is some relationship between \(X\) and \(Y\) .
Based on our model: this translates to
\(H_0\) : \(\beta_1=0\) .
\(H_a\) : \(\beta_1\neq 0\) .
Test statistic:
Under the null hypothesis, this has a \(t\) -distribution with \(n-2\) degrees of freedom.
Sample output: advertising data #
Interpreting the hypothesis test #.
If we reject the null hypothesis, can we assume there is an exact linear relationship?
No. A quadratic relationship may be a better fit, for example. This test assumes the simple linear regression model is correct which precludes a quadratic relationship.
If we don’t reject the null hypothesis, can we assume there is no relationship between \(X\) and \(Y\) ?
No. This test is based on the model we posited above and is only powerful against certain monotone alternatives. There could be more complex non-linear relationships.
Linear regression - Hypothesis testing
by Marco Taboga , PhD
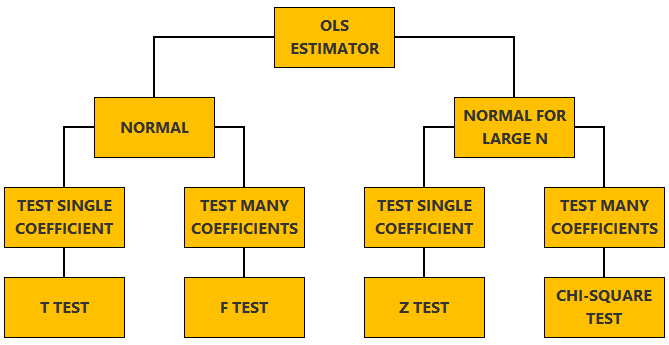
This lecture discusses how to perform tests of hypotheses about the coefficients of a linear regression model estimated by ordinary least squares (OLS).
Table of contents

Normal vs non-normal model
The linear regression model, matrix notation, tests of hypothesis in the normal linear regression model, test of a restriction on a single coefficient (t test), test of a set of linear restrictions (f test), tests based on maximum likelihood procedures (wald, lagrange multiplier, likelihood ratio), tests of hypothesis when the ols estimator is asymptotically normal, test of a restriction on a single coefficient (z test), test of a set of linear restrictions (chi-square test), learn more about regression analysis.
The lecture is divided in two parts:
in the first part, we discuss hypothesis testing in the normal linear regression model , in which the OLS estimator of the coefficients has a normal distribution conditional on the matrix of regressors;
in the second part, we show how to carry out hypothesis tests in linear regression analyses where the hypothesis of normality holds only in large samples (i.e., the OLS estimator can be proved to be asymptotically normal).
We also denote:
We now explain how to derive tests about the coefficients of the normal linear regression model.
It can be proved (see the lecture about the normal linear regression model ) that the assumption of conditional normality implies that:
How the acceptance region is determined depends not only on the desired size of the test , but also on whether the test is:
one-tailed (only one of the two things, i.e., either smaller or larger, is possible).
For more details on how to determine the acceptance region, see the glossary entry on critical values .
![null hypothesis in regression [eq28]](https://www.statlect.com/images/linear-regression-hypothesis-testing__90.png)
The F test is one-tailed .
A critical value in the right tail of the F distribution is chosen so as to achieve the desired size of the test.
Then, the null hypothesis is rejected if the F statistics is larger than the critical value.
In this section we explain how to perform hypothesis tests about the coefficients of a linear regression model when the OLS estimator is asymptotically normal.
As we have shown in the lecture on the properties of the OLS estimator , in several cases (i.e., under different sets of assumptions) it can be proved that:
These two properties are used to derive the asymptotic distribution of the test statistics used in hypothesis testing.
The test can be either one-tailed or two-tailed . The same comments made for the t-test apply here.
![null hypothesis in regression [eq50]](https://www.statlect.com/images/linear-regression-hypothesis-testing__175.png)
Like the F test, also the Chi-square test is usually one-tailed .
The desired size of the test is achieved by appropriately choosing a critical value in the right tail of the Chi-square distribution.
The null is rejected if the Chi-square statistics is larger than the critical value.
Want to learn more about regression analysis? Here are some suggestions:
R squared of a linear regression ;
Gauss-Markov theorem ;
Generalized Least Squares ;
Multicollinearity ;
Dummy variables ;
Selection of linear regression models
Partitioned regression ;
Ridge regression .
How to cite
Please cite as:
Taboga, Marco (2021). "Linear regression - Hypothesis testing", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/fundamentals-of-statistics/linear-regression-hypothesis-testing.
Most of the learning materials found on this website are now available in a traditional textbook format.
- F distribution
- Beta distribution
- Conditional probability
- Central Limit Theorem
- Binomial distribution
- Mean square convergence
- Delta method
- Almost sure convergence
- Mathematical tools
- Fundamentals of probability
- Probability distributions
- Asymptotic theory
- Fundamentals of statistics
- About Statlect
- Cookies, privacy and terms of use
- Loss function
- Almost sure
- Type I error
- Precision matrix
- Integrable variable
- To enhance your privacy,
- we removed the social buttons,
- but don't forget to share .
9.1 Null and Alternative Hypotheses
The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.
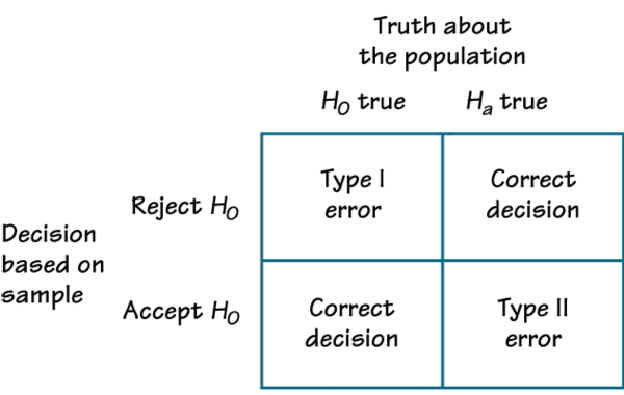
H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .
Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.
After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.
Mathematical Symbols Used in H 0 and H a :
| equal (=) | not equal (≠) greater than (>) less than (<) |
| greater than or equal to (≥) | less than (<) |
| less than or equal to (≤) | more than (>) |
H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.
Example 9.1
H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30
A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.
Example 9.2
We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0
We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ __ 66
- H a : μ __ 66
Example 9.3
We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5
We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : μ __ 45
- H a : μ __ 45
Example 9.4
An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066
On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.
- H 0 : p __ 0.40
- H a : p __ 0.40
Collaborative Exercise
Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.
Access for free at https://openstax.org/books/statistics/pages/1-introduction
- Authors: Barbara Illowsky, Susan Dean
- Publisher/website: OpenStax
- Book title: Statistics
- Publication date: Mar 27, 2020
- Location: Houston, Texas
- Book URL: https://openstax.org/books/statistics/pages/1-introduction
- Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses
© Apr 16, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
User Preferences
Content preview.
Arcu felis bibendum ut tristique et egestas quis:
- Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
- Duis aute irure dolor in reprehenderit in voluptate
- Excepteur sint occaecat cupidatat non proident
Keyboard Shortcuts
6.2.3 - more on model-fitting.
Suppose two models are under consideration, where one model is a special case or "reduced" form of the other obtained by setting \(k\) of the regression coefficients (parameters) equal to zero. The larger model is considered the "full" model, and the hypotheses would be
\(H_0\): reduced model versus \(H_A\): full model
Equivalently, the null hypothesis can be stated as the \(k\) predictor terms associated with the omitted coefficients have no relationship with the response, given the remaining predictor terms are already in the model. If we fit both models, we can compute the likelihood-ratio test (LRT) statistic:
\(G^2 = −2 (\log L_0 - \log L_1)\)
where \(L_0\) and \(L_1\) are the max likelihood values for the reduced and full models, respectively. The degrees of freedom would be \(k\), the number of coefficients in question. The p-value is the area under the \(\chi^2_k\) curve to the right of \( G^2)\).
To perform the test in SAS, we can look at the "Model Fit Statistics" section and examine the value of "−2 Log L" for "Intercept and Covariates." Here, the reduced model is the "intercept-only" model (i.e., no predictors), and "intercept and covariates" is the full model. For our running example, this would be equivalent to testing "intercept-only" model vs. full (saturated) model (since we have only one predictor).
| Model Fit Statistics | |||
|---|---|---|---|
| Criterion | Intercept Only | Intercept and Covariates | |
| Log Likelihood | Full Log Likelihood | ||
| AIC | 5178.510 | 5151.390 | 19.242 |
| SC | 5185.100 | 5164.569 | 32.421 |
| -2 Log L | 5176.510 | 5147.390 | 15.242 |
Larger differences in the "-2 Log L" values lead to smaller p-values more evidence against the reduced model in favor of the full model. For our example, \( G^2 = 5176.510 − 5147.390 = 29.1207\) with \(2 − 1 = 1\) degree of freedom. Notice that this matches the deviance we got in the earlier text above.
Also, notice that the \(G^2\) we calculated for this example is equal to 29.1207 with 1df and p-value <.0001 from "Testing Global Hypothesis: BETA=0" section (the next part of the output, see below).
Testing the Joint Significance of All Predictors Section
Testing the null hypothesis that the set of coefficients is simultaneously zero. For example, consider the full model
\(\log\left(\dfrac{\pi}{1-\pi}\right)=\beta_0+\beta_1 x_1+\cdots+\beta_k x_k\)
and the null hypothesis \(H_0\colon \beta_1=\beta_2=\cdots=\beta_k=0\) versus the alternative that at least one of the coefficients is not zero. This is like the overall F−test in linear regression. In other words, this is testing the null hypothesis of the intercept-only model:
\(\log\left(\dfrac{\pi}{1-\pi}\right)=\beta_0\)
versus the alternative that the current (full) model is correct. This corresponds to the test in our example because we have only a single predictor term, and the reduced model that removes the coefficient for that predictor is the intercept-only model.
In the SAS output, three different chi-square statistics for this test are displayed in the section "Testing Global Null Hypothesis: Beta=0," corresponding to the likelihood ratio, score, and Wald tests. Recall our brief encounter with them in our discussion of binomial inference in Lesson 2.
| Testing Global Null Hypothesis: BETA=0 | |||
|---|---|---|---|
| Test | Chi-Square | DF | Pr > ChiSq |
| Likelihood Ratio | 29.1207 | 1 | <.0001 |
| Score | 27.6766 | 1 | <.0001 |
| Wald | 27.3361 | 1 | <.0001 |
Large chi-square statistics lead to small p-values and provide evidence against the intercept-only model in favor of the current model. The Wald test is based on asymptotic normality of ML estimates of \(\beta\)s. Rather than using the Wald, most statisticians would prefer the LR test. If these three tests agree, that is evidence that the large-sample approximations are working well and the results are trustworthy. If the results from the three tests disagree, most statisticians would tend to trust the likelihood-ratio test more than the other two.
In our example, the "intercept only" model or the null model says that student's smoking is unrelated to parents' smoking habits. Thus the test of the global null hypothesis \(\beta_1=0\) is equivalent to the usual test for independence in the \(2\times2\) table. We will see that the estimated coefficients and standard errors are as we predicted before, as well as the estimated odds and odds ratios.
Residual deviance is the difference between −2 logL for the saturated model and −2 logL for the currently fit model. The high residual deviance shows that the model cannot be accepted. The null deviance is the difference between −2 logL for the saturated model and −2 logL for the intercept-only model. The high residual deviance shows that the intercept-only model does not fit.
In our \(2\times2\) table smoking example, the residual deviance is almost 0 because the model we built is the saturated model. And notice that the degree of freedom is 0 too. Regarding the null deviance, we could see it equivalent to the section "Testing Global Null Hypothesis: Beta=0," by likelihood ratio in SAS output.
For our example, Null deviance = 29.1207 with df = 1. Notice that this matches the deviance we got in the earlier text above.
The Homer-Lemeshow Statistic Section
An alternative statistic for measuring overall goodness-of-fit is the Hosmer-Lemeshow statistic .
This is a Pearson-like chi-square statistic that is computed after the data are grouped by having similar predicted probabilities. It is more useful when there is more than one predictor and/or continuous predictors in the model too. We will see more on this later.
\(H_0\): the current model fits well \(H_A\): the current model does not fit well
To calculate this statistic:
- Group the observations according to model-predicted probabilities ( \(\hat{\pi}_i\))
- The number of groups is typically determined such that there is roughly an equal number of observations per group
- The Hosmer-Lemeshow (HL) statistic, a Pearson-like chi-square statistic, is computed on the grouped data but does NOT have a limiting chi-square distribution because the observations in groups are not from identical trials. Simulations have shown that this statistic can be approximated by a chi-squared distribution with \(g − 2\) degrees of freedom, where \(g\) is the number of groups.
Warning about the Hosmer-Lemeshow goodness-of-fit test:
- It is a conservative statistic, i.e., its value is smaller than what it should be, and therefore the rejection probability of the null hypothesis is smaller.
- It has low power in predicting certain types of lack of fit such as nonlinearity in explanatory variables.
- It is highly dependent on how the observations are grouped.
- If too few groups are used (e.g., 5 or less), it almost always fails to reject the current model fit. This means that it's usually not a good measure if only one or two categorical predictor variables are involved, and it's best used for continuous predictors.
In the model statement, the option lackfit tells SAS to compute the HL statistic and print the partitioning. For our example, because we have a small number of groups (i.e., 2), this statistic gives a perfect fit (HL = 0, p-value = 1). Instead of deriving the diagnostics, we will look at them from a purely applied viewpoint. Recall the definitions and introductions to the regression residuals and Pearson and Deviance residuals.
Residuals Section
The Pearson residuals are defined as
\(r_i=\dfrac{y_i-\hat{\mu}_i}{\sqrt{\hat{V}(\hat{\mu}_i)}}=\dfrac{y_i-n_i\hat{\pi}_i}{\sqrt{n_i\hat{\pi}_i(1-\hat{\pi}_i)}}\)
The contribution of the \(i\)th row to the Pearson statistic is
\(\dfrac{(y_i-\hat{\mu}_i)^2}{\hat{\mu}_i}+\dfrac{((n_i-y_i)-(n_i-\hat{\mu}_i))^2}{n_i-\hat{\mu}_i}=r^2_i\)
and the Pearson goodness-of fit statistic is
\(X^2=\sum\limits_{i=1}^N r^2_i\)
which we would compare to a \(\chi^2_{N-p}\) distribution. The deviance test statistic is
\(G^2=2\sum\limits_{i=1}^N \left\{ y_i\text{log}\left(\dfrac{y_i}{\hat{\mu}_i}\right)+(n_i-y_i)\text{log}\left(\dfrac{n_i-y_i}{n_i-\hat{\mu}_i}\right)\right\}\)
which we would again compare to \(\chi^2_{N-p}\), and the contribution of the \(i\)th row to the deviance is
\(2\left\{ y_i\log\left(\dfrac{y_i}{\hat{\mu}_i}\right)+(n_i-y_i)\log\left(\dfrac{n_i-y_i}{n_i-\hat{\mu}_i}\right)\right\}\)
We will note how these quantities are derived through appropriate software and how they provide useful information to understand and interpret the models.
Null Hypothesis for Multiple Regression
Table of Contents
What is a Null Hypothesis and Why Does it Matter?
In multiple regression analysis, a null hypothesis is a crucial concept that plays a central role in statistical inference and hypothesis testing. A null hypothesis, denoted by H0, is a statement that proposes no significant relationship between the independent variables and the dependent variable. In other words, the null hypothesis suggests that the independent variables do not explain the variation in the dependent variable.
The null hypothesis is essential in multiple regression because it provides a basis for testing the significance of the regression coefficients. By formulating a null hypothesis, researchers can determine whether the observed relationships between variables are due to chance or if they reflect a real phenomenon. A well-crafted null hypothesis also helps to avoid false positives, ensuring that the results are not merely a result of chance.
In the context of multiple regression, the null hypothesis is typically tested against an alternative hypothesis, denoted by H1. The alternative hypothesis proposes that there is a significant relationship between the independent variables and the dependent variable. By comparing the null and alternative hypotheses , researchers can determine the probability of observing the results assuming that the null hypothesis is true. This probability, known as the p-value, is a critical component of hypothesis testing in multiple regression.
Formulating a null hypothesis for multiple regression is a critical step in the research process, as it directly impacts the interpretation of the results. A null hypothesis that is poorly formulated or irrelevant to the research question can lead to misleading conclusions and incorrect decisions. Therefore, it is essential to understand the role of the null hypothesis in multiple regression analysis and how to formulate it correctly.
https://www.youtube.com/watch?v=cpL38ZeIecE
How to Formulate a Null Hypothesis for Multiple Regression
Formulating a null hypothesis for multiple regression is a crucial step in the research process . A well-crafted null hypothesis provides a clear direction for the research and ensures that the results are meaningful and relevant. In this section, we will provide a step-by-step guide on how to formulate a null hypothesis for multiple regression.
Step 1: Identify the Research Question
The first step in formulating a null hypothesis is to identify the research question. The research question should be specific, clear, and concise, and it should guide the entire research process. For example, “Is there a significant relationship between the amount of exercise and blood pressure in adults?”
Step 2: Select the Dependent and Independent Variables
The next step is to select the dependent and independent variables . The dependent variable is the outcome variable that we are trying to predict, while the independent variables are the predictor variables that we use to explain the variation in the dependent variable. In our example, the dependent variable is blood pressure, and the independent variable is the amount of exercise.
Step 3: State the Null Hypothesis
The null hypothesis is a statement that proposes no significant relationship between the independent variables and the dependent variable. In our example, the null hypothesis would be “There is no significant relationship between the amount of exercise and blood pressure in adults.” This null hypothesis is denoted by H0.
Step 4: State the Alternative Hypothesis
The alternative hypothesis is a statement that proposes a significant relationship between the independent variables and the dependent variable. In our example, the alternative hypothesis would be “There is a significant relationship between the amount of exercise and blood pressure in adults.” This alternative hypothesis is denoted by H1.
By following these steps, researchers can formulate a clear and concise null hypothesis for multiple regression. A well-crafted null hypothesis provides a clear direction for the research and ensures that the results are meaningful and relevant. In the next section, we will discuss the importance of the null hypothesis in multiple regression modeling.

The Role of Null Hypothesis in Multiple Regression Modeling
In multiple regression modeling, the null hypothesis plays a crucial role in guiding the analysis and interpretation of results. The null hypothesis serves as a benchmark against which the alternative hypothesis is tested, and its formulation has a direct impact on the outcome of the analysis.
The null hypothesis influences model interpretation by determining the significance of the regression coefficients. If the null hypothesis is rejected, it implies that the in dependent variable s have a significant effect on the dependent variable, and the regression coefficients can be used to make predictions. On the other hand , if the null hypothesis is not rejected, it suggests that the independent variables do not have a significant effect on the dependent variable, and the regression coefficients are not reliable.
The null hypothesis also affects coefficient estimation in multiple regression. The null hypothesis is used to test the significance of each regression coefficient, and if the null hypothesis is rejected, the coefficient is considered statistically significant. This, in turn, affects the interpretation of the results, as statistically significant coefficients are used to make predictions and draw conclusions.
Furthermore, the null hypothesis is essential for p-value calculation in multiple regression. The p-value represents the probability of observing the results assuming that the null hypothesis is true. A low p-value indicates that the null hypothesis can be rejected, implying that the independent variables have a significant effect on the dependent variable. A high p-value, on the other hand, suggests that the null hypothesis cannot be rejected, and the independent variables do not have a significant effect on the dependent variable.
In summary, the null hypothesis is a critical component of multiple regression modeling, as it guides the analysis and interpretation of results. Its formulation has a direct impact on model interpretation, coefficient estimation, and p-value calculation. By understanding the role of the null hypothesis in multiple regression, researchers can ensure that their analysis is accurate and reliable, leading to meaningful conclusions and informed decision-making.

Understanding Type I and Type II Errors in Multiple Regression
In multiple regression analysis, Type I and Type II errors are critical concepts that researchers must understand to ensure accurate and reliable results. These errors occur when testing the null hypothesis, and their consequences can be far-reaching.
A Type I error occurs when the null hypothesis is rejected, but it is actually true. This means that the researcher has incorrectly concluded that there is a significant relationship between the in dependent variable s and the dependent variable. The probability of committing a Type I error is denoted by α (alpha) and is typically set to 0.05. A Type I error can lead to false conclusions and misinformed decision-making.
On the other hand , a Type II error occurs when the null hypothesis is not rejected, but it is actually false. This means that the researcher has failed to detect a significant relationship between the independent variables and the dependent variable. The probability of committing a Type II error is denoted by β (beta) and is related to the power of the test. A Type II error can lead to missed opportunities and incorrect assumptions.
The consequences of committing Type I and Type II errors can be significant. A Type I error can lead to the implementation of ineffective solutions or the allocation of resources to non-essential areas. A Type II error can lead to the failure to identify important relationships or the underestimation of the impact of independent variables.
To minimize the risk of Type I and Type II errors, researchers must carefully formulate the null hypothesis, select an appropriate significance level, and ensure adequate sample size and data quality. By understanding the concepts of Type I and Type II errors, researchers can ensure that their multiple regression analysis is accurate, reliable, and informative.
Interpreting the Results of Multiple Regression Analysis
Once the multiple regression analysis is complete, interpreting the results is crucial to understanding the relationships between the independent variables and the dependent variable. In this section, we will discuss how to interpret the coefficient of determination (R-squared), F-statistic, and p-values.
The coefficient of determination, denoted by R-squared, measures the proportion of variance in the dependent variable that is explained by the independent variables. An R-squared value close to 1 indicates a strong relationship between the independent variables and the dependent variable, while a value close to 0 indicates a weak relationship . In multiple regression analysis, R-squared is used to evaluate the goodness of fit of the model.
The F-statistic is a measure of the overall significance of the regression model. It is used to test the null hypothesis that all the regression coefficients are equal to zero. A high F-statistic value indicates that the regression model is significant, and the independent variables have a significant effect on the dependent variable.
P-values are used to determine the significance of each regression coefficient. A p-value less than the significance level (typically 0.05) indicates that the regression coefficient is statistically significant, and the independent variable has a significant effect on the dependent variable. On the other hand, a p-value greater than the significance level indicates that the regression coefficient is not statistically significant, and the independent variable does not have a significant effect on the dependent variable.
When interpreting the results of multiple regression analysis, it is essential to consider the null hypothesis for multiple regression. The null hypothesis is used to test the significance of the regression coefficients, and its formulation has a direct impact on the interpretation of the results. By understanding the null hypothesis and its role in multiple regression analysis, researchers can ensure that their results are accurate and reliable.
Common Pitfalls to Avoid When Working with Null Hypotheses
When working with null hypotheses in multiple regression analysis, it is essential to avoid common pitfalls that can lead to inaccurate or misleading results. In this section, we will discuss some of the most common mistakes to avoid when working with null hypotheses.
One of the most critical mistakes is incorrect hypothesis formulation. A poorly formulated null hypothesis can lead to incorrect conclusions and misinformed decision-making. To avoid this, researchers must carefully identify the research question, select the dependent and independent variables , and state the null hypothesis clearly and concisely.
Inadequate sample size is another common pitfall. A sample size that is too small can lead to inaccurate estimates of the regression coefficients and p-values, making it difficult to draw meaningful conclusions. Researchers must ensure that the sample size is sufficient to detect significant relationships between the independent variables and the dependent variable.
Misinterpretation of results is also a common mistake. Researchers must be careful not to overinterpret the results of multiple regression analysis, especially when it comes to the null hypothesis. A failure to reject the null hypothesis does not necessarily mean that there is no significant relationship between the independent variables and the dependent variable. Rather, it may indicate that the sample size is too small or the data is too noisy to detect a significant relationship.
Additionally, researchers must avoid ignoring the assumptions of multiple regression analysis. Violating the assumptions of linearity, independence, homoscedasticity, normality, and no or little multicollinearity can lead to inaccurate results and incorrect conclusions. By checking the assumptions of multiple regression analysis, researchers can ensure that the results are reliable and accurate.
Finally, researchers must avoid using multiple regression analysis as a black box . Multiple regression analysis is a powerful tool, but it requires a deep understanding of the underlying statistical concepts and assumptions. By understanding the null hypothesis for multiple regression and its role in statistical inference and hypothesis testing, researchers can ensure that their results are accurate, reliable, and informative.

Real-World Applications of Multiple Regression Analysis
Multiple regression analysis has numerous real-world applications across various fields, including finance, marketing, healthcare, and more. In this section, we will explore some of the most significant applications of multiple regression analysis.
In finance, multiple regression analysis is used to predict stock prices, analyze portfolio risk, and identify factors that influence investment returns. For instance, a financial analyst may use multiple regression to examine the relationship between a company’s stock price and various economic indicators, such as GDP, inflation rate, and unemployment rate.
In marketing, multiple regression analysis is employed to analyze customer behavior, predict sales, and optimize marketing campaigns. Marketers may use multiple regression to identify the factors that influence customer purchasing decisions, such as demographics, advertising spend, and price.
In healthcare, multiple regression analysis is used to identify risk factors for diseases, predict patient outcomes, and evaluate the effectiveness of treatments. For example, a healthcare researcher may use multiple regression to examine the relationship between patient characteristics, such as age, gender, and lifestyle, and the risk of developing a particular disease.
In addition to these fields, multiple regression analysis has applications in economics, social sciences, and environmental studies. It is a powerful tool for analyzing complex relationships between variables and making informed decisions.
In all these applications, the null hypothesis for multiple regression plays a critical role in statistical inference and hypothesis testing. By formulating a clear and concise null hypothesis, researchers can ensure that their results are accurate, reliable, and informative.
By understanding the real-world applications of multiple regression analysis, researchers and practitioners can unlock the full potential of this powerful statistical technique and make data-driven decisions that drive business success and improve lives.

Best Practices for Implementing Multiple Regression in Your Research
When implementing multiple regression in research, it is essential to follow best practices to ensure accurate, reliable, and informative results. In this section, we will discuss some of the most critical best practices for implementing multiple regression in research.
Data Preparation: Before conducting multiple regression analysis, it is crucial to prepare the data properly. This includes checking for missing values, outliers, and multicollinearity, as well as transforming variables to meet the assumptions of multiple regression.
Model Validation: Validating the multiple regression model is critical to ensuring that the results are accurate and reliable. This includes checking the model’s assumptions, such as linearity, independence, homoscedasticity, normality, and no or little multicollinearity.
Result Reporting: When reporting the results of multiple regression analysis, it is essential to provide clear and concise information about the model, including the null hypothesis for multiple regression, the coefficient of determination (R-squared), F-statistic, and p-values.
Interpretation of Results: Interpreting the results of multiple regression analysis requires a deep understanding of the null hypothesis for multiple regression and its role in statistical inference and hypothesis testing. Researchers must be careful not to overinterpret the results, especially when it comes to the null hypothesis.
Avoiding Common Pitfalls: Finally, researchers must avoid common pitfalls when working with null hypotheses in multiple regression, such as incorrect hypothesis formulation, inadequate sample size, and misinterpretation of results.
By following these best practices, researchers can ensure that their multiple regression analysis is accurate, reliable, and informative, and that the results are useful for making informed decisions.
Remember, the null hypothesis for multiple regression is a critical component of statistical inference and hypothesis testing, and it plays a vital role in ensuring that the results of multiple regression analysis are accurate and reliable.

Understanding Correlation, Distribution, and Hypothesis Testing:
Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
Changing null hypothesis in linear regression
I have some data that is highly correlated. If I run a linear regression I get a regression line with a slope close to one (= 0.93). What I'd like to do is test if this slope is significantly different from 1.0. My expectation is that it is not. In other words, I'd like to change the null hypothesis of the linear regression from a slope of zero to a slope of one. Is this a sensible approach? I'd also really appreciate it you could include some R code in your answer so I could implement this method (or a better one you suggest!). Thanks.
- correlation
- hypothesis-testing
5 Answers 5
- $\begingroup$ Thank you! I just couldn't figure out how to change the lm command. $\endgroup$ – Nick Crawford Commented Apr 21, 2011 at 14:35
- $\begingroup$ Then is it exactly the same "lm(y-x ~ x)" than "lm(y ~ x, offset= 1.00*x)" (or without that 1.00) ? Wouldn't that substraction be problem with the assumptions for least squares or with collinearity? I want to use it for a logistic regression with random effects glmer(....). It would be great to have a simple but correct method to get the p-values. $\endgroup$ – skan Commented May 19, 2017 at 15:43
- $\begingroup$ Here stats.stackexchange.com/questions/111559/… Matifou says this method is worse than using Wald the test. $\endgroup$ – skan Commented May 19, 2017 at 15:45
Your hypothesis can be expressed as $R\beta=r$ where $\beta$ is your regression coefficients and $R$ is restriction matrix with $r$ the restrictions. If our model is
$$y=\beta_0+\beta_1x+u$$
then for hypothesis $\beta_1=0$, $R=[0,1]$ and $r=1$.
For these type of hypotheses you can use linearHypothesis function from package car :
- $\begingroup$ Can this be used for a one-sided test? $\endgroup$ – user66430 Commented Feb 7, 2017 at 15:17
It seems you're still trying to reject a null hypothesis. There are loads of problems with that, not the least of which is that it's possible that you don't have enough power to see that you're different from 1. It sounds like you don't care that the slope is 0.07 different from 1. But what if you can't really tell? What if you're actually estimating a slope that varies wildly and may actually be quite far from 1 with something like a confidence interval of ±0.4. Your best tactic here is not changing the null hypothesis but actually speaking reasonably about an interval estimate. If you apply the command confint() to your model you can get a 95% confidence interval around your slope. Then you can use this to discuss the slope you did get. If 1 is within the confidence interval you can state that it is within the range of values you believe likely to contain the true value. But more importantly you can also state what that range of values is.
The point of testing is that you want to reject your null hypothesis, not confirm it. The fact that there is no significant difference, is in no way a proof of the absence of a significant difference. For that, you'll have to define what effect size you deem reasonable to reject the null.
Testing whether your slope is significantly different from 1 is not that difficult, you just test whether the difference $slope - 1$ differs significantly from zero. By hand this would be something like :
Now you should be aware of the fact that the effect size for which a difference becomes significant, is
provided that we have a decent estimator of the standard error on the slope. Hence, if you decide that a significant difference should only be detected from 0.1, you can calculate the necessary DF as follows :
Mind you, this is pretty dependent on the estimate of the seslope. To get a better estimate on seslope, you could do a resampling of your data. A naive way would be :
putting seslope2 in the optimization function, returns :
All this will tell you that your dataset will return a significant result faster than you deem necessary, and that you only need 7 degrees of freedom (in this case 9 observations) if you want to be sure that non-significant means what you want it means.
You can simply not make probability or likelihood statements about the parameter using a confidence interval, this is a Bayesian paradigm.
What John is saying is confusing because it there is an equivalence between CIs and Pvalues, so at a 5%, saying that your CI includes 1 is equivalent to saying that Pval>0.05.
linearHypothesis allows you to test restrictions different from the standard beta=0
Your Answer
Sign up or log in, post as a guest.
Required, but never shown
By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .
Not the answer you're looking for? Browse other questions tagged regression correlation hypothesis-testing or ask your own question .
- Featured on Meta
- We've made changes to our Terms of Service & Privacy Policy - July 2024
- Bringing clarity to status tag usage on meta sites
Hot Network Questions
- How does static resources help prevent security vulnerabilities?
- What does it mean to have a truth value of a 'nothing' type instance?
- In compound nouns is there a way to distinguish which is the subject or the object?
- The relation between aerodynamic center and lift
- Physical basis of "forced harmonics" on a violin
- Solve an integral analytically
- What majority age is taken into consideration when travelling from country to country?
- UART pin acting as power pin
- Easyjet denied EU261 compensation for flight cancellation during Crowdstrike: Any escalation or other recourse?
- Where will the ants position themselves so that they are precisely twice as far from vinegar as they are from peanut butter?
- Simple JSON parser in lisp
- Will the product of electrolysis of all dilute aqueous solutions be hydrogen or oxygen?
- are "lie low" and "keep a low profile" interchangeable?
- What is the translation of point man in French?
- How did Jason Bourne know the garbage man isn't CIA?
- Unexpected behaviour during implicit conversion in C
- Venus’ LIP period starts today, can we save the Venusians?
- How predictable are the voting records of members of the US legislative branch?
- Bottom bracket: What to do about rust in cup + blemish on spindle?
- Density matrices and locality
- The complement of a properly embedded annulus in a handlebody is a handlebody
- How can I cover all my skin (face+neck+body) while swimming outside (sea or outdoor pool) to avoid UV radiations?
- Where exactly was this picture taken?
- How do you "stealth" a relativistic superweapon?

IMAGES
COMMENTS
x: The value of the predictor variable. Simple linear regression uses the following null and alternative hypotheses: H0: β1 = 0. HA: β1 ≠ 0. The null hypothesis states that the coefficient β1 is equal to zero. In other words, there is no statistically significant relationship between the predictor variable, x, and the response variable, y.
c plot.9.2 Statistical hypothesesFor simple linear regression, the chief null hypothesis is H0 : β1 = 0, and the corresponding alter. ative hypothesis is H1 : β1 6= 0. If this null hypothesis is true, then, from E(Y ) = β0 + β1x we can see that the population mean of Y is β0 for every x value, which t.
The formula for the t-test statistic is t = b1 (MSE SSxx)√. Use the t-distribution with degrees of freedom equal to n − p − 1. The t-test for slope has the same hypotheses as the F-test: Use a t-test to see if there is a significant relationship between hours studied and grade on the exam, use α = 0.05.
Null Hypothesis H 0: Group means are equal in the population: ... Correlation and Regression Coefficients. Some studies assess the relationship between two continuous variables rather than differences between groups. In these studies, analysts often use either correlation or regression analysis. For these tests, the null states that there is no ...
Multiple linear regression uses the following null and alternative hypotheses: H 0: β 1 = β 2 = … = β k = 0; H A: β 1 = β 2 = … = β k ≠ 0; The null hypothesis states that all coefficients in the model are equal to zero. In other words, none of the predictor variables have a statistically significant relationship with the response ...
The null hypothesis [latex]\beta_1=0[/latex] is the claim that the regression coefficient for the independent variable [latex]x_1[/latex] is zero. That is, the null hypothesis is the claim that there is no relationship between the dependent variable and the independent variable "hours of unpaid work per week."
Regression, like all other analyses, will test a null hypothesis in our data. In regression, we are interested in predicting \(Y\) scores and explaining variance using a line, the slope of which is what allows us to get closer to our observed scores than the mean of \(Y\) can. Thus, our hypotheses concern the slope of the line, which is ...
Simple Linear Regression ANOVA Hypothesis Test Example: Rainfall and sales of sunglasses We will now describe a hypothesis test to determine if the regression model is meaningful; in other words, does the value of \(X\) in any way help predict the expected value of \(Y\)?
Hypothesis test. Null hypothesis H 0: There is no relationship between X and Y. Alternative hypothesis H a: There is some relationship between X and Y. Based on our model: this translates to. H 0: β 1 = 0. H a: β 1 ≠ 0. Test statistic: t = β ^ 1 − 0 SE ( β ^ 1). Under the null hypothesis, this has a t -distribution with n − 2 degrees ...
For Bob's simple linear regression example, he wants to see how changes in the number of critical areas (the predictor variable) impact the dollar amount for land development (the response variable). ... Remember from hypothesis testing, we test the null hypothesis that a value is zero. We extend this principle to the slope, with a null ...
The null hypothesis is rejected if falls outside the acceptance region. How ... Usually this is obtained by performing an F test of the null hypothesis that all the regression coefficients are equal to (except the coefficient on the intercept). Tests based on maximum likelihood procedures (Wald, Lagrange multiplier, likelihood ratio) ...
In regression, as described partially in the other two answers, the null model is the null hypothesis that all the regression parameters are 0. So you can interpret this as saying that under the null hypothesis, there is no trend and the best estimate/predictor of a new observation is the mean, which is 0 in the case of no intercept.
The P-value is the probability — if the null hypothesis were true — that we would get an F-statistic larger than 32.7554. Comparing our F-statistic to an F-distribution with 1 numerator degree of freedom and 28 denominator degrees of freedom, ... The regression parameter for \(x_{2}\) represents the difference between the estimated ...
A population model for a multiple linear regression model that relates a y -variable to p -1 x -variables is written as. y i = β 0 + β 1 x i, 1 + β 2 x i, 2 + … + β p − 1 x i, p − 1 + ϵ i. We assume that the ϵ i have a normal distribution with mean 0 and constant variance σ 2. These are the same assumptions that we used in simple ...
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. H 0, the —null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
The null hypothesis and the alternative hypothesis are types of conjectures used in statistical tests to make statistical inferences, which are formal methods of reaching conclusions and separating scientific claims from statistical noise.. The statement being tested in a test of statistical significance is called the null hypothesis. The test of significance is designed to assess the strength ...
METHOD 1: Using a p-value to make a decision. To calculate the p-value using LinRegTTEST: On the LinRegTTEST input screen, on the line prompt for β or ρ, highlight " ≠ 0 ". The output screen shows the p-value on the line that reads " p = ". (Most computer statistical software can calculate the p-value .)
6.2.3 - More on Model-fitting. Suppose two models are under consideration, where one model is a special case or "reduced" form of the other obtained by setting k of the regression coefficients (parameters) equal to zero. The larger model is considered the "full" model, and the hypotheses would be. H 0: reduced model versus H A: full model.
A null hypothesis, denoted by H0, is a statement that proposes no significant relationship between the independent variables and the dependent variable. In other words, the null hypothesis suggests that the independent variables do not explain the variation in the dependent variable. The null hypothesis is essential in multiple regression ...
H 0 (Null Hypothesis): Population parameter =, ≤, ≥ some value. H A (Alternative Hypothesis): Population parameter <, >, ≠ some value. Note that the null hypothesis always contains the equal sign. We interpret the hypotheses as follows: Null hypothesis: The sample data provides no evidence to support some claim being made by an individual.
First, the hypotheses: Null hypothesis (H0) : The model with no predictor variables (also known as an intercept-only model) fits the data as well as the regression model. Alternative hypothesis (H1) : The regression model fits the data better than the intercept-only model. Least squares give: y = 1.0571 + 1.0738 x.
Why does null hypothesis in simple linear regression (i.e. slope = 0) have distribution? A null hypothesis is not a random variable; it doesn't have a distribution. A test statistic has a distribution. In particular we can compute what the distribution of some test statistic would be if the null hypothesis were true.
This paper focuses on the problem of testing the null hypothesis that the regression functions of several populations are equal under a general nonparametric homoscedastic regression model. It is well known that linear kernel regression estimators are sensitive to atypical responses. These distorted estimates will influence the test statistic ...
In hypothesis testing, the null hypothesis is typically denoted by: a) H0 b) H1 c) α d) β Ans: A. Why is this page out of focus? Because this is a premium document. Subscribe to unlock this document and more. ... The relationship between two variables in a regression analysis d) The number of failures in a binomial experiment Ans: B 19.
7. Your hypothesis can be expressed as Rβ = r R β = r where β β is your regression coefficients and R R is restriction matrix with r r the restrictions. If our model is. y = β +β x + u y = β 0 + β 1 x + u. then for hypothesis β1 = 0 β 1 = 0, R = [0, 1] R = [ 0, 1] and r = 1 r = 1.