8.3 Inverse Trigonometric Functions
Learning objectives.
In this section, you will:
- Understand and use the inverse sine, cosine, and tangent functions.
- Find the exact value of expressions involving the inverse sine, cosine, and tangent functions.
- Use a calculator to evaluate inverse trigonometric functions.
- Find exact values of composite functions with inverse trigonometric functions.
For any right triangle , given one other angle and the length of one side, we can figure out what the other angles and sides are. But what if we are given only two sides of a right triangle? We need a procedure that leads us from a ratio of sides to an angle. This is where the notion of an inverse to a trigonometric function comes into play. In this section, we will explore the inverse trigonometric functions .

Understanding and Using the Inverse Sine, Cosine, and Tangent Functions
In order to use inverse trigonometric functions, we need to understand that an inverse trigonometric function “undoes” what the original trigonometric function “does,” as is the case with any other function and its inverse. In other words, the domain of the inverse function is the range of the original function, and vice versa, as summarized in Figure 1 .
For example, if f ( x ) = sin x , f ( x ) = sin x , then we would write f − 1 ( x ) = sin − 1 x . f − 1 ( x ) = sin − 1 x . Be aware that sin − 1 x sin − 1 x does not mean 1 sin x . 1 sin x . The following examples illustrate the inverse trigonometric functions:
- Since sin ( π 6 ) = 1 2 , sin ( π 6 ) = 1 2 , then π 6 = sin − 1 ( 1 2 ) . π 6 = sin − 1 ( 1 2 ) .
- Since cos ( π ) = − 1 , cos ( π ) = − 1 , then π = cos − 1 ( − 1 ) . π = cos − 1 ( − 1 ) .
- Since tan ( π 4 ) = 1 , tan ( π 4 ) = 1 , then π 4 = tan − 1 ( 1 ) . π 4 = tan − 1 ( 1 ) .
In previous sections, we evaluated the trigonometric functions at various angles, but at times we need to know what angle would yield a specific sine, cosine, or tangent value. For this, we need inverse functions. Recall that, for a one-to-one function , if f ( a ) = b , f ( a ) = b , then an inverse function would satisfy f − 1 ( b ) = a . f − 1 ( b ) = a .
Bear in mind that the sine, cosine, and tangent functions are not one-to-one functions. The graph of each function would fail the horizontal line test. In fact, no periodic function can be one-to-one because each output in its range corresponds to at least one input in every period, and there are an infinite number of periods. As with other functions that are not one-to-one, we will need to restrict the domain of each function to yield a new function that is one-to-one. We choose a domain for each function that includes the number 0. Figure 2 shows the graph of the sine function limited to [ − π 2 , π 2 ] [ − π 2 , π 2 ] and the graph of the cosine function limited to [ 0 , π ] . [ 0 , π ] .
Figure 3 shows the graph of the tangent function limited to ( − π 2 , π 2 ) . ( − π 2 , π 2 ) .
These conventional choices for the restricted domain are somewhat arbitrary, but they have important, helpful characteristics. Each domain includes the origin and some positive values, and most importantly, each results in a one-to-one function that is invertible. The conventional choice for the restricted domain of the tangent function also has the useful property that it extends from one vertical asymptote to the next instead of being divided into two parts by an asymptote.
On these restricted domains, we can define the inverse trigonometric functions .
- The inverse sine function y = sin − 1 x y = sin − 1 x means x = sin y . x = sin y . The inverse sine function is sometimes called the arcsine function, and notated arcsin x . arcsin x . y = sin − 1 x has domain [ −1 , 1 ] and range [ − π 2 , π 2 ] y = sin − 1 x has domain [ −1 , 1 ] and range [ − π 2 , π 2 ]
- The inverse cosine function y = cos − 1 x y = cos − 1 x means x = cos y . x = cos y . The inverse cosine function is sometimes called the arccosine function, and notated arccos x . arccos x . y = cos − 1 x has domain [ −1 , 1 ] and range [ 0 , π ] y = cos − 1 x has domain [ −1 , 1 ] and range [ 0 , π ]
- The inverse tangent function y = tan − 1 x y = tan − 1 x means x = tan y . x = tan y . The inverse tangent function is sometimes called the arctangent function, and notated arctan x . arctan x . y = tan − 1 x has domain ( −∞ , ∞ ) and range ( − π 2 , π 2 ) y = tan − 1 x has domain ( −∞ , ∞ ) and range ( − π 2 , π 2 )
The graphs of the inverse functions are shown in Figure 4 , Figure 5 , and Figure 6 . Notice that the output of each of these inverse functions is a number, an angle in radian measure. We see that sin − 1 x sin − 1 x has domain [ −1 , 1 ] [ −1 , 1 ] and range [ − π 2 , π 2 ] , [ − π 2 , π 2 ] , cos − 1 x cos − 1 x has domain [ −1 ,1 ] [ −1 ,1 ] and range [ 0 , π ] , [ 0 , π ] , and tan − 1 x tan − 1 x has domain of all real numbers and range ( − π 2 , π 2 ) . ( − π 2 , π 2 ) . To find the domain and range of inverse trigonometric functions, switch the domain and range of the original functions. Each graph of the inverse trigonometric function is a reflection of the graph of the original function about the line y = x . y = x .
Relations for Inverse Sine, Cosine, and Tangent Functions
For angles in the interval [ − π 2 , π 2 ] , [ − π 2 , π 2 ] , if sin y = x , sin y = x , then sin − 1 x = y . sin − 1 x = y .
For angles in the interval [ 0 , π ] , [ 0 , π ] , if cos y = x , cos y = x , then cos − 1 x = y . cos − 1 x = y .
For angles in the interval ( − π 2 , π 2 ) , ( − π 2 , π 2 ) , if tan y = x , tan y = x , then tan − 1 x = y . tan − 1 x = y .
Writing a Relation for an Inverse Function
Given sin ( 5 π 12 ) ≈ 0.96593 , sin ( 5 π 12 ) ≈ 0.96593 , write a relation involving the inverse sine.
Use the relation for the inverse sine. If sin y = x , sin y = x , then sin − 1 x = y sin − 1 x = y .
In this problem, x = 0.96593 , x = 0.96593 , and y = 5 π 12 . y = 5 π 12 .
Given cos ( 0.5 ) ≈ 0.8776, cos ( 0.5 ) ≈ 0.8776, write a relation involving the inverse cosine.
Finding the Exact Value of Expressions Involving the Inverse Sine, Cosine, and Tangent Functions
Now that we can identify inverse functions, we will learn to evaluate them. For most values in their domains, we must evaluate the inverse trigonometric functions by using a calculator, interpolating from a table, or using some other numerical technique. Just as we did with the original trigonometric functions, we can give exact values for the inverse functions when we are using the special angles, specifically π 6 π 6 (30°), π 4 π 4 (45°), and π 3 π 3 (60°), and their reflections into other quadrants.
Given a “special” input value, evaluate an inverse trigonometric function.
- Find angle x x for which the original trigonometric function has an output equal to the given input for the inverse trigonometric function.
- If x x is not in the defined range of the inverse, find another angle y y that is in the defined range and has the same sine, cosine, or tangent as x , x , depending on which corresponds to the given inverse function.
Evaluating Inverse Trigonometric Functions for Special Input Values
Evaluate each of the following.
- ⓐ sin − 1 ( 1 2 ) sin − 1 ( 1 2 )
- ⓑ sin − 1 ( − 2 2 ) sin − 1 ( − 2 2 )
- ⓒ cos − 1 ( − 3 2 ) cos − 1 ( − 3 2 )
- ⓓ tan − 1 ( 1 ) tan − 1 ( 1 )
- ⓐ Evaluating sin − 1 ( 1 2 ) sin − 1 ( 1 2 ) is the same as determining the angle that would have a sine value of 1 2 . 1 2 . In other words, what angle x x would satisfy sin ( x ) = 1 2 ? sin ( x ) = 1 2 ? There are multiple values that would satisfy this relationship, such as π 6 π 6 and 5 π 6 , 5 π 6 , but we know we need the angle in the interval [ − π 2 , π 2 ] , [ − π 2 , π 2 ] , so the answer will be sin − 1 ( 1 2 ) = π 6 . sin − 1 ( 1 2 ) = π 6 . Remember that the inverse is a function, so for each input, we will get exactly one output.
- ⓑ To evaluate sin − 1 ( − 2 2 ) , sin − 1 ( − 2 2 ) , we know that 5 π 4 5 π 4 and 7 π 4 7 π 4 both have a sine value of − 2 2 , − 2 2 , but neither is in the interval [ − π 2 , π 2 ] . [ − π 2 , π 2 ] . For that, we need the negative angle coterminal with 7 π 4 : 7 π 4 : sin − 1 ( − 2 2 ) = − π 4 . sin − 1 ( − 2 2 ) = − π 4 .
- ⓒ To evaluate cos − 1 ( − 3 2 ) , cos − 1 ( − 3 2 ) , we are looking for an angle in the interval [ 0 , π ] [ 0 , π ] with a cosine value of − 3 2 . − 3 2 . The angle that satisfies this is cos − 1 ( − 3 2 ) = 5 π 6 . cos − 1 ( − 3 2 ) = 5 π 6 .
- ⓓ Evaluating tan − 1 ( 1 ) , tan − 1 ( 1 ) , we are looking for an angle in the interval ( − π 2 , π 2 ) ( − π 2 , π 2 ) with a tangent value of 1. The correct angle is tan − 1 ( 1 ) = π 4 . tan − 1 ( 1 ) = π 4 .
- ⓐ sin −1 ( −1 ) sin −1 ( −1 )
- ⓑ tan −1 ( −1 ) tan −1 ( −1 )
- ⓒ cos −1 ( −1 ) cos −1 ( −1 )
- ⓓ cos −1 ( 1 2 ) cos −1 ( 1 2 )
Using a Calculator to Evaluate Inverse Trigonometric Functions
To evaluate inverse trigonometric functions that do not involve the special angles discussed previously, we will need to use a calculator or other type of technology. Most scientific calculators and calculator-emulating applications have specific keys or buttons for the inverse sine, cosine, and tangent functions. These may be labeled, for example, SIN −1 −1 , ARCSIN , or ASIN .
In the previous chapter, we worked with trigonometry on a right triangle to solve for the sides of a triangle given one side and an additional angle. Using the inverse trigonometric functions, we can solve for the angles of a right triangle given two sides, and we can use a calculator to find the values to several decimal places.
In these examples and exercises, the answers will be interpreted as angles and we will use θ θ as the independent variable. The value displayed on the calculator may be in degrees or radians, so be sure to set the mode appropriate to the application.
Evaluating the Inverse Sine on a Calculator
Evaluate sin − 1 ( 0.97 ) sin − 1 ( 0.97 ) using a calculator.
Because the output of the inverse function is an angle, the calculator will give us a degree value if in degree mode and a radian value if in radian mode. Calculators also use the same domain restrictions on the angles as we are using.
In radian mode, sin − 1 ( 0.97 ) ≈ 1.3252. sin − 1 ( 0.97 ) ≈ 1.3252. In degree mode, sin − 1 ( 0.97 ) ≈ 75.93°. sin − 1 ( 0.97 ) ≈ 75.93°. Note that in calculus and beyond we will use radians in almost all cases.
Evaluate cos − 1 ( − 0.4 ) cos − 1 ( − 0.4 ) using a calculator.
Given two sides of a right triangle like the one shown in Figure 7 , find an angle.
- If one given side is the hypotenuse of length h h and the side of length a a adjacent to the desired angle is given, use the equation θ = cos − 1 ( a h ) . θ = cos − 1 ( a h ) .
- If one given side is the hypotenuse of length h h and the side of length p p opposite to the desired angle is given, use the equation θ = sin − 1 ( p h ) . θ = sin − 1 ( p h ) .
- If the two legs (the sides adjacent to the right angle) are given, then use the equation θ = tan − 1 ( p a ) . θ = tan − 1 ( p a ) .
Applying the Inverse Cosine to a Right Triangle
Solve the triangle in Figure 8 for the angle θ . θ .
Because we know the hypotenuse and the side adjacent to the angle, it makes sense for us to use the cosine function.
Solve the triangle in Figure 9 for the angle θ . θ .
Finding Exact Values of Composite Functions with Inverse Trigonometric Functions
There are times when we need to compose a trigonometric function with an inverse trigonometric function. In these cases, we can usually find exact values for the resulting expressions without resorting to a calculator. Even when the input to the composite function is a variable or an expression, we can often find an expression for the output. To help sort out different cases, let f ( x ) f ( x ) and g ( x ) g ( x ) be two different trigonometric functions belonging to the set { sin ( x ) , cos ( x ) , tan ( x ) } { sin ( x ) , cos ( x ) , tan ( x ) } and let f − 1 ( y ) f − 1 ( y ) and g − 1 ( y ) g − 1 ( y ) be their inverses.
Evaluating Compositions of the Form f ( f −1 ( y )) and f −1 ( f ( x ))
For any trigonometric function, f ( f − 1 ( y ) ) = y f ( f − 1 ( y ) ) = y for all y y in the proper domain for the given function. This follows from the definition of the inverse and from the fact that the range of f f was defined to be identical to the domain of f − 1 . f − 1 . However, we have to be a little more careful with expressions of the form f − 1 ( f ( x ) ) . f − 1 ( f ( x ) ) .
Compositions of a trigonometric function and its inverse
Is it correct that sin − 1 ( sin x ) = x ? sin − 1 ( sin x ) = x ?
No. This equation is correct if x x belongs to the restricted domain [ − π 2 , π 2 ] , [ − π 2 , π 2 ] , but sine is defined for all real input values, and for x x outside the restricted interval, the equation is not correct because its inverse always returns a value in [ − π 2 , π 2 ] . [ − π 2 , π 2 ] . The situation is similar for cosine and tangent and their inverses. For example, sin − 1 ( sin ( 3 π 4 ) ) = π 4 . sin − 1 ( sin ( 3 π 4 ) ) = π 4 .
Given an expression of the form f −1 (f(θ)) where f ( θ ) = sin θ , cos θ , or tan θ , f ( θ ) = sin θ , cos θ , or tan θ , evaluate.
- If θ θ is in the restricted domain of f , then f − 1 ( f ( θ ) ) = θ . f , then f − 1 ( f ( θ ) ) = θ .
- If not, then find an angle ϕ ϕ within the restricted domain of f f such that f ( ϕ ) = f ( θ ) . f ( ϕ ) = f ( θ ) . Then f − 1 ( f ( θ ) ) = ϕ . f − 1 ( f ( θ ) ) = ϕ .
Using Inverse Trigonometric Functions
Evaluate the following:
- ⓐ sin − 1 ( sin ( π 3 ) ) sin − 1 ( sin ( π 3 ) )
- ⓑ sin − 1 ( sin ( 2 π 3 ) ) sin − 1 ( sin ( 2 π 3 ) )
- ⓒ cos − 1 ( cos ( 2 π 3 ) ) cos − 1 ( cos ( 2 π 3 ) )
- ⓓ cos − 1 ( cos ( − π 3 ) ) cos − 1 ( cos ( − π 3 ) )
- ⓐ π 3 is in [ − π 2 , π 2 ] , π 3 is in [ − π 2 , π 2 ] , so sin − 1 ( sin ( π 3 ) ) = π 3 . sin − 1 ( sin ( π 3 ) ) = π 3 .
- ⓑ 2 π 3 is not in [ − π 2 , π 2 ] , 2 π 3 is not in [ − π 2 , π 2 ] , but sin ( 2 π 3 ) = sin ( π 3 ) , sin ( 2 π 3 ) = sin ( π 3 ) , so sin − 1 ( sin ( 2 π 3 ) ) = π 3 . sin − 1 ( sin ( 2 π 3 ) ) = π 3 .
- ⓒ 2 π 3 is in [ 0 , π ] , 2 π 3 is in [ 0 , π ] , so cos − 1 ( cos ( 2 π 3 ) ) = 2 π 3 . cos − 1 ( cos ( 2 π 3 ) ) = 2 π 3 .
- ⓓ − π 3 is not in [ 0 , π ] , − π 3 is not in [ 0 , π ] , but cos ( − π 3 ) = cos ( π 3 ) cos ( − π 3 ) = cos ( π 3 ) because cosine is an even function. π 3 is in [ 0 , π ] , π 3 is in [ 0 , π ] , so cos − 1 ( cos ( − π 3 ) ) = π 3 . cos − 1 ( cos ( − π 3 ) ) = π 3 .
Evaluate tan − 1 ( tan ( π 8 ) ) and tan − 1 ( tan ( 11 π 9 ) ) . tan − 1 ( tan ( π 8 ) ) and tan − 1 ( tan ( 11 π 9 ) ) .
Evaluating Compositions of the Form f −1 ( g ( x ))
Now that we can compose a trigonometric function with its inverse, we can explore how to evaluate a composition of a trigonometric function and the inverse of another trigonometric function. We will begin with compositions of the form f − 1 ( g ( x ) ) . f − 1 ( g ( x ) ) . For special values of x , x , we can exactly evaluate the inner function and then the outer, inverse function. However, we can find a more general approach by considering the relation between the two acute angles of a right triangle where one is θ , θ , making the other π 2 − θ . π 2 − θ . Consider the sine and cosine of each angle of the right triangle in Figure 10 .
Because cos θ = b c = sin ( π 2 − θ ) , cos θ = b c = sin ( π 2 − θ ) , we have sin − 1 ( cos θ ) = π 2 − θ sin − 1 ( cos θ ) = π 2 − θ if 0 ≤ θ ≤ π . 0 ≤ θ ≤ π . If θ θ is not in this domain, then we need to find another angle that has the same cosine as θ θ and does belong to the restricted domain; we then subtract this angle from π 2 . π 2 . Similarly, sin θ = a c = cos ( π 2 − θ ) , sin θ = a c = cos ( π 2 − θ ) , so cos − 1 ( sin θ ) = π 2 − θ cos − 1 ( sin θ ) = π 2 − θ if − π 2 ≤ θ ≤ π 2 . − π 2 ≤ θ ≤ π 2 . These are just the function-cofunction relationships presented in another way.
Given functions of the form sin − 1 ( cos x ) sin − 1 ( cos x ) and cos − 1 ( sin x ) , cos − 1 ( sin x ) , evaluate them.
- If x is in [ 0 , π ] , x is in [ 0 , π ] , then sin − 1 ( cos x ) = π 2 − x . sin − 1 ( cos x ) = π 2 − x .
- If x is not in [ 0 , π ] , x is not in [ 0 , π ] , then find another angle y in [ 0 , π ] y in [ 0 , π ] such that cos y = cos x . cos y = cos x . sin − 1 ( cos x ) = π 2 − y sin − 1 ( cos x ) = π 2 − y
- If x is in [ − π 2 , π 2 ] , x is in [ − π 2 , π 2 ] , then cos − 1 ( sin x ) = π 2 − x . cos − 1 ( sin x ) = π 2 − x .
- If x is not in [ − π 2 , π 2 ] , x is not in [ − π 2 , π 2 ] , then find another angle y in [ − π 2 , π 2 ] y in [ − π 2 , π 2 ] such that sin y = sin x . sin y = sin x . cos − 1 ( sin x ) = π 2 − y cos − 1 ( sin x ) = π 2 − y
Evaluating the Composition of an Inverse Sine with a Cosine
Evaluate sin − 1 ( cos ( 13 π 6 ) ) sin − 1 ( cos ( 13 π 6 ) )
- ⓐ by direct evaluation.
- ⓑ by the method described previously.
Now, we can evaluate the inverse function as we did earlier.
- ⓑ We have x = 13 π 6 , y = π 6 , x = 13 π 6 , y = π 6 , and sin − 1 ( cos ( 13 π 6 ) ) = π 2 − π 6 = π 3 sin − 1 ( cos ( 13 π 6 ) ) = π 2 − π 6 = π 3
Evaluate cos − 1 ( sin ( − 11 π 4 ) ) . cos − 1 ( sin ( − 11 π 4 ) ) .
Evaluating Compositions of the Form f ( g −1 ( x ))
To evaluate compositions of the form f ( g − 1 ( x ) ) , f ( g − 1 ( x ) ) , where f f and g g are any two of the functions sine, cosine, or tangent and x x is any input in the domain of g − 1 , g − 1 , we have exact formulas, such as sin ( cos − 1 x ) = 1 − x 2 . sin ( cos − 1 x ) = 1 − x 2 . When we need to use them, we can derive these formulas by using the trigonometric relations between the angles and sides of a right triangle, together with the use of Pythagoras’s relation between the lengths of the sides. We can use the Pythagorean identity, sin 2 x + cos 2 x = 1 , sin 2 x + cos 2 x = 1 , to solve for one when given the other. We can also use the inverse trigonometric functions to find compositions involving algebraic expressions.
Evaluating the Composition of a Sine with an Inverse Cosine
Find an exact value for sin ( cos − 1 ( 4 5 ) ) . sin ( cos − 1 ( 4 5 ) ) .
Beginning with the inside, we can say there is some angle such that θ = cos − 1 ( 4 5 ) , θ = cos − 1 ( 4 5 ) , which means cos θ = 4 5 , cos θ = 4 5 , and we are looking for sin θ . sin θ . We can use the Pythagorean identity to do this.
Since θ = cos − 1 ( 4 5 ) θ = cos − 1 ( 4 5 ) is in quadrant I, sin θ sin θ must be positive, so the solution is 3 5 . 3 5 . See Figure 11 .
We know that the inverse cosine always gives an angle on the interval [ 0 , π ] , [ 0 , π ] , so we know that the sine of that angle must be positive; therefore sin ( cos − 1 ( 4 5 ) ) = sin θ = 3 5 . sin ( cos − 1 ( 4 5 ) ) = sin θ = 3 5 .
Evaluate cos ( tan − 1 ( 5 12 ) ) . cos ( tan − 1 ( 5 12 ) ) .
Evaluating the Composition of a Sine with an Inverse Tangent
Find an exact value for sin ( tan − 1 ( 7 4 ) ) . sin ( tan − 1 ( 7 4 ) ) .
While we could use a similar technique as in Example 6 , we will demonstrate a different technique here. From the inside, we know there is an angle such that tan θ = 7 4 . tan θ = 7 4 . We can envision this as the opposite and adjacent sides on a right triangle, as shown in Figure 12 .
Using the Pythagorean Theorem, we can find the hypotenuse of this triangle.
Now, we can evaluate the sine of the angle as the opposite side divided by the hypotenuse.
This gives us our desired composition.
Evaluate cos ( sin − 1 ( 7 9 ) ) . cos ( sin − 1 ( 7 9 ) ) .
Finding the Cosine of the Inverse Sine of an Algebraic Expression
Find a simplified expression for cos ( sin − 1 ( x 3 ) ) cos ( sin − 1 ( x 3 ) ) for − 3 ≤ x ≤ 3. − 3 ≤ x ≤ 3.
We know there is an angle θ θ such that sin θ = x 3 . sin θ = x 3 .
Because we know that the inverse sine must give an angle on the interval [ − π 2 , π 2 ] , [ − π 2 , π 2 ] , we can deduce that the cosine of that angle must be positive.
Find a simplified expression for sin ( tan − 1 ( 4 x ) ) sin ( tan − 1 ( 4 x ) ) for − 1 4 ≤ x ≤ 1 4 . − 1 4 ≤ x ≤ 1 4 .
Access this online resource for additional instruction and practice with inverse trigonometric functions.
- Evaluate Expressions Involving Inverse Trigonometric Functions
8.3 Section Exercises
Why do the functions f ( x ) = sin − 1 x f ( x ) = sin − 1 x and g ( x ) = cos − 1 x g ( x ) = cos − 1 x have different ranges?
Since the functions y = cos x y = cos x and y = cos − 1 x y = cos − 1 x are inverse functions, why is cos − 1 ( cos ( − π 6 ) ) cos − 1 ( cos ( − π 6 ) ) not equal to − π 6 ? − π 6 ?
Explain the meaning of π 6 = arcsin ( 0.5 ) . π 6 = arcsin ( 0.5 ) .
Most calculators do not have a key to evaluate sec − 1 ( 2 ) . sec − 1 ( 2 ) . Explain how this can be done using the cosine function or the inverse cosine function.
Why must the domain of the sine function, sin x , sin x , be restricted to [ − π 2 , π 2 ] [ − π 2 , π 2 ] for the inverse sine function to exist?
Discuss why this statement is incorrect: arccos ( cos x ) = x arccos ( cos x ) = x for all x . x .
Determine whether the following statement is true or false and explain your answer: arccos ( − x ) = π − arccos x . arccos ( − x ) = π − arccos x .
For the following exercises, evaluate the expressions.
sin − 1 ( 2 2 ) sin − 1 ( 2 2 )
sin − 1 ( − 1 2 ) sin − 1 ( − 1 2 )
cos − 1 ( 1 2 ) cos − 1 ( 1 2 )
cos − 1 ( − 2 2 ) cos − 1 ( − 2 2 )
tan − 1 ( 1 ) tan − 1 ( 1 )
tan − 1 ( − 3 ) tan − 1 ( − 3 )
tan − 1 ( − 1 ) tan − 1 ( − 1 )
tan − 1 ( 3 ) tan − 1 ( 3 )
tan − 1 ( − 1 3 ) tan − 1 ( − 1 3 )
For the following exercises, use a calculator to evaluate each expression. Express answers to the nearest hundredth.
cos − 1 ( − 0.4 ) cos − 1 ( − 0.4 )
arcsin ( 0.23 ) arcsin ( 0.23 )
arccos ( 3 5 ) arccos ( 3 5 )
cos − 1 ( 0.8 ) cos − 1 ( 0.8 )
tan − 1 ( 6 ) tan − 1 ( 6 )
For the following exercises, find the angle θ θ in the given right triangle. Round answers to the nearest hundredth.
For the following exercises, find the exact value, if possible, without a calculator. If it is not possible, explain why.
sin − 1 ( cos ( π ) ) sin − 1 ( cos ( π ) )
tan − 1 ( sin ( π ) ) tan − 1 ( sin ( π ) )
cos − 1 ( sin ( π 3 ) ) cos − 1 ( sin ( π 3 ) )
tan − 1 ( sin ( π 3 ) ) tan − 1 ( sin ( π 3 ) )
sin − 1 ( cos ( − π 2 ) ) sin − 1 ( cos ( − π 2 ) )
tan − 1 ( sin ( 4 π 3 ) ) tan − 1 ( sin ( 4 π 3 ) )
sin − 1 ( sin ( 5 π 6 ) ) sin − 1 ( sin ( 5 π 6 ) )
tan − 1 ( sin ( − 5 π 2 ) ) tan − 1 ( sin ( − 5 π 2 ) )
cos ( sin − 1 ( 4 5 ) ) cos ( sin − 1 ( 4 5 ) )
sin ( cos − 1 ( 3 5 ) ) sin ( cos − 1 ( 3 5 ) )
sin ( tan − 1 ( 4 3 ) ) sin ( tan − 1 ( 4 3 ) )
cos ( tan − 1 ( 12 5 ) ) cos ( tan − 1 ( 12 5 ) )
cos ( sin − 1 ( 1 2 ) ) cos ( sin − 1 ( 1 2 ) )
For the following exercises, find the exact value of the expression in terms of x x with the help of a reference triangle.
tan ( sin − 1 ( x − 1 ) ) tan ( sin − 1 ( x − 1 ) )
sin ( cos − 1 ( 1 − x ) ) sin ( cos − 1 ( 1 − x ) )
cos ( sin − 1 ( 1 x ) ) cos ( sin − 1 ( 1 x ) )
cos ( tan − 1 ( 3 x − 1 ) ) cos ( tan − 1 ( 3 x − 1 ) )
tan ( sin − 1 ( x + 1 2 ) ) tan ( sin − 1 ( x + 1 2 ) )
For the following exercises, evaluate the expression without using a calculator. Give the exact value.
sin − 1 ( 1 2 ) − cos − 1 ( 2 2 ) + sin − 1 ( 3 2 ) − cos − 1 ( 1 ) cos − 1 ( 3 2 ) − sin − 1 ( 2 2 ) + cos − 1 ( 1 2 ) − sin − 1 ( 0 ) sin − 1 ( 1 2 ) − cos − 1 ( 2 2 ) + sin − 1 ( 3 2 ) − cos − 1 ( 1 ) cos − 1 ( 3 2 ) − sin − 1 ( 2 2 ) + cos − 1 ( 1 2 ) − sin − 1 ( 0 )
For the following exercises, find the function if sin t = x x + 1 . sin t = x x + 1 .
cos t cos t
sec t sec t
cot t cot t
cos ( sin − 1 ( x x + 1 ) ) cos ( sin − 1 ( x x + 1 ) )
tan − 1 ( x 2 x + 1 ) tan − 1 ( x 2 x + 1 )
Graph y = sin − 1 x y = sin − 1 x and state the domain and range of the function.
Graph y = arccos x y = arccos x and state the domain and range of the function.
Graph one cycle of y = tan − 1 x y = tan − 1 x and state the domain and range of the function.
For what value of x x does sin x = sin − 1 x ? sin x = sin − 1 x ? Use a graphing calculator to approximate the answer.
For what value of x x does cos x = cos − 1 x ? cos x = cos − 1 x ? Use a graphing calculator to approximate the answer.
Real-World Applications
Suppose a 13-foot ladder is leaning against a building, reaching to the bottom of a second-floor window 12 feet above the ground. What angle, in radians, does the ladder make with the building?
Suppose you drive 0.6 miles on a road so that the vertical distance changes from 0 to 150 feet. What is the angle of elevation of the road?
An isosceles triangle has two congruent sides of length 9 inches. The remaining side has a length of 8 inches. Find the angle that a side of 9 inches makes with the 8-inch side.
Without using a calculator, approximate the value of arctan ( 10 , 000 ) . arctan ( 10 , 000 ) . Explain why your answer is reasonable.
A truss (interior beam structure) for the roof of a house is constructed from two identical right triangles. Each has a base of 12 feet and height of 4 feet. Find the measure of the acute angle adjacent to the 4-foot side.
The line y = 3 5 x y = 3 5 x passes through the origin in the x , y -plane. What is the measure of the angle that the line makes with the positive x -axis?
The line y = − 3 7 x y = − 3 7 x passes through the origin in the x , y -plane. What is the measure of the angle that the line makes with the negative x -axis?
What percentage grade should a road have if the angle of elevation of the road is 4 degrees? (The percentage grade is defined as the change in the altitude of the road over a 100-foot horizontal distance. For example a 5% grade means that the road rises 5 feet for every 100 feet of horizontal distance.)
A 20-foot ladder leans up against the side of a building so that the foot of the ladder is 10 feet from the base of the building. If specifications call for the ladder's angle of elevation to be between 35 and 45 degrees, does the placement of this ladder satisfy safety specifications?
Suppose a 15-foot ladder leans against the side of a house so that the angle of elevation of the ladder is 42 degrees. How far is the foot of the ladder from the side of the house?
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/algebra-and-trigonometry-2e/pages/1-introduction-to-prerequisites
- Authors: Jay Abramson
- Publisher/website: OpenStax
- Book title: Algebra and Trigonometry 2e
- Publication date: Dec 21, 2021
- Location: Houston, Texas
- Book URL: https://openstax.org/books/algebra-and-trigonometry-2e/pages/1-introduction-to-prerequisites
- Section URL: https://openstax.org/books/algebra-and-trigonometry-2e/pages/8-3-inverse-trigonometric-functions
© Jun 28, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Chapter 8: More Functions and Identities
Exercises: 8.2 Inverse Trigonometric Functions Exercises
Practice each skill in the Homework Problems listed.
- Decide whether a function has an inverse function #1–8
- Evaluate the inverse trig functions #9–20
- Model problems with inverse trig functions #21–24
- Solve formulas #25–30
- Simplify expressions involving the inverse trig functions #31–42, 51–68
- Graph the inverse trig functions #43–50, 69 and 70
Suggested Homework
Exercises for 8.2 Inverse Trigonometric Functions
Exercise group.
In Problems 1–4, which functions have an inverse function? Explain your answer.
For Problems 5–8, graph the function and decide if it has an inverse function.
[latex]f(x)=\sin 2x - \cos x[/latex]
[latex]g(x)=4e^{-(x/4)^2}[/latex]
[latex]G(x)=\sqrt{25-x^2}[/latex]
[latex]F(x)=\ln(x^3+8)[/latex]
For Problems 9–14, use a calculator to evaluate. Round your answers to the nearest tenth of a degree.
[latex]\sin^{-1}(0.2838)[/latex]
[latex]\tan^{-1}(4.8972)[/latex]
[latex]\cos^{-1}(0.6894)[/latex]
[latex]\arccos(-0.8134)[/latex]
[latex]\arctan(-1.2765)[/latex]
[latex]\arcsin(-07493)[/latex]
For Problems 15–20, give exact values in radians.
[latex]\cos^{-1} \dfrac{-1}{\sqrt{2}}[/latex]
[latex]\tan^{-1}(-1)[/latex]
[latex]\sin^{-1}\dfrac{-1}{2}[/latex]
[latex]\arccos\dfrac{\sqrt{3}}{2}[/latex]
[latex]\arctan \dfrac{1}{\sqrt{3}}[/latex]
[latex]\arcsin (-1)[/latex]
For Problems 21–26, sketch a figure to help you model each problem.
Delbert is watching the launch of a satellite at Cape Canaveral. The viewing area is 500 yards from the launch site. The angle of elevation, [latex]\theta{,}[/latex] of Delbert’s line of sight increases as the booster rocket rises.
- Write a formula for the height, [latex]h{,}[/latex] of the rocket as a function of [latex]\theta{.}[/latex]
- Write a formula for [latex]\theta[/latex] as a function of [latex]h{.}[/latex]
- Evaluate the formula in part (b) for [latex]h=1000{,}[/latex] and interpret the result.
Francine’s house lies under the flight path from the city airport, and commercial airliners pass overhead at an altitude of 35,000 feet. As Francine watches an airplane recede, its angle of elevation, [latex]\theta{,}[/latex] decreases.
- Write a formula for the horizontal distance, [latex]d{,}[/latex] to the airplane as a function of [latex]\theta{.}[/latex]
- Write a formula for [latex]\theta[/latex] as a function of [latex]d{.}[/latex]
- Evaluate the formula in part (b) for [latex]d=20,000{,}[/latex] and interpret the result.
While driving along the interstate, you approach an enormous 50-foot-wide billboard that sits just beside the road. Your viewing angle, [latex]\theta{,}[/latex] increases as you get closer to the billboard.
- Write a formula for your distance, [latex]d{,}[/latex] from the billboard as a function of [latex]\theta{.}[/latex]
- Evaluate the formula in part (b) for [latex]d=200{,}[/latex] and interpret the result.
Emma is walking along the bank of a straight river toward a 20-meter-long bridge over the river. Let [latex]\theta[/latex] be the angle subtended horizontally by Emma’s view of the bridge.
- Write a formula for Emma’s distance from the bridge, [latex]d{,}[/latex] as a function of [latex]\theta{.}[/latex]
- Evaluate the formula in part (b) for [latex]d=500{,}[/latex] and interpret the result.
Martin is viewing a 4-meter-tall painting whose base is 1 meter above his eye level.
- Write a formula for [latex]\alpha{,}[/latex] the angle subtended from Martin’s eye level to the bottom of the painting, when he stands [latex]x[/latex] meters from the wall.
- Write a formula for [latex]\beta{,}[/latex] the angle subtended by the painting, in terms of [latex]x{.}[/latex]
- Evaluate the formula in part (b) for [latex]x=5{,}[/latex] and interpret the result.
A 5-foot mirror is positioned so that its bottom is 1.5 feet below Jane’s eye level.
- Write a formula for [latex]\alpha{,}[/latex] the angle subtended by the section of mirror below Jane’s eye level, when she stands [latex]x[/latex] feet from the mirror.
- Write a formula for [latex]\theta{,}[/latex] the angle subtended by the entire mirror, in terms of [latex]x{.}[/latex]
- Evaluate the formula in part (b) for [latex]x=10{,}[/latex] and interpret the result.
For Problems 27–32, solve the formula for the given variable.
[latex]V=V_0 \sin(2\pi\omega t+\phi){,}[/latex] for [latex]t[/latex]
[latex]R=\dfrac{1}{32} v_0^2\sin (2\theta){,}[/latex] for [latex]\theta[/latex]
[latex]\dfrac{a}{\sin A}= \dfrac{b}{\sin B}{,}[/latex] for [latex]A[/latex]
[latex]c^2=a^2 + b^2 - 2ab\cos C{,}[/latex] for [latex]C[/latex]
[latex]P=\dfrac{k}{R^4\cos \theta}[/latex] for [latex]\theta[/latex]
[latex]\dfrac{r}{z}=\dfrac{1}{\tan (\alpha + \beta)}{,}[/latex] for [latex]\alpha[/latex]
For Problems 33–38, find exact values without using a calculator.
[latex]\tan\left(\sin^{-1}\left(\dfrac{2}{3}\right)\right)[/latex]
[latex]\tan\left(\cos^{-1}\left(\dfrac{3}{4}\right)\right)[/latex]
[latex]\cos\left[\tan^{-1}(-2)\right][/latex]
[latex]\sin \left[\tan^{-1}\left(\dfrac{-3}{\sqrt{5}}\right)\right][/latex]
[latex]\sin\left[\cos^{-1}\left(\dfrac{-2\sqrt{6}}{7}\right)\right][/latex]
[latex]\cos\left[\sin^{-1}\left(\dfrac{-2}{7}\right)\right][/latex]
For Problems 39–44, simplify the expression.
[latex]\tan(\cos^{-1}x)[/latex]
[latex]\cos(\tan^{-1}a)[/latex]
[latex]\cos(\sin^{-1}h)[/latex]
[latex]\sin(\cos^{-1}v)[/latex]
[latex]\sin(\tan^{-1}2t)[/latex]
[latex]\tan(\sin^{-1}3b)[/latex]
For Problems 45–47, complete the table of values and sketch the function.
| [latex]x[/latex] | [latex]-1[/latex] | [latex]\dfrac{-\sqrt{3}}{2}[/latex] | [latex]\dfrac{-\sqrt{2}}{2}[/latex] | [latex]\dfrac{-1}{2}[/latex] | [latex]0[/latex] | [latex]\dfrac{1}{2}[/latex] | [latex]\dfrac{\sqrt{2}}{2}[/latex] | [latex]\dfrac{\sqrt{3}}{2}[/latex] | [latex]1[/latex] |
| [latex]\cos^{-1}x[/latex] | [latex]\hphantom{0000}[/latex] | [latex]\hphantom{0000}[/latex] | [latex]\hphantom{0000}[/latex] | [latex]\hphantom{0000}[/latex] | [latex]\hphantom{0000}[/latex] | [latex]\hphantom{0000}[/latex] | [latex]\hphantom{0000}[/latex] | [latex]\hphantom{0000}[/latex] | [latex]\hphantom{0000}[/latex] |
| [latex]x[/latex] | [latex]-1[/latex] | [latex]\dfrac{-\sqrt{3}}{2}[/latex] | [latex]\dfrac{-\sqrt{2}}{2}[/latex] | [latex]\dfrac{-1}{2}[/latex] | [latex]0[/latex] | [latex]\dfrac{1}{2}[/latex] | [latex]\dfrac{\sqrt{2}}{2}[/latex] | [latex]\dfrac{\sqrt{3}}{2}[/latex] | [latex]1[/latex] |
| [latex]\sin^{-1}x[/latex] | [latex]\hphantom{0000}[/latex] | [latex]\hphantom{0000}[/latex] | [latex]\hphantom{0000}[/latex] | [latex]\hphantom{0000}[/latex] | [latex]\hphantom{0000}[/latex] | [latex]\hphantom{0000}[/latex] | [latex]\hphantom{0000}[/latex] | [latex]\hphantom{0000}[/latex] | [latex]\hphantom{0000}[/latex] |
| [latex]x[/latex] | [latex]-\sqrt{3}[/latex] | [latex]-1[/latex] | [latex]\dfrac{-1}{\sqrt{3}}[/latex] | [latex]0[/latex] | [latex]\dfrac{1}{\sqrt{3}}[/latex] | [latex]1[/latex] | [latex]\sqrt{3}[/latex] |
| [latex]\tan^{-1}x[/latex] | [latex]\hphantom{0000}[/latex] | [latex]\hphantom{0000}[/latex] | [latex]\hphantom{0000}[/latex] | [latex]\hphantom{0000}[/latex] | [latex]\hphantom{0000}[/latex] | [latex]\hphantom{0000}[/latex] | [latex]\hphantom{0000}[/latex] |
Use a graphing calculator to answer each of the following questions. Then explain the results.
- Does [latex]\cos^{-1}x=\dfrac{1}{\cos x}{?}[/latex]
- Does [latex]\sin^{-1}x=\dfrac{1}{\sin x}{?}[/latex]
- Does [latex]\tan^{-1}x=\dfrac{1}{\tan x}{?}[/latex]
- Sketch a graph of [latex]y=\cos^{-1}x{,}[/latex] and label the scales on the axes.
- Use transformations to sketch graphs of [latex]y=2\cos^{-1}x[/latex] and [latex]y=\cos^{-1}(2x){.}[/latex]
Does [latex]2\cos^{-1}x=\cos^{-1}(2x){?}[/latex]
- Sketch a graph of [latex]y=\sin^{-1}x{,}[/latex] and label the scales on the axes.
- Use transformations to sketch graphs of [latex]y=\dfrac{1}{2}\sin^{-1}x[/latex] and [latex]y=\cos^{-1}\left(\dfrac{1}{2}x\right){.}[/latex]
- Does [latex]\dfrac{1}{2}\sin^{-1}x=\cos^{-1}\left(\dfrac{1}{2}x\right){?}[/latex]
- Sketch a graph of [latex]y=\tan^{-1}x{,}[/latex] and label the scales on the axes.
- Use your calculator to graph [latex]y=\dfrac{\sin^{-1}x}{\cos^{-1}x}[/latex] on a suitable domain.
- Does [latex]\tan^{-1}x=\dfrac{\sin^{-1}x}{\cos^{-1}x}{?}[/latex]
- Use your calculator to sketch [latex]y=\sqrt[3]{x}[/latex] and [latex]\tan^{-1}x[/latex] on [latex][-10, 10]{.}[/latex]
- Describe the similarities and differences in the two graphs.
Use the identities from Section 8.1 to help you find exact values for the expressions in Problems 53–58.
[latex]\sin (2\tan^{-1}4)[/latex]
[latex]\cos\left(2\sin^{-1}\left(\dfrac{5}{13}\right)\right)[/latex]
[latex]\tan\left(2\cos^{-1}\left(\dfrac{3}{4}\right)\right)[/latex]
[latex]\sin\left(2\cos^{-1}\left(\dfrac{-4}{5}\right)\right)[/latex]
[latex]\tan\left(2\sin^{-1}\left(\dfrac{1}{3}\right)\right)[/latex]
[latex]\cos\left(2\tan^{-1}\left(\dfrac{3}{2}\right)\right)[/latex]
Let [latex]\alpha= \cos^{-1}\left(\dfrac{-4}{5}\right),~\beta=\sin^{-1}\left(\dfrac{5}{13}\right){.}[/latex] Find exact values for the following:
[latex]\displaystyle \sin (\alpha+\beta)[/latex]
[latex]\displaystyle \cos (\alpha-\beta)[/latex]
[latex]\displaystyle \sin (\alpha-\beta)[/latex]
Let [latex]\alpha= \sin^{-1}\left(\dfrac{-15}{17}\right),~\beta=\tan^{-1}\left(\dfrac{4}{3}\right){.}[/latex] Find exact values for the following:
Find an exact value for [latex]\sin\left(\tan^{-1}\left(\dfrac{3}{4}\right)-\sin^{-1}\left(\dfrac{-4}{5}\right)\right){.}[/latex]
Find an exact value for [latex]\cos\left(\tan^{-1}\left(\dfrac{5}{12}\right)+\sin^{-1}\left(\dfrac{-3}{5}\right)\right){.}[/latex]
Express in terms of [latex]x[/latex] without trigonometric functions.
[latex]\displaystyle \cos(2\sin^{-1}x)[/latex]
Express in terms of [latex]w[/latex] without trigonometric functions.
[latex]\displaystyle \cos(2\tan^{-1}w)[/latex]
If [latex]x=5\sin \theta,~0° \lt \theta \lt 90°{,}[/latex] express [latex]\sin 2\theta[/latex] and [latex]\cos 2\theta[/latex] in terms of [latex]x{.}[/latex]
If [latex]x-1=2\cos \theta,~0° \lt \theta \lt 90°{,}[/latex] express [latex]\sin 2\theta[/latex] and [latex]\cos 2\theta[/latex] in terms of [latex]x{.}[/latex]
If [latex]x=3\tan \theta{,}[/latex] write [latex]\theta +\dfrac{1}{4}\sin 2\theta[/latex] in terms of [latex]x{.}[/latex]
If [latex]x=5\cos \theta{,}[/latex] write [latex]\dfrac{\theta}{2}-\cos 2\theta[/latex] in terms of [latex]x{.}[/latex]
- For what values of [latex]x[/latex] is the function [latex]f(x)=\sin (\arcsin x)[/latex] defined?
- Is [latex]\sin (\arcsin x)=x[/latex] for all [latex]x[/latex] where it is defined? If not, for what values of [latex]x[/latex] is the equation false?
- For what values of [latex]x[/latex] is the function [latex]g(x)=\arcsin(\sin x)[/latex] defined?
- Is [latex]\arcsin (\sin x)=x[/latex] for all [latex]x[/latex] where it is defined? If not, for what values of [latex]x[/latex] is the equation false?
- For what values of [latex]x[/latex] is the function [latex]f(x)=\cos (\arccos x)[/latex] defined?
- Is [latex]\cos (\arccos x)=x[/latex] for all [latex]x[/latex] where it is defined? If not, for what values of [latex]x[/latex] is the equation false?
- For what values of [latex]x[/latex] is the function [latex]g(x)=\arccos(\cos x)[/latex] defined?
- Is [latex]\arccos (\cos x)=x[/latex] for all [latex]x[/latex] where it is defined? If not, for what values of [latex]x[/latex] is the equation false?
Use your calculator to graph [latex]y=\sin^{-1}x+\cos^{-1}x{.}[/latex]
- State the domain and range of the graph.
- Explain why the graph looks as it does.
Use your calculator to graph [latex]y=\tan^{-1}x+\tan^{-1}(\dfrac{1}{x}){.}[/latex]
In Problems 73–74, we find a formula for the area under part of a semicircle.
- Write an expression for the area of the shaded sector in terms of [latex]\theta{.}[/latex]
- How are [latex]\theta[/latex] and [latex]t[/latex] related in the figure? (Hint: Write an expression for [latex]\sin \theta{.}[/latex])
- Combine your answers to (a) and (b) to write an expression for the area of the sector in terms of [latex]t{.}[/latex]
- Write an expression for the height of the shaded triangle in terms of [latex]t{.}[/latex] (Hint: Use the Pythagorean theorem.)
- Write an expression for the area of the triangle in terms of [latex]t{.}[/latex]
- Combine your answers to (b) and to Problem 73 to write an expression for the area bounded above by the upper semicircle, below by the [latex]x[/latex]-axis, on the left by the [latex]y[/latex]-axis, and on the right by [latex]x=t{,}[/latex] when [latex]0 \le t \le 1{.}[/latex]
Trigonometry Copyright © 2024 by Bimal Kunwor; Donna Densmore; Jared Eusea; and Yi Zhen. All Rights Reserved.
Share This Book
Inverse trigonometry functions
The inverses of sec,cot,csc are written in a similar way, but rarely used
On a calculator
You will always use a calculator to find the values of trig functions and their inverses. On a calculator the inverse buttons may be marked for example arcsin, asin, or sin -1 .
( Be careful : The latter form - sin -1 - can be very misleading since raising something to the power negative one implies the reciprocal, which is not the same thing as the inverse function).
--> Solving a right triangle
In a right triangle , when you know any two sides, you can use the inverse trig functions to find all the angles. In the figure below we are given the three sides. We can find the angles A,B,C
Using arcsin
Using arccos, using arctan.
So all three produce the same result, as they should. Use whichever function you like, depending on which sides you are given to start.
Large and negative angles
Recall that we can apply trig functions to any angle , including large and negative angles. But when we consider the inverse function we run into a problem.
What if we were asked to find the inverse sine of say 0.5? In other words, what angle has a sine of 0.5?
If we look at the curve above we see four angles whose sine is 0.5 (red dots). In fact, since the graph goes on forever in both directions, there are an infinite number of angles that have a sine of a 0.5. (See Graph of the sine function ).
How is this resolved?
Other trigonometry topics.
- Angle definition, properties of angles
- Standard position on an angle
- Initial side of an angle
- Terminal side of an angle
- Quadrantal angles
- Coterminal angles
- Reference angle
Trigonometric functions
- Introduction to the six trig functions
- Functions of large and negative angles
- Inverse trig functions
- SOH CAH TOA memory aid
- Sine function (sin) in right triangles
- Inverse sine function (arcsin)
- Graphing the sine function
- Cosine function (cos) in right triangles
- Inverse cosine function (arccos)
- Graphing the cosine function
- Tangent function (tan) in right triangles
- Inverse tangent function (arctan)
- Graphing the tangent function
- Cotangent function cot (in right triangles)
- Secant function sec (in right triangles)
- Cosecant function csc (in right triangles)
Solving trigonometry problems
- The general approach
- Finding slant distance along a slope or ramp
- Finding the angle of a slope or ramp
- Derivatives of trigonometric functions
Inverse Trigonometric Functions
Introduction to Inverse Trig Functions
The same principles apply for the inverses of six trigonometric functions , but since the trig functions are periodic (repeating), these functions don’t have inverses, unless we restrict the domain . As shown below, we restrict the domains to certain quadrants so the original function passes the horizontal line test and thus the inverse function passes the vertical line test . Thus, the inverse trig functions are one-to-one functions , meaning every element of the range of the function corresponds to exactly one element of the domain.
As an example, in order to make an inverse trig function an actual function, only take the values between $ \displaystyle -\frac{\pi }{2}$ and $ \displaystyle \frac{\pi }{2}$, so the sin function passes the horizontal line test (meaning its inverse is a function):
Important Note: There is a subtle distinction between finding inverse trig functions and solving for trig functions . If we want $ \displaystyle {{\sin }^{{-1}}}\left( {\frac{{\sqrt{2}}}{2}} \right)$ for example, we only pick the answers from Quadrants I and IV , so we get $ \displaystyle \frac{\pi }{4}$ only. But if we are solving $ \displaystyle \sin \left( x \right)=\frac{{\sqrt{2}}}{2}$ like in the Solving Trigonometric Functions section , there are no domain restrictions, so we get $ \displaystyle \frac{\pi }{4}$ and $ \displaystyle \frac{{3\pi }}{4}$ in the interval $ \left( {0,2\pi } \right)$, and $ \displaystyle \frac{\pi }{4}+2\pi k$ and $ \displaystyle \frac{3\pi }{4}+2\pi k$ over all reals.
Graphs of Inverse Trig Functions
Evaluating inverse trig functions – special angles.
When you are asked to evaluate inverse functions, you may see the notation $ {{\sin }^{-1}}$ or arcsin ; they mean the same thing. The following examples use angles that are special values or special angles : angles that have trig values that we can compute exactly, since they come right off the Unit Circle:
When using the Unit Circle , when the answer is in Quadrant IV , it must be negative (go backwards from the $ (1, 0)$ point). For example, for the $ \displaystyle {{\sin }^{-1}}\left( -\frac{1}{2} \right)$ or $ \displaystyle \arcsin \left( -\frac{1}{2} \right)$, the angle is 330° , or $ \displaystyle \frac{11\pi }{6}$. But since our answer has to be between $ \displaystyle -\frac{\pi }{2}$ and $ \displaystyle \frac{\pi }{2}$, we need to change this to the co-terminal angle $ -30{}^\circ $, or $ \displaystyle -\frac{\pi }{6}$.
To get the inverses for the reciprocal functions , take the reciprocal of what’s in the parentheses and then use the “normal” trig functions. For example, to get $ {{\sec }^{-1}}\left( -\sqrt{2} \right)$, look for $ \displaystyle {{\cos }^{-1}}\left( -\frac{1}{\sqrt{2}} \right)$, which is $ \displaystyle {{\cos }^{-1}}\left( -\frac{\sqrt{2}}{2} \right)$, which is $ \displaystyle \frac{3\pi }{4}$, or 135° .
Check your work : For all inverse trig functions of a positive argument (given the correct domain ), we should get an angle in Quadrant I ($ \displaystyle 0\le \theta \le \frac{\pi }{2}$). For the arcsin , arccsc , and arctan functions, if we have a negative argument, we’ll end up in Quadrant IV (specifically $ \displaystyle -\frac{\pi }{2}\le \theta \le \frac{\pi }{2}$), and for the arccos , arcsec , and arccot functions, if we have a negative argument, we’ll end up in Quadrant II ($ \displaystyle \frac{\pi }{2}\le \theta \le \pi $). For arguments outside the domains of the trig functions for arcsin , arccsc , arccos , and arcsec , we’ll get no solution .
Trig Inverses in the Calculator
IMPORTANT NOTE : When getting trig inverses in the calculator, we only get one value back (which we should, because of the domain restrictions , and thus quadrant restrictions ). When solving trig equations , however, we typically get many solutions, for example, if we want values in the interval $ \left[ {0,2\pi } \right)$, or over the reals. We’ll see how to use the inverse trig function in the calculator when solving trig equations here in the Solving Trigonometric Equations section .
Transformations of the Inverse Trig Functions
We learned how to transform Basic Parent Functions here in the Parent Functions and Transformations section, and we learned how to transform the six Trigonometric Functions here. Now we will transform the Inverse Trig Functions .
T-Charts for the Six Inverse Trigonometric Functions
Some prefer to do all the transformations with t-charts like we did earlier, and some prefer it without t-charts ; most of the examples will show t-charts.
Composite Inverse Trig Functions with Special Values/Angles
Trig composites on the calculator.
You can also put trig composites in the graphing calculator (and they don’t have to be special angles), but remember to add $ \pi $ to the answer that you get (or 180° if in degrees) when you are getting the arccot or $ {{\cot }^{{-1}}}$ of a negative number (see last example).
Note again for the reciprocal functions, you put 1 over the whole trig function when you work with the regular trig functions (like cos ), and you take the reciprocal of what’s in the parentheses when you work with the inverse trig functions (like arccos ).
Note : We do have to be careful when using $ \displaystyle \frac{1}{{\tan \left( x \right)}}$ for $ \cot \left( x \right)$ in the calculator. For angles $ \displaystyle \frac{\pi }{2},\frac{{3\pi }}{2}$, the results won’t be correct; it shows an error, instead of 0 (try it!). It would be better to use $ \displaystyle \frac{{\cos \left( x \right)}}{{\sin \left( x \right)}}$ in this case.
Composite Inverse Trig Functions with Non-Special Angles
You might also have to find composite inverse trig functions with non-special angles , which means that they are not found on the Unit Circle. (Examples of special angles are 0°, 45°, 60°, 270°, and their radian equivalents.) The easiest way to do this is to draw triangles on they coordinate system, and (if necessary) use the Pythagorean Theorem to find the missing sides.
Note : If the angle we’re dealing with is on one of the axes, such as with the arctan( 0° ), we don’t have to draw a triangle, but just draw a line on the $ x$- or $ y$-axis. Be careful with division by 0 ; an answer will be “undefined” in these cases.
Learn these rules, and practice, practice, practice!
Click on Submit (the arrow to the right of the problem) to solve this problem. You can also type in more problems, or click on the 3 dots in the upper right hand corner to drill down for example problems.
If you click on “Tap to view steps”, you will go to the Mathway site, where you can register for the full version (steps included) of the software. You can even get math worksheets.
You can also go to the Mathway site here , where you can register, or just use the software for free without the detailed solutions. There is even a Mathway App for your mobile device. Enjoy!
On to Solving Trigonometric Equations – you are ready!
Math 112 (Online) Walkthrough Text
Walkthrough of unit 5: inverse trig functions and solving trig equations, learning outcomes.
- Understand and use the inverse sine, cosine, and tangent functions.
- Find the exact value of expressions involving the inverse sine, cosine, and tangent functions.
- Use a calculator to evaluate inverse trigonometric functions.
- Use inverse trigonometric functions to solve right triangles.
- Find exact values of composite functions with inverse trigonometric functions.
Understanding and Using the Inverse Sine, Cosine, and Tangent Functions
In order to use inverse trigonometric functions, we need to understand that an inverse trigonometric function “undoes” what the original trigonometric function “does,” as is the case with any other function and its inverse. In other words, the domain of the inverse function is the range of the original function, and vice versa, as summarized in Figure 1.

For example, if [latex]f(x)=\sin x[/latex], then we would write [latex]f^{1}(x)={\sin}^{-1}{x}[/latex]. Be aware that [latex]{\sin}^{-1}x[/latex] does not mean [latex]\frac{1}{\sin{x}}[/latex]. The following examples illustrate the inverse trigonometric functions:
- Since [latex]\sin\left(\frac{\pi}{6}\right)=\frac{1}{2}[/latex], then [latex]\frac{\pi}{6}=\sin^{−1}(\frac{1}{2})[/latex].
- Since [latex]\cos(\pi)=−1[/latex], then [latex]\pi=\cos^{−1}(−1)[/latex].
- Since [latex]\tan\left(\frac{\pi}{4}\right)=1[/latex], then [latex]\frac{\pi}{4}=\tan^{−1}(1)[/latex].
In previous sections, we evaluated the trigonometric functions at various angles, but at times we need to know what angle would yield a specific sine, cosine, or tangent value. For this, we need inverse functions. Recall that, for a one-to-one function , if [latex]f(a)=b[/latex], then an inverse function would satisfy [latex]f^{−1}(b)=a[/latex].
Bear in mind that the sine, cosine, and tangent functions are not one-to-one functions. The graph of each function would fail the horizontal line test. In fact, no periodic function can be one-to-one because each output in its range corresponds to at least one input in every period, and there are an infinite number of periods. As with other functions that are not one-to-one, we will need to restrict the domain of each function to yield a new function that is one-to-one. We choose a domain for each function that includes the number 0. Figure 2 shows the graph of the sine function limited to [latex]\left[\frac{−\pi}{2}\text{, }\frac{\pi}{2}\right][/latex] and the graph of the cosine function limited to [0, π].
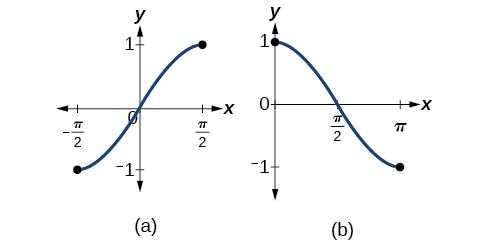
Figure 2. (a) Sine function on a restricted domain of [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right][/latex]; (b) Cosine function on a restricted domain of [0, π]
Figure 3 shows the graph of the tangent function limited to [latex]\left(−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right)[/latex].
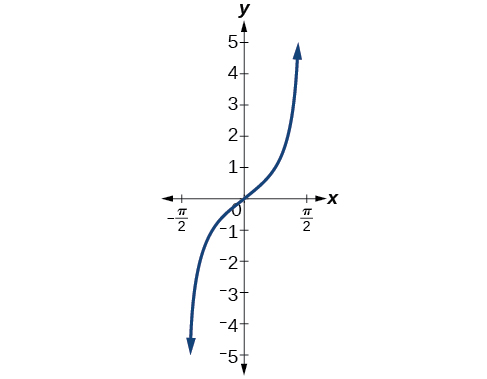
Figure 3. Tangent function on a restricted domain of [latex]\left(−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right)[/latex]
These conventional choices for the restricted domain are somewhat arbitrary, but they have important, helpful characteristics. Each domain includes the origin and some positive values, and most importantly, each results in a one-to-one function that is invertible. The conventional choice for the restricted domain of the tangent function also has the useful property that it extends from one vertical asymptote to the next instead of being divided into two parts by an asymptote.
On these restricted domains, we can define the inverse trigonometric functions .
- The inverse sine function [latex]y=\sin^{−1}x[/latex] means [latex]x=\sin y[/latex]. The inverse sine function is sometimes called the arcsine function, and notated arcsin x . [latex]y=\sin^{−1}x[/latex] has domain [−1, 1] and range [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right][/latex]
- The inverse cosine function [latex]y=\cos^{−1}x[/latex] means [latex]x=\cos y[/latex]. The inverse cosine function is sometimes called the arccosine function, and notated arccos x . [latex]y=\cos^{−1}x[/latex] has domain [−1, 1] and range [0, π]
- The inverse tangent function [latex]y=\tan^{−1}x[/latex] means [latex]x=\tan y[/latex]. The inverse tangent function is sometimes called the arctangent function, and notated arctan x . [latex]y=\tan^{−1}x[/latex] has domain (−∞, ∞) and range [latex]\left(−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right)[/latex]
The graphs of the inverse functions are shown in Figure 4, Figure 5, and Figure 6. Notice that the output of each of these inverse functions is a number, an angle in radian measure. We see that [latex]\sin^{−1}x[/latex] has domain [−1, 1] and range [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right][/latex], [latex]\cos^{−1}x[/latex] has domain [−1, 1] and range [0, π], and [latex]\tan^{−1}x[/latex] has domain of all real numbers and range [latex]\left(−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right)[/latex]. To find the domain and range of inverse trigonometric functions, switch the domain and range of the original functions. Each graph of the inverse trigonometric function is a reflection of the graph of the original function about the line [latex]y=x[/latex].
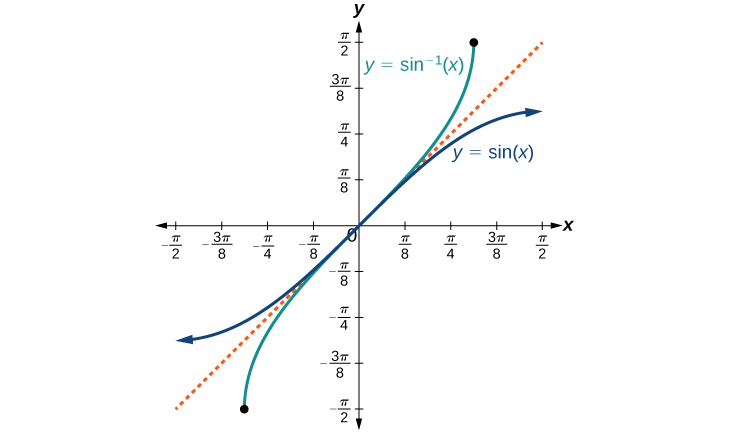
Figure 4. The sine function and inverse sine (or arcsine) function
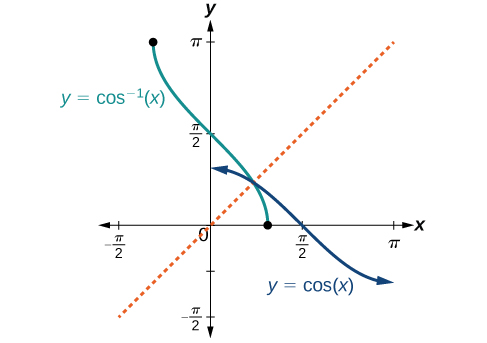
Figure 5. The cosine function and inverse cosine (or arccosine) function
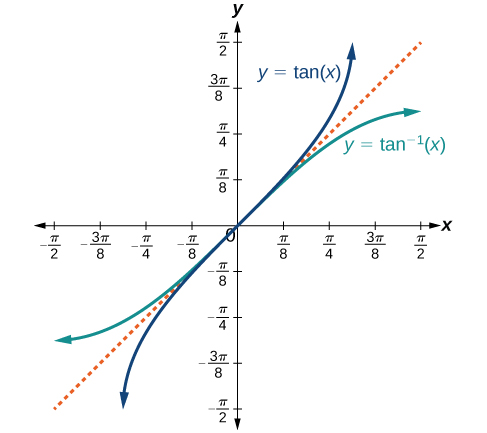
Figure 6. The tangent function and inverse tangent (or arctangent) function
A General Note: Relations for Inverse Sine, Cosine, and Tangent Functions
For angles in the interval [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right][/latex], if [latex]\sin y=x[/latex], then [latex]\sin^{−1}x=y[/latex].
For angles in the interval [0, π], if [latex]\cos y=x[/latex], then [latex]\cos^{−1}x=y[/latex].
For angles in the interval [latex]\left(−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right)[/latex], if [latex]\tan y=x[/latex], then [latex]\tan^{−1}x=y[/latex].
Example 1: Writing a Relation for an Inverse Function
Given [latex]\sin\left(\frac{5\pi}{12}\right)\approx 0.96593[/latex], write a relation involving the inverse sine.
Use the relation for the inverse sine. If [latex]\sin y=x[/latex], then [latex]\sin^{−1}x=y[/latex].
In this problem, [latex]x=0.96593[/latex], and [latex]y=\frac{5\pi}{12}[/latex].
[latex]\sin^{−1}(0.96593)\approx \frac{5\pi}{12}[/latex]
Given [latex]\cos(0.5)\approx 0.8776[/latex], write a relation involving the inverse cosine.
[latex]\arccos(0.8776)\approx0.5[/latex]
Finding the Exact Value of Expressions Involving the Inverse Sine, Cosine, and Tangent Functions
Now that we can identify inverse functions, we will learn to evaluate them. For most values in their domains, we must evaluate the inverse trigonometric functions by using a calculator, interpolating from a table, or using some other numerical technique. Just as we did with the original trigonometric functions, we can give exact values for the inverse functions when we are using the special angles, specifically [latex]\frac{\pi}{ 6} (30^\circ)\text{, }\frac{\pi}{ 4} (45^\circ),\text{ and } \frac{\pi}{ 3} (60^\circ)[/latex], and their reflections into other quadrants.
How To: Given a “special” input value, evaluate an inverse trigonometric function.
- Find angle x for which the original trigonometric function has an output equal to the given input for the inverse trigonometric function.
- If x is not in the defined range of the inverse, find another angle y that is in the defined range and has the same sine, cosine, or tangent as x , depending on which corresponds to the given inverse function.
Example 2: Evaluating Inverse Trigonometric Functions for Special Input Values
Evaluate each of the following.
a. [latex]\sin−1\left(\frac{1}{2}\right)[/latex]
b. [latex]\sin−1\left(−\frac{2}{\sqrt{2}}\right)[/latex]
c. [latex]\cos−1\left(−\frac{3}{\sqrt{2}}\right)[/latex]
d. [latex]\tan^{− 1}(1)[/latex]
a. Evaluating [latex]\sin^{−1}(\frac{1}{2})[/latex] is the same as determining the angle that would have a sine value of [latex]\frac{1}{2}[/latex]. In other words, what angle x would satisfy [latex]\sin(x)=\frac{1}{2}[/latex]? There are multiple values that would satisfy this relationship, such as [latex]\frac{\pi}{6}[/latex] and [latex]\frac{5\pi}{6}[/latex], but we know we need the angle in the interval [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right][/latex], so the answer will be [latex]\sin^{−1}(\frac{1}{2})=\frac{\pi}{6}[/latex]. Remember that the inverse is a function, so for each input, we will get exactly one output.
b. To evaluate [latex]\sin^{−1}\left(−\frac{\sqrt{2}}{2}\right)[/latex], we know that [latex]\frac{5\pi}{4}[/latex] and [latex]\frac{7\pi}{4}[/latex] both have a sine value of [latex]−\frac{\sqrt{2}}{2}[/latex], but neither is in the interval [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right][/latex]. For that, we need the negative angle coterminal with [latex]\frac{7\pi}{4}:\sin^{−1}\left(−\frac{\sqrt{2}}{2}\right)=−\frac{\pi}{4}[/latex].
c. To evaluate [latex]\cos^{−1}\left(−\frac{\sqrt{3}}{2}\right)[/latex], we are looking for an angle in the interval [0,π] with a cosine value of [latex]−\frac{\sqrt{3}}{2}[/latex]. The angle that satisfies this is [latex]\cos^{−1}\left(−\frac{\sqrt{3}}{2}\right)=\frac{5\pi}{6}[/latex].
d. Evaluating [latex]\tan^{−1}(1)[/latex], we are looking for an angle in the interval [latex](−\frac{\pi}{2}\text{, }\frac{\pi}{2})[/latex] with a tangent value of 1. The correct angle is [latex]\tan^{−1}(1)=\frac{\pi}{4}[/latex].
- [latex]\sin^{−1}(−1)[/latex]
- [latex]\tan^{−1}(−1)[/latex]
- [latex]\cos^{−1}(−1)[/latex]
- [latex]\cos^{−1}(\frac{1}{2})[/latex]
1. [latex]−\frac{\pi}{2}[/latex];
2. [latex]−\frac{\pi}{4}[/latex]
3. [latex]\pi[/latex]
4. [latex]\frac{\pi}{3}[/latex]
Using a Calculator to Evaluate Inverse Trigonometric Functions
To evaluate inverse trigonometric functions that do not involve the special angles discussed previously, we will need to use a calculator or other type of technology. Most scientific calculators and calculator-emulating applications have specific keys or buttons for the inverse sine, cosine, and tangent functions. These may be labeled, for example, SIN-1, ARCSIN, or ASIN.
In the previous chapter, we worked with trigonometry on a right triangle to solve for the sides of a triangle given one side and an additional angle. Using the inverse trigonometric functions, we can solve for the angles of a right triangle given two sides, and we can use a calculator to find the values to several decimal places.
In these examples and exercises, the answers will be interpreted as angles and we will use θ as the independent variable. The value displayed on the calculator may be in degrees or radians, so be sure to set the mode appropriate to the application.
Example 3: Evaluating the Inverse Sine on a Calculator
Evaluate [latex]\sin^{−1}(0.97)[/latex] using a calculator.
Because the output of the inverse function is an angle, the calculator will give us a degree value if in degree mode and a radian value if in radian mode. Calculators also use the same domain restrictions on the angles as we are using.
In radian mode, [latex]\sin^{−1}(0.97)\approx1.3252[/latex]. In degree mode, [latex]\sin^{−1}(0.97)\approx75.93^{\circ}[/latex]. Note that in calculus and beyond we will use radians in almost all cases.
Evaluate [latex]\cos^{−1}(−0.4)[/latex] using a calculator.
1.9823 or 113.578°
How To: Given two sides of a right triangle like the one shown in Figure 7, find an angle.
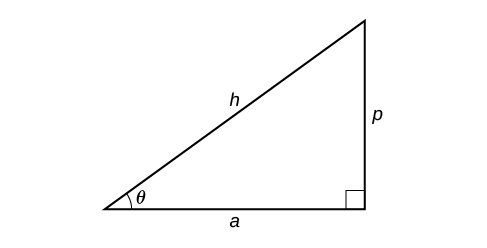
- If one given side is the hypotenuse of length h and the side of length a adjacent to the desired angle is given, use the equation [latex]\theta=\cos^{−1}\left(\frac{a}{h}\right)[/latex].
- If one given side is the hypotenuse of length h and the side of length p opposite to the desired angle is given, use the equation [latex]\theta=\sin^{−1}\left(\frac{p}{h}\right)[/latex].
- If the two legs (the sides adjacent to the right angle) are given, then use the equation [latex]\theta=\tan^{−1}\left(\frac{p}{a}\right)[/latex].
Example 4: Applying the Inverse Cosine to a Right Triangle
Solve the triangle in Figure 8 for the angle θ.
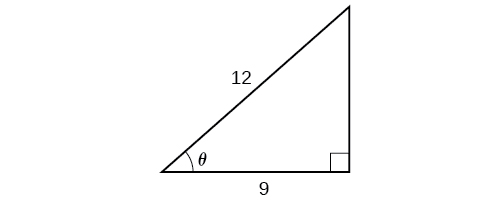
Because we know the hypotenuse and the side adjacent to the angle, it makes sense for us to use the cosine function.
[latex]\begin{align}&\cos\theta=\frac{9}{12}\\ &\theta=\cos^{−1}\left(\frac{9}{12}\right) && \text{Apply definition of the inverse.} \\ &\theta\approx0.7227\text{ or about }41.4096^{\circ} && \text{Evaluate.} \end{align}[/latex]
Solve the triangle in Figure 9 for the angle θ.
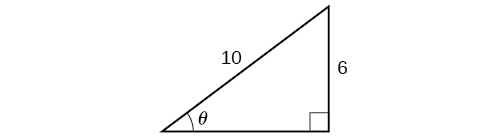
[latex]\sin^{−1}(0.6)=36.87^{\circ}=0.6435[/latex] radians
Finding Exact Values of Composite Functions with Inverse Trigonometric Functions
There are times when we need to compose a trigonometric function with an inverse trigonometric function. In these cases, we can usually find exact values for the resulting expressions without resorting to a calculator. Even when the input to the composite function is a variable or an expression, we can often find an expression for the output. To help sort out different cases, let f ( x ) and g ( x ) be two different trigonometric functions belonging to the set {sin( x ), cos( x ), tan( x )} and let [latex]f^{−1}(y)[/latex] and [latex]g^{−1}(y)[/latex] be their inverses.
Evaluating Compositions of the Form [latex]f\left(f^{−1}(y)\right)[/latex] and [latex]f^{−1}(f(x))[/latex]
For any trigonometric function, [latex]f(f^{−1}(y))=y[/latex] for all y in the proper domain for the given function. This follows from the definition of the inverse and from the fact that the range of f was defined to be identical to the domain of [latex]f^{−1}[/latex]. However, we have to be a little more careful with expressions of the form [latex]f^{−1}(f(x))[/latex].
A General Note: Compositions of a trigonometric function and its inverse
[latex]\begin{align} &\sin(\sin^{−1}x)=x\text{ for }−1\leq x\leq1\\ &\cos(\cos^{−1}x)=x\text{ for }−\infty\leq x\leq1 \\ &\tan(\tan^{−1}x)=x\text{ for }−\infty\text{ < }x\text{ < }\infty \end{align}[/latex]
[latex]\begin{align} \hfill &\sin^{−1}(\sin x)=x\text{ only for }−\frac{\pi}{2} \leq x \leq \frac{\pi}{2} \hfill \\ &\cos^{−1}(\cos x)=x\text{ only for }0\leq x\leq\pi \hfill \\ &\tan^{−1}(\tan x)=x\text{ only for }−\frac{\pi}{2}\text{ < }x\text{ < }\frac{\pi}{2} \end{align}[/latex]
Is it correct that [latex]\sin^{−1}(\sin x)=x[/latex]?
No. This equation is correct if x belongs to the restricted domain [latex]\left[−\frac{\pi}{2},\frac{\pi}{2}\right][/latex], but sine is defined for all real input values, and for x outside the restricted interval, the equation is not correct because its inverse always returns a value in [latex]\left[−\frac{\pi}{2},\frac{\pi}{2}\right][\latex] . The situation is similar for cosine and tangent and their inverses. For example, [latex]\sin^{−1}\left(\sin\left(\frac{3\pi}{4}\right)\right)=\frac{\pi}{4}[/latex].
Given an expression of the form [latex]f^{−1}(f(\theta))[/latex] where [latex]f(\theta)=\sin\theta\text{, }\cos\theta\text{, or }\tan\theta[/latex], evaluate.
- If θ is in the restricted domain of f , then [latex]f^{−1}(f(\theta))=\theta[/latex].
- If not, then find an angle ϕ within the restricted domain of f such that [latex]f(\phi)=f(\theta)[/latex]. Then [latex]f^{−1}(f(\theta))=\phi[/latex].
Example 5: Using Inverse Trigonometric Functions
Evaluate the following:
- [latex]\sin^{−1}(\sin(\frac{\pi}{3}))[/latex]
- [latex]\sin^{−1}(\sin(\frac{2\pi}{3}))[/latex]
- [latex]\cos^{−1}(\cos(\frac{2\pi}{3}))[/latex]
- [latex]\cos^{−1}(\cos(−\frac{\pi}{3}))[/latex]
- [latex]\frac{\pi}{3}[/latex] is in [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right][/latex], so [latex]\sin^{−1}(\sin(\frac{\pi}{3}))=\frac{\pi}{3}[/latex].
- [latex]\frac{2\pi}{3}[/latex] is not in [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right][/latex], but [latex]\sin\left(\frac{2\pi}{3}\right)=\sin\left(\frac{\pi}{3}\right)[/latex], so [latex]\sin^{−1}\left(\sin\left(\frac{2\pi}{3}\right)\right)=\frac{\pi}{3}[/latex].
- [latex]\frac{2\pi}{3}[/latex] is in [0,π], so [latex]\cos^{−1}\left(\cos\left(\frac{2\pi}{3}\right)\right)=\frac{2\pi}{3}[/latex].
- [latex]−\frac{\pi}{3}[/latex] is not in [0,π], but [latex]\cos(−\frac{\pi}{3})=\cos\left(\frac{\pi}{3}\right)[/latex] because cosine is an even function.
Evaluate [latex]\tan^{−1}\left(\tan\left(\frac{\pi}{8}\right)\right)[/latex] and [latex]\tan^{−1}\left(\tan\left(\frac{11\pi}{9}\right)\right)[/latex].
[latex]\frac{\pi}{8}\text{; }\frac{2\pi}{9}[/latex]
Evaluating Compositions of the Form [latex]f^{−1}(g(x))[/latex]
Now that we can compose a trigonometric function with its inverse, we can explore how to evaluate a composition of a trigonometric function and the inverse of another trigonometric function. We will begin with compositions of the form [latex]f^{−1}(g(x))[/latex]. For special values of x , we can exactly evaluate the inner function and then the outer, inverse function. However, we can find a more general approach by considering the relation between the two acute angles of a right triangle where one is θ, making the other [latex]\frac{\pi}{2}−\theta[/latex]. Consider the sine and cosine of each angle of the right triangle in Figure 10.
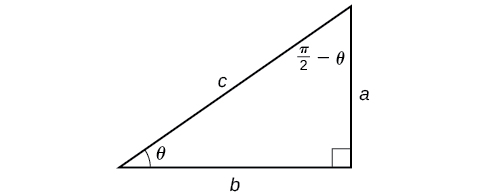
Figure 10. Right triangle illustrating the cofunction relationships
Because [latex]\cos\theta=\frac{b}{c}=\sin\left(\frac{\pi}{2}−\theta\right)[/latex], we have [latex]\sin^{−1}(\cos\theta)=\frac{\pi}{2}−\theta\text{ if }0\leq\theta\leq\pi[/latex]. If θ is not in this domain, then we need to find another angle that has the same cosine as θ and does belong to the restricted domain; we then subtract this angle from [latex]\frac{\pi}{2}[/latex]. Similarly, [latex]\sin\theta=\frac{a}{c}=\cos\left(\frac{\pi}{2}−\theta\right)[/latex], so [latex]\cos^{−1}(\sin\theta)=\frac{\pi}{2}−\theta\text{ if }−\frac{\pi}{2}\leq\theta\leq\frac{\pi}{2}[/latex]. These are just the function-cofunction relationships presented in another way.
How To: Given functions of the form [latex]\sin^{−1}(\cos x)\text{ and }\cos^{−1}(\sin x)[/latex], evaluate them.
- If x is in [0,π], then [latex]\sin^{−1}(\cos x)=\frac{\pi}{2}−x[/latex].
- If x is not in [0,π], then find another angle y in [0,π] such that [latex]\cos y=\cos x[/latex]. [latex]\sin^{−1}(\cos x)=\frac{\pi}{2}−y[/latex]
- If x is in [latex]\left[−\frac{\pi}{2},\frac{\pi}{2}\right][/latex], then [latex]\cos^{−1}(\sin x)=\frac{\pi}{2}−x[/latex].
- If x is not in [latex]\left[−\frac{\pi}{2},\frac{\pi}{2}\right][/latex], then find another angle y in [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right][/latex] such that [latex]\sin y=\sin x[/latex]. [latex]\cos^{−1}(\sin x)=\frac{\pi}{2}−y[/latex]
Example 6: Evaluating the Composition of an Inverse Sine with a Cosine
Evaluate [latex]\sin^{−1}(\cos(\frac{13\pi}{6}))[/latex]
- by direct evaluation.
- by the method described previously.
Now, we can evaluate the inverse function as we did earlier.
- We have [latex]x=\frac{13\pi}{6}[/latex], [latex]y=\frac{\pi}{6}[/latex], and [latex]\begin{align}\sin^{−1}\left(\cos\left(\frac{13\pi}{6}\right)\right)=\frac{\pi}{2}−\frac{\pi}{6} =\frac{\pi}{3} \end{align}[/latex]
Evaluate [latex]\cos^{−1}(\sin(−\frac{11\pi}{4}))[/latex].
[latex]\frac{3\pi}{4}[/latex]
Evaluating Compositions of the Form [latex]f(g^{−1}(x))[/latex]
To evaluate compositions of the form [latex]f(g^{−1}(x))[/latex], where f and g are any two of the functions sine, cosine, or tangent and x is any input in the domain of [latex]g−1[/latex], we have exact formulas, such as [latex]\sin\left({\cos}^{−1}x\right)=\sqrt{1−{x}^{2}}[/latex]. When we need to use them, we can derive these formulas by using the trigonometric relations between the angles and sides of a right triangle, together with the use of Pythagoras’s relation between the lengths of the sides. We can use the Pythagorean identity, [latex]\sin^{2}x+cos^{2}x=1[/latex], to solve for one when given the other. We can also use the inverse trigonometric functions to find compositions involving algebraic expressions.
Example 7: Evaluating the Composition of a Sine with an Inverse Cosine
Find an exact value for [latex]\sin\left(\cos^{−1}\left(\frac{4}{5}\right)\right)[/latex].
Beginning with the inside, we can say there is some angle such that [latex]\theta=\cos^{−1}(\frac{4}{5})[/latex], which means [latex]\cos\theta=\frac{4}{5}[/latex], and we are looking for [latex]\sin\theta[/latex]. We can use the Pythagorean identity to do this.
[latex]\begin{align} &\sin^{2}\theta+\cos^{2}\theta=1 && \text{Use our known value for cosine.} \\ &\sin^{2}\theta+\left(\frac{4}{5}\right)^{2}=1 && \text{Solve for sine.} \\ &\sin^{2}\theta=1−\frac{16}{25} \\ &\sin\theta=\pm\sqrt{\frac{9}{25}}=\pm\frac{3}{5} \end{align}[/latex]
Since [latex]\theta=\cos^{−1}(\frac{4}{5})[/latex] is in quadrant I, [latex]\sin{\theta}[/latex] must be positive, so the solution is [latex]\frac{3}{5}[/latex]. See Figure 11.
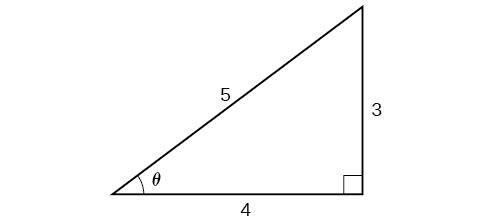
Figure 11. Right triangle illustrating that if [latex]\cos\theta=\frac{4}{5}[/latex], then [latex]\sin\theta=\frac{3}{5}[/latex]
We know that the inverse cosine always gives an angle on the interval [0, π], so we know that the sine of that angle must be positive; therefore [latex]\sin\left(\cos^{−1}\left(\frac{4}{5}\right)\right)=\sin\theta=\frac{3}{5}[/latex].
Evaluate [latex]\cos(\tan^{−1}(\frac{5}{12}))[/latex].
[latex]\frac{12}{13}[/latex]
Example 8: Evaluating the Composition of a Sine with an Inverse Tangent
Find an exact value for [latex]\sin\left(\tan^{−1}\left(\frac{7}{4}\right)\right)[/latex].
While we could use a similar technique as in Example 6, we will demonstrate a different technique here. From the inside, we know there is an angle such that [latex]\tan\theta=\frac{7}{4}[/latex]. We can envision this as the opposite and adjacent sides on a right triangle, as shown in Figure 12.
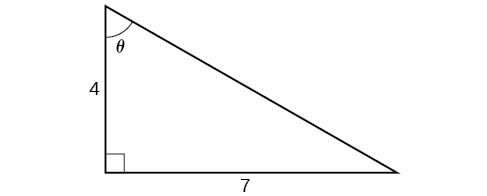
Figure 12. A right triangle with two sides known
Using the Pythagorean Theorem, we can find the hypotenuse of this triangle.
[latex]\begin{gathered}4^{2}+7^{2}=\text{hypotenuse}^{2} \\ \text{hypotenuse}=\sqrt{65} \end{gathered}[/latex]
Evaluate [latex]\cos(\sin^{−1}(\frac{7}{9}))[/latex].
[latex]\frac{4\sqrt{2}}{9}[/latex]

Example 9: Finding the Cosine of the Inverse Sine of an Algebraic Expression
Find a simplified expression for [latex]\cos\left(\sin^{−1}\left(\frac{x}{3}\right)\right)[/latex] for [latex]−3\leq x\leq3[/latex].
We know there is an angle θ such that [latex]\sin\theta=\frac{x}{3}\\[/latex]
[latex]\begin{align}&\sin^{2}\theta+\cos^{2}\theta=1 7&& \text{Use the Pythagorean Theorem.} \\ &\left(\frac{x}{3}\right)^{2}+\cos^{2}+\cos^2\theta=1 && \text{Solve for cosine.} \\ &\cos^{2}\theta=1−\frac{x^{2}}{9} \\ &\cos\theta=\pm\sqrt{\frac{9−x^{2}}{9}}=\pm\frac{\sqrt{9−x^{2}}}{3} \end{align}[/latex]
Because we know that the inverse sine must give an angle on the interval [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right][/latex], we can deduce that the cosine of that angle must be positive.
[latex]\cos\left(\sin^{−1}\left(\frac{x}{3}\right)\right)=\frac{\sqrt{9−x^{2}}}{3}[/latex]
Find a simplified expression for [latex]\sin\left(\tan^{−1}\left(4x\right)\right)\\[/latex] for [latex]−\frac{1}{4}\leq x \leq\frac{1}{4}[/latex].
[latex]\frac{4x}{\sqrt{16x^{2}+1}}[/latex]
Solving Linear Trigonometric Equations in Sine and Cosine
Trigonometric equations are, as the name implies, equations that involve trigonometric functions. Similar in many ways to solving polynomial equations or rational equations, only specific values of the variable will be solutions, if there are solutions at all. Often we will solve a trigonometric equation over a specified interval. However, just as often, we will be asked to find all possible solutions, and as trigonometric functions are periodic, solutions are repeated within each period. In other words, trigonometric equations may have an infinite number of solutions. Additionally, like rational equations, the domain of the function must be considered before we assume that any solution is valid. The period of both the sine function and the cosine function is [latex]2\pi [/latex]. In other words, every [latex]2\pi [/latex] units, the y- values repeat. If we need to find all possible solutions, then we must add [latex]2\pi k[/latex], where [latex]k[/latex] is an integer, to the initial solution. Recall the rule that gives the format for stating all possible solutions for a function where the period is [latex]2\pi :[/latex]
There are similar rules for indicating all possible solutions for the other trigonometric functions. Solving trigonometric equations requires the same techniques as solving algebraic equations. We read the equation from left to right, horizontally, like a sentence. We look for known patterns, factor, find common denominators, and substitute certain expressions with a variable to make solving a more straightforward process. However, with trigonometric equations, we also have the advantage of using the identities we developed in the previous sections.
Example 10: Solving a Linear Trigonometric Equation Involving the Cosine Function
Find all possible exact solutions for the equation [latex]\cos \theta =\frac{1}{2}[/latex].
From the unit circle , we know that
[latex]\begin{gathered}\cos \theta =\frac{1}{2} \\ \theta =\frac{\pi }{3},\frac{5\pi }{3} \end{gathered}[/latex]
These are the solutions in the interval [latex]\left[0,2\pi \right][/latex]. All possible solutions are given by
[latex]\theta =\frac{\pi }{3}\pm 2k\pi \text{ and }\theta =\frac{5\pi }{3}\pm 2k\pi [/latex]
where [latex]k[/latex] is an integer.
Example 11: Solving a Linear Equation Involving the Sine Function
Find all possible exact solutions for the equation [latex]\sin t=\frac{1}{2}[/latex].
Solving for all possible values of t means that solutions include angles beyond the period of [latex]2\pi [/latex]. From the unit circle, we can see that the solutions are [latex]t=\frac{\pi }{6}[/latex] and [latex]t=\frac{5\pi }{6}[/latex]. But the problem is asking for all possible values that solve the equation. Therefore, the answer is
[latex]t=\frac{\pi }{6}\pm 2\pi k\text{ and }t=\frac{5\pi }{6}\pm 2\pi k[/latex]
How To: Given a trigonometric equation, solve using algebra.
- Look for a pattern that suggests an algebraic property, such as the difference of squares or a factoring opportunity.
- Substitute the trigonometric expression with a single variable, such as [latex]x[/latex] or [latex]u[/latex].
- Solve the equation the same way an algebraic equation would be solved.
- Substitute the trigonometric expression back in for the variable in the resulting expressions.
- Solve for the angle.
Example 12: Solve the Trigonometric Equation in Linear Form
Solve the equation exactly: [latex]2\cos \theta -3=-5,0\le \theta <2\pi [/latex].
[latex]\begin{gathered}2\cos \theta -3=-5 \\ \cos \theta =-2 \\ \cos \theta =-1 \\ \theta =\pi \end{gathered}[/latex]
Solve exactly the following linear equation on the interval [latex]\left[0,2\pi \right):2\sin x+1=0[/latex].
[latex]x=\frac{7\pi }{6},\frac{11\pi }{6}[/latex]
Solve Trigonometric Equations Using a Calculator
Not all functions can be solved exactly using only the unit circle. When we must solve an equation involving an angle other than one of the special angles, we will need to use a calculator. Make sure it is set to the proper mode, either degrees or radians, depending on the criteria of the given problem.
Example 13: Using a Calculator to Solve a Trigonometric Equation Involving Sine
Use a calculator to solve the equation [latex]\sin \theta =0.8[/latex], where [latex]\theta [/latex] is in radians.
Make sure mode is set to radians. To find [latex]\theta [/latex], use the inverse sine function. On most calculators, you will need to push the 2 ND button and then the SIN button to bring up the [latex]{\sin }^{-1}[/latex] function. What is shown on the screen is [latex]{\sin}^{-1}[/latex](. The calculator is ready for the input within the parentheses. For this problem, we enter [latex]{\sin }^{-1}\left(0.8\right)[/latex], and press ENTER. Thus, to four decimals places,
[latex]{\sin }^{-1}\left(0.8\right)\approx 0.9273[/latex]
This is the solution in quadrant I. There is also a solution in quadrant II. To find this we subtract [latex]/pi - 0.9273 \approx 2.2143 [/latex]
The general solution is
[latex]\theta \approx 0.9273\pm 2\pi k \text{ and } \theta \approx 2.2143 \pm 2\pi k[/latex]
The angle measurement in degrees is
[latex]\begin{align} \theta &\approx {53.1}^{\circ } \\ \theta &\approx {180}^{\circ }-{53.1}^{\circ } \\ &\approx {126.9}^{\circ } \end{align}[/latex]
Analysis of the Solution
Note that a calculator will only return an angle in quadrants I or IV for the sine function, since that is the range of the inverse sine. The other angle is obtained by using [latex]\pi -\theta [/latex].
Example 14: Using a Calculator to Solve a Trigonometric Equation Involving Secant
Use a calculator to solve the equation [latex]\sec \theta =-4[/latex], giving your answer in radians.
We can begin with some algebra.
[latex]\begin{gathered}\sec \theta =-4\\ \frac{1}{\cos \theta }=-4\\ \cos \theta =-\frac{1}{4}\end{gathered}[/latex]
Check that the MODE is in radians. Now use the inverse cosine function.
[latex]\begin{gathered}{\cos }^{-1}\left(-\frac{1}{4}\right)\approx 1.8235 \\ \theta \approx 1.8235+2\pi k \end{gathered}[/latex]
Since [latex]\frac{\pi }{2}\approx 1.57[/latex] and [latex]\pi \approx 3.14[/latex], 1.8235 is between these two numbers, thus [latex]\theta \approx \text{1}\text{.8235}[/latex] is in quadrant II. Cosine is also negative in quadrant III. Note that a calculator will only return an angle in quadrants I or II for the cosine function, since that is the range of the inverse cosine.
So, we also need to find the measure of the angle in quadrant III. In quadrant III, the reference angle is [latex]\theta \text{ }\text{ }\text{‘}\approx \pi -\text{1}\text{.8235}\approx \text{1}\text{.3181}\text{.}[/latex] The other solution in quadrant III is [latex]\theta \text{ }\text{ }\text{‘}\approx \pi +\text{1}\text{.3181}\approx \text{4}\text{.4597}\text{.}[/latex]
The solutions are [latex]\theta \approx 1.8235\pm 2\pi k[/latex] and [latex]\theta \approx 4.4597\pm 2\pi k[/latex].
Solve [latex]\cos \theta =-0.2[/latex].
[latex]\theta \approx 1.7722\pm 2\pi k[/latex] and [latex]\theta \approx 4.5110\pm 2\pi k[/latex]
Solving Equations Involving a Single Trigonometric Function
When we are given equations that involve only one of the six trigonometric functions, their solutions involve using algebraic techniques and the unit circle. We need to make several considerations when the equation involves trigonometric functions other than sine and cosine. Problems involving the reciprocals of the primary trigonometric functions need to be viewed from an algebraic perspective. In other words, we will write the reciprocal function, and solve for the angles using the function. Also, an equation involving the tangent function is slightly different from one containing a sine or cosine function. First, as we know, the period of tangent is [latex]\pi [/latex], not [latex]2\pi [/latex]. Further, the domain of tangent is all real numbers with the exception of odd integer multiples of [latex]\frac{\pi }{2}[/latex], unless, of course, a problem places its own restrictions on the domain.
Example 15: Solving a Problem Involving a Single Trigonometric Function
Solve the problem exactly: [latex]2{\sin }^{2}\theta -1=0,0\le \theta <2\pi [/latex].
As this problem is not easily factored, we will solve using the square root property. First, we use algebra to isolate [latex]\sin \theta [/latex]. Then we will find the angles.
[latex]\begin{gathered}2{\sin }^{2}\theta -1=0 \\ 2{\sin }^{2}\theta =1 \\ {\sin }^{2}\theta =\frac{1}{2} \\ \sqrt{{\sin }^{2}\theta }=\pm \sqrt{\frac{1}{2}} \\ \sin \theta =\pm \frac{1}{\sqrt{2}}=\pm \frac{\sqrt{2}}{2} \\ \theta =\frac{\pi }{4},\frac{3\pi }{4},\frac{5\pi }{4},\frac{7\pi }{4} \end{gathered}[/latex]
Example 16: Solving a Trigonometric Equation Involving Cosecant
Solve the following equation exactly: [latex]\csc \theta =-2,0\le \theta <4\pi [/latex].
We want all values of [latex]\theta [/latex] for which [latex]\csc \theta =-2[/latex] over the interval [latex]0\le \theta <4\pi [/latex].
[latex]\begin{gathered}\csc \theta =-2 \\ \frac{1}{\sin \theta }=-2 \\ \sin \theta =-\frac{1}{2} \\ \theta =\frac{7\pi }{6},\frac{11\pi }{6},\frac{19\pi }{6},\frac{23\pi }{6} \end{gathered}[/latex]
As [latex]\sin \theta =-\frac{1}{2}[/latex], notice that all four solutions are in the third and fourth quadrants.
Example 17: Solving an Equation Involving Tangent
Solve the equation exactly: [latex]\tan \left(\theta -\frac{\pi }{2}\right)=1,0\le \theta <2\pi [/latex].
Recall that the tangent function has a period of [latex]\pi [/latex]. On the interval [latex]\left[0,\pi \right)[/latex], and at the angle of [latex]\frac{\pi }{4}[/latex], the tangent has a value of 1. However, the angle we want is [latex]\left(\theta -\frac{\pi }{2}\right)[/latex]. Thus, if [latex]\tan \left(\frac{\pi }{4}\right)=1[/latex], then
[latex]\begin{gathered}\theta -\frac{\pi }{2}=\frac{\pi }{4}\\ \theta =\frac{3\pi }{4}\pm k\pi \end{gathered}[/latex]
Over the interval [latex]\left[0,2\pi \right)[/latex], we have two solutions:
[latex]\theta =\frac{3\pi }{4}\text{ and }\theta =\frac{3\pi }{4}+\pi =\frac{7\pi }{4}[/latex]
Find all solutions for [latex]\tan x=\sqrt{3}[/latex].
[latex]\frac{\pi }{3}\pm \pi k[/latex]
Example 18: Identify all Solutions to the Equation Involving Tangent
Identify all exact solutions to the equation [latex]2\left(\tan x+3\right)=5+\tan x,0\le x<2\pi [/latex].
We can solve this equation using only algebra. Isolate the expression [latex]\tan x[/latex] on the left side of the equals sign.
[latex]\begin{gathered} 2\left(\tan x\right)+2\left(3\right) =5+\tan x \\ 2\tan x+6 =5+\tan x \\ 2\tan x-\tan x =5 - 6 \\ \tan x =-1\end{gathered}[/latex]
There are two angles on the unit circle that have a tangent value of [latex]-1:\theta =\frac{3\pi }{4}[/latex] and [latex]\theta =\frac{7\pi }{4}[/latex].
Solving Trigonometric Equations in Quadratic Form
Solving a quadratic equation may be more complicated, but once again, we can use algebra as we would for any quadratic equation. Look at the pattern of the equation. Is there more than one trigonometric function in the equation, or is there only one? Which trigonometric function is squared? If there is only one function represented and one of the terms is squared, think about the standard form of a quadratic. Replace the trigonometric function with a variable such as [latex]x[/latex] or [latex]u[/latex]. If substitution makes the equation look like a quadratic equation, then we can use the same methods for solving quadratics to solve the trigonometric equations.
Example 19: Solving a Trigonometric Equation in Quadratic Form
Solve the equation exactly: [latex]{\cos }^{2}\theta +3\cos \theta -1=0,0\le \theta <2\pi[/latex].
We begin by using substitution and replacing cos [latex]\theta[/latex] with [latex]x[/latex]. It is not necessary to use substitution, but it may make the problem easier to solve visually. Let [latex]\cos \theta =x[/latex]. We have
[latex]{x}^{2}+3x - 1=0[/latex]
The equation cannot be factored, so we will use the quadratic formula [latex]x=\frac{-b\pm \sqrt{{b}^{2}-4ac}}{2a}[/latex].
[latex]\begin{align} x&=\frac{-3\pm \sqrt{{\left(-3\right)}^{2}-4\left(1\right)\left(-1\right)}}{2}&=\frac{-3\pm \sqrt{13}}{2} \end{align}[/latex]
Replace [latex]x[/latex] with [latex]\cos \theta[/latex], and solve. Thus,
[latex]\begin{gathered} \cos \theta =\frac{-3\pm \sqrt{13}}{2}\theta ={\cos }^{-1}\left(\frac{-3+\sqrt{13}}{2}\right)\end{gathered}[/latex]
Note that only the + sign is used. This is because we get an error when we solve [latex]\theta ={\cos }^{-1}\left(\frac{-3-\sqrt{13}}{2}\right)[/latex] on a calculator, since the domain of the inverse cosine function is [latex]\left[-1,1\right][/latex]. However, there is a second solution:
[latex]\begin{align}\theta &={\cos }^{-1}\left(\frac{-3+\sqrt{13}}{2}\right) \\ &\approx 1.26 \end{align}[/latex]
This terminal side of the angle lies in quadrant I. Since cosine is also positive in quadrant IV, the second solution is
[latex]\begin{align}\theta &=2\pi -{\cos }^{-1}\left(\frac{-3+\sqrt{13}}{2}\right) \\ &\approx 5.02 \end{align}[/latex]
Example 20: Solving a Trigonometric Equation in Quadratic Form by Factoring
Solve the equation exactly: [latex]2{\sin }^{2}\theta -5\sin \theta +3=0,0\le \theta \le 2\pi[/latex].
Using grouping, this quadratic can be factored. Either make the real substitution, [latex]\sin \theta =u[/latex], or imagine it, as we factor:
[latex]\begin{gathered}2{\sin }^{2}\theta -5\sin \theta +3=0 \\ \left(2\sin \theta -3\right)\left(\sin \theta -1\right)=0 \end{gathered}[/latex]
Now set each factor equal to zero.
[latex]\begin{gathered}2\sin \theta -3=0 \\ 2\sin \theta =3 \\ \sin \theta =\frac{3}{2} \\ \text{ } \\ \sin \theta -1=0 \\ \sin \theta =1 \end{gathered}[/latex]
Next solve for [latex]\theta :\sin \theta \ne \frac{3}{2}[/latex], as the range of the sine function is [latex]\left[-1,1\right][/latex]. However, [latex]\sin \theta =1[/latex], giving the solution [latex]\theta =\frac{\pi }{2}[/latex].
Make sure to check all solutions on the given domain as some factors have no solution.
Solve [latex]{\sin }^{2}\theta =2\cos \theta +2,0\le \theta \le 2\pi[/latex]. [Hint: Make a substitution to express the equation only in terms of cosine.]
[latex]\cos \theta =-1,\theta =\pi [/latex]
Example 21: Solving a Trigonometric Equation Using Algebra
Solve exactly:
[latex]2{\sin }^{2}\theta +\sin \theta =0;0\le \theta <2\pi[/latex]
This problem should appear familiar as it is similar to a quadratic. Let [latex]\sin \theta =x[/latex]. The equation becomes [latex]2{x}^{2}+x=0[/latex]. We begin by factoring:
[latex]\begin{gathered}2{x}^{2}+x=0\\ x\left(2x+1\right)=0\end{gathered}[/latex]
Set each factor equal to zero.
[latex]\begin{gathered}x=0 \\ 2x+1=0 \\ x=-\frac{1}{2} \end{gathered}[/latex]
Then, substitute back into the equation the original expression [latex]\sin \theta[/latex] for [latex]x[/latex]. Thus,
[latex]\begin{gathered}\sin \theta =0 \\ \theta =0,\pi \\ \text{ } \\ \sin \theta =-\frac{1}{2} \\ \theta =\frac{7\pi }{6},\frac{11\pi }{6} \end{gathered}[/latex]
The solutions within the domain [latex]0\le \theta <2\pi[/latex] are [latex]\theta =0,\pi ,\frac{7\pi }{6},\frac{11\pi }{6}[/latex].
If we prefer not to substitute, we can solve the equation by following the same pattern of factoring and setting each factor equal to zero.
[latex]\begin{gathered}2{\sin }^{2}\theta +\sin \theta =0 \\ \sin \theta \left(2\sin \theta +1\right)=0 \\ \sin \theta =0 \\ \theta =0,\pi \\ \text{ } \\ 2\sin \theta +1=0 \\ 2\sin \theta =-1 \\ \sin \theta =-\frac{1}{2} \\ \theta =\frac{7\pi }{6},\frac{11\pi }{6} \end{gathered}[/latex]
We can see the solutions on the graph in Figure 3. On the interval [latex]0\le \theta <2\pi[/latex], the graph crosses the x- axis four times, at the solutions noted. Notice that trigonometric equations that are in quadratic form can yield up to four solutions instead of the expected two that are found with quadratic equations. In this example, each solution (angle) corresponding to a positive sine value will yield two angles that would result in that value.
We can verify the solutions on the unit circle in Sum and Difference Identities as well.
Example 22: Solving a Trigonometric Equation Quadratic in Form
Solve the equation quadratic in form exactly: [latex]2{\sin }^{2}\theta -3\sin \theta +1=0,0\le \theta <2\pi[/latex].
We can factor using grouping. Solution values of [latex]\theta[/latex] can be found on the unit circle:
[latex]\begin{gathered}\left(2\sin \theta -1\right)\left(\sin \theta -1\right)=0 \\ 2\sin \theta -1=0 \\ \sin \theta =\frac{1}{2} \\ \theta =\frac{\pi }{6},\frac{5\pi }{6} \\ \text{ } \\ \sin \theta =1 \\ \theta =\frac{\pi }{2} \end{gathered}[/latex]
Solve the quadratic equation [latex]2{\cos }^{2}\theta +\cos \theta =0[/latex].
[latex]\frac{\pi }{2},\frac{2\pi }{3},\frac{4\pi }{3},\frac{3\pi }{2}[/latex]
Key Concepts
- An inverse function is one that “undoes” another function. The domain of an inverse function is the range of the original function and the range of an inverse function is the domain of the original function.
- Because the trigonometric functions are not one-to-one on their natural domains, inverse trigonometric functions are defined for restricted domains.
- For any trigonometric function [latex]f(x)[/latex], if [latex]x=f^{−1}(y)[/latex], then [latex]f(x)=y[/latex]. However, [latex]f(x)=y[/latex] only implies [latex]x=f^{−1}(y)[/latex] if x is in the restricted domain of f .
- Special angles are the outputs of inverse trigonometric functions for special input values; for example, [latex]\frac{\pi}{4}=\tan^{−1}( 1 )\text{ and }\frac{\pi}{6}=\sin^{−1}(\frac{1}{2})[/latex].
- A calculator will return an angle within the restricted domain of the original trigonometric function.
- Inverse functions allow us to find an angle when given two sides of a right triangle.
- In function composition, if the inside function is an inverse trigonometric function, then there are exact expressions; for example, [latex]\sin\left(\cos^{−1}\left(x\right)\right)=\sqrt{1−x^{2}}[/latex].
- If the inside function is a trigonometric function, then the only possible combinations are [latex]\sin^{−1}\left(\cos x\right)=\frac{\pi}{2}−x[/latex] if [latex]0\leq x\leq\pi[/latex] and [latex]\cos^{−1}\left(\sin x\right)=\frac{\pi}{2}−x[/latex] if [latex]−\frac{\pi}{2}\leq x \leq\frac{\pi}{2}[/latex].
- When evaluating the composition of a trigonometric function with an inverse trigonometric function, draw a reference triangle to assist in determining the ratio of sides that represents the output of the trigonometric function.
- When evaluating the composition of a trigonometric function with an inverse trigonometric function, you may use trig identities to assist in determining the ratio of sides.
- When solving linear trigonometric equations, we can use algebraic techniques just as we do solving algebraic equations. Look for patterns, like the difference of squares, quadratic form, or an expression that lends itself well to substitution.
- Equations involving a single trigonometric function can be solved or verified using the unit circle.
- We can also solve trigonometric equations using a graphing calculator.
- Many equations appear quadratic in form. We can use substitution to make the equation appear simpler, and then use the same techniques we use solving an algebraic quadratic: factoring, the quadratic formula, etc.
- Precalculus. Authored by : OpenStax College. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:1/Preface . License : CC BY: Attribution
- Français
- Preparatory
Lesson Explainer: Solving Equations Using Inverse Trigonometric Functions Mathematics • First Year of Secondary School
Join nagwa classes.
Attend live Mathematics sessions on Nagwa Classes to learn more about this topic from an expert teacher!

- Remaining Seats: 13
In this explainer, we will learn how to solve equations by using inverse trigonometric functions in the first quadrant.
The first quadrant means we only consider acute angles 𝜃 , where 0 𝜃 9 0 ∘ ∘ or 0 𝜃 𝜋 2 in radians .
The inverse trigonometric functions have a number of real-world applications in many disciplines including engineering, navigation, physics, and geometry. For example, if you are doing carpentry and you want to make sure that the end of a piece of wood is cut at a particular angle, you can do this by measuring the sides and using an inverse trigonometric function to determine the angle. Or suppose you want to climb a mountain but do not want to climb up an elevation greater than a particular angle; you can measure the horizontal distance to the mountain from your starting position and the distance of your path up the mountain and use inverse trigonometric functions to ensure you do not exceed your maximum elevation angle or to determine which mountain to climb if you want to reach the top.
Before we talk about the inverse trigonometric functions, let’s begin by recalling the trigonometric functions, whose inverses we will examine in this explainer. Consider the right triangle shown.
The trigonometric functions can be expressed in terms of the ratio of the sides of the triangle as s i n O H c o s A H t a n O A 𝜃 = , 𝜃 = , 𝜃 = .
These functions satisfy the following trigonometric identities: s i n c o s t a n s i n c o s 𝜃 + 𝜃 ≡ 1 , 𝜃 ≡ 𝜃 𝜃 .
The domain (the set of possible inputs) and range (the set of possible outputs) of the trigonometric functions are beyond the scope of this explainer. We will only consider input values in the first quadrant for acute angles, for the trigonometric functions.
The common trigonometric values, in degrees and radians , are given in the following table.
| Angle | |||
|---|---|---|---|
| 1 |
We can remember these from the following special right triangles.
We can see the use of the inverse trigonometric functions by considering the following question. Suppose a 14 m ladder is placed against a wall. If the bottom of the ladder is 7 m away from the base of the wall, what angle does the bottom of the ladder make with the ground?
For this problem, the length of the hypotenuse side is 14 m and the length of the side adjacent to the angle 𝜃 is 7 m . Since cosine is the ratio between the lengths of the adjacent and hypotenuse in a right triangle, we have c o s A H m m 𝜃 = = 7 1 4 = 1 2 .
In order to find the angle 𝜃 , which is an acute angle, we can look up the common trigonometric values to see which value of 𝜃 satisfies this equation for c o s 𝜃 . Therefore, the angle made by the bottom of the ladder with the ground is given by 𝜃 = 6 0 , 𝜋 3 . ∘ o r r a d i a n s
In this problem, we found the angle just by inspecting different values of 𝜃 for the cosine function. We can then ask the question: what if 𝜃 is not a common trigonometric value that we can deduce by working backward? This is where we turn to the inverse trigonometric functions that essentially allow us to make 𝜃 the subject of the equation.
The sine, cosine, and tangent trigonometric functions are periodic functions. Their domains have to be restricted to a particular subset, known as the principle branch, in order to have inverse functions. This is not an issue in this explainer, since we restrict the domain to the first quadrant, 0 , 𝜋 2 in radians or ] 0 , 9 0 [ ∘ ∘ in degrees .
Definition: Inverse Trigonometric Functions
The inverse trigonometric functions denoted by s i n , c o s , and t a n are the inverse functions of the trigonometric functions s i n , c o s , and t a n . This means they work in reverse or “go backward” from the usual trigonometric functions. For acute angles, 𝑦 ∈ 0 , 𝜋 2 in radians or 𝑦 ∈ ] 0 , 9 0 [ ∘ ∘ in degrees ; they are defined by 𝑦 = 𝑥 ⟺ 𝑥 = 𝑦 , 𝑦 = 𝑥 ⟺ 𝑥 = 𝑦 , 𝑦 = 𝑥 ⟺ 𝑥 = 𝑦 . s i n s i n c o s c o s t a n t a n
These can also be written as a r c s i n 𝑥 , a r c c o s 𝑥 , and a r c t a n 𝑥 .
For example, if we have s i n ( 3 0 ) = 1 2 ∘ , then this is equivalent to s i n ∘ 1 2 = 3 0 . (The inverse of a function, 𝑓 ( 𝑥 ) , can also be denoted as 𝑓 ( 𝑥 ) , so if 𝑥 = 𝑓 ( 𝑦 ) = 𝑦 s i n , then 𝑦 = 𝑓 ( 𝑥 ) = 𝑥 s i n , and vice versa. This will be covered in more detail in another explainer on inverse functions in general.)
From the definition of the inverse function and for acute angles 𝜃 ∈ 0 , 𝜋 2 in radians or ] 0 , 9 0 [ ∘ ∘ in degrees , the inverse trigonometric functions satisfy the properties s i n s i n c o s c o s t a n t a n ( 𝜃 ) = 𝜃 , ( 𝜃 ) = 𝜃 , ( 𝜃 ) = 𝜃 .
The input and output values are interchanged for the inverse trigonometric functions from the usual trigonometric functions. For the inverse trigonometric functions, we only consider output values in the first quadrant for acute angles, corresponding to the input values of the trigonometric functions which we mentioned earlier.
We can also express the angle 𝜃 in our right triangle in terms of the given sides by using the inverse trigonometric functions: s i n O H s i n s i n s i n O H s i n O H 𝜃 = , ( 𝜃 ) = , 𝜃 = , and similarly for the other expressions: 𝜃 = , 𝜃 = . c o s A H t a n O A
For our problem with the ladder, we could have used the inverse cosine function to find the angle 𝜃 in a similar way: c o s c o s c o s c o s c o s 𝜃 = 1 2 , ( 𝜃 ) = 1 2 , 𝜃 = 1 2 , 𝜃 = 6 0 . ∘
By using the table for trigonometric values in reverse, we can also create a table for the common inverse trigonometric values as follows.
| 1 | |||
|---|---|---|---|
These types of problems can be solved for any acute angle and not just those given by the common values. Suppose we want to solve the equation 3 𝜃 − 2 . 9 4 6 = 0 , s i n to determine the acute angle 𝜃 to the nearest degree . We begin by rearranging the equation to isolate s i n 𝜃 : 3 𝜃 − 2 . 9 4 6 = 0 3 𝜃 = 2 . 9 4 6 𝜃 = 2 . 9 4 6 3 𝜃 = 0 . 9 8 2 . s i n s i n s i n s i n
Now, we apply the inverse sine function, s i n , to make 𝜃 subject: s i n s i n s i n ∘ ( 𝜃 ) = ( 0 . 9 8 2 ) 𝜃 = 7 9 . 1 1 2 5 … .
We obtained the value of s i n ( 0 . 9 8 2 ) by using the a r c s i n function on a calculator, set to degrees mode. Therefore, to the nearest degree , we have 𝜃 = 7 9 . ∘
Now, suppose for an acute angle 𝑋 measured in radians we want to solve the equation 2 √ 3 𝑋 − 2 𝑋 = 0 . s i n c o s
We want to find the value of 𝑋 , in radians , such that this equation is satisfied. We begin by rearranging the equation and using a trigonometric identity to rewrite the expression in terms of t a n 𝑋 : 2 √ 3 𝑋 − 2 𝑋 = 0 2 √ 3 𝑋 = 2 𝑋 𝑋 = 1 √ 3 𝑋 𝑋 𝑋 = 1 √ 3 𝑋 = √ 3 3 . s i n c o s s i n c o s s i n c o s s i n c o s t a n
Finally, we apply the inverse tangent function, a r c t a n , to make 𝑋 the subject and find the appropriate value from the table of common angles or using the a r c t a n function on a calculator, set to radians mode: t a n t a n t a n ( 𝑋 ) = √ 3 3 , 𝑋 = 𝜋 6 .
We will now look at a few examples to practice and deepen our understanding.
For the first example, we will apply the inverse sine function to determine a particular angle, in degrees , to the nearest tenth of a degree .
Example 1: Using Inverse Trigonometric Functions to Solve a Trigonometric Equation
Given that 𝐴 is an acute angle and that s i n 𝐴 = 0 . 8 1 9 3 , determine 𝑚 ∠ A to the nearest tenth of a degree .
In this example, we want to determine an angle using the inverse sine function, to the nearest tenth of a degree .
In particular, we will make use of the sine property for acute angles, 𝑥 ∈ ] 0 , 9 0 [ ∘ ∘ : s i n s i n ( 𝑥 ) = 𝑥 .
We begin by taking the inverse sine function s i n of both sides of the equation: s i n s i n s i n s i n 𝐴 = 0 . 8 1 9 3 ( 𝐴 ) = ( 0 . 8 1 9 3 ) 𝐴 = 5 5 . 0 1 4 7 … . ∘
We obtained the value of s i n ( 0 . 8 1 9 3 ) by using the a r c s i n function on a calculator, set to degrees mode.
Therefore, to the nearest tenth of a degree , 𝑚 ∠ 𝐴 = 5 5 . 0 . ∘
In our next example, we will use the inverse cosine function to determine a particular angle in radians .
Example 2: Using Inverse Trigonometric Functions to Solve Trigonometric Equations Involving Special Angles
Given that 𝑥 is an acute angle and 4 ( 𝑥 ) = 2 √ 3 c o s , determine the value of 𝑥 in radians .
In this example, we want to determine an angle using the inverse cosine function, in radians .
In particular, we will make use of the cosine property for acute angles, 𝑥 ∈ 0 , 𝜋 2 : c o s c o s ( ( 𝑥 ) ) = 𝑥 .
We begin by rearranging the equation to make c o s ( 𝑥 ) the subject: 4 ( 𝑥 ) = 2 √ 3 ( 𝑥 ) = 2 √ 3 4 ( 𝑥 ) = √ 3 2 . c o s c o s c o s
Now, we apply the inverse cosine function c o s to both sides of the equation and use the table of common angles or the a r c c o s function on a calculator, set to radians mode, to determine the value of 𝑥 : c o s c o s c o s ( ( 𝑥 ) ) = √ 3 2 𝑥 = 𝜋 6 .
In our next example, we will use the inverse cosine function again to determine a particular angle, but this time in degrees by using the knowledge of the tangent of a common angle.
Example 3: Using Inverse Trigonometric Functions to Solve Trigonometric Equations Involving Special Angles
Find the measure of ∠ 𝑋 in degrees given 2 𝑋 = 6 0 c o s t a n ∘ where 𝑋 is an acute angle.
In this example, we want to determine an angle using the inverse cosine function.
In particular, we will make use of the cosine property for acute angles, 𝑥 ∈ ] 0 , 9 0 [ ∘ ∘ : c o s c o s ( 𝑥 ) = 𝑥 .
First note that t a n 6 0 = √ 3 ∘ . We begin by rearranging the equation to isolate c o s 𝑋 : 2 𝑋 = √ 3 𝑋 = √ 3 2 . c o s c o s
Now, we apply the inverse cosine function c o s to both sides of the equation and use the table of common angles or the a r c c o s function on a calculator, set to degrees mode, to determine the value of 𝑋 : c o s c o s c o s ∘ ( 𝑋 ) = √ 3 2 𝑋 = 3 0 .
In our next example, we will use the inverse tangent function to determine a particular angle and give our answer to the nearest second .
Example 4: Using Inverse Trigonometric Functions to Solve Trigonometric Equations
Find 𝑚 ∠ 𝐸 given t a n 𝐸 = 1 8 . 5 8 4 5 and ∠ 𝐸 is an acute angle. Give the answer to the nearest second .
In this example, we want to determine an angle using the inverse tangent function to the nearest second .
In particular, we will make use of the tangent property for acute angles, 𝑥 ∈ ] 0 , 9 0 [ ∘ ∘ : t a n t a n ( 𝑥 ) = 𝑥 .
We begin by taking the inverse tangent function of both sides of the equation: t a n t a n t a n t a n 𝐸 = 1 8 . 5 8 4 5 ( 𝐸 ) = ( 1 8 . 5 8 4 5 ) 𝐸 = 8 6 . 9 1 9 9 … . ∘
We obtained the value of t a n ( 1 8 . 5 8 4 5 ) by using the a r c t a n function on a calculator, set to degrees mode.
Now, we convert this angle into the right form by expressing it as 8 6 . 9 1 9 9 8 2 8 6 … = 8 6 + 5 5 6 0 + 1 1 . 9 3 8 2 … 6 0 = 8 6 5 5 ′ 1 1 . 9 3 8 2 … ′ ′ . ∘ ∘
Therefore, to the nearest second , we have 𝑚 ∠ 𝐸 = 8 6 5 5 ′ 1 2 ′ ′ . ∘
In our next example, we will use the inverse tangent and inverse cosine functions to solve two equations involving trigonometric functions.
Example 5: Solving Trigonometric Equations Involving Multiple Trigonometric Functions and Special Angles
Find the smallest positive angle that satisfies both 2 𝜃 − √ 2 = 0 c o s and t a n 𝜃 − 1 = 0 .
In this example, we want to solve a pair of equations by using the inverse cosine and tangent functions.
Since we are looking for the smallest positive angle solving these equations, let’s begin by looking for acute solutions. In particular, we will make use of the cosine and tangent property for acute angles, 𝑥 ∈ ] 0 , 9 0 [ ∘ ∘ : c o s c o s t a n t a n ( 𝑥 ) = 𝑥 , ( 𝑥 ) = 𝑥 .
We begin by rearranging the first equation to make c o s 𝜃 the subject of the equation: 2 𝜃 − √ 2 = 0 2 𝜃 = √ 2 𝜃 = √ 2 2 . c o s c o s c o s
Now, we can take the inverse cosine function c o s of both sides of the equation and use the table of common angles or the a r c c o s function on a calculator, set to degrees mode, to determine the value of 𝜃 : c o s c o s c o s ∘ ( 𝜃 ) = √ 2 2 𝜃 = 4 5 .
We now check that this satisfies the second condition by substituting 𝜃 = 4 5 ∘ into the second equation to check that it is satisfied, or we determine the angle directly from the second equation. For the latter, we begin by rearranging the equation to isolate t a n 𝜃 : t a n t a n 𝜃 − 1 = 0 𝜃 = 1 .
Next, we apply the inverse tangent function t a n to both sides of the equation and use the table for the common angles or the a r c t a n function on a calculator, set to degrees mode, to determine the angle 𝜃 : t a n t a n t a n ∘ ( 𝜃 ) = ( 1 ) 𝜃 = 4 5 .
Thus, the smallest positive angle that satisfies both 2 𝜃 − √ 2 = 0 c o s and t a n 𝜃 − 1 = 0 is 𝜃 = 4 5 . ∘
In our next example, we will use the inverse cosine function to determine a particular angle different from the common angles, in radians .
Example 6: Using Inverse Trigonometric Functions to Solve Trigonometric Equations Involving Special Angles
Given that 𝑥 is an acute angle and 2 √ 2 ( 𝑥 ) = 1 + √ 3 c o s , determine the value of 𝑥 in radians .
In this example, we want to determine the value of an acute angle using the inverse cosine function, in radians .
We begin by rearranging the equation to make c o s ( 𝑥 ) the subject: 2 √ 2 ( 𝑥 ) = 1 + √ 3 ( 𝑥 ) = 1 + √ 3 2 √ 2 . c o s c o s
Now, we apply the inverse tangent function c o s to both sides of the equation and use the a r c c o s function on a calculator, set to radians mode, to determine the angle 𝑥 : c o s c o s c o s ( ( 𝑥 ) ) = 1 + √ 3 2 √ 2 𝑥 = 𝜋 1 2 .
In our final example, we will use the inverse tangent function to determine a particular angle.
Example 7: Using Inverse Trigonometric Functions to Solve Trigonometric Equations Involving Special Angles
Find the value of 𝑋 given t a n 𝑋 4 = √ 3 where 𝑋 4 is an acute angle.
In this example, we want to determine an angle using the inverse tangent function.
We begin by taking the inverse tangent function, t a n , of both sides of the equation and use the table for the common angles or the a r c t a n function on a calculator, set to degrees mode, to determine the acute angle 𝑋 4 : t a n t a n t a n t a n 𝑋 4 = √ 3 𝑋 4 = √ 3 𝑋 4 = 6 0 . ∘
Therefore, the value of 𝑋 is given by 𝑋 = 2 4 0 . ∘
- We can use the inverse trigonometric functions s i n , c o s , and t a n to solve trigonometric equations.
- For some values of s i n 𝜃 , c o s 𝜃 , or t a n 𝜃 , where 𝜃 is an acute angle, we can use the inverse trigonometric functions to find the missing angle in degrees or radians .
- The key properties to solve these problems for acute angles 𝜃 ∈ ] 0 , 9 0 [ ∘ ∘ in degrees or 𝜃 ∈ 0 , 𝜋 2 in radians are s i n s i n c o s c o s t a n t a n ( 𝜃 ) = 𝜃 , ( 𝜃 ) = 𝜃 , ( 𝜃 ) = 𝜃 .
Attend live sessions on Nagwa Classes to boost your learning with guidance and advice from an expert teacher!
- Interactive Sessions
- Chat & Messaging
- Realistic Exam Questions

Nagwa uses cookies to ensure you get the best experience on our website. Learn more about our Privacy Policy

- Math Forum/Help
- Problem Solver
- College Math
- Inverse Trigonometric Functions
Inverse Trigonometric Functions: Problems with Solutions
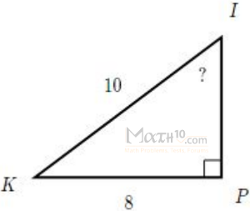
- Math Article
Inverse Trigonometric Functions

Inverse trigonometric functions are defined as the inverse functions of the basic trigonometric functions, which are sine, cosine, tangent, cotangent, secant and cosecant functions. They are also termed arcus functions, antitrigonometric functions or cyclometric functions. These inverse functions in trigonometry are used to get the angle with any of the trigonometry ratios . The inverse trigonometry functions have major applications in the field of engineering, physics, geometry and navigation.
Table of Contents
- Derivatives
What Are Inverse Trigonometric Functions?
Inverse trigonometric functions are also called “ arc functions ” since, for a given value of trigonometric functions, they produce the length of arc needed to obtain that particular value. The inverse trigonometric functions perform the opposite operation of the trigonometric functions such as sine, cosine, tangent, cosecant, secant and cotangent. We know that trigonometric functions are applicable, especially to the right-angle triangle. These six important functions are used to find the angle measure in the right-angle triangle when two sides of the triangle measures are known.
The basic inverse trigonometric formulas are as follows:
| Arcsine | sin (-x) = -sin (x), x ∈ [-1, 1] |
| Arccosine | cos (-x) = π -cos (x), x ∈ [-1, 1] |
| Arctangent | tan (-x) = -tan (x), x ∈ R |
| Arccotangent | cot (-x) = π – cot (x), x ∈ R |
| Arcsecant | sec (-x) = π -sec (x), |x| ≥ 1 |
| Arccosecant | cosec (-x) = -cosec (x), |x| ≥ 1 |
Inverse Trigonometric Functions Graphs
There are particularly six inverse trig functions for each trigonometry ratio . The inverse of six important trigonometric functions are
- Arccotangent
- Arccosecant
Let us discuss all six important types of inverse trigonometric functions, along with its definition, formulas, graphs, properties and solved examples.
Arcsine Function
The arcsine function is an inverse of the sine function denoted by sin -1 x . It is represented in the graph as shown below.
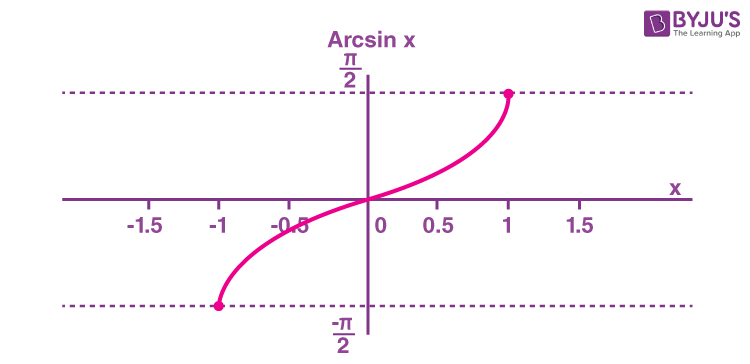
| -1 ≤ x ≤ 1 | |
| -π/2 ≤ y ≤ π/2 |
Arccosine Function
The arccosine function is the inverse of the cosine function denoted by cos -1 x . It is represented in the graph as shown below.
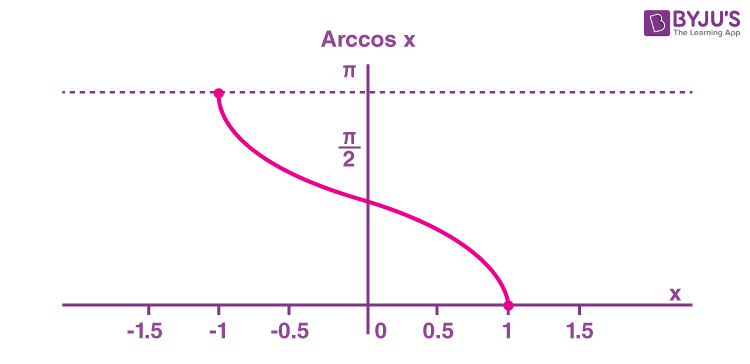
Therefore, the inverse of the cos function can be expressed as y = cos -1 x (arccosine x )
Domain and range of arcsine function are as follows:
| -1≤x≤1 | |
| 0 ≤ y ≤ π |
Arctangent Function
The arctangent function is the inverse of the tangent function denoted by tan -1 x . It is represented in the graph as shown below.
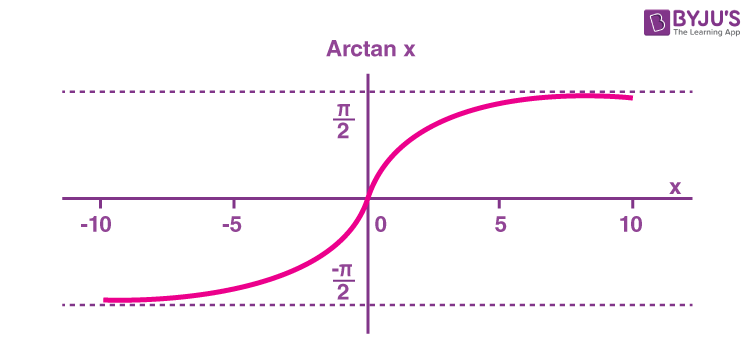
Therefore, the inverse of the tangent function can be expressed as y = tan -1 x (arctangent x )
Domain and range of arctangent are as follows:
| -∞ < x < ∞ | |
| -π/2 < y < π/2 |
Arccotangent (Arccot) Function
The arccotangent function is the inverse of the cotangent function denoted by cot -1 x .
Therefore, the inverse of the cotangent function can be expressed as y = cot -1 x (arccotangent x )
Domain and range of arccotangent are as follows:
| -∞ < x < ∞ | |
| 0 < y < π |
Arcsecant Function
What is the arcsecant (arcsec) function? The arcsecant function is the inverse of the secant function denoted by sec -1 x . It is represented in the graph as shown below.
Therefore, the inverse of the secant function can be expressed as y = sec -1 x (arcsecant x )
Domain and range of arcsecant are as follows:
| -∞ ≤ x ≤ -1 or 1 ≤ x ≤ ∞ | |
| 0 ≤ y ≤ π, y ≠ π/2 |
Arccosecant Function
What is the arccosecant (arccsc x ) function? The arccosecant function is the inverse of the cosecant function denoted by cosec -1 x . It is represented in the graph as shown below.
Therefore, the inverse of the cosecant function can be expressed as y = cosec -1 x (arccosecant x )
Domain and range of arccosecant are:
| -∞ ≤ x ≤ -1 or 1 ≤ x ≤ ∞ | |
| -π/2 ≤ y ≤ π/2, y ≠ 0 |
Inverse Trigonometric Functions Table
Let us look at all the inverse trigonometric functions with their notation, definition, domain and range.
| Arcsine or inverse sine | y = sin (x) | x=sin y | −1 ≤ x ≤ 1 | °≤ y ≤ 90° |
| Arccosine or inverse cosine | y=cos (x) | x=cos y | −1 ≤ x ≤ 1 | |
| Arctangent or inverse tangent | y=tan (x) | x=tan y | For all real numbers | °< y < 90° |
| Arccotangent or inverse cot | y=cot (x) | x=cot y | For all real numbers | |
| Arcsecant or inverse secant | y = sec (x) | x=sec y | x ≤ −1 or 1 ≤ x | |
| Arccosecant | y=csc (x) | x=csc y | x ≤ −1 or 1 ≤ x |
Inverse Trigonometric Functions Derivatives
The derivatives of inverse trigonometric functions are first-order derivatives. Let us check out the derivatives of all six inverse functions here.
| y = sin (x) | 1/√(1-x ) |
| y = cos (x) | -1/√(1-x ) |
| y = tan (x) | 1/(1+x ) |
| y = cot (x) | -1/(1+x ) |
| y = sec (x) | 1/[|x|√(x -1)] |
| y = csc (x) | -1/[|x|√(x -1)] |
Learn in detail the derivation of these functions here: Derivative Inverse Trigonometric Functions
Inverse Trigonometric Functions Properties
The inverse trigonometric functions are also known as arc functions. Inverse trigonometric functions are defined in a certain interval (under restricted domains). Read more on inverse trigonometric properties here .
Trigonometry Basics
Trigonometry basics include the basic trigonometry and trigonometric ratios, such as sin x, cos x, tan x, cosec x, sec x and cot x.
Video Lessons on Inverse Trigonometric Functions

Multiple Angles

Inverse Trigonometric Functions Problems
Example 1: Find the value of x for sin(x) = 2.
Solution: Given: sin x = 2
x =sin -1 (2), which is not possible.
Hence, there is no value of x for which sin x = 2, so the domain of sin -1 x is -1 to 1 for the values of x.
Example 2: Find the value of sin -1 (sin (π/6)).
sin -1 (sin (π/6) = π/6 (Using identity sin -1 (sin (x) ) = x)
Example 3: Find sin (cos -1 3/5).
Suppose that, cos -1 3/5 = x
So, cos x = 3/5
This implies, sin x = sin (cos -1 3/5) = 4/5
Example 4:
Practice Problems
Problem 1: Solve: tan(arcsin 12/13)
Problem 2: Find the value of x, cos(arccos 1) = cos x
Learn more about inverse trigonometric functions at BYJU’S. Download BYJU’S – The Learning App for other Maths-related articles and access various interactive videos to make the subject easy.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz
Visit BYJU’S for all Maths related queries and study materials
Your result is as below
Request OTP on Voice Call
| MATHS Related Links | |
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Post My Comment
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
Inverse trigonometric function
An Inverse trigonometric function is an inverse function of trigonometric functions, such as sin and cosine.
Something appears to not have loaded correctly.
Click to refresh .
- Problems on Inverse Trigonometric Function
We will solve different types of problems on inverse trigonometric function.
1. Find the values of sin (cos\(^{-1}\) 3/5)
Solution:
Let, cos\(^{-1}\) 3/5 = θ
Therefore, cos θ = 3/5
Therefore, sin θ = √(1 - cos\(^{2}\) θ) = √(1 - 9/25) = √(16/25) = 4/5 .
Therefore, sin (cos\(^{-1}\) 3/5) = sin θ = 4/5.
2. Find the values of tan\(^{-1}\) sin (- π/2)
tan\(^{-1}\) sin (- π/2)
= tan\(^{-1}\) (- sin π/2)
= tan\(^{-1}\) (- 1), [Since - sin π/2 = -1]
= tan\(^{-1}\)(- tan π/4), [Since tan π/4 = 1]
= tan\(^{-1}\) tan (-π/4)
= - π/4.
Therefore, tan\(^{-1}\) sin (- π/2) = - π/4
3. Evaluate: sin\(^{-1}\) (sin 10)
We know that sin\(^{-1}\) (sin θ) = θ, if - \(\frac{π}{2}\) ≤ θ ≤ \(\frac{π}{2}\).
Here, θ = 10 radians which does not lie between - \(\frac{π}{2}\) and \(\frac{π}{2}\). But 3π - θ i.e., 3π - 10 lies between - \(\frac{π}{2}\) and \(\frac{π}{2}\) and sin (3π - 10) = sin 10.
Now, sin\(^{-1}\) (sin 10)
= sin^-1 (sin (3π - 10)
Therefore, sin\(^{-1}\) (sin 10) = 3π - 10.
4. Find the values of cos (tan\(^{-1}\) ¾)
Let, tan\(^{-1}\) ¾ = θ
Therefore, tan θ = ¾
We know that sec\(^{2}\) θ - tan\(^{2}\) θ = 1
⇒ sec θ = √(1 + tan\(^{2}\) θ)
⇒ sec θ = √(1 + (3/4)\(^{2}\))
⇒ sec θ = √(1 + 9/16)
⇒ sec θ = √(25/16)
⇒ sec θ = 5/4
Therefore, cos θ = 4/5
⇒ θ = cos\(^{-1}\) 4/5
Now, cos (tan\(^{-1}\) ¾) = cos (cos\(^{-1}\) 4/5) = 4/5
Therefore, cos (tan\(^{-1}\) ¾) = 4/5
5. Find the values of sec csc\(^{-1}\) (2/√3)
sec csc\(^{-1}\) (2/√3)
= sec csc\(^{-1}\) (csc π/3)
= sec (csc\(^{-1}\)csc π/3)
Therefore, sec csc\(^{-1}\) (2/√3) = 2
● Inverse Trigonometric Functions
- General and Principal Values of sin\(^{-1}\) x
- General and Principal Values of cos\(^{-1}\) x
- General and Principal Values of tan\(^{-1}\) x
- General and Principal Values of csc\(^{-1}\) x
- General and Principal Values of sec\(^{-1}\) x
- General and Principal Values of cot\(^{-1}\) x
- Principal Values of Inverse Trigonometric Functions
- General Values of Inverse Trigonometric Functions
- arcsin(x) + arccos(x) = \(\frac{π}{2}\)
- arctan(x) + arccot(x) = \(\frac{π}{2}\)
- arctan(x) + arctan(y) = arctan(\(\frac{x + y}{1 - xy}\))
- arctan(x) - arctan(y) = arctan(\(\frac{x - y}{1 + xy}\))
- arctan(x) + arctan(y) + arctan(z)= arctan\(\frac{x + y + z – xyz}{1 – xy – yz – zx}\)
- arccot(x) + arccot(y) = arccot(\(\frac{xy - 1}{y + x}\))
- arccot(x) - arccot(y) = arccot(\(\frac{xy + 1}{y - x}\))
- arcsin(x) + arcsin(y) = arcsin(x \(\sqrt{1 - y^{2}}\) + y\(\sqrt{1 - x^{2}}\))
- arcsin (x) - arcsin(y) = arcsin (x \(\sqrt{1 - y^{2}}\) - y\(\sqrt{1 - x^{2}}\))
- arccos (x) + arccos(y) = arccos(xy - \(\sqrt{1 - x^{2}}\)\(\sqrt{1 - y^{2}}\))
- arccos(x) - arccos(y) = arccos(xy + \(\sqrt{1 - x^{2}}\)\(\sqrt{1 - y^{2}}\))
- 2 arcsin(x) = arcsin(2x\(\sqrt{1 - x^{2}}\))
- 2 arccos(x) = arccos(2x\(^{2}\) - 1)
- 2 arctan(x) = arctan(\(\frac{2x}{1 - x^{2}}\)) = arcsin(\(\frac{2x}{1 + x^{2}}\)) = arccos(\(\frac{1 - x^{2}}{1 + x^{2}}\))
- 3 arcsin(x) = arcsin(3x - 4x\(^{3}\))
- 3 arccos(x) = arccos(4x\(^{3}\) - 3x)
- 3 arctan(x) = arctan(\(\frac{3x - x^{3}}{1 - 3 x^{2}}\))
- Inverse Trigonometric Function Formula
11 and 12 Grade Math From Problems on Inverse Trigonometric Function to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.
New! Comments
Share this page: What’s this?
- Preschool Activities
- Kindergarten Math
- 1st Grade Math
- 2nd Grade Math
- 3rd Grade Math
- 4th Grade Math
- 5th Grade Math
- 6th Grade Math
- 7th Grade Math
- 8th Grade Math
- 9th Grade Math
- 10th Grade Math
- 11 & 12 Grade Math
- Concepts of Sets
- Probability
- Boolean Algebra
- Math Coloring Pages
- Multiplication Table
- Cool Maths Games
- Math Flash Cards
- Online Math Quiz
- Math Puzzles
- Binary System
- Math Dictionary
- Conversion Chart
- Homework Sheets
- Math Problem Ans
- Free Math Answers
- Printable Math Sheet
- Funny Math Answers
- Employment Test
- Math Patterns
- Link Partners
- Privacy Policy
| E-mail Address | |
| First Name | |
| to send you Math Only Math. |
Recent Articles
5th grade geometry worksheet | angles | triangles | classification.
Aug 23, 24 02:58 PM

Worksheet on Word Problems on Percentage | Real Life Problems on Per
Aug 23, 24 10:21 AM
Data Handling | Data Analysis | Data Processing | Numerical Data | Def
Aug 23, 24 02:28 AM
Construction of Angles by using Compass, Construction of Angles
Aug 22, 24 02:01 AM
Bisecting an Angle | Bisecting an Angle by Using a Protractor | Rules
Aug 21, 24 01:22 AM
© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.
Solve Inverse Trigonometric Functions Questions
| Problems on inverse trigonometric functions are solved and detailed solutions are presented. Also exercises with answers are presented at the end of this page. We first review some of the theorems and properties of the inverse functions. 1. with 2. with 3. with Find the exact value of 1. arcsin(- √3 / 2) 2. arctan(- 1 ) 3. arccos(- 1 / 2) Simplify cos(arcsin x ) Simplify csc ( arctan x ) Evaluate the following 1. arcsin( sin (7 ? / 4)) 2. arccos( cos (4 ? / 3 ))
1. Evaluate arcsin( sin (13 ? / 4)) 2. Simplify sec ( arctan x ) 3. Find the exact value of arccos(- √3 / 2) |
More References and Links to Inverse Trigonometric Functions
Scholarships
Test Series NEW
Inverse Trigonometric Functions
Inverse Trigonometric Functions , also known as arcus, anti-trigonometric, or cyclometric functions, are the inverse counterparts of the fundamental trigonometric functions: sine, cosine, tangent, cotangent, secant, and cosecant. They are instrumental in determining angles based on trigonometric ratios. Widely utilized in engineering, Physics, Geometry, and navigation, these functions play pivotal roles in various applications.
Inverse trigonometry functions are crucial in Mathematics, especially in Calculus and Trigonometry. They are the inverse operations of trigonometric functions and have diverse applications in solving equations, finding angles, and analyzing periodic phenomena. In this thorough exploration, we will delve deep into inverse trigonometric functions, exploring their formulas, derivatives, graphs, properties, and much more.
- 1.0 What Are Inverse Trigonometric Functions?
Inverse trigonometric functions are functions that yield angles when given the ratios of sides in a right triangle. They are denoted by sin −1 x, cos −1 x, tan −1 x, cot −1 x, sec −1 x, and cosec −1 x. These functions have restricted domains and ranges to ensure their inverse nature.
- 2.0 Graphs of Inverse Trigonometric Functions:
The graphs of inverse trigonometric functions exhibit unique characteristics due to their restricted domains and ranges. Here are the graphs of the six primary inverse trigonometric functions:
- Graph of Arcsine Function (sin −1 x):
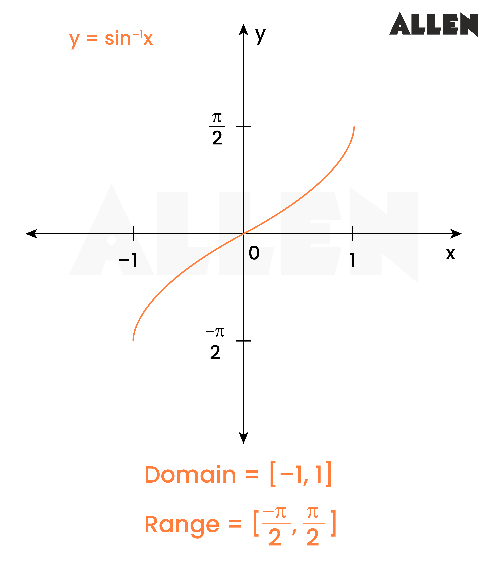
- Graph of Arccosine Function (cos −1 x):
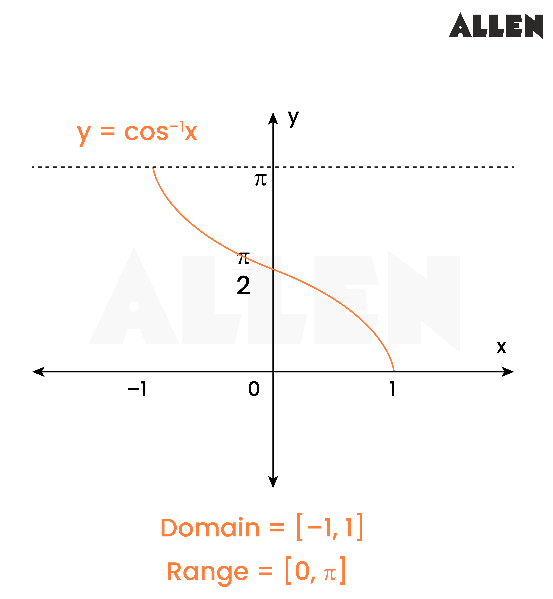
- Graph of Arctangent Function (tan −1 x):
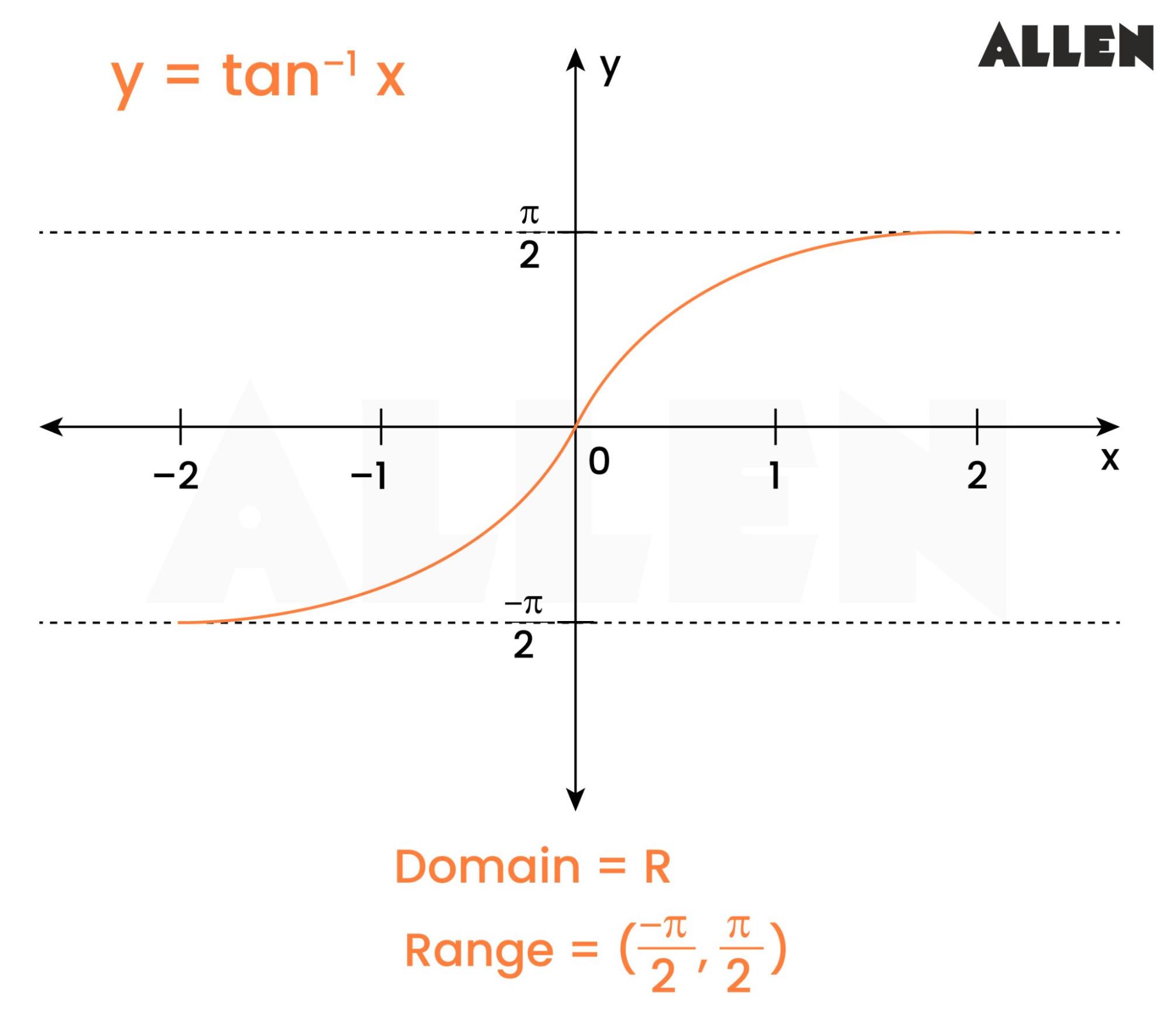
- Graph of Arc cotangent Function (cot −1 x):
- Graph of Arcsecant Function (sec −1 x):
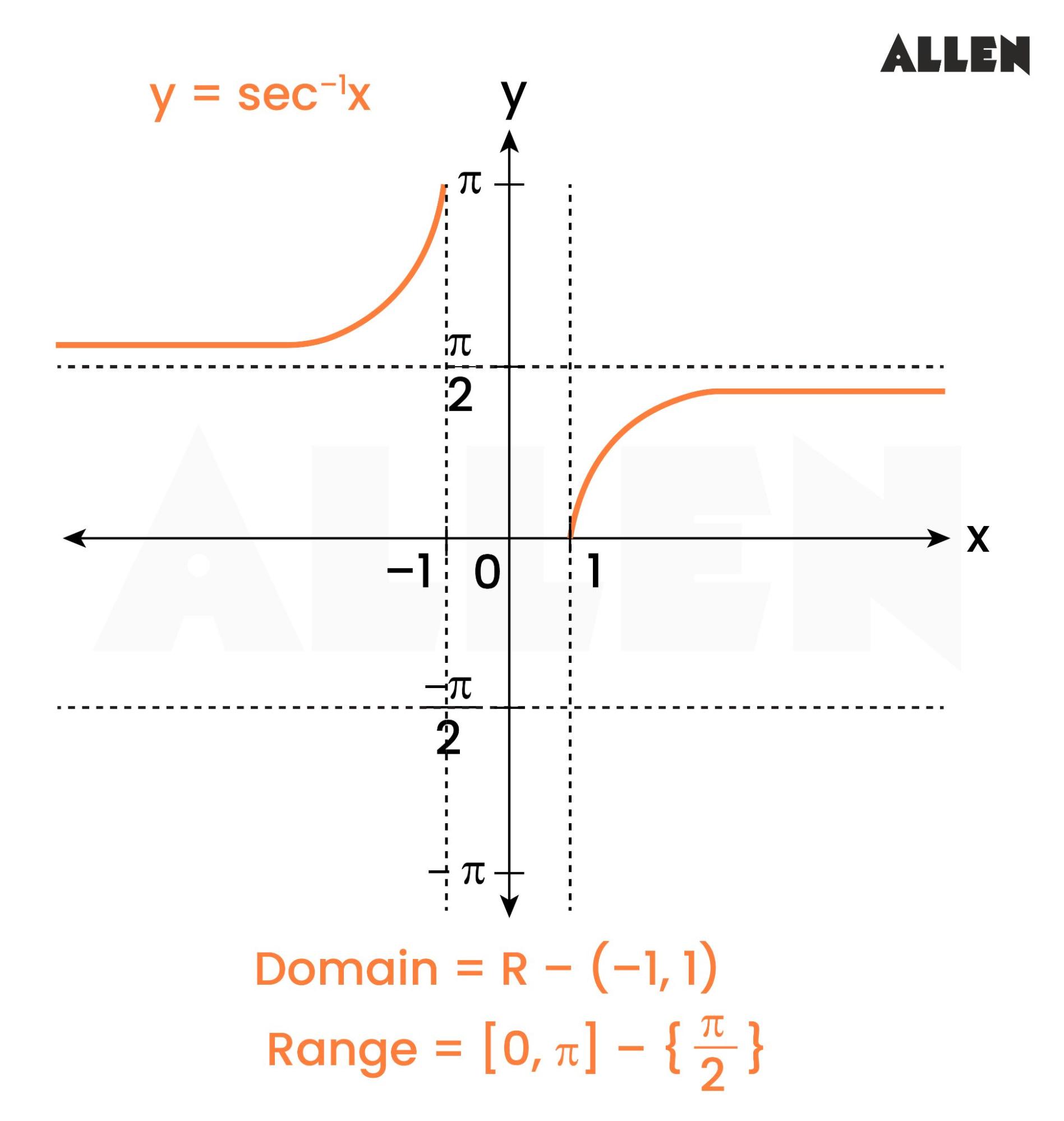
- Graph of Arccosecant Function (cosec −1 x):
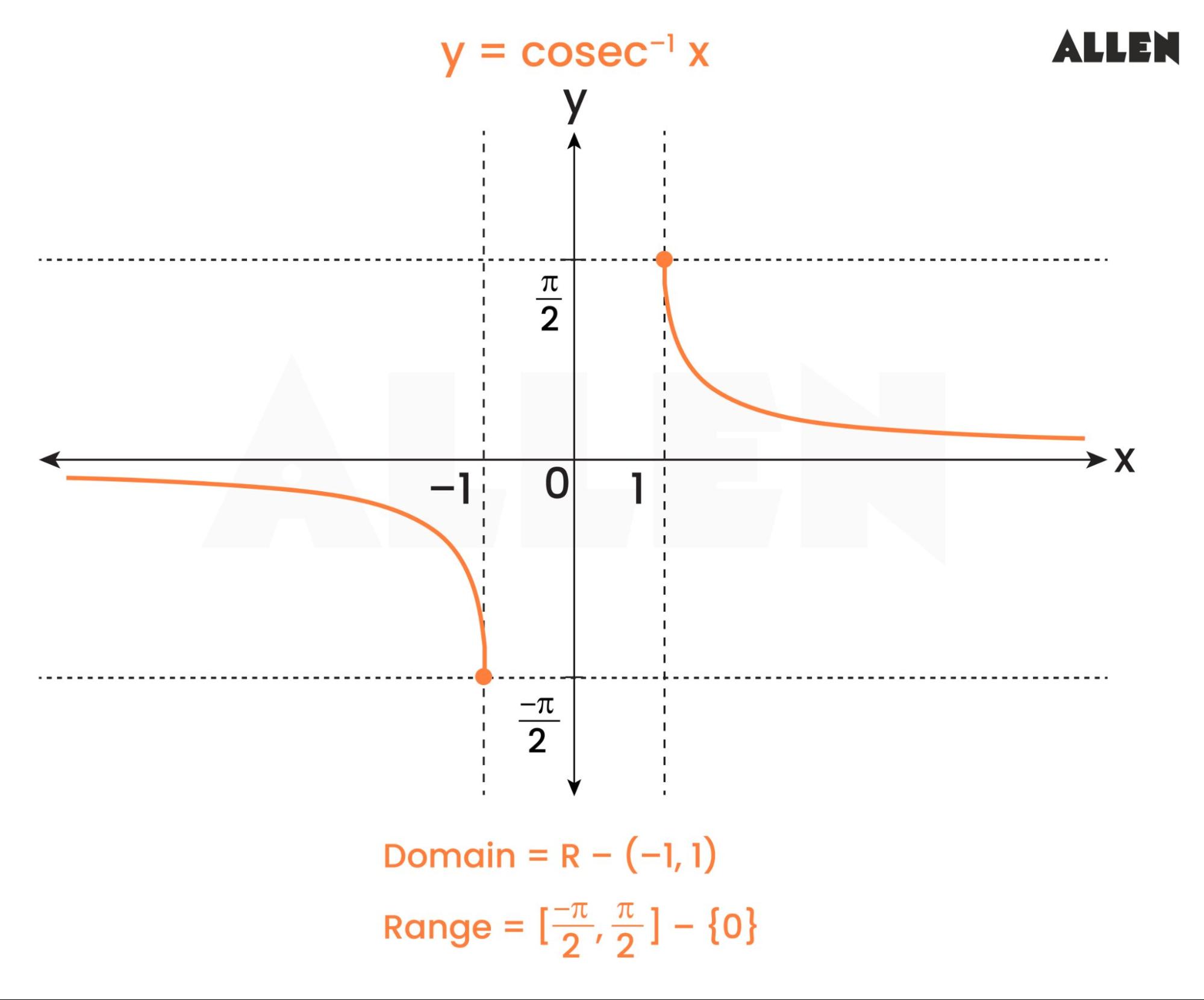
- 3.0 Domain and Range of Inverse Trigonometric Functions:
The domain and range of inverse trigonometric functions are determined by their definitions and properties. For example, the domain of sin –1 x is [–1,1], and its range is [ 2 − π , 2 π ] . Understanding these domains and ranges is essential for solving equations and analyzing functions.
Here are the domain and range of the six primary inverse trigonometric functions:
|
|
|
| [–1,1] | [2−π,2π] |
| [–1,1] | [0, π] |
|
| (2−π,2π) |
|
| (0, π) |
| – (–1,1) | [0,π]−{2π} |
| (–1,1) | [2−π,2π]−{0} |
Domain of Inverse Trigonometric Functions
The domain of inverse trigonometric functions is limited to ensure their inverse nature. For example, the domain of sin −1 x and cos −1 x is [−1, 1], while the domain of tan −1 x is R. Understanding these domains is crucial for determining where the functions are defined. Domains of the six primary inverse trigonometric functions are given above.
Range of Inverse Trigonometric Functions
The range of inverse trigonometric functions varies depending on the function. For example, the range of sin –1 x is [ − 2 π , 2 π ] , while the range of cos –1 x is [0, π] These ranges reflect the restrictions imposed on the outputs of inverse trigonometric functions. Range of the six primary inverse trigonometric functions are given above.
- 4.0 Inverse Trigonometric Functions Identities
Inverse trigonometric functions have several identities that relate them to their corresponding trigonometric functions. For example, sin(sin −1 x) = x and sin −1 (sin x) = x in specific domains are identities that demonstrate the relationship between sine and arcsine. These identities are useful in simplifying expressions and solving equations.
- 5.0 Properties of Inverse Trigonometric Functions
Inverse trigonometric functions possess various properties that govern their behavior. These properties include symmetry, periodicity, and monotonicity. For instance, sin −1 (−x) = −sin −1 x reflects the odd symmetry of arcsine function. Understanding these properties enhances our comprehension of inverse trigonometric functions.
Property – 1
(i) sin − 1 x + cos − 1 x = 2 π ; |x| < 1
(ii) tan − 1 x + cot − 1 x = 2 π ; x ∈ R
(iii) cosec − 1 x + sec − 1 x = 2 π ; |x| ≥ 1
Property – 2
(i) sin –1 (–x) = –sin –1 x; |x| ≤ 1
(ii) cosec –1 (–x) = – cosec –1 x |x| > 1
(iii) tan –1 (–x) = –tan –1 x; x ∈ R
(iv) cot –1 (–x) = π – cot –1 x; x∈ R
(v) cos –1 (–x) = π – cos –1 x; |x| < 1
(vi) sec –1 (–x) = π – sec –1 x; |x| > 1
Property – 3
(i) cosec − 1 x = sin − 1 x 1 ; |x| ≥1
(ii) sec − 1 x = cos − 1 x 1 ; |x| ≥ 1
(iii) cot − 1 x = { tan − 1 x 1 π + tan − 1 x 1 ; ; x > 0 x < 0
Property – 4
(i) (a) tan − 1 x + tan − 1 y = ⎩ ⎨ ⎧ tan − 1 1 − x y x + y π + tan − 1 1 − x y x + y 2 π , where where where x > 0 , y > 0& x y < 1 x > 0 , y > 0& x y > 1 x > 0 , y > 0& x y = 1
(b) tan − 1 x − tan − 1 y = tan − 1 1 + x y x − y w h ere x > 0 , y > 0
(c) tan − 1 x + tan − 1 y + tan − 1 z = tan − 1 [ 1 − x y − yz − z x x + y + z − x yz ]
if x > 0, y > 0, z > 0 and xy + yz + zx < 1
(ii) (a) sin − 1 x + sin − 1 y =
⎩ ⎨ ⎧ sin − 1 [ x 1 − y 2 + y 1 − x 2 ] π − sin − 1 [ x 1 − y 2 + y 1 − x 2 ] where x > 0 , y > 0& ( x 2 + y 2 ) ≤ 1 where x > 0 , y > 0& x 2 + y 2 > 1
(b) sin − 1 − sin − 1 y = sin − 1 [ x 1 − y 2 − y 1 − x 2 ] w h ere x > 0 , y > 0
(iii) (a) cos − 1 x + cos − 1 y = cos − 1 [ x y − 1 − x 2 1 − y 2 ] w h ere x > 0 , y > 0
(b) cos − 1 x − cos − 1 y = ⎩ ⎨ ⎧ cos − 1 ( x y + 1 − x 2 1 − y 2 ) ; − cos − 1 ( x y + 1 − x 2 1 − y 2 ) ; x < y , x , y > 0 x > y , x , y > 0
- 6.0 Inverse Trigonometric Functions Solved Problems
Example 1: The value of sin − 1 ( − 3 /2 ) is -
(A) –π/3 (B) –2π/3 (C) 4π/3 (D) 5π/3
Solution:
sin − 1 ( − 2 3 ) = − sin − 1 ( 2 3 ) = − 3 π
Example 2: Domain of the function y = sin − 1 ( lo g 2 x )
(A) [1, 2] (B) [–1, 2] (C) [–2, 2] (D) [–3, 3]
Solution: sin –1 (log 2 x) ≥ 0 and –1 ≤ log 2 x ≤ 1 and x > 0
0 ≤ sin − 1 ( lo g 2 x ) ≤ 2 π
0 ≤ (log 2 x) ≤ 1
Example 3: Range of sin –1 x + cosec –1 x is -
(A) {–π, π} (B) (-π, π)
(C) { 0 , 2 π } (D) none of these
Solution: Domain of sin –1 x is [–1, 1]
domain of cosec –1 x is (–∞, –1] ∪ [1, ∞)
The common domain is {–1, 1} only.
range = sin –1 (–1) + cosec –1 (–1) = –π
or sin –1 (1) + cosec –1 (1) =π
Hence, range = {–π, π}
Example 4: Find domain and range of y = sin –1 (x) + cos –1 (x) + tan –1 (x)
Solution: D f : x ∈ [–1,1] and x ∈ [–1,1] and x ∈ R
⇒ x ∈ [–1,1]
∴ D f : [–1,1]
f ( x ) = 2 π + tan − 1 ( x )
–1 ≤ x ≤ –1
⇒ − 4 π ≤ tan − 1 x ≤ 4 π
⇒ 4 π ≤ 2 π + tan − 1 x ≤ 4 3 π
∴ R f : [ 4 π , 4 3 π ]
Example 5: Prove that sec 2 (tan –1 2) + cosec 2 (cot –1 ) 3) = 15
Solution: We have,
sec 2 (tan -1 2) + cosec 2 (cot –1 3)
= { sec ( tan − 1 2 ) } 2 + { cosec ( cot − 1 3 ) } 2
= { sec ( tan − 1 1 2 ) } 2 + { cosec ( cot − 1 1 3 ) } 2
= { sec ( sec − 1 5 ) } 2 + { cosec ( cosec − 1 10 } 2
= { sec ( sec − 1 5 ) } 2 + { cosec ( cosec − 1 10 } 2
= ( 5 ) 2 + ( 10 ) 2 = 15
- 7.0 Sample Questions on Inverse Trigonometric Functions
Q. What are inverse trigonometric functions?
Ans: Inverse trigonometric functions are functions that provide angles given the ratios of sides in a right triangle. They are denoted by sin −1 x, cos −1 x , tan −1 x , cot −1 x , sec −1 x , and cosec −1 x .
Q. What are some common identities involving inverse trigonometric functions?
Ans: Common identities include sin(sin −1 x) = x, cos(cos −1 x) = x, and tan(tan −1 x) = x. These identities express the relationships between trigonometric functions and their inverses.
Table of Contents
- 3.1 Domain of Inverse Trigonometric Functions
- 3.2 Range of Inverse Trigonometric Functions
The domain and range vary depending on the function. Generally, the domain of inverse trigonometric functions is restricted to ensure their inverse nature, while the range is determined by the properties of the functions.
Inverse trigonometric functions are used to find angles when given trigonometric ratios in equations. They provide a way to "undo" the effects of trigonometric functions and retrieve the original angles.
The main properties include symmetry, periodicity, and monotonicity. For example, the arcsine and arccosine functions are odd and even functions, respectively, and the arctangent function is periodic with a period of π.
Inverse trigonometric functions are used in various fields such as engineering, physics, geometry, and navigation. They help in solving problems involving angles, distances, velocities, and more.
The graphs of inverse trigonometric functions exhibit unique characteristics due to their restricted domains and ranges. They often resemble segments or curves on the coordinate plane, with specific intervals and points of intersection.
In calculus, inverse trigonometric functions are essential for finding derivatives, integrals, and solving differential equations. They play a crucial role in analyzing functions and their behavior.

IMAGES
COMMENTS
I: Graphs of inverses. Exercise 6.1e. 138. Graph y = sin − 1x and state the domain and range of the function. 139. Graph y = arccosx and state the domain and range of the function. 140. Graph one cycle of y = tan − 1x and state the domain and range of the function. Answers to odd exercises.
To do so: -Enter 0.30 on your calculator. -Find the Inverse button, then the Cosine button (This could also be the Second Function button, or the Arccosine button). Should come out to 72.542397, rounded. To round to the nearest hundredth of a degree, we round to 2 decimal, places, giving the answer 72.54.
Translation: f(3) = 5 means f−1(5) = 3. For any function f to have an inverse, it must be 1-1. That means two inputs cannot have the same output (f(x1) 6=f(x2)). Functions that are not 1-1 can still have an inverse, but only after the inputs are restricted. Given a function, there are two ways to graph its inverse.
In this problem, x = 0.96593, x = 0.96593, and y = 5 ... Using the inverse trigonometric functions, we can solve for the angles of a right triangle given two sides, and we can use a calculator to find the values to several decimal places. In these examples and exercises, ...
Do you want to review the concepts and properties of inverse trigonometric functions, such as arcsin, arccos, and arctan? Do you want to practice solving problems involving inverse trig functions and right triangles? Then check out this article from Khan Academy, a nonprofit organization that offers free, world-class education for anyone, anywhere.
Practice each skill in the Homework Problems listed. Decide whether a function has an inverse function #1-8. Evaluate the inverse trig functions #9-20. Model problems with inverse trig functions #21-24. Solve formulas #25-30. Simplify expressions involving the inverse trig functions #31-42, 51-68. Graph the inverse trig functions ...
Figure 4.1.7. If one given side is the hypotenuse of length h and the side of length a adjacent to the desired angle is given, use the equation θ = cos − 1(a h). If one given side is the hypotenuse of length h and the side of length p opposite to the desired angle is given, use the equation θ = sin − 1(p h).
Solving Equations Using the Inverse Trigonometric Functions. Example 10.6.7; 10.6.5. Exercises; 10.6.6 Answers; Reference; As the title indicates, in this section we concern ourselves with finding inverses of the (circular) trigonometric functions. Our immediate problem is that, owing to their periodic nature, none of the six circular functions ...
To solve this problem, the range of inverse trig function are limited in such a way that the inverse functions is one-to-one, that is, there is only one result for each input value. The range can be different for each function, but as an example, the range of arcsin is conventionally limited to -90 to +90° or So if you were asked for the ...
Have you seen how inverse trig functions (arcsin, arccos, arctan) work, but still get stuck on problems? In this video we work through five problems, from th...
Introduction to Inverse Trig Functions. We studied Inverses of Functions here; we remember that getting the inverse of a function is basically switching the $ x$- and $ y$-values and solving for the other variable.The inverse of a function is symmetrical (a mirror image) around the line $ y=x$. Here's an example of how we'd find an inverse algebraically with a trig function:
Using the inverse trigonometric functions, we can solve for the angles of a right triangle given two sides, and we can use a calculator to find the values to several decimal places. ... Example 15: Solving a Problem Involving a Single Trigonometric Function. Solve the problem exactly: [latex]2{\sin }^{2}\theta -1=0,0\le \theta <2\pi [/latex].
In this explainer, we will learn how to solve equations by using inverse trigonometric functions in the first quadrant. The first quadrant means we only consider acute angles 𝜃, where 0 < 𝜃 < 9 0 ∘ ∘ or 0 < 𝜃 < 𝜋 2 in radians. The inverse trigonometric functions have a number of real-world applications in many disciplines ...
If $0\leq P\leq \pi $, find the value of $P=\arcsin (\frac{\sqrt{2}}{2})+\arccos (-\frac{1}{2})+\arctan(1)$
Inverse trigonometric functions are defined as the inverse functions of the basic trigonometric functions, which are sine, cosine, tangent, cotangent, secant and cosecant functions. They are also termed arcus functions, antitrigonometric functions or cyclometric functions. These inverse functions in trigonometry are used to get the angle with any of the trigonometry ratios.
An Inverse trigonometric function is an inverse function of trigonometric functions, such as sin and cosine.
In other words, the domain of the inverse function is the range of the original function, and vice versa, as summarized in Figure 6.3.1. Figure 6.3.1. For example, if f(x) = sin x, then we would write f − 1(x) = sin − 1x. Be aware that sin − 1x does not mean 1 sin x. The following examples illustrate the inverse trigonometric functions:
Problems on Inverse Trigonometric Function. We will solve different types of problems on inverse trigonometric function. 1. Find the values of sin (cos −1 − 1 3/5) Solution: Let, cos −1 − 1 3/5 = θ. Therefore, cos θ = 3/5. Therefore, sin θ = √ (1 - cos 2 2 θ) = √ (1 - 9/25) = √ (16/25) = 4/5 . Therefore, sin (cos −1 − 1 3/ ...
This trigonometry video tutorial provides a basic introduction on evaluating inverse trigonometric functions. It has plenty of examples such as inverse sin...
Problems on inverse trigonometric functions are solved and detailed solutions are presented. Also exercises with answers are presented at the end of this page. We first review some of the theorems and properties of the inverse functions. Theorem 1. y = arcsin x is equivalent to sin y = x with -1 ? x ? 1 and - ? / 2 ? y ? ? / 2 2
The following problems are real-world problems that can be solved using the trigonometric functions. In everyday life, indirect measurement is used to obtain answers to problems that are impossible to solve using measurement tools. However, mathematics will come to the rescue in the form of trigonometry to calculate these unknown measurements.
3.0 Domain and Range of Inverse Trigonometric Functions:. The domain and range of inverse trigonometric functions are determined by their definitions and properties. For example, the domain of sin -1 x is [-1,1], and its range is [2 − π , 2 π ].Understanding these domains and ranges is essential for solving equations and analyzing functions.
In mathematics, specifically differential calculus, the inverse function theorem gives a sufficient condition for a function to be invertible in a neighborhood of a point in its domain: namely, that its derivative is continuous and non-zero at the point.The theorem also gives a formula for the derivative of the inverse function.In multivariable calculus, this theorem can be generalized to any ...
Radian Measure. To use trigonometric functions, we first must understand how to measure the angles. Although we can use both radians and degrees, radians are a more natural measurement because they are related directly to the unit circle, a circle with radius 1.The radian measure of an angle is defined as follows.