- 12.1 - Logistic Regression
Logistic regression models a relationship between predictor variables and a categorical response variable. For example, we could use logistic regression to model the relationship between various measurements of a manufactured specimen (such as dimensions and chemical composition) to predict if a crack greater than 10 mils will occur (a binary variable: either yes or no). Logistic regression helps us estimate a probability of falling into a certain level of the categorical response given a set of predictors. We can choose from three types of logistic regression, depending on the nature of the categorical response variable:
Binary Logistic Regression :
Used when the response is binary (i.e., it has two possible outcomes). The cracking example given above would utilize binary logistic regression. Other examples of binary responses could include passing or failing a test, responding yes or no on a survey, and having high or low blood pressure.
Nominal Logistic Regression :
Used when there are three or more categories with no natural ordering to the levels. Examples of nominal responses could include departments at a business (e.g., marketing, sales, HR), type of search engine used (e.g., Google, Yahoo!, MSN), and color (black, red, blue, orange).
Ordinal Logistic Regression :
Used when there are three or more categories with a natural ordering to the levels, but the ranking of the levels do not necessarily mean the intervals between them are equal. Examples of ordinal responses could be how students rate the effectiveness of a college course (e.g., good, medium, poor), levels of flavors for hot wings, and medical condition (e.g., good, stable, serious, critical).
Particular issues with modelling a categorical response variable include nonnormal error terms, nonconstant error variance, and constraints on the response function (i.e., the response is bounded between 0 and 1). We will investigate ways of dealing with these in the binary logistic regression setting here. Nominal and ordinal logistic regression are not considered in this course.
The multiple binary logistic regression model is the following:
\[\begin{align}\label{logmod} \pi(\textbf{X})&=\frac{\exp(\beta_{0}+\beta_{1}X_{1}+\ldots+\beta_{k}X_{k})}{1+\exp(\beta_{0}+\beta_{1}X_{1}+\ldots+\beta_{k}X_{k})}\notag \\ & =\frac{\exp(\textbf{X}\beta)}{1+\exp(\textbf{X}\beta)}\\ & =\frac{1}{1+\exp(-\textbf{X}\beta)}, \end{align}\]
where here \(\pi\) denotes a probability and not the irrational number 3.14....
- \(\pi\) is the probability that an observation is in a specified category of the binary Y variable, generally called the "success probability."
- Notice that the model describes the probability of an event happening as a function of X variables. For instance, it might provide estimates of the probability that an older person has heart disease.
- The numerator \(\exp(\beta_{0}+\beta_{1}X_{1}+\ldots+\beta_{k}X_{k})\) must be positive, because it is a power of a positive value ( e ).
- The denominator of the model is (1 + numerator), so the answer will always be less than 1.
- With one X variable, the theoretical model for \(\pi\) has an elongated "S" shape (or sigmoidal shape) with asymptotes at 0 and 1, although in sample estimates we may not see this "S" shape if the range of the X variable is limited.
For a sample of size n , the likelihood for a binary logistic regression is given by:
\[\begin{align*} L(\beta;\textbf{y},\textbf{X})&=\prod_{i=1}^{n}\pi_{i}^{y_{i}}(1-\pi_{i})^{1-y_{i}}\\ & =\prod_{i=1}^{n}\biggl(\frac{\exp(\textbf{X}_{i}\beta)}{1+\exp(\textbf{X}_{i}\beta)}\biggr)^{y_{i}}\biggl(\frac{1}{1+\exp(\textbf{X}_{i}\beta)}\biggr)^{1-y_{i}}. \end{align*}\]
This yields the log likelihood:
\[\begin{align*} \ell(\beta)&=\sum_{i=1}^{n}[y_{i}\log(\pi_{i})+(1-y_{i})\log(1-\pi_{i})]\\ & =\sum_{i=1}^{n}[y_{i}\textbf{X}_{i}\beta-\log(1+\exp(\textbf{X}_{i}\beta))]. \end{align*}\]
Maximizing the likelihood (or log likelihood) has no closed-form solution, so a technique like iteratively reweighted least squares is used to find an estimate of the regression coefficients, $\hat{\beta}$.
To illustrate, consider data published on n = 27 leukemia patients. The data ( leukemia_remission.txt ) has a response variable of whether leukemia remission occurred (REMISS), which is given by a 1.
The predictor variables are cellularity of the marrow clot section (CELL), smear differential percentage of blasts (SMEAR), percentage of absolute marrow leukemia cell infiltrate (INFIL), percentage labeling index of the bone marrow leukemia cells (LI), absolute number of blasts in the peripheral blood (BLAST), and the highest temperature prior to start of treatment (TEMP).
The following output shows the estimated logistic regression equation and associated significance tests
- Select Stat > Regression > Binary Logistic Regression > Fit Binary Logistic Model.
- Select "REMISS" for the Response (the response event for remission is 1 for this data).
- Select all the predictors as Continuous predictors.
- Click Options and choose Deviance or Pearson residuals for diagnostic plots.
- Click Graphs and select "Residuals versus order."
- Click Results and change "Display of results" to "Expanded tables."
- Click Storage and select "Coefficients."
Coefficients Term Coef SE Coef 95% CI Z-Value P-Value VIF Constant 64.3 75.0 ( -82.7, 211.2) 0.86 0.391 CELL 30.8 52.1 ( -71.4, 133.0) 0.59 0.554 62.46 SMEAR 24.7 61.5 ( -95.9, 145.3) 0.40 0.688 434.42 INFIL -25.0 65.3 (-152.9, 103.0) -0.38 0.702 471.10 LI 4.36 2.66 ( -0.85, 9.57) 1.64 0.101 4.43 BLAST -0.01 2.27 ( -4.45, 4.43) -0.01 0.996 4.18 TEMP -100.2 77.8 (-252.6, 52.2) -1.29 0.198 3.01
The Wald test is the test of significance for individual regression coefficients in logistic regression (recall that we use t -tests in linear regression). For maximum likelihood estimates, the ratio
\[\begin{equation*} Z=\frac{\hat{\beta}_{i}}{\textrm{s.e.}(\hat{\beta}_{i})} \end{equation*}\]
can be used to test $H_{0}: \beta_{i}=0$. The standard normal curve is used to determine the $p$-value of the test. Furthermore, confidence intervals can be constructed as
\[\begin{equation*} \hat{\beta}_{i}\pm z_{1-\alpha/2}\textrm{s.e.}(\hat{\beta}_{i}). \end{equation*}\]
Estimates of the regression coefficients, $\hat{\beta}$, are given in the Coefficients table in the column labeled "Coef." This table also gives coefficient p -values based on Wald tests. The index of the bone marrow leukemia cells (LI) has the smallest p -value and so appears to be closest to a significant predictor of remission occurring. After looking at various subsets of the data, we find that a good model is one which only includes the labeling index as a predictor:
Coefficients Term Coef SE Coef 95% CI Z-Value P-Value VIF Constant -3.78 1.38 (-6.48, -1.08) -2.74 0.006 LI 2.90 1.19 ( 0.57, 5.22) 2.44 0.015 1.00
Regression Equation P(1) = exp(Y')/(1 + exp(Y')) Y' = -3.78 + 2.90 LI
Since we only have a single predictor in this model we can create a Binary Fitted Line Plot to visualize the sigmoidal shape of the fitted logistic regression curve:


Odds, Log Odds, and Odds Ratio
There are algebraically equivalent ways to write the logistic regression model:
The first is
\[\begin{equation}\label{logmod1} \frac{\pi}{1-\pi}=\exp(\beta_{0}+\beta_{1}X_{1}+\ldots+\beta_{k}X_{k}), \end{equation}\]
which is an equation that describes the odds of being in the current category of interest. By definition, the odds for an event is π / (1 - π ) such that P is the probability of the event. For example, if you are at the racetrack and there is a 80% chance that a certain horse will win the race, then his odds are 0.80 / (1 - 0.80) = 4, or 4:1.
The second is
\[\begin{equation}\label{logmod2} \log\biggl(\frac{\pi}{1-\pi}\biggr)=\beta_{0}+\beta_{1}X_{1}+\ldots+\beta_{k}X_{k}, \end{equation}\]
which states that the (natural) logarithm of the odds is a linear function of the X variables (and is often called the log odds ). This is also referred to as the logit transformation of the probability of success, \(\pi\).
The odds ratio (which we will write as $\theta$) between the odds for two sets of predictors (say $\textbf{X}_{(1)}$ and $\textbf{X}_{(2)}$) is given by
\[\begin{equation*} \theta=\frac{(\pi/(1-\pi))|_{\textbf{X}=\textbf{X}_{(1)}}}{(\pi/(1-\pi))|_{\textbf{X}=\textbf{X}_{(2)}}}. \end{equation*}\]
For binary logistic regression, the odds of success are:
\[\begin{equation*} \frac{\pi}{1-\pi}=\exp(\textbf{X}\beta). \end{equation*}\]
By plugging this into the formula for $\theta$ above and setting $\textbf{X}_{(1)}$ equal to $\textbf{X}_{(2)}$ except in one position (i.e., only one predictor differs by one unit), we can determine the relationship between that predictor and the response. The odds ratio can be any nonnegative number. An odds ratio of 1 serves as the baseline for comparison and indicates there is no association between the response and predictor. If the odds ratio is greater than 1, then the odds of success are higher for higher levels of a continuous predictor (or for the indicated level of a factor). In particular, the odds increase multiplicatively by $\exp(\beta_{j})$ for every one-unit increase in $\textbf{X}_{j}$. If the odds ratio is less than 1, then the odds of success are less for higher levels of a continuous predictor (or for the indicated level of a factor). Values farther from 1 represent stronger degrees of association.
For example, when there is just a single predictor, \(X\), the odds of success are:
\[\begin{equation*} \frac{\pi}{1-\pi}=\exp(\beta_0+\beta_1X). \end{equation*}\]
If we increase \(X\) by one unit, the odds ratio is
\[\begin{equation*} \theta=\frac{\exp(\beta_0+\beta_1(X+1))}{\exp(\beta_0+\beta_1X)}=\exp(\beta_1). \end{equation*}\]
To illustrate, the relevant output from the leukemia example is:
Odds Ratios for Continuous Predictors Odds Ratio 95% CI LI 18.1245 (1.7703, 185.5617)
The regression parameter estimate for LI is $2.89726$, so the odds ratio for LI is calculated as $\exp(2.89726)=18.1245$. The 95% confidence interval is calculated as $\exp(2.89726\pm z_{0.975}*1.19)$, where $z_{0.975}=1.960$ is the $97.5^{\textrm{th}}$ percentile from the standard normal distribution. The interpretation of the odds ratio is that for every increase of 1 unit in LI, the estimated odds of leukemia remission are multiplied by 18.1245. However, since the LI appears to fall between 0 and 2, it may make more sense to say that for every 0.1 unit increase in L1, the estimated odds of remission are multiplied by $\exp(2.89726\times 0.1)=1.336$. Then
- At LI=0.9, the estimated odds of leukemia remission is $\exp\{-3.77714+2.89726*0.9\}=0.310$.
- At LI=0.8, the estimated odds of leukemia remission is $\exp\{-3.77714+2.89726*0.8\}=0.232$.
- The resulting odds ratio is $\frac{0.310}{0.232}=1.336$, which is the ratio of the odds of remission when LI=0.9 compared to the odds when L1=0.8.
Notice that $1.336\times 0.232=0.310$, which demonstrates the multiplicative effect by $\exp(0.1\hat{\beta_{1}})$ on the odds.
Likelihood Ratio (or Deviance) Test
The likelihood ratio test is used to test the null hypothesis that any subset of the $\beta$'s is equal to 0. The number of $\beta$'s in the full model is k +1 , while the number of $\beta$'s in the reduced model is r +1 . (Remember the reduced model is the model that results when the $\beta$'s in the null hypothesis are set to 0.) Thus, the number of $\beta$'s being tested in the null hypothesis is \((k+1)-(r+1)=k-r\). Then the likelihood ratio test statistic is given by:
\[\begin{equation*} \Lambda^{*}=-2(\ell(\hat{\beta}^{(0)})-\ell(\hat{\beta})), \end{equation*}\]
where $\ell(\hat{\beta})$ is the log likelihood of the fitted (full) model and $\ell(\hat{\beta}^{(0)})$ is the log likelihood of the (reduced) model specified by the null hypothesis evaluated at the maximum likelihood estimate of that reduced model. This test statistic has a $\chi^{2}$ distribution with \(k-r\) degrees of freedom. Statistical software often presents results for this test in terms of "deviance," which is defined as \(-2\) times log-likelihood. The notation used for the test statistic is typically $G^2$ = deviance (reduced) – deviance (full).
This test procedure is analagous to the general linear F test procedure for multiple linear regression. However, note that when testing a single coefficient, the Wald test and likelihood ratio test will not in general give identical results.
To illustrate, the relevant software output from the leukemia example is:
Deviance Table Source DF Adj Dev Adj Mean Chi-Square P-Value Regression 1 8.299 8.299 8.30 0.004 LI 1 8.299 8.299 8.30 0.004 Error 25 26.073 1.043 Total 26 34.372
Since there is only a single predictor for this example, this table simply provides information on the likelihood ratio test for LI ( p -value of 0.004), which is similar but not identical to the earlier Wald test result ( p -value of 0.015). The Deviance Table includes the following:
- The null (reduced) model in this case has no predictors, so the fitted probabilities are simply the sample proportion of successes, \(9/27=0.333333\). The log-likelihood for the null model is \(\ell(\hat{\beta}^{(0)})=-17.1859\), so the deviance for the null model is \(-2\times-17.1859=34.372\), which is shown in the "Total" row in the Deviance Table.
- The log-likelihood for the fitted (full) model is \(\ell(\hat{\beta})=-13.0365\), so the deviance for the fitted model is \(-2\times-13.0365=26.073\), which is shown in the "Error" row in the Deviance Table.
- The likelihood ratio test statistic is therefore \(\Lambda^{*}=-2(-17.1859-(-13.0365))=8.299\), which is the same as \(G^2=34.372-26.073=8.299\).
- The p -value comes from a $\chi^{2}$ distribution with \(2-1=1\) degrees of freedom.
When using the likelihood ratio (or deviance) test for more than one regression coefficient, we can first fit the "full" model to find deviance (full), which is shown in the "Error" row in the resulting full model Deviance Table. Then fit the "reduced" model (corresponding to the model that results if the null hypothesis is true) to find deviance (reduced), which is shown in the "Error" row in the resulting reduced model Deviance Table. For example, the relevant Deviance Tables for the Disease Outbreak example on pages 581-582 of Applied Linear Regression Models (4th ed) by Kutner et al are:
Full model:
Source DF Adj Dev Adj Mean Chi-Square P-Value Regression 9 28.322 3.14686 28.32 0.001 Error 88 93.996 1.06813 Total 97 122.318
Reduced model:
Source DF Adj Dev Adj Mean Chi-Square P-Value Regression 4 21.263 5.3159 21.26 0.000 Error 93 101.054 1.0866 Total 97 122.318
Here the full model includes four single-factor predictor terms and five two-factor interaction terms, while the reduced model excludes the interaction terms. The test statistic for testing the interaction terms is \(G^2 = 101.054-93.996 = 7.058\), which is compared to a chi-square distribution with \(10-5=5\) degrees of freedom to find the p -value = 0.216 > 0.05 (meaning the interaction terms are not significant at a 5% significance level).
Alternatively, select the corresponding predictor terms last in the full model and request the software to output Sequential (Type I) Deviances. Then add the corresponding Sequential Deviances in the resulting Deviance Table to calculate \(G^2\). For example, the relevant Deviance Table for the Disease Outbreak example is:
Source DF Seq Dev Seq Mean Chi-Square P-Value Regression 9 28.322 3.1469 28.32 0.001 Age 1 7.405 7.4050 7.40 0.007 Middle 1 1.804 1.8040 1.80 0.179 Lower 1 1.606 1.6064 1.61 0.205 Sector 1 10.448 10.4481 10.45 0.001 Age*Middle 1 4.570 4.5697 4.57 0.033 Age*Lower 1 1.015 1.0152 1.02 0.314 Age*Sector 1 1.120 1.1202 1.12 0.290 Middle*Sector 1 0.000 0.0001 0.00 0.993 Lower*Sector 1 0.353 0.3531 0.35 0.552 Error 88 93.996 1.0681 Total 97 122.318
The test statistic for testing the interaction terms is \(G^2 = 4.570+1.015+1.120+0.000+0.353 = 7.058\), the same as in the first calculation.
Goodness-of-Fit Tests
Overall performance of the fitted model can be measured by several different goodness-of-fit tests. Two tests that require replicated data (multiple observations with the same values for all the predictors) are the Pearson chi-square goodness-of-fit test and the deviance goodness-of-fit test (analagous to the multiple linear regression lack-of-fit F-test). Both of these tests have statistics that are approximately chi-square distributed with c - k - 1 degrees of freedom, where c is the number of distinct combinations of the predictor variables. When a test is rejected, there is a statistically significant lack of fit. Otherwise, there is no evidence of lack of fit.
By contrast, the Hosmer-Lemeshow goodness-of-fit test is useful for unreplicated datasets or for datasets that contain just a few replicated observations. For this test the observations are grouped based on their estimated probabilities. The resulting test statistic is approximately chi-square distributed with c - 2 degrees of freedom, where c is the number of groups (generally chosen to be between 5 and 10, depending on the sample size) .
Goodness-of-Fit Tests Test DF Chi-Square P-Value Deviance 25 26.07 0.404 Pearson 25 23.93 0.523 Hosmer-Lemeshow 7 6.87 0.442
Since there is no replicated data for this example, the deviance and Pearson goodness-of-fit tests are invalid, so the first two rows of this table should be ignored. However, the Hosmer-Lemeshow test does not require replicated data so we can interpret its high p -value as indicating no evidence of lack-of-fit.
The calculation of R 2 used in linear regression does not extend directly to logistic regression. One version of R 2 used in logistic regression is defined as
\[\begin{equation*} R^{2}=\frac{\ell(\hat{\beta_{0}})-\ell(\hat{\beta})}{\ell(\hat{\beta_{0}})-\ell_{S}(\beta)}, \end{equation*}\]
where $\ell(\hat{\beta_{0}})$ is the log likelihood of the model when only the intercept is included and $\ell_{S}(\beta)$ is the log likelihood of the saturated model (i.e., where a model is fit perfectly to the data). This R 2 does go from 0 to 1 with 1 being a perfect fit. With unreplicated data, $\ell_{S}(\beta)=0$, so the formula simplifies to:
\[\begin{equation*} R^{2}=\frac{\ell(\hat{\beta_{0}})-\ell(\hat{\beta})}{\ell(\hat{\beta_{0}})}=1-\frac{\ell(\hat{\beta})}{\ell(\hat{\beta_{0}})}. \end{equation*}\]
Model Summary Deviance Deviance R-Sq R-Sq(adj) AIC 24.14% 21.23% 30.07
Recall from above that \(\ell(\hat{\beta})=-13.0365\) and \(\ell(\hat{\beta}^{(0)})=-17.1859\), so:
\[\begin{equation*} R^{2}=1-\frac{-13.0365}{-17.1859}=0.2414. \end{equation*}\]
Note that we can obtain the same result by simply using deviances instead of log-likelihoods since the $-2$ factor cancels out:
\[\begin{equation*} R^{2}=1-\frac{26.073}{34.372}=0.2414. \end{equation*}\]
Raw Residual
The raw residual is the difference between the actual response and the estimated probability from the model. The formula for the raw residual is
\[\begin{equation*} r_{i}=y_{i}-\hat{\pi}_{i}. \end{equation*}\]
Pearson Residual
The Pearson residual corrects for the unequal variance in the raw residuals by dividing by the standard deviation. The formula for the Pearson residuals is
\[\begin{equation*} p_{i}=\frac{r_{i}}{\sqrt{\hat{\pi}_{i}(1-\hat{\pi}_{i})}}. \end{equation*}\]
Deviance Residuals
Deviance residuals are also popular because the sum of squares of these residuals is the deviance statistic. The formula for the deviance residual is
\[\begin{equation*} d_{i}=\pm\sqrt{2\biggl[y_{i}\log\biggl(\frac{y_{i}}{\hat{\pi}_{i}}\biggr)+(1-y_{i})\log\biggl(\frac{1-y_{i}}{1-\hat{\pi}_{i}}\biggr)\biggr]}. \end{equation*}\]
Here are the plots of the Pearson residuals and deviance residuals for the leukemia example. There are no alarming patterns in these plots to suggest a major problem with the model.

The hat matrix serves a similar purpose as in the case of linear regression – to measure the influence of each observation on the overall fit of the model – but the interpretation is not as clear due to its more complicated form. The hat values (leverages) are given by
\[\begin{equation*} h_{i,i}=\hat{\pi}_{i}(1-\hat{\pi}_{i})\textbf{x}_{i}^{\textrm{T}}(\textbf{X}^{\textrm{T}}\textbf{W}\textbf{X})\textbf{x}_{i}, \end{equation*}\]
where W is an $n\times n$ diagonal matrix with the values of $\hat{\pi}_{i}(1-\hat{\pi}_{i})$ for $i=1 ,\ldots,n$ on the diagonal. As before, we should investigate any observations with $h_{i,i}>3p/n$ or, failing this, any observations with $h_{i,i}>2p/n$ and very isolated .
Studentized Residuals
We can also report Studentized versions of some of the earlier residuals. The Studentized Pearson residuals are given by
\[\begin{equation*} sp_{i}=\frac{p_{i}}{\sqrt{1-h_{i,i}}} \end{equation*}\]
and the Studentized deviance residuals are given by
\[\begin{equation*} sd_{i}=\frac{d_{i}}{\sqrt{1-h_{i, i}}}. \end{equation*}\]
Cook's Distances
An extension of Cook's distance for logistic regression measures the overall change in fitted logits due to deleting the $i^{\textrm{th}}$ observation. It is defined by:
\[\begin{equation*} \textrm{C}_{i}=\frac{p_{i}^{2}h _{i,i}}{(k+1)(1-h_{i,i})^{2}}. \end{equation*}\]
Fits and Diagnostics for Unusual Observations Observed Obs Probability Fit SE Fit 95% CI Resid Std Resid Del Resid HI 8 0.000 0.849 0.139 (0.403, 0.979) -1.945 -2.11 -2.19 0.149840 Obs Cook’s D DFITS 8 0.58 -1.08011 R R Large residual
The residuals in this output are deviance residuals, so observation 8 has a deviance residual of \(-1.945\), a studentized deviance residual of \(-2.19\), a leverage (h) of \(0.149840\), and a Cook's distance (C) of 0.58.
Start Here!
- Welcome to STAT 462!
- Search Course Materials
- Lesson 1: Statistical Inference Foundations
- Lesson 2: Simple Linear Regression (SLR) Model
- Lesson 3: SLR Evaluation
- Lesson 4: SLR Assumptions, Estimation & Prediction
- Lesson 5: Multiple Linear Regression (MLR) Model & Evaluation
- Lesson 6: MLR Assumptions, Estimation & Prediction
- Lesson 7: Transformations & Interactions
- Lesson 8: Categorical Predictors
- Lesson 9: Influential Points
- Lesson 10: Regression Pitfalls
- Lesson 11: Model Building
- 12.2 - Further Logistic Regression Examples
- 12.3 - Poisson Regression
- 12.4 - Generalized Linear Models
- 12.5 - Nonlinear Regression
- 12.6 - Exponential Regression Example
- 12.7 - Population Growth Example
- Website for Applied Regression Modeling, 2nd edition
- Notation Used in this Course
- R Software Help
- Minitab Software Help

Copyright © 2018 The Pennsylvania State University Privacy and Legal Statements Contact the Department of Statistics Online Programs
Introduction to Regression Analysis in R
Chapter 19 inference in logistic regression.
\(\newcommand{\E}{\mathrm{E}}\) \(\newcommand{\Var}{\mathrm{Var}}\) \(\newcommand{\bmx}{\mathbf{x}}\) \(\newcommand{\bmH}{\mathbf{H}}\) \(\newcommand{\bmI}{\mathbf{I}}\) \(\newcommand{\bmX}{\mathbf{X}}\) \(\newcommand{\bmy}{\mathbf{y}}\) \(\newcommand{\bmY}{\mathbf{Y}}\) \(\newcommand{\bmbeta}{\boldsymbol{\beta}}\) \(\newcommand{\bmepsilon}{\boldsymbol{\epsilon}}\) \(\newcommand{\bmmu}{\boldsymbol{\mu}}\) \(\newcommand{\bmSigma}{\boldsymbol{\Sigma}}\) \(\newcommand{\XtX}{\bmX^\mT\bmX}\) \(\newcommand{\mT}{\mathsf{T}}\) \(\newcommand{\XtXinv}{(\bmX^\mT\bmX)^{-1}}\)
19.1 Maximum Likelihood
For estimating \(\beta\) ’s in the logistic regression model \[logit(p_i) = \beta_0 + \beta_1x_{i1} + \beta_2x_{i2} + \dots + \beta_kx_{ik},\] we can’t minimize the residual sum of squares like was done in linear regression. Instead, we use a statistical technique called maximum likelihood.
To demonstrate the idea of maximum likelihood, we first consider examples of flipping a coin.
Example 19.1 Suppose we that we have a (possibly biased) coin that has probability \(p\) of landing heads. We flip it twice. What is the probability that we get two heads?
Consider the random variable \(Y_i\) such that \(Y_i= 1\) if the \(i\) th coin flip is heads, and \(Y_i = 0\) if the \(i\) th coin flip is tails. Clearly, \(P(Y_i=1) = p\) and \(P(Y_i=0) = 1- p\) . More generally, we can write \(P(Y_i = y) = p^y(1-p)^{(1-y)}\) . To determine the probability of getting two heads in two flips, we need to compute \(P(Y_1=1 \text{ and }Y_2 = 1)\) . Since the flips are independent, we have \(P(Y_1=1 \text{ and }Y_2 = 1) = P(Y_1 = 1)P(Y_2 =1)= p*p = p^2\) .
Using the same logic, we find the probabiltiy of obtaining two tails to be \((1-p)^2\) .
Lastly, we could calculate the probability of obtaining 1 heads and 1 tails (from two coin flips) as \(p(1-p) + (1-p)p = 2p(1-p)\) . Notice that we sum two values here, corresponding to different orderings: heads then tails or tails then heads. Both occurences lead to 1 heads and 1 tails in total.
Example 19.2 Suppose again we have a biased coin, that has probability \(p\) of landing heads. We flip it 100 times. What is the probability of getting 64 heads?
\[\begin{equation} P(\text{64 heads in 100 flips}) = \text{constant} \times p^{64}(1-p)^{100 - 64} \tag{19.1} \end{equation}\] In this equation, the constant term 16 accounts for the possible orderings.
19.1.1 Likelihood function
Now consider reversing the question of Example 19.2 . Suppose we flipped a coin 100 times and observed 64 heads and 36 tails. What would be our best guess of the probability of landing heads for this coin? We can calculate by considering the likelihood :
\[L(p) = \text{constant} \times p^{64}(1-p)^{100 - 64}\]
This likelihood function is very similar to (19.1) , but is written as a function of the parameter \(p\) rather than the random variable \(Y\) . The likelihood function indicates how likely the data are if the probability of heads is \(p\) . This value depends on the data (in this case, 64 heads) and the probability of heads ( \(p\) ).
In maximum likelihood, we seek to find the value of \(p\) that gives the largest possible value of \(L(p)\) . We call this value the maximum likelihood estimate of \(p\) and denote it as \(\hat p\) .

Figure 19.1: Likelihood function \(L(p)\) when 64 heads are observed out of 100 coin flips.
19.1.2 Maximum Likelihood in Logistic Regression
We use this approach to calculate \(\hat\beta_j\) ’s in logistic regression. The likelihood function for \(n\) independent binary random variables can be written: \[L(p_1, \dots, p_n) \propto \prod_{i=1}^n p_i^{y_i}(1-p_i)^{1-y_i}\]
Important differences from the coin flip example are that now \(p_i\) is different for each observation and \(p_i\) depends on \(\beta\) ’s. Taking this into account, we can write the likelihood function for logistic regression as: \[L(\beta_0, \beta_1, \dots, \beta_k) = L(\boldsymbol{\beta}) = \prod_{i=1}^n p_i(\boldsymbol{\beta})^y_i(1-p_i(\boldsymbol{\beta}))^{1-y_i}\] The goal of maximum likelihood is to find the values of \(\boldsymbol\beta\) that maximize \(L(\boldsymbol\beta)\) . Our data have the highest probability of occurring when \(\boldsymbol\beta\) takes these values (compared to other values of \(\boldsymbol\beta\) ).
Unfortunately, there is not simple closed-form solution to finding \(\hat{\boldsymbol\beta}\) . Instead, we use an iterative procedure called Iteratively Reweighted Least Squares (IRLS). This is done automatically by the glm() function in R, so we will skip over the details of the procedure.
If you want to know the value of the likelihood function for a logistic regression model, use the logLik() function on the fitted model object. This will return the logarithm of the likelihood. Alternatively, the summary output for glm() provides the deviance , which is \(-2\) times the logarithm of the likelihood.
19.2 Hypothesis Testing for \(\beta\) ’s
Like with linear regression, a common inferential question in logistic regression is whether a \(\beta_j\) is different from zero. This corresponds to there being a difference in the log odds of the outcome among observations that differen in the value of the predictor variable \(x_j\) .
There are three possible tests of \(H_0: \beta_j = 0\) vs. \(H_A: \beta_j \ne 0\) in logistic regression:
- Likelihood Ratio Test
In linear regression, all three are equivalent. In logistic regression (and other GLM’s), they are not equivalent.
19.2.1 Likelihood Ratio Test (LRT)
The LRT asks the question: Are the data significantly more likely when \(\beta_j = \hat\beta_j\) than when \(\beta_j = 0\) ? To do this, it compares the values of the log-likelihood for models with and without \(\beta_j\) The test statistic is: \[\begin{align*} \text{LR Statistic } \Lambda &= -2 \log \frac{L(\widehat{reduced})}{L(\widehat{full})}\\ &= -2 \log L(\widehat{reduced}) + 2 \log L(\widehat{full}) \end{align*}\]
\(\Lambda\) follows a \(\chi^2_{r}\) distribution when \(H_0\) is true and \(n\) is large ( \(r\) is the number of variables set to zero, in this case \(=1\) ). We reject the null hypothesis when \(\Lambda > \chi^2_{r}(\alpha)\) . This means that larger values of \(\Lambda\) lead to rejecting \(H_0\) . Conceptually, if \(\beta_j\) greatly improves the model fit, then \(L(\widehat{full})\) is much bigger than \(L(\widehat{reduced})\) . This makes \(\frac{L(\widehat{reduced})}{L(\widehat{full})} \approx 0\) and thus \(\Lambda\) large.
A key advantage of the LRT is that the test doesn’t depend upon the model parameterization. We obtain same answer testing (1) \(H_0: \beta_j = 0\) vs. \(H_A: \beta_j \ne 0\) as we would testing (2) \(H_0: \exp(\beta_j) = 1\) vs. \(H_A: \exp(\beta_j) \ne 1\) . A second advantage is that the LRT easily extends to testing multiple parmaeters at once.
Although the LRT requires fitting the model twice (once with all variables and once with the variables being tested held out), this is trivially fast for most modern computers.
19.2.2 LRT in R
To fit the LRT in R, use the anova(reduced, full, test="LRT") command. Here, reduced is the lm -object for the reduced model and full is the lm -object for the full model.
Example 19.3 Is there a relationship between smoking status and CHD among US men with the same age, EKG status, and systolic blood pressure (SBP)?
To answer this, we fit two models: one with age, EKG status, SBP, and smoking status as predictors, and another with only the first three.
We have strong evidence to reject that null hypothesis that smoking is not related to CHD in men, when adjusting for age, EKG status, and systolic blood pressure ( \(p = 0.0036\) ).
19.2.3 Hypothesis Testing for \(\beta\) ’s
19.2.4 wald test.
A Wald test is, on the surface, the same type of test used in linear regression. The idea behind a Wald test is to calculate how many standard deviations \(\hat\beta_j\) is from zero, and compare that value to a \(Z\) -statistic.
\[\begin{align*} \text{Wald Statistic } W &= \frac{\hat\beta_j - 0}{se(\hat\beta_j)} \end{align*}\]
\(W\) follows a \(N(0, 1)\) distribution when \(H_0\) is true and \(n\) is large. We reject the \(H: \beta_j = 0\) when \(|W| > z_{1-\alpha/2}\) or when \(W^2 > \chi^2_1(\alpha)\) . That is, larger values of \(W\) lead to rejecting \(H_0\) .
Generally, an LRT is preferred to a Wald test, since the Wald test has several drawbacks. A Wald test does depend upon the model parameterization: \[\frac{\hat\beta - 0}{se(\hat\beta)} \ne \frac{\exp(\hat\beta) - 1}{se(\exp(\hat\beta))}\] Wald tests can also have low power when truth is far from \(H_0\) and are based on a normal approximation that is less reliable in small samples. The primary advantage to a Wald test is that it is easy to compute–and often provided by default in most statistical programs.
R can calculate the Wald test for you:
19.2.5 Score Test
The score test relies on the fact that the slope of the log-likelihood function is 0 when \(\beta = \hat\beta\) 17
The idea is to evaluate the slope of the log-likelihood for the “reduced” model (does not include \(\beta_1\) ) and see if it is “significantly” steep. The score test is also called Rao test. The test statistic, \(S\) , follows a \(\chi^2_{r}\) distribution when \(H_0\) is true and \(n\) is large ( \(r\) is the numnber of of variables set to zero, in this case \(=1\) ). The null hypothesis is rejected when \(S > \chi^2_{r}(\alpha)\) .
An advantage of the score test is that is only requires fitting the reduced model. This provides computational advantages in some complex situations (generally not an issue for logistic regression). Like the LRT, the score test doesn’t depend upon the model parameterization
Calculate the score test using with test="Rao"
19.3 Interval Estimation
There are two ways for computing confidence intervals in logistic regression. Both are based on inverting testing approaches.
19.3.1 Wald Confidence Intervals
Consider the Wald hypothesis test:
\[W = \frac{{\hat\beta_j} - {\beta_j^0}}{{se(\hat\beta_j)}}\] If \(|W| \ge z_{1 - \alpha/2}\) , then we would reject the null hypothesis \(H_0 : \beta_j = \beta^0_j\) at the \(\alpha\) level.
Reverse the formula for \(W\) to get:
\[{\hat\beta_k} - z_{1 - \alpha/2}{se(\hat\beta_j)} \le {\beta_j^0} \le {\hat\beta_k} + z_{1 - \alpha/2}{se(\hat\beta_j)}\]
Thus, a \(100\times (1-\alpha) \%\) Wald confidence interval for \(\beta_j\) is:
\[\left(\hat\beta_k - z_{1 - \alpha/2}se(\hat\beta_j), \hat\beta_k + z_{1 - \alpha/2}se(\hat\beta_j)\right)\]
19.3.2 Profile Confidence Intervals
Wald confidence intervals have a simple formula, but don’t always work well–especially in small sample sizes (which is also when Wald Tests are not as good). Profile Confidence Intervals “reverse” a LRT similar to how a Wald CI “reverses” a Wald Hypothesis test.
- Profile confidence intervals are usually better to use than Wald CI’s.
- Interpretation is the same for both.
- This is also what tidy() will use when conf.int=TRUE
To get a confidence interval for an OR, exponentiate the confidence interval for \(\hat\beta_j\)
19.4 Generalized Linear Models (GLMs)
Logistic regression is one example of a generalized linear model (GLM). GLMs have three pieces:
| GLM Part | Explanation | Logistic Regression |
|---|---|---|
| Probability Distribution from Exponential Family | Describes generating mechanism for observed data and mean-variance relationship. | \(Y_i \sim Bernoilli(p_i)\) \(\Var(Y_i) \propto p_i(1-p_i)\) |
| Linear Predictor \(\eta = \mathbf{X}\boldsymbol\beta\) | Describes how \(\eta\) depends on linear combination of parameters and predictor variables | \(\eta = \mathbf{X}\boldsymbol\beta\) |
| Link function \(g\). \(\E[Y] = g^{-1}(\eta)\) | Connection between mean of distribution and linear predictor | \(p = \frac{\exp(\eta)}{1 + \exp(\eta)}\) or \(logit(p) = \eta\) |
Another common GLM is Poisson regression (“log-linear” models)
| GLM Part | Explanation | Poisson Regression |
|---|---|---|
| Probability Distribution from Exponential Family | Describes generating mechanism for observed data and mean-variance relationship. | \(Y_i \sim Poisson(\lambda_i)\) \(\Var(Y_i) \propto \lambda_i\) |
| Linear Predictor \(\eta = \bmX\bmbeta\) | Describes how \(\eta\) depends on linear combination of parameters and predictor variables | \(\eta = \bmX\bmbeta\) |
| Link function \(g\). \(\E[Y] = g^{-1}(\eta)\) | Connection between mean of distribution and linear predictor | \(\lambda_i = \exp(\eta)\) or \(\log(\lambda_i) = \eta\) |
The value of the constant is a binomial coefficient , but it’s exact value is not important for our needs here. ↩︎
This follows from the first derivative of a function always equally zero at a local extremum. ↩︎
An Introduction to Data Analysis
15.2 logistic regression.
Suppose \(y \in \{0,1\}^n\) is an \(n\) -placed vector of binary outcomes, and \(X\) a predictor matrix for a linear regression model. A Bayesian logistic regression model has the following form:
\[ \begin{align*} \beta, \sigma & \sim \text{some prior} \\ \xi & = X \beta && \text{[linear predictor]} \\ \eta_i & = \text{logistic}(\xi_i) && \text{[predictor of central tendency]} \\ y_i & \sim \text{Bernoulli}(\eta_i) && \text{[likelihood]} \\ \end{align*} \] The logistic function used as a link function is a function in \(\mathbb{R} \rightarrow [0;1]\) , i.e., from the reals to the unit interval. It is defined as:
\[\text{logistic}(\xi_i) = (1 + \exp(-\xi_i))^{-1}\] It’s shape (a sigmoid, or S-shaped curve) is this:

We use the Simon task data as an example application. So far we only tested the first of two hypotheses about the Simon task data, namely the hypothesis relating to reaction times. The second hypothesis which arose in the context of the Simon task refers to the accuracy of answers, i.e., the proportion of “correct” choices:
\[ \text{Accuracy}_{\text{correct},\ \text{congruent}} > \text{Accuracy}_{\text{correct},\ \text{incongruent}} \] Notice that correctness is a binary categorical variable. Therefore, we use logistic regression to test this hypothesis.
Here is how to set up a logistic regression model with brms . The only thing that is new here is that we specify explicitly the likelihood function and the (inverse!) link function. 70 This is done using the syntax family = bernoulli(link = "logit") . For later hypothesis testing we also use proper priors and take samples from the prior as well.
The Bayesian summary statistics of the posterior samples of values for regression coefficients are:
What do these specific numerical estimates for coefficients mean? The mean estimate for the linear predictor \(\xi_\text{cong}\) for the “congruent” condition is roughly 3.204. The mean estimate for the linear predictor \(\xi_\text{inc}\) for the “incongruent” condition is roughly 3.204 + -0.726, so roughly 2.478. The central predictors corresponding to these linear predictors are:
\[ \begin{align*} \eta_\text{cong} & = \text{logistic}(3.204) \approx 0.961 \\ \eta_\text{incon} & = \text{logistic}(2.478) \approx 0.923 \end{align*} \]
These central estimates for the latent proportion of “correct” answers in each condition tightly match the empirically observed proportion of “correct” answers in the data:
Testing hypothesis for a logistic regression model is the exact same as for a standard regression model. And so, we find very strong support for hypothesis 2, suggesting that (given model and data), there is reason to believe that the accuracy in incongruent trials is lower than in congruent trials.
Notice that the logit function is the inverse of the logistic function. ↩︎
Companion to BER 642: Advanced Regression Methods
Chapter 10 binary logistic regression, 10.1 introduction.
Logistic regression is a technique used when the dependent variable is categorical (or nominal). Examples: 1) Consumers make a decision to buy or not to buy, 2) a product may pass or fail quality control, 3) there are good or poor credit risks, and 4) employee may be promoted or not.
Binary logistic regression - determines the impact of multiple independent variables presented simultaneously to predict membership of one or other of the two dependent variable categories.
Since the dependent variable is dichotomous we cannot predict a numerical value for it using logistic regression so the usual regression least squares deviations criteria for best fit approach of minimizing error around the line of best fit is inappropriate (It’s impossible to calculate deviations using binary variables!).
Instead, logistic regression employs binomial probability theory in which there are only two values to predict: that probability (p) is 1 rather than 0, i.e. the event/person belongs to one group rather than the other.
Logistic regression forms a best fitting equation or function using the maximum likelihood (ML) method, which maximizes the probability of classifying the observed data into the appropriate category given the regression coefficients.
Like multiple regression, logistic regression provides a coefficient ‘b’, which measures each independent variable’s partial contribution to variations in the dependent variable.
The goal is to correctly predict the category of outcome for individual cases using the most parsimonious model.
To accomplish this goal, a model (i.e. an equation) is created that includes all predictor variables that are useful in predicting the response variable.
10.2 The Purpose of Binary Logistic Regression
- The logistic regression predicts group membership
Since logistic regression calculates the probability of success over the probability of failure, the results of the analysis are in the form of an odds ratio.
Logistic regression determines the impact of multiple independent variables presented simultaneously to predict membership of one or other of the two dependent variable categories.
- The logistic regression also provides the relationships and strengths among the variables ## Assumptions of (Binary) Logistic Regression
Logistic regression does not assume a linear relationship between the dependent and independent variables.
- Logistic regression assumes linearity of independent variables and log odds of dependent variable.
The independent variables need not be interval, nor normally distributed, nor linearly related, nor of equal variance within each group
- Homoscedasticity is not required. The error terms (residuals) do not need to be normally distributed.
The dependent variable in logistic regression is not measured on an interval or ratio scale.
- The dependent variable must be a dichotomous ( 2 categories) for the binary logistic regression.
The categories (groups) as a dependent variable must be mutually exclusive and exhaustive; a case can only be in one group and every case must be a member of one of the groups.
Larger samples are needed than for linear regression because maximum coefficients using a ML method are large sample estimates. A minimum of 50 cases per predictor is recommended (Field, 2013)
Hosmer, Lemeshow, and Sturdivant (2013) suggest a minimum sample of 10 observations per independent variable in the model, but caution that 20 observations per variable should be sought if possible.
Leblanc and Fitzgerald (2000) suggest a minimum of 30 observations per independent variable.
10.3 Log Transformation
The log transformation is, arguably, the most popular among the different types of transformations used to transform skewed data to approximately conform to normality.
- Log transformations and sq. root transformations moved skewed distributions closer to normality. So what we are about to do is common.
This log transformation of the p values to a log distribution enables us to create a link with the normal regression equation. The log distribution (or logistic transformation of p) is also called the logit of p or logit(p).
In logistic regression, a logistic transformation of the odds (referred to as logit) serves as the depending variable:
\[\log (o d d s)=\operatorname{logit}(P)=\ln \left(\frac{P}{1-P}\right)\] If we take the above dependent variable and add a regression equation for the independent variables, we get a logistic regression:
\[\ logit(p)=a+b_{1} x_{1}+b_{2} x_{2}+b_{3} x_{3}+\ldots\] As in least-squares regression, the relationship between the logit(P) and X is assumed to be linear.
10.4 Equation
\[P=\frac{\exp \left(a+b_{1} x_{1}+b_{2} x_{2}+b_{3} x_{3}+\ldots\right)}{1+\exp \left(a+b_{1} x_{1}+b_{2} x_{2}+b_{3} x_{3}+\ldots\right)}\] In the equation above: P can be calculated with the following formula
P = the probability that a case is in a particular category,
exp = the exponential function (approx. 2.72),
a = the constant (or intercept) of the equation and,
b = the coefficient (or slope) of the predictor variables.
10.5 Hypothesis Test
In logistic regression, hypotheses are of interest:
the null hypothesis , which is when all the coefficients in the regression equation take the value zero, and
the alternate hypothesis that the model currently under consideration is accurate and differs significantly from the null of zero, i.e. gives significantly better than the chance or random prediction level of the null hypothesis.
10.6 Likelihood Ratio Test for Nested Models
The likelihood ratio test is based on -2LL ratio. It is a test of the significance of the difference between the likelihood ratio (-2LL) for the researcher’s model with predictors (called model chi square) minus the likelihood ratio for baseline model with only a constant in it.
Significance at the .05 level or lower means the researcher’s model with the predictors is significantly different from the one with the constant only (all ‘b’ coefficients being zero). It measures the improvement in fit that the explanatory variables make compared to the null model.
Chi square is used to assess significance of this ratio.
10.7 R Lab: Running Binary Logistic Regression Model
10.7.1 data explanations ((data set: class.sav)).
A researcher is interested in how variables, such as GRE (Graduate Record Exam scores), GPA (grade point average) and prestige of the undergraduate institution, effect admission into graduate school. The response variable, admit/don’t admit, is a binary variable.
This dataset has a binary response (outcome, dependent) variable called admit, which is equal to 1 if the individual was admitted to graduate school, and 0 otherwise.
There are three predictor variables: GRE, GPA, and rank. We will treat the variables GRE and GPA as continuous. The variable rank takes on the values 1 through 4. Institutions with a rank of 1 have the highest prestige, while those with a rank of 4 have the lowest.
10.7.2 Explore the data
This dataset has a binary response (outcome, dependent) variable called admit. There are three predictor variables: gre, gpa and rank. We will treat the variables gre and gpa as continuous. The variable rank takes on the values 1 through 4. Institutions with a rank of 1 have the highest prestige, while those with a rank of 4 have the lowest. We can get basic descriptives for the entire data set by using summary. To get the standard deviations, we use sapply to apply the sd function to each variable in the dataset.
Before we run a binary logistic regression, we need check the previous two-way contingency table of categorical outcome and predictors. We want to make sure there is no zero in any cells.

10.7.3 Running a logstic regression model
In the output above, the first thing we see is the call, this is R reminding us what the model we ran was, what options we specified, etc.
Next we see the deviance residuals, which are a measure of model fit. This part of output shows the distribution of the deviance residuals for individual cases used in the model. Below we discuss how to use summaries of the deviance statistic to assess model fit.
The next part of the output shows the coefficients, their standard errors, the z-statistic (sometimes called a Wald z-statistic), and the associated p-values. Both gre and gpa are statistically significant, as are the three terms for rank. The logistic regression coefficients give the change in the log odds of the outcome for a one unit increase in the predictor variable.
How to do the interpretation?
For every one unit change in gre, the log odds of admission (versus non-admission) increases by 0.002.
For a one unit increase in gpa, the log odds of being admitted to graduate school increases by 0.804.
The indicator variables for rank have a slightly different interpretation. For example, having attended an undergraduate institution with rank of 2, versus an institution with a rank of 1, changes the log odds of admission by -0.675.
Below the table of coefficients are fit indices, including the null and deviance residuals and the AIC. Later we show an example of how you can use these values to help assess model fit.
Why the coefficient value of rank (B) are different with the SPSS outputs? - In R, the glm automatically made the Rank 1 as the references group. However, in our SPSS example, we set the rank 4 as the reference group.
We can test for an overall effect of rank using the wald.test function of the aod library. The order in which the coefficients are given in the table of coefficients is the same as the order of the terms in the model. This is important because the wald.test function refers to the coefficients by their order in the model. We use the wald.test function. b supplies the coefficients, while Sigma supplies the variance covariance matrix of the error terms, finally Terms tells R which terms in the model are to be tested, in this case, terms 4, 5, and 6, are the three terms for the levels of rank.
The chi-squared test statistic of 20.9, with three degrees of freedom is associated with a p-value of 0.00011 indicating that the overall effect of rank is statistically significant.
We can also test additional hypotheses about the differences in the coefficients for the different levels of rank. Below we test that the coefficient for rank=2 is equal to the coefficient for rank=3. The first line of code below creates a vector l that defines the test we want to perform. In this case, we want to test the difference (subtraction) of the terms for rank=2 and rank=3 (i.e., the 4th and 5th terms in the model). To contrast these two terms, we multiply one of them by 1, and the other by -1. The other terms in the model are not involved in the test, so they are multiplied by 0. The second line of code below uses L=l to tell R that we wish to base the test on the vector l (rather than using the Terms option as we did above).
The chi-squared test statistic of 5.5 with 1 degree of freedom is associated with a p-value of 0.019, indicating that the difference between the coefficient for rank=2 and the coefficient for rank=3 is statistically significant.
You can also exponentiate the coefficients and interpret them as odds-ratios. R will do this computation for you. To get the exponentiated coefficients, you tell R that you want to exponentiate (exp), and that the object you want to exponentiate is called coefficients and it is part of mylogit (coef(mylogit)). We can use the same logic to get odds ratios and their confidence intervals, by exponentiating the confidence intervals from before. To put it all in one table, we use cbind to bind the coefficients and confidence intervals column-wise.
Now we can say that for a one unit increase in gpa, the odds of being admitted to graduate school (versus not being admitted) increase by a factor of 2.23.
For more information on interpreting odds ratios see our FAQ page: How do I interpret odds ratios in logistic regression? Link:
Note that while R produces it, the odds ratio for the intercept is not generally interpreted.
You can also use predicted probabilities to help you understand the model. Predicted probabilities can be computed for both categorical and continuous predictor variables. In order to create predicted probabilities we first need to create a new data frame with the values we want the independent variables to take on to create our predictions
We will start by calculating the predicted probability of admission at each value of rank, holding gre and gpa at their means.
These objects must have the same names as the variables in your logistic regression above (e.g. in this example the mean for gre must be named gre). Now that we have the data frame we want to use to calculate the predicted probabilities, we can tell R to create the predicted probabilities. The first line of code below is quite compact, we will break it apart to discuss what various components do. The newdata1$rankP tells R that we want to create a new variable in the dataset (data frame) newdata1 called rankP, the rest of the command tells R that the values of rankP should be predictions made using the predict( ) function. The options within the parentheses tell R that the predictions should be based on the analysis mylogit with values of the predictor variables coming from newdata1 and that the type of prediction is a predicted probability (type=“response”). The second line of the code lists the values in the data frame newdata1. Although not particularly pretty, this is a table of predicted probabilities.
In the above output we see that the predicted probability of being accepted into a graduate program is 0.52 for students from the highest prestige undergraduate institutions (rank=1), and 0.18 for students from the lowest ranked institutions (rank=4), holding gre and gpa at their means.
Now, we are going to do something that do not exist in our SPSS section
The code to generate the predicted probabilities (the first line below) is the same as before, except we are also going to ask for standard errors so we can plot a confidence interval. We get the estimates on the link scale and back transform both the predicted values and confidence limits into probabilities.
It can also be helpful to use graphs of predicted probabilities to understand and/or present the model. We will use the ggplot2 package for graphing.

We may also wish to see measures of how well our model fits. This can be particularly useful when comparing competing models. The output produced by summary(mylogit) included indices of fit (shown below the coefficients), including the null and deviance residuals and the AIC. One measure of model fit is the significance of the overall model. This test asks whether the model with predictors fits significantly better than a model with just an intercept (i.e., a null model). The test statistic is the difference between the residual deviance for the model with predictors and the null model. The test statistic is distributed chi-squared with degrees of freedom equal to the differences in degrees of freedom between the current and the null model (i.e., the number of predictor variables in the model). To find the difference in deviance for the two models (i.e., the test statistic) we can use the command:
10.8 Things to consider
Empty cells or small cells: You should check for empty or small cells by doing a crosstab between categorical predictors and the outcome variable. If a cell has very few cases (a small cell), the model may become unstable or it might not run at all.
Separation or quasi-separation (also called perfect prediction), a condition in which the outcome does not vary at some levels of the independent variables. See our page FAQ: What is complete or quasi-complete separation in logistic/probit regression and how do we deal with them? for information on models with perfect prediction. Link
Sample size: Both logit and probit models require more cases than OLS regression because they use maximum likelihood estimation techniques. It is sometimes possible to estimate models for binary outcomes in datasets with only a small number of cases using exact logistic regression. It is also important to keep in mind that when the outcome is rare, even if the overall dataset is large, it can be difficult to estimate a logit model.
Pseudo-R-squared: Many different measures of psuedo-R-squared exist. They all attempt to provide information similar to that provided by R-squared in OLS regression; however, none of them can be interpreted exactly as R-squared in OLS regression is interpreted. For a discussion of various pseudo-R-squareds see Long and Freese (2006) or our FAQ page What are pseudo R-squareds? Link
Diagnostics: The diagnostics for logistic regression are different from those for OLS regression. For a discussion of model diagnostics for logistic regression, see Hosmer and Lemeshow (2000, Chapter 5). Note that diagnostics done for logistic regression are similar to those done for probit regression.
10.9 Supplementary Learning Materials
Agresti, A. (1996). An Introduction to Categorical Data Analysis. Wiley & Sons, NY.
Burns, R. P. & Burns R. (2008). Business research methods & statistics using SPSS. SAGE Publications.
Field, A (2013). Discovering statistics using IBM SPSS statistics (4th ed.). Los Angeles, CA: Sage Publications
Data files from Link1 , Link2 , & Link3 .
Introduction to Statistics and Data Science
Chapter 18 logistic regression, 18.1 what is logistic regression used for.
Logistic regression is useful when we have a response variable which is categorical with only two categories. This might seem like it wouldn’t be especially useful, however with a little thought we can see that this is actually a very useful thing to know how to do. Here are some examples where we might use logistic regression .
- Predict whether a customer will visit your website again using browsing data
- Predict whether a voter will vote for the democratic candidate in an upcoming election using demographic and polling data
- Predict whether a patient given a surgery will survive for 5+ years after the surgery using health data
- Given the history of a stock, market trends predict if the closing price tomorrow will be higher or lower than today?
With many other possible examples. We can often phrase important questions as yes/no or (0-1) answers where we want to use some data to better predict the outcome. This is a simple case of what is called a classification problem in the machine learning/data science community. Given some information we want to use a computer to decide make a prediction which can be sorted into some finite number of outcomes.
18.2 GLM: Generalized Linear Models
Our linear regression techniques thus far have focused on cases where the response ( \(Y\) ) variable is continuous in nature. Recall, they take the form: \[ \begin{equation} Y_i=\alpha+ \sum_{j=1}^N \beta_j X_{ij} \end{equation} \] Where \(alpha\) is the intercept and \(\{\beta_1, \beta_2, ... \beta_N\}\) are the slope parameters for the explanatory variables ( \(\{X_1, X_2, ...X_N\}\) ). However, our outputs \(Y_i\) should give the probability that \(Y_i\) takes the value 1 given the \(X_j\) values. The right hand side of our model above will produce values in \(\mathbb{R}=(-\infty, \infty)\) while the left hand side should live in \([0,1]\) .
Therefore to use a model like this we need to transform our outputs from [0,1] to the whole real line \(\mathbb{R}\) .

\[y_i=g \left( \alpha+ \sum_{j=1}^N \beta_j X_{ij} \right)\]
18.3 A Starting Example
Let’s consider the shot logs data set again. We will use the shot distance column SHOT_DIST and the FGM columns for a logistic regression. The FGM column is 1 if the shot was made and 0 otherwise (perfect candidate for the response variable in a logistic regression). We expect that the further the shot is from the basket (SHOT_DIST) the less likely it will be that the shot is made (FGM=1).
To build this model in R we will use the glm() command and specify the link function we are using a the logit function.
\[logit(p)=0.392-0.04 \times SD \implies p=logit^{-1}(0.392-0.04 \times SD)\] So we can find the probability of a shot going in 12 feet from the basket as:
Here is a plot of the probability of a shot going in as a function of the distance from the basket using our best fit coefficients.

18.3.1 Confidence Intervals for the Parameters
A major point of this book is that you should never be satisfied with a single number summary in statistics. Rather than just considering a single best fit for our coefficients we should really form some confidence intervals for their values.
As we saw for simple regression we can look at the confidence intervals for our intercepts and slopes using the confint command.
Note, these values are still in the logit transformed scale.
18.4 Equivalence of Logistic Regression and Proportion Tests
Suppose we want to use the categorical variable of the individual player in our analysis. In the interest of keeping our tables and graphs visible we will limit our players to just those who took more than 820 shots in the data set.
| Name | Number of Shots |
|---|---|
| blake griffin | 878 |
| chris paul | 851 |
| damian lillard | 925 |
| gordon hayward | 833 |
| james harden | 1006 |
| klay thompson | 953 |
| kyle lowry | 832 |
| kyrie irving | 919 |
| lamarcus aldridge | 1010 |
| lebron james | 947 |
| mnta ellis | 1004 |
| nikola vucevic | 889 |
| rudy gay | 861 |
| russell westbrook | 943 |
| stephen curry | 941 |
| tyreke evans | 875 |
Now we can get a reduced data set with just these players.
Lets form a logistic regression using just a categorical variable as the explanatory variable. \[ \begin{equation} logit(p)=\beta Player \end{equation} \]
If we take the inverse logit of the coefficients we get the field goal percentage of the players in our data set.
Now suppose we want to see if the players in our data set truly differ in their field goal percentages or whether the differences we observe could just be caused by random effects. To do this we want to compare a model without the players information included with one that includes this information. Let’s create a null model to compare against our player model.
This null model contains no explanatory variables and takes the form: \[logit(p_i)=\alpha\]
Thus, the shooting percentage is not allowed to vary between the players. We find based on this data an overall field goal percentage of:
Now we may compare logistic regression models using the anova command in R.
The second line contains a p value of 2.33e-5 telling us to reject the null hypothesis that the two models are equivalent. So we found that knowledge of the player does matter in calculating the probability of a shot being made.
Notice we could have performed this analysis as a proportion test using the null that all players shooting percentages are the same \(p_1=p_2=...p_{15}\)
Notice the p-value obtained matches the logistic regression ANOVA almost exactly. Thus, a proportion test can be viewed as a special case of a logistic regression.
18.5 Example: Building a More Accurate Model
Now we can form a model for the shooting percentages using the individual players data:
\[ logit(p_i)=\alpha+\beta_1 SF+\beta_2DD+\beta_3 \text{player_dummy} \]
18.6 Example: Measuring Team Defense Using Logistic Regression
\[ logit(p_i)=\alpha+\beta_1 SD+\beta_2 \text{Team}+\beta_3 (\text{Team}) (SD) \] Since the team defending is a categorical variable R will store it as a dummy variable when forming the regression. Thus the first level of this variable will not appear in our regression (or more precisely it will be included in the intercept \(\alpha\) and slope \(\beta_1\) ). Before we run the model we can see which team will be missing.
The below plot shows the expected shooting percentages at each distance for the teams in the data set.

#Better Approach
Kahneman, Daniel. 2011. Thinking, Fast and Slow . Macmillan.
Wickham, Hadley, and Garrett Grolemund. 2016. R for Data Science: Import, Tidy, Transform, Visualize, and Model Data . " O’Reilly Media, Inc.".
Xie, Yihui. 2019. Bookdown: Authoring Books and Technical Documents with R Markdown . https://CRAN.R-project.org/package=bookdown .

Applied Data Science Meeting, July 4-6, 2023, Shanghai, China . Register for the workshops: (1) Deep Learning Using R, (2) Introduction to Social Network Analysis, (3) From Latent Class Model to Latent Transition Model Using Mplus, (4) Longitudinal Data Analysis, and (5) Practical Mediation Analysis. Click here for more information .
- Example Datasets
- Basics of R
- Graphs in R
- Hypothesis testing
- Confidence interval
- Simple Regression
- Multiple Regression
- Logistic regression
- Moderation analysis
- Mediation analysis
- Path analysis
- Factor analysis
- Multilevel regression
- Longitudinal data analysis
- Power analysis
Logistic Regression
Logistic regression is widely used in social and behavioral research in analyzing the binary (dichotomous) outcome data. In logistic regression, the outcome can only take two values 0 and 1. Some examples that can utilize the logistic regression are given in the following.
- The election of Democratic or Republican president can depend on the factors such as the economic status, the amount of money spent on the campaign, as well as gender and income of the voters.
- Whether an assistant professor can be tenured may be predicted from the number of publications and teaching performance in the first three years.
- Whether or not someone has a heart attack may be related to age, gender and living habits.
- Whether a student is admitted may be predicted by her/his high school GPA, SAT score, and quality of recommendation letters.
We use an example to illustrate how to conduct logistic regression in R.
In this example, the aim is to predict whether a woman is in compliance with mammography screening recommendations from four predictors, one reflecting medical input and three reflecting a woman's psychological status with regarding to screening.
- Outcome y: whether a woman is in compliance with mammography screening recommendations (1: in compliance; 0: not in compliance)
- x1: whether she has received a recommendation for screening from a physician;
- x2: her knowledge about breast cancer and mammography screening;
- x3: her perception of benefit of such a screening;
- x4: her perception of the barriers to being screened.
Basic ideas
With a binary outcome, the linear regression does not work any more. Simply speaking, the predictors can take any value but the outcome cannot. Therefore, using a linear regression cannot predict the outcome well. In order to deal with the problem, we model the probability to observe an outcome 1 instead, that is $p = \Pr(y=1)$. Using the mammography example, that'll be the probability for a woman to be in compliance with the screening recommendation.
Even directly modeling the probability would work better than predicting the 1/0 outcome, intuitively. A potential problem is that the probability is bound between 0 and 1 but the predicted values are generally not. To further deal with the problem, we conduct a transformation using
\[ \eta = \log\frac{p}{1-p}.\]
After transformation, $\eta$ can take any value from $-\infty$ when $p=0$ to $\infty$ when $p=1$. Such a transformation is called logit transformation, denoted by $\text{logit}(p)$. Note that $p_{i}/(1-p_{i})$ is called odds, which is simply the ratio of the probability for the two possible outcomes. For example, if for one woman, the probability that she is in compliance is 0.8, then the odds is 0.8/(1-0.2)=4. Clearly, for equal probability of the outcome, the odds=1. If odds>1, there is a probability higher than 0.5 to observe the outcome 1. With the transformation, the $\eta$ can be directly modeled.
Therefore, the logistic regression is
\[ \mbox{logit}(p_{i})=\log(\frac{p_{i}}{1-p_{i}})=\eta_i=\beta_{0}+\beta_{1}x_{1i}+\ldots+\beta_{k}x_{ki} \]
where $p_i = \Pr(y_i = 1)$. Different from the regular linear regression, no residual is used in the model.
Why is this?
For a variable $y$ with two and only two outcome values, it is often assumed it follows a Bernoulli or binomial distribution with the probability $p$ for the outcome 1 and probability $1-p$ for 0. The density function is
\[ p^y (1-p)^{1-y}. \]
Note that when $y=1$, $p^y (1-p)^{1-y} = p$ exactly.
Furthermore, we assume there is a continuous variable $y^*$ underlying the observed binary variable. If the continuous variable takes a value larger than certain threshold, we would observe 1, otherwise 0. For logistic regression, we assume the continuous variable has a logistic distribution with the density function:
\[ \frac{e^{-y^*}}{1+e^{-y^*}} .\]
The probability for observing 1 is therefore can be directly calculated using the logistic distribution as:
\[ p = \frac{1}{1 + e^{-y^*}},\]
which transforms to
\[ \log\frac{p}{1-p} = y^*.\]
For $y^*$, since it is a continuous variable, it can be predicted as in a regular regression model.
Fitting a logistic regression model in R
In R, the model can be estimated using the glm() function. Logistic regression is one example of the generalized linear model (glm). Below gives the analysis of the mammography data.
- glm uses the model formula same as the linear regression model.
- family = tells the distribution of the outcome variable. For binary data, the binomial distribution is used.
- link = tell the transformation method. Here, the logit transformation is used.
- The output includes the regression coefficients and their z-statistics and p-values.
- The dispersion parameter is related to the variance of the response variable.
Interpret the results
We first focus on how to interpret the parameter estimates from the analysis. For the intercept, when all the predictors take the value 0, we have
\[ \beta_0 = \log(\frac{p}{1-p}), \]
which is the log odds that the observed outcome is 1.
We now look at the coefficient for each predictor. For the mammography example, let's assume $x_2$, $x_3$, and $x_4$ are the same and look at $x_1$ only. If a woman has received a recommendation ($x_1=1$), then the odds is
\[ \log(\frac{p}{1-p})|(x_1=1)=\beta_{0}+\beta_{1}+\beta_{2}x_{2}+\beta_{3}x_{3}+\beta_{4}x_{4}.\]
If a woman has not received a recommendation ($x_1=0$), then the odds is
\[\log(\frac{p}{1-p})|(x_1=0)=\beta_{0}+\beta_{2}x_{2}+\beta_{3}x_{3}+\beta_{4}x_{4}.\]
The difference is
\[\log(\frac{p}{1-p})|(x_1=1)-\log(\frac{p}{1-p})|(x_1=0)=\beta_{1}.\]
Therefore, the logistic regression coefficient for a predictor is the difference in the log odds when the predictor changes 1 unit given other predictors unchanged.
This above equation is equivalent to
\[\log\left(\frac{\frac{p(x_1=1)}{1-p(x_1=1)}}{\frac{p(x_1=0)}{1-p(x_1=0)}}\right)=\beta_{1}.\]
More descriptively, we have
\[\log\left(\frac{\mbox{ODDS(received recommendation)}}{\mbox{ODDS(not received recommendation)}}\right)=\beta_{1}.\]
Therefore, the regression coefficients is the log odds ratio. By a simple transformation, we have
\[\frac{\mbox{ODDS(received recommendation)}}{\mbox{ODDS(not received recommendation)}}=\exp(\beta_{1})\]
\[\mbox{ODDS(received recommendation)} = \exp(\beta_{1})*\mbox{ODDS(not received recommendation)}.\]
Therefore, the exponential of a regression coefficient is the odds ratio. For the example, $exp(\beta_{1})$=exp(1.7731)=5.9. Thus, the odds in compliance to screening for those who received recommendation is about 5.9 times of those who did not receive recommendation.
For continuous predictors, the regression coefficients can also be interpreted the same way. For example, we may say that if high school GPA increase one unit, the odds a student to be admitted can be increased to 6 times given other variables the same.
Although the output does not directly show odds ratio, they can be calculated easily in R as shown below.
By using odds ratios, we can intercept the parameters in the following.
- For x1, if a woman receives a screening recommendation, the odds for her to be in compliance with screening is about 5.9 times of the odds of a woman who does not receive a recommendation given x2, x3, x4 the same. Alternatively (may be more intuitive), if a woman receives a screening recommendation, the odds for her to be in compliance with screening will increase 4.9 times (5.889 – 1 = 4.889 =4.9), given other variables the same.
- For x2, if a woman has one unit more knowledge on breast cancer and mammography screening, the odds for her to be in compliance with screening decreases 58.1% (.419-1=-58.1%, negative number means decrease), keeping other variables constant.
- For x3, if a woman's perception about the benefit increases one unit, the odds for her to be in compliance with screening increases 81% (1.81-1=81%, positive number means increase), keeping other variables constant.
- For x4, if a woman's perception about the barriers increases one unit, the odds for her to be in compliance with screening decreases 14.2% (.858-1=-14.2%, negative number means decrease), keeping other variables constant.

Statistical inference for logistic regression
Statistical inference for logistic regression is very similar to statistical inference for simple linear regression. We can (1) conduct significance testing for each parameter, (2) test the overall model, and (3) test the overall model.
Test a single coefficient (z-test and confidence interval)
For each regression coefficient of the predictors, we can use a z-test (note not the t-test). In the output, we have z-values and corresponding p-values. For x1 and x3, their coefficients are significant at the alpha level 0.05. But for x2 and x4, they are not. Note that some software outputs Wald statistic for testing significance. Wald statistic is the square of the z-statistic and thus Wald test gives the same conclusion as the z-test.
We can also conduct the hypothesis testing by constructing confidence intervals. With the model, the function confint() can be used to obtain the confidence interval. Since one is often interested in odds ratio, its confidence interval can also be obtained.
Note that if the CI for odds ratio includes 1, it means nonsignificance. If it does not include 1, the coefficient is significant. This is because for the original coefficient, we compare the CI with 0. For odds ratio, exp(0)=1.
If we were reporting the results in terms of the odds and its CI, we could say, “The odds of in compliance to screening increases by a factor of 5.9 if receiving screening recommendation (z=3.66, P = 0.0002; 95% CI = 2.38 to 16.23) given everything else the same.”
Test the overall model
For the linear regression, we evaluate the overall model fit by looking at the variance explained by all the predictors. For the logistic regression, we cannot calculate a variance. However, we can define and evaluate the deviance instead. For a model without any predictor, we can calculate a null deviance, which is similar to variance for the normal outcome variable. After including the predictors, we have the residual deviance. The difference between the null deviance and the residual deviance tells how much the predictors help predict the outcome. If the difference is significant, then overall, the predictors are significant statistically.
The difference or the decease in deviance after including the predictors follows a chi-square ($\chi^{2}$) distribution. The chi-square ($\chi^{2}$) distribution is a widely used distribution in statistical inference. It has a close relationship to F distribution. For example, the ratio of two independent chi-square distributions is a F distribution. In addition, a chi-square distribution is the limiting distribution of an F distribution as the denominator degrees of freedom goes to infinity.
There are two ways to conduct the test. From the output, we can find the Null and Residual deviances and the corresponding degrees of freedom. Then we calculate the difference. For the mammography example, we first get the difference between the Null deviance and the Residual deviance, 203.32-155.48= 47.84. Then, we find the difference in the degrees of freedom 163-159=4. Then, the p-value can be calculated based on a chi-square distribution with the degree of freedom 4. Because the p-value is smaller than 0.05, the overall model is significant.
The test can be conducted simply in another way. We first fit a model without any predictor and another model with all the predictors. Then, we can use anova() to get the difference in deviance and the chi-square test result.
Test a subset of predictors
We can also test the significance of a subset of predictors. For example, whether x3 and x4 are significant above and beyond x1 and x2. This can also be done using the chi-square test based on the difference. In this case, we can compare a model with all predictors and a model without x3 and x4 to see if the change in the deviance is significant. In this example, the p-value is 0.002, indicating the change is signficant. Therefore, x3 and x4 are statistically significant above and beyond x1 and x2
To cite the book, use: Zhang, Z. & Wang, L. (2017-2022). Advanced statistics using R . Granger, IN: ISDSA Press. https://doi.org/10.35566/advstats. ISBN: 978-1-946728-01-2. To take the full advantage of the book such as running analysis within your web browser, please subscribe .

Logistic Regression in Python
Table of Contents
What Is Classification?
When do you need classification, math prerequisites, problem formulation, methodology, classification performance, single-variate logistic regression, multi-variate logistic regression, regularization, logistic regression python packages, logistic regression in python with scikit-learn: example 1, logistic regression in python with scikit-learn: example 2, logistic regression in python with statsmodels: example, logistic regression in python: handwriting recognition, beyond logistic regression in python.
As the amount of available data, the strength of computing power, and the number of algorithmic improvements continue to rise, so does the importance of data science and machine learning . Classification is among the most important areas of machine learning, and logistic regression is one of its basic methods. By the end of this tutorial, you’ll have learned about classification in general and the fundamentals of logistic regression in particular, as well as how to implement logistic regression in Python.
In this tutorial, you’ll learn:
- What logistic regression is
- What logistic regression is used for
- How logistic regression works
- How to implement logistic regression in Python, step by step
Free Bonus: Click here to get access to a free NumPy Resources Guide that points you to the best tutorials, videos, and books for improving your NumPy skills.
Classification
Classification is a very important area of supervised machine learning . A large number of important machine learning problems fall within this area. There are many classification methods, and logistic regression is one of them.
Supervised machine learning algorithms define models that capture relationships among data. Classification is an area of supervised machine learning that tries to predict which class or category some entity belongs to, based on its features.
For example, you might analyze the employees of some company and try to establish a dependence on the features or variables , such as the level of education, number of years in a current position, age, salary, odds for being promoted, and so on. The set of data related to a single employee is one observation . The features or variables can take one of two forms:
- Independent variables , also called inputs or predictors, don’t depend on other features of interest (or at least you assume so for the purpose of the analysis).
- Dependent variables , also called outputs or responses, depend on the independent variables.
In the above example where you’re analyzing employees, you might presume the level of education, time in a current position, and age as being mutually independent, and consider them as the inputs. The salary and the odds for promotion could be the outputs that depend on the inputs.
Note: Supervised machine learning algorithms analyze a number of observations and try to mathematically express the dependence between the inputs and outputs. These mathematical representations of dependencies are the models .
The nature of the dependent variables differentiates regression and classification problems. Regression problems have continuous and usually unbounded outputs. An example is when you’re estimating the salary as a function of experience and education level. On the other hand, classification problems have discrete and finite outputs called classes or categories . For example, predicting if an employee is going to be promoted or not (true or false) is a classification problem.
There are two main types of classification problems:
- Binary or binomial classification: exactly two classes to choose between (usually 0 and 1, true and false, or positive and negative)
- Multiclass or multinomial classification: three or more classes of the outputs to choose from
If there’s only one input variable, then it’s usually denoted with 𝑥. For more than one input, you’ll commonly see the vector notation 𝐱 = (𝑥₁, …, 𝑥ᵣ), where 𝑟 is the number of the predictors (or independent features). The output variable is often denoted with 𝑦 and takes the values 0 or 1.
You can apply classification in many fields of science and technology. For example, text classification algorithms are used to separate legitimate and spam emails, as well as positive and negative comments. You can check out Practical Text Classification With Python and Keras to get some insight into this topic. Other examples involve medical applications, biological classification, credit scoring, and more.
Image recognition tasks are often represented as classification problems. For example, you might ask if an image is depicting a human face or not, or if it’s a mouse or an elephant, or which digit from zero to nine it represents, and so on. To learn more about this, check out Traditional Face Detection With Python and Face Recognition with Python, in Under 25 Lines of Code .
Logistic Regression Overview
Logistic regression is a fundamental classification technique. It belongs to the group of linear classifiers and is somewhat similar to polynomial and linear regression . Logistic regression is fast and relatively uncomplicated, and it’s convenient for you to interpret the results. Although it’s essentially a method for binary classification, it can also be applied to multiclass problems.
You’ll need an understanding of the sigmoid function and the natural logarithm function to understand what logistic regression is and how it works.
This image shows the sigmoid function (or S-shaped curve) of some variable 𝑥:
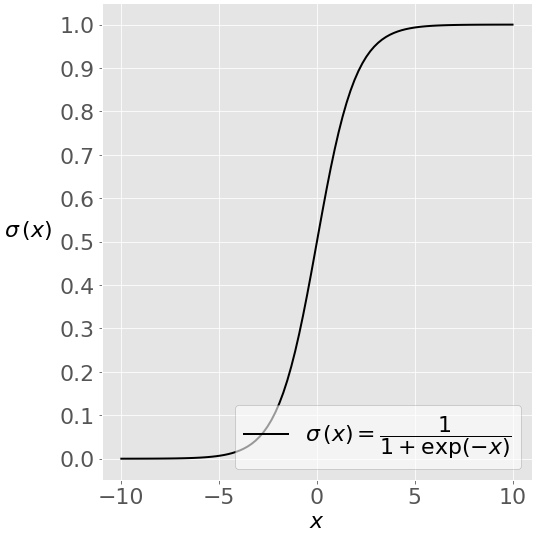
The sigmoid function has values very close to either 0 or 1 across most of its domain. This fact makes it suitable for application in classification methods.
This image depicts the natural logarithm log(𝑥) of some variable 𝑥, for values of 𝑥 between 0 and 1:

As 𝑥 approaches zero, the natural logarithm of 𝑥 drops towards negative infinity. When 𝑥 = 1, log(𝑥) is 0. The opposite is true for log(1 − 𝑥).
Note that you’ll often find the natural logarithm denoted with ln instead of log . In Python, math.log(x) and numpy.log(x) represent the natural logarithm of x , so you’ll follow this notation in this tutorial.
In this tutorial, you’ll see an explanation for the common case of logistic regression applied to binary classification. When you’re implementing the logistic regression of some dependent variable 𝑦 on the set of independent variables 𝐱 = (𝑥₁, …, 𝑥ᵣ), where 𝑟 is the number of predictors ( or inputs), you start with the known values of the predictors 𝐱ᵢ and the corresponding actual response (or output) 𝑦ᵢ for each observation 𝑖 = 1, …, 𝑛.
Your goal is to find the logistic regression function 𝑝(𝐱) such that the predicted responses 𝑝(𝐱ᵢ) are as close as possible to the actual response 𝑦ᵢ for each observation 𝑖 = 1, …, 𝑛. Remember that the actual response can be only 0 or 1 in binary classification problems! This means that each 𝑝(𝐱ᵢ) should be close to either 0 or 1. That’s why it’s convenient to use the sigmoid function.
Once you have the logistic regression function 𝑝(𝐱), you can use it to predict the outputs for new and unseen inputs, assuming that the underlying mathematical dependence is unchanged.
Logistic regression is a linear classifier, so you’ll use a linear function 𝑓(𝐱) = 𝑏₀ + 𝑏₁𝑥₁ + ⋯ + 𝑏ᵣ𝑥ᵣ, also called the logit . The variables 𝑏₀, 𝑏₁, …, 𝑏ᵣ are the estimators of the regression coefficients, which are also called the predicted weights or just coefficients .
The logistic regression function 𝑝(𝐱) is the sigmoid function of 𝑓(𝐱): 𝑝(𝐱) = 1 / (1 + exp(−𝑓(𝐱)). As such, it’s often close to either 0 or 1. The function 𝑝(𝐱) is often interpreted as the predicted probability that the output for a given 𝐱 is equal to 1. Therefore, 1 − 𝑝(𝑥) is the probability that the output is 0.
Logistic regression determines the best predicted weights 𝑏₀, 𝑏₁, …, 𝑏ᵣ such that the function 𝑝(𝐱) is as close as possible to all actual responses 𝑦ᵢ, 𝑖 = 1, …, 𝑛, where 𝑛 is the number of observations. The process of calculating the best weights using available observations is called model training or fitting .
To get the best weights, you usually maximize the log-likelihood function (LLF) for all observations 𝑖 = 1, …, 𝑛. This method is called the maximum likelihood estimation and is represented by the equation LLF = Σᵢ(𝑦ᵢ log(𝑝(𝐱ᵢ)) + (1 − 𝑦ᵢ) log(1 − 𝑝(𝐱ᵢ))).
When 𝑦ᵢ = 0, the LLF for the corresponding observation is equal to log(1 − 𝑝(𝐱ᵢ)). If 𝑝(𝐱ᵢ) is close to 𝑦ᵢ = 0, then log(1 − 𝑝(𝐱ᵢ)) is close to 0. This is the result you want. If 𝑝(𝐱ᵢ) is far from 0, then log(1 − 𝑝(𝐱ᵢ)) drops significantly. You don’t want that result because your goal is to obtain the maximum LLF. Similarly, when 𝑦ᵢ = 1, the LLF for that observation is 𝑦ᵢ log(𝑝(𝐱ᵢ)). If 𝑝(𝐱ᵢ) is close to 𝑦ᵢ = 1, then log(𝑝(𝐱ᵢ)) is close to 0. If 𝑝(𝐱ᵢ) is far from 1, then log(𝑝(𝐱ᵢ)) is a large negative number.
There are several mathematical approaches that will calculate the best weights that correspond to the maximum LLF, but that’s beyond the scope of this tutorial. For now, you can leave these details to the logistic regression Python libraries you’ll learn to use here!
Once you determine the best weights that define the function 𝑝(𝐱), you can get the predicted outputs 𝑝(𝐱ᵢ) for any given input 𝐱ᵢ. For each observation 𝑖 = 1, …, 𝑛, the predicted output is 1 if 𝑝(𝐱ᵢ) > 0.5 and 0 otherwise. The threshold doesn’t have to be 0.5, but it usually is. You might define a lower or higher value if that’s more convenient for your situation.
There’s one more important relationship between 𝑝(𝐱) and 𝑓(𝐱), which is that log(𝑝(𝐱) / (1 − 𝑝(𝐱))) = 𝑓(𝐱). This equality explains why 𝑓(𝐱) is the logit . It implies that 𝑝(𝐱) = 0.5 when 𝑓(𝐱) = 0 and that the predicted output is 1 if 𝑓(𝐱) > 0 and 0 otherwise.
Binary classification has four possible types of results :
- True negatives: correctly predicted negatives (zeros)
- True positives: correctly predicted positives (ones)
- False negatives: incorrectly predicted negatives (zeros)
- False positives: incorrectly predicted positives (ones)
You usually evaluate the performance of your classifier by comparing the actual and predicted outputsand counting the correct and incorrect predictions.
The most straightforward indicator of classification accuracy is the ratio of the number of correct predictions to the total number of predictions (or observations). Other indicators of binary classifiers include the following:
- The positive predictive value is the ratio of the number of true positives to the sum of the numbers of true and false positives.
- The negative predictive value is the ratio of the number of true negatives to the sum of the numbers of true and false negatives.
- The sensitivity (also known as recall or true positive rate) is the ratio of the number of true positives to the number of actual positives.
- The specificity (or true negative rate) is the ratio of the number of true negatives to the number of actual negatives.
The most suitable indicator depends on the problem of interest. In this tutorial, you’ll use the most straightforward form of classification accuracy.
Single-variate logistic regression is the most straightforward case of logistic regression. There is only one independent variable (or feature), which is 𝐱 = 𝑥. This figure illustrates single-variate logistic regression:
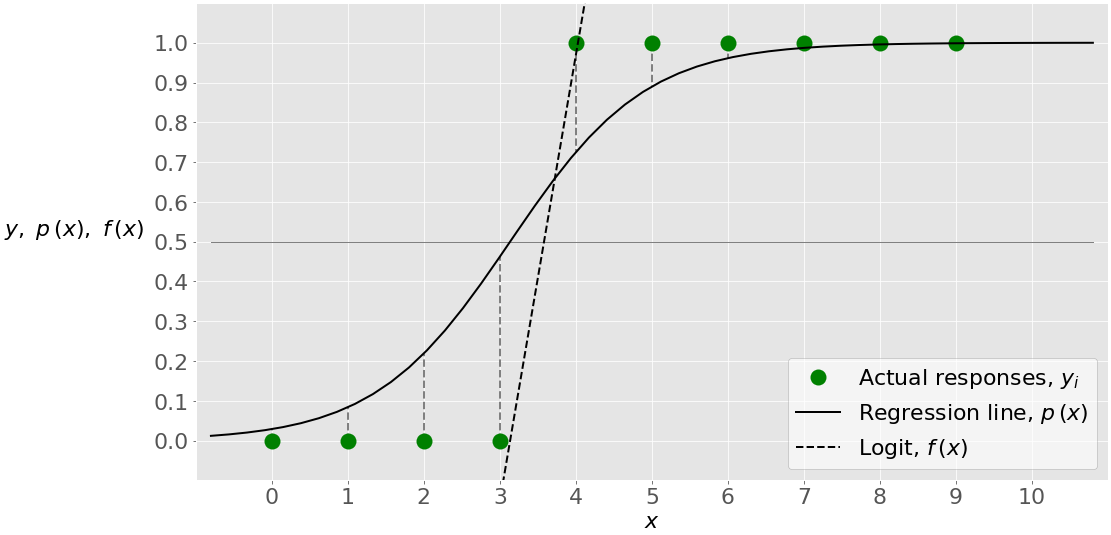
Here, you have a given set of input-output (or 𝑥-𝑦) pairs, represented by green circles. These are your observations. Remember that 𝑦 can only be 0 or 1. For example, the leftmost green circle has the input 𝑥 = 0 and the actual output 𝑦 = 0. The rightmost observation has 𝑥 = 9 and 𝑦 = 1.
Logistic regression finds the weights 𝑏₀ and 𝑏₁ that correspond to the maximum LLF. These weights define the logit 𝑓(𝑥) = 𝑏₀ + 𝑏₁𝑥, which is the dashed black line. They also define the predicted probability 𝑝(𝑥) = 1 / (1 + exp(−𝑓(𝑥))), shown here as the full black line. In this case, the threshold 𝑝(𝑥) = 0.5 and 𝑓(𝑥) = 0 corresponds to the value of 𝑥 slightly higher than 3. This value is the limit between the inputs with the predicted outputs of 0 and 1.
Multi-variate logistic regression has more than one input variable. This figure shows the classification with two independent variables, 𝑥₁ and 𝑥₂:

The graph is different from the single-variate graph because both axes represent the inputs. The outputs also differ in color. The white circles show the observations classified as zeros, while the green circles are those classified as ones.
Logistic regression determines the weights 𝑏₀, 𝑏₁, and 𝑏₂ that maximize the LLF. Once you have 𝑏₀, 𝑏₁, and 𝑏₂, you can get:
- The logit 𝑓(𝑥₁, 𝑥₂) = 𝑏₀ + 𝑏₁𝑥₁ + 𝑏₂𝑥₂
- The probabilities 𝑝(𝑥₁, 𝑥₂) = 1 / (1 + exp(−𝑓(𝑥₁, 𝑥₂)))
The dash-dotted black line linearly separates the two classes. This line corresponds to 𝑝(𝑥₁, 𝑥₂) = 0.5 and 𝑓(𝑥₁, 𝑥₂) = 0.
Overfitting is one of the most serious kinds of problems related to machine learning. It occurs when a model learns the training data too well. The model then learns not only the relationships among data but also the noise in the dataset. Overfitted models tend to have good performance with the data used to fit them (the training data), but they behave poorly with unseen data (or test data, which is data not used to fit the model).
Overfitting usually occurs with complex models. Regularization normally tries to reduce or penalize the complexity of the model. Regularization techniques applied with logistic regression mostly tend to penalize large coefficients 𝑏₀, 𝑏₁, …, 𝑏ᵣ:
- L1 regularization penalizes the LLF with the scaled sum of the absolute values of the weights: |𝑏₀|+|𝑏₁|+⋯+|𝑏ᵣ|.
- L2 regularization penalizes the LLF with the scaled sum of the squares of the weights: 𝑏₀²+𝑏₁²+⋯+𝑏ᵣ².
- Elastic-net regularization is a linear combination of L1 and L2 regularization.
Regularization can significantly improve model performance on unseen data.
Now that you understand the fundamentals, you’re ready to apply the appropriate packages as well as their functions and classes to perform logistic regression in Python. In this section, you’ll see the following:
- A summary of Python packages for logistic regression (NumPy, scikit-learn, StatsModels, and Matplotlib)
- Two illustrative examples of logistic regression solved with scikit-learn
- One conceptual example solved with StatsModels
- One real-world example of classifying handwritten digits
Let’s start implementing logistic regression in Python!
There are several packages you’ll need for logistic regression in Python. All of them are free and open-source, with lots of available resources. First, you’ll need NumPy , which is a fundamental package for scientific and numerical computing in Python. NumPy is useful and popular because it enables high-performance operations on single- and multi-dimensional arrays.
NumPy has many useful array routines. It allows you to write elegant and compact code, and it works well with many Python packages. If you want to learn NumPy, then you can start with the official user guide . The NumPy Reference also provides comprehensive documentation on its functions, classes, and methods.
Note: To learn more about NumPy performance and the other benefits it can offer, check out Pure Python vs NumPy vs TensorFlow Performance Comparison and Look Ma, No for Loops: Array Programming With NumPy .
Another Python package you’ll use is scikit-learn . This is one of the most popular data science and machine learning libraries. You can use scikit-learn to perform various functions:
- Preprocess data
- Reduce the dimensionality of problems
- Validate models
- Select the most appropriate model
- Solve regression and classification problems
- Implement cluster analysis
You’ll find useful information on the official scikit-learn website , where you might want to read about generalized linear models and logistic regression implementation . If you need functionality that scikit-learn can’t offer, then you might find StatsModels useful. It’s a powerful Python library for statistical analysis. You can find more information on the official website .
Finally, you’ll use Matplotlib to visualize the results of your classification. This is a Python library that’s comprehensive and widely used for high-quality plotting. For additional information, you can check the official website and user guide . There are several resources for learning Matplotlib you might find useful, like the official tutorials , the Anatomy of Matplotlib , and Python Plotting With Matplotlib (Guide) .
The first example is related to a single-variate binary classification problem. This is the most straightforward kind of classification problem. There are several general steps you’ll take when you’re preparing your classification models:
- Import packages, functions, and classes
- Get data to work with and, if appropriate, transform it
- Create a classification model and train (or fit) it with your existing data
- Evaluate your model to see if its performance is satisfactory
A sufficiently good model that you define can be used to make further predictions related to new, unseen data. The above procedure is the same for classification and regression.
Step 1: Import Packages, Functions, and Classes
First, you have to import Matplotlib for visualization and NumPy for array operations. You’ll also need LogisticRegression , classification_report() , and confusion_matrix() from scikit-learn:
Now you’ve imported everything you need for logistic regression in Python with scikit-learn!
Step 2: Get Data
In practice, you’ll usually have some data to work with. For the purpose of this example, let’s just create arrays for the input (𝑥) and output (𝑦) values:
The input and output should be NumPy arrays (instances of the class numpy.ndarray ) or similar objects. numpy.arange() creates an array of consecutive, equally-spaced values within a given range. For more information on this function, check the official documentation or NumPy arange(): How to Use np.arange() .
The array x is required to be two-dimensional . It should have one column for each input, and the number of rows should be equal to the number of observations. To make x two-dimensional, you apply .reshape() with the arguments -1 to get as many rows as needed and 1 to get one column. For more information on .reshape() , you can check out the official documentation . Here’s how x and y look now:
x has two dimensions:
- One column for a single input
- Ten rows , each corresponding to one observation
y is one-dimensional with ten items. Again, each item corresponds to one observation. It contains only zeros and ones since this is a binary classification problem.
Step 3: Create a Model and Train It
Once you have the input and output prepared, you can create and define your classification model. You’re going to represent it with an instance of the class LogisticRegression :
The above statement creates an instance of LogisticRegression and binds its references to the variable model . LogisticRegression has several optional parameters that define the behavior of the model and approach:
penalty is a string ( 'l2' by default) that decides whether there is regularization and which approach to use. Other options are 'l1' , 'elasticnet' , and 'none' .
dual is a Boolean ( False by default) that decides whether to use primal (when False ) or dual formulation (when True ).
tol is a floating-point number ( 0.0001 by default) that defines the tolerance for stopping the procedure.
C is a positive floating-point number ( 1.0 by default) that defines the relative strength of regularization. Smaller values indicate stronger regularization.
fit_intercept is a Boolean ( True by default) that decides whether to calculate the intercept 𝑏₀ (when True ) or consider it equal to zero (when False ).
intercept_scaling is a floating-point number ( 1.0 by default) that defines the scaling of the intercept 𝑏₀.
class_weight is a dictionary, 'balanced' , or None (default) that defines the weights related to each class. When None , all classes have the weight one.
random_state is an integer, an instance of numpy.RandomState , or None (default) that defines what pseudo-random number generator to use.
solver is a string ( 'liblinear' by default) that decides what solver to use for fitting the model. Other options are 'newton-cg' , 'lbfgs' , 'sag' , and 'saga' .
max_iter is an integer ( 100 by default) that defines the maximum number of iterations by the solver during model fitting.
multi_class is a string ( 'ovr' by default) that decides the approach to use for handling multiple classes. Other options are 'multinomial' and 'auto' .
verbose is a non-negative integer ( 0 by default) that defines the verbosity for the 'liblinear' and 'lbfgs' solvers.
warm_start is a Boolean ( False by default) that decides whether to reuse the previously obtained solution.
n_jobs is an integer or None (default) that defines the number of parallel processes to use. None usually means to use one core, while -1 means to use all available cores.
l1_ratio is either a floating-point number between zero and one or None (default). It defines the relative importance of the L1 part in the elastic-net regularization.
You should carefully match the solver and regularization method for several reasons:
- 'liblinear' solver doesn’t work without regularization.
- 'newton-cg' , 'sag' , 'saga' , and 'lbfgs' don’t support L1 regularization.
- 'saga' is the only solver that supports elastic-net regularization.
Once the model is created, you need to fit (or train) it. Model fitting is the process of determining the coefficients 𝑏₀, 𝑏₁, …, 𝑏ᵣ that correspond to the best value of the cost function. You fit the model with .fit() :
.fit() takes x , y , and possibly observation-related weights. Then it fits the model and returns the model instance itself:
This is the obtained string representation of the fitted model.
You can use the fact that .fit() returns the model instance and chain the last two statements. They are equivalent to the following line of code:
At this point, you have the classification model defined.
You can quickly get the attributes of your model. For example, the attribute .classes_ represents the array of distinct values that y takes:
This is the example of binary classification, and y can be 0 or 1 , as indicated above.
You can also get the value of the slope 𝑏₁ and the intercept 𝑏₀ of the linear function 𝑓 like so:
As you can see, 𝑏₀ is given inside a one-dimensional array, while 𝑏₁ is inside a two-dimensional array. You use the attributes .intercept_ and .coef_ to get these results.
Step 4: Evaluate the Model
Once a model is defined, you can check its performance with .predict_proba() , which returns the matrix of probabilities that the predicted output is equal to zero or one:
In the matrix above, each row corresponds to a single observation. The first column is the probability of the predicted output being zero, that is 1 - 𝑝(𝑥). The second column is the probability that the output is one, or 𝑝(𝑥).
You can get the actual predictions, based on the probability matrix and the values of 𝑝(𝑥), with .predict() :
This function returns the predicted output values as a one-dimensional array.
The figure below illustrates the input, output, and classification results:

The green circles represent the actual responses as well as the correct predictions. The red × shows the incorrect prediction. The full black line is the estimated logistic regression line 𝑝(𝑥). The grey squares are the points on this line that correspond to 𝑥 and the values in the second column of the probability matrix. The black dashed line is the logit 𝑓(𝑥).
The value of 𝑥 slightly above 2 corresponds to the threshold 𝑝(𝑥)=0.5, which is 𝑓(𝑥)=0. This value of 𝑥 is the boundary between the points that are classified as zeros and those predicted as ones.
For example, the first point has input 𝑥=0, actual output 𝑦=0, probability 𝑝=0.26, and a predicted value of 0. The second point has 𝑥=1, 𝑦=0, 𝑝=0.37, and a prediction of 0. Only the fourth point has the actual output 𝑦=0 and the probability higher than 0.5 (at 𝑝=0.62), so it’s wrongly classified as 1. All other values are predicted correctly.
When you have nine out of ten observations classified correctly, the accuracy of your model is equal to 9/10=0.9, which you can obtain with .score() :
.score() takes the input and output as arguments and returns the ratio of the number of correct predictions to the number of observations.
You can get more information on the accuracy of the model with a confusion matrix . In the case of binary classification, the confusion matrix shows the numbers of the following:
- True negatives in the upper-left position
- False negatives in the lower-left position
- False positives in the upper-right position
- True positives in the lower-right position
To create the confusion matrix, you can use confusion_matrix() and provide the actual and predicted outputs as the arguments:
The obtained matrix shows the following:
- Three true negative predictions: The first three observations are zeros predicted correctly.
- No false negative predictions: These are the ones wrongly predicted as zeros.
- One false positive prediction: The fourth observation is a zero that was wrongly predicted as one.
- Six true positive predictions: The last six observations are ones predicted correctly.
It’s often useful to visualize the confusion matrix. You can do that with .imshow() from Matplotlib, which accepts the confusion matrix as the argument:
The code above creates a heatmap that represents the confusion matrix:
In this figure, different colors represent different numbers and similar colors represent similar numbers. Heatmaps are a nice and convenient way to represent a matrix. To learn more about them, check out the Matplotlib documentation on Creating Annotated Heatmaps and .imshow() .
You can get a more comprehensive report on the classification with classification_report() :
This function also takes the actual and predicted outputs as arguments. It returns a report on the classification as a dictionary if you provide output_dict=True or a string otherwise.
Note: It’s usually better to evaluate your model with the data you didn’t use for training. That’s how you avoid bias and detect overfitting. You’ll see an example later in this tutorial.
For more information on LogisticRegression , check out the official documentation . In addition, scikit-learn offers a similar class LogisticRegressionCV , which is more suitable for cross-validation . You can also check out the official documentation to learn more about classification reports and confusion matrices .
Improve the Model
You can improve your model by setting different parameters. For example, let’s work with the regularization strength C equal to 10.0 , instead of the default value of 1.0 :
Now you have another model with different parameters. It’s also going to have a different probability matrix and a different set of coefficients and predictions:
As you can see, the absolute values of the intercept 𝑏₀ and the coefficient 𝑏₁ are larger. This is the case because the larger value of C means weaker regularization, or weaker penalization related to high values of 𝑏₀ and 𝑏₁.
Different values of 𝑏₀ and 𝑏₁ imply a change of the logit 𝑓(𝑥), different values of the probabilities 𝑝(𝑥), a different shape of the regression line, and possibly changes in other predicted outputs and classification performance. The boundary value of 𝑥 for which 𝑝(𝑥)=0.5 and 𝑓(𝑥)=0 is higher now. It’s above 3. In this case, you obtain all true predictions, as shown by the accuracy, confusion matrix, and classification report:
The score (or accuracy) of 1 and the zeros in the lower-left and upper-right fields of the confusion matrix indicate that the actual and predicted outputs are the same. That’s also shown with the figure below:
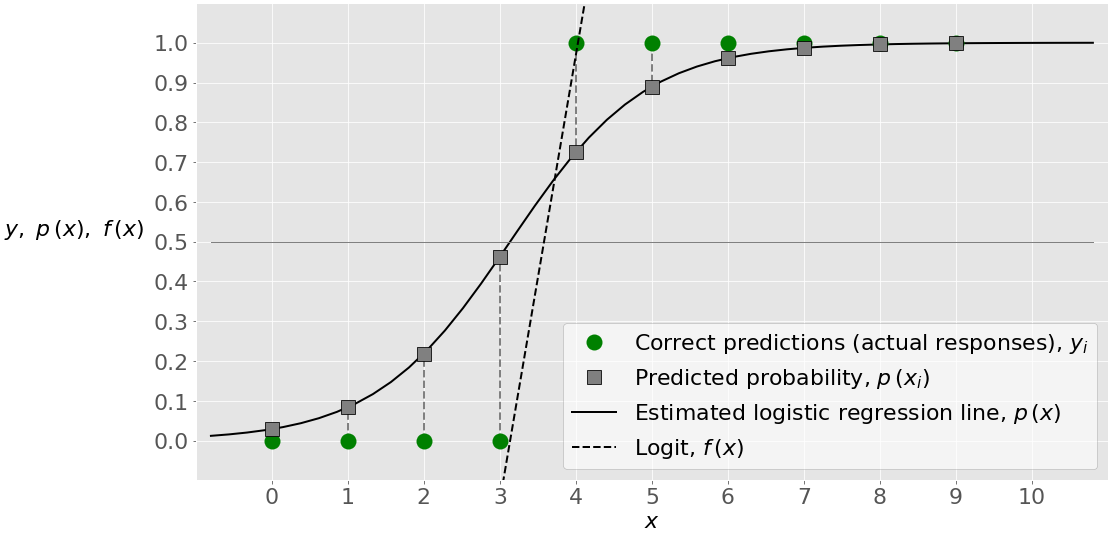
This figure illustrates that the estimated regression line now has a different shape and that the fourth point is correctly classified as 0. There isn’t a red ×, so there is no wrong prediction.
Let’s solve another classification problem. It’s similar to the previous one, except that the output differs in the second value. The code is similar to the previous case:
This classification code sample generates the following results:
In this case, the score (or accuracy) is 0.8. There are two observations classified incorrectly. One of them is a false negative, while the other is a false positive.
The figure below illustrates this example with eight correct and two incorrect predictions:

This figure reveals one important characteristic of this example. Unlike the previous one, this problem is not linearly separable . That means you can’t find a value of 𝑥 and draw a straight line to separate the observations with 𝑦=0 and those with 𝑦=1. There is no such line. Keep in mind that logistic regression is essentially a linear classifier, so you theoretically can’t make a logistic regression model with an accuracy of 1 in this case.
You can also implement logistic regression in Python with the StatsModels package. Typically, you want this when you need more statistical details related to models and results. The procedure is similar to that of scikit-learn.
Step 1: Import Packages
All you need to import is NumPy and statsmodels.api :
Now you have the packages you need.
You can get the inputs and output the same way as you did with scikit-learn. However, StatsModels doesn’t take the intercept 𝑏₀ into account, and you need to include the additional column of ones in x . You do that with add_constant() :
add_constant() takes the array x as the argument and returns a new array with the additional column of ones. This is how x and y look:
This is your data. The first column of x corresponds to the intercept 𝑏₀. The second column contains the original values of x .
Your logistic regression model is going to be an instance of the class statsmodels.discrete.discrete_model.Logit . This is how you can create one:
Note that the first argument here is y , followed by x .
Now, you’ve created your model and you should fit it with the existing data. You do that with .fit() or, if you want to apply L1 regularization, with .fit_regularized() :
The model is now ready, and the variable result holds useful data. For example, you can obtain the values of 𝑏₀ and 𝑏₁ with .params :
The first element of the obtained array is the intercept 𝑏₀, while the second is the slope 𝑏₁. For more information, you can look at the official documentation on Logit , as well as .fit() and .fit_regularized() .
You can use results to obtain the probabilities of the predicted outputs being equal to one:
These probabilities are calculated with .predict() . You can use their values to get the actual predicted outputs:
The obtained array contains the predicted output values. As you can see, 𝑏₀, 𝑏₁, and the probabilities obtained with scikit-learn and StatsModels are different. This is the consequence of applying different iterative and approximate procedures and parameters. However, in this case, you obtain the same predicted outputs as when you used scikit-learn.
You can obtain the confusion matrix with .pred_table() :
This example is the same as when you used scikit-learn because the predicted ouptuts are equal. The confusion matrices you obtained with StatsModels and scikit-learn differ in the types of their elements (floating-point numbers and integers).
.summary() and .summary2() get output data that you might find useful in some circumstances:
These are detailed reports with values that you can obtain with appropriate methods and attributes. For more information, check out the official documentation related to LogitResults .
The previous examples illustrated the implementation of logistic regression in Python, as well as some details related to this method. The next example will show you how to use logistic regression to solve a real-world classification problem. The approach is very similar to what you’ve already seen, but with a larger dataset and several additional concerns.
This example is about image recognition . To be more precise, you’ll work on the recognition of handwritten digits. You’ll use a dataset with 1797 observations, each of which is an image of one handwritten digit. Each image has 64 px, with a width of 8 px and a height of 8 px.
Note: To learn more about this dataset, check the official documentation .
The inputs (𝐱) are vectors with 64 dimensions or values. Each input vector describes one image. Each of the 64 values represents one pixel of the image. The input values are the integers between 0 and 16, depending on the shade of gray for the corresponding pixel. The output (𝑦) for each observation is an integer between 0 and 9, consistent with the digit on the image. There are ten classes in total, each corresponding to one image.
You’ll need to import Matplotlib, NumPy, and several functions and classes from scikit-learn:
That’s it! You have all the functionality you need to perform classification.
Step 2a: Get Data
You can grab the dataset directly from scikit-learn with load_digits() . It returns a tuple of the inputs and output:
Now you have the data. This is how x and y look:
That’s your data to work with. x is a multi-dimensional array with 1797 rows and 64 columns. It contains integers from 0 to 16. y is an one-dimensional array with 1797 integers between 0 and 9.
Step 2b: Split Data
It’s a good and widely-adopted practice to split the dataset you’re working with into two subsets. These are the training set and the test set . This split is usually performed randomly. You should use the training set to fit your model. Once the model is fitted, you evaluate its performance with the test set. It’s important not to use the test set in the process of fitting the model. This approach enables an unbiased evaluation of the model.
One way to split your dataset into training and test sets is to apply train_test_split() :
train_test_split() accepts x and y . It also takes test_size , which determines the size of the test set, and random_state to define the state of the pseudo-random number generator, as well as other optional arguments. This function returns a list with four arrays:
- x_train : the part of x used to fit the model
- x_test : the part of x used to evaluate the model
- y_train : the part of y that corresponds to x_train
- y_test : the part of y that corresponds to x_test
Once your data is split, you can forget about x_test and y_test until you define your model.
Step 2c: Scale Data
Standardization is the process of transforming data in a way such that the mean of each column becomes equal to zero, and the standard deviation of each column is one. This way, you obtain the same scale for all columns. Take the following steps to standardize your data:
- Calculate the mean and standard deviation for each column.
- Subtract the corresponding mean from each element.
- Divide the obtained difference by the corresponding standard deviation.
It’s a good practice to standardize the input data that you use for logistic regression, although in many cases it’s not necessary. Standardization might improve the performance of your algorithm. It helps if you need to compare and interpret the weights. It’s important when you apply penalization because the algorithm is actually penalizing against the large values of the weights.
You can standardize your inputs by creating an instance of StandardScaler and calling .fit_transform() on it:
.fit_transform() fits the instance of StandardScaler to the array passed as the argument, transforms this array, and returns the new, standardized array. Now, x_train is a standardized input array.
This step is very similar to the previous examples. The only difference is that you use x_train and y_train subsets to fit the model. Again, you should create an instance of LogisticRegression and call .fit() on it:
When you’re working with problems with more than two classes, you should specify the multi_class parameter of LogisticRegression . It determines how to solve the problem:
- 'ovr' says to make the binary fit for each class.
- 'multinomial' says to apply the multinomial loss fit.
The last statement yields the following output since .fit() returns the model itself:
These are the parameters of your model. It’s now defined and ready for the next step.
You should evaluate your model similar to what you did in the previous examples, with the difference that you’ll mostly use x_test and y_test , which are the subsets not applied for training. If you’ve decided to standardize x_train , then the obtained model relies on the scaled data, so x_test should be scaled as well with the same instance of StandardScaler :
That’s how you obtain a new, properly-scaled x_test . In this case, you use .transform() , which only transforms the argument, without fitting the scaler.
You can obtain the predicted outputs with .predict() :
The variable y_pred is now bound to an array of the predicted outputs. Note that you use x_test as the argument here.
You can obtain the accuracy with .score() :
Actually, you can get two values of the accuracy, one obtained with the training set and other with the test set. It might be a good idea to compare the two, as a situation where the training set accuracy is much higher might indicate overfitting. The test set accuracy is more relevant for evaluating the performance on unseen data since it’s not biased.
You can get the confusion matrix with confusion_matrix() :
The obtained confusion matrix is large. In this case, it has 100 numbers. This is a situation when it might be really useful to visualize it:
The code above produces the following figure of the confusion matrix:
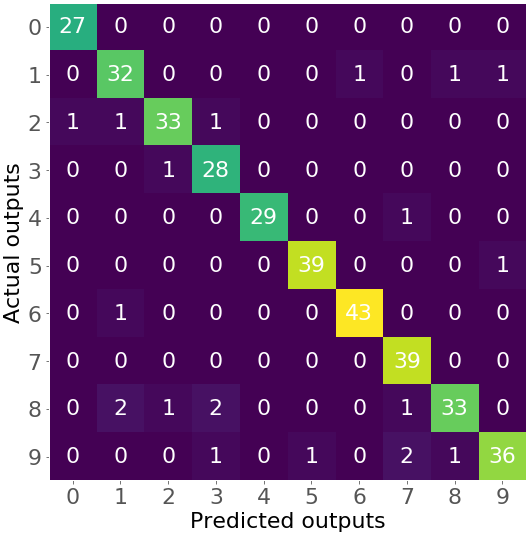
This is a heatmap that illustrates the confusion matrix with numbers and colors. You can see that the shades of purple represent small numbers (like 0, 1, or 2), while green and yellow show much larger numbers (27 and above).
The numbers on the main diagonal (27, 32, …, 36) show the number of correct predictions from the test set. For example, there are 27 images with zero, 32 images of one, and so on that are correctly classified. Other numbers correspond to the incorrect predictions. For example, the number 1 in the third row and the first column shows that there is one image with the number 2 incorrectly classified as 0.
Finally, you can get the report on classification as a string or dictionary with classification_report() :
This report shows additional information, like the support and precision of classifying each digit.
Logistic regression is a fundamental classification technique. It’s a relatively uncomplicated linear classifier. Despite its simplicity and popularity, there are cases (especially with highly complex models) where logistic regression doesn’t work well. In such circumstances, you can use other classification techniques:
- k-Nearest Neighbors
- Naive Bayes classifiers
- Support Vector Machines
- Decision Trees
- Random Forests
- Neural Networks
Fortunately, there are several comprehensive Python libraries for machine learning that implement these techniques. For example, the package you’ve seen in action here, scikit-learn, implements all of the above-mentioned techniques, with the exception of neural networks.
For all these techniques, scikit-learn offers suitable classes with methods like model.fit() , model.predict_proba() , model.predict() , model.score() , and so on. You can combine them with train_test_split() , confusion_matrix() , classification_report() , and others.
Neural networks (including deep neural networks) have become very popular for classification problems. Libraries like TensorFlow, PyTorch , or Keras offer suitable, performant , and powerful support for these kinds of models.
You now know what logistic regression is and how you can implement it for classification with Python. You’ve used many open-source packages, including NumPy, to work with arrays and Matplotlib to visualize the results. You also used both scikit-learn and StatsModels to create, fit, evaluate, and apply models.
Generally, logistic regression in Python has a straightforward and user-friendly implementation. It usually consists of these steps:
- Create a classification model and train (or fit) it with existing data
- Apply your model to make predictions
You’ve come a long way in understanding one of the most important areas of machine learning! If you have questions or comments, then please put them in the comments section below.
🐍 Python Tricks 💌
Get a short & sweet Python Trick delivered to your inbox every couple of days. No spam ever. Unsubscribe any time. Curated by the Real Python team.

About Mirko Stojiljković

Mirko has a Ph.D. in Mechanical Engineering and works as a university professor. He is a Pythonista who applies hybrid optimization and machine learning methods to support decision making in the energy sector.
Each tutorial at Real Python is created by a team of developers so that it meets our high quality standards. The team members who worked on this tutorial are:

Master Real-World Python Skills With Unlimited Access to Real Python
Join us and get access to thousands of tutorials, hands-on video courses, and a community of expert Pythonistas:
Join us and get access to thousands of tutorials, hands-on video courses, and a community of expert Pythonistas:
What Do You Think?
What’s your #1 takeaway or favorite thing you learned? How are you going to put your newfound skills to use? Leave a comment below and let us know.
Commenting Tips: The most useful comments are those written with the goal of learning from or helping out other students. Get tips for asking good questions and get answers to common questions in our support portal . Looking for a real-time conversation? Visit the Real Python Community Chat or join the next “Office Hours” Live Q&A Session . Happy Pythoning!
Keep Learning
Related Topics: intermediate data-science machine-learning
Keep reading Real Python by creating a free account or signing in:
Already have an account? Sign-In
Almost there! Complete this form and click the button below to gain instant access:

NumPy: The Best Learning Resources (A Free PDF Guide)
🔒 No spam. We take your privacy seriously.
- Data Science
- Data Analysis
- Data Visualization
- Machine Learning
- Deep Learning
- Computer Vision
- Artificial Intelligence
- AI ML DS Interview Series
- AI ML DS Projects series
- Data Engineering
- Web Scrapping
Logistic Regression in Machine Learning
Logistic regression is a supervised machine learning algorithm used for classification tasks where the goal is to predict the probability that an instance belongs to a given class or not. Logistic regression is a statistical algorithm which analyze the relationship between two data factors. The article explores the fundamentals of logistic regression, it’s types and implementations.
Table of Content
What is Logistic Regression?
Logistic function – sigmoid function, types of logistic regression, assumptions of logistic regression, how does logistic regression work, code implementation for logistic regression, precision-recall tradeoff in logistic regression threshold setting, how to evaluate logistic regression model, differences between linear and logistic regression.
Logistic regression is used for binary classification where we use sigmoid function , that takes input as independent variables and produces a probability value between 0 and 1.
For example, we have two classes Class 0 and Class 1 if the value of the logistic function for an input is greater than 0.5 (threshold value) then it belongs to Class 1 otherwise it belongs to Class 0. It’s referred to as regression because it is the extension of linear regression but is mainly used for classification problems.
Key Points:
- Logistic regression predicts the output of a categorical dependent variable. Therefore, the outcome must be a categorical or discrete value.
- It can be either Yes or No, 0 or 1, true or False, etc. but instead of giving the exact value as 0 and 1, it gives the probabilistic values which lie between 0 and 1.
- In Logistic regression, instead of fitting a regression line, we fit an “S” shaped logistic function, which predicts two maximum values (0 or 1).
- The sigmoid function is a mathematical function used to map the predicted values to probabilities.
- It maps any real value into another value within a range of 0 and 1. The value of the logistic regression must be between 0 and 1, which cannot go beyond this limit, so it forms a curve like the “S” form.
- The S-form curve is called the Sigmoid function or the logistic function.
- In logistic regression, we use the concept of the threshold value, which defines the probability of either 0 or 1. Such as values above the threshold value tends to 1, and a value below the threshold values tends to 0.
On the basis of the categories, Logistic Regression can be classified into three types:
- Binomial: In binomial Logistic regression, there can be only two possible types of the dependent variables, such as 0 or 1, Pass or Fail, etc.
- Multinomial: In multinomial Logistic regression, there can be 3 or more possible unordered types of the dependent variable, such as “cat”, “dogs”, or “sheep”
- Ordinal: In ordinal Logistic regression, there can be 3 or more possible ordered types of dependent variables, such as “low”, “Medium”, or “High”.
We will explore the assumptions of logistic regression as understanding these assumptions is important to ensure that we are using appropriate application of the model. The assumption include:
- Independent observations: Each observation is independent of the other. meaning there is no correlation between any input variables.
- Binary dependent variables: It takes the assumption that the dependent variable must be binary or dichotomous, meaning it can take only two values. For more than two categories SoftMax functions are used.
- Linearity relationship between independent variables and log odds: The relationship between the independent variables and the log odds of the dependent variable should be linear.
- No outliers: There should be no outliers in the dataset.
- Large sample size: The sample size is sufficiently large
Terminologies involved in Logistic Regression
Here are some common terms involved in logistic regression:
- Independent variables: The input characteristics or predictor factors applied to the dependent variable’s predictions.
- Dependent variable: The target variable in a logistic regression model, which we are trying to predict.
- Logistic function: The formula used to represent how the independent and dependent variables relate to one another. The logistic function transforms the input variables into a probability value between 0 and 1, which represents the likelihood of the dependent variable being 1 or 0.
- Odds: It is the ratio of something occurring to something not occurring. it is different from probability as the probability is the ratio of something occurring to everything that could possibly occur.
- Log-odds: The log-odds, also known as the logit function, is the natural logarithm of the odds. In logistic regression, the log odds of the dependent variable are modeled as a linear combination of the independent variables and the intercept.
- Coefficient: The logistic regression model’s estimated parameters, show how the independent and dependent variables relate to one another.
- Intercept: A constant term in the logistic regression model, which represents the log odds when all independent variables are equal to zero.
- Maximum likelihood estimation : The method used to estimate the coefficients of the logistic regression model, which maximizes the likelihood of observing the data given the model.
The logistic regression model transforms the linear regression function continuous value output into categorical value output using a sigmoid function, which maps any real-valued set of independent variables input into a value between 0 and 1. This function is known as the logistic function.
Let the independent input features be:
[Tex]X = \begin{bmatrix} x_{11} & … & x_{1m}\\ x_{21} & … & x_{2m} \\ \vdots & \ddots & \vdots \\ x_{n1} & … & x_{nm} \end{bmatrix}[/Tex]
and the dependent variable is Y having only binary value i.e. 0 or 1.
[Tex]Y = \begin{cases} 0 & \text{ if } Class\;1 \\ 1 & \text{ if } Class\;2 \end{cases} [/Tex]
then, apply the multi-linear function to the input variables X.
[Tex]z = \left(\sum_{i=1}^{n} w_{i}x_{i}\right) + b [/Tex]
Here [Tex]x_i [/Tex] is the ith observation of X, [Tex]w_i = [w_1, w_2, w_3, \cdots,w_m] [/Tex] is the weights or Coefficient, and b is the bias term also known as intercept. simply this can be represented as the dot product of weight and bias.
[Tex]z = w\cdot X +b [/Tex]
whatever we discussed above is the linear regression .
Sigmoid Function
Now we use the sigmoid function where the input will be z and we find the probability between 0 and 1. i.e. predicted y.
[Tex]\sigma(z) = \frac{1}{1+e^{-z}} [/Tex]
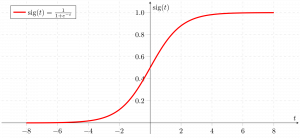
Sigmoid function
As shown above, the figure sigmoid function converts the continuous variable data into the probability i.e. between 0 and 1.
- [Tex]\sigma(z) [/Tex] tends towards 1 as [Tex]z\rightarrow\infty [/Tex]
- [Tex]\sigma(z) [/Tex] tends towards 0 as [Tex]z\rightarrow-\infty [/Tex]
- [Tex]\sigma(z) [/Tex] is always bounded between 0 and 1
where the probability of being a class can be measured as:
[Tex]P(y=1) = \sigma(z) \\ P(y=0) = 1-\sigma(z) [/Tex]
Logistic Regression Equation
The odd is the ratio of something occurring to something not occurring. it is different from probability as the probability is the ratio of something occurring to everything that could possibly occur. so odd will be:
[Tex]\frac{p(x)}{1-p(x)} = e^z[/Tex]
Applying natural log on odd. then log odd will be:
[Tex]\begin{aligned} \log \left[\frac{p(x)}{1-p(x)} \right] &= z \\ \log \left[\frac{p(x)}{1-p(x)} \right] &= w\cdot X +b \\ \frac{p(x)}{1-p(x)}&= e^{w\cdot X +b} \;\;\cdots\text{Exponentiate both sides} \\ p(x) &=e^{w\cdot X +b}\cdot (1-p(x)) \\p(x) &=e^{w\cdot X +b}-e^{w\cdot X +b}\cdot p(x)) \\p(x)+e^{w\cdot X +b}\cdot p(x))&=e^{w\cdot X +b} \\p(x)(1+e^{w\cdot X +b}) &=e^{w\cdot X +b} \\p(x)&= \frac{e^{w\cdot X +b}}{1+e^{w\cdot X +b}} \end{aligned}[/Tex]
then the final logistic regression equation will be:
[Tex]p(X;b,w) = \frac{e^{w\cdot X +b}}{1+e^{w\cdot X +b}} = \frac{1}{1+e^{-w\cdot X +b}}[/Tex]
Likelihood Function for Logistic Regression
The predicted probabilities will be:
- for y=1 The predicted probabilities will be: p(X;b,w) = p(x)
- for y = 0 The predicted probabilities will be: 1-p(X;b,w) = 1-p(x)
[Tex]L(b,w) = \prod_{i=1}^{n}p(x_i)^{y_i}(1-p(x_i))^{1-y_i}[/Tex]
Taking natural logs on both sides
[Tex]\begin{aligned}\log(L(b,w)) &= \sum_{i=1}^{n} y_i\log p(x_i)\;+\; (1-y_i)\log(1-p(x_i)) \\ &=\sum_{i=1}^{n} y_i\log p(x_i)+\log(1-p(x_i))-y_i\log(1-p(x_i)) \\ &=\sum_{i=1}^{n} \log(1-p(x_i)) +\sum_{i=1}^{n}y_i\log \frac{p(x_i)}{1-p(x_i} \\ &=\sum_{i=1}^{n} -\log1-e^{-(w\cdot x_i+b)} +\sum_{i=1}^{n}y_i (w\cdot x_i +b) \\ &=\sum_{i=1}^{n} -\log1+e^{w\cdot x_i+b} +\sum_{i=1}^{n}y_i (w\cdot x_i +b) \end{aligned}[/Tex]
Gradient of the log-likelihood function
To find the maximum likelihood estimates, we differentiate w.r.t w,
[Tex]\begin{aligned} \frac{\partial J(l(b,w)}{\partial w_j}&=-\sum_{i=n}^{n}\frac{1}{1+e^{w\cdot x_i+b}}e^{w\cdot x_i+b} x_{ij} +\sum_{i=1}^{n}y_{i}x_{ij} \\&=-\sum_{i=n}^{n}p(x_i;b,w)x_{ij}+\sum_{i=1}^{n}y_{i}x_{ij} \\&=\sum_{i=n}^{n}(y_i -p(x_i;b,w))x_{ij} \end{aligned} [/Tex]
Binomial Logistic regression:
Target variable can have only 2 possible types: “0” or “1” which may represent “win” vs “loss”, “pass” vs “fail”, “dead” vs “alive”, etc., in this case, sigmoid functions are used, which is already discussed above.
Importing necessary libraries based on the requirement of model. This Python code shows how to use the breast cancer dataset to implement a Logistic Regression model for classification.
# import the necessary libraries from sklearn.datasets import load_breast_cancer from sklearn.linear_model import LogisticRegression from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score # load the breast cancer dataset X , y = load_breast_cancer ( return_X_y = True ) # split the train and test dataset X_train , X_test , \ y_train , y_test = train_test_split ( X , y , test_size = 0.20 , random_state = 23 ) # LogisticRegression clf = LogisticRegression ( random_state = 0 ) clf . fit ( X_train , y_train ) # Prediction y_pred = clf . predict ( X_test ) acc = accuracy_score ( y_test , y_pred ) print ( "Logistic Regression model accuracy (in %):" , acc * 100 )
Logistic Regression model accuracy (in %): 95.6140350877193
Multinomial Logistic Regression:
Target variable can have 3 or more possible types which are not ordered (i.e. types have no quantitative significance) like “disease A” vs “disease B” vs “disease C”.
In this case, the softmax function is used in place of the sigmoid function. Softmax function for K classes will be:
[Tex]\text{softmax}(z_i) =\frac{ e^{z_i}}{\sum_{j=1}^{K}e^{z_{j}}}[/Tex]
Here, K represents the number of elements in the vector z, and i, j iterates over all the elements in the vector.
Then the probability for class c will be:
[Tex]P(Y=c | \overrightarrow{X}=x) = \frac{e^{w_c \cdot x + b_c}}{\sum_{k=1}^{K}e^{w_k \cdot x + b_k}}[/Tex]
In Multinomial Logistic Regression, the output variable can have more than two possible discrete outputs . Consider the Digit Dataset.
from sklearn.model_selection import train_test_split from sklearn import datasets , linear_model , metrics # load the digit dataset digits = datasets . load_digits () # defining feature matrix(X) and response vector(y) X = digits . data y = digits . target # splitting X and y into training and testing sets X_train , X_test , \ y_train , y_test = train_test_split ( X , y , test_size = 0.4 , random_state = 1 ) # create logistic regression object reg = linear_model . LogisticRegression () # train the model using the training sets reg . fit ( X_train , y_train ) # making predictions on the testing set y_pred = reg . predict ( X_test ) # comparing actual response values (y_test) # with predicted response values (y_pred) print ( "Logistic Regression model accuracy(in %):" , metrics . accuracy_score ( y_test , y_pred ) * 100 )
Logistic Regression model accuracy(in %): 96.52294853963839
We can evaluate the logistic regression model using the following metrics:
- Accuracy: Accuracy provides the proportion of correctly classified instances. [Tex]Accuracy = \frac{True \, Positives + True \, Negatives}{Total} [/Tex]
- Precision: Precision focuses on the accuracy of positive predictions. [Tex]Precision = \frac{True \, Positives }{True\, Positives + False \, Positives} [/Tex]
- Recall (Sensitivity or True Positive Rate): Recall measures the proportion of correctly predicted positive instances among all actual positive instances. [Tex]Recall = \frac{ True \, Positives}{True\, Positives + False \, Negatives} [/Tex]
- F1 Score: F1 score is the harmonic mean of precision and recall. [Tex]F1 \, Score = 2 * \frac{Precision * Recall}{Precision + Recall} [/Tex]
- Area Under the Receiver Operating Characteristic Curve (AUC-ROC): The ROC curve plots the true positive rate against the false positive rate at various thresholds. AUC-ROC measures the area under this curve, providing an aggregate measure of a model’s performance across different classification thresholds.
- Area Under the Precision-Recall Curve (AUC-PR): Similar to AUC-ROC, AUC-PR measures the area under the precision-recall curve, providing a summary of a model’s performance across different precision-recall trade-offs.
Logistic regression becomes a classification technique only when a decision threshold is brought into the picture. The setting of the threshold value is a very important aspect of Logistic regression and is dependent on the classification problem itself.
The decision for the value of the threshold value is majorly affected by the values of precision and recall. Ideally, we want both precision and recall being 1, but this seldom is the case.
In the case of a Precision-Recall tradeoff , we use the following arguments to decide upon the threshold:
- Low Precision/High Recall: In applications where we want to reduce the number of false negatives without necessarily reducing the number of false positives, we choose a decision value that has a low value of Precision or a high value of Recall. For example, in a cancer diagnosis application, we do not want any affected patient to be classified as not affected without giving much heed to if the patient is being wrongfully diagnosed with cancer. This is because the absence of cancer can be detected by further medical diseases, but the presence of the disease cannot be detected in an already rejected candidate.
- High Precision/Low Recall: In applications where we want to reduce the number of false positives without necessarily reducing the number of false negatives, we choose a decision value that has a high value of Precision or a low value of Recall. For example, if we are classifying customers whether they will react positively or negatively to a personalized advertisement, we want to be absolutely sure that the customer will react positively to the advertisement because otherwise, a negative reaction can cause a loss of potential sales from the customer.
The difference between linear regression and logistic regression is that linear regression output is the continuous value that can be anything while logistic regression predicts the probability that an instance belongs to a given class or not.
Linear Regression | Logistic Regression |
|---|---|
Linear regression is used to predict the continuous dependent variable using a given set of independent variables. | Logistic regression is used to predict the categorical dependent variable using a given set of independent variables. |
Linear regression is used for solving regression problem. | It is used for solving classification problems. |
In this we predict the value of continuous variables | In this we predict values of categorical variables |
In this we find best fit line. | In this we find S-Curve. |
Least square estimation method is used for estimation of accuracy. | Maximum likelihood estimation method is used for Estimation of accuracy. |
The output must be continuous value, such as price, age, etc. | Output must be categorical value such as 0 or 1, Yes or no, etc. |
It required linear relationship between dependent and independent variables. | It not required linear relationship. |
There may be collinearity between the independent variables. | There should be little to no collinearity between independent variables. |
Logistic Regression – Frequently Asked Questions (FAQs)
What is logistic regression in machine learning.
Logistic regression is a statistical method for developing machine learning models with binary dependent variables, i.e. binary. Logistic regression is a statistical technique used to describe data and the relationship between one dependent variable and one or more independent variables.
What are the three types of logistic regression?
Logistic regression is classified into three types: binary, multinomial, and ordinal. They differ in execution as well as theory. Binary regression is concerned with two possible outcomes: yes or no. Multinomial logistic regression is used when there are three or more values.
Why logistic regression is used for classification problem?
Logistic regression is easier to implement, interpret, and train. It classifies unknown records very quickly. When the dataset is linearly separable, it performs well. Model coefficients can be interpreted as indicators of feature importance.
What distinguishes Logistic Regression from Linear Regression?
While Linear Regression is used to predict continuous outcomes, Logistic Regression is used to predict the likelihood of an observation falling into a specific category. Logistic Regression employs an S-shaped logistic function to map predicted values between 0 and 1.
What role does the logistic function play in Logistic Regression?
Logistic Regression relies on the logistic function to convert the output into a probability score. This score represents the probability that an observation belongs to a particular class. The S-shaped curve assists in thresholding and categorising data into binary outcomes.
Please Login to comment...
Similar reads.
- Best PS5 SSDs in 2024: Top Picks for Expanding Your Storage
- Best Nintendo Switch Controllers in 2024
- Xbox Game Pass Ultimate: Features, Benefits, and Pricing in 2024
- Xbox Game Pass vs. Xbox Game Pass Ultimate: Which is Right for You?
- #geekstreak2024 – 21 Days POTD Challenge Powered By Deutsche Bank
Improve your Coding Skills with Practice
What kind of Experience do you want to share?
Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
Hypothesis Testing in Logistic Regression
In Linear Regression, the book Introduction to Statistical Learning argued that we should use the $F$ statistic to decide if s $\beta_1 = \beta_2 = ... = 0$ instead of looking at individual p-values for the $t$ statistic.
For instance, consider an example in which p = 100 and $\beta_1 = \beta_2 = ... = 0$ is true, so no variable is truly associated with the response. In this situation, about 5 % of the p-values associated with each variable will be below 0.05 by chance.
But when discussing Logistic Regression, we settled with looking at individual p-values of the coefficients,as also seen in this tutorial.
Is there a $F$ statistic counterpart for Logistic Regression?
- machine-learning
- hypothesis-testing
- statistical-significance
The likelihood-ratio test on a model fit by maximum likelihood, (for example, a logistic regression or another generalized linear model), is a counterpart to the $F$ test on a linear regression model. Both allow for testing the overall model against the null model (in R, outcome ~ 1 ), as in your question, and generally for testing nested models against each other.
In R, the anova() function applied to 2 nested glm models will provide a likelihood-ratio test if you set test = "LR" . Unlike anova() for linear regression with an $F$ test default, you need to specify the test.
For testing the full model against the null, you can construct the test yourself from the values of likelihoods or deviances and degrees of freedom typically reported for the full and null models. In R, from summary(model) you take the difference between the reported null and residual deviances, and test against chi-square with degrees of freedom equal to the difference between the null and residual degrees of freedom.
See the related UCLA IDRE page for a worked-through example and further information on testing things like combinations of predictors or different levels of a categorical predictor.
Your Answer
Sign up or log in, post as a guest.
Required, but never shown
By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .
Not the answer you're looking for? Browse other questions tagged machine-learning hypothesis-testing self-study statistical-significance or ask your own question .
- Featured on Meta
- Site maintenance - Mon, Sept 16 2024, 21:00 UTC to Tue, Sept 17 2024, 2:00...
- User activation: Learnings and opportunities
- Join Stack Overflow’s CEO and me for the first Stack IRL Community Event in...
Hot Network Questions
- Why does Sfas Emes start his commentary on Parshat Noach by saying he doesn't know it? Is the translation faulty?
- Did Queen (or Freddie Mercury) really not like Star Wars?
- Does the word vaishnava appear even once in Srimad Bhagavatam?
- MSSQL - query runs for too long when filtering after a certain date
- How do I go about writing a tragic ending in a story while making it overall satisfying to the reader?
- Does any row of Pascal's triangle contain a Pythagorean triple?
- Why are my empty files not being assigned the correct mimetype?
- What is this stats overlay that's appeared?
- Attacks exploiting decryption failures in KYBER
- 4/4 time change to 6/8 time
- Engaging students in the beauty of mathematics
- Should I write an email to a Latino teacher working in the US in English or Spanish?
- Navigating career options after a disastrous PhD performance and a disappointed advisor?
- How do elected politicians get away with not giving straight answers?
- How is switching of measurement ranges in instruments, like oscilloscopes, realized nowadays?
- How do you ensure that calendar invites won't be moved out of your inbox when your rules are executed?
- Definition of annuity
- Is it defamatory to publish nonsense under somebody else's name?
- Paying a parking fine when I don't trust the recipient
- Taylor Swift - Use of "them" in her text "she fights for the rights and causes I believe need a warrior to champion them"
- How much technological progress could a group of modern people make in a century?
- Gridded plane colouring problem. Can a 2x2 black square be created on a white gridded plane using 3x3 and 4x4 "stamps" that invert the grid colour?
- Why was Esther included in the canon?
- Is saying "Both A and not-A can do B" contradictory?
This week: the arXiv Accessibility Forum
Help | Advanced Search
Statistics > Methodology
Title: global and simultaneous hypothesis testing for high-dimensional logistic regression models.
Abstract: High-dimensional logistic regression is widely used in analyzing data with binary outcomes. In this paper, global testing and large-scale multiple testing for the regression coefficients are considered in both single- and two-regression settings. A test statistic for testing the global null hypothesis is constructed using a generalized low-dimensional projection for bias correction and its asymptotic null distribution is derived. A lower bound for the global testing is established, which shows that the proposed test is asymptotically minimax optimal over some sparsity range. For testing the individual coefficients simultaneously, multiple testing procedures are proposed and shown to control the false discovery rate (FDR) and falsely discovered variables (FDV) asymptotically. Simulation studies are carried out to examine the numerical performance of the proposed tests and their superiority over existing methods. The testing procedures are also illustrated by analyzing a data set of a metabolomics study that investigates the association between fecal metabolites and pediatric Crohn's disease and the effects of treatment on such associations.
| Comments: | Typos corrected |
| Subjects: | Methodology (stat.ME); Statistics Theory (math.ST) |
| Cite as: | [stat.ME] |
| (or [stat.ME] for this version) | |
| Focus to learn more arXiv-issued DOI via DataCite | |
| Journal reference: | Journal of the American Statistical Association (2019) |
| : | Focus to learn more DOI(s) linking to related resources |
Submission history
Access paper:.
- Other Formats
References & Citations
- Google Scholar
- Semantic Scholar
BibTeX formatted citation
Bibliographic and Citation Tools
Code, data and media associated with this article, recommenders and search tools.
- Institution
arXivLabs: experimental projects with community collaborators
arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.
Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.
Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

VIDEO
COMMENTS
Testing a single logistic regression coefficient in R To test a single logistic regression coefficient, we will use the Wald test, βˆ j −β j0 seˆ(βˆ) ∼ N(0,1), where seˆ(βˆ) is calculated by taking the inverse of the estimated information matrix. This value is given to you in the R output for β j0 = 0. As in linear regression ...
Simple logistic regression uses the following null and alternative hypotheses: H0: β1 = 0. HA: β1 ≠ 0. The null hypothesis states that the coefficient β1 is equal to zero. In other words, there is no statistically significant relationship between the predictor variable, x, and the response variable, y. The alternative hypothesis states ...
GLOBAL TESTS OF PARAMETERS. In OLS regression, if we wanted to test the hypothesis that all β's = 0 versus the alternative that at least one did not, we used a global F test. In logistic regression, we use a likelihood ratio chi-square test instead. Stata calls this LR chi2. The value in this case is 15.40.
12.1 - Logistic Regression. Logistic regression models a relationship between predictor variables and a categorical response variable. For example, we could use logistic regression to model the relationship between various measurements of a manufactured specimen (such as dimensions and chemical composition) to predict if a crack greater than 10 ...
19.2 Hypothesis Testing for \(\beta\) 's. Like with linear regression, a common inferential question in logistic regression is whether a \(\beta_j\) is different from zero. This corresponds to there being a difference in the log odds of the outcome among observations that differen in the value of the predictor variable \(x_j\).
comes to Logistic regression. I'm trying to more or less follow Menard, but you'll have to learn to adapt to whatever the author or statistical program happens to use. Overview. In this handout, we'll examine hypothesis testing in logistic regression and make comparisons between logistic regression and OLS.
Besides such single logistic regression problems, hypothesis testing involving two logistic regression models with regression coe cients (1) and (2) in Rp is also important. Speci cally, one is interested in testing the global null hypothesis H 0: (1) = (2), or identifying the di erentially associated covariates through simultaneously testing ...
The logistic regression classifier will predict "Male" if: This is because the logistic regression " threshold " is set at g (z)=0.5, see the plot of the logistic regression function above for verification. For our data set the values of θ are: To get access to the θ parameters computed by scikit-learn one can do: # For theta_0: print ...
Logistic regression is just one example of this type of model. All generalized linear models have the following three characteristics: A probability distribution describing the outcome variable. A linear model. = 0 + 1X1 + + nXn. A link function that relates the linear model to the parameter of the outcome distribution.
Like standard multiple regression, logistic regression carries hypothesis tests for the significance of each variable, along with other tests, estimates, and goodness-of-fit assessments. In the classification setting, the variable significance tests can be used for feature selection: modern computational implementations incorporate several ...
Testing hypothesis for a logistic regression model is the exact same as for a standard regression model. And so, we find very strong support for hypothesis 2, suggesting that (given model and data), there is reason to believe that the accuracy in incongruent trials is lower than in congruent trials.
Logistic regression: dependence of outcome on predictors quantified by odds ratios. Key challenge for understanding logistic regression is being able to interpret ... Two ways to test if null hypothesis is true at significance level ("alpha") 0.05 1. p-value < 0.05 (0.0009 < 0.05 significance) ...
10.5 Hypothesis Test. In logistic regression, hypotheses are of interest: the null hypothesis, which is when all the coefficients in the regression equation take the value zero, and. the alternate hypothesis that the model currently under consideration is accurate and differs significantly from the null of zero, i.e. gives significantly better than the chance or random prediction level of the ...
18.6 Example: Measuring Team Defense Using Logistic Regression. logit(pi) = α+β1SD+β2Team+β3(Team)(SD) l o g i t (p i) = α + β 1 S D + β 2 Team + β 3 (Team) (S D) Since the team defending is a categorical variable R will store it as a dummy variable when forming the regression. Thus the first level of this variable will not appear in ...
Use multiple logistic regression when you have one nominal and two or more measurement variables. The nominal variable is the dependent (Y) variable; you are studying the effect that the independent (X) variables have on the probability of obtaining a particular value of the dependent variable. For example, you might want to know the effect ...
Linear Regression VS Logistic Regression Graph| Image: Data Camp. We can call a Logistic Regression a Linear Regression model but the Logistic Regression uses a more complex cost function, this cost function can be defined as the 'Sigmoid function' or also known as the 'logistic function' instead of a linear function. The hypothesis of logistic regression tends it to limit the cost ...
Logistic regression is widely used in social and behavioral research in analyzing the binary (dichotomous) outcome data. In logistic regression, the outcome can only take two values 0 and 1. ... Wald statistic is the square of the z-statistic and thus Wald test gives the same conclusion as the z-test. We can also conduct the hypothesis testing ...
📚Chapter: 5 -Logistic Regression Introduction. Let's start talking about logistic regression. In this tutorial, I'd like to show you the hypothesis representation, that is, what is the ...
Problem Formulation. In this tutorial, you'll see an explanation for the common case of logistic regression applied to binary classification. When you're implementing the logistic regression of some dependent variable 𝑦 on the set of independent variables 𝐱 = (𝑥₁, …, 𝑥ᵣ), where 𝑟 is the number of predictors ( or inputs), you start with the known values of the ...
1 Logistic regression models have been applied widely in genetics, finance, and business analytics. ... A test statistic for testing the global null hypothesis is constructed using a generalized low-dimensional projection for bias correction and its asymptotic null distribution is derived. A lower bound for the global testing is established ...
Logistic regression is a supervised machine learning algorithm used for classification tasks where the goal is to predict the probability that an instance belongs to a given class or not. Logistic regression is a statistical algorithm which analyze the relationship between two data factors. The article explores the fundamentals of logistic regression, it's types and implementations.
5. The likelihood-ratio test on a model fit by maximum likelihood, (for example, a logistic regression or another generalized linear model), is a counterpart to the F F test on a linear regression model. Both allow for testing the overall model against the null model (in R, outcome ~ 1), as in your question, and generally for testing nested ...
High-dimensional logistic regression is widely used in analyzing data with binary outcomes. In this paper, global testing and large-scale multiple testing for the regression coefficients are considered in both single- and two-regression settings. A test statistic for testing the global null hypothesis is constructed using a generalized low-dimensional projection for bias correction and its ...