{{ article.displayTitle }}
| {{ 'ml-lesson-number-slides' | message : article.intro.bblockCount }} | |
| {{ 'ml-lesson-number-exercises' | message : article.intro.exerciseCount }} | |
| {{ 'ml-lesson-time-estimation' | message }} |
- {{ item.file.title }} {{ presentation }}

Catch-Up and Review
Here are a few recommended readings before getting started with this lesson.
- The concept of similarity .
- Conditions for similarity of polygons .
- The concept of congruence .
- Conditions that guarantee the congruence of triangles .
Using Similarity of Triangles to Solve Problems
Find the ratio of the length of a diagonal and a side of a regular pentagon .
Investigating Triangles With Two Pairs of Congruent Angles
In the applet, move points Q and R . The applet copies ∠ B and ∠ C on Q R and labels the intersection of the corresponding rays by P .
- What do you notice about the angles and side lengths of the two triangles ?
- Are the two triangles similar ?
Angle-Angle Similarity Theorem
Two polygons are similar if corresponding angles are congruent and corresponding sides are proportional . For triangles, the congruence of two angles already implies similarity.
If two angles of a triangle are congruent to two angles of another triangle, then the triangles are similar .
If ∠ A ≅ ∠ D and ∠ B ≅ ∠ E , then △ A B C ∼ △ D E F .
Consider two triangles △ A B C and △ D E F , whose two corresponding angles are congruent.
These triangles can be proven to be similar by identifying a similarity transformation that maps one triangle onto the other. First, △ D E F can be dilated with the scale factor k = D E A B about D , forming the new triangle △ D E ′ F ′ .
Therefore, it can be concluded that △ A B C and △ D E F are similar triangles.
△ A B C ∼ △ D E F
The proof is now complete.
Solving Problems Using Angle-Angle-Similarity Theorem
The Grim Reaper, who is 5 feet tall, stands 1 6 feet away from a street lamp at night. The Grim Reaper's shadow cast by the streetlamp light is 8 feet long. How tall is the street lamp?
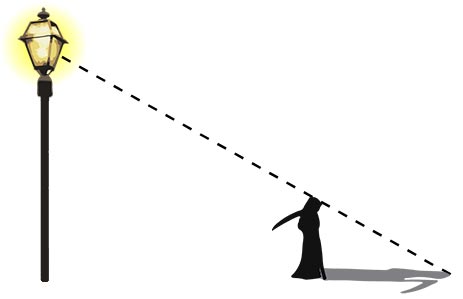
Both the lamp post and the Grim Reaper stand vertically on horizontal ground.
A sketch of the situation is helpful for finding the solution. Under the assumption that the lamp post and the Grim Reaper make right angles in relation to the ground, two right triangles can be drawn. The unknown height of the lamp post is labeled as x .
As these triangles both have a right angle and share the angle on the right-hand side, they are similar by the Angle-Angle (AA) Similarity Theorem . Notice that the base of the larger triangle measures to be 2 4 feet.
Calculate quotient
LHS ⋅ 5 = RHS ⋅ 5
The street lamp at 1 5 feet high towers over The Grimp Reaper.
Practice Solving Problems Using Similar Triangles
For the given diagram, find the missing length.
Side-Side-Side Similarity Theorem
A second theorem allows for determining triangle similarity when only the lengths of corresponding sides are known.
If corresponding sides of two triangles are proportional , then the triangles are similar .
If D E A B = E F B C = F D C A , then △ A B C ∼ △ D E F .
Consider two triangles △ A B C and △ D E F , whose corresponding sides are proportional .
The combination of this rigid motion and the dilation performed earlier forms a similarity transformation that maps △ D E F onto △ A B C .
Solving Problems Using Similar Triangles
There are four congruent angles in the figure. Try to identify them.
∠ D B A ≅ ∠ B C E ≅ ∠ B E C ≅ ∠ D B E
Look for similar triangles and an isosceles triangle.
First, notice that segments B E and B C are equal in length.
Two of the triangles, △ A B D and △ A C E look similar .
Because the lengths of the sides are given, the ratio of corresponding sides can be calculated.
| Ratio | Expression | Simplification |
|---|---|---|
| ABAC | 459459+1275=4591734 | 934 |
| ADAE | 405405+1125=4051530 | 934 |
| DBEC | 3601360 | 934 |
In addition to the proportions in Step 2 showing that △ A C E and △ A B D are similar, they also show the two triangles are dilations of each other from the common vertex A . Since dilations map a segment to a parallel segment, segments D B and E C are parallel.
Answering the Question
Side-angle-side similarity theorem.
Two theorems have been covered, now a third theorem that can be used to prove triangle similarity will be investigated. This third theorem allows for determining triangle similarity when the lengths of two corresponding sides and the measure of the included angles are known.
If two sides of a triangle are proportional to two sides of another triangle and the included angles are congruent , then the triangles are similar .
If D E A B = D F A C and ∠ A ≅ ∠ D , then △ A B C ∼ △ D E F .
Consider two triangles △ A B C and △ D E F , whose two pairs of corresponding sides are proportional and the included angles are congruent.
Proving Similarity Between Triangles Given Sides
The diagram shows the distances between points on a figure.
Show that △ A B C and △ A E D are similar triangles. Then find D E .
Use the Side-Angle-Side (SAS) Similarity Theorem .
Triangles △ A B C and △ A E D have a common angle at A .
The table below contains the ratios of two pairs of corresponding sides of the two triangles.
| Ratio | Expression | Simplified Form |
|---|---|---|
| AEAB | 5+97=147 | 21 |
| ADAC | 7+35=105 | 21 |
LHS ⋅ D E = RHS ⋅ D E
LHS ⋅ 2 = RHS ⋅ 2
Rearrange equation
Applying Triangle Similarity Theorems to Solve Problems
Through applying the theorems of similar triangles, the ratio of the lengths of a diagonal and the sides of a regular pentagon can be found.
Begin by determining the angle measures of the figure.
m ∠ A E B = m ∠ A B E , m ∠ A = 1 0 8
LHS − 1 0 8 = RHS − 1 0 8
a + a = 2 a
LHS / 2 = RHS / 2
Substitute values
LHS − ( 3 6 + 3 6 ) = RHS − ( 3 6 + 3 6 )
Next, focus on △ A C E . In this triangle, A C and E C are diagonals of the pentagon, and A E is a side.
Substitute expressions
Simplify quotient
Factor out s
b a = b / s a / s
LHS ⋅ ( x − 1 ) = RHS ⋅ ( x − 1 )
Multiply parentheses
LHS − 1 = RHS − 1
Use the Quadratic Formula: a = 1 , b = - 1 , c = - 1
- ( - a ) = a
Calculate power and product
a − ( - b ) = a + b
Length of side Length of diagonal = 2 1 + 5 ≈ 1 . 6 1 8
The ratio of the diagonal to the side of a regular pentagon can be used to prove that the following construction creates a regular pentagon. This is a construction created by Yosifusa Hirano in the 19th century.

- Math Forum/Help
- Problem Solver
- College Math
Similar Triangles

Generally, two triangles are said to be similar if they have the same shape, even if they are scaled, rotated or even flipped over.
The mathematical presentation of two similar triangles A 1 B 1 C 1 and A 2 B 2 C 2 as shown by the figure beside is:
ΔA 1 B 1 C 1 ~ ΔA 2 B 2 C 2
Two triangles are similar if:
1. Each angle in one triangle is congruent with (equal to) its corresponding angle in the other triangle i.e.: ∠A 1 = ∠A 2 , ∠B 1 = ∠B 2 and ∠C 1 = ∠C 2
2. The ratio of the length of one side of one triangle to the corresponding side in the other triangle is the same i.e.: $\frac{A_1B_1}{A_2B_2}=\frac{A_1C_1}{A_2C_2}=\frac{B_1C_1}{B_2C_2}$
3. The ratio of the length of two sides of one triangle to the corresponding sides in the other triangle is the same and the angles between these sides are equal i.e.: $\frac{B_1A_1}{B_2A_2}=\frac{A_1C_1}{A_2C_2}$ and $\angle A_1 = \angle A_2$ or $\frac{A_1B_1}{A_2B_2}=\frac{B_1C_1}{B_2C_2}$ and $\angle B_1 = \angle B_2$ or $\frac{B_1C_1}{B_2C_2}=\frac{C_1A_1}{C_2A_2}$ and $\angle C_1 = \angle C_2$
Be careful not to mix similar triangles with identical triangle. Identical triangles are those having the same corresponding sides’ lengths. Therefore, for identical triangles:
$\frac{A_1B_1}{A_2B_2}=\frac{A_1C_1}{A_2C_2}=\frac{B_1C_1}{B_2C_2}=1$
Therefore, all identical triangles are similar. However, not all similar triangles are identical.
Although the above shows that we need to know the measures of the three angles or the lengths of the three sides of each triangle in order to decide whether the two triangles are similar or not, it would be sufficient, for solving problems involving similar triangles, to know only three of the above measures for each triangle. These measures can be any of the following combinations:
1) the three angles of each triangle (without the need to know the lengths of their sides). Or at least 2 angles of the first triangle are equal to 2 angles of the second triangle. Because if 2 angles are equal the third angles are equal too.(The third angles are 180 - angle1 - angle2)
2) the lengths of the sides of each triangle (without the need to know the measures of their angles);
3) the lengths of two sides and the measure of one angle of each triangle. This angle should be the one formed by the two known sides.
In what follows we shall explain the solution of some problems involving similar triangles. We will start with those problems that can be solved with the direct application of the above rules, and then we will upgrade our discussion to explain some practical problems which use the similar triangles principle to be solved.
Direct Application of Problems Involving Similar Triangles

Solution: Since the lengths of the sides of both triangles are known, the second condition can be checked:
$\frac{PQ}{AB}=\frac{6}{2}=3$ $\frac{QR}{CB}=\frac{12}{4}=3$ $\frac{PR}{AC}=\frac{15}{5}=3$

Solution: ∠A = ∠P and ∠B = ∠Q, ∠C = ∠R (because ∠C = 180 - ∠A - ∠B and ∠R = 180 - ∠P - ∠Q)
Therefore, the two triangles ΔABC and ΔPQR are similar. Consequently: $\frac{AB}{PQ}=\frac{BC}{QR}=\frac{AC}{PR}$
$\frac{BC}{QR}=\frac{6}{12}=\frac{AB}{PQ}=\frac{4}{PQ} \Rightarrow PQ=\frac{4\times12}{6} = 8$ and $\frac{BC}{QR}=\frac{6}{12}=\frac{AC}{PR}=\frac{7}{PR} \Rightarrow PR=\frac{7\times12}{6} = 14$

∠ABC = ∠ADE, ∠ACB = ∠AED and ∠A is common => the two triangles ΔABC and ΔADE are similar.
$\frac{BC}{DE} = \frac{3}{6} = \frac{AB}{AD} = \frac{AB}{AB + BD} = \frac{AB}{AB + 4} = \frac{1}{2} \Rightarrow 2\times AB = AB + 4 \Rightarrow AB = 4$

The two triangles ΔABC and ΔCDE appear to be similar since AB || DE and they have the same apex angle C. It appears that one triangle is a scaled version of the other. However, we need to prove this mathematically.
AB || DE, CD || AC and BC || EC ∠BAC = ∠EDC and ∠ABC = ∠DEC
Considering the above and the common angle C , we may conclude that the two triangles ΔABC and ΔCDE are similar.
Therefore: $\frac{DE}{AB} = \frac{7}{11} = \frac{CD}{CA} = \frac{15}{CA} \Rightarrow CA = \frac{15 \times 11}{7} = 23.57$ x = AC - DC = 23.57 - 15 = 8.57
Practical Examples

The factory wants to extend its conveyor to reach a new Level 2 which is 9m above Level 1 while maintaining the inclination angle of the conveyor.
Find the distance at which a new post is to be installed to support the conveyor at its new end at Level 2. Also, calculate the additional distance that the product has to travel to reach the new level.
First, let us denote each intersection point by a letter as shown in Red on the figure above.
Following the same explanation provided in the examples above, we can conclude that the two triangles ΔABC and ΔADE are similar. Therefore,
$\frac{DE}{BC} = \frac{3}{9} = \frac{AD}{AB} = \frac{8}{AB} \Rightarrow AB = \frac{8 \times 9}{3} = 24m$ x = AB - 8 = 24 - 8 = 16m
Hence, the new post should be placed at a distance of 16m from the existing post.
Since the construction is forming right-angle triangles, we can calculate the travel distance of the product as follows:
$AE = \sqrt{AD^2 + DE^2} = \sqrt{8^2 + 3^2} = 8.54m$
Similarly, $AC = \sqrt{AB^2 + BC^2} = \sqrt{24^2 + 9^2} = 25.63m$ which is the distance the product is currently travelling to reach the existing level.
y = AC - AE = 25.63 - 8.54 = 17.09m which is the additional distance that the product has to travel to reach the new level.

You may notice that the two triangles ΔABC and ΔCDE are similar and therefore: $\frac{AB}{DE} = \frac{BC}{CD} = \frac{AC}{CE}$
From the problem description, we have:
AB = 15km, AC = 13.13km, CD = 4.41km and DE = 5km
From the above, we can calculate the following lengths:
$BC = \frac{AB \times CD}{DE} = \frac{15 \times 4.41}{5} = 13.23km$ $CE = \frac{AC \times CD}{BC} = \frac{13.13 \times 4.41}{13.23} = 4.38km$
In order for Steve to reach his friend’s house, he may follow any of the following routes:
A -> B -> C -> E -> G which has a total length of 7.5+13.23+4.38+2.5=27.61km
F -> B -> C -> D -> G which has a total length of 7.5+13.23+4.41+2.5=27.64km
F -> A -> C -> E -> G which has a total length of 7.5+13.13+4.38+2.5=27.51km
F -> A -> C -> D -> G which has a total length of 7.5+13.13+4.41+2.5=27.54km
Therefore, Route number 3 is to shortest one to be recommended to Steve.
Example 7: Trisha wants to measure the height of a building but she does not have the tools to do so. She noticed that there is a tree located in front of the building so she decided to use her smartness and the geometry knowledge that she got at school to measure the building height. She measured the distance between the tree and the building and found that it is 30m. She stood in front of the tree and started backing until she could see the top edge of the building from above the tree top. She marked her place and measured it from the tree. It was 5m.

First, let us make use of the similarity between the triangles ΔABC and ΔADE.
$\frac{BC}{DE} = \frac{1.6}{2.8} = \frac{AC}{AE} = \frac{AC}{5 + AC} \Rightarrow 2.8 \times AC = 1.6 \times (5 + AC) = 8 + 1.6 \times AC$
$(2.8 - 1.6) \times AC = 8 \Rightarrow AC = \frac{8}{1.2} = 6.67$
We can then use the similarity between triangles ΔACB and ΔAFG or between the triangles ΔADE and ΔAFG. Let us take the first option.
$\frac{BC}{FG} = \frac{1.6}{H} = \frac{AC}{AG} = \frac{6.67}{6.67 + 5 + 30} = 0.16 \Rightarrow H = \frac{1.6}{0.16} = 10m$
Helping with Math
Similar Triangles
Introduction.
In the variety of geometrical shapes we encounter daily, have you ever wondered how to relate two shapes about their size and orientation? Turns out, mathematicians have made an answer to this—the concept of similarity .
In this article, we introduce this concept by comparing triangles. We first look back at the definition and properties of a triangle with some relevant equations, then we show different theorems associated with similar triangles. Along the way, we will also try some examples as a supplement for learning.
What is a Triangle?
In geometry, a triangle is a shape that consists of a set of three straight lines or sides , three interior angles that are formed by a pair of sides, and three vertices or intersection points of the lines forming the triangle.

A triangle can also have an exterior angle . This occurs when we extend one side of a triangle and take the angle the extended line forms at its vertex with another side.
What are some Properties of Triangles?
First, we note that the sum of the length of two sides of a triangle is greater than the length of its third side. Conversely, we can say that the difference between the length of two sides is always less than the length of the third side.
Second, we observe that for any triangle the sum of its interior angles adds up to a measure of 180°. This is called the Angle Sum Property .
Third, we note that the sum of the measures of a triangle’s interior angle and its adjacent exterior angle is supplementary. In other words, these angles add up to a measure of 180°.
What is the Law of Sines?
The Law of Sines , also known by other names such as Sine Law, Sine Rule, or Sine Formula, is an equation relating the angles of a triangle with the corresponding side opposite its vertex.
It states that the ratio between the length of a triangle’s side and the sine of the angle at an opposite vertex is equal for all sides and angles of any triangle:
$\frac{a}{sinsin A} = \frac{b}{sinsin B} = \frac{c}{sinsin C}$
We can use the Law of Sines to find the unknown sides or angles of a triangle, through a set of given information:
- Two angles of a triangle and one included side
- Two angles of a triangle and one non-included side
- Two sides of a triangle and one angle opposite either side
What is the Law of Cosines?
The Law of Cosines , also called the Cosine Law, Cosine Rule, or Cosine Formula, is another equation that relates the angles of a triangle with the lengths of its sides.
It states that the square of the length of one side of a triangle is equal to the sum of the squares of the lengths of the other two sides, minus twice their product and the cosine of their included angle:
c 2 = a 2 + b 2 – 2ab coscos C
Alternatively, we can write similar equations for the remaining two sides:
a 2 = b 2 + c 2 – 2ab coscos A b 2 = a 2 + c 2 – 2ac coscos B
We can use the Law of Cosines to find the following unknown:
- Unknown side of a triangle given two sides and one included angle
- Unknown angles of a triangle given all three sides
Now, we move from the underlying concepts to the main topic. Similarity , by definition, is the likeliness or resemblance of two geometrical objects. When we say two objects are similar, we observe that they look alike. Whether it is by their size or orientation, we recognize how we get from one shape to another in similar shapes .
For the case of triangles, we say that two triangles are similar if their sizes are proportional and/or one triangle is either a rotated or flipped version of the other:

To be specific, two triangles ABC and XYZ are said to be similar if the following conditions hold:
The lengths of their sides are proportional to each other
$\frac{AB}{XY} = \frac{AC}{XZ} = \frac{BC}{YZ}$
The measures of their corresponding angles are equal
∠A≅∠X ∠B≅∠Y ∠C≅∠Z
In the above example, we have triangles ABC and XYZ which are scaled, rotated versions of each other. This means that they are similar triangles, or in mathematical notation: ABC∼XYZ where “” is the symbol denoting similarity.
With these conditions, we have the following theorems that involve similarity between triangles: the Angle-Angle Similarity Theorem, the Side-Angle-Side Similarity Theorem, and the Side-Side-Side Similarity Theorem.
AA Similarity Theorem
The Angle-Angle (AA) Similarity Theorem determines similar triangles based on a pair of two angles in triangles. It states that if the measure of two angles of a triangle is equal to the measure of two angles in another triangle, then the two triangles are similar.
This also refers to the Angle-Angle-Angle (AAA) Similarity Theorem, since by the Angle Sum Property we can tell that the third angle and its corresponding angle are equal.
SAS Similarity Theorem
The Side-Angle-Side (SAS) Similarity Theorem determines the similarity between two triangles by comparing a set of two angles and the angle formed between these sides.
It states that if the measure of the lengths of any two sides in a triangle is proportional to the length of two sides in another triangle, and the measures of the included angles in both triangles are equal, then they are similar triangles.
SSS Similarity Theorem
The Side-Side-Side (SSS) Similarity Theorem checks whether two triangles are similar based on the sides of both triangles being compared.
It states that if the measures of the lengths of all sides of a triangle are proportional to the lengths of the sides of the other triangle, then they are similar.
Problem-Solving Examples
We can now proceed to solve sample problems to apply what we have learned so far. Each problem tackles different formulas discussed and gives us a challenge on how to solve through the information given to us.
Using the AA Similarity Theorem
Sample Problem 1:
In the figure below, we have two triangles FGH and JKL. Are the two triangles similar?
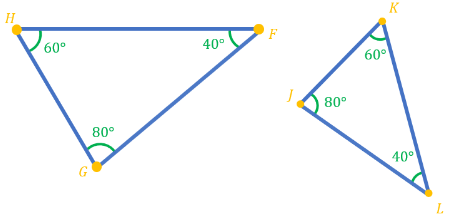
We first note the given measures of each angle:
∠F=40° ∠G=80° ∠H=60° ∠J=80° ∠K=60° ∠L=40°
We then relate the corresponding angles of both triangles to establish the following equalities:
∠F≅∠L ∠G≅∠J ∠H≅∠K
Now, since at least two pairs of angles have the same measure, we conclude that by the AA Similarity Theorem the given triangles are similar :
Sample Problem 2:
Two triangles CAT and DOG whose angles are given are shown below:

We are asked the following questions:
- What is the measure of the unknown angle ∠C?
- What is the measure of the unknown angle ∠D?
- Are CAT and DOG similar triangles?
- We first consider triangle CAT. Two of its angles are given with measures:
∠A=35° ∠T=75°
Then, by the Angle Sum Property we can relate the sum of the interior angles of CAT as:
∠C+∠A+∠T=180°
Substituting the given angle measures, we have:
∠C+35°+75°=180°
Next, we rewrite the equation in terms of the unknown angle by transposing terms to the right-hand side of the equation:
∠C=180°-35°-75°
Finally, we subtract the measures of the angles to get the measure of the unknown angle:
Therefore, the measure of ∠C is 70°.
- Following the steps performed in Part A, we consider the other triangle DOG and note the given measures of its angles:
∠O=70° ∠G=75°
Then, by the Angle Sum Property we can relate the measures of the interior angles of DOG as follows:
∠D+∠O+∠G=180°
Substituting the given angle measures, we get:
∠D+∠70°+∠75°=180°
We then rewrite the equation in terms of the unknown angle:
∠D=180°-70°-75°
Lastly, we subtract the given measures to obtain the measure of the unknown angle:
Therefore, the measure of ∠D is 35°.
- From the angle measures obtained from Part A and Part B, we relate the corresponding angles of both triangles to establish the following equalities:
∠C≅∠O ∠A≅∠D ∠T≅∠G
Sample Problem 3:
Suppose we have two triangles △ELF and △ORC whose sides and angles are given as shown below:

Show that the two triangles are similar via the AA Similarity Theorem.
To use the AA Similarity Theorem, we must show that at least two pairs of angles in △ELF and △ORC are equal in measure. However, only one angle is given for triangle ELF. Hence, we first solve for the measure of either ∠L or ∠F.
In this case, we choose to solve for ∠L using the Law of Sines. We recall that for triangle ELF, the following equality holds following the Sine Law:
$\frac{e}{sinsin E} = \frac{l}{sinsin L} = \frac{f}{sinsin F}$
Focusing on the given angle and side lengths, we have:
$\frac{8}{sinsin 75°} = \frac{7}{sinsin L}$
Re-writing the equation in terms of the unknown angle measure L, we get:
sinsin L = $\frac{7}{8}$ x sinsin 75°
Solving for the value of sin 75° , we simplify the right-hand side of the equation into:
sinsin L= $\frac{7}{8}$ × 0.97
Then, we can multiply the numbers together to obtain:
sinsin L=0.85
Finally, we take the arcsine of both sides of the equation to solve for the measure of ∠L:
L=arcsin arcsin (0.85)
Now, we observe that for the given triangles we have the following congruent angles:
Therefore, by the AA Similarity Theorem we conclude that both triangles are similar :
Using the SAS Similarity Theorem
Sample Problem 4:
We consider the same pair of triangles from Sample Problem 3:

This time, show that △ELF∼△ORC using the SAS Similarity Theorem.
From the given figure, we know the angle measures of both triangles to be:
∠E=75° ∠O=47° ∠R=58°
From the given angles, we note that the measure of angles ∠E and ∠C are equal:
Next, we observe the given lengths of the sides of both triangles:
EF=7 LF=8 OC=21 OR=24
If we consider the side opposite to the congruent angles, and one side adjacent to it, we compare the ratio of their measures between triangles △ELF and △ORC, we get:
$\frac{EF}{OC} = \frac{7}{21} = \frac{1}{3}$ $\frac{LF}{OR} = \frac{8}{24} = \frac{1}{3}$
Hence, we can say that the two sides of both triangles are proportional to each other:
$\frac{EF}{OC} = \frac{LF}{OR}$
Since ∠E≅∠C, and $\frac{EF}{OC} = \frac{LF}{OR}$, by the SAS Similarity Theorem we therefore conclude that the given triangles are similar :
△ELF ∼ △ORC
Sample Problem 5:
In the figure shown below, we have two isosceles triangles whose sides and angles are known:

- Are the two triangles similar?
We first note that the given triangles are isosceles. This means that the lengths of two sides are equal, and the measures of two internal angles are also equal. In this case, we have the following information given to us:
∠E=∠R=65° RD=ED=13 TI=TN=26
We wish to find the measure of the unknown angle ∠D. By the Angle Sum Property, we can relate the internal angles of RED such that:
∠R+∠E+∠D=180°
65°+65°+∠D=180°
Then, we transpose terms to isolate the unknown angle ∠D:
∠D=180°-65°-65°
Hence, we can determine the measure of angle ∠D by subtracting the numbers on the right-hand side of the equation:
We note that this angle has a measure equal to that of ∠T. As such, we can say that both angles are congruent:
Next, if we consider the equal sides of both triangles and take their ratio, we get the following equalities:
$\frac{RD}{TI}=\frac{13}{26}=\frac{1}{2}$ $\frac{ED}{TN}=\frac{13}{26}=\frac{1}{2}$
Thus, we can say that the two sides of both triangles are proportional to each other:
$\frac{RD}{TI}=\frac{ED}{TN}$
Finally, since ∠D≅∠T, and $\frac{RD}{TI}=\frac{ED}{TN}$, we therefore conclude by the SAS Similarity Theorem that both triangles are similar :
△RED ∼ △TIN
Using the SSS Similarity Theorem
Sample Problem 6:
Suppose we have two equilateral triangles △ABC and △XYZ:
- If their side lengths are given by AB=1 and XY=10, are the two triangles similar?
- If the side lengths of △ABC are changed to AB=20 and △XYZ remains unchanged, are they still similar triangles?
- In general, can we say that all equilateral triangles are similar? Why or why not?
- We recall that for equilateral triangles, all sides have equal length. This implies that the side lengths for both triangles are given as:
AB=AC=BC=1 XY=XZ=YZ=10
Now, if we take the ratio between corresponding sides of both triangles, we observe that they have the same value:
$\frac{AB}{XY}=\frac{1}{10}$ $\frac{AC}{XZ}=\frac{1}{10}$ $\frac{BC}{YZ}=\frac{1}{10}$
Hence, we can say that all sides of both triangles are proportional to each other:
$\frac{AB}{XY}=\frac{AC}{XZ}=\frac{BC}{YZ}$
Therefore, by the SSS Similarity Theorem we conclude that the given triangles are similar :
- We repeat the same steps done in Part A. Since the given lengths are:
AB=AC=BC=20 XY=XZ=YZ=10
We know that the ratio between their corresponding sides is equal:
$\frac{AB}{XY}=\frac{AC}{XZ}=\frac{BC}{YZ}=\frac{20}{10}$
Thus, we conclude by the SSS Similarity Theorem that the two triangles are also similar :
- We have observed that changing the side lengths of either triangle still preserves similarity between the two triangles. Since the side lengths of one triangle change in proportion to its other sides, we expect the ratio between the side lengths of both triangles to remain equal.
Through this observation, we can say that all equilateral triangles are similar .
Sample Problem 7:
Two triangles △RST and △UVW are shown whose side lengths and angle measures are given:

- What is the length of side RS of triangle △RST?
- We observe that for triangle △RST, two sides and their included angle are given. We need to know all three sides of both triangles to use the SSS Similarity Theorem. Hence, we can apply the Law of Cosines to solve for the length of side RS.
We recall from the Cosine Law that the lengths of the sides of △RST can be expressed as follows:
RS 2 =ST 2 +RT 2 – (2×ST×RT×coscos T )
Substituting the given side lengths and included angle, we have:
RS 2 =16 2 +14 2 -(2×16×14×coscos 47°)
We then evaluate the value of the trigonometric function:
RS 2 =16 2 +14 2 -(2×16×14×0.682)
Next, we multiply the numbers enclosed within parentheses:
RS 2 =16 2 +14 2 -305.536
We also take the square of both numbers on the right-hand side of the equation:
RS 2 =256+196-304.64
Thus, we can simplify the equation by adding/subtracting the numbers together:
RS 2 =146.464
We take the square root of both sides to get the length of side RS:
Rounding off to the nearest whole number, we conclude that the length of RS is 12:
- Now that we know the side lengths of both triangles to be:
| RS=12 | RT=14 | ST=16 |
| VW=36 | UW=42 | UV=48 |
If we take the ratio between the corresponding sides of both triangles, we have the following values:
$\frac{RS}{VW}=\frac{12}{36}=\frac{1}{3}$ $\frac{RT}{UW}=\frac{14}{42}=\frac{1}{3}$ $\frac{ST}{UV}=\frac{16}{48}=\frac{1}{3}$
Thus, we can say that all sides of both RST and UVW are proportional to each other:
$\frac{RS}{VW}=\frac{RT}{UW}=\frac{ST}{UV}$
Therefore, by the SSS Similarity Theorem we conclude that both triangles are similar :
Sample Problem 8:
In the figure shown below, we have two right triangles △LMN and △OPQ:

- What is the length of the hypotenuse of △LMN?
- What is the length of side OP of △OPQ?
- Are the given triangles similar?
- We begin by solving for the length of the hypotenuse of △LMN by applying the Pythagorean Theorem. We recall for a right triangle, the length of the hypotenuse is given by:
LN 2 =LM 2 +MN 2
Substituting the given side lengths, we have:
LN 2 =8 2 +6 2
We then take the square of both numbers we have substituted earlier to get:
LN 2 =64+36
Then, we add both numbers on the right-hand side of the equation:
Lastly, we take the square root of both sides of the equation to get the length of the hypotenuse:
Therefore, the length of the hypotenuse LN is 10.
- We then proceed to solve for the length of the unknown side of △OPQ through the Pythagorean Theorem. Again, for a right triangle, their side lengths are related as:
OQ 2 =OP 2 +PQ 2
Re-writing the equation in terms of the unknown side OP, we get:
OP 2 =OQ 2 -PQ 2
OP 2 =30 2 -18 2
OP 2 =900-324
Subtracting both numbers on the right-hand side of the equation, we have:
Finally, we take the square root of both sides of the equation to get the length of the unknown side OP:
Therefore, the length of side OP is 24.
- From the computations made in Part A and Part B, we know the side lengths of both triangles to be:
| LM=8 | MN=6 | LN=10 |
| OP=24 | PQ=18 | OQ=30 |
$\frac{LM}{OP}=\frac{8}{24}=\frac{1}{3}$
$\frac{MN}{PQ}=\frac{6}{18}=\frac{1}{3}$
$\frac{LN}{OQ}=\frac{10}{30}=\frac{1}{3}$
Thus, we can say that all sides of both LMN and OPQ are proportional to each other:
$\frac{LM}{OP}=\frac{MN}{PQ}=\frac{LN}{OQ}$
A triangle is a shape formed by a set of three sides , three interior angles , formed between the sides of the triangle, and three vertices , or intersections of the sides of the triangle. It can also have exterior angles , formed by extending one of its sides.
The Angle Sum Property states that the sum of all interior angles in a triangle adds up to a measure of 180°.
The Law of Sines states that the ratio between the length of a triangle’s side and the sine of the angle at an opposite vertex is equal for all sides and angles of any triangle:
On the other hand, the Law of Cosines relates the squares of the lengths of sides of a triangle and the cosine of their included angles:
c 2 =a 2 +b 2 – 2ab coscos C
Two triangles are said to be similar if the following conditions hold:
To determine whether two triangles are similar, we use the following similarity theorems:
The Angle-Angle (AA) Similarity Theorem states that if the measure of two angles of a triangle is equal to the measure of two angles in another triangle, then the two triangles are similar.
The Side-Angle-Side (SAS) Similarity Theorem states that if the measure of the lengths of any two sides in a triangle is proportional to the length of two sides in another triangle, and the measures of the included angles in both triangles are equal, then they are similar triangles.
The Side-Side-Side (SSS) Similarity Theorem states that if the measures of the lengths of all sides of a triangle are proportional to the lengths of the sides of the other triangle, then they are similar.
Frequently Asked Questions (FAQs)
What is an included side.
An included side is a side that coincides with two angles. For example, for a triangle FGH, the side $\overline{HF}$ is an included side between two angles ∠H and angle ∠F:

We can also say from this figure that $\overline{HG}$ is an included side between ∠H and ∠G, and $\overline{GF}$ is an included side between ∠G and ∠F.
What is an included angle?
An included angle is an angle that coincides with two sides. Using the previous example, the angle ∠H is an included angle between two sides $\overline{HF}$ and $\overline{HG}$:

We can also say from this figure that ∠G is an included angle between $\overline{HG}$ and $\overline{GF}$, and ∠F is an included angle between $\overline{HF}$ and $\overline{GF}$.
What is a non-included side?
A non-included side is a side that does not coincide with two angles. For example, for a triangle △FGH, the sides $\overline{HG}$ and $\overline{GF}$ are non-included sides between two angles ∠H and angle ∠F:
We can also say from this figure that $\overline{HF}$ and $\overline{GF}$ are non-included sides between ∠H and ∠G, and that $\overline{HG}$ and $\overline{HF}$ are non-included sides between ∠G and ∠F.

What is a non-included angle?
A non-included angle is an angle that does not coincide with two sides. Using the previous example, the angles G and ∠F are non-included angles between two sides $\overline{HF}$ and $\overline{GF}$:
We can also say from this figure that H and ∠F are non-included angles between $\overline{HG}$ and $\overline{GF}$, and that H and ∠G are non-included angles between $\overline{HF}$ and $\overline{GF}$.
What is the Pythagorean Theorem?
The Pythagorean Theorem relates all three sides of a right triangle in an equation. It states that the square of the length of its hypotenuse is equal to the sum of the squares of the lengths of its other sides:

c 2 =a 2 +b 2
How do we use the Pythagorean Theorem?
If we know the lengths of the sides of a right triangle, we substitute their lengths to the formula. Then, we square their lengths and add them to get the squared length of the hypotenuse. After taking the square root of the sum, we then get the length of the hypotenuse c.
Recommended Worksheets
Perimeter of a Triangle (Thanksgiving Themed) Math Worksheets Right Triangles (Halloween Themed) Math Worksheets Spatial Skills: Triangles and Quadrilaterals (Winter Solstice Themed) Math Worksheets
Link/Reference Us
We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!
<a href="https://helpingwithmath.com/similar-triangles/">Similar Triangles</a>
"Similar Triangles". Helping with Math . Accessed on August 13, 2024. https://helpingwithmath.com/similar-triangles/.
"Similar Triangles". Helping with Math , https://helpingwithmath.com/similar-triangles/. Accessed 13 August, 2024.
Additional Geometry Theory:
Latest worksheets.
The worksheets below are the mostly recently added to the site.
August Free Bundle of Worksheets

Multiplying Mixed Numbers by Fractions 5th Grade Math Worksheets

Dividing Mixed Numbers by Fractions 5th Grade Math Worksheets

July Free Bundle of Worksheets

Grade 1 Geometry Free Bundle

Grade 1 Measurement and Data Free Bundle

Grade 1 Operations and Algebraic Thinking Free Bundle

Grade 1 Number and Operations in Base Ten Free Bundle

June Free Bundle of Worksheets

Comparing Data Using “Less” and “More” 1st Grade Math Worksheets

Similarity (geometry)
Informally, two objects are similar if they are similar in every aspect except possibly size or orientation. For example, a globe and the surface of the earth are, in theory, similar.
More formally, we say two objects are congruent if they are the same up to translation, rotation and reflection ( rigid motions ). We say two objects are similar if they are congruent up to a dilation .
Determining Similarity
- All circles are similar.
- If two of the triangles' corresponding angles are the same, the triangles are similar by AA Similarity . Note that by the Triangle Angle Theorem, the third corresponding angle is also the same from the two triangles.
- Two triangles are similar if all their corresponding sides are in equal ratios by SSS Similarity.
- If two of the triangles' corresponding sides are in equal ratio and the corresponding angle between the two sides are the same the triangles are similar by SAS Similarity.
- Two polygons are similar if their corresponding angles are equal and corresponding sides are in a fixed ratio. Note that for polygons with 4 or more sides, both of these conditions are necessary. For instance, all rectangles have the same angles, but not all rectangles are similar.
Applications to Similarity
Once two figures are determined to be similar, the corresponding sides are proportional and the corresponding angles are congruent.
Similar figures (especially triangles) can be usually found in figures that contain many pairs of equal angles.
Something appears to not have loaded correctly.
Click to refresh .
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
High school geometry
Course: high school geometry > unit 4.
- Solving similar triangles
- Solve similar triangles (basic)
- Solving similar triangles: same side plays different roles
Solve similar triangles (advanced)
- Your answer should be
- an integer, like 6
- a simplified proper fraction, like 3 / 5
- a simplified improper fraction, like 7 / 4
- a mixed number, like 1 3 / 4
- an exact decimal, like 0.75
- a multiple of pi, like 12 pi or 2 / 3 pi
ANGLE ANGLE SIMILARITY
Similar figures have the same shape but may have different sizes. Two triangles are similar if their corresponding angles are congruent and the lengths of their corresponding sides are proportional.
Angle-Angle (AA) Similarity Postulate
If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar.
Discovering Angle Angle Similarity
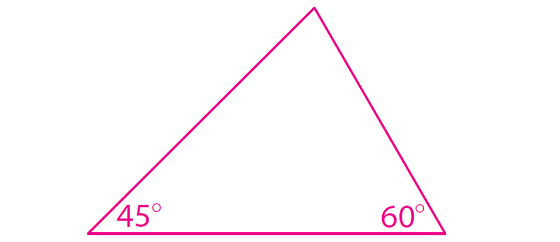
Use your protractor and a straightedge to draw a triangle. Make one angle measure 45° and another angle measure 60°.
Step 2 :
Compare your triangle to those drawn by your classmates. Triangle drawn by you and the triangles drawn by your classmates will have same shape and different in sizes.
Step 3 :
Use the Triangle Sum Theorem to find the measure of the third angle of your triangle.
180° - (45° + 60°) = 180° - 105° = 75°
1. If two angles in one triangle are congruent to two angles in another triangle, what do you know about the third pair of angles ?
They must also be congruent.
2. Are two pairs of congruent angles enough information to conclude that two triangles are similar ? Explain.
By the Triangle Sum Theorem, the third pair of angles must have the same angle measure and thus are congruent, so the triangles must be similar.
Solved Problems
Problem 1 :
Explain whether the triangles PQR and STU are similar.
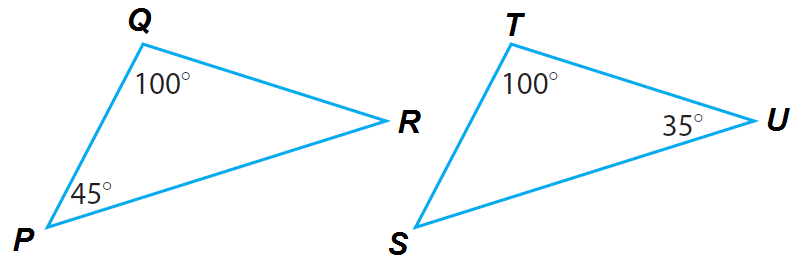
The figure shows only one pair of congruent angles. Find the measure of the third angle in each triangle.
Triangle PQR :
Write the Triangle Sum Theorem for this triangle.
m ∠P + m ∠Q + m ∠R = 180°
Substitute the given angle measures.
45 ° + 100° + m ∠R = 180 °
145° + m ∠R = 180 °
Subtract 145° from both sides.
145° + m ∠R - 145 ° = 180 ° - 145 °
m ∠R = 35 °
Triangle STU :
m ∠S + m ∠T + m ∠U = 180°
m ∠S + 100° + 35° = 180°
m ∠S + 135° = 180 °
Subtract 135° from both sides.
m ∠S + 135° - 135 ° = 180° - 135 °
m ∠S = 45 °
Conclusion :
Three Angles of triangle PQR are 45 °, 100° and 35 °.
Three Angles of triangle STU are 45 °, 100° and 35 °.
Because two angles in one triangle are congruent to two angles in the other triangle, the two triangles are similar.
Problem 2 :
Explain whether the triangles ABC and DEF are similar.
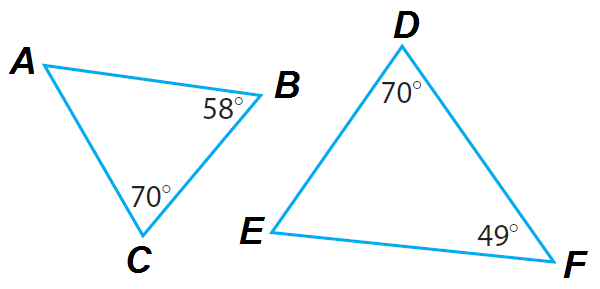
Triangle ABC :
m ∠A + m ∠B + m ∠C = 180°
m ∠A + 58° + 70° = 180°
m ∠A + 128 ° = 180 °
Subtract 128° from both sides.
m ∠A + 128 ° - 128 ° = 180° - 128 °
m ∠A = 52 °
Triangle DEF :
m ∠D + m ∠E + m ∠F = 180°
70° + m ∠E + 49° = 180°
m ∠E + 119 ° = 180 °
Subtract 119° from both sides.
m ∠E + 119 ° - 119 ° = 180° - 119 °
m ∠E = 61 °
Three Angles of triangle ABC are 52 °, 58° and 70°.
Three Angles of triangle DEF are 70 °, 61° and 49°.
Because only one angle is congruent, the two triangles are not similar.
Kindly mail your feedback to [email protected]
We always appreciate your feedback.
© All rights reserved. onlinemath4all.com
- Sat Math Practice
- SAT Math Worksheets
- PEMDAS Rule
- BODMAS rule
- GEMDAS Order of Operations
- Math Calculators
- Transformations of Functions
- Order of rotational symmetry
- Lines of symmetry
- Compound Angles
- Quantitative Aptitude Tricks
- Trigonometric ratio table
- Word Problems
- Times Table Shortcuts
- 10th CBSE solution
- PSAT Math Preparation
- Privacy Policy
- Laws of Exponents
Recent Articles
Derivative problems and solutions (part - 6).
Aug 13, 24 12:32 PM
SAT Math Resources (Videos, Concepts, Worksheets and More)
Aug 12, 24 12:42 PM
Digital SAT Math Problems and Solutions (Part - 26)
Aug 12, 24 12:40 PM
Geometry: Common Core (15th Edition)
By charles, randall i., chapter 7 - similarity - 7-2 similar polygons - practice and problem-solving exercises - page 444: 9, work step by step, update this answer.
You can help us out by revising, improving and updating this answer.
After you claim an answer you’ll have 24 hours to send in a draft. An editor will review the submission and either publish your submission or provide feedback.


IMAGES
COMMENTS
Practice and Problem Solving: A/B 1. ΔABC has angle measures 42°, 50°, 88°, and ΔFGH has angle measures 42°, 50°, 88°. The triangles are similar because two angles in one triangle are congruent to two angles in the other triangle. 2. ΔXYZ has angle measures 41°, 55°, 84°, and ΔPRQ has angle measures 38°, 55°, 87°.
Angle Relationships Practice and Problem Solving: D For Exercises 1-3, use the figure. The first one is done for you. 1. Name a pair of vertical angles. _____ 2. Name a pair of complementary angles. _____ 3. Name a pair of supplementary angles. _____ Use the diagram to find each angle measure. The first one is done for you. 4. If m 3 = 60q ...
Which triangles are similar to A B C ? 58 ° 68 ° A B C. Choose 1 answer: Choose 1 answer: (Choice A) 54 ° 93 ° Q R S. Q R S only. A. 54 ° 93 ° Q R S.
Problem. In the diagram below, D R → is perpendicular to O P ― . P O A U D R M 4.5 4.0 10.0 3.75. Find the area of D U O . If entering your answer as a decimal, round your final answer to the nearest hundredth. square units. Report a problem. Learn for free about math, art, computer programming, economics, physics, chemistry, biology ...
3. Explain whether the triangles are similar. Because corresponding angles are congruent and corresponding sides are proportional in similar triangles, you can use similar triangles to solve real-world problems. While playing tennis, Matt is 12 meters from the net, which is 0.9 meter high.
No, there is not a similarity criterion using only angles for quadrilaterals. This is because some figures can have all corresponding pairs of angles congruent and still not be similar. For example, all angles in a rectangle are 90 degrees, but a 3-by-4 rectangle is not similar to a 3-by-5 rectangle. Feel free to give me any feedback or critiques!
Angle-Angle Similarity Practice and Problem Solving: A/B ... Angle-Angle Similarity Practice and Problem Solving: C Solve. 1. Which of the triangles at the right are ... Can you assume that the similar triangles in problem 1 are congruent? Explain. _____ _____ Find the unknown measure. 3. A tree casts a shadow 21 feet long, while 4. ...
Subtract 130° from both sides. m∠D + 139° - 139° = 180° - 139°. Simplify. m∠D = 41°. Conclusion : Three Angles of triangle ABC are 41°, 109° and 30°. Three Angles of triangle DEF are 41°, 109° and 30°. Because two angles in one triangle are congruent to two angles in the other triangle, the two triangles are similar.
Using the angle bisector theorem. Report a problem. Do 4 problems. Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education for anyone, anywhere.
How to solve problems that involve similar triangles? 1. Sketch a diagram of the problem, identifying the similar triangles. 2. Set up the proportion. 3. Cross multiply. 4. Divide. Word Problems with Similar Triangles and Proportions Examples: 1. Two ladders are leaning against a wall at the same angle as shown. How long is the shorter ladder? 2.
The sum interior angles of a triangle is equal to 180. Therefore, , and . We can write the equation: , acknowledging the fact that and . To conclude, by subtracting by both equations, we get . See also. Similarity (geometry) SAS similarity; SSS similarity; This article is a stub. Help us out by expanding it.
Angle-Angle (AA) Similarity Postulate. If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar. 100° 100° 45° A B 35° The triangles above only show one pair of congruent angles. Find the measure of the third angle in each triangle. m∠A = 35° m∠B = 45° Are the triangles similar? Yes ...
* Since the ratios are not equal, we know that the triangles are not similar. As for D, we have one pair of congruent angles. Since we have also been given the lengths of the sides that have an included angle, we can investigate if D and A are similar by the Side-Angle-Side Similarity Theorem. Again, since sides with the same relative length ...
You have two pairs of congruent angles, x ft. so the triangles are similar by the 5 ft 4 in. AA Similarity Theorem. 40 in. 50 ft. You can use a proportion to fi nd the height x. Write 5 feet 4 inches as 64 inches so that you can form two ratios of feet to inches. x ft 50 ft — 64 in. = — 40 in. Write proportion of side lengths. 40x 3200.
Determine similar triangles: Angles. 4 questions. Practice. Determine similar triangles: SSS. 4 questions. Practice. ... Challenging similarity problem (Opens a modal) Practice. Use similar triangles. 4 questions. ... Solving similar triangles. Angle bisector theorem.
ΔA 1 B 1 C 1 ~ ΔA 2 B 2 C 2. Two triangles are similar if: 1. Each angle in one triangle is congruent with (equal to) its corresponding angle in the other triangle i.e.: ∠A1 = ∠A2, ∠B1 = ∠B2 and ∠C1 = ∠C2. 2. The ratio of the length of one side of one triangle to the corresponding side in the other triangle is the same i.e.:
Then, we transpose terms to isolate the unknown angle ∠D: ∠D=180°-65°-65° Hence, we can determine the measure of angle ∠D by subtracting the numbers on the right-hand side of the equation: ∠D=50° We note that this angle has a measure equal to that of ∠T. As such, we can say that both angles are congruent: ∠D≅∠T
Practice and Problem Solving: D Tell whether the shapes are similar. Explain your answer. The first ... Tell whether the four-sided figures are similar. Explain your answer. ... LESSON 4-1 Yes; All the angles are right angles, and the ratio of corresponding sides is 1:3. No; Corresponding side lengths are not proportional.
All circles are similar. There are three ways of determining if two triangles are similar. If two of the triangles' corresponding angles are the same, the triangles are similar by AA Similarity. Note that by the Triangle Angle Theorem, the third corresponding angle is also the same from the two triangles. Two triangles are similar if all their ...
Problem. Solve for x . x =. A E D B C 3 2 x 11. Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education for anyone, anywhere.
Discovering Angle Angle Similarity. Step 1 : Use your protractor and a straightedge to draw a triangle. Make one angle measure 45° and another angle measure 60°. Step 2 : Compare your triangle to those drawn by your classmates. Triangle drawn by you and the triangles drawn by your classmates will have same shape and different in sizes.
Angle Theorems for Triangles Practice and Problem Solving: A/B Find the unknown angle measure in each triangle. Choose the letter for the best answer. 1. 2. A 45° C 90° A 40° C 60° B 55° D 135° B 50° D 70° Find the unknown angle measure in each triangle. 3. 4. 5. _____ _____ _____
Geometry: Common Core (15th Edition) answers to Chapter 7 - Similarity - 7-2 Similar Polygons - Practice and Problem-Solving Exercises - Page 444 9 including work step by step written by community members like you. Textbook Authors: Charles, Randall I., ISBN-10: 0133281159, ISBN-13: 978--13328-115-6, Publisher: Prentice Hall