problem solving ratio questions gcse

• International
• Education Jobs
• Schools directory
• Resources Education Jobs Schools directory News Search

Ratio problem solving for 9-1 GCSE with answers

Subject: Mathematics

Age range: 14-16

Resource type: Worksheet/Activity

Last updated

27 September 2017

• Share through email
• Share through twitter
• Share through linkedin
• Share through facebook
• Share through pinterest

Creative Commons "Sharealike"

Your rating is required to reflect your happiness.

It's good to leave some feedback.

Something went wrong, please try again later.

clareturnertutor

A good set of ratio questions that require problem-solving. Thank you for sharing.

Empty reply does not make any sense for the end user

Nice selection of questions, thank you.

This is an excellent worksheet for the most able students because it focuses on the harder questions that initially cause them problems that are reasonably easy to overcome.

Lovely selection of questions, thank you.

Report this resource to let us know if it violates our terms and conditions. Our customer service team will review your report and will be in touch.

Not quite what you were looking for? Search by keyword to find the right resource:

• 5,000+ Topicwise Questions & Answers Included
• Best for 11+ Grammar & Independent School Exams
• Improve Speed, Accuracy & Time Management

GCSE Ratio & Proportion Questions and Answers

These detailed solutions are visible only for premium members

Please register to unlock over 135+ GCSE Maths Solved Past & Predicted Papers. 5,000+ Topicwise Questions with Step by Step Solutions

GCSE Topics

• Comparing Statistical Measures (1)
• Geometric Mean (1)
• Arithmetic Mean (1)
• Rounding Numbers (87)
• Reverse Percentages (13)
• Odd and Even Numbers (28)
• Estimation (80)
• Decimals to Percentages (6)
• Multiplication and Division (96)
• Percentage Change (56)
• lcm word problems (11)
• Laws of Indices (16)
• Significant Figures (77)
• Order of Operations (13)
• HCF Word Problems (2)
• Profit and Loss (1)
• Decimals (137)
• Percentage Profit and Loss (21)
• Square Roots (41)
• Decimal Places (77)
• Ordering Fractions (5)
• Recurring Decimals (19)
• Repeated Percentage Change (11)
• Rounding Numbers, Estimation, Significant Figures, Decimal Places (14)
• Percentage to Fractions (8)
• Multiplying Decimals (19)
• Calculator Skills (50)
• Product Rule (11)
• Place Value (11)
• Dividing Decimals (27)
• Standard form (48)
• Error Intervals (26)
• Cube Roots (14)
• Pecentage Change (8)
• Ordering Decimals (8)
• Counting Strategies (24)
• Negative Numbers (14)
• Fractions (173)
• Square Numbers (48)
• Upper and Lower Bounds (25)
• Mixed Numbers (27)
• Cube Numbers (30)
• Limits of Accuracy (20)
• Operations with fractions (41)
• HCF, LCM (34)
• Comparing Numbers (24)
• Factors, Multiples and Primes (88)
• Equivalent Fractions (16)
• Fractions of amounts (15)
• Simple and Compound Interest (36)
• Division (1)
• Fractions to decimals (29)
• Multipliers (21)
• Addition and Subtraction (57)
• Multiplication (1)
• Fractions to percentages (12)
• Fraction problems (22)
• Arithmetic Word Problems (182)
• Percentages (222)
• Ordering Numbers, (18)
• Decimals to Fractions (23)
• Time Series Graphs (1)
• Interpreting and Comparing Data (1)
• Scatter Graph (1)
• Negative Indices (16)
• Quadratic Sequences (19)
• Factorizing Quadratics (11)
• Formulae (3)
• Algebraic Fractions (23)
• Coordinates (101)
• Cubic and Reciprocal Graphs (19)
• Linear Equations (190)
• Gradient of a line (67)
• Transforming Graphs (8)
• Simultaneous Equations (42)
• Equations of Straight Lines (91)
• Areas under curves (17)
• Geometric Sequences (11)
• Quadratics and Fractions (1)
• Quadratic Equations (104)
• Straight Line Graphs (74)
• Algebraic Proof (39)
• Algebraic Equations (308)
• Writing Formulae (1)
• Quadratic Formula (22)
• Real-life Graphs (14)
• Function Notation (26)
• Completing the Square (11)
• Trigonometric Graphs (18)
• Inverse Functions (14)
• Factorising Expressions (30)
• Substitution (59)
• Graphs of inequalities (12)
• Equation of a Circle (22)
• Composite Functions (14)
• Factorising Quadratics (27)
• Speed Distance Time (74)
• Velocity-time Graphs (18)
• Iterative Methods (16)
• Time Tables (4)
• Expanding Brackets (61)
• Expanding Double Brackets (4)
• Rearranging Formulae (40)
• Algebraic Expressions (190)
• Factorizing Expressions (14)
• Parallel and Perpendicular Lines (36)
• Function Machine (20)
• Algebraic Formulae (20)
• Simplifying Expressions (128)
• Quadratic Graphs (51)
• Collecting like Terms (50)
• Linear Inequalities (48)
• Turning Points (22)
• Indices (112)
• Quadratic Inequalities (10)
• Sketching Graphs (67)
• Order of Operations (BIDMAS) (16)
• Laws of Indices (70)
• Fractional Indices (28)
• Sequences (74)
• Exponential Graphs (16)
• Cubic Equations (18)
• Algebraic Indices (16)
• Arithmetic Sequences (43)
• Gradients of Curves (13)
• Rates of Change (5)
• Scale diagrams and maps (17)
• Ratio & Proportion (248)
• Compound Measures (26)
• Proportion and Graphs (12)
• Unit Conversions (84)
• Growth and Decay (9)
• Density (24)
• Direct and Inverse Proportion (62)
• Angles (135)
• Rhombus (7)
• Trigonometry Angles (98)
• 3D trigonometry (6)
• Pythagoras Theorem (45)
• Trapeziums (31)
• Sine Rule (21)
• Circles (1)
• 3D Pythagoras Theorem (8)
• Prisms (23)
• Cosine Rule (19)
• Constructing Perpendicular Lines (11)
• Circles, Sectors and Arcs (110)
• Vectors (55)
• Constructions (32)
• Cylinders (17)
• Plans and Elevations (15)
• Circle Theorems (33)
• Scale Drawings and Maps (26)
• Transformations (54)
• Reflection (30)
• Polygons (39)
• Pyramid (12)
• Area and Perimeter (179)
• Rotations (25)
• Scale Factor (39)
• 3D Shapes (74)
• Translations (25)
• Parallel Lines (22)
• Rotational Symmetry (9)
• Volume & Surface Area (87)
• Enlargement (27)
• Triangles (189)
• Similar Shapes (34)
• Squares (41)
• Congruent Triangles (27)
• Symmetry (18)
• Rectangles (68)
• Bearings (19)
• Line Symmetry (14)
• Nets of solids (2)
• Parallelograms (23)
• Trigonometry Lengths (73)
• Unit Conversion (2)
• Cumulative Frequency (29)
• Mean, mode and Median (94)
• Comparing Data (16)
• Stem and Leaf Diagrams (4)
• Data and Sampling (13)
• Histograms (23)
• Bar charts (29)
• Pictograms (14)
• Pie charts (26)
• Frequency Polygon (6)
• Box plots (18)
• Scatter graphs (28)
• Time series graphs (14)
• Averages and Range (33)
• Sampling (2)
• Line Graphs (14)
• Frequency Table (50)
• Probability (2)
• Sample space diagram (20)
• AND & OR Rules (56)
• Two way Tables (7)
• Relative Frequency (24)
• Tree diagrams (38)
• Frequency and Outcomes (12)
• Venn Diagrams (42)
• Set Notation (11)
• Conditional Probability (13)
• Independent Events (14)
• interpreting via collected data and calculated probabilitites (1)
• Comparing Probabilities (1)

The main topics in GCSE Maths are:

• Ratio, Proportion and Rates of Change 
• Geometry and Measures
• Statistics 
• Probability 
• Statistical Measures 
• Data Visualisation 

With regular practice of GCSE Maths topic-wise questions and GCSE Maths past pacers , you can easily score high marks.

Although many people think of GCSE maths as a difficult subject, with the correct training and preparation,you can master it in time. You can practice GCSE Maths  topic-wise questions daily to improve speed, accuracy, and time and to score high marks in the GCSE Maths exam.

A grade of 4 or 5 would be considered "good" because the government has established a 4 as the passing grade; a grade of 5 is seen as a strong pass. Therefore, anything that exceeds this level would be considered good. You can practice GCSE Maths topic-wise questions to score good grades in the GCSE Maths exam.

You can get a high score in GCSE Maths through meticulous practice of GCSE Maths topic-wise questions and GCSE Maths past papers .

Subscribe to Newsletter

** Get 10% off coupon code on your first order, valid sitewide.

PiAcademy Partners

Follow us on

More than 20,000 registered members!

Exam papers.

© 2014 - 2024 PiAcademy Limited, All Rights Reserved

Ratio: Problem Solving Textbook Answers

Click here for answers, gcse revision cards.

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

GCSE Tutoring Programme

"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."

GCSE Maths Topics

This topic is relevant for:

Ratio and Proportion

Ratio And Proportion – Maths GCSE

Here we will learn about ratio and proportion, including forming and sharing with ratios, using solving problems involving direct or inverse proportion, solving problems involving compound measures and finding rates of change.

There are also ratio and proportion worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is ratio and proportion?

Ratio and proportion is an area of mathematics which deals with the relationship between two or more quantities. The understanding of ratio and proportion is a vital part of GCSE mathematics and it links to many of the number, algebra, geometry, probability and statistics topics.

In this page we will link to lots of other pages that will help with a variety of ratio and proportion topics that are examined in both foundation and higher GCSE mathematics. Some have already been seen in key stages 2 and 3.

Each of the sections will include exam practice questions and mark schemes.

Ratio is a relationship between two or more quantities showing the number of times one is contained within the other(s).

Ratios are written in the form a:b, which is said “ a to b ” where a and b are normally integers, fractions or decimals.

They can also be represented in the form \frac{a}{b} (a fraction).

The order of the quantities in the ratio is important.

For example, there are 10 boys in a class and 15 girls. The ratio of boys to girls is 10:15 which we say as “ 10 to 15 ”.

We can use ratios in a variety of ways,

• Working out ratio
• Simplifying ratios
• Dividing (sharing) in ratios
• Ratios to fractions
• Ratio problem solving
• Ratio scales

Step-by-step guide: Ratio

Proportion is a type of relationship between two variables linked by a constant . 

There are two types of proportion, direct proportion and inverse proportion . They can also be referred to as direct variation and inverse variation . 

Equations can be formed to represent proportional relationships.

The symbol ‘\propto’ means ‘is proportional to’.

If y is directly proportional to x we can write it as y\propto{x}.

We can then rewrite this using a constant of proportionality usually denoted by the letter ‘k’. 

The direct proportion formula is y=kx.

If y is inversely proportional to x we can write it as y\propto\frac{1}{x} .

We can then rewrite this using a constant of proportionality usually denoted by the letter ‘k’.

The inverse proportion formula is y=\frac{k}{x}.

We can also have proportional relationships involving powers with equations such as y=k{x}^{n}, \ y=k\sqrt[n]{x}, \ y=\frac{k}{{x}^{n}} and y=\frac{k}{\sqrt[n]{x}}.

Step-by-step guide: Proportion

Ratio and proportion worksheet

Over 30 ratio and proportion worksheets ready to download and give to your GCSE students. Each with functional and applied reasoning questions and exam style questions.

Compound measures

Compound measures are measures which are found from two other measures.

The most common compound measures studied at GCSE Maths are speed , density and pressure .

There are other compound measures such as rates of pay (for example, pounds (£) per hour) or flow rate (for example, litres per minute). We can also use compound measures when calculating a best buy (for example, grams per pence).

Step-by-step guide: Compound measures (coming soon)

Speed is a compound measure made from dividing a unit of distance by a unit of time. Speed is a measure of how much an object has travelled over a certain time period . The different units for speed include metres per second (m/s) and kilometres per hour (km/h).

The speed formula is,

Step-by-step guide: Speed distance time

Density is a compound measure made from dividing a unit of mass by a unit of volume. Density is a measure of how the amount of matter there is in a certain volume . The different units for density include grams per cubic centimetre (g/cm^{3}) and kilograms per cubic metre (kg/m^{3}).

The density formula is,

Step-by-step guide: Mass density volume

Pressure is a compound measure made from dividing a unit of force by a unit of area. Pressure is defined as the force per unit area . The standard unit of pressure is Pascals (Pa). One Pascal is equal to 1 \ N/m^{2}. We need to know that pressure is calculated by dividing the amount of force by the area.

The pressure formula is,

Step-by-step guide: Pressure force area

Best buy problems involve assessing which item is the best value for money.

To do this we we could use the following methods,

Unitary method

This involves calculating the price per unit for each item.

Common multiples

Here we find a common multiple of the number of units we have and use this to make comparisons.

We interpret deals such as ‘3 for 2’, ‘buy one get one free’ or a percentage extra free.

Exchange rates

If the prices are in different currencies, we convert them to the same currency to compare them.

Step-by-step guide: Best buy maths

Scale maths

Scale maths is a way of enlarging an object.

If we have two shapes that are similar, one will be a scale diagram of the other. Usually we need to find the scale factor of enlargement or find a missing length, area or volume .

Scale maths is used for real world scale drawings as it is much easier to create a scale drawing of an object, than to draw the object using actual distances . 

The ratio usually takes the form 1:n of the model/plan to the actual distance. 

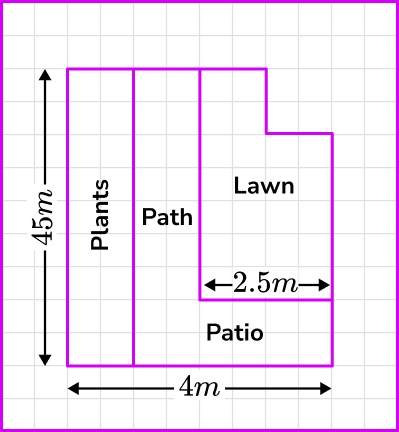
For example, below is a scale diagram of a garden where 1 square is equal to 0.5 metres.

Writing this as a ratio we get \bf{1} square: \bf{0.5 \ m} .

Step-by-step guide: Scale maths

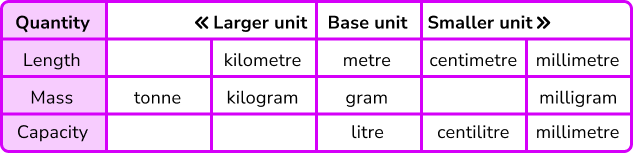
• Units of measurement

Units of measurement are used to measure different quantities.

The main metric units of measurement are here,

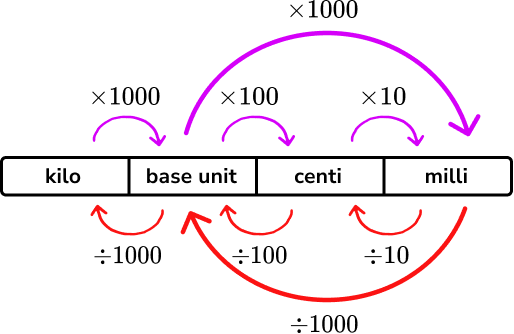
We also need to know how to convert between different units of measurement.

We also need to know about imperial units of measurement and units of measurement for area and volume.

Step-by-step guide: Units of measurement

Flow rate is the term used to describe the rate at which a fluid or substance flows into or out of an object.

To calculate flow rate we can use information about the change in capacity of the substance and the amount of time taken for that change to occur.

For example, a tap is used to fill a container in the shape of a cuboid measuring 1.5 \ m by 2 \ m by 0.4 \ m.

The tap releases water at a flow rate of 5 litres per minute. 

Find the time taken for the container to be filled.

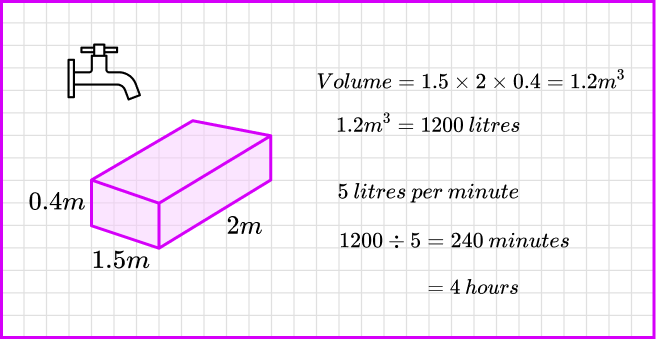
Step-by-step guide: Flow rate

Conversion graphs

Conversion graphs are straight line graphs that show a relationship between two units and can be used to convert from one to another. They are very useful to solve real-life problems.

Some conversion graphs can show a direct proportion between two units, for example, converting between two currencies to show an exchange rate, such as Pounds Sterling to US Dollars.

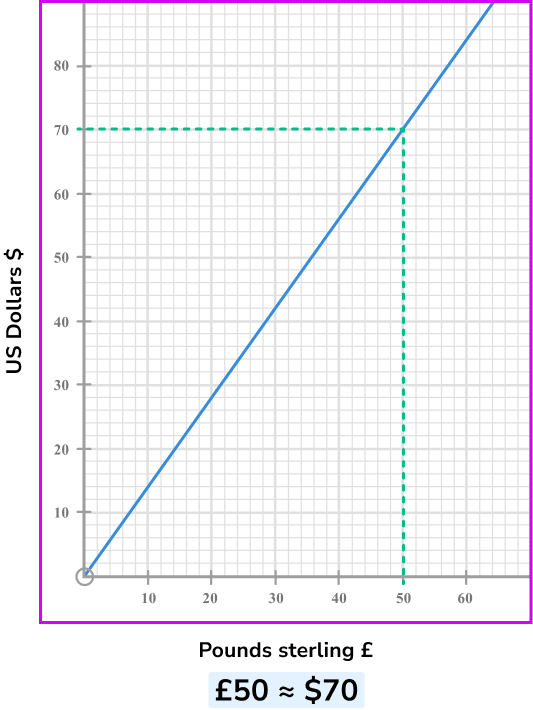
Step-by-step guide: Conversion graphs

An exchange rate is the rate at which the money of one country can be exchanged for the money of another country. Using the exchange rate we can convert between two currencies.

To convert from British pounds to a foreign currency you must multiply the currency in pounds by the exchange rate.

For example, £1 is equivalent to \$1.87 \ AUD and so for any amount given in British pounds, we multiply that value by 1.87 to get the number of Australian dollars.

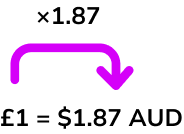
To convert from a foreign currency into British pounds you must divide by the exchange rate.

For example, to convert Australian dollars back to British pounds, we divide the number of Australian dollars by 1.87.

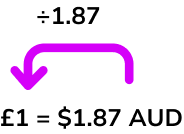
Step-by-step guide: Exchange rates

Rate of change

Rates of change relate to what degree one variable changes in relation to another.  

A rate of change can be calculated by finding the gradient of a straight line, either at a point or between two points.

For example, below is a straight line graph.

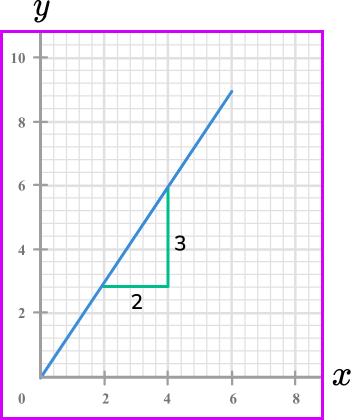
The gradient of the line is

Sometimes we need to find the instantaneous rate of change. This is the rate of change at a specific point. It is found by calculating the gradient of a curve/line at a particular point using a tangent line.

A tangent line is a line that just touches a curve at a single point, it matches the curve’s gradient at that point.

We may also need to find the average rate of change from a curve. This is the rate of change between two points where the rate of change is not constant. It is found by calculating the gradient of a chord between two points.

Step-by-step guide: Rate of change

Common misconceptions

• Ratio written in the wrong order

A common error is to write the parts of the ratio in the wrong order.  For example, the number of dogs to cats is given as the ratio 12:13 but the solution is incorrectly written as 13:12.

• Ratios and fractions confusion

For example, the ratio 2:3 is incorrectly expressed as the fraction \frac{2}{3} and rather than the correct answer of \frac{2}{5}. This is a misunderstanding of the sum of the parts of the ratio. The sum of all of the parts of the ratio gives us the denominator of the fraction.

• Incorrect use of the exchange rate when converting currencies

If £1= \$1.30, to convert £ to \$ we need to multiply by 1.30. To convert \$ to £ we need to divide by 1.30, not the other way around.

• Converting units

Sometimes the units need to be converted, so it is important to be able to confidently convert between different metric units. For example, a map scale is given as 1:25000 which means that 1 \ cm on the map is equivalent to 25000 \ cm in real life. If the answer needs to be written in kilometres, the real life value in centimetres must be divided by 100 \ 000 to get the same measurement in kilometres. 1:25 \ 000 = 1 \ cm: 0.25 \ km.

Practice ratio and proportion questions

1. The fraction of bananas in a bowl is \frac{8}{15}. Calculate the ratio of bananas to other pieces of fruit in the bowl.

Let the total number of pieces of fruit be 15. The number of bananas is 8. The number of other pieces of fruit is therefore 7. The ratio of bananas to other pieces of fruit is therefore 8:7.

2. If it takes 5 workers 12 hours to do a job, how long would it take 9 workers to complete the same job? Give your answer in hours and minutes.

3 hours 45 minutes

21 hours 6 minutes

7 hours 6 minutes

6 hours 40 minutes

This is an inverse proportion problem.

The total time needed to complete the job is

k=5\times 12=60 hours.

This means that y=\frac{60}{x} where y is the number of hours it takes x people to complete a job.

Sharing this time between 9 workers would be

Two thirds of an hour ( 60 minutes) is calculated by multiplying 60 by two thirds.

60\times\frac{2}{3}=40 minutes

The final answer would be 6 hours 40 minutes.

3. Which of these graphs indicates that y\propto\frac{1}{x}?

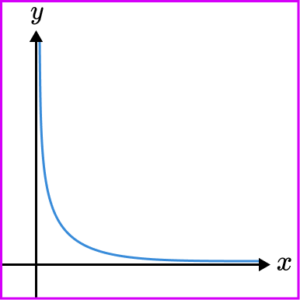
y\propto\frac{1}{x} becomes y=\frac{k}{x} and so a reciprocal graph is required. The graph must be a smooth curve, and does not touch either axis.

4. Find the density of an object when the mass of the object is 350 \ g and its volume is 25 \ cm^{3}.

5. A hose pipe is used to fill a water butt. Water flows at a rate of 3.5 litres per minute and fills the water butt in 12 minutes and 52 seconds. Calculate the volume of the water butt to the nearest litre.

Convert the time into the decimalised form, then use the formula

  \text{Flow rate}=\frac{\text{change in volume}}{\text{time taken}}.

  By multiplying both sides of the formula by the time taken, we can change the subject to be the volume.

  \text{Volume}=\text{flow rate}\times \text{time taken}.   Substituting the values for the flow rate and the time into the formula, we have  

3.5\times{12}\frac{52}{60}=45.0\dot{3}.  

The volume will be 45 litres, to the nearest litre.

6. Lucy is buying some items from an online shop which will accept payments in pounds and euros.

She buys a watch costing £150, a pendant costing £280 and a frame costing £17.

The exchange rate is £1 = €1.27 . Work out the cost of her bill in euros.

Adding up the prices first, we have

  \pounds 150 + \pounds 280+ \pounds 17=\pounds 447.

  Multiplying the total by the exchange rate 1.27, we have

  This gives €567.69.

Ratio and proportion GCSE questions

1. Imogen and Samuel share some sweets in the ratio of 7:5.

Imogen has 12 more sweets than Samuel. How many sweets were there altogether

2 shares is equivalent to 12 sweets or 1 share is equivalent to 6 sweets.

2. Stones of different mass M \ kg are dropped into sand and make a circular crater of diameter D \ cm.

The diameter of the crater is directly proportional to the square root of the mass.

A stone of mass 4 \ kg makes a crater of diameter 6 \ cm.

(a) Write a formula for D in terms of M.

(b) Find the diameter of the crater made by a stone of mass 9 \ kg.

(c) Find the mass of the stone that makes a crater of diameter 12 \ cm.

Form an equation with k, \ D=k\sqrt{M} .

Substitute M=9 into the equation, D=3\sqrt{9} .

Substitute D=12 into the equation, 12=3\sqrt{M} .

3. Joseph buys a camera in the USA for \$330.

Amelia buys the same camera in the UK for £255.

The exchange rate is £1 = \$1.32.

Where is the camera the cheapest, USA or UK?

255 \times 1.32 or 330 \div 1.32

The most popular lessons are

• Converting metric units
• Dividing ratios

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Privacy Overview

Resourceaholic

Ideas and resources for teaching secondary school mathematics

• Blog Archive

20 December 2017

New gcse: ratio.

• Mel from JustMaths collated ratio Higher GCSE questions from sample and specimen papers here , and has written up her solutions here . 
• If you subscribe to MathsPad then you'll be pleased to hear that they have lovely resources for ratio including a set of questions for Higher GCSE  with loads of examples like the problems I've featured in this post.  
• Don Steward has plenty of ratio tasks  including his set of ' Harder Ratio Questions ' and a really helpful collection of GCSE ratio and proportion questions .
• On MathsBot you can generate ratio questions, revision grids and practice papers. Select 'ratio, proportion and rates of change' at the top.
• There are exam style questions in this collection from Lucy Kilgariff on TES.
• OCR has a 'Calculations with Ratio' Topic Check In  and AQA has a Ratio and Proportion Topic Test .
• David Morse of Maths4Everyone has shared a set of revision exercises and ratio exam style questions .

20 comments:

My ratio pages don't get much attention - not sure why since I think they're instructive and easy to use. They don't support the particular type of harder questions described in the post (but I'll look to add something along those lines), but they do help understanding the concept of a ratio and it's utility. Manipulation of ratio quantities: http://thewessens.net/ClassroomApps/Main/ratios.html?topic=number&path=Main&id=7 Introduction to the ratio concept: http://www.thewessens.net/blog/2015/03/19/ratios-the-super-fractions/ Bar model visualisation of ratios: http://thewessens.net/ClassroomApps/Models/BarModels/visualfractionratio.html?topic=models&path=Models&id=17 Multiplicative word problems: http://thewessens.net/ClassroomApps/Models/BarModels/multiplicationwordproblems.html?topic=models&path=Models&id=8 Ken

Fantastic! Thanks Ken.

Thanks so much for your blog on ratio question types. Although I've been a maths teacher/tutor for over 30 year, ratio has always been a bug bear for me. I could wing it with old style gcse because I learnt the types of solutions required, however I have been stressed on the new types. This blog has made me think through ratios and I am certainly a lot happier. Bryan

Excellent, I'm so pleased it helps.

On your fractions approach, a quick trick is to realise that a/c = a/b x b/c. Makes it quite quick to work out (That is, if the students are good with cancelling down when multiplying). However, what I find confuses students about writing ratios as fractions is that it confuses the part:part idea of a ratio with the part:whole idea of a fraction. Perhaps that's why it's somewhat counter-intuitive. Also, final point is that ratios (fractions) and vectors is another application of harder ratio questions that often pops up on the new GCSE. Thanks for the post, Farah

Thanks for the comment!

This is a fabulous resource on work that is missing from the new GCSE texts that I have seen. Lovely challeging questions to make students think.

Thanks! Glad it's helpful.

I've been using equivalent ratios for these type of questions. Find what doesn't change - the total number of sweets. Write ratios as equivalent ratios where the parts that doesn't change are the same. 3:7 has 10 parts, 3:5 has 8 parts LCM of 8 and 10 is 40 Ratios are 12:28 and 15:25 Number of sweets given is 3. Also works for following question Ratio of blue to red counters in a bag is 1:2, I add 12 blue counters and the ratio is 5:7. How many red counters are in the bag? What doesn't change? Red counters LCM of 2 and 7 is 14 Ratios are 7:14 and 10:14 3 parts are 12 counters, 1 part is 4 counters and 14 parts are 56 red counters. Also Jill is 4 times older than Jack. In 14 years time the ratio of Jack's age to Jill is 5:7. How old is Jill now? Ratios are 1:4 and 5:7. What doesn't change? The difference between their ages Find two equivalent ratios where difference between them is the same. 4 - 1 = 3 and 7 - 5 = 2 LCM of 2 and 3 is 6 Equivalent ratios are 2:8 and 15:21 13 parts = 26 years, 1 part is 2 years, Jill is 16.

This is the approach I use. I think it's logical.

Thank you! Yes, this is logical. Same approach as bar modelling (but without the visual).

Oops, my mistake, third example should be .....in 26 years time the ratio of their ages is 5:7 ..... I did try to represent these using bar modelling at first but struggled to find a model that was intuitive and actually helped with the question. I would be grateful if anyone has ideas on this.

Although some bar modelling experts would disagree, I don't think bar modelling is intuitive/helpful for harder ratio questions. Bar modelling is fantastic for easier ratio questions, but when the questions get more complicated it's often really hard to figure out how to draw the scenario - definitely not as easy as some people make out!

Thank you for the post. Brilliant as usual. I actually did the sweets question in my class once. I simply said that Alice fraction of sweets changed from 7/10 to 5/8 when she gave the 3 sweets away. If we just subtract those fractions, the fraction remaining, 7/10 - 5/8 = 3/40. This means that Alice originally had 40 sweets.

Hadnt considered tis method but I love it

Thanks Stephen. I guess it makes sense, as the fraction lost is equivalent to the 3 sweets divided by the total.

Love this! Thanks for sharing.

Hi Jo, thanks for the post which I came across via a tweet you put out a couple of days ago - which also tied in with a question and the same method I saw in my step-daughters book the very next day - freaky! It is a more compact method than I would normally use in my teaching and will be switching to it. I think the only tweak I might make is to write the algebra ratio above the numeric one so the starting fractions are (7x-3)/5 : (3x+3)/3 The reason being that some students might get a little scared seeing algebra as part of the denominator but less so when faced with a number.

Good idea - thank you!

Hi Jo, One method I use when teaching questions like the first one above (Alice gives 3 sweets to Olivia) is the following. To begin with Alice has 7/10 of the sweets and then after giving three to Olivia, her share has reduced to 5/8 of the sweets. So Alice's share has reduced by (7/10 - 5/8=) 3/40 which is equivalent to 3 sweets, therefore there must be 40 sweets in total. Students can then proceed in answering the relevant question. I must admit I only use this method with the top sets.

Multiple Ratios ( Edexcel GCSE Maths )

Revision note.

Multiple Ratios

How do i combine two ratios to make a 3 - part ratio.

• Sometimes you may be given two separate ratios, that link together in some way, so that you can form a 3-part ratio
• Suppose that on a farm with 85 animals
• The ratio of cows to sheep is 2:3
• The ratio of sheep to pigs is 6:7
• We want to find the number of each animal on the farm
• We can’t just share 85 in the ratio 2:3 or 6:7, because these ratios don’t account for all the animals on the farm on their own
• We need to find a combined, 3-part ratio that shows the relative portions of all the animals together
• Notice that sheep appear in both ratios, so we can use sheep as the link between the two
• C:S = 2:3 and S:P = 6:7
• We can multiply both sides of the C:S ratio by 2, so that both ratios are comparing relative to 6 sheep
• C:S = 4:6 and S:P = 6:7
• These can now be joined together
• C:S:P = 4:6:7
• We can now use this to share the 85 animals in the ratio 4:6:7
• There are 17 parts in total (4 + 6 + 7 = 17)
• Each part is worth 5 animals (85 ÷ 17 = 5)
• There are 20 cows (4 × 5), 30 sheep (6 × 5), and 35 pigs (7 × 5)

How do I answer a 'changed ratio' question ?

• 4+3=7, so the ratio divides the sweets into 7 parts
• 28÷7=4, so each part contains 4 sweets
• Therefore there are 4×4=16 lemon sweets, and 3×4=12 blackcurrant sweets
• So far, so 'I'm smashing ratios'!
• You can still use all your usual ratio 'tricks' here, the only difference is that more steps will be involved
• The question  may give you this info
• If it doesn't, you will need to work it out from the info given (like we just did above)
• We know there were 16 lemon sweets in the bag, and that now those only represent  2 parts in the ratio
• So now one part is equal to 16÷2=8 sweets
• And blackcurrant sweets are now 5 parts in the ratio
• So there are now 5×8=40 blackcurrant sweets in the bag
• And originally there were 12 blackcurrant sweets in the bag
• Therefore Natasha added 40-12=28 blackcurrant sweets to the bag
• Your job in answering is to break the question down into those simple bits
• e.g. The ratio of circles to squares is 3 : 4
• 3 circles are removed and the ratio now becomes 3 : 5
• The number of squares has remained the same so change the "4" and "5" into a common multiple
• 3 : 4 = 15 : 20 and 3 : 5 = 12 : 20
• So there were 15 circles and 20 squares originally

Worked example

In Jamie’s sock drawer there are only black socks, striped socks, and white socks.  The ratio of black socks to striped socks is 5:2, and the ratio of striped socks to white socks 6:7.

Given that there are 18 striped socks in the drawer, determine the total number of socks that are in the drawer.

Because the 'striped socks' number is different in the two ratios, we can't use those ratios yet to talk about all the socks in the drawer. However, 'striped socks' appears in both ratios, so we can use that to link the two ratios together into one overall ratio. If we 'scale up' the black : striped ratio by multiplying it by 3, then the 'striped socks' number will be the same in both ratios.

Now that the 'striped socks' number is the same in both ratios, we can join them together into a 3-part ratio.

Now we can say that 'striped socks' represent 6 parts of the overall ratio. And there are 18 striped socks overall. So divide 18 by 6 to find the size of 1 part.

In the overall ratio, black socks are 15 parts and white socks are 7 parts. Multiply those by 3 to find how many of each type of sock there are.

Finally add all those numbers together to find the total number of socks.

84 socks in total

At Antonio's llamas and quokkas sanctuary there are originally 12 llamas, and the ratio of llamas to quokkas is 3:7.

After some new quokkas arrive at the sanctuary, the ratio of llamas to quokkas changes to 4:13.

Given that the number of llamas has not changed, determine the number of quokkas that arrived at the sanctuary.

First figure out the number of quokkas that were there originally. 12 llamas represents 3 parts in the original ratio. So divide 12 by 3 to find the size of one part.

Quokkas represent 7 parts in the original ratio. So multiply 4 by 7 to find the original number of quokkas.

After the new quokkas arrive, there are still 12 llamas. But now those 12 llamas represent 4 parts in the changed ratio. So divide 12 by 4 to find the size of one part.

And now quokkas represent 13 parts in the changed ratio. So multiply 3 by 13 to find the number of quokkas after the new arrivals.

And finally subtract 28 from 39 to find out how many quokkas arrived.

11 quokkas arrived at the sanctuary

You've read 0 of your 10 free revision notes

Unlock more, it's free, join the 100,000 + students that ❤️ save my exams.

the (exam) results speak for themselves:

Did this page help you?

• Ratio Problem Solving
• Direct & Inverse Proportion
• Standard & Compound Units
• Exchange Rates & Best Buys
• Geometry Toolkit
• Angles in Polygons & Parallel Lines
• Bearings, Scale Drawing, Constructions & Loci
• Circle Theorems
• Area & Perimeter
• Circles, Arcs & Sectors

Author: Roger

Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.