joint variation problem solving examples

Texas Go Math
Big Ideas Math
Engageny Math
McGraw Hill My Math
enVision Math
180 Days of Math
Math in Focus Answer Key
Math Expressions Answer Key
Privacy Policy

$CCSS Math Answers$

Joint Variation – Formula, Examples | How to Solve Problems Involving Joint Variation?

Joint Variation definition, rules, methods and formulae are here. Check the joint variation problems and solutions to prepare for the exam. Refer to problems of direct and inverse variations and the relationship between the variables. Know the different type of variations like inverse, direct, combined and joint variation. Go through the below sections to check definition, various properties, example problems, value tables, concepts etc.

Joint Variation – Introduction

Joint Variation refers to the scenario where the value of 1 variable depends on 2 or more and other variables that are held constant. For example, if C varies jointly as A and B, then C = ABX for which constant “X”. The joint variation will be useful to represent interactions of multiple variables at one time.

Most of the situations are complicated than the basic inverse or direct variation model. One or the other variables depends on the multiple other variables. Joint Variation is nothing but the variable depending on 2 or more variables quotient or product. To understand clearly with an example, The amount of busing candidates for each of the school trip varies with the no of candidates attending the distance from the school. The variable c (cost) varies jointly with n (number of students) and d (distance).

Joint Variation problems are very easy once you get the perfection of the lingo. These problems involve simple formulae or relationships which involves one variable which is equal to the “one” term which may be linear (with just an “x” axis), a quadratic equation (like “x²) where more than one variable (like “hr²”), and square root (like “\sqrt{4 – r^2\,}4−r2”) etc.

Functions of 2 or More Variables

It is very uncommon for the output variable to depend on 2 or more inputs. Most of the familiar formulas describe the several variables functions. For suppose, if the rectangle perimeter depends on the length and width. The cylinder volume depends on its height and radius. The travelled distance depends on the time and speed while travelling. The function notation of the formulas can be written as

P = f(l,w) = 2l + 2w where P is the perimeter and is a function of width and length

V = f(r,h) = Πr²h where V is the volume and is a function of radius and height

d = f(r,t) = rt where d is the distance and is a function of time and rate.

Tables of Values

Just for the single variable functions, we use the tables to describe two-variable functions. The heading of the table shows row and column and it shows the value if two input variables and the complete table shows the values of the output variable.

You can easily make graphs in three dimensions for two-variable functions. Instead of representing graphs, we represent functions by holding two or one variable constants.

Also, Read:

What is Variation
Practice Test on Ratio and Proportion

How to Solve Joint Variation Problems?

Follow the step by step procedure provided below to solve problems involving Joint Variation and arrive at the solution easily. They are along the lines

Step 1: Write the exact equation. The problems of joint variation can be solved using the equation y =kxz. While dealing with the word problems. you should also consider using variables other than x,y and z. Use the variables which are relevant to the problem being solved. Read the problem carefully and determine the changes in the equation of joint variation such as cubes, squares or square roots.

Step 2: With the help of the information in the problem, you have to find the value of k which is called the constant of proportionality and variation.

Step 3: Rewrite the equation starting with 1 substituting the value of k and found in step 2.

Step 4: Use the equation in step 3 and the information in the problem to answer the question. While solving the word problems, remember including the units in the final answer.

Joint Variation Problems with Solutions

The area of a triangle varies jointly as the base and the height. Area = 12m² when base = 6m and height = 4m. Find base when Area = 36m² and height = 8m?

The area of the triangle is represented with A

The base is represented with b

Height is represented with h

As given in the question,

A = 12m² when B = 6m and H = 4m

We know the equation,

A = kbh where k is the constant value

12 = k(6)(4)

Divide by 24 on both sides, we get

12/24 = k(24)/24

The value of k = 1/2

As the equation is

To find the base of the triangle of A = 36m² and H = 8m

36 = 1/2(b)(8)

Dividing both sides by 4, we get

36/4 = 4b/4

The value of base = 9m

Hence, the base of the triangle when A = 36m² and H = 8m is 9m

Wind resistance varies jointly as an object’s surface velocity and area. If the object travels at 80 miles per hour and has a surface area of 30 square feet which experiences 540 newtons wind resistance. How much fast will the car move with 40 square feet of the surface area in order to experience a wind resistance of 495 newtons?

Let w be the wind resistance

Let s be the object’s surface area

Let v be the object velocity

The object’s surface area = 80 newtons

The wind resistance = 540 newtons

The object velocity = 30

w = ksv where k is the constant

(540) = k (80) (30)

540 = k (2400)

540/2400 = k

The value of k is 9/40

To find the velocity of the car with s = 40, w = 495 newtons and k = 9/40

Substitute the values in the equation

495 = (9/40) (40) v

The velocity of a car is 55mph for which the object’s surface area is 40 and wind resistance is 495 newtons

Hence, the final solution is 55mph

For the given interest, SI (simple interest) varies jointly as principal and time. If 2,500 Rs left in an account for 5 years, then the interest of 625 Rs. How much interest would be earned, if you deposit 7,000 Rs for 9 years?

Let i be the interest

Let p be the principal

Let t be the time

The interest is 625 Rs

The principal is 2500

The time is 5 hours

i = kpt where k is the constant

Substituting the values in the equation,

(625) = k(2500)(5)

625 = k(12,500)

Dividing 12,500 on both the sides

625/12,500 = k (12,500)/12,500

The value of k = 1/20

To find the interest where the deposit is 7000Rs for 9 years, use the equation

i = (1/20) (7000) (9)

i = (350) (9)

Therefore, the interest is 3,150 Rs, if you deposit 7,000 Rs for 9 years

Thus, the final solution is Rs. 3,150

The volume of a pyramid varies jointly as its height and the area of the base. A pyramid with a height of 21 feet and a base with an area of 24 square feet has a volume of 168 cubic feet. Find the volume of a pyramid with a height of 18 feet and a base with an area of 42 square feet?

Let v be the volume of a pyramid

Let h be the height of a pyramid

Let a be the area of a pyramid

The volume v = 168 cubic feet

The height h = 21 feet

The area a = 24 square feet

V = Kha where K is the constant,

168 = k(21)(24)

168 = k(504)

Divide 504 on both sides

168/504 = k(504)/504

The value of k = 1/3

To find the volume of a pyramid with a height of 18 feet and a base with an area of 42 square feet

h = 18 feet

a = 42 square feet

V = (1/3) (18) (42)

V = (6) (42)

V = 252 ft³

The volume of the pyramid = 252 ft³ which has a height of 18 feet and a base with an area of 42 square feet

Therefore, the final solution is 252 ft³

The amount of oil used by a ship travelling at a uniform speed varies jointly with the distance and the square of the speed. If the ship uses 200 barrels of oil in travelling 200 miles at 36 miles per hour, determine how many barrels of oil are used when the ship travels 360 miles at 18 miles per hour?

No of barrels of oil = 200

The distance at which the oil is travelling = 200 miles

The distance at which the ship is travelling = 36 miles per hour

A = kds² where k is constant

200 = k.200.(36)²

Dividing both sides by 200

200/200 = k.200.(36)²/200

1 = k.(36)²

The value of k is 1/1296

To find the no of barrels when the ship travels 360 miles at 18 miles per hour

A = 1/1296 * 360 * 18²

Therefore, 90 barrels of oil is used when the ship travels 360 miles at 18 miles per hour

Thus, the final solution is 90 barrels

New! Comments

Share this page: What’s this?

Preschool Activities
Kindergarten Math
1st Grade Math
2nd Grade Math
3rd Grade Math
4th Grade Math
5th Grade Math
6th Grade Math
7th Grade Math
8th Grade Math
9th Grade Math
10th Grade Math
11 & 12 Grade Math
Concepts of Sets
Probability
Boolean Algebra
Math Coloring Pages
Multiplication Table
Cool Maths Games
Math Flash Cards
Online Math Quiz
Math Puzzles
Binary System
Math Dictionary
Conversion Chart
Homework Sheets
Math Problem Ans
Free Math Answers
Printable Math Sheet
Funny Math Answers
Employment Test
Math Patterns
Link Partners
Privacy Policy

E-mail Address

First Name

to send you Math Only Math.

Recent Articles

2nd grade place value | definition | explanation | examples |worksheet.

Sep 06, 24 02:33 AM

Worksheet on Bar Graphs | Bar Graphs or Column Graphs | Graphing Bar

Sep 04, 24 03:48 PM

1st Grade Numbers Worksheet | Before, After and Between | Compare Numb

Sep 03, 24 03:33 PM

$1st Grade Color by Numbers$

Subtraction Word Problems - 2-Digit Numbers | Subtraction Problems

Sep 03, 24 02:26 AM

Days of the Week | 7 Days of the Week | What are the Seven Days?

Sep 03, 24 01:58 AM

$Days of the Weeks$

Joint or Combined Variation

These lessons help Algebra students learn about joint or combined variation.

Related Pages: Proportions Joint Variation Word Problems Direct Variation Inverse Variation More Algebra Lessons

The following figure shows Joint Variation. Scroll down the page for more examples and solutions of Joint and Combine Variations.

What is Joint Variation or Combined Variation?

Joint Variation or Combined Variation is when one quantity varies directly as the product of at least two other quantities.

For example: y = kxz y varies jointly as x and z, when there is some nonzero constant k

Joint Variation Examples

Example: Suppose y varies jointly as x and z. What is y when x = 2 and z = 3, if y = 20 when x = 4 and z = 3?

Example: z varies jointly with x and y. When x = 3, y = 8, z = 6. Find z, when x = 6 and y = 4.

Joint Variation Application

Example: The energy that an item possesses due to its motion is called kinetic energy. The kinetic energy of an object (which is measured in joules) varies jointly with the mass of the object and the square of its velocity. If the kinetic energy of a 3 kg ball traveling 12 m/s is 216 Joules, how is the mass of a ball that generates 250 Joules of energy when traveling at 10 m/s?

Distinguish between Direct, Inverse and Joint Variation

Example: Determine whether the data in the table is an example of direct, inverse or joint variation. Then, identify the equation that represents the relationship.

Combined Variation

In Algebra, sometimes we have functions that vary in more than one element. When this happens, we say that the functions have joint variation or combined variation. Joint variation is direct variation to more than one variable (for example, d = (r)(t)). With combined variation, we have both direct variation and indirect variation.

How to set up and solve combined variation problems?

Example: Suppose y varies jointly with x and z. When y = 20, x = 6 and z = 10. Find y when x = 8 and z =15.

Lesson on combining direct and inverse or joint and inverse variation

Example: y varies directly as x and inversely as the square of z, and when x = 32, y = 6 and z = 4. Find x when y = 10 and z = 3.

How to solve problems involving joint and combined variation?

If t varies jointly with u and the square of v, and t is 1152 when u is 8 and v is 4, find t when v is 5 and u is 5.

The amount of oil used by a ship traveling at a uniform speed varies jointly with the distance and the square of the speed. If the ship uses 200 barrels of oil in traveling 200 miles at 36 miles per hour, determine how many barrels of oil are used when the ship travels 360 miles at 18 miles per hour.

Designer Dolls found that its number of Dress-Up Dolls sold, N, varies directly with their advertising budget, A, and inversely proportional with the price of each doll, P. When $54,00 was spent on advertising and the price of the doll is $90, then 9,600 units are sold. Determine the number of dolls sold if the amount of advertising budget is increased to $144,000.

Example: y varies jointly as x and z and inversely as w, and y = 3/2, when x = 2, z =3 and w = 4. Find the equation of variation.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Direct, Inverse, Joint and Combined Variation

When you start studying algebra, you will also study how two (or more) variables can relate to each other specifically. The cases you’ll study are:

Direct Variation , where one variable is a constant multiple of another. For example, the number of dollars I make varies directly (or varies proportionally ) to the number of hours I work. Or, the perimeter of a square varies directly with the length of a side of the square.
Inverse or Indirect Variation , where when one of the variables increases, the other one decreases (their product is constant). For example, the temperature in my house varies indirectly (same or inversely ) with the amount of time the air conditioning is running. Or, the number of people I invite to my bowling party varies inversely with the number of games they might get to play (or you can say is proportional to the inverse of ).
Joint Variation , where at least two variables are related directly. For example, the area of a triangle is jointly related to both its height and base.
Combined Variation , which involves a combination of direct or joint variation, and indirect variation. For example, the average number of phone calls per day between two cities has found to be jointly proportional to the populations of the cities, and inversely proportional to the square of the distance between the two cities.
Partial (Direct) Variation , where two variables are related by a formula, such as the formula for a straight line (with a non-zero $ y$-intercept). For example, the total cost of my phone bill consists of a fixed cost per month, and also a charge per minute.

Note : Just because two variables have a direct relationship, the relationship may not necessarily be a causal relationship (causation) , meaning one variable directly affects the other. There may be another variable that affects both of the variables. For example, there may be a correlation between the number of people buying ice cream and the number of people buying shorts. People buying ice cream do not cause people to buy shorts, but most likely warm weather outside is causing both to happen.

Here is a table for the types of variation we’ll be discussing:

Direct or Proportional Variation

When two variables are related directly, the ratio of their values is always the same. If $ k$, the constant ratio is positive, the variables go up and down in the same direction. (If $ k$ is negative, as one variable goes up, the other goes down; this is still considered a direct variation, but is not seen often in these problems.) Note that $ k\ne 0$.

Think of linear direct variation as a “$ y=mx$” line, where the ratio of $ y$ to $ x$ is the slope ($ m$). With direct variation, the $ y$-intercept is always 0 (zero); this is how it’s defined. Direct variation problems are typically written: → $ \boldsymbol {y=kx}$, where $ k$ is the ratio of $ y$ to $ x$ (which is the same as the slope or rate ).

Some problems will ask for that $ k$ value (which is called the constant ratio , constant of variation or constant of proportionality – it’s like a slope!); others will just give you 3 out of the 4 values for $ x$ and $ y$ and you can simply set up a ratio to find the other value. I’m thinking the $ k$ comes from the word “constant” in another language.

Remember the example of making $10 an hour at the mall ($ y=10x$)? This is an example of direct variation, since the ratio of how much you make to how many hours you work is always constant.

We can also set up direct variation problems in a ratio , as long as we have the same variable in either the top or bottom of the ratio, or on the same side . This will look like the following. Don’t let this scare you; the subscripts just refer to either the first set of variables $ ({{x}_{1}},{{y}_{1}})$, or the second $ ({{x}_{2}},{{y}_{2}})$: $ \displaystyle \frac{{{{y}_{1}}}}{{{{x}_{1}}}}\,\,=\,\,\frac{{{{y}_{2}}}}{{{{x}_{2}}}}$.

Notes: Partial Variation (see below), or “varies partly” means that there is an extra fixed constant, so we’ll have an equation like $ y=mx+b$, which is our typical linear equation. Also, I’m assuming in these examples that direct variation is linear ; sometime I see it where it’s not, like in a Direct Square Variation where $ y=k{{x}^{2}}$. There is a word problem example of this here .

Direct Variation Word Problem: We can solve the following direct variation problem in one of two ways, as shown. We do these methods when we are given any three of the four values for $ x$ and $ y$.

It’s really that easy. Can you see why the proportion method can be the preferred method, unless you are asked to find the $ k$ constant in the formula? Again, if the problem asks for the equation that models this situation , it would be “$ y=10x$”.

Direct Variation Word Problem:

Here’s another; let’s use the proportion method :

See how similar these types of problems are to the Proportions problems we did earlier?

Direct Square Variation Word Problem:

Again, a Direct Square Variation is when $ y$ is proportional to the square of $ x$, or $ y=k{{x}^{2}}$. Let’s work a word problem with this type of variation and show both the formula and proportion methods:

Inverse or Indirect Variation

Inverse or Indirect Variation refers to relationships of two variables that go in the opposite direction (their product is a constant, $ k$). Let’s suppose you are comparing how fast you are driving (average speed) to how fast you get to your school. You might have measured the following speeds and times:

Do you see how when the $ x$ variable goes up, the $ y$ goes down, and when you multiply the $ x$ with the $ y$, we always get the same number? (Note that this is different than a negative slope, or negative $ k$ value, since with a negative slope, we can’t multiply the $ x$’s and $ y$’s to get the same number).

The formula for inverse or indirect variation is: → $ \displaystyle \boldsymbol{y=\frac{k}{x}}$ or $ \boldsymbol{xy=k}$, where $ k$ is always the same number.

(Note that you could also have an Indirect Square Variation or Inverse Square Variation , like we saw above for a Direct Variation. This would be of the form $ \displaystyle y=\frac{k}{{{{x}^{2}}}}\text{ or }{{x}^{2}}y=k$.)

We might have a problem like this; we can solve this problem in one of two ways, as shown. We do these methods when we are given any three of the four values for $ x$ and $ y$:

Here’s a more advanced problem that uses inverse proportions in a “work” word problem ; we’ll see more “work problems” here in the Systems of Linear Equations Section and here in the Rational Functions and Equations section .

In the problem below, the three different values are inversely proportional; for example, the more women you have, the less days it takes to paint the mural, and the more hours in a day the women paint, the less days they need to complete the mural:

Recognizing Direct or Indirect Variation

You might be asked to look at functions (equations or points that compare $ x$’s to unique $ y$’s – we’ll discuss later in the Algebraic Functions section) and determine if they are direct, inverse, or neither:

Joint Variation and Combined Variation

Joint variation is just like direct variation, but involves more than one other variable. All the variables are directly proportional, taken one at a time. Let’s set this up like we did with direct variation, find the $ k$, and then solve for $ y$; we need to use the Formula Method:

Another Joint Variation Word Problem:

Combined Variation

Combined variation involves a combination of direct or joint variation, and indirect variation. Since these equations are a little more complicated, you probably want to plug in all the variables, solve for $ k$, and then solve back to get what’s missing. Let’s try a problem:

Here’s another; this one looks really tough, but it’s really not that bad if you take it one step at a time:

Combined Variation Word Problem:

Partial Variation

You don’t hear about Partial Variation or something being partly varied or part varied very often, but it means that two variables are related by the sum of two or more variables (one of which may be a constant). An example of part variation is the relationship modeled by an equation of a line that doesn’t go through the origin. Here are a few examples:

We’re doing really difficult problems now – but see how, if you know the rules, they really aren’t bad at all?

Learn these rules, and practice, practice, practice!

For Practice : Use the Mathway widget below to try a Variation problem. Click on Submit (the blue arrow to the right of the problem) and click on Find the Constant of Variation to see the answer.

You can also type in your own problem, or click on the three dots in the upper right hand corner and click on “Examples” to drill down by topic.

If you click on Tap to view steps , or Click Here , you can register at Mathway for a free trial , and then upgrade to a paid subscription at any time (to get any type of math problem solved!).

On to Introduction to the Graphing Display Calculator (GDC) . I’m proud of you for getting this far!

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 2: Linear Equations

2.7 Variation Word Problems

Direct variation problems.

There are many mathematical relations that occur in life. For instance, a flat commission salaried salesperson earns a percentage of their sales, where the more they sell equates to the wage they earn. An example of this would be an employee whose wage is 5% of the sales they make. This is a direct or a linear variation, which, in an equation, would look like:

[latex]\text{Wage }(x)=5\%\text{ Commission }(k)\text{ of Sales Completed }(y)[/latex]

[latex]x=ky[/latex]

A historical example of direct variation can be found in the changing measurement of pi, which has been symbolized using the Greek letter π since the mid 18th century. Variations of historical π calculations are Babylonian [latex]\left(\dfrac{25}{8}\right),[/latex] Egyptian [latex]\left(\dfrac{16}{9}\right)^2,[/latex] and Indian [latex]\left(\dfrac{339}{108}\text{ and }10^{\frac{1}{2}}\right).[/latex] In the 5th century, Chinese mathematician Zu Chongzhi calculated the value of π to seven decimal places (3.1415926), representing the most accurate value of π for over 1000 years.

Pi is found by taking any circle and dividing the circumference of the circle by the diameter, which will always give the same value: 3.14159265358979323846264338327950288419716… (42 decimal places). Using an infinite-series exact equation has allowed computers to calculate π to 10 13 decimals.

[latex]\begin{array}{c} \text{Circumference }(c)=\pi \text{ times the diameter }(d) \\ \\ \text{or} \\ \\ c=\pi d \end{array}[/latex]

All direct variation relationships are verbalized in written problems as a direct variation or as directly proportional and take the form of straight line relationships. Examples of direct variation or directly proportional equations are:

[latex]x[/latex] varies directly as [latex]y[/latex]
[latex]x[/latex] varies as [latex]y[/latex]
[latex]x[/latex] varies directly proportional to [latex]y[/latex]
[latex]x[/latex] is proportional to [latex]y[/latex]
[latex]x[/latex] varies directly as the square of [latex]y[/latex]
[latex]x[/latex] varies as [latex]y[/latex] squared
[latex]x[/latex] is proportional to the square of [latex]y[/latex]
[latex]x[/latex] varies directly as the cube of [latex]y[/latex]
[latex]x[/latex] varies as [latex]y[/latex] cubed
[latex]x[/latex] is proportional to the cube of [latex]y[/latex]
[latex]x[/latex] varies directly as the square root of [latex]y[/latex]
[latex]x[/latex] varies as the root of [latex]y[/latex]
[latex]x[/latex] is proportional to the square root of [latex]y[/latex]

Example 2.7.1

Find the variation equation described as follows:

The surface area of a square surface [latex](A)[/latex] is directly proportional to the square of either side [latex](x).[/latex]

[latex]\begin{array}{c} \text{Area }(A) =\text{ constant }(k)\text{ times side}^2\text{ } (x^2) \\ \\ \text{or} \\ \\ A=kx^2 \end{array}[/latex]

Example 2.7.2

When looking at two buildings at the same time, the length of the buildings’ shadows [latex](s)[/latex] varies directly as their height [latex](h).[/latex] If a 5-story building has a 20 m long shadow, how many stories high would a building that has a 32 m long shadow be?

The equation that describes this variation is:

[latex]h=kx[/latex]

Breaking the data up into the first and second parts gives:

[latex]\begin{array}{ll} \begin{array}{rrl} \\ &&\textbf{1st Data} \\ s&=&20\text{ m} \\ h&=&5\text{ stories} \\ k&=&\text{find 1st} \\ \\ &&\text{Find }k\text{:} \\ h&=&kx \\ 5\text{ stories}&=&k\text{ (20 m)} \\ k&=&5\text{ stories/20 m}\\ k&=&0.25\text{ story/m} \end{array} & \hspace{0.5in} \begin{array}{rrl} &&\textbf{2nd Data} \\ s&=&\text{32 m} \\ h&=&\text{find 2nd} \\ k&=&0.25\text{ story/m} \\ \\ &&\text{Find }h\text{:} \\ h&=&kx \\ h&=&(0.25\text{ story/m})(32\text{ m}) \\ h&=&8\text{ stories} \end{array} \end{array}[/latex]

Inverse Variation Problems

Inverse variation problems are reciprocal relationships. In these types of problems, the product of two or more variables is equal to a constant. An example of this comes from the relationship of the pressure [latex](P)[/latex] and the volume [latex](V)[/latex] of a gas, called Boyle’s Law (1662). This law is written as:

[latex]\begin{array}{c} \text{Pressure }(P)\text{ times Volume }(V)=\text{ constant} \\ \\ \text{ or } \\ \\ PV=k \end{array}[/latex]

Written as an inverse variation problem, it can be said that the pressure of an ideal gas varies as the inverse of the volume or varies inversely as the volume. Expressed this way, the equation can be written as:

[latex]P=\dfrac{k}{V}[/latex]

Another example is the historically famous inverse square laws. Examples of this are the force of gravity [latex](F_{\text{g}}),[/latex] electrostatic force [latex](F_{\text{el}}),[/latex] and the intensity of light [latex](I).[/latex] In all of these measures of force and light intensity, as you move away from the source, the intensity or strength decreases as the square of the distance.

In equation form, these look like:

[latex]F_{\text{g}}=\dfrac{k}{d^2}\hspace{0.25in} F_{\text{el}}=\dfrac{k}{d^2}\hspace{0.25in} I=\dfrac{k}{d^2}[/latex]

These equations would be verbalized as:

The force of gravity [latex](F_{\text{g}})[/latex] varies inversely as the square of the distance.
Electrostatic force [latex](F_{\text{el}})[/latex] varies inversely as the square of the distance.
The intensity of a light source [latex](I)[/latex] varies inversely as the square of the distance.

All inverse variation relationship are verbalized in written problems as inverse variations or as inversely proportional. Examples of inverse variation or inversely proportional equations are:

[latex]x[/latex] varies inversely as [latex]y[/latex]
[latex]x[/latex] varies as the inverse of [latex]y[/latex]
[latex]x[/latex] varies inversely proportional to [latex]y[/latex]
[latex]x[/latex] is inversely proportional to [latex]y[/latex]
[latex]x[/latex] varies inversely as the square of [latex]y[/latex]
[latex]x[/latex] varies inversely as [latex]y[/latex] squared
[latex]x[/latex] is inversely proportional to the square of [latex]y[/latex]
[latex]x[/latex] varies inversely as the cube of [latex]y[/latex]
[latex]x[/latex] varies inversely as [latex]y[/latex] cubed
[latex]x[/latex] is inversely proportional to the cube of [latex]y[/latex]
[latex]x[/latex] varies inversely as the square root of [latex]y[/latex]
[latex]x[/latex] varies as the inverse root of [latex]y[/latex]
[latex]x[/latex] is inversely proportional to the square root of [latex]y[/latex]

Example 2.7.3

The force experienced by a magnetic field [latex](F_{\text{b}})[/latex] is inversely proportional to the square of the distance from the source [latex](d_{\text{s}}).[/latex]

[latex]F_{\text{b}} = \dfrac{k}{{d_{\text{s}}}^2}[/latex]

Example 2.7.4

The time [latex](t)[/latex] it takes to travel from North Vancouver to Hope varies inversely as the speed [latex](v)[/latex] at which one travels. If it takes 1.5 hours to travel this distance at an average speed of 120 km/h, find the constant [latex]k[/latex] and the amount of time it would take to drive back if you were only able to travel at 60 km/h due to an engine problem.

[latex]t=\dfrac{k}{v}[/latex]

[latex]\begin{array}{ll} \begin{array}{rrl} &&\textbf{1st Data} \\ v&=&120\text{ km/h} \\ t&=&1.5\text{ h} \\ k&=&\text{find 1st} \\ \\ &&\text{Find }k\text{:} \\ k&=&tv \\ k&=&(1.5\text{ h})(120\text{ km/h}) \\ k&=&180\text{ km} \end{array} & \hspace{0.5in} \begin{array}{rrl} \\ \\ \\ &&\textbf{2nd Data} \\ v&=&60\text{ km/h} \\ t&=&\text{find 2nd} \\ k&=&180\text{ km} \\ \\ &&\text{Find }t\text{:} \\ t&=&\dfrac{k}{v} \\ \\ t&=&\dfrac{180\text{ km}}{60\text{ km/h}} \\ \\ t&=&3\text{ h} \end{array} \end{array}[/latex]

Joint or Combined Variation Problems

In real life, variation problems are not restricted to single variables. Instead, functions are generally a combination of multiple factors. For instance, the physics equation quantifying the gravitational force of attraction between two bodies is:

[latex]F_{\text{g}}=\dfrac{Gm_1m_2}{d^2}[/latex]

[latex]F_{\text{g}}[/latex] stands for the gravitational force of attraction
[latex]G[/latex] is Newton’s constant, which would be represented by [latex]k[/latex] in a standard variation problem
[latex]m_1[/latex] and [latex]m_2[/latex] are the masses of the two bodies
[latex]d^2[/latex] is the distance between the centres of both bodies

To write this out as a variation problem, first state that the force of gravitational attraction [latex](F_{\text{g}})[/latex] between two bodies is directly proportional to the product of the two masses [latex](m_1, m_2)[/latex] and inversely proportional to the square of the distance [latex](d)[/latex] separating the two masses. From this information, the necessary equation can be derived. All joint variation relationships are verbalized in written problems as a combination of direct and inverse variation relationships, and care must be taken to correctly identify which variables are related in what relationship.

Example 2.7.5

The force of electrical attraction [latex](F_{\text{el}})[/latex] between two statically charged bodies is directly proportional to the product of the charges on each of the two objects [latex](q_1, q_2)[/latex] and inversely proportional to the square of the distance [latex](d)[/latex] separating these two charged bodies.

[latex]F_{\text{el}}=\dfrac{kq_1q_2}{d^2}[/latex]

Solving these combined or joint variation problems is the same as solving simpler variation problems.

First, decide what equation the variation represents. Second, break up the data into the first data given—which is used to find [latex]k[/latex]—and then the second data, which is used to solve the problem given. Consider the following joint variation problem.

Example 2.7.6

[latex]y[/latex] varies jointly with [latex]m[/latex] and [latex]n[/latex] and inversely with the square of [latex]d[/latex]. If [latex]y = 12[/latex] when [latex]m = 3[/latex], [latex]n = 8[/latex], and [latex]d = 2,[/latex] find the constant [latex]k[/latex], then use [latex]k[/latex] to find [latex]y[/latex] when [latex]m=-3[/latex], [latex]n = 18[/latex], and [latex]d = 3[/latex].

[latex]y=\dfrac{kmn}{d^2}[/latex]

[latex]\begin{array}{ll} \begin{array}{rrl} \\ \\ \\ && \textbf{1st Data} \\ y&=&12 \\ m&=&3 \\ n&=&8 \\ d&=&2 \\ k&=&\text{find 1st} \\ \\ &&\text{Find }k\text{:} \\ y&=&\dfrac{kmn}{d^2} \\ \\ 12&=&\dfrac{k(3)(8)}{(2)^2} \\ \\ k&=&\dfrac{12(2)^2}{(3)(8)} \\ \\ k&=& 2 \end{array} & \hspace{0.5in} \begin{array}{rrl} &&\textbf{2nd Data} \\ y&=&\text{find 2nd} \\ m&=&-3 \\ n&=&18 \\ d&=&3 \\ k&=&2 \\ \\ &&\text{Find }y\text{:} \\ y&=&\dfrac{kmn}{d^2} \\ \\ y&=&\dfrac{(2)(-3)(18)}{(3)^2} \\ \\ y&=&12 \end{array} \end{array}[/latex]

For questions 1 to 12, write the formula defining the variation, including the constant of variation [latex](k).[/latex]

[latex]x[/latex] is jointly proportional to [latex]y[/latex] and [latex]z[/latex]
[latex]x[/latex] varies jointly as [latex]z[/latex] and [latex]y[/latex]
[latex]x[/latex] is jointly proportional with the square of [latex]y[/latex] and the square root of [latex]z[/latex]
[latex]x[/latex] is inversely proportional to [latex]y[/latex] to the sixth power
[latex]x[/latex] is jointly proportional with the cube of [latex]y[/latex] and inversely to the square root of [latex]z[/latex]
[latex]x[/latex] is inversely proportional with the square of [latex]y[/latex] and the square root of [latex]z[/latex]
[latex]x[/latex] varies jointly as [latex]z[/latex] and [latex]y[/latex] and is inversely proportional to the cube of [latex]p[/latex]
[latex]x[/latex] is inversely proportional to the cube of [latex]y[/latex] and square of [latex]z[/latex]

For questions 13 to 22, find the formula defining the variation and the constant of variation [latex](k).[/latex]

If [latex]A[/latex] varies directly as [latex]B,[/latex] find [latex]k[/latex] when [latex]A=15[/latex] and [latex]B=5.[/latex]
If [latex]P[/latex] is jointly proportional to [latex]Q[/latex] and [latex]R,[/latex] find [latex]k[/latex] when [latex]P=12, Q=8[/latex] and [latex]R=3.[/latex]
If [latex]A[/latex] varies inversely as [latex]B,[/latex] find [latex]k[/latex] when [latex]A=7[/latex] and [latex]B=4.[/latex]
If [latex]A[/latex] varies directly as the square of [latex]B,[/latex] find [latex]k[/latex] when [latex]A=6[/latex] and [latex]B=3.[/latex]
If [latex]C[/latex] varies jointly as [latex]A[/latex] and [latex]B,[/latex] find [latex]k[/latex] when [latex]C=24, A=3,[/latex] and [latex]B=2.[/latex]
If [latex]Y[/latex] is inversely proportional to the cube of [latex]X,[/latex] find [latex]k[/latex] when [latex]Y=54[/latex] and [latex]X=3.[/latex]
If [latex]X[/latex] is directly proportional to [latex]Y,[/latex] find [latex]k[/latex] when [latex]X=12[/latex] and [latex]Y=8.[/latex]
If [latex]A[/latex] is jointly proportional with the square of [latex]B[/latex] and the square root of [latex]C,[/latex] find [latex]k[/latex] when [latex]A=25, B=5[/latex] and [latex]C=9.[/latex]
If [latex]y[/latex] varies jointly with [latex]m[/latex] and the square of [latex]n[/latex] and inversely with [latex]d,[/latex] find [latex]k[/latex] when [latex]y=10, m=4, n=5,[/latex] and [latex]d=6.[/latex]
If [latex]P[/latex] varies directly as [latex]T[/latex] and inversely as [latex]V,[/latex] find [latex]k[/latex] when [latex]P=10, T=250,[/latex] and [latex]V=400.[/latex]

For questions 23 to 37, solve each variation word problem.

The electrical current [latex]I[/latex] (in amperes, A) varies directly as the voltage [latex](V)[/latex] in a simple circuit. If the current is 5 A when the source voltage is 15 V, what is the current when the source voltage is 25 V?
The current [latex]I[/latex] in an electrical conductor varies inversely as the resistance [latex]R[/latex] (in ohms, Ω) of the conductor. If the current is 12 A when the resistance is 240 Ω, what is the current when the resistance is 540 Ω?
Hooke’s law states that the distance [latex](d_s)[/latex] that a spring is stretched supporting a suspended object varies directly as the mass of the object [latex](m).[/latex] If the distance stretched is 18 cm when the suspended mass is 3 kg, what is the distance when the suspended mass is 5 kg?
The volume [latex](V)[/latex] of an ideal gas at a constant temperature varies inversely as the pressure [latex](P)[/latex] exerted on it. If the volume of a gas is 200 cm 3 under a pressure of 32 kg/cm 2 , what will be its volume under a pressure of 40 kg/cm 2 ?
The number of aluminum cans [latex](c)[/latex] used each year varies directly as the number of people [latex](p)[/latex] using the cans. If 250 people use 60,000 cans in one year, how many cans are used each year in a city that has a population of 1,000,000?
The time [latex](t)[/latex] required to do a masonry job varies inversely as the number of bricklayers [latex](b).[/latex] If it takes 5 hours for 7 bricklayers to build a park wall, how much time should it take 10 bricklayers to complete the same job?
The wavelength of a radio signal (λ) varies inversely as its frequency [latex](f).[/latex] A wave with a frequency of 1200 kilohertz has a length of 250 metres. What is the wavelength of a radio signal having a frequency of 60 kilohertz?
The number of kilograms of water [latex](w)[/latex] in a human body is proportional to the mass of the body [latex](m).[/latex] If a 96 kg person contains 64 kg of water, how many kilograms of water are in a 60 kg person?
The time [latex](t)[/latex] required to drive a fixed distance [latex](d)[/latex] varies inversely as the speed [latex](v).[/latex] If it takes 5 hours at a speed of 80 km/h to drive a fixed distance, what speed is required to do the same trip in 4.2 hours?
The volume [latex](V)[/latex] of a cone varies jointly as its height [latex](h)[/latex] and the square of its radius [latex](r).[/latex] If a cone with a height of 8 centimetres and a radius of 2 centimetres has a volume of 33.5 cm 3 , what is the volume of a cone with a height of 6 centimetres and a radius of 4 centimetres?
The centripetal force [latex](F_{\text{c}})[/latex] acting on an object varies as the square of the speed [latex](v)[/latex] and inversely to the radius [latex](r)[/latex] of its path. If the centripetal force is 100 N when the object is travelling at 10 m/s in a path or radius of 0.5 m, what is the centripetal force when the object’s speed increases to 25 m/s and the path is now 1.0 m?
The maximum load [latex](L_{\text{max}})[/latex] that a cylindrical column with a circular cross section can hold varies directly as the fourth power of the diameter [latex](d)[/latex] and inversely as the square of the height [latex](h).[/latex] If an 8.0 m column that is 2.0 m in diameter will support 64 tonnes, how many tonnes can be supported by a column 12.0 m high and 3.0 m in diameter?
The volume [latex](V)[/latex] of gas varies directly as the temperature [latex](T)[/latex] and inversely as the pressure [latex](P).[/latex] If the volume is 225 cc when the temperature is 300 K and the pressure is 100 N/cm 2 , what is the volume when the temperature drops to 270 K and the pressure is 150 N/cm 2 ?
The electrical resistance [latex](R)[/latex] of a wire varies directly as its length [latex](l)[/latex] and inversely as the square of its diameter [latex](d).[/latex] A wire with a length of 5.0 m and a diameter of 0.25 cm has a resistance of 20 Ω. Find the electrical resistance in a 10.0 m long wire having twice the diameter.
The volume of wood in a tree [latex](V)[/latex] varies directly as the height [latex](h)[/latex] and the diameter [latex](d).[/latex] If the volume of a tree is 377 m 3 when the height is 30 m and the diameter is 2.0 m, what is the height of a tree having a volume of 225 m 3 and a diameter of 1.75 m?

Answer Key 2.7

Share This Book

joint variation problem solving examples

Solutions Integral Calculator Derivative Calculator Algebra Calculator Matrix Calculator More...
Graphing Line Graph Exponential Graph Quadratic Graph Sine Graph More...
Calculators BMI Calculator Compound Interest Calculator Percentage Calculator Acceleration Calculator More...
Geometry Pythagorean Theorem Calculator Circle Area Calculator Isosceles Triangle Calculator Triangles Calculator More...
Tools Notebook Groups Cheat Sheets Worksheets Study Guides Practice Verify Solution

Study Guides > College Algebra CoRequisite Course

Inverse and joint variation, learning outcomes.

Solve an Inverse variation problem.
Write a formula for an inversely proportional relationship.

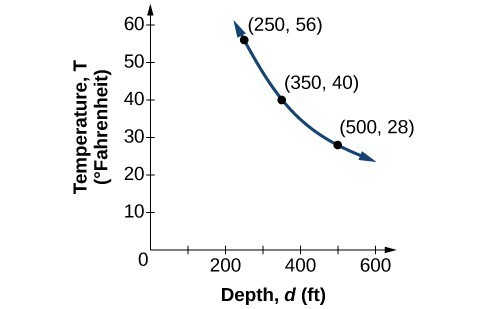
[latex]d[/latex], depth	[latex]T=\frac{\text{14,000}}{d}[/latex]	Interpretation
500 ft	[latex]\frac{14,000}{500}=28[/latex]	At a depth of 500 ft, the water temperature is 28° F.
350 ft	[latex]\frac{14,000}{350}=40[/latex]	At a depth of 350 ft, the water temperature is 40° F.
250 ft	[latex]\frac{14,000}{250}=56[/latex]	At a depth of 250 ft, the water temperature is 56° F.

Graph of y=(14000)/x where the horizontal axis is labeled,

A General Note: Inverse Variation

Isolating the constant of variation, example: writing a formula for an inversely proportional relationship.

[latex]\begin{align}t\left(v\right)&=\dfrac{100}{v} \\[1mm] &=100{v}^{-1} \end{align}[/latex]

How To: Given a description of an inverse variation problem, solve for an unknown.

Identify the input, [latex]x[/latex], and the output, [latex]y[/latex].
Determine the constant of variation. You may need to multiply [latex]y[/latex] by the specified power of [latex]x[/latex] to determine the constant of variation.
Use the constant of variation to write an equation for the relationship.
Substitute known values into the equation to find the unknown.

Example: Solving an Inverse Variation Problem

[latex]\begin{align}k&={x}^{3}y \\[1mm] &={2}^{3}\cdot 25 \\[1mm] &=200 \end{align}[/latex]

[latex]\begin{align}y&=\dfrac{k}{{x}^{3}},\hspace{2mm}k=200 \\[1mm] y&=\dfrac{200}{{x}^{3}} \end{align}[/latex]

[latex]\begin{align}y&=\dfrac{200}{{6}^{3}} \\[1mm] &=\dfrac{25}{27} \end{align}[/latex]

Analysis of the Solution

Graph of y=25/(x^3) with the labeled points (2, 25) and (6, 25/27).

Answer: [latex-display]\dfrac{9}{2}[/latex-display]

Joint Variation

A general note: joint variation, example: solving problems involving joint variation.

[latex]x=\dfrac{k{y}^{2}}{\sqrt[3]{z}}[/latex]

[latex]\begin{align}6&=\dfrac{k{2}^{2}}{\sqrt[3]{8}} \\[1mm] 6&=\dfrac{4k}{2} \\[1mm] 3&=k \end{align}[/latex]

[latex]x=\dfrac{3{y}^{2}}{\sqrt[3]{z}}[/latex]

[latex]\begin{align}x&=\dfrac{3{\left(1\right)}^{2}}{\sqrt[3]{27}} \\[1mm] &=1 \end{align}[/latex]

Answer: [latex-display]x=20[/latex-display]

Licenses & Attributions

Cc licensed content, original.

Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution .

CC licensed content, Shared previously

Question ID 91393,91394. Authored by: Jenck,Michael (for Lumen Learning). License: CC BY: Attribution . License terms: IMathAS Community License CC-BY + GPL.
College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution . License terms: Download for free at http://cnx.org/contents/ [email protected] .
Inverse Variation. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution .
Joint Variation: Determine the Variation Constant (Volume of a Cone). Provided by: Joint Variation: Determine the Variation Constant (Volume of a Cone) Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. License: CC BY: Attribution .

We want your feedback

Please add a message.

Message received. Thanks for the feedback.

> Algebra
> Relations and Functions

Joint and Combined Variation: Formulas, Examples, and Applications Unlock the power of joint and combined variation! Learn essential formulas, explore real-world applications, and master problem-solving techniques to excel in advanced algebra and beyond.

Get the most by viewing this topic in your current grade. Pick your course now .

Introduction to joint and combined variation
Review: direct variation vs. inverse variation
What is a joint variation?
What is a combined variation and how is it different from a joint variation?
How to solve a variation problem?
x x x varies jointly as y y y and the square of z z z .
The speed of a race car varies directly as the distance and inversely as the time.
a a a varies directly with b b b and c c c . If a = 336 a=336 a = 336 when b = 4 b=4 b = 4 and c = 7 c=7 c = 7 , find a a a when b = 2 b=2 b = 2 and c = 11 c=11 c = 11 .
p p p varies directly as q q q but inversely as r r r . If p = 14 p=14 p = 14 when q = 2 q=2 q = 2 and r = 5 r=5 r = 5 , find q q q when p = 105 p=105 p = 105 and r = 18 r=18 r = 18 .
Find the constant of variation k k k . Round your answer to 2 decimal places.
What is the volume of a can that has a 7 cm height and 3 cm radius?
The time required to process a shipment at Mamazon varies directly with the number of orders being made and inversely with the number of workers. If 1344 orders can be processed by 7 workers in 12 hours, how long will it take 125 workers to process 20,000 items?

Free to Join!

Join for Free

Easily See Your Progress

Make Use of Our Learning Aids

Last Viewed

Practice accuracy, suggested tasks.

Get quick access to the topic you're currently learning.

See how well your practice sessions are going over time.

Stay on track with our daily recommendations.

Earn Achievements as You Learn

Create and Customize Your Avatar

In this lesson, we will learn:

Identifying Types of Variations
Translating Variation Statements Into Equations
Solving Variation Problems
Word Problems of Variations
Joint variation is a direct variation, but with two or more variables. It has the equation y = k ⋅ x ⋅ z y=k \cdot x \cdot z y = k ⋅ x ⋅ z where k k k is the constant of variation and k ≠ 0 k \neq 0 k  = 0 .
A combined variation is formed when we combine any of the variations together (direct, inverse and joint). In most cases, we combine direct and inverse variations to form a combined variation. i.e. y y y varies directly with x x x and inversely with z z z ( y = k ⋅ x z ) (y = k \cdot \frac{x}{z}) ( y = k ⋅ z x )
Steps to solving a variation problem:
Write the general variation formula of the problem.
Find the constant of variation k k k .
Rewrite the formula with the value of k k k .
Solve the problem by inputting known information.

Introduction to Joint and Combined Variation

Welcome to our exploration of joint and combined variation! These fascinating mathematical concepts are essential in understanding how multiple variables can influence each other simultaneously. Our introduction video serves as an excellent starting point, providing clear explanations and visual examples to help you grasp these ideas. Joint variation occurs when one variable is directly proportional to two or more other variables, while combined variation involves both direct and inverse relationships. As we delve deeper into these concepts, you'll discover their wide-ranging applications in fields like physics, engineering, and economics. The video will guide you through step-by-step examples, making these complex topics more accessible and relatable. By mastering joint and combined variation, you'll enhance your problem-solving skills and gain a deeper appreciation for the interconnectedness of mathematical relationships. So, let's dive in and unravel the intricacies of these important concepts together!

Solving Variation Problems Find the missing variables. a a a varies directly with b b b and c c c . If a = 336 a=336 a = 336 when b = 4 b=4 b = 4 and c = 7 c=7 c = 7 , find a a a when b = 2 b=2 b = 2 and c = 11 c=11 c = 11 .

Step 1: Identify the Type of Variation

The first step in solving this problem is to identify the type of variation we are dealing with. In this case, a a a varies directly with both b b b and c c c . This means that a a a is directly proportional to the product of b b b and c c c . This type of relationship is known as joint variation.

Step 2: Write the General Formula

Since a a a varies directly with b b b and c c c , we can write the general formula for this relationship as: a = k ⋅ b ⋅ c a = k \cdot b \cdot c a = k ⋅ b ⋅ c Here, k k k is the constant of variation. Our goal is to find the value of k k k using the given information.

Step 3: Substitute the Given Values to Find k k k

We are given that a = 336 a = 336 a = 336 when b = 4 b = 4 b = 4 and c = 7 c = 7 c = 7 . We can substitute these values into the general formula to find k k k : 336 = k ⋅ 4 ⋅ 7 336 = k \cdot 4 \cdot 7 336 = k ⋅ 4 ⋅ 7 Simplify the right-hand side: 336 = k ⋅ 28 336 = k \cdot 28 336 = k ⋅ 28 To solve for k k k , divide both sides by 28: k = 336 28 k = \frac{336}{28} k = 28 336 Simplify the division to find the value of k k k .

Step 4: Update the Formula with the Constant k k k

Once we have found the value of k k k , we can update our general formula. Suppose k k k is found to be 12 (as an example): a = 12 ⋅ b ⋅ c a = 12 \cdot b \cdot c a = 12 ⋅ b ⋅ c This updated formula will be used to find the new value of a a a when b = 2 b = 2 b = 2 and c = 11 c = 11 c = 11 .

Step 5: Substitute the New Values to Find a a a

Now, we need to find a a a when b = 2 b = 2 b = 2 and c = 11 c = 11 c = 11 . Substitute these values into the updated formula: a = 12 ⋅ 2 ⋅ 11 a = 12 \cdot 2 \cdot 11 a = 12 ⋅ 2 ⋅ 11 Simplify the multiplication: a = 12 ⋅ 22 a = 12 \cdot 22 a = 12 ⋅ 22 Continue simplifying to find the value of a a a .

Step 6: Verify the Solution

After calculating the value of a a a , it is always a good practice to verify the solution. Check if the calculated value of a a a makes sense in the context of the problem and ensure that all steps were followed correctly.

By following these steps, you can solve any joint variation problem where one variable varies directly with the product of two other variables. The key is to identify the type of variation, write the general formula, find the constant of variation, update the formula, and then substitute the new values to find the missing variable.

Here are some frequently asked questions about joint and combined variation:

1. What is the difference between joint variation and combined variation?

Joint variation occurs when one variable is directly proportional to two or more other variables, expressed as y = kxz. Combined variation involves both direct and inverse relationships, typically expressed as y = k(x/z), where y varies directly with x and inversely with z.

2. What is an example of joint variation in real life?

A real-life example of joint variation is the volume of a rectangular prism. The volume (V) varies jointly with its length (l), width (w), and height (h), expressed as V = l × w × h.

3. How do you solve a combined variation problem?

To solve a combined variation problem: 1) Identify the variables and their relationships. 2) Write the equation (e.g., y = k(x/z)). 3) Use given information to find the constant k. 4) Substitute known values to solve for the unknown variable.

4. What are the four types of variation in mathematics?

The four main types of variation in mathematics are: 1) Direct variation, 2) Inverse variation, 3) Joint variation, and 4) Combined variation. Each type describes a different relationship between variables.

5. How can you identify the type of variation in a problem?

To identify the type of variation: Look for keywords like "directly," "inversely," or "jointly." If a variable increases as another increases, it's likely direct variation. If it decreases as another increases, it's probably inverse variation. When more than two variables are involved, consider joint or combined variation.

Understanding joint and combined variation is crucial in advanced algebra and real-world applications. To fully grasp this concept, it's essential to have a solid foundation in several prerequisite topics. One of the most fundamental is direct variation , which forms the basis for understanding how variables change in proportion to each other. The direct variation formula is a key component in recognizing and solving problems involving joint variation.

Equally important is the concept of inverse variation , where one variable increases as another decreases in a specific proportion. Mastering the inverse variation formula is crucial for tackling complex problems in joint and combined variation scenarios. These two types of variation are often combined in real-world situations, making their understanding vital.

To effectively work with joint and combined variation, students must be proficient in understanding tables of values of linear relationships . This skill helps in identifying proportional relationships and interpreting data, which is essential when dealing with multiple variables in joint variation problems.

Additionally, familiarity with distance and time related questions in linear equations provides practical context for joint variation. This knowledge is particularly useful when solving inverse variation problems, as many real-world scenarios involving joint variation relate to distance, time, and rate.

While it might seem unrelated at first, understanding volume of rectangular prisms word problems can be surprisingly relevant. These problems often involve multiple variables changing in relation to each other, mirroring the principles of joint variation in a three-dimensional context.

Lastly, knowledge of Newton's Second Law of Motion provides an excellent real-world application of joint variation. This law demonstrates how force, mass, and acceleration are related in a way that perfectly exemplifies the principles of joint variation.

By mastering these prerequisite topics, students will be well-equipped to tackle the complexities of joint and combined variation. Each concept builds upon the others, creating a comprehensive understanding that is essential for success in advanced algebra and its applications in science and engineering. Remember, a strong foundation in these basics will make the journey into more complex mathematical concepts smoother and more intuitive.

Become a member to get more!

No Javascript

It looks like you have javascript disabled.

You can still navigate around the site and check out our free content, but some functionality, such as sign up, will not work.

If you do have javascript enabled there may have been a loading error; try refreshing your browser.

HW Guidelines
Study Skills Quiz
Find Local Tutors
Demo MathHelp.com
Join MathHelp.com

Select a Course Below

ACCUPLACER Math
Math Placement Test
PRAXIS Math
+ more tests
5th Grade Math
6th Grade Math
Pre-Algebra
College Pre-Algebra
Introductory Algebra
Intermediate Algebra
College Algebra

Variation Word Problems

Equations Word Problems More Prob's

It's one thing to be able to take the words for a variation equation (such as " y varies directly as the square of x and inversely as the cube root of z ") and turn this into an equation that you can solve or use. It's another thing to extract the words from a word problem. But, because the lingo for variation equations is so specific, it's not really that hard. Just look for the keywords, and you're nearly home and dry.

The only other keywords (or "key-phrases", really) you might need to know are "is proportional to" which, in the strictly-mathematical sense, means "varies directly as"; and "is inversely proportional to" which means "varies inversely with".

Content Continues Below

MathHelp.com

Suppose that y is inversely proportional to x , and that y = 0.4 when x = 2.5 . Find y when x = 4 .

Translating the above from the English into algebra, I see the key-phrase "inversely proportional to", which means "varies indirectly as". In practical terms, it means that the variable part that does the varying is going to be in the denominator. So I get the formula:

Plugging in the data point they gave me, I can solve for the value of k :

0.4 = k /(2.5)

(0.4)(2.5) = k = 1

Now that I have found the value of the variation constant, I can plug in the x -value they gave me, and find the value of y when x = 4 :

Then my answer is:

Most word problems, of course, are not nearly as simple as the above example (or the ones on the previous page). Instead, you have to figure out which values go where, what the equation is, and how to interpret it. Fortunately, the keywords and key-phrases should generally be fairly clear, telling you exactly what format to use.

According to Hooke's Law, the force needed to stretch a spring is proportional to the amount the spring is stretched. If fifty pounds of force stretches a spring five inches, how much will the spring be stretched by a force of 120 pounds?

"Is proportional to" means "varies directly with", so the formula for Hooke's Law is:

...where " F " is the force and " d " is the distance that the spring is stretched.

Note: In physics, "weight" is a force. These Hooke's Law word problems, among other types, are often stated in terms of weight, and the weight they list is the force they mean.

First I have to solve for the value of k . They've given me the data point ( d , F) = (5, 50) , so I'll plug this in to the formula:

Now I know that the formula for this particular spring is:

(Hooke's Law doesn't change, but each spring is different, so each spring will have its own " k ".)

Once I know the formula, I can answer their question: "How much will the spring be stretched by a force of 120 pounds?" I'll plug the value they've given me for the force into the equation I've found:

Note that they did not ask "What is the value of ' d '?". They asked me for a distance. I need to be sure to answer the question that they actually asked. That final answer is the distance that the spring is stretched, including the units (which are "inches", in this case):

Note: If you give the above answer as being only " 12 ", the grader will be perfectly correct to count your answer as being at least partly wrong. The answer is not a number, but is a number of units.

Kepler's third law of planetary motion states that the square of the time required for a planet to make one revolution about the sun varies directly as the cube of the average distance of the planet from the sun. If you assume that Mars is 1.5 times as far from the sun as is the earth, find the approximate length of a Martian year.

This one is a bit different from the previous exercise. Normally, I've given given a relation in terms of variation with a plain old variable, like y . In this case, though, the variation relationship is between the square of the time and the cube of the distance. This means that the left-hand side of my equation will have a squared variable!

My variation formula is:

t 2 = k d 3

If I take " d = 1 " to mean "the distance is one AU", an AU being an "astronomical unit" (the distance of earth from the sun), then the distance for Mars is 1.5 AU. Also, I will take " t = 1 " to stand for "one earth year". Then, in terms of the planet Earth, I get:

(1) 2 = k (1) 3

Then the formula, in terms of Earth, is:

Now I'll plug in the information for Mars (in comparison to earth):

t 2 = (1.5) 3

This is one of those times when a calculator's decimal approximation is probably going to be a little more useful in answering the question. I'll show the exact answer in my working, but I'll use a sensible approximation in my final answer. The decimal expansion starts as:

In other words, the Martian year is approximately the length of:

1.837 earth years

By the way, you can make the above answer more intuitive by finding the number of (Earth) days, approximately, represented by that " 0.837 " part of the answer above. Since the average Earth year, technically, has about 365.25 days, then the 0.837 of an Earth year is:

0.837 × 365.25 = 305.71425

Letting the "average" month have 365.25 ÷ 12 = 30.4375 days, then the above number of (Earth) days is:

305.71425 ÷ 30.4375 = 10.044

In other words, the Martian year is almost exactly one Earth year and ten Earth months long.

If you were writing for an audience (like a fellow student, as you'll be required to do in some class projects or essay questions), this "one year and ten months" form would probably be the best way to go.

The weight of a body varies inversely as the square of its distance from the center of the earth. If the radius of the earth is 4000 miles, how much would a 200 -pound man weigh 1000 miles above the surface of the earth?

Remembering that "weight" is a force, I'll let the weight be designated by " F ". The distance of a body from the center of the earth is " d ". Then my variation formula is the following:

(200)(16,000,000) = k

3,200,000,000 = k

(Hey; there's nothing that says that the value of the variation constant k has to be small!)

The distance is always measured from the center of the earth. If the guy is in orbit a thousand miles up (from the surface of the planet), then his distance (from the center of the planet) is the 4000 miles from the center to the surface plus the 1000 miles from the surface to his ship. That is, d = 5000 . I'll plug this in to my equation, and solve for the value of the force (which is here called "weight") F :

Remembering my units, my answer is that, up in his spacecraft, the guy weighs:

URL: https://www.purplemath.com/modules/variatn2.htm

Page 1 Page 2 Page 3

Standardized Test Prep

College math, homeschool math, share this page.

Terms of Use
About Purplemath
About the Author
Tutoring from PM
Advertising
Linking to PM
Site licencing

Visit Our Profiles

JOINT VARIATION WORD PROBLEMS

Problem 1 :

z varies directly with the sum of squares of x and y. z = 5 when x = 3 and y = 4. Find the value of z when x = 2 and y = 4.

Since z varies directly with the sum of squares of x and y,

z ∝ x 2 + x 2

z = k(x 2 + y 2 ) ----(1)

Substitute z = 5, x = 3 and y = 4 to find the value k.

5 = k(3 2 + 4 2 )

5 = k(9 + 16)

Divide both sides by 25.

Substitute k = 1/5 in (1).

z = (1/5)(x 2 + y 2 )

Substitute x = 2, y = 4 and evaluate z.

z = (1/5)( (2 2 + 4 2 )

z = (1/5)( (4 + 16)

z = (1/5)( (20)

Problem 2 :

M varies directly with the square of d and inversely with the square root of x. M = 24 when d = 4 and x = 9. Find the value of M when d = 5 and x = 4.

Since m varies directly with the square of d and inversely with the square root of x

M ∝ d 2 √ x

M = kd 2 √ x ----(1)

Substitute M = 24, d = 4 and x = 9 to find the value k.

24 = k4 2 √9

24 = k(16)(3)

Divide both sides by 48.

Substitute k = 1/2 in (1).

M = (1/2)(d 2 √ x )

Substitute d = 5, x = 4 and evaluate M.

M = (1/2) (5 2 √4 )

M = (1/2)( (25)(2)

Problem 3 :

Square of T varies directly with the cube of a and inversely with the square of d. T = 2 when a = 2 and d = 4. Find the value of s quare of T when a = 4 and d = 2

Since square of T varies directly with the cube of a and inversely with the square of d

T 2 ∝ a 3 d 2

T 2 = ka 3 d 2 ----(1)

Substitute T = 2, a = 2 and d = 4 to find the value k.

2 2 = k2 3 4 2

4 = k(4)(16)

Divide both sides by 64.

Substitute k = 1/16 in (1).

T 2 = (1/16)a 3 d 2

Substitute a = 4, d = 2 and evaluate T 2 .

T 2 = (1/16)(4 3 )(2 2 )

T 2 = (1/16)(64)(4)

T 2 = 16

Problem 4 :

The area of a rectangle varies directly with its length and square of its width. When the length is 5 cm and width is 4 cm, the area is 160 cm 2 . Find the area of the rectangle when the length is 7 cm and the width is 3 cm.

Let A represent the area of the rectangle, l represent the length and w represent width.

Since the area of the rectangle varies directly with its length and square of its width,

A ∝ lw 2

A = klw 2 ----(1)

Substitute A = 160, l = 5 and d = 4 to find the value k.

160 = k(5)(4 2 )

160 = k(5)(16 )

160 = 80k

Divide both sides by 80.

Substitute k = 2 in (1).

Substitute l = 7, w = 3 and evaluate A.

A = 2(7)(3 2 )

A = 2(7)(9)

Area of the rectangle = 126 cm 2

Problem 5 :

The volume of a cylinder varies jointly as the square of radius and two times of its height. A cylinder with radius 4 cm and height 8 cm has a volume 128 π cm 3 . Find the volume of a cylinder with radius 3 cm and height 10 cm.

Let V represent volume of the cylinder, r represent radius and h represent height.

Since t he volume of a cylinder varies jointly as the radius and the sum of the radius and the height.

V ∝ r 2 (2h)

V = kr 2 (2h) ----(1)

Substitute V = 128 π , r = 4 and h = 8 to find the value of k.

128π = k(4 2 )(2 ⋅ 8)

128π = k(16)(16)

128π = 256k

Divide both sides by 256.

π/2 = k

Substitute k = π/2 in (1).

V = ( π/2) r 2 (2h)

V = π r 2 h

Substitute r = 3, h = 10 and evaluate V.

V = π(3 2 )(10)

V = π(9) (10)

Volume of the cylinder = 90 π cm 3

Kindly mail your feedback to [email protected]

We always appreciate your feedback.

Sat Math Practice
SAT Math Worksheets
PEMDAS Rule
BODMAS rule
GEMDAS Order of Operations
Math Calculators
Transformations of Functions
Order of rotational symmetry
Lines of symmetry
Compound Angles
Quantitative Aptitude Tricks
Trigonometric ratio table
Word Problems
Times Table Shortcuts
10th CBSE solution
PSAT Math Preparation
Privacy Policy
Laws of Exponents

Recent Articles

Logical reasoning blood relations.

Sep 05, 24 09:06 PM

Digital SAT Math Problems and Solutions (Part - 22)

Sep 05, 24 08:55 PM

SAT Math Resources (Videos, Concepts, Worksheets and More)

Sep 05, 24 08:19 PM

Module 10: Rational and Radical Functions

Inverse and joint variation, learning outcomes.

Solve an Inverse variation problem.
Write a formula for an inversely proportional relationship.

Water temperature in an ocean varies inversely to the water’s depth. Between the depths of 250 feet and 500 feet, the formula [latex]T=\frac{14,000}{d}[/latex] gives us the temperature in degrees Fahrenheit at a depth in feet below Earth’s surface. Consider the Atlantic Ocean, which covers 22% of Earth’s surface. At a certain location, at the depth of 500 feet, the temperature may be 28°F.

If we create a table we observe that, as the depth increases, the water temperature decreases.

[latex]d[/latex], depth	[latex]T=\frac{\text{14,000}}{d}[/latex]	Interpretation
500 ft	[latex]\frac{14,000}{500}=28[/latex]	At a depth of 500 ft, the water temperature is 28° F.
350 ft	[latex]\frac{14,000}{350}=40[/latex]	At a depth of 350 ft, the water temperature is 40° F.
250 ft	[latex]\frac{14,000}{250}=56[/latex]	At a depth of 250 ft, the water temperature is 56° F.

We notice in the relationship between these variables that, as one quantity increases, the other decreases. The two quantities are said to be inversely proportional and each term varies inversely with the other. Inversely proportional relationships are also called inverse variations .

For our example, the graph depicts the inverse variation . We say the water temperature varies inversely with the depth of the water because, as the depth increases, the temperature decreases. The formula [latex]y=\dfrac{k}{x}[/latex] for inverse variation in this case uses [latex]k=14,000[/latex].

A General Note: Inverse Variation

If [latex]x[/latex] and [latex]y[/latex] are related by an equation of the form

[latex]y=\dfrac{k}{{x}^{n}}[/latex]

where [latex]k[/latex] is a nonzero constant, then we say that [latex]y[/latex] varies inversely with the [latex]n[/latex]th power of [latex]x[/latex]. In inversely proportional relationships, or inverse variations , there is a constant multiple [latex]k={x}^{n}y[/latex].

Example: Writing a Formula for an Inversely Proportional Relationship

A tourist plans to drive 100 miles. Find a formula for the time the trip will take as a function of the speed the tourist drives.

Recall that multiplying speed by time gives distance. If we let [latex]t[/latex] represent the drive time in hours, and [latex]v[/latex] represent the velocity (speed or rate) at which the tourist drives, then [latex]vt=[/latex] distance. Because the distance is fixed at 100 miles, [latex]vt=100[/latex]. Solving this relationship for the time gives us our function.

[latex]\begin{align}t\left(v\right)&=\dfrac{100}{v} \\[1mm] &=100{v}^{-1} \end{align}[/latex]

We can see that the constant of variation is 100 and, although we can write the relationship using the negative exponent, it is more common to see it written as a fraction.

How To: Given a description of an indirect variation problem, solve for an unknown.

Identify the input, [latex]x[/latex], and the output, [latex]y[/latex].
Determine the constant of variation. You may need to multiply [latex]y[/latex] by the specified power of [latex]x[/latex] to determine the constant of variation.
Use the constant of variation to write an equation for the relationship.
Substitute known values into the equation to find the unknown.

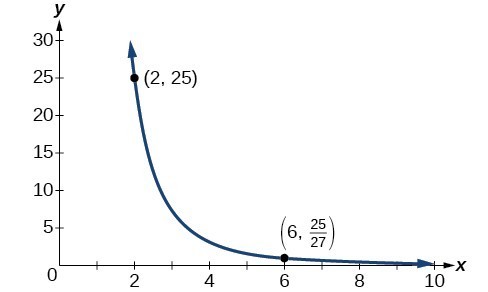
Example: Solving an Inverse Variation Problem

A quantity [latex]y[/latex] varies inversely with the cube of [latex]x[/latex]. If [latex]y=25[/latex] when [latex]x=2[/latex], find [latex]y[/latex] when [latex]x[/latex] is 6.

The general formula for inverse variation with a cube is [latex]y=\dfrac{k}{{x}^{3}}[/latex]. The constant can be found by multiplying [latex]y[/latex] by the cube of [latex]x[/latex].

[latex]\begin{align}k&={x}^{3}y \\[1mm] &={2}^{3}\cdot 25 \\[1mm] &=200 \end{align}[/latex]

Now we use the constant to write an equation that represents this relationship.

[latex]\begin{align}y&=\dfrac{k}{{x}^{3}},\hspace{2mm}k=200 \\[1mm] y&=\dfrac{200}{{x}^{3}} \end{align}[/latex]

Substitute [latex]x=6[/latex] and solve for [latex]y[/latex].

[latex]\begin{align}y&=\dfrac{200}{{6}^{3}} \\[1mm] &=\dfrac{25}{27} \end{align}[/latex]

Analysis of the Solution

The graph of this equation is a rational function.

A quantity [latex]y[/latex] varies inversely with the square of [latex]x[/latex]. If [latex]y=8[/latex] when [latex]x=3[/latex], find [latex]y[/latex] when [latex]x[/latex] is 4.

[latex]\dfrac{9}{2}[/latex]

The following video presents a short lesson on inverse variation and includes more worked examples.

Joint Variation

Many situations are more complicated than a basic direct variation or inverse variation model. One variable often depends on multiple other variables. When a variable is dependent on the product or quotient of two or more variables, this is called joint variation . For example, the cost of busing students for each school trip varies with the number of students attending and the distance from the school. The variable [latex]c[/latex], cost, varies jointly with the number of students, [latex]n[/latex], and the distance, [latex]d[/latex].

A General Note: Joint Variation

Joint variation occurs when a variable varies directly or inversely with multiple variables.

For instance, if [latex]x[/latex] varies directly with both [latex]y[/latex] and [latex]z[/latex], we have [latex]x=kyz[/latex]. If [latex]x[/latex] varies directly with [latex]y[/latex] and inversely with [latex]z[/latex], we have [latex]x=\dfrac{ky}{z}[/latex]. Notice that we only use one constant in a joint variation equation.

Example: Solving Problems Involving Joint Variation

A quantity [latex]x[/latex] varies directly with the square of [latex]y[/latex] and inversely with the cube root of [latex]z[/latex]. If [latex]x=6[/latex] when [latex]y=2[/latex] and [latex]z=8[/latex], find [latex]x[/latex] when [latex]y=1[/latex] and [latex]z=27[/latex].

Begin by writing an equation to show the relationship between the variables.

[latex]x=\dfrac{k{y}^{2}}{\sqrt[3]{z}}[/latex]

Substitute [latex]x=6[/latex], [latex]y=2[/latex], and [latex]z=8[/latex] to find the value of the constant [latex]k[/latex].

[latex]\begin{align}6&=\dfrac{k{2}^{2}}{\sqrt[3]{8}} \\[1mm] 6&=\dfrac{4k}{2} \\[1mm] 3&=k \end{align}[/latex]

Now we can substitute the value of the constant into the equation for the relationship.

[latex]x=\dfrac{3{y}^{2}}{\sqrt[3]{z}}[/latex]

To find [latex]x[/latex] when [latex]y=1[/latex] and [latex]z=27[/latex], we will substitute values for [latex]y[/latex] and [latex]z[/latex] into our equation.

[latex]\begin{align}x&=\dfrac{3{\left(1\right)}^{2}}{\sqrt[3]{27}} \\[1mm] &=1 \end{align}[/latex]

[latex]x[/latex] varies directly with the square of [latex]y[/latex] and inversely with [latex]z[/latex]. If [latex]x=40[/latex] when [latex]y=4[/latex] and [latex]z=2[/latex], find [latex]x[/latex] when [latex]y=10[/latex] and [latex]z=25[/latex].

[latex]x=20[/latex]

The following video provides another worked example of a joint variation problem.

Contribute!

Improve this page Learn More

Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
Question ID 91393,91394. Authored by : Jenck,Michael (for Lumen Learning). License : CC BY: Attribution . License Terms : IMathAS Community License CC-BY + GPL
College Algebra. Authored by : Abramson, Jay et al.. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
Inverse Variation. Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/awp2vxqd-l4 . License : CC BY: Attribution
Joint Variation: Determine the Variation Constant (Volume of a Cone). Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Provided by : Joint Variation: Determine the Variation Constant (Volume of a Cone). Located at : https://youtu.be/JREPATMScbM . License : CC BY: Attribution

5.8 Modeling Using Variation

Learning objectives.

In this section, you will:

Solve direct variation problems.
Solve inverse variation problems.
Solve problems involving joint variation.

A pre-owned car dealer has just offered their best candidate, Nicole, a position in sales. The position offers 16% commission on her sales. Her earnings depend on the amount of her sales. For instance, if she sells a vehicle for $4,600, she will earn $736. As she considers the offer, she takes into account the typical price of the dealer's cars, the overall market, and how many she can reasonably expect to sell. In this section, we will look at relationships, such as this one, between earnings, sales, and commission rate.

Solving Direct Variation Problems

In the example above, Nicole’s earnings can be found by multiplying her sales by her commission. The formula e = 0.16 s e = 0.16 s tells us her earnings, e , e , come from the product of 0.16, her commission, and the sale price of the vehicle. If we create a table, we observe that as the sales price increases, the earnings increase as well, which should be intuitive. See Table 1 .

, sales price		Interpretation
$4,600		A sale of a $4,600 vehicle results in $736 earnings.
$9,200		A sale of a $9,200 vehicle results in $1472 earnings.
$18,400		A sale of a $18,400 vehicle results in $2944 earnings.

Notice that earnings are a multiple of sales. As sales increase, earnings increase in a predictable way. Double the sales of the vehicle from $4,600 to $9,200, and we double the earnings from $736 to $1,472. As the input increases, the output increases as a multiple of the input. A relationship in which one quantity is a constant multiplied by another quantity is called direct variation . Each variable in this type of relationship varies directly with the other.

Figure 1 represents the data for Nicole’s potential earnings. We say that earnings vary directly with the sales price of the car. The formula y = k x n y = k x n is used for direct variation. The value k k is a nonzero constant greater than zero and is called the constant of variation . In this case, k = 0.16 k = 0.16 and n = 1. n = 1. We saw functions like this one when we discussed power functions.

Direct Variation

If x and y x and y are related by an equation of the form

then we say that the relationship is direct variation and y y varies directly with, or is proportional to, the n n th power of x . x . In direct variation relationships, there is a nonzero constant ratio k = y x n , k = y x n , where k k is called the constant of variation , which help defines the relationship between the variables.

Given a description of a direct variation problem, solve for an unknown.

Identify the input, x , x , and the output, y . y .
Determine the constant of variation. You may need to divide y y by the specified power of x x to determine the constant of variation.
Use the constant of variation to write an equation for the relationship.
Substitute known values into the equation to find the unknown.

Solving a Direct Variation Problem

The quantity y y varies directly with the cube of x . x . If y = 25 y = 25 when x = 2 , x = 2 , find y y when x x is 6.

The general formula for direct variation with a cube is y = k x 3 . y = k x 3 . The constant can be found by dividing y y by the cube of x . x .

Now use the constant to write an equation that represents this relationship.

Substitute x = 6 x = 6 and solve for y . y .

The graph of this equation is a simple cubic, as shown in Figure 2 .

Do the graphs of all direct variation equations look like Example 1 ?

No. Direct variation equations are power functions—they may be linear, quadratic, cubic, quartic, radical, etc. But all of the graphs pass through ( 0,0 ) . ( 0,0 ) .

The quantity y y varies directly with the square of x . x . If y = 24 y = 24 when x = 3 , x = 3 , find y y when x x is 4.

Solving Inverse Variation Problems

Water temperature in an ocean varies inversely to the water’s depth. The formula T = 14,000 d T = 14,000 d gives us the temperature in degrees Fahrenheit at a depth in feet below Earth’s surface. Consider the Atlantic Ocean, which covers 22% of Earth’s surface. At a certain location, at the depth of 500 feet, the temperature may be 28°F.

If we create Table 2 , we observe that, as the depth increases, the water temperature decreases.

depth		Interpretation
500 ft		At a depth of 500 ft, the water temperature is 28° F.
1000 ft		At a depth of 1,000 ft, the water temperature is 14° F.
2000 ft		At a depth of 2,000 ft, the water temperature is 7° F.

For our example, Figure 3 depicts the inverse variation . We say the water temperature varies inversely with the depth of the water because, as the depth increases, the temperature decreases. The formula y = k x y = k x for inverse variation in this case uses k = 14,000. k = 14,000.

Inverse Variation

If x x and y y are related by an equation of the form

where k k is a nonzero constant, then we say that y y varies inversely with the n th n th power of x . x . In inversely proportional relationships, or inverse variations , there is a constant multiple k = x n y . k = x n y .

Writing a Formula for an Inversely Proportional Relationship

A tourist plans to drive 100 miles. Find a formula for the time the trip will take as a function of the speed the tourist drives.

Recall that multiplying speed by time gives distance. If we let t t represent the drive time in hours, and v v represent the velocity (speed or rate) at which the tourist drives, then v t = distance . v t = distance . Because the distance is fixed at 100 miles, v t = 100 v t = 100 so t = 100/ v . t = 100/ v . Because time is a function of velocity, we can write t ( v ) . t ( v ) .

We can see that the constant of variation is 100 and, although we can write the relationship using the negative exponent, it is more common to see it written as a fraction. We say that time varies inversely with velocity.

Given a description of an indirect variation problem, solve for an unknown.

Determine the constant of variation. You may need to multiply y y by the specified power of x x to determine the constant of variation.

Solving an Inverse Variation Problem

A quantity y y varies inversely with the cube of x . x . If y = 25 y = 25 when x = 2 , x = 2 , find y y when x x is 6.

The general formula for inverse variation with a cube is y = k x 3 . y = k x 3 . The constant can be found by multiplying y y by the cube of x . x .

Now we use the constant to write an equation that represents this relationship.

The graph of this equation is a rational function, as shown in Figure 4 .

A quantity y y varies inversely with the square of x . x . If y = 8 y = 8 when x = 3 , x = 3 , find y y when x x is 4.

Solving Problems Involving Joint Variation

Many situations are more complicated than a basic direct variation or inverse variation model. One variable often depends on multiple other variables. When a variable is dependent on the product or quotient of two or more variables, this is called joint variation . For example, the cost of busing students for each school trip varies with the number of students attending and the distance from the school. The variable c , c , cost, varies jointly with the number of students, n , n , and the distance, d . d .

Joint Variation

Joint variation occurs when a variable varies directly or inversely with multiple variables.

For instance, if x x varies directly with both y y and z , z , we have x = k y z . x = k y z . If x x varies directly with y y and inversely with z , z , we have x = k y z . x = k y z . Notice that we only use one constant in a joint variation equation.

A quantity x x varies directly with the square of y y and inversely with the cube root of z . z . If x = 6 x = 6 when y = 2 y = 2 and z = 8 , z = 8 , find x x when y = 1 y = 1 and z = 27. z = 27.

Begin by writing an equation to show the relationship between the variables.

Substitute x = 6 , x = 6 , y = 2 , y = 2 , and z = 8 z = 8 to find the value of the constant k . k .

Now we can substitute the value of the constant into the equation for the relationship.

To find x x when y = 1 y = 1 and z = 27 , z = 27 , we will substitute values for y y and z z into our equation.

A quantity x x varies directly with the square of y y and inversely with z . z . If x = 40 x = 40 when y = 4 y = 4 and z = 2 , z = 2 , find x x when y = 10 y = 10 and z = 25. z = 25.

Access these online resources for additional instruction and practice with direct and inverse variation.

Direct and Inverse Variation

5.8 Section Exercises

What is true of the appearance of graphs that reflect a direct variation between two variables?

If two variables vary inversely, what will an equation representing their relationship look like?

Is there a limit to the number of variables that can vary jointly? Explain.

For the following exercises, write an equation describing the relationship of the given variables.

y y varies directly as x x and when x = 6 , y = 12. x = 6 , y = 12.

y y varies directly as the square of x x and when x = 4 , y = 80 . x = 4 , y = 80 .

y y varies directly as the square root of x x and when x = 36 , y = 24. x = 36 , y = 24.

y y varies directly as the cube of x x and when x = 36 , y = 24. x = 36 , y = 24.

y y varies directly as the cube root of x x and when x = 27 , y = 15. x = 27 , y = 15.

y y varies directly as the fourth power of x x and when x = 1 , y = 6. x = 1 , y = 6.

y y varies inversely as x x and when x = 4 , y = 2. x = 4 , y = 2.

y y varies inversely as the square of x x and when x = 3 , y = 2. x = 3 , y = 2.

y y varies inversely as the cube of x x and when x = 2 , y = 5. x = 2 , y = 5.

y y varies inversely as the fourth power of x x and when x = 3 , y = 1. x = 3 , y = 1.

y y varies inversely as the square root of x x and when x = 25 , y = 3. x = 25 , y = 3.

y y varies inversely as the cube root of x x and when x = 64 , y = 5. x = 64 , y = 5.

y y varies jointly with x x and z z and when x = 2 x = 2 and z = 3 , y = 36. z = 3 , y = 36.

y y varies jointly as x , z , x , z , and w w and when x = 1 , z = 2 , w = 5 , x = 1 , z = 2 , w = 5 , then y = 100. y = 100.

y y varies jointly as the square of x x and the square of z z and when x = 3 x = 3 and z = 4 , z = 4 , then y = 72. y = 72.

y y varies jointly as x x and the square root of z z and when x = 2 x = 2 and z = 25 , z = 25 , then y = 100. y = 100.

y y varies jointly as the square of x x the cube of z z and the square root of W . W . When x = 1 , z = 2 , x = 1 , z = 2 , and w = 36 , w = 36 , then y = 48. y = 48.

y y varies jointly as x x and z z and inversely as w w . When x = 3 , z = 5 x = 3 , z = 5 , and w = 6 w = 6 , then y = 10. y = 10.

y y varies jointly as the square of x x and the square root of z z and inversely as the cube of w . w . When x = 3 , z = 4 , x = 3 , z = 4 , and w = 3 , w = 3 , then y = 6. y = 6.

y y varies jointly as x x and z z and inversely as the square root of w w and the square of t . t . When x = 3 , z = 1 , w = 25 , x = 3 , z = 1 , w = 25 , and t = 2 , t = 2 , then y = 6. y = 6.

For the following exercises, use the given information to find the unknown value.

y y varies directly as x . x . When x = 3 , x = 3 , then y = 12. y = 12. Find y y wneh x = 20. x = 20.

y y varies directly as the square of x . x . When x = 2 , x = 2 , then y = 16. y = 16. Find y y when x = 8. x = 8.

y y varies directly as the cube of x . x . When x = 3 , x = 3 , then y = 5. y = 5. Find y y when x = 4. x = 4.

y y varies directly as the square root of x . x . When x = 16 , x = 16 , then y = 4. y = 4. Find y y when x = 36. x = 36.

y y varies directly as the cube root of x . x . When x = 125 , x = 125 , then y = 15. y = 15. Find y y when x = 1,000. x = 1,000.

y y varies inversely with x . x . When x = 3 , x = 3 , then y = 2. y = 2. Find y y when x = 1. x = 1.

y y varies inversely with the square of x . x . When x = 4 , x = 4 , then y = 3. y = 3. Find y y when x = 2. x = 2.

y y varies inversely with the cube of x . x . When x = 3 , x = 3 , then y = 1. y = 1. Find y y when x = 1. x = 1.

y y varies inversely with the square root of x . x . When x = 64 , x = 64 , then y = 12. y = 12. Find y y when x = 36. x = 36.

y y varies inversely with the cube root of x . x . When x = 27 , x = 27 , then y = 5. y = 5. Find y y when x = 125. x = 125.

y y varies jointly as x and z . x and z . When x = 4 x = 4 and z = 2 , z = 2 , then y = 16. y = 16. Find y y when x = 3 x = 3 and z = 3. z = 3.

y y varies jointly as x , z , and w . x , z , and w . When x = 2 , x = 2 , z = 1 , z = 1 , and w = 12 , w = 12 , then y = 72. y = 72. Find y y when x = 1 , x = 1 , z = 2 , z = 2 , and w = 3. w = 3.

y y varies jointly as x x and the square of z. z. When x = 2 x = 2 and z = 4 , z = 4 , then y = 144. y = 144. Find y y when x = 4 x = 4 and z = 5. z = 5.

y y varies jointly as the square of x x and the square root of z . z . When x = 2 x = 2 and z = 9 , z = 9 , then y = 24. y = 24. Find y y when x = 3 x = 3 and z = 25. z = 25.

y y varies jointly as x x and z z and inversely as w . w . When x = 5 , x = 5 , z = 2 , z = 2 , and w = 20 , w = 20 , then y = 4. y = 4. Find y y when x = 3 x = 3 and z = 8 , z = 8 , and w = 48. w = 48.

y y varies jointly as the square of x x and the cube of z z and inversely as the square root of w . w . When x = 2 , x = 2 , z = 2 , z = 2 , and w = 64 , w = 64 , then y = 12. y = 12. Find y y when x = 1 , x = 1 , z = 3 , z = 3 , and w = 4. w = 4.

y y varies jointly as the square of x x and of z z and inversely as the square root of w w and of t . t . When x = 2 , x = 2 , z = 3 , z = 3 , w = 16 , w = 16 , and t = 3 , t = 3 , then y = 1. y = 1. Find y y when x = 3 , x = 3 , z = 2 , z = 2 , w = 36 , w = 36 , and t = 5. t = 5.

For the following exercises, use a calculator to graph the equation implied by the given variation.

y y varies directly with the square of x x and when x = 2 , y = 3. x = 2 , y = 3.

y y varies directly as the cube of x x and when x = 2 , y = 4. x = 2 , y = 4.

y y varies directly as the square root of x x and when x = 36 , y = 2. x = 36 , y = 2.

y y varies inversely with x x and when x = 6 , y = 2. x = 6 , y = 2.

y y varies inversely as the square of x x and when x = 1 , y = 4. x = 1 , y = 4.

For the following exercises, use Kepler’s Law, which states that the square of the time, T , T , required for a planet to orbit the Sun varies directly with the cube of the mean distance, a , a , that the planet is from the Sun.

Using Earth’s time of 1 year and mean distance of 93 million miles, find the equation relating T T and a . a .

Use the result from the previous exercise to determine the time required for Mars to orbit the Sun if its mean distance is 142 million miles.

Using Earth’s distance of 150 million kilometers, find the equation relating T T and a . a .

Use the result from the previous exercise to determine the time required for Venus to orbit the Sun if its mean distance is 108 million kilometers.

Using Earth’s distance of 1 astronomical unit (A.U.), determine the time for Saturn to orbit the Sun if its mean distance is 9.54 A.U.

Real-World Applications

For the following exercises, use the given information to answer the questions.

The distance s s that an object falls varies directly with the square of the time, t , t , of the fall. If an object falls 16 feet in one se c ond, how long for it to fall 144 feet?

The velocity v v of a falling object varies directly to the time, t t , of the fall. If after 2 seconds, the velocity of the object is 64 feet per second, what is the velocity after 5 seconds?

The rate of vibration of a string under constant tension varies inversely with the length of the string. If a string is 24 inches long and vibrates 128 times per second, what is the length of a string that vibrates 64 times per second?

The volume of a gas held at constant temperature varies indirectly as the pressure of the gas. If the volume of a gas is 1200 cubic centimeters when the pressure is 200 millimeters of mercury, what is the volume when the pressure is 300 millimeters of mercury?

The weight of an object above the surface of Earth varies inversely with the square of the distance from the center of Earth. If a body weighs 50 pounds when it is 3960 miles from Earth’s center, what would it weigh it were 3970 miles from Earth’s center?

The intensity of light measured in foot-candles varies inversely with the square of the distance from the light source. Suppose the intensity of a light bulb is 0.08 foot-candles at a distance of 3 meters. Find the intensity level at 8 meters.

The current in a circuit varies inversely with its resistance measured in ohms. When the current in a circuit is 40 amperes, the resistance is 10 ohms. Find the current if the resistance is 12 ohms.

The force exerted by the wind on a plane surface varies jointly with the square of the velocity of the wind and with the area of the plane surface. If the area of the surface is 40 square feet surface and the wind velocity is 20 miles per hour, the resulting force is 15 pounds. Find the force on a surface of 65 square feet with a velocity of 30 miles per hour.

The horsepower (hp) that a shaft can safely transmit varies jointly with its speed (in revolutions per minute (rpm) and the cube of the diameter. If the shaft of a certain material 3 inches in diameter can transmit 45 hp at 100 rpm, what must the diameter be in order to transmit 60 hp at 150 rpm?

The kinetic energy K K of a moving object varies jointly with its mass m m and the square of its velocity v . v . If an object weighing 40 kilograms with a velocity of 15 meters per second has a kinetic energy of 1000 joules, find the kinetic energy if the velocity is increased to 20 meters per second.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites

Authors: Jay Abramson
Publisher/website: OpenStax
Book title: College Algebra 2e
Publication date: Dec 21, 2021
Location: Houston, Texas
Book URL: https://openstax.org/books/college-algebra-2e/pages/1-introduction-to-prerequisites
Section URL: https://openstax.org/books/college-algebra-2e/pages/5-8-modeling-using-variation

© Jun 28, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Search Menu
Sign in through your institution
Volume 239, Issue 2, November 2024 (In Progress)
Volume 239, Issue 1, October 2024 (In Progress)
Volume 238, Issue 3, September 2024
Advance Access
Applied and Marine Geophysics
General Geophysical Methods
Geodynamics and Tectonics
Geomagnetism and Electromagnetism
Gravity, Geodesy and Tides
Heat Flow and Volcanology
Rock and Mineral Physics, Rheology
Mount Etna Virtual Issue
Advances in Induced Polarization
100 Influential Papers
Advance Articles
Express Letters
Hunga Volcano Special Issue
East Anatolia Fault Special Issue
Special Issues
Why Publish
Author Guidelines
Submission Site
Read & Publish
Developing Countries Initiative
Author Resources
Self-Archiving policy
Rights and Permissions
About Geophysical Journal International
Editorial Board
About the Royal Astronomical Society
About the DGG
Journals on Oxford Academic
Books on Oxford Academic

Article Contents

1 introduction, 2 joint inversion by variable splitting and alternating minimization, 3 regularization and coupling, 4 application to mt, fatt and gravity, 5 numerical examples, 6 conclusions, acknowledgements, data availability.

< Previous

Decoupled joint inversion with variable splitting: example scheme for magnetotelluric, seismic and gravity data

Article contents
Figures & tables
Supplementary Data

Dmitry Molodtsov, Duygu Kiyan, Christopher J Bean, Decoupled joint inversion with variable splitting: example scheme for magnetotelluric, seismic and gravity data, Geophysical Journal International , Volume 239, Issue 1, October 2024, Pages 706–724, https://doi.org/10.1093/gji/ggae292

Permissions Icon Permissions

We present a general framework for multiphysics joint inversion of any number of geophysical data sets. Its main feature is the use of the variable splitting approach: an auxiliary multiparameter model space is introduced in which minimization of the coupling and stabilizing functionals is carried out. The use of rediscretization and interpolation to map between this auxiliary space and the model spaces allows the coupled models to have completely different parametrizations. Joint inversion is decoupled into the individual inversion and the coupling-regularization subproblems, each of which can be solved by a different optimization algorithm. For each subproblem, the linking term controlling the distance between the model and the corresponding auxiliary variable takes the form of a quadratic regularization with a reference model. As a result, any existing inversion code supporting such regularization can be integrated without modifications into the developed framework. As a concrete example scheme, we consider an application of the framework to 3-D joint inversion of magnetotelluric, seismic refraction and gravity data. We discuss different coupling functionals, mainly those corresponding to the more universal structural constraints: joint total variation, joint minimum support, cross-gradient, one-way cross-gradient and their combinations for a general multimodel case. The use of coupling based on explicit ‘petrophysical’ relationship between the properties is also considered. Performance of the developed framework is studied on three synthetic cases: a time-lapse joint inversion of full-tensor gravity gradiometry and seismic data, a joint inversion of magnetotelluric, seismic and gravity data and a joint inversion for electrical resistivity tomography and audio-magnetotellurics.

Joint inversion is an actively developing approach to the integration of multiple geophysical methods that aims at reducing the uncertainties inherent to the geophysical inversions and subsequent geological interpretation. Related approach, when a model obtained with one geophysical method is incorporated in the inversion of another method, is termed ‘model fusion’ (Haber & Holtzman Gazit 2013 ) or ‘cooperative inversion’ (Moorkamp et al . 2016 ). Both approaches can be applied to methods sensitive to the same physical property, for example magnetotellurics and electrical resistivity tomography, which are both sensitive to the resistivity (see Vozoff & Jupp 1975 ), or to methods sensitive to different properties. In the latter case, some coupling between the models has to be assumed (the single-property joint/cooperative inversion can be viewed as a special case with trivial coupling).

Depending on the nature of the available prior information, coupling between the geophysical models can be based on structural similarity (see Crestel et al . 2018 , for an overview), explicitly defined common structural parameters (e.g. Juhojuntti & Kamm 2015 ; Zheglova et al . 2018 ) or relationships between the physical properties, defined either analytically (e.g. Heincke et al . 2017 ; Colombo & Rovetta 2018 ) or using statistical data analysis techniques such as fuzzy clustering (e.g. Lelièvre et al . 2012 ; Sun & Li 2016 ) and Gaussian mixture models (Astic et al . 2021 ). A promising approach to model coupling is based on maximization of various measures of statistical dependence: Haber & Holtzman Gazit ( 2013 ) and Mandolesi & Jones ( 2014 ) experimented with the mutual information; as an alternative, the use of the variation of information (Moorkamp 2021 ) and the joint entropy (Zhdanov et al . 2022 ) have been suggested. Gramian constraints (Zhdanov et al . 2012 ; Malovichko et al . 2020 ) allow for efficient maximization of the correlation coefficients between the models or their transforms. Alternatively to the coupling of geophysical models, a joint inverse problem can be solved directly for lithologies (Bosch 1999 ) or for thermochemical (Khan et al . 2007 ; Afonso et al . 2013 ) or petrophysical (Chen et al . 2007 ; Gao et al . 2012 ) parameters.

Deterministic inversion methods based on local optimization have well-known limitations: the uncertainty estimation, when available, is restricted to linearized estimates, solutions depend on the choice of the regularization parameters (as a scalarization of a multiobjective optimization problem) and, for nonlinear problems, on the initial model. However, at the present time, for most 3-D inverse problems with a large number of unknowns, stochastic, global optimization methods are not computationally feasible. This situation may change with the advances in techniques like the reduced order modelling (Manassero et al . 2021 ) and deep learning (Colombo et al . 2021 ).

In this paper we consider a deterministic 3-D joint inversion framework, with the primary aim of applying it to large magnetotelluric (MT), gravity and seismic first-arrival traveltime (FATT) data sets, on both regional and local scales. During the preparation of this publication, magnetic data inversion was added to the framework. In the future, we plan to add inversion of seismic surface wave dispersion data. Thus, we need a framework to which geophysical methods can be easily added, preferably as existing inversion codes. Model discretization required by a particular method is dictated by the physics (resolution, boundary conditions, etc.) and by the numerical implementation of the forward problem. Although it is possible to use a common grid for the joint inverse problem and individual, problem-specific grids for the forward problems (e.g. see Moorkamp et al . 2011 , Heincke et al . 2017 ), our choice here is to use an individual grid for each inverse problem—this makes it easier to adapt inversion codes and ensures that a model parametrization is capable of entirely explaining each data set. The ‘philosophy’ of our approach is that the priority is given to the individual inversions (i.e. the model parametrization, the forward solver and the optimization method are optimal for each data set in the sense that the same choices would have been made in a ‘separate’ inversion case), while the ‘joint’ part, that is the coupling, is added as a logically independent and easily modifiable block. We show how this can be achieved with a simple technique, often referred to as variable splitting (e.g. Wang et al . 2008 ): terms of an objective function are decoupled by introducing an auxiliary variable and penalizing the distance between this variable and the model vector. By combining this technique with interpolation between the grids, the joint inverse problem is decoupled into the separate inversion (with standard quadratic regularization) and the coupling (and regularization) subproblems that are solved in an alternating manner.

The paper is organized as follows. First, we derive a general split-variable formulation of joint inversion and discuss its practical implementation as an alternating minimization algorithm. Next, we describe several structure-coupling functionals, which are implemented in our joint inversion framework: the joint total variation (JTV), the joint minimum support (JMS), the cross-gradient (XG) and the one-way cross-gradient (OWXG). We then discuss the main aspects of the application of the proposed scheme to MT, FATT and gravity problems. Finally, performance of the framework is demonstrated on synthetic data: in the first example we consider a time-lapse joint inversion of FATT and gravity gradiometry data using JMS constraints, in the second example we compare performance of several combinations of JTV, XG, OWXG and ‘petrophysical’ constraints in a joint inversion of MT, FATT and gravity data, and in the third example we consider joint inversion of audio-magnetotelluric (AMT) and electrical resistivity tomography (ERT) data combining 2-D finite-element and 3-D finite-difference grids.

Consider a multiphysics joint inverse problem—the same region of the Earth’s interior is imaged with N geophysical methods, each sensitive to a different physical property of the medium and modelled by a forward operator |$\mathbf {f}_i$|⁠ ; the goal is, given N observed data vectors |$\mathbf {d}_i$|⁠ , to simultaneously recover the physical properties described by the model vectors |$\mathbf {m}_i$|⁠ :

For each method, assuming the noise |$\boldsymbol{\epsilon }_i$| is Gaussian with zero mean, the maximum likelihood solution can be found by minimizing the data misfit functional

where |$\mathbf {C}_{d_i}$| is the covariance matrix of the observed data. Because this solution is generally non-unique due to ill-posedness of the inverse problem ( 1 ) and unattainable for local optimization due to nonlinearity of |$\mathbf {f}_i(\mathbf {m}_i)$|⁠ , prior information about the model must be introduced—in the form of regularization and, in the case of the multiphysics joint inversion, also by postulating some coupling between the individual models. This coupling, as well as the regularization, can generally be imposed as a penalty functional. Denoting by |$\mathcal {R}$| the combination of all the ‘prior’ functionals, we can set the joint inversion as an unconstrained optimization problem:

Coefficients |$\lambda _i \gt 0$| weight the individual data misfit functionals relative to each other and to the ‘prior’ terms. Practical implementation of eq. ( 3 ) can be difficult due to the complexity and heterogeneity of the objective function—the individual inverse problems, as well as the ‘prior’ terms, often have different requirements to model parametrization and optimization techniques (and regardless of this, maximum reuse of the existing codes is always desirable). A straightforward workaround is based on the block coordinate descent (BCD) approach (Hu et al . 2009 ; Haber & Holtzman Gazit 2013 ) or alternating minimization : the idea is to cycle through the models |$\mathbf {m}_i$| (i.e. blocks of |$[\mathbf {m}_0^{\mathrm{T}}, \mathbf {m}_1^{\mathrm{T}}, \dots , \mathbf {m}_{N\!-\!1}^{\mathrm{T}}]^{\mathrm{T}}$|⁠ ) each time minimizing eq. ( 3 ) with respect to one model while keeping the other models fixed; this decouples the |$\Phi _{d_i}$| terms, significantly simplifying practical implementation of the joint inversion (at the cost of theoretically slower convergence). We develop a different alternating minimization approach, whose advantages over BCD will be demonstrated below.

Let us introduce for each |$\mathbf {m}_i \in {\mathbb R}^{M_i}$| an auxiliary variable |$\mathbf {u}_i \in \mathbb {R}^{M_i}$| and, instead of eq. ( 3 ), write:

With all |$\alpha _i \rightarrow \infty$|⁠ , this problem is equivalent to eq. ( 3 ). This technique, known as variable splitting, following the works of Wang et al . ( 2008 ) and Goldstein & Osher ( 2009 ) is widely used with |$\ell _1$| -regularized problems as a means of separating the non-differentiable |$\ell _1$| and the |$\ell _2$| terms of the objective function. Here it separates the |$\Phi _{d_i}$| terms from the regularization and coupling term |$\mathcal {R}$|⁠ .

Assume that each vector |$\mathbf {m}_i = [m_{i,1},m_{i,2}, \dots , m_{i,M_i}]^{\mathrm{T}}$| parametrizes a grid-based discretization of a physical property |$m_i(\mathbf {x})$| of the medium in the following form:

where |$\varphi _{i,j}(\mathbf {x})$| are some basis functions defining a 3-D grid. Thus, we assume that individual models are discretized independently and the model regions |$\Omega _i$| are, in general, different (with a necessary limitation that the intersection of all |$\Omega _i$| is not empty). In contrast to |$\mathbf {m}_i$|⁠ , vectors |$\mathbf {u}_i$| in eq. ( 4 ) are coupled by the term |$\mathcal {R}$| which implies that they must, at some point, be mapped to the same basis. Let us discretize all |$\mathbf {u}_i$| by the same grid, that is analogously to eq. ( 5 ), |$u_i(\mathbf {x}) = \sum _{j=1}^M u_{i,j} \varphi _j(\mathbf {x})$|⁠ , with |$\mathbf {x} \in \Omega : \bigcap _{i=0}^{N\!-\!1} \Omega _i \subset \Omega$|⁠ , and denote by matrix |$\mathbf {P}_i$| interpolation onto this grid from the grid of |$\mathbf {m}_i$|⁠ . Let us also define the multiparameter model vector |$\mathbf {u} = [\mathbf {u}_0^{\mathrm{T}},\mathbf {u}_1^{\mathrm{T}}, \dots , \mathbf {u}_{N\!-\!1}^{\mathrm{T}}]^{\mathrm{T}}$|⁠ . Using this notation, we can rewrite problem ( 4 ) as follows:

The problem is thus decomposed into a system of N data-fitting ( inversion ) subproblems, each regularized by a simple quadratic functional, and the coupling-regularization subproblem. Derivatives of the linking terms with respect to |$\mathbf {m}_i$| required by the inversion subproblems include transpose |$\mathbf {P}_i^{\mathrm{T}}$| of the interpolation operators, which is often difficult to implement; an iterative solver such as the conjugate gradient method would require computationally expensive (for large 3-D grids) application of |$\mathbf {P}_i$| and |$\mathbf {P}_i^{\mathrm{T}}$| at each iteration. However, given that both |$\mathbf {m}_i$| and |$\mathbf {u}_i$| adequately represent the models (e.g. satisfy the Nyquist criterion), distance between the models can as well be calculated in the |$\mathbf {m}_i$| space. Another difficulty with the inversion subproblems, especially when the gradient of |$\Phi _{d_i}(\mathbf {m}_i)$| is ‘rough’ (as, e.g. in ray-based tomography), is that, even if the smoothness of |$\mathbf {u}_i$| is controlled by |$\mathcal {R}(\mathbf {u})$|⁠ , lack of smoothness in the updates to |$\mathbf {m}_i$| at early stages, when |$\mathbf {m}_i$| and |$\mathbf {u}_i$| are far apart, may lead to instability and breakdown of the inversion. The required additional smoothing can be introduced by replacing the Euclidean norm in the linking terms by a Sobolev norm. Applying these changes to system ( 6 ), we get:

where |$\hat{\alpha }_i = \alpha _i / \lambda _i$|⁠ , |$\mathbf {Q}_i$| is interpolation from the grid of |$\mathbf {u}$| onto the grid of |$\mathbf {m}_i$| and |$W^1_2$| denotes (weighted) discretized Sobolev norm of order one:

where |$\mathbf {L}$| is a negative discrete Laplacian and w is a weighting coefficient. In the coupling-regularization subproblem, we omit additional smoothing since in the cases considered here it is either redundant or conflicting with the regularization present in |$\mathcal {R}$|⁠ . Note that if all the models and |$\mathbf {u}$| use the same discretization and |$\alpha _i \rightarrow \infty$|⁠ , problem ( 7 ) is equivalent to eq. ( 3 ).

Discretizations of |$\mathbf {m}_i$| are dictated by the inverse problems. Since the regularization and coupling should not create excessive details, discretizing |$\mathbf {u}$| by a grid that is not coarser than the finest |$\mathbf {m}_i$| grid is always safe. However, this is not always necessary and computationally feasible. For example, inversion of MT data often requires a very fine grid in the near surface, while its joint inversion with tomography and/or gravity aims at resolving the deeper (and larger scale) structures. In this case, discretizing |$\mathbf {u}$| by a regular grid with the smallest step from the resistivity grid would be prohibitively expensive, but since |$\mathbf {u}$| enters MT inversion as a reference model only, using a coarser grid will still allow for recovery of a fine resistivity structure in the near surface (see Section 5.2 ).

System ( 7 ) can be solved by alternating minimization: several (or one, for Newton-type methods) iterations of the inversion subproblems are followed by several iterations of the coupling-regularization subproblem, after which this cycle, which we will refer to as the outer iteration, is repeated. We use a continuation (see, e.g. Nocedal & Wright 1999 ) in |$\alpha _i$| and |$\hat{\alpha }_i$|⁠ : following Wang et al . ( 2008 ), |$\alpha _i$| are gradually increased with the outer iterations as a geometric series |$\alpha _{i,n} = q^n \alpha _{i,0}$|⁠ , where |$q\gt 1$|⁠ . On the other hand, |$\hat{\alpha }_i = \alpha _i / \lambda _i$|⁠ . Recalling eq. ( 3 ), we recognize |$\lambda _i$| as the Lagrange multipliers of the constraints |$2\Phi _{d_i}(\mathbf {m}_i) = N_{d_i}$|⁠ , where |$N_{d_i}$| is the dimension of |$\mathbf {d}_i$|⁠ ; a common practical approach to determining these Lagrange multipliers, known as cooling or adaptive regularization, is to use continuation |$\lambda _{i,n} = q_\lambda ^n \lambda _{i,0}$| with |$q_\lambda \gt 1$|⁠ , starting from a “small” value |$\lambda _{i,0}$|⁠ , until the constraint is satisfied (see, e.g. Haber et al . 2000 ; Zhdanov 2002 ). Assuming that |$q_\lambda \approx q$|⁠ , we can keep |$\hat{\alpha }_i$| constant during the inversion–this simplification was used in all our numerical examples and proved to be working satisfactorily. Overall, with |$\hat{\alpha }_i$| fixed and |$\alpha _i$| increasing, the balance is gradually shifted from the prior |$\mathcal {R}$| towards the data terms, similar to the (separate inversion) cooling. A finer tuning of |$\alpha _i$| and |$\hat{\alpha }_i$| is usually needed at the final iterations in order to prevent overfitting and to assure simultaneous convergence of all the methods (see lines 11–15 of Algorithm 1 below). Convergence is controlled through the root-mean-square (RMS) values of the covariance-weighted data misfits:

and the relative mean misfits between the models and the auxiliary variables:

Parameters |$\alpha _{i,0}$| and |$\hat{\alpha }_i$| are problem-dependent and are selected in such a way that the effects of coupling and regularization are maximized while acceptable values of |$\text{RMS}_i$| and |$r_i$| are reached. Moreover, |$\alpha _{i,0}$| control relative importance of the individual methods in the joint inversion. Practical aspects of this are discussed in Section 5.1 .

The resulting inversion scheme is summarized below as Algorithm 1 .

Decoupling minimization problems for the different data misfit functionals simplifies programming and allows each inverse subproblem to be solved using both numerical grid and optimization method tailored to the specific physics. Compared to the BCD, Algorithm 1 does not require implementation of |$\mathcal {R}$| on the side of each inversion subproblem. Another advantage over the BCD is that the steps in different |$\mathbf {m}_i$| can be taken simultaneously, that is the inverse problems can be run in parallel. The linking terms act as the standard quadratic ‘damping + smoothing’ stabilizers and the information exchange between the subproblems is performed by means of the reference models, thus most existing (separate) inversion codes can be used without any modification. With |$N\!=\!1$|⁠ , Algorithm 1 effectively changes regularization in an existing inversion code. Similarly, isolation of the coupling-regularization subproblem simplifies its implementation and modification and allows the use of tailored optimization methods. Strategies of Um et al . ( 2014 ) and Gao & Zhang ( 2018 ) demonstrate a similar level of decoupling, but instead of variable splitting they essentially rely on sequential minimization of components of the joint objective function: decoupled inversions are restarted from the models that are ‘preconditioned’ by minimization of cross-gradient with damping. Another similar strategy, although restricted to the case of explicit petrophysical relationships between the models, is that of Heincke et al . ( 2017 ) and Kamm et al . ( 2015 ).

Here we give several illustrative examples of |$\mathcal {R}(\mathbf {u})$|⁠ , focusing on the more universal structural priors.

For discretization of the regularization-coupling subproblem, we use a ‘voxel’ regular grid with step h and |$M=M_x \times M_y \times M_z$| cells. With ( ⁠|$\mathbf {x}_1,\mathbf {x}_2, \dots , \mathbf {x}_M$|⁠ ) being lexicographically ordered coordinates |$\mathbf {x}_{i,j,k}=(x_i,y_j,z_k)$| of the cell centres, the multiparameter model vector is defined as follows:

Partial derivatives are approximated by forward differences and zero Neumann boundary conditions are applied:

which we write in matrix form as |$\partial _x u_i \approx \mathbf {D}_x \mathbf {u}_i$|⁠ , and analogously for y and z directions.

To update |$\bf u$| at each inner iteration of Algorithm 1, the following system of linear equations is solved:

where |$\mathbf {H}_{\mathcal {R}}$| is some approximation of the Hessian of |$\mathcal {R}$|⁠ , |${\bf A}=\operatorname{diag}[\alpha _i] \otimes \mathbf {I}$|⁠ , |$\mathbf {I}$| is |$M \times M$| identity matrix and |$\otimes$| denotes Kronecker product. Then, |$\mathbf {u} \leftarrow \mathbf {u} + \mu \delta \mathbf {u}$| with the step length |$\mu \le 1$| determined by backtracking line search. Here we focus on Gauss–Newton-like forms of eq. ( 13 ), as from our experience they combine ease of implementation with reasonable efficiency; the provided expressions for the gradient can be used to implement gradient-based and quasi-Newton schemes.

3.1 Joint total variation

Total variation (TV) regularization is efficient in many inverse problems because of its edge-preserving properties (Rudin et al . 1992 ). The TV is defined as |$\ell _1$| norm of the magnitude of the model’s gradient; in order to make the absolute value differentiable at zero it is commonly ‘smoothed’ using a small positive constant |$\beta$|⁠ :

TV of the multiparameter model |$\bf u$| can be defined simply as a sum of TV functionals of the individual models: |$\mathcal {R_{\text{TV}}} ({\bf u}) = \sum _i \mathcal {R_{\text{TV}}} ({\bf u}_i)$|⁠ .

Another way to generalize TV to the multiparameter model case is by using the |$\ell _{1,2}$| mixed norm: taking |$\ell _2$| norm of the vector |$[|\nabla u_0|,|\nabla u_1|, \dots , |\nabla u_{N\!-\!1}|]^{\mathrm{T}}$| at each spatial position and then |$\ell _1$| norm of the result gives functional known as colour, vectorial or joint total variation (JTV, Blomgren & Chan 1998 ; Haber & Holtzman Gazit 2013 ; Crestel et al . 2018 ). We use a slightly generalized, weighted version of JTV:

where |$\mathbf {W}_i = \operatorname{diag}[w_{i,x},w_{i,y},w_{i,z}]$|⁠ , |$w_{i,\xi }\gt 0$|⁠ . This functional is convex (see the references above) and thus a stabilizing functional according to Tikhonov & Arsenin ( 1977 ), at the same time it introduces coupling between the models by aligning their edges , that is local maxima of the magnitude of the gradient. The coupling property of JTV can be illustrated by the following example: consider |$\bf u$| consisting of two piecewise constant models with the jumps of unit amplitude and with unit values of the total variation; it is clear that if the jumps in the two models are disjoint, then |$\mathcal {R_{\text{JTV}}} ({\bf u}) = 2$|⁠ , but if instead they are fully coincident, |$\mathcal {R_{\text{JTV}}} ({\bf u}) =\sqrt{2}$|⁠ .

A simple and relatively efficient way to minimize TV and JTV functionals is by using the iteratively reweighted least squares (IRLS) method (Vogel & Oman 1996 ; Molodtsov & Troyan 2017 ). It leads to an approximation of the Hessian of JTV that is block-diagonal, that is system ( 13 ) is decoupled into the following N systems:

and |$g_{w;i,j} = \sqrt{w_{i,x} [\mathbf {D}_x \mathbf {u}_i]_j^2 + w_{i,y} [\mathbf {D}_y \mathbf {u}_i]_j^2 + w_{i,z} [\mathbf {D}_z \mathbf {u}_i]_j^2}$|⁠ .

Matrix |$\mathbf {L}_{w;i}$| can be viewed as a finite-difference diffusion operator with anisotropic (due to the weighting |$\mathbf {W}_i$|⁠ ) diffusivity that depends on the |$\mathbf {u}$| computed at the previous IRLS iteration. The edges (large |$g_{w;i,j}$|⁠ ) locally reduce all the diffusivities and in this way persist between the iterations, resulting in edge-preserving smoothing (similar to TV), and between the models, resulting in coupling. It follows that coincident edges are more resistant to smoothing, but new edges can only be introduced by |$\mathbf {u}_{\text{ref}}$|⁠ , that is by the data.

Because systems ( 16 ) are symmetric positive definite, they can be efficiently solved by the preconditioned conjugate gradient (PCG) method. We use Jacobi preconditioner and, as usual in Gauss–Newton-like schemes (see, e.g. Nocedal & Wright 1999 ), terminate PCG early by setting relative tolerance to 0.001–0.01. The condition number of the system depends on |$\beta$|⁠ ; if |$\beta$| is too small (and when |$\alpha _i$| are small) PCG may stagnate. We find that, given the model gradients are reasonably scaled (see below), |$\beta =10^{-7}$| provides a good balance between PCG convergence rate and the accuracy of |$\ell _1$| norm approximation.

Scaling of the models, which represent different physical quantities, is important for efficient coupling; apart from the bounding transforms that are discussed below, it is achieved by defining |$\mathbf {W}_i = s_i^{-1} \operatorname{diag}[w_x,w_y,w_z]$|⁠ , where |$s_i$| is the RMS magnitude of the gradient of |$\mathbf {u}_{\text{ref},i}$|⁠ . Similarly to the classical |$\ell _2$| -norm regularization case (e.g. Li & Oldenburg 1998 ), constants |$w_x=w_y \approx 10$| and |$w_z=1$| usually work well for ‘subhorizontal’ structures, while some scenarios with steeply dipping geology may benefit from |$w_z \gt w_x = w_y$|⁠ .

3.2 Joint minimum support

For linear inverse problems, regularization based on the |$\ell _1$| norm leads to sparse solutions (Loris et al . 2007 ). Similarly, the |$\ell _{1,2}$| mixed norm promotes joint sparsity—same sparsity pattern between the individual model vectors (e.g. Gramfort et al . 2012 ). These approaches are particularly efficient because the corresponding stabilizers are convex. Non-convex stabilizers are more problematic from the optimization standpoint, but have stronger sparsity-promoting properties; a well-known example is the minimum support (MS) functional introduced by Last & Kubik ( 1983 ) and generalized by Portniaguine & Zhdanov ( 1999 ):

With |$\beta \rightarrow 0$|⁠ , it approximates the volume of the regions of |$\Omega$| where |$u_i$| deviates from a (known) background model |$u_{b;i}$|⁠ , that is the volume of the support of |$u_i ({\bf x}) - u_{b;i} ({\bf x})$|⁠ . In the multiparameter case, by analogy with mixed norms, we arrive at the joint minimum support (JMS) functional (Molodtsov & Troyan 2017 ):

Similarly to the |$\ell _{1,2}$| norm, JMS is a stabilizing functional and introduces coupling through joint sparsity. The coupling property follows from the fact that the integrand of eq. ( 19 ), the function |$t \mapsto t/(t+\beta )$| with |$t \ge 0$|⁠ , is subadditive. JMS regularization tends to ‘focus’ the models |$u_i - u_{b;i}$| such that they have the same support, which can be especially useful in time-lapse problems. It was applied to magnetic, gravity and marine controlled-source electromagnetic data (Jorgensen & Zhdanov 2021 ; Tu & Zhdanov 2022 ).

To illustrate the behaviour of JMS, let us consider an ‘inverse problem’ with one data point |$d=f(\mathbf {m}_0)$| and two model parameters |$\mathbf {m}_0=(m_{0,1},m_{0,2})$| representing two voxels and let |$\mathbf {m}_1=(m_{1,1},m_{1,2})$| be a ‘fixed’ reference model. JMS of |$\mathbf {m}_0$| and |$\mathbf {m}_1$| (with zero background models and |$\beta =0.001$|⁠ ) is plotted in Fig. 1 : at |$\mathbf {m}_1 \!=\! \mathbf {0}$|⁠ , JMS regularization selects two sparse solutions to |$d=f(\mathbf {m}_0)$|⁠ , but as we move away from zero along |$m_{1,1}$|⁠ , only the solution having the same sparsity pattern as |$\mathbf {m}_1$| remains.

$Joint minimum support (JMS) of two 2-D model vectors $\mathbf {m}_0 = (m_{0,1}, m_{0,2})$ and $\mathbf {m}_1 = (m_{1,1}, m_{1,2})$ plotted as a function of $\mathbf {m}_0$ for four different values of $\mathbf {m}_1$. Minimization of JMS under the constraint $d = f(\mathbf {m}_0)$ (black line) leads to sparse $\mathbf {m}_0$ with the same sparsity pattern as $\mathbf {m}_1$.$

Joint minimum support (JMS) of two 2-D model vectors |$\mathbf {m}_0 = (m_{0,1}, m_{0,2})$| and |$\mathbf {m}_1 = (m_{1,1}, m_{1,2})$| plotted as a function of |$\mathbf {m}_0$| for four different values of |$\mathbf {m}_1$|⁠ . Minimization of JMS under the constraint |$d = f(\mathbf {m}_0)$| (black line) leads to sparse |$\mathbf {m}_0$| with the same sparsity pattern as |$\mathbf {m}_1$|⁠ .

Minimization of JMS can be carried out using IRLS (by analogy with MS, following Last & Kubik ( 1983 ) and Portniaguine & Zhdanov ( 1999 )). In the vicinity of a model |$\mathbf {u}^{(k)}$| found at IRLS iteration k , (eq. 19 ) is approximated by a quadratic functional:

Substituting it into the eq. ( 13 ) and taking unit step length, we get an explicit formula for the updated model vector components:

for |$i=0,\dots ,N\!-\!1$|⁠ , |$j=1,\dots ,M$|⁠ . JMS is straightforward to modify to include scaling of the models similarly to JTV (but with the coefficients |$s_i$| equal to RMS values of |$\mathbf {u}_{\text{ref},i} - \mathbf {u}_{b;i}$|⁠ ).

3.3 Modifications of cross-gradient

The cross-gradient constraint of Gallardo & Meju ( 2003 ) can be imposed, for a pair of models, by minimizing |$\ell _2$| norm of the cross product of the model gradients:

The cross product is zero if the gradients (and, consequently, the level sets of the models) are parallel or if a gradient vanishes. The latter means that the constraint is rather inefficient for piecewise-constant models and also demonstrates that (eq. 23 ) is not a stabilizing functional. JTV, on the other hand, does not efficiently couple smooth models since diffusivity in eq. ( 17 ) depends only on the magnitude of the gradients. Naturally occurring models are usually combinations of the smooth and the piecewise constant cases, so it seems reasonable to use JTV as a stabilizing functional for the cross-gradient. Considering all pairs of the models and introducing for each pair a positive weighting coefficient |$\gamma _{ij}$|⁠ , we have

The gradient of eq. ( 24 ) consists of the blocks

where |$\mathbf {r}_{ij,\xi }$| is the discretized |$\xi$| component of |$\nabla u_j \times (\nabla u_i \times \nabla u_j)$|⁠ . Using Gauss–Newton approximation for the cross-gradient terms, the Hessian of eq. ( 24 ) is approximated by

The resulting linear system ( 13 ) is solved by the PCG analogously to the JTV case, the main difference is that the search directions |$\delta \mathbf {u}_i$| for the individual models are now coupled.

Denoting by |$\theta$| the angle between the two gradients, we can factorize the cross-gradient as follows:

The first two factors zero the cross-gradient when the corresponding gradient vanishes, the third factor—when the gradients are antiparallel and the fourth—parallel. In many cases, the sign |$\sigma _{ij}$| of correlation between the two reconstructed properties is known a priori and this information should be incorporated into the coupling constraints. This can be done (following Molodtsov et al . 2011 ) by selecting either the ‘parallel’ or the ‘antiparallel’ factor of eq. ( 29 ) and taking |$\ell _2$| norm of the result, which leads to the one-way cross-gradient functional:

where |$\sigma _{ij} = \pm 1$|⁠ . Minimization of this functional with |$\sigma _{ij}=1$| forces model gradients to be parallel, with |$\sigma _{ij}=-1$| – antiparallel and in both cases the gradients are free to vanish.

The gradient and Gauss–Newton approximation to the Hessian of eq. ( 30 ) are given by the following expressions:

where |$\mathbf {r}_{ij}$| is the discretized |$|\nabla u_i| |\nabla u_j| - \sigma _{ij} \nabla u_i \cdot \nabla u_j$|⁠ ,

and |$g_{i,k} = \sqrt{\sum _\xi [\mathbf {D}_\xi \mathbf {u}_i]_k^2 + \beta }$|⁠ . These expressions are substituted into eqs ( 25 ) and ( 26 ) when some of the cross-gradient terms in the functional ( 24 ) are replaced by eq. ( 30 ).

Regularization and coupling can be easily generalized by appending fixed models to the vector |$\mathbf {u}$|⁠ , for example in order to use geological or legacy geophysical models as a structural reference. Extra regularization (such as ‘damping’ towards a reference model) and coupling (such as ad hoc petrophysical relations, as demonstrated in the numerical example in Section 5.2 ) terms are often required when dealing with real data and are straightforward to implement.

Here we outline the implementation of the inversion subproblems used in the numerical examples.

3-D MT inversion is performed using the nonlinear conjugate gradient (NLCG) method implemented in the ModEM software package (Kelbert et al . 2014 ). Resistivity is discretized on a non-uniform rectangular grid, with the cells increasing in size with the decay of the MT resolution with depth and laterally outside of the data-covered area; the model vector |$\mathbf {m}$| is formed from the natural logarithm of the cells’ resistivities. Regularization in ModEM has the form |$(\mathbf {m} - \mathbf {m}_{\text{ref}})^{\mathrm{T}} \mathbf {C}_m^{-1} (\mathbf {m} - \mathbf {m}_{\text{ref}})$|⁠ , with the model covariance |$\mathbf {C}_m$| implemented as a first-order autoregressive smoothing operator; it can be shown (Yanovskaya & Ditmar 1990 ; Xu 2005 ) that it is equivalent to a squared |$W^1_2$| Sobolev norm. NLCG iterations are performed in transformed model space |$\tilde{\mathbf {m}} = \mathbf {C}_m^{-1/2} (\mathbf {m} - \mathbf {m}_{\text{ref}})$|⁠ . In |$\mathbf {u}$|⁠ , a logarithmic resistivity vector is used, so |$\mathbf {m}$| is transformed to |$\tilde{\mathbf {m}}$| and back at each outer iteration of Algorithm 1. To make use of conjugacy, several NLCG iterations are needed at each outer iteration; at the same time, for the alternating minimization with continuation, this number should not be too large. In our experiments, five iterations were sufficient for a satisfactory convergence rate.

Seismic first-arrival traveltime tomography (FATT) is implemented using the Gauss–Newton method, a single iteration of which is performed at each outer iteration of Algorithm 1. Velocity |$v_p$| is defined over a voxel grid. The forward problem is solved by the 3-D finite-difference method of Podvin & Lecomte ( 1991 ) and its Jacobian is computed using our implementation of the ‘backtracking’ ray tracing, principle of which is described in the same paper; normal equations are solved by PCG; computations are parallelized over the sources. Inversion (as well as regularization and coupling) is performed in the transformed model domain, with the transform

which guarantees that the slowness |$s=1/v_p$| lies within the predefined interval |$(s_{\min }, s_{\max })$|⁠ . Details on the bounding transform eq. ( 34 ) can be found in Commer & Newman ( 2008 ).

Our implementation of 3-D gravity inversion is based on the works of Li & Oldenburg ( 1998 , 2003 ). A single Gauss–Newton iteration with PCG as a linear solver is performed at each outer iteration of Algorithm 1. The model is discretized with a non-uniform rectangular grid and analytical expressions for the gravity field of a constant-density rectangular prism are used to precompute the sensitivity matrix. Each row of the sensitivity matrix is compressed using a 3-D discrete wavelet transform (DWT) with the D4 Daubechies wavelet. Trade-off between the compression ratio and the forward problem accuracy is controlled by setting the relative error of the sensitivity reconstruction. The depth (or distance) weighting (Li & Oldenburg 1998 ) is applied prior to the compression; in addition to improving the recovery of deep structures, it also reduces the dynamic range of the sensitivity thus reducing the compression artefacts. Inversion is performed in the depth/distance-weighted model space, but the vector |$\mathbf {u}_i$| is unweighted, that is the weighting is only applied to the linking terms in the inversion subproblem. To constrain the density range, instead of a logarithmic barrier method used by Li & Oldenburg ( 2003 ), we use the bounding transform eq. ( 34 ).

Trilinear interpolation is used for |$\mathbf {P}_i$|⁠ , |$\mathbf {Q}_i$|⁠ , which is quite efficient when all the grids are rectangular. In case of a mismatch between the regions |$\Omega$| and |$\Omega _i$|⁠ , nearest-neighbour extrapolation is invoked and the interpolation-extrapolation result m is smoothly merged with the prior (or initial) model |$m_0$| outside the interpolation region via a sigmoid function s centred on the regions boundary as |$m \leftarrow sm + (1-s)m_0$|⁠ .

5.1 Example 1: time-lapse seismic–gravity joint inversion using JMS regularization

Joint inversion attempting to reconstruct compact, highly (co)localized features can be efficiently performed with the help of the joint minimum support regularization. To demonstrate this, we consider a simple synthetic example combining time-lapse FATT and full-tensor gravity gradiometry (FTG). Seismic tomography is widely used for time-lapse applications at various scales (e.g. Patanè et al . 2006 ; Ajo-Franklin et al . 2007 ; Hilbich 2010 ). The feasibility of time-lapse applications of FTG was studied, for example by Droujinine et al . ( 2007 ) and by Reitz et al . ( 2015 ); in this example, we use six components of the gravity gradient tensor ( ⁠|$U_{xx}$|⁠ , |$U_{yy}$|⁠ , |$U_{zz}$|⁠ , |$U_{xy}$|⁠ , |$U_{xz}$|⁠ , |$U_{yz}$|⁠ ) and the vertical gravity component |$U_z$|⁠ .

Using notation introduced in Section 2 , let us consider two experiments–FATT ( ⁠|$i=0$|⁠ ) and FTG ( ⁠|$i=1$|⁠ ), both performed twice—at time |$t_0$| and |$t_1$|⁠ :

In the context of time-lapse inversion, the states at |$t_0$| and |$t_1$| are usually referred to as baseline and monitor, respectively. If the data acquisition geometry stays constant, it is advantageous to work with the difference of monitor and baseline data, |$\Delta \mathbf {d}_i = \mathbf {d}_i(t_1) - \mathbf {d}_i(t_0)$|⁠ . A common strategy is: (1) find |$\mathbf {m}_i(t_0)$| by inverting baseline data and (2) find the model temporal perturbation |$\Delta \mathbf {m}_i$| by minimizing the double-difference data misfit functional (Waldhauser & Ellsworth 2000 ):

Given smallness of |$\Delta \mathbf {m}_i$|⁠ , the second step is relatively fast and both observational and modelling systematic errors are cancelled in eq. ( 36 ), increasing sensitivity to the temporal changes, compared with a straightforward sequential inversion of baseline and monitor data. The gravity forward problem is linear with respect to the density, so for the FTG inversion, eq. ( 36 ) simplifies to

that is there is no need for the baseline density model if we are only interested in the temporal changes of density. Thus, after the reconstruction of the baseline velocity, which we perform by stand-alone FATT, time-lapse joint inversion reduces to the problem ( 7 ), in which the unknown models |$\mathbf {m}_i$| are replaced with |$\Delta \mathbf {m}_i$|⁠ . Nevertheless, baseline gravity data can still be used in a scenario where baseline velocity model can be improved by joint inversion with gravity.

The SEG/EAGE Overthrust Model (Aminzadeh et al . 1997 ) is used as the baseline velocity model. The time-lapse velocity perturbation is a 1 km s −1 cube with a 600 m edge, positioned horizontally at the centre of the model, at 1825 m depth (Fig. 2a ). The true models are discretized by a regular cubic grid with 50 m spacing. 50 sources and 900 receivers are placed over a regular grid at 25 m depth (Fig. 2a ); every source is registered by all the receivers. In the FTG problem, we directly model the time-lapse data difference. The density perturbation is 0.1 g cm −3 cube coincident with the velocity perturbation. Because there is no baseline density and discretizations of FTG and FATT are independent, a smaller grid can be used for density as shown in Fig. 2(b) . The grid consists of a uniform core with 100 m horizontal and 90 m vertical steps padded at the lateral edges by three padding layers expanding by a factor of two, a total of |$64^3$| cells. Vertical gravity and the gravity gradient components are calculated at |$13^2$| points at 10 m height (Fig. 2b ). Synthetic data are contaminated with Gaussian noise with the standard deviation of 1 ms for the traveltimes, 1 μGal for the gravity and 1 mE for the gravity gradient.

Time-lapse inversion. (a) True monitor ( ⁠|$t_1$|⁠ ) velocity model; locations of seismic sources and receivers are shown by big and small dots, respectively. (b) Corresponding density model (the time-lapse change) and FTG data locations; two faces display the model grid. (c) Baseline ( ⁠|$t_0$|⁠ ) velocity model recovered by FATT.

Gravity inversion is performed on the same grid that is used for generating the synthetic data. However, in the inversion, unlike in the synthetic data calculation, the sensitivity is compressed using DWT with the relative reconstruction error of 1 per cent, resulting in the compression ratio of 58; the depth weighting is set proportional to |$1/z$|⁠ . For the tomography, the model region that was used for the forward modelling is rediscretized with a 100 m step. Bounding transform eq. ( 34 ) is applied to the models such that |$v_p \in (0.2, 6.5)$| km s −1 and the density |$\sigma \in (-0.2, 0.2)$| g cm −3 . Baseline traveltimes are inverted using Algorithm 1 with the TV regularization; initial model is 1-D, velocity linearly increases with depth from 2 to 6 km s −1 ; reconstructed baseline model is shown in Fig. 2(c) . The subsequent time-lapse inversion is essentially a simple ‘spike test’ (in which FTG problem is linear, but FATT is, of course, nonlinear and depends on the baseline).

Regularization for the time-lapse inversion is chosen based on the assumption that the volume of the support of the temporal changes is much smaller than the whole model volume—this corresponds to the MS functional (eq. 18 ) for separate inversions and the JMS functional (eq. 19 ) for joint inversion. The regularization-coupling grid is identical to the FATT inversion grid ( ⁠|$200 \times 200 \times 46$| cells, 100 m spacing).

To assess the coupling effect of JMS regularization separately from its regularizing effect and to quantify the degree of alignment of the reconstructed anomalies, we introduce the following quantity:

Given that the anomalous part of |${\bf u}$| does not vanish everywhere, it follows from the definitions of MS and JMS functionals that |$1/N \le \gamma ({\bf u}) \le 1$| (recall that |$\mathcal {R}_{\text{MS}}$| approximates the volume of the support of an individual model and |$\mathcal {R}_{\text{JMS}}$| —that of the multiparameter model, i.e. volume of the union of the individual supports). The upper bound, |$\gamma ({\bf u}) = 1$|⁠ , corresponds to fully disjoint anomalies, whose supports do not intersect, and the lower bound, |$1/N$|⁠ ,—to full alignment, when the supports of all N anomalies are identical.

To determine the regularization parameters |$\alpha _i$| (to simplify the notation, instead of writing |$\alpha _{i,0}$| we will understand |$\alpha _i$| as the initial values) and |$\hat{\alpha _i}$|⁠ , we use the following strategy:

1. Determine |$\hat{\alpha _0}$|⁠ , |$\hat{\alpha _1}$|⁠ . For each method, run a series of separate inversions with fixed |$\mathbf {m}_{\text{ref},i}$| (i.e. Algorithm 1 without the coupling-regularization step) and varying |$\hat{\alpha _i}$| and select its optimal value according to the Occam/discrepancy principle—maximum |$\hat{\alpha _i}$| for which |$\text{RMS}_i \approx 1$|⁠ .

2. Determine |$\alpha _0$|⁠ , |$\alpha _1$|⁠ . A reasonable starting point is |$\alpha _i = \hat{\alpha _i}$|⁠ . Run a series of joint inversions with varying |$\alpha _i$| and select those that return minimum values of |$\mathcal {R}$| (of course, while the inversion converges in |$\text{RMS}_i$| and |$r_i$|⁠ ). Such combinations of |$\alpha _i$| are, in general, non-unique. At the same time, we usually want to equalize contributions of the methods/data sets to the joint inversion as much as possible. Since the inverse problems are decoupled, relative weights of the data sets are primarily controlled by |$\alpha _i$| and not |$\hat{\alpha _i}$|⁠ : increasing |$\alpha _i$| increases the influence of i th data set on the joint inversion. It follows that good balance between the data sets can be achieved through similar final values of |$r_i$|⁠ .

The values of |$\hat{\alpha _i}$| selected with separate inversions ensure convergence of the joint inversion in the data RMS; however, since in joint inversion, |$\mathbf {m}_{\text{ref},i}$| are no longer fixed but move towards |$\mathbf {m}_i$|⁠ , it is usually possible to increase |$\hat{\alpha _i}$| slightly (usually less than by an order of magnitude) to enhance the regularization and coupling. In the current example we simply use the values found at the step 1: |$\hat{\alpha _0} = 100$| and |$\hat{\alpha _1} = 10^8$|⁠ .

With the |$\hat{\alpha _i}$| fixed, we perform grid search for |$\alpha _0$| and |$\alpha _1$|⁠ . For the purpose of finding the optimal parameters, full grid search is redundant, here it serves the illustrative purpose. By changing |$\alpha _i$| by an order of magnitude, we build a 15 |$\times$| 15 logarithmic grid, centred roughly on ( ⁠|$\hat{\alpha _0}$|⁠ , |$\hat{\alpha _1}$|⁠ ). At each grid point |$(\alpha _0, \alpha _1)$|⁠ , we run the joint inversion with the maximum number of outer iterations set to 30, |$q=2$| and the number of the coupling-regularization iterations |$n_{\text{itn}}=100$|⁠ . To slightly optimize the search, if joint inversion does not reach the target value of |$r_0$|⁠ , then the current |$\alpha _0$| is deemed too low and exploration of the current column of the grid is terminated, and analogously for |$r_1$| and the respective rows. Fig. 3 shows the grid with the final values of JMS, |$\gamma (\mathbf {u})$|⁠ , |$\text{RMS}_0$|⁠ , |$\text{RMS}_1$|⁠ , |$r_0-r_1$| and the iteration count. For each i , as expected, as |$\alpha _i$| increases, |$r_i$| and |$\text{RMS}_i$| decrease and JMS increases. We are interested in the minimum of JMS and, to balance FTG and FATT, |$r_0 \approx r_1$|⁠ . The region satisfying these criteria, outlined by the rectangle in Fig. 3 , is explored with a finer grid, with a factor of two step (Fig. 4 ). This time we use |$q=1.5$|⁠ , which increases the iteration count and, since the maximum number of iterations is unchanged, shifts the region of convergence towards larger |$\alpha _i$|⁠ . At the expense of more iterations, reducing q usually improves the inversion results. As we see from the fine grid, the quantities vary smoothly enough that determining |$\alpha _i$| to an order of magnitude should give satisfactory results.

$Scanning the initial values of $\alpha _0$ and $\alpha _1$ (index 0 corresponds to FATT, 1–to FTG) for JMS-regularized joint inversion, using grid with the step of a factor of ten; $\hat{\alpha _0} = 100$, $\hat{\alpha _1} = 10^8$, the outer iterations limit is set to 30 and $q=2$. Final values of (a) $\mathcal {R_{\text{JMS}}}$, (b) $\gamma$, (c) the iteration count, (d) $r_0-r_1$, (e) RMS$_0$ and (f) RMS$_1$. Hatching indicates positions where the inversion fails to converge; unexplored areas are grey. We are interested in minimizing $\mathcal {R_{\text{JMS}}}$ and $\gamma$ and, if there is no reason to prioritize either FATT or FTG, we also want $r_0 \approx r_1$. The region of interest, sampled with a finer grid in Fig. 4, is outlined by the rectangle.$

Scanning the initial values of |$\alpha _0$| and |$\alpha _1$| (index 0 corresponds to FATT, 1–to FTG) for JMS-regularized joint inversion, using grid with the step of a factor of ten; |$\hat{\alpha _0} = 100$|⁠ , |$\hat{\alpha _1} = 10^8$|⁠ , the outer iterations limit is set to 30 and |$q=2$|⁠ . Final values of (a) |$\mathcal {R_{\text{JMS}}}$|⁠ , (b) |$\gamma$|⁠ , (c) the iteration count, (d) |$r_0-r_1$|⁠ , (e) RMS |$_0$| and (f) RMS |$_1$|⁠ . Hatching indicates positions where the inversion fails to converge; unexplored areas are grey. We are interested in minimizing |$\mathcal {R_{\text{JMS}}}$| and |$\gamma$| and, if there is no reason to prioritize either FATT or FTG, we also want |$r_0 \approx r_1$|⁠ . The region of interest, sampled with a finer grid in Fig. 4 , is outlined by the rectangle.

$Same as in Fig. 3, but using a factor of two grid step to sample the central region of interest and with $q=1.5$. Note that decreasing q from 2 to 1.5 increases the iteration count and shifts the region of convergence towards higher $\alpha _i$, however, other quantities are less affected. Point ($6 \times 10^4, 10^{10}$) marked with ‘+’ corresponds to the models shown in Figs 6 c–d and point ($10^5, 10^8$) marked with ‘$\Delta$’ corresponds to the models shown in Fig. 5 and Figs 6 e–f.$

Same as in Fig. 3 , but using a factor of two grid step to sample the central region of interest and with |$q=1.5$|⁠ . Note that decreasing q from 2 to 1.5 increases the iteration count and shifts the region of convergence towards higher |$\alpha _i$|⁠ , however, other quantities are less affected. Point ( ⁠|$6 \times 10^4, 10^{10}$|⁠ ) marked with ‘+’ corresponds to the models shown in Figs 6 c–d and point ( ⁠|$10^5, 10^8$|⁠ ) marked with ‘ |$\Delta$| ’ corresponds to the models shown in Fig. 5 and Figs 6 e–f.

The minimum of |$\mathcal {R_{\text{JMS}}}$| is associated with FATT dominating FTG (Figs 4a and d ), which is consistent with the overall higher resolution of FATT. For the point |$(10^5, 10^8)$| in this region, marked with ‘ |$\Delta$| ’ in Fig. 4 , the reconstructed velocity and density models are shown in Figs 5 and 6(e) and (f) . Best balance between FTG and FATT, in terms of the smallest |$|r_0 - r_1|$|⁠ , along the |$\mathcal {R_{\text{JMS}}}$| valley bottom is reached at the point |$(6 \times 10^4, 10^{10})$| marked with ‘+’ in Fig. 4 ; the corresponding models are shown in Figs 6(c) and (d) .

$Time-lapse perturbations of (a) velocity and (b) density recovered by joint FATT–FTG inversion with JMS regularization, using initial $\alpha _0 = 10^5$, $\alpha _1 = 10^8$ and $q=1.5$. Axes mark the full extent of the inversion grids; true structure is shown by the green outline.$

Time-lapse perturbations of (a) velocity and (b) density recovered by joint FATT–FTG inversion with JMS regularization, using initial |$\alpha _0 = 10^5$|⁠ , |$\alpha _1 = 10^8$| and |$q=1.5$|⁠ . Axes mark the full extent of the inversion grids; true structure is shown by the green outline.

$A close view of the reconstructed velocity and density perturbations. (a–b) Separate inversions with MS regularization, $\alpha _0 = 10^6$, $\alpha _1 = 10^{10}$ and $n_{\text{itn}}=100$. Joint inversion with JMS regularization: (c–d) $\alpha _0 = 6 \times 10^4$, $\alpha _1 = 10^{10}$, $n_{\text{itn}}=100$, (e–f) $\alpha _0 = 10^5$, $\alpha _1 = 10^8$, $n_{\text{itn}}=100$ (same models as in Fig. 5) and (g–h) $\alpha _0 = 10^5$, $\alpha _1 = 10^8$, $n_{\text{itn}}=5$. True structure is shown by the green outline.$

A close view of the reconstructed velocity and density perturbations. (a–b) Separate inversions with MS regularization, |$\alpha _0 = 10^6$|⁠ , |$\alpha _1 = 10^{10}$| and |$n_{\text{itn}}=100$|⁠ . Joint inversion with JMS regularization: (c–d) |$\alpha _0 = 6 \times 10^4$|⁠ , |$\alpha _1 = 10^{10}$|⁠ , |$n_{\text{itn}}=100$|⁠ , (e–f) |$\alpha _0 = 10^5$|⁠ , |$\alpha _1 = 10^8$|⁠ , |$n_{\text{itn}}=100$| (same models as in Fig. 5 ) and (g–h) |$\alpha _0 = 10^5$|⁠ , |$\alpha _1 = 10^8$|⁠ , |$n_{\text{itn}}=5$|⁠ . True structure is shown by the green outline.

For separate inversion with MS regularization, grid search results in |$\alpha _0 = 10^6$| and |$\alpha _1 = 10^{10}$|⁠ , and the corresponding reconstructed models are shown in Figs 6(a) and (b) . Not surprisingly, FTG inversion correctly positions the density anomaly in the horizontal plane but not vertically and its upward displacement is compensated by its greatly reduced amplitude. Joint inversion with |$\alpha _0 = 6 \times 10^4$| and |$\alpha _1 = 10^{10}$| (the best FTG–FATT balance) moves the density anomaly downwards (Figs 6c and d ), but both velocity and density anomalies are poorly focused, as a result of the trade-off in JMS. Increasing the relative weight of FATT by moving down the valley of |$\mathcal {R_{\text{JMS}}}$| to |$\alpha _0 = 10^5$|⁠ , |$\alpha _1 = 10^8$| results in both anomalies satisfactorily aligned and positioned (Figs 6e and f ); note the stronger focusing of the velocity anomaly compared to the separate FATT inversion.

Fig. 7 shows the progress of the inversions corresponding to the models in Fig. 6 , in terms of |$\text{RMS}_i$|⁠ , |$r_i$|⁠ , |$\gamma ({\bf u})$| and |$\mathcal {R_{\text{JMS}}}$|⁠ . The target RMS values are reached after the first few iterations, after which the models and the auxiliary variables continue to be gradually brought together by increasing |$\alpha _i$| until their relative difference |$r_i$| reaches the target value of 0.1. Note that FATT is ahead of FTG in terms of |$r_i$|⁠ , except in Fig. 7(b) where they converge simultaneously. While the stabilizer, |$\mathcal {R_{\text{JMS}}}$|⁠ , is being minimized, the structure of |$\mathbf {u}$| develops (by the transfer from |$\mathbf {m}_i$|⁠ ), resulting in the overall growth of |$\mathcal {R_{\text{JMS}}}$|⁠ . At the same time, in the joint inversions, |$\gamma ({\bf u})$| decreases as the support of the anomalies becomes more similar. In the MS-regularized separate inversion (Fig. 7a ), the values of |$\mathcal {R_{\text{JMS}}}$| are similar, but |$\gamma ({\bf u})$| stays close to 1 as the anomalies are almost disjoint (Figs 6a and b ). Note that the points of the |$\gamma ({\bf u})$| and |$\mathcal {R_{\text{JMS}}}$| curves correspond to the inner IRLS iterations of the coupling-regularization subproblem. The sawtooth-like appearance of these curves is a result of the continuation—at each following outer iteration, IRLS starts with new |$\mathbf {u}_{\text{ref}}$| and higher values of |$\alpha _i$|⁠ , the increased relative weight of the linking terms causes a jump in |$\mathcal {R_{\text{JMS}}}$|⁠ . With |$n_{\text{itn}} = 100$|⁠ , we can clearly see the convergence of the IRLS. Terminating the IRLS very early with |$n_{\text{itn}} = 5$| (Fig. 7d ) results in higher final value of |$\mathcal {R_{\text{JMS}}}$|⁠ , which is manifested as somewhat smoother models in Figs 6(a) and (b) , but the coupling remains satisfactory, both visually and as indicated by |$\gamma ({\bf u})$|⁠ .

$Progress of the inversions whose final models are shown in Fig. 6. (a) Separate inversions with MS regularization, $\alpha _0 = 10^6$, $\alpha _1 = 10^{10}$ and $n_{\text{itn}}=100$. Joint inversion with JMS regularization: (b) $\alpha _0 = 6 \times 10^4$, $\alpha _1 = 10^{10}$, $n_{\text{itn}}=100$, (c) $\alpha _0 = 10^5$, $\alpha _1 = 10^8$, $n_{\text{itn}}=100$, (d) $\alpha _0 = 10^5$, $\alpha _1 = 10^8$, $n_{\text{itn}}=5$. For $\gamma (\mathbf {u})$ and $\mathcal {R_{\text{JMS}}}$, points of the curves correspond to the inner iterations of the coupling-regularization subproblem.$

Progress of the inversions whose final models are shown in Fig. 6 . (a) Separate inversions with MS regularization, |$\alpha _0 = 10^6$|⁠ , |$\alpha _1 = 10^{10}$| and |$n_{\text{itn}}=100$|⁠ . Joint inversion with JMS regularization: (b) |$\alpha _0 = 6 \times 10^4$|⁠ , |$\alpha _1 = 10^{10}$|⁠ , |$n_{\text{itn}}=100$|⁠ , (c) |$\alpha _0 = 10^5$|⁠ , |$\alpha _1 = 10^8$|⁠ , |$n_{\text{itn}}=100$|⁠ , (d) |$\alpha _0 = 10^5$|⁠ , |$\alpha _1 = 10^8$|⁠ , |$n_{\text{itn}}=5$|⁠ . For |$\gamma (\mathbf {u})$| and |$\mathcal {R_{\text{JMS}}}$|⁠ , points of the curves correspond to the inner iterations of the coupling-regularization subproblem.

5.2 Example 2: MT–seismic–gravity joint inversion using different regularization and coupling

This example is based on a modification of MT checkerboard-type benchmark model presented in Egbert & Kelbert ( 2012 ). Electrical resistivity, P -wave velocity and density models are displayed in Fig. 8 ; the models have the same pattern except for the top checkerboard layer (with the anomalous blocks being coincident, up to the grid discretization error). The ‘checkers’ are bounded by the planes |$x,y=\lbrace -27.6,-11.7,-8.7,7.2,10.2,26.1\rbrace$| km and |$z=\lbrace 0,1,1.8,5,5.8,10.6\rbrace$| km.

$Example 2, true models showing the full-extent inversion grids and the data geometry. (a) Resistivity model and MT data locations. (b) Velocity model: section through $y=20$ km and the $\pm 0.4$ km s−1 velocity anomalies; seismic sources (green dots) and receivers. (c) Density model and gravity data locations. The regularization-coupling grid is identical to the FATT grid.$

Example 2, true models showing the full-extent inversion grids and the data geometry. (a) Resistivity model and MT data locations. (b) Velocity model: section through |$y=20$| km and the |$\pm 0.4$| km s −1 velocity anomalies; seismic sources (green dots) and receivers. (c) Density model and gravity data locations. The regularization-coupling grid is identical to the FATT grid.

The resistivity values are 10, 100 and 1000 |$\Omega \cdot$| m. The resistivity model grid contains |$66 \times 66 \times 59$| cells. It consists of the core area with the horizontal cell size of 1 km |$\times$| 1 km and four lateral padding layers. In the vertical direction, the cell size increases with depth from 50 m to 16 km. Impedance tensor and vertical magnetic transfer functions data are computed over 15 |$\times$| 15 regular grid of stations at the surface (Figs 8a and 9 ) for 12 logarithmically equispaced periods in 0.1–100 s range. Gaussian noise is added to the data, its standard deviation is 3 per cent of |$\sqrt{|Z_{xy}||Z_{yx}|}$| for all components of the impedance tensor and 0.03 for the tipper.

Slices through the core parts of the true models shown in Fig. 8 , locations of MT, seismic and gravity stations (green dots) and seismic sources (black dots). Black lines denote positions of the slices (note that 3 and 8 km horizontal slices are displayed in one subplot).

The background velocity is linearly increasing from 4 km s −1 at the surface to 6.8 km s −1 at 20 km depth, the checkerboard pattern imposes |$\pm 0.4$| km s −1 anomalies with respect to this trend; the model is discretized on a regular cubic grid with 500 m step, resulting in |$140 \times 140 \times 40$| cells. 64 sources and 225 receivers are placed at the surface over the regular grid with 8 and 4 km spacing, respectively (Figs 8b and 9 ); for each source, first arrival traveltimes are computed at all receivers within 60 km radius and contaminated with Gaussian noise with the standard deviation of 12.5 ms.

The density model contains two layers with |$\pm 0.1$| g cm −3 anomalies and is discretized into |$64^3$| cells; the cells are approximately 1 km |$\times$| 1 km |$\times$| 0.5 km in the core area, which is surrounded by two padding layers expanding with a factor of two (Figs 8c and 9 ). Vertical component of the gravity field is computed at 10 m above the surface at 225 points horizontally coinciding with the MT locations and Gaussian noise with a standard deviation of 0.1 mGal is added.

The synthetic data are inverted using Algorithm 1 with different stabilizing and coupling functionals: (a) TV, corresponding to separate inversions, (b) JTV, (c) JTV combined with the cross-gradient (XG), (d) TV combined with XG and the one-way cross-gradient (OWXG), (e) JTV combined with XG and OWXG and (f) JTV combined with XG, OWXG and a ‘petrophysics’ coupling; the corresponding reconstructed models are shown in Fig. 11 . Apart from the choice of the stabilizing and coupling functionals, all the inversions are run with the same settings, which are summarized below.

$Progress of the inversions using different regularization and coupling functionals, corresponding to the final models shown in Fig. 11: (a) TV (separate inversions), (b) JTV, (c) JTV + XG, (d) TV + (OW)XG, (e) JTV + (OW)XG, (f) JTV + (OW)XG + functional (41). For $\gamma _{\operatorname{TV}} (\mathbf {u})$ and the ‘cross-gradient’ terms, points of the curves correspond to the inner iterations of the coupling-regularization subproblem.$

Progress of the inversions using different regularization and coupling functionals, corresponding to the final models shown in Fig. 11 : (a) TV (separate inversions), (b) JTV, (c) JTV + XG, (d) TV + (OW)XG, (e) JTV + (OW)XG, (f) JTV + (OW)XG + functional ( 41 ). For |$\gamma _{\operatorname{TV}} (\mathbf {u})$| and the ‘cross-gradient’ terms, points of the curves correspond to the inner iterations of the coupling-regularization subproblem.

Slices through the core parts of the resistivity, velocity and density models reconstructed using different regularization and coupling. Each column corresponds to one inversion, with the column caption indicating the coupling-regularization functionals used. Where ‘(OW)XG’ is specified, XG is applied to resistivity–density and resistivity–velocity pairs and OWXG—to velocity–density. Dashed lines denote the true structures, solid lines in the first column—positions of the slices (note that horizontal slices combine two depth levels). In vertical slices, vertical exaggeration is 2:1.

The MT inversion is started from the homogeneous 100 |$\Omega \cdot$| m model. The number of NLCG iterations is set to five; the initial line-search step length is set to 20. The model covariance smoothing is applied twice with the factor 0.3 along each coordinate axis. FATT is started from the 1-D model corresponding to the true background velocity trend, with the model transform bounds 0.96 and 7.2 km s −1 ; the relative tolerance of PCG is set to 0.01. Gravity inversion is started from a zero density model, with the model transform bounds −2.5 and 2.5 g cm −3 . Depth weighting |$\sim 1/z$| is used and the DWT reconstruction error is set to 5 per cent, resulting in the compression ratio of 77; PCG tolerance is set to |$10^{-3}$|⁠ . All the inversion grids are the same as those of the true models used for computing the synthetic data.

In order to determine the regularization parameters |$\alpha _i$| and |$\hat{\alpha _i}$|⁠ , we follow the same strategy as in Example 1: first find |$\hat{\alpha _i}$| using separate inversions, then find |$\alpha _i$| that minimize JTV in the JTV-regularized joint inversion; however, because of the higher dimensionality and numerical complexity of the problem, we determine |$\alpha _i$| by trial and error (using order-of-magnitude steps) without exhaustive grid search, understanding that the results may be suboptimal. The same values of |$\alpha _i$| and |$\hat{\alpha _i}$| are then used in the rest of the inversions (with XG, OWXG and ‘petrophysics’ coupling), as we attempt to compare the effects of the coupling constraints. For all the cases, the results appear to be satisfactory, however, they probably can be improved by changing |$\alpha _i$|⁠ . To determine |$\gamma _{ij}$|⁠ , with |$\alpha _i$| and |$\hat{\alpha _i}$| fixed, we choose the maximum values for which the convergence is maintained and the models are sufficiently ‘smooth’ (in terms of (J)TV).

Using the above procedure, the parameters are set as follows (with index 0 denoting FATT, 1–gravity, 2–MT): |$\alpha _0=200$|⁠ , |$\hat{\alpha }_0=20$|⁠ , |$\alpha _1=10^5$|⁠ , |$\hat{\alpha }_1=10^6$|⁠ , |$\alpha _2=1$|⁠ , |$\hat{\alpha }_2=10$| and |$q=1.3$|⁠ . In the inversions with XG, |$\gamma _{01} =\gamma _{02}=200$|⁠ , |$\gamma _{12}=20$| and when OWXG is applied to the FATT–gravity pair, |$\gamma _{01}=2000$| and |$\sigma _{01}=-1$|⁠ .

For FATT and gravity, the Sobolev norm weight |$w=1000$|⁠ . For TV and JTV, |$w_x = w_y = 10$| and |$w_z=1$|⁠ . The number of Gauss–Newton iterations |$n_{\text{itn}} = 4$| and PCG tolerance is set to 0.01. The regularization-coupling grid is the same as the FATT grid.

To measure the alignment of the models’ edges, similarly to the JMS case considered in Example 1, we normalize JTV and define

which is bounded by |$1/\sqrt{N}$| and 1.

The change of RMS data misfits, relative distances |$r_i$| between |$\mathbf {m}_i$| and |$\mathbf {u}_i$|⁠ , XG and OWXG functionals and |$\gamma _{\text{TV}} ({\bf u})$| with the outer iterations is plotted in Fig. 10 . Note that, except for the Fig. 10(c) , the same functionals are plotted irrespective of whether or not they are part of the corresponding objective function. Table 1 summarizes the relative performance of the inversions in terms of the relative mean error with respect to the true models: |$\text{mRMS} = \Vert \mathbf {m}_i - \mathbf {m}_{i,\text{true}}\Vert / \Vert \mathbf {m}_{i,\text{true}}\Vert \cdot 100\%$|⁠ , as well as the RMS covariance-weighted data misfits and the number of iterations.

Number of outer iterations, data and model normalized RMS errors for the models in Figs 11 and 12 .

.	.	MT .		FATT .		Gravity .
.	itn .	RMS .	mRMS [%] .	RMS .	mRMS [%] .	RMS .	mRMS [%] .
Separate (TV)	24	1.10	13.63	1.06	73.25	0.99	107.37
JTV	24	1.10	13.34	1.04	73.41	1.08	106.40
JTV + XG	28	1.10	13.06	1.08	70.56	1.06	109.11
TV + (OW)XG	26	1.10	13.22	1.04	73.32	1.05	81.28
JTV + (OW)XG	29	1.10	12.88	1.08	71.56	1.09	67.91
JTV + (OW)XG + ( )	25	1.10	11.49	1.07	67.96	1.10	65.16
25%, separate (TV)	18	1.10	16.88	1.01	82.85	0.72	97.85
25%, JTV + OWXG	22	1.09	15.81	0.96	79.92	0.80	68.32

.	.	MT .		FATT .		Gravity .
.	itn .	RMS .	mRMS [%] .	RMS .	mRMS [%] .	RMS .	mRMS [%] .
Separate (TV)	24	1.10	13.63	1.06	73.25	0.99	107.37
JTV	24	1.10	13.34	1.04	73.41	1.08	106.40
JTV + XG	28	1.10	13.06	1.08	70.56	1.06	109.11
TV + (OW)XG	26	1.10	13.22	1.04	73.32	1.05	81.28
JTV + (OW)XG	29	1.10	12.88	1.08	71.56	1.09	67.91
JTV + (OW)XG + ( )	25	1.10	11.49	1.07	67.96	1.10	65.16
25%, separate (TV)	18	1.10	16.88	1.01	82.85	0.72	97.85
25%, JTV + OWXG	22	1.09	15.81	0.96	79.92	0.80	68.32

Fig. 11 presents a comparison of the models obtained with different combinations of the structural constraints. Using JTV instead of TV mainly increases the contrast of the anomalies, while the improvement in their structural similarity is minor, most visible in vertical sections of the density model. Adding XG further increases the structural similarity, as evidenced, for example by the shape of the low-velocity blocks (see 3 km depth slices) and the reduced ‘bleeding’ in the resistivity models. Postulating positivity of the velocity–density correlation via the use of OWXG appears to be critical for the reconstruction of density ( cf . columns 3 and 4–6 of Fig. 11 )—essentially, it brings depth resolution into the gravity inversion. This effect is similar to the effect of the positivity constraint on the susceptibility in magnetic data inversion (Li & Oldenburg 1998 ). However, also applying OWXG to the resistivity only marginally improves the models and does not result in reconstruction of the bottom-layer resistive blocks since their absence satisfies the OWXG constraint (see the irregular-geometry test below). Note that the pattern of the upper checkerboard layer is different for velocity, resistivity and density, that is structure present in one of the properties is absent in the others, and all the tested structural constraints work fine in this situation, producing no artefacts.

In the next test, we examine the effects of direct ‘petrophysics’ coupling, assuming such information is available for a certain subset of the model parameters. With the exception of the top checkerboard layer, true velocity |$v_p$| and logarithm of resistivity |$\rho$| are linearly related as follows:

where |$u_0$| is the slowness model transformed by eq. ( 34 ), |$u_2 = \ln \rho$| and |$v_{p,0}$| is the background velocity. This constraint is enforced for the bottom checkerboard layer only by adding to |$\mathcal {R}(\mathbf {u})$| the term

where |$\mathbf {W}$| is diagonal matrix whose entries are 1000 for the cells below |$z=5$| km and zero otherwise. Adding it to the combination of JTV, XG and OWXG from the previous test somewhat accelerates convergence of the inversion and dramatically improves models of all the properties (see Table 1 ), in particular, resistive blocks of the bottom checkerboard layer are now recovered (last column of Fig. 11 ).

To simulate an irregular acquisition geometry often encountered in the real data, particularly in regional studies, we randomly draw from the regular-grid data sets 25 per cent of the MT and gravity locations and 50 per cent of seismic sources and receivers (Fig. 12 ). These subsamples of the data are inverted separately using TV (Fig. 12a ) and jointly using JTV and OWXG (Fig. 12b ). OWXG is applied to all pairs of the models with |$\gamma _{01}=\gamma _{02}=2000$|⁠ , |$\gamma _{12}=200$| and |$\sigma _{01}=\sigma _{02}=-1$|⁠ , |$\sigma _{12}=1$|⁠ . Data and model RMS errors and the number of iterations for separate and joint inversions are summarized in Table 1 . As we can see from Fig. 12 (especially the resistivity model), joint inversion, by making use of the spatially complementary sensitivities, improves recovery of the features that are poorly resolved by the individual inversions due to the missing stations.

$Slices through the core parts of the models reconstructed using randomly selected 25 per cent of the data. (a) Separate inversions, TV regularization. (b) Joint inversion, JTV + OWXG ($\sigma _{01}=\sigma _{02}=-1$, $\sigma _{12}=1$). Dashed lines denote the true structures, dots—horizontal positions of stations, ‘+’— horizontal positions of seismic sources.$

Slices through the core parts of the models reconstructed using randomly selected 25 per cent of the data. (a) Separate inversions, TV regularization. (b) Joint inversion, JTV + OWXG ( ⁠|$\sigma _{01}=\sigma _{02}=-1$|⁠ , |$\sigma _{12}=1$|⁠ ). Dashed lines denote the true structures, dots—horizontal positions of stations, ‘+’— horizontal positions of seismic sources.

5.3 Example 3: joint inversion of MT and electrical resistivity tomography data

In this example we demonstrate how the proposed approach can be applied to the situation where the coupled inverse problems use radically different grids. It is inspired by field data from Furnas Volcano, Azores (Hogg et al . 2018 ), where a 1.5 km electrical resistivity tomography (ERT) profile was acquired across a fault-zone associated fumarole area together with audio-magnetotelluric (AMT) data. For ERT we use 2-D finite-element modelling and inversion implemented in pyGIMLI (Rücker et al . 2017 ). For AMT, the 3-D version of ModEM (Kelbert et al . 2014 ) is used. The true model is 2-D, consisting of a 1 |$\Omega \cdot$| m ‘fault’, 10 |$\Omega \cdot$| m ‘clay cap’ and a 1000 |$\Omega \cdot$| m resistor embedded in 100 |$\Omega \cdot$| m background with topography (Fig. 13 ). The ERT data are generated using 64 electrodes with 24 m spacing in the Wenner configuration and contaminated by Gaussian noise with the standard deviation of 2 per cent + 1 μV. The AMT data are calculated for four stations with 380 m spacing at nine frequencies in 1–100 Hz range and contaminated by Gaussian noise with 3 per cent standard deviation; only the off-diagonal components of the impedance tensor are inverted.

$Resistivity models used for generating the synthetic (a) ERT and (b) AMT data. Red dots–positions of ERT electrodes, white–AMT stations. In (b), air cells and cells at $y\gt 0$ are removed, the grid is symmetric with respect to $y=0$.$

Resistivity models used for generating the synthetic (a) ERT and (b) AMT data. Red dots–positions of ERT electrodes, white–AMT stations. In (b), air cells and cells at |$y\gt 0$| are removed, the grid is symmetric with respect to |$y=0$|⁠ .

The AMT data are inverted using a |$46 \times 16 \times 40$| model grid consisting of a core area with the horizontal cell size of 50 m |$\times$| 50 m which is expanded by 5 padding cells in each horizontal direction, with the cell size increasing by a factor of 2.5. In the vertical direction, the cell size increases with depth from 5 m to 1.4 km. The model covariance smoothing is applied twice with a factor of 0.3 along the x - and z -directions and 0.9 along the y -direction. The ERT data are inverted using 2-D Delaunay triangulation grid with the cells expanding with depth starting from two edges between neighbouring electrodes at the surface. Both ERT and AMT inversions start with 100 |$\Omega \cdot$| m homogeneous initial models.

For the joint inversion, using eq. ( 7 ) with |$\mathcal {R}(\mathbf {u}) = \Vert \mathbf {u}_0 - \mathbf {u}_1\Vert ^2 = 0$|⁠ , we get

so the reference models for the inverse subproblems are essentially the weighted average of the ERT and AMT models from the previous outer iteration. As both model vectors are logarithms of resistivity, this corresponds to the weighted geometric mean of the resistivities. We define |$\mathbf {u}$| on a |$340\times 130$| regular grid with a 5 m step and use bilinear interpolation between the cell centres for |$\mathbf {P}_i$| and |$\mathbf {Q}_i$|⁠ . In the AMT case, when mapping from the 3-D model to the 2-D |$\mathbf {u}$|⁠ , we average along the y -direction over the core part of the grid, to minimize the effect of the model ‘fading’ away from the profile, and when mapping back, ‘broadcast’ along the y -direction over the whole grid.

At each outer iteration of the joint inversion, the ERT inversion is terminated after three Gauss–Newton iterations and the AMT inversion—after 10 NLCG iterations. The regularization parameters are set as follows for all the inversions: |$\hat{\alpha }_0 = 40$| (ERT) and |$\hat{\alpha }_1 = 1$| (AMT) and are kept constant. To analyse the effect of ERT/AMT weighting we test three values of |$\alpha _0 / \alpha _1$|⁠ : 0.1, 1 and 10.

The models resulting from the joint and separate inversions are shown in Fig. 14 . As we can see from the separate inversion results, the near-surface part of the model is well resolved by ERT, but not by AMT, due to large spacing between the stations and the lack of high frequencies, while the deeper structure is resolved by AMT. Joint inversions achieve better reconstruction of the whole model, but at the expense of slightly higher RMS values in AMT: all joint inversions were terminated after 30 outer iterations without the RMS falling below 1.1. Fig. 15 shows the progress of the joint inversions in terms of RMS and |$r_i$|⁠ . The high RMS values in AMT are largely due to the resistive artefact to the left of the ‘fault’, which is produced by the ERT inversion on the edge of its high-sensitivity region. Using, instead of scalar |$\alpha _i$|⁠ , weighting matrices proportional to the integrated sensitivities should suppress such artefacts and further improve the joint inversion results. We see that the mapping between different grids based on a simple linear interpolation works reasonably well at least when the methods have comparable resolution lengths and the resistivity models are smooth. However, in more extreme cases accurate mapping of resistivities may require material averaging (see, e.g. Commer & Newman 2008 ) which will replace |$\mathbf {P}_i$| and |$\mathbf {Q}_i$| by nonlinear operators.

$Resistivity models recovered by separate ERT ($i=0$) and AMT ($i=1$) inversions and joint inversions with three different values of $\alpha _0 / \alpha _1$. For the joint inversions, $\mathbf {u}_i$ are also shown. The corresponding RMS, mRMS and $r_i$ values are indicated. The ERT models are masked according to the integrated sensitivity and for the AMT models the $y=0$ slices through the core part of the grid are shown. True structure is indicated by the black contour, positions of the electrodes/stations—by red dots.$

Resistivity models recovered by separate ERT ( ⁠|$i=0$|⁠ ) and AMT ( ⁠|$i=1$|⁠ ) inversions and joint inversions with three different values of |$\alpha _0 / \alpha _1$|⁠ . For the joint inversions, |$\mathbf {u}_i$| are also shown. The corresponding RMS, mRMS and |$r_i$| values are indicated. The ERT models are masked according to the integrated sensitivity and for the AMT models the |$y=0$| slices through the core part of the grid are shown. True structure is indicated by the black contour, positions of the electrodes/stations—by red dots.

$Progress of the ERT–AMT joint inversions for three different values of $\alpha _0 / \alpha _1$.$

Progress of the ERT–AMT joint inversions for three different values of |$\alpha _0 / \alpha _1$|⁠ .

We have developed a flexible general framework for multiphysics joint inversion of any number of geophysical data sets. It is based on the variable splitting technique that introduces an auxiliary multiparameter model space in which minimization of the coupling and stabilizing functionals is carried out. By defining a mapping between this space and the model spaces via interpolation, completely different parametrizations can be applied to different models. Each of the inversion supbroblems and the coupling-regularization subproblem can be solved using a different optimization algorithm. For each subproblem, the linking term controlling the distance between the model and the corresponding auxiliary variable takes the form of a quadratic regularization with a reference model. Thus, any existing inversion code supporting such regularization can be integrated, without modifications, into this joint inversion framework. Using the developed framework, we have implemented 3-D joint inversion of magnetotelluric, seismic refraction and gravity data. We have implemented and tested on synthetic data different combinations of coupling constraints based on joint total variation, joint minimum support, cross-gradient and one-way cross-gradient, as well as an explicit relationship between the properties. The joint minimum support is a promising coupling regularization for multiphysics time-lapse inversions. The joint total variation and the cross-gradient are complementary, with JTV providing regularization and coupling edge-like features of the models by aligning their positions and XG coupling smoother features of the models by aligning gradient directions. The one-way cross-gradient can dramatically improve the effects of structural coupling in certain problems: in particular, for the gravity inversion it eliminates the non-uniqueness related to the lack of depth resolution. We expect that the developed approach will be especially useful for joint inversion with more complicated priors.

We would like to thank the editors, Colin Farquharson and two anonymous reviewers for their constructive comments that helped to improve the manuscript. This work has emanated from research supported in part by: a research grant to iCRAG from Science Foundation Ireland (SFI) under Grant Number 13/RC/2092 and co-funded under the European Regional Development Fund and by iCRAG industry partners; and a research grant to iCRAG2 from SFI under Grant Number 13/RC/2092_P2. Finally, we would like to thank Gary Egbert, Anna Kelbert and Naser Meqbel for making their ModEM code available to us.

The data underlying this paper will be shared on request to the corresponding author.

Afonso J.C. , Fullea J. , Yang Y. , Connolly J. , Jones A. , 2013 . 3-D multi-observable probabilistic inversion for the compositional and thermal structure of the lithosphere and upper mantle. II: general methodology and resolution analysis , J. geophys. Res. , 118 ( 4 ), 1650 – 1676 . 10.1002/jgrb.50123

Google Scholar

Ajo-Franklin J.B. , Minsley B.J. , Daley T.M. , 2007 . Applying compactness constraints to differential traveltime tomography , Geophysics , 72 ( 4 ), R67 – R75 . 10.1190/1.2742496

Aminzadeh F. , Jean B. , Kunz T. , 1997 . 3-D Salt and Overthrust Models , Society of Exploration Geophysicists .

Google Preview

Astic T. , Heagy L.J. , Oldenburg D.W. , 2021 . Petrophysically and geologically guided multi-physics inversion using a dynamic gaussian mixture model , J. geophys. Int. , 224 ( 1 ), 40 – 68 . 10.1093/gji/ggaa378

Blomgren P. , Chan T.F. , 1998 . Color TV: total variation methods for restoration of vector-valued images , IEEE Trans. Image Process. , 7 ( 3 ), 304 – 309 . 10.1109/83.661180

Bosch M. , 1999 . Lithologic tomography: from plural geophysical data to lithology estimation , J. geophys. Res. , 104 ( B1 ), 749 – 766 . 10.1029/1998JB900014

Chen J. , Hoversten G.M. , Vasco D. , Rubin Y. , Hou Z. , 2007 . A Bayesian model for gas saturation estimation using marine seismic AVA and CSEM data , Geophysics , 72 ( 2 ), WA85 – WA95 . 10.1190/1.2435082

Colombo D. , Rovetta D. , 2018 . Coupling strategies in multiparameter geophysical joint inversion , J. geophys. Int. , 215 ( 2 ), 1171 – 1184 . 10.1093/gji/ggy341

Colombo D. , Turkoglu E. , Li W. , Rovetta D. , 2021 . Coupled physics-deep learning inversion , Comput. Geosci. , 157 , doi:10.1016/j.cageo.2021.104917. 10.1016/j.cageo.2021.104917

Commer M. , Newman G.A. , 2008 . New advances in three-dimensional controlled-source electromagnetic inversion , J. geophys. Int. , 172 ( 2 ), 513 – 535 . 10.1111/j.1365-246X.2007.03663.x

Crestel B. , Stadler G. , Ghattas O. , 2018 . A comparative study of structural similarity and regularization for joint inverse problems governed by pdes , Inverse Problems , 35 ( 2 ), doi:10.1088/1361-6420/aaf129. 10.1088/1361-6420/aaf129

Droujinine A. , Vasilevsky A. , Evans R. , 2007 . Feasibility of using full tensor gradient (FTG) data for detection of local lateral density contrasts during reservoir monitoring , J. geophys. Int. , 169 ( 3 ), 795 – 820 . 10.1111/j.1365-246X.2007.02806.x

Egbert G.D. , Kelbert A. , 2012 . Computational recipes for electromagnetic inverse problems , J. geophys. Int. , 189 ( 1 ), 251 – 267 . 10.1111/j.1365-246X.2011.05347.x

Gallardo L.A. , Meju M.A. , 2003 . Characterization of heterogeneous near-surface materials by joint 2D inversion of dc resistivity and seismic data , Geophys. Res. Lett. , 30 ( 13 ), doi:10.1029/2003GL017370. 10.1029/2003GL017370

Gao G. , Abubakar A. , Habashy T.M. , 2012 . Joint petrophysical inversion of electromagnetic and full-waveform seismic datajoint petrophysical em and seismic inversion , Geophysics , 77 ( 3 ), WA3 – WA18 . 10.1190/geo2011-0157.1

Gao J. , Zhang H. , 2018 . An efficient sequential strategy for realizing cross-gradient joint inversion: method and its application to 2-D cross borehole seismic traveltime and dc resistivity tomography , J. geophys. Int. , 213 ( 2 ), 1044 – 1055 . 10.1093/gji/ggy026

Goldstein T. , Osher S. , 2009 . The split Bregman method for l1-regularized problems , SIAM J. Imag. Sci. , 2 ( 2 ), 323 – 343 . 10.1137/080725891

Gramfort A. , Kowalski M. , Hämäläinen M. , 2012 . Mixed-norm estimates for the M/EEG inverse problem using accelerated gradient methods , Phys. Med. Biol. , 57 ( 7 ), doi:10.1088/0031-9155/57/7/1937. 10.1088/0031-9155/57/7/1937

Haber E. , Holtzman Gazit M. , 2013 . Model fusion and joint inversion , Surv. Geophys. , 34 ( 5 ), 675 – 695 . 10.1007/s10712-013-9232-4

Haber E. , Ascher U.M. , Oldenburg D. , 2000 . On optimization techniques for solving nonlinear inverse problems , Inverse Problems , 16 ( 5 ), doi:10.1088/0266-5611/16/5/309. 10.1088/0266-5611/16/5/309

Heincke B. , Jegen M. , Moorkamp M. , Hobbs R.W. , Chen J. , 2017 . An adaptive coupling strategy for joint inversions that use petrophysical information as constraints , J. appl. Geophys. , 136 , 279 – 297 . 10.1016/j.jappgeo.2016.10.028

Hilbich C. , 2010 . Time-lapse refraction seismic tomography for the detection of ground ice degradation , Cryosphere , 4 ( 3 ), 243 – 259 . 10.5194/tc-4-243-2010

Hogg C. et al. , 2018 . 3-d interpretation of short-period magnetotelluric data at Furnas Volcano, Azores Islands , J. geophys. Int. , 213 ( 1 ), 371 – 386 . 10.1093/gji/ggx512

Hu W. , Abubakar A. , Habashy T.M. , 2009 . Joint electromagnetic and seismic inversion using structural constraints , Geophysics , 74 ( 6 ), R99 – R109 . 10.1190/1.3246586

Jorgensen M. , Zhdanov M.S. , 2021 . Recovering magnetization of rock formations by jointly inverting airborne gravity gradiometry and total magnetic intensity data , Minerals , 11 ( 4 ), doi:10.3390/min11040366. 10.3390/min11040366

Juhojuntti N. , Kamm J. , 2015 . Joint inversion of seismic refraction and resistivity data using layered models-applications to groundwater investigation , Geophysics , 80 ( 1 ), EN43 – EN55 . 10.1190/geo2013-0476.1

Kamm J. , Lundin I.A. , Bastani M. , Sadeghi M. , Pedersen L.B. , 2015 . Joint inversion of gravity, magnetic, and petrophysical data—a case study from a Gabbro intrusion in Boden, Sweden joint potential-field inversion , Geophysics , 80 ( 5 ), B131 – B152 . 10.1190/geo2014-0122.1

Kelbert A. , Meqbel N. , Egbert G.D. , Tandon K. , 2014 . Modem: a modular system for inversion of electromagnetic geophysical data , Comput. Geosci. , 66 , 40 – 53 . 10.1016/j.cageo.2014.01.010

Khan A. , Connolly J. , Maclennan J. , Mosegaard K. , 2007 . Joint inversion of seismic and gravity data for lunar composition and thermal state , J. geophys. Int. , 168 ( 1 ), 243 – 258 . 10.1111/j.1365-246X.2006.03200.x

Last B. , Kubik K. , 1983 . Compact gravity inversion , Geophysics , 48 ( 6 ), 713 – 721 . 10.1190/1.1441501

Lelièvre P.G. , Farquharson C.G. , Hurich C.A. , 2012 . Joint inversion of seismic traveltimes and gravity data on unstructured grids with application to mineral exploration , Geophysics , 77 ( 1 ), K1 – K15 .

Li Y. , Oldenburg D.W. , 1998 . 3-D inversion of gravity data , Geophysics , 63 ( 1 ), 109 – 119 . 10.1190/1.1444302

Li Y. , Oldenburg D.W. , 2003 . Fast inversion of large-scale magnetic data using wavelet transforms and a logarithmic barrier method , J. geophys. Int. , 152 ( 2 ), 251 – 265 . 10.1046/j.1365-246X.2003.01766.x

Loris I. , Nolet G. , Daubechies I. , Dahlen F. , 2007 . Tomographic inversion using |$\ell$| 1-norm regularization of wavelet coefficients , J. geophys. Int. , 170 ( 1 ), 359 – 370 . 10.1111/j.1365-246X.2007.03409.x

Malovichko M. , Khokhlov N. , Yavich N. , Zhdanov M.S. , 2020 . Incorporating known petrophysical model in the seismic full-waveform inversion using the Gramian constraint , Geophys. Prospect. , 68 ( 4 ), 1361 – 1378 . 10.1111/1365-2478.12932

Manassero M. , Afonso J.C. , Zyserman F. , Jones A. , Zlotnik S. , Fomin I. , 2021 . A reduced order approach for probabilistic inversions of 3D magnetotelluric data II: joint inversion of mt and surface-wave data , J. geophys. Res. , 126 ( 12 ), 1 – 33 . 10.1029/2021JB021962

Mandolesi E. , Jones A.G. , 2014 . Magnetotelluric inversion based on mutual information , J. geophys. Int. , 199 ( 1 ), 242 – 252 . 10.1093/gji/ggu258

Molodtsov D. , Troyan V. , 2017 . Multiphysics joint inversion through joint sparsity regularization , in SEG Technical Program Expanded Abstracts 2017 , 1262 – 1267 ., Society of Exploration Geophysicists .

Molodtsov D. , Kashtan B. , Roslov Y. , 2011 . Joint inversion of seismic and magnetotelluric data with structural constraint based on dot product of image gradients , in SEG Technical Program Expanded Abstracts 2011 , 740 – 744 ., Society of Exploration Geophysicists .

Moorkamp M. , 2021 . Joint inversion of gravity and magnetotelluric data from the ernest-henry iocg deposit with a variation of information constraint , in First International Meeting for Applied Geoscience & Energy , 1711 – 1715 ., Society of Exploration Geophysicists . 10.1190/segam2021-3582000.1

Moorkamp M. , Heincke B. , Jegen M. , Roberts A.W. , Hobbs R.W. , 2011 . A framework for 3-D joint inversion of mt, gravity and seismic refraction data , J. geophys. Int. , 184 ( 1 ), 477 – 493 . 10.1111/j.1365-246X.2010.04856.x

Moorkamp M. , Lelièvre P.G. , Linde N. , Khan A. , 2016 . Integrated Imaging of the Earth: Theory and Applications , Vol. 218 , John Wiley & Sons . 10.1002/9781118929063

Nocedal J. , Wright S.J. , 1999 . Numerical Optimization , Springer . 10.1007/b98874

Patanè D. , Barberi G. , Cocina O. , De Gori P. , Chiarabba C. , 2006 . Time-resolved seismic tomography detects magma intrusions at mount etna , Science , 313 ( 5788 ), 821 – 823 . 10.1126/science.1127724

Podvin P. , Lecomte I. , 1991 . Finite difference computation of traveltimes in very contrasted velocity models: a massively parallel approach and its associated tools , J. geophys. Int. , 105 ( 1 ), 271 – 284 . 10.1111/j.1365-246X.1991.tb03461.x

Portniaguine O. , Zhdanov M.S. , 1999 . Focusing geophysical inversion images , Geophysics , 64 ( 3 ), 874 – 887 . 10.1190/1.1444596

Reitz A. , Krahenbuhl R. , Li Y. , 2015 . Feasibility of time-lapse gravity and gravity gradiometry monitoring for steam-assisted gravity drainage reservoirs , Geophysics , 80 ( 2 ), WA99 – WA111 . 10.1190/geo2014-0217.1

Rücker C. , Günther T. , Wagner F.M. , 2017 . pyGIMLi: an open-source library for modelling and inversion in geophysics , Comput. Geosci. , 109 , 106 – 123 .

Rudin L.I. , Osher S. , Fatemi E. , 1992 . Nonlinear total variation based noise removal algorithms , Physica D , 60 ( 1–4 ), 259 – 268 . 10.1016/0167-2789(92)90242-F

Sun J. , Li Y. , 2016 . Joint inversion of multiple geophysical and petrophysical data using generalized fuzzy clustering algorithms , Geophys. Suppl. Mon. Not. R. astr. Soc. , 208 ( 2 ), 1201 – 1216 . 10.1093/gji/ggw442

Tikhonov A.N. , Arsenin V.Y. , 1977 . Solutions of Ill-Posed Problems , Vol. 330 , WH Winston .

Tu X. , Zhdanov M.S. , 2022 . Joint focusing inversion of marine controlled-source electromagnetic and full tensor gravity gradiometry data , Geophysics , 87 ( 5 ), K35 – K47 . 10.1190/geo2021-0691.1

Um E.S. , Commer M. , Newman G.A. , 2014 . A strategy for coupled 3D imaging of large-scale seismic and electromagnetic data sets: application to subsalt imaging , Geophysics , 79 ( 3 ), ID1 – ID13 . 10.1190/geo2013-0053.1

Vogel C.R. , Oman M.E. , 1996 . Iterative methods for total variation denoising , SIAM J. Sci. Comput. , 17 ( 1 ), 227 – 238 . 10.1137/0917016

Vozoff K. , Jupp D. , 1975 . Joint inversion of geophysical data , J. geophys. Int. , 42 ( 3 ), 977 – 991 . 10.1111/j.1365-246X.1975.tb06462.x

Waldhauser F. , Ellsworth W.L. , 2000 . A double-difference earthquake location algorithm: method and application to the Northern Hayward Fault, California , Bull. seism. Soc. Am. , 90 ( 6 ), 1353 – 1368 . 10.1785/0120000006

Wang Y. , Yang J. , Yin W. , Zhang Y. , 2008 . A new alternating minimization algorithm for total variation image reconstruction , SIAM J. Imag. Sci. , 1 ( 3 ), 248 – 272 . 10.1137/080724265

Xu Q. , 2005 . Representations of inverse covariances by differential operators , Adv. Atmos. Sci. , 22 ( 2 ), 181 – 198 . 10.1007/BF02918508

Yanovskaya T. , Ditmar P. , 1990 . Smoothness criteria in surface wave tomography , J. geophys. Int. , 102 ( 1 ), 63 – 72 . 10.1111/j.1365-246X.1990.tb00530.x

Zhdanov M.S. , 2002 . Geophysical Inverse Theory and Regularization Problems , Vol. 36 , Elsevier .

Zhdanov M.S. , Gribenko A. , Wilson G. , 2012 . Generalized joint inversion of multimodal geophysical data using Gramian constraints , Geophys. Res. Lett. , 39 ( 9 ), doi:10.1029/2012GL051233. 10.1029/2012GL051233

Zhdanov M.S. , Tu X. , Čuma M. , 2022 . Cooperative inversion of multiphysics data using joint minimum entropy constraints , Near Surf. Geophys. , 20 ( 6 ), 623 – 636 . 10.1002/nsg.12203

Zheglova P. , Lelièvre P.G. , Farquharson C.G. , 2018 . Multiple level-set joint inversion of traveltime and gravity data with application to ore delineation: a synthetic study , Geophysics , 83 ( 1 ), R13 – R30 . 10.1190/geo2016-0675.1

Month:	Total Views:
August 2024	62

Email alerts

Astrophysics data system, citing articles via.

Recommend to your Library
Advertising and Corporate Services
Journals Career Network

Affiliations

Online ISSN 1365-246X
About Oxford Academic
Publish journals with us
University press partners
What we publish
New features
Open access
Institutional account management
Rights and permissions
Get help with access
Accessibility
Advertising
Media enquiries
Oxford University Press
Oxford Languages
University of Oxford

Oxford University Press is a department of the University of Oxford. It furthers the University's objective of excellence in research, scholarship, and education by publishing worldwide

Cookie settings
Cookie policy
Privacy policy
Legal notice

This Feature Is Available To Subscribers Only

This PDF is available to Subscribers Only

For full access to this pdf, sign in to an existing account, or purchase an annual subscription.

IMAGES

Solve using Joint Variation
Joint Variation
Pre-Calculus
Joint Variation
Solving Joint Variation Problems (3 of 3)
Chapter 7 Section ppt download

VIDEO

JOINT VARIATION
JOINT VARIATION
Joint Variation
Joint Variation (and Combined Variation)
Joint Variation (Variation Statement)
Joint Variation Kaise nikale ll How to solve joint Variation ll short tricks ll

COMMENTS

Joint And Combined Variation Word Problems
Example 1: A quantity varies inversely as two or more other quantities. The figure below shows a rectangular solid with a fixed volume. Express its width, w, as a joint variation in terms of its length, l, and height, h. Solution: w ∝ 1/ (lh) In other words, the longer the length l or the height h, the narrower is the width w.
Solve problems involving joint variation
Example 4: Solving Problems Involving Joint Variation. A quantity x varies directly with the square of y and inversely with the cube root of z.If x = 6 when y = 2 and z = 8, find x when y = 1 and z = 27.
Joint Variation: Solving Joint Variation Problems in Algebra
Joint variation is a variation in which the quotient of a variable and the product of two variables is a constant. Joint variation states that if y varies directly as the product of x and z, if there is a constant k such that y = kxz or k = y / xz, y varies jointly as x and z. It occurs when a variable varies directly or inversely with multiple ...
Study Guide
A General Note: Joint Variation. Joint variation occurs when a variable varies directly or inversely with multiple variables. For instance, if x varies directly with both y and z, we have x = kyz. If x varies directly with y and inversely with z, we have x=\frac {ky} {z} x = zky. Notice that we only use one constant in a joint variation equation.
Joint Variation
Go through the below sections to check definition, various properties, example problems, value tables, concepts etc. Joint Variation - Introduction. Joint Variation refers to the scenario where the value of 1 variable depends on 2 or more and other variables that are held constant. For example, if C varies jointly as A and B, then C = ABX for ...
Joint Variation
The equation for the given problem of joint variation is. x = Kyz where K is the constant. For the given data. 16 = K × 4 × 6. or, K = 46 4 6. So substituting the value of K the equation becomes. x = 4yz 6 4 y z 6. Now for the required condition. x = 4×8×126 4 × 8 × 12 6.
JOINT VARIATION (Definition, Examples, Solving Problems) Made Easy
This video is about the definition and examples of joint variation and translating statements into the equation of variation. It also includes examples of so...
Direct Inverse and Joint Variation Word Problems
This algebra video tutorial focuses on solving direct, inverse, and joint variation word problems. It shows you how to write the appropriate equation / form...
Joint or Combined Variation (video lessons, examples and solutions)
Example: Suppose y varies jointly with x and z. When y = 20, x = 6 and z = 10. Find y when x = 8 and z =15. Show Video Lesson. Lesson on combining direct and inverse or joint and inverse variation. Example: y varies directly as x and inversely as the square of z, and when x = 32, y = 6 and z = 4. Find x when y = 10 and z = 3.
1.8: Variation
Solving Problems involving Direct, Inverse, and Joint variation. Certain relationships occur so frequently in applied situations that they are given special names. Variation equations show how one quantity changes in relation to other quantities. The relationship between the quantities can be described as direct, inverse, or joint variation.
Direct, Inverse, Joint and Combined Variation
Joint Variation, where at least two variables are related directly. For example, the area of a triangle is jointly related to both its height and base. Combined Variation, which involves a combination of direct or joint variation, and indirect variation. For example, the average number of phone calls per day between two cities has found to be ...
Lesson 9.5
The following video goes over two examples on how to apply joint variation to solve problems.
2.7 Variation Word Problems
A historical example of direct variation can be found in the changing measurement of pi, which has been symbolized using the Greek letter π since the mid 18th century. ... Solving these combined or joint variation problems is the same as solving simpler variation problems. First, decide what equation the variation represents. ...
Study Guide
Example: Solving an Inverse Variation Problem. A quantity y y varies inversely with the cube of x x. If y=25 y = 25 when x=2 x = 2, find y y when x x is 6. Answer: The general formula for inverse variation with a cube is y=\dfrac {k} { {x}^ {3}} y = x3k. The constant can be found by multiplying y y by the cube of x x .
Master Joint and Combined Variation: Formulas & Examples
Joint variation is a direct variation, but with two or more variables. It has the equation. y = k ⋅ x ⋅ z. y=k \cdot x \cdot z y = k⋅x⋅z where. k. k k is the constant of variation and. k ≠ 0. k \neq 0 k = 0. A combined variation is formed when we combine any of the variations together (direct, inverse and joint).
Variation Word Problems
Purplemath. It's one thing to be able to take the words for a variation equation (such as " y varies directly as the square of x and inversely as the cube root of z ") and turn this into an equation that you can solve or use. It's another thing to extract the words from a word problem. But, because the lingo for variation equations is so ...
Joint and Combined Variation
Write the variation equation and answer the given question in each problem. 1. If 20 volunteers can wash 100 cars in 2.5 hours, find the constant of variation and find out how many cars 30 volunteers can wash in 3 hours. 2. If 10 students from the environmental club can clean up trash on a 2-mile stretch of road in 1 hour, find the constant of ...
JOINT VARIATION WORD PROBLEMS
JOINT VARIATION WORD PROBLEMS. Problem 1 : z varies directly with the sum of squares of x and y. z = 5 when x = 3 and y = 4. Find the value of z when x = 2 and y = 4. Solution : Since z varies directly with the sum of squares of x and y, z ∝ x2 + x2. z = k (x2 + y2) ---- (1)
Joint Variation Examples and Word Problems
This is a video about Joint Variation Examples and Word Problems. In joint variation one variable is jointly proportional or jointly varies to two or more va...
Exploring Combined Variation Examples and Joint Variation Insights
Here, the variable z varies jointly with x and y, and k is the constant of variation. Here are some examples of joint variation. Here, l is the rectangle's length, w its width, and the constant of variation k is 1. Here, l and w are the length and the width of the base, respectively, while h is the pyramid's height.
Inverse and Joint Variation
A General Note: Joint Variation. Joint variation occurs when a variable varies directly or inversely with multiple variables. For instance, if x x varies directly with both y y and z z, we have x = kyz x = k y z. If x x varies directly with y y and inversely with z z, we have x= ky z x = k y z. Notice that we only use one constant in a joint ...
5.8 Modeling Using Variation
Solving Problems Involving Joint Variation. Many situations are more complicated than a basic direct variation or inverse variation model. One variable often depends on multiple other variables. When a variable is dependent on the product or quotient of two or more variables, this is called joint variation. For example, the cost of busing ...
Joint Variation: Definition & Examples
Example 1 - Abstract. Let's look at some examples of joint variation problems. If y varies jointly with x, z, and w, and the value of y is 60 when x = 2, z = 3, and w = 5, what is the value of y ...
Decoupled joint inversion with variable splitting: example scheme for
where |$\mathbf {C}_{d_i}$| is the covariance matrix of the observed data. Because this solution is generally non-unique due to ill-posedness of the inverse problem and unattainable for local optimization due to nonlinearity of |$\mathbf {f}_i(\mathbf {m}_i)$|⁠, prior information about the model must be introduced—in the form of regularization and, in the case of the multiphysics joint ...

Joint Variation – Formula, Examples | How to Solve Problems Involving Joint Variation?

Joint Variation – Introduction

Functions of 2 or More Variables

Tables of Values

How to Solve Joint Variation Problems?

Joint Variation Problems with Solutions

Leave a Comment Cancel Reply

New! Comments

Recent Articles

Worksheet on Bar Graphs | Bar Graphs or Column Graphs | Graphing Bar

1st Grade Numbers Worksheet | Before, After and Between | Compare Numb

Subtraction Word Problems - 2-Digit Numbers | Subtraction Problems

Days of the Week | 7 Days of the Week | What are the Seven Days?

Joint or Combined Variation

What is Joint Variation or Combined Variation?

Direct, Inverse, Joint and Combined Variation

Direct or Proportional Variation

Inverse or Indirect Variation

Recognizing Direct or Indirect Variation

Joint Variation and Combined Variation

Combined Variation

Partial Variation

2.7 Variation Word Problems

Inverse Variation Problems

Joint or Combined Variation Problems

Share This Book

Study Guides > College Algebra CoRequisite Course

A General Note: Inverse Variation

How To: Given a description of an inverse variation problem, solve for an unknown.

Example: Solving an Inverse Variation Problem

Analysis of the Solution

Joint Variation

Licenses & Attributions

CC licensed content, Shared previously

We want your feedback

Joint and Combined Variation: Formulas, Examples, and Applications Unlock the power of joint and combined variation! Learn essential formulas, explore real-world applications, and master problem-solving techniques to excel in advanced algebra and beyond.

Free to Join!

Easily See Your Progress

Make Use of Our Learning Aids

Last Viewed

Earn Achievements as You Learn

Create and Customize Your Avatar

Introduction to Joint and Combined Variation

Step 1: Identify the Type of Variation

Step 2: Write the General Formula

Step 3: Substitute the Given Values to Find k k k

Step 4: Update the Formula with the Constant k k k

Step 5: Substitute the New Values to Find a a a

Step 6: Verify the Solution

1. What is the difference between joint variation and combined variation?

2. What is an example of joint variation in real life?

3. How do you solve a combined variation problem?

4. What are the four types of variation in mathematics?

5. How can you identify the type of variation in a problem?

Become a member to get more!

Select a Course Below

Variation Word Problems

MathHelp.com

Suppose that y is inversely proportional to x , and that y = 0.4 when x = 2.5 . Find y when x = 4 .

According to Hooke's Law, the force needed to stretch a spring is proportional to the amount the spring is stretched. If fifty pounds of force stretches a spring five inches, how much will the spring be stretched by a force of 120 pounds?

The weight of a body varies inversely as the square of its distance from the center of the earth. If the radius of the earth is 4000 miles, how much would a 200 -pound man weigh 1000 miles above the surface of the earth?

Standardized Test Prep

Visit Our Profiles

JOINT VARIATION WORD PROBLEMS

Recent Articles

Digital SAT Math Problems and Solutions (Part - 22)

SAT Math Resources (Videos, Concepts, Worksheets and More)

Module 10: Rational and Radical Functions

A General Note: Inverse Variation

Example: Writing a Formula for an Inversely Proportional Relationship

How To: Given a description of an indirect variation problem, solve for an unknown.

Example: Solving an Inverse Variation Problem

Analysis of the Solution

Joint Variation

A General Note: Joint Variation

Example: Solving Problems Involving Joint Variation

Contribute!

5.8 Modeling Using Variation

Solving Direct Variation Problems

Solving a Direct Variation Problem