
Solving Linear Inequalities Worksheets with Solutions
Solving linear inequalities is a foundational skill that you will build throughout your studies of elementary and high school algebra. While it isn’t the hardest concept you will encounter in the entire class, there are a few tips and tricks you should get used to. And the best way to do that is by practicing!
That’s why I put together this collection of solving linear inequalities worksheets! Let’s dig in so that you can master this important algebra concept!
What is a Linear Inequality?
A linear inequality is a type of statement in algebra that compares two linear equations. To make this comparison, we place an inequality symbol in between the two sides of the inequality. For example, \(x+1>2x-1\).
Take a moment to review this inequality symbol list:
- < (less than)
- > (greater than)
- ≤ (less than or equal to)
- ≥ (greater than or equal to)
Linear inequalities are similar to linear equations, however instead of an equals sign, a linear inequality contains one of the inequality symbols from the above list.
How to Solve a Linear Inequality
The steps that you take to solve a linear inequality are a very similar to those that you would take while solving an algebraic equation . When solving linear inequalities, you often perform similar operations as you would when solving linear equations .
Just like in linear equations, you can add or subtract terms on both sides, and multiply or divide by constants on both sides. However, unlike solving linear equations, linear inequalities have one very important rule:
Remember: If you multiply or divide both sides of an inequality by a negative number, the inequality sign must be flipped!
You will see some examples of this in the solving linear inequalities worksheets linked below!
Another important difference between solving a linear equation and solving a linear inequality is that the solution to a linear inequality will be the set of all values that make the inequality true (rather than just a single value that makes the equation true).
The solution to a linear inequality will tell you the places on the graph where one line is greater than or less than the other.
For example, consider the coordinate plane below that shows two lines in slope-intercept form.
As you can see, the red line is above the green line as long as \(x<2\). After this, the green line is above the red line. So if we wanted to write the solution to \(x+1>2x-1\), we would say that the solution set is \(x<2\), or all x-values less than 2 (note that we do not include 2 in the solution set since that is the point where the lines are equal ).
Solving Algebraically
In order to solve \(x+1>2x-1\) algebraically, we will use the same algebra strategies that we use when solving linear equations. We will collect all x-terms on the left side of the equation, and all non-variable terms on the right side of the equation.
\begin{split} x+1&>2x-1 \\ \\ -x&>-2 \\ \\ x&<2 \end{split}
Since we had to divide both sides by -1, notice that we flipped the sign of the inequality symbol! Therefore, the solution to this inequality is x<2 (which we can confirm using the coordinate plane above).
Another way that we can represent this solution is on a number line . We draw a line to the left of 2 with a hollow circle at 2 to indicate that 2 is not part of our solution set. We would use a filled in dot to indicate a value that is part of the solution set.
There are many ways to solve linear inequalities and represent their solutions. In the math worksheets that follow below, you will focus mainly on solving algebraically and representing your answer on a number line!
One-Step Inequalities Math Worksheet
To get started, try the set of one-step inequalities in the worksheet linked below. These problems will help you become familiar with solving a linear equality algebraically, and representing the solution on a number line.
I have created this worksheet in PDF format for your convenience. Remember to check the answer key provided to make sure that you understand the basics of solving linear inequalities.
Download the PDF worksheet by clicking below!
Multi-Step Inequalities Math Worksheet
Now that you have had some practice with solving one-step inequality problems, use the following worksheet to try your hand at some more complex linear inequality problems. This worksheet contains two-step inequalities as well as some more difficult multi-step linear inequality problems!
This worksheet is also provided in PDF format for ease of access. Remember to check the answer key to confirm your understanding of solving more complex linear inequalities.
Practice Solving Linear Inequalities
Inequalities may seem scary at first because of the inequality symbol, but as you have seen, they are actually solved in a very similar way to linear equations.
Use the math worksheets linked above to practice getting comfortable with solving a variety of linear inequality problems. Like any math concept, the more you practice the more familiar the concept will start to feel.
I hope these solving linear inequalities worksheets have helped you practice your inequality solving skills, as well as representing the solution set on a number line!
Ready to start applying your skills? Check out this linear inequalities word problems worksheet !
Did you find these solving linear inequalities worksheets helpful? Share this post and subscribe to Math By The Pixel on YouTube for more helpful mathematics content!
RECOMMENDED FOR YOU
Examples of One Solution Equations, Zero, and Infinite
Linear Equations Word Problems Worksheet with Solutions

- Parallelogram
- Quadrilateral
- Parallelepiped
- Tetrahedron
- Dodecahedron
- Fraction Calculator
- Mixed Fraction Calculator
- Greatest Common Factor Calulator
- Decimal to Fraction Calculator
- Whole Numbers
- Rational Numbers
- Place Value
- Irrational Numbers
- Natural Numbers
- Binary Operation
- Numerator and Denominator
- Order of Operations (PEMDAS)
- Scientific Notation
Table of Contents
Last modified on June 8th, 2024
#ezw_tco-2 .ez-toc-title{ font-size: 120%; ; ; } #ezw_tco-2 .ez-toc-widget-container ul.ez-toc-list li.active{ background-color: #ededed; } chapter outline
Linear inequalities.
Linear inequalities are algebraic expressions where the power of the unknown variable is no more than one, and the variable is connected with an inequality sign (>, <, ≤, or ≥).
7x – 12 > 16 and 5x + 11 < 2 are examples of linear inequalities
Rules to Solve
For adding or subtracting .
Adding or subtracting a number on or from both sides of the inequality does not change its direction.
If a < b, then a + c < b + c
If a > b, then a + c > b + c
If a < b, then a – c < b – c
If a > b, then a – c > b – c
For Multiplying or Dividing
Like adding and subtracting, multiplying, or dividing an inequality by the same positive number also does not change the direction of the inequality.
If a < b and c > 0, then ac < bc
If a > b and c > 0, then ac > bc
If a < b and c < 0, then ac > bc
If a > b and c < 0, then ac < bc
If a < b and c > 0, then ${\dfrac{a}{c} <\dfrac{b}{c}}$
If a > b and c > 0, then ${\dfrac{a}{c} >\dfrac{b}{c}}$
If a < b and c < 0, then ${\dfrac{a}{c} >\dfrac{b}{c}}$
If a > b and c < 0, then ${\dfrac{a}{c} <\dfrac{b}{c}}$
Solving and Graphing
When solving a linear inequality, the solution is typically represented as an ordered pair (x, y) that satisfies the inequality, which is then graphed on a number line.
Using the above rules, we solve the inequality x + 3 > 10
Step 1: Using the Subtraction Property
x + 3 – 3 > 10 -3
Step 3: Graphing the Solution

For One Variable
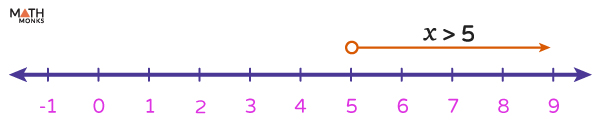
Let us try solving the inequality with one variable as 4x + 3 > 23
4x + 3 – 3 > 23 – 3
⇒ 4x > 20
Step 2: Using the Division Property
${\dfrac{4x}{4} >\dfrac{20}{4}}$
Thus, the solution is x > 5
For Two Variables:
Now, we solve the inequality 7y – 5x ≤ 6y – 3x + 3
Step 1: Solve for ‘x’ Using the Addition Property
7y – 5x + 5x ≤ 6y – 3x + 5x + 3
⇒ 7y ≤ 6y + 2x + 3
Step 2: Solve for ‘y’ Using the Subtraction Property
7y – 6y ≤ 6y + 2x + 3 – 6y
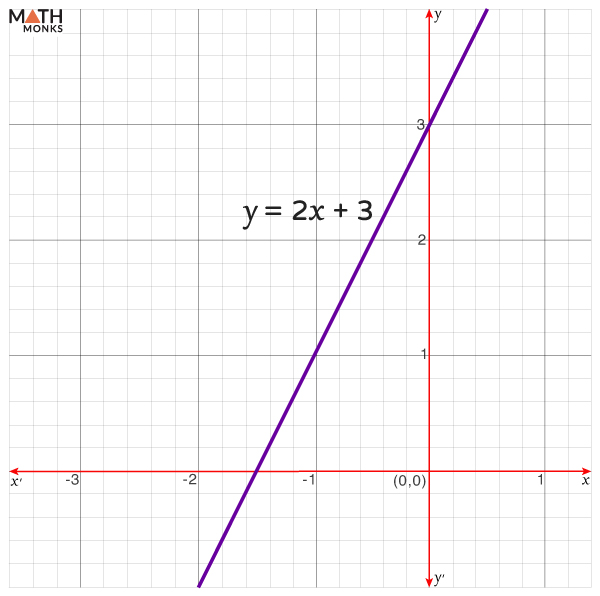
⇒ y ≤ 2x + 3
To plot a graph of the inequality y ≤ 2x + 3, we consider ‘≤’ as ‘=’ sign. Now, plotting the graph y = 2x + 3, we get
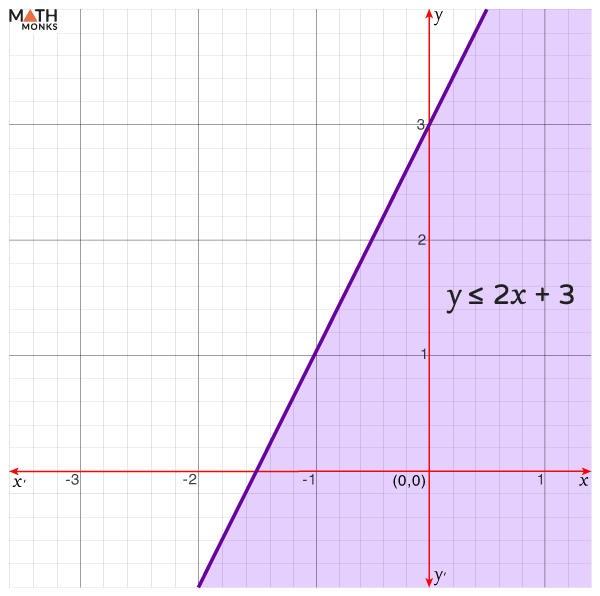
Since the inequality is ‘≥,’ the graph of the equation is formed as a solid line.
Now, considering a point (x, y) as (-2, 0), we get
2x + 3 = 2(-2) + 3 = -4 + 3 = -1, which is not greater than 0
Thus, y ≰ 2x + 3 at (-2, 0)
Now, shading the region that does not contain (-2, 0) shows the following graph.
Solved Examples
Solve and Graph the inequality with one variable: 2x + 5 < 3x

Given, 2x + 5 < 3x Step 1: Using the Subtraction Property 2x + 5 – 2x < 3x – 2x ⇒ 5 < x ⇒ x > 5, which is graphed on the number line as shown.
Solve and Graph the inequality with the variables on both sides: 7x – 5 > 3x + 13
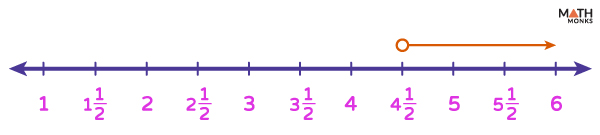
Given, 7x – 5 > 3x + 13 Step 1: Using the Addition and Subtraction Property 7x – 5 + 5 – 3x > 3x + 13 + 5 – 3x ⇒ 4x > 18 Step 2: Using the Division Property ⇒ x > ${\dfrac{18}{4}}$ (by division property) ⇒ x > ${\dfrac{9}{2}}$ However, linear inequalities with the same solution are called equivalent inequalities . Thus, 7x – 5 > 3x + 13 is equivalent to x > ${\dfrac{9}{2}}$ or x > ${4\dfrac{1}{2}}$ By plotting the solution on the number line, we get the shown graph.
Special Cases
Sometimes, plotting the solution of linear inequalities can form a horizontal line parallel to the x-axis or a vertical line parallel to the y-axis.
Case 1: When we plot the graph of the linear inequality y > 1 (‘y’ is greater than 1, excluding 1), the graph includes the entire region above the line y = 1, without the line y = 1 (shown in dotted form).
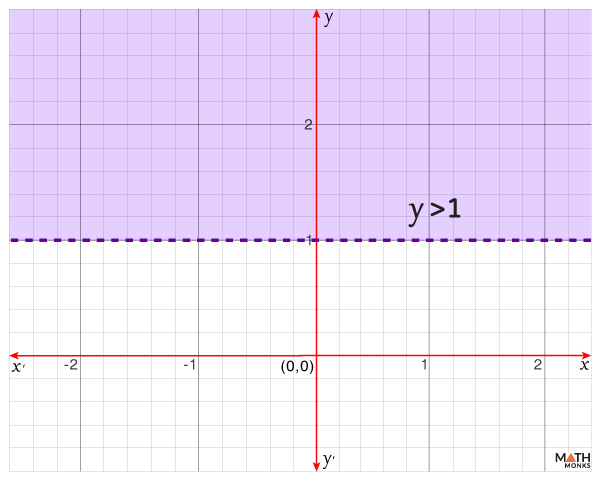
Case 2: When we plot the graph of the linear inequality x < 4 (‘x’ is less than 4, excluding 4), the graph includes the entire region left of line x = 4, without the line x = 4 (shown in dotted form).

System of Linear Inequalities
A system of linear inequalities consists of two or more linear inequalities with the same variables. Its solution includes all ordered pairs that simultaneously satisfy each inequality in the system.
Graphically, the solution set is depicted as the intersection of the regions represented by each individual inequality on the coordinate plane.
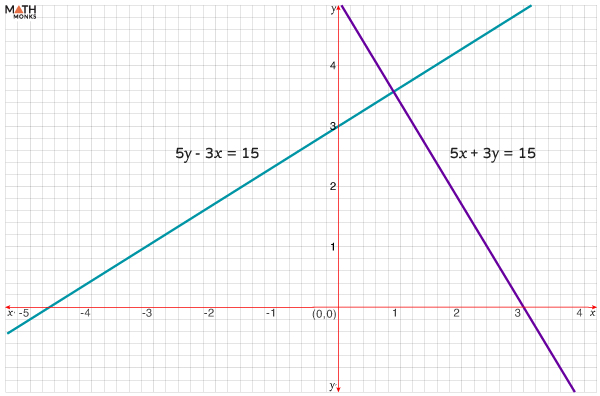
Let us consider the system of inequalities:
5y – 3x < 15 and 5x + 3y > 15
First, we graph each inequality separately, as shown.
Now, let us pick a point that is not on the two given lines and verify whether this point satisfies the inequalities.
Considering the point (x, y) as (2, 1), we get
5y – 3x = 5(1) – 3(2) = 5 – 6 = -1, which is less than 15
5x + 3y = 5(2) + 3(1) = 10 + 3 = 13, which is not greater than 15
Thus, the individual shaded regions and their overlapped region are shaded:
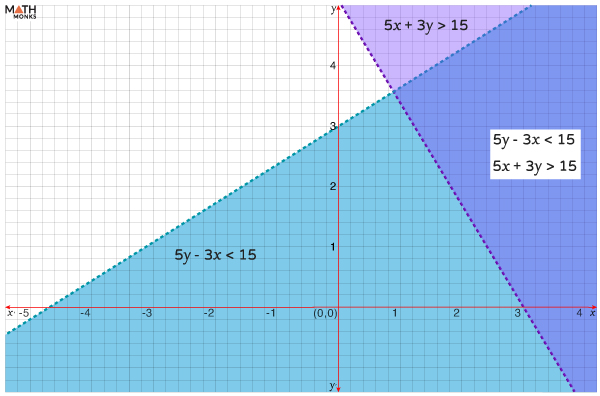
Here, the graphs are formed as dotted lines for the strict inequalities (‘<’ and ‘>’).
Solve and graph the linear inequality 6(x – 3) > 30

Here, 6(x – 3) > 30 ⇒ x – 3 > 5 (by division property) ⇒ x > 5 + 3 (by addition property) ⇒ x > 8 Thus, the solution is x > 8, and its graph is as follows.
Solve the inequality 6(y – 5) < 5(4 + y)
Here, 6(y – 5) < 5(4 + y) ⇒ 6y – 30 < 20 + 5y ⇒ 6y – 5y – 30 + 30 < 20 + 5y – 5y + 30 (by addition and subtraction property) ⇒ y < 50 Thus, the solution is y < 50

Here, the given graph represents the linear inequality x ≥ -2 for any variable x.
Related Materials

- Privacy Policy
- Trigonometry
Join Our Newsletter
© 2024 Mathmonks.com . All rights reserved. Reproduction in whole or in part without permission is prohibited.

- HW Guidelines
- Study Skills Quiz
- Find Local Tutors
- Demo MathHelp.com
- Join MathHelp.com
Select a Course Below
- ACCUPLACER Math
- Math Placement Test
- PRAXIS Math
- + more tests
- 5th Grade Math
- 6th Grade Math
- Pre-Algebra
- College Pre-Algebra
- Introductory Algebra
- Intermediate Algebra
- College Algebra
Examples of Solving Harder Linear Inequalities
Intro & Formatting Worked Examples Harder Examples & Word Prob's
Once you'd learned how to solve one-variable linear equations, you were then given word problems. To solve these problems, you'd have to figure out a linear equation that modelled the situation, and then you'd have to solve that equation to find the answer to the word problem.
Content Continues Below
MathHelp.com
Solving Inequalities
So, now that you know how to solve linear inequalities — you guessed it! — they give you word problems.
- The velocity of an object fired directly upward is given by V = 80 − 32 t , where the time t is measured in seconds. When will the velocity be between 32 and 64 feet per second (inclusive)?
This question is asking when the velocity, V , will be between two given values. So I'll take the expression for the velocity,, and put it between the two values they've given me. They've specified that the interval of velocities is inclusive, which means that the interval endpoints are included. Mathematically, this means that the inequality for this model will be an "or equal to" inequality. Because the solution is a bracket (that is, the solution is within an interval), I'll need to set up a three-part (that is, a compound) inequality.
I will set up the compound inequality, and then solve for the range of times t :
32 ≤ 80 − 32 t ≤ 64
32 − 80 ≤ 80 − 80 − 32 t ≤ 64 − 80
−48 ≤ −32 t ≤ −16
−48 / −32 ≥ −32 t / −32 ≥ −16 / −32
1.5 ≥ t ≥ 0.5
Note that, since I had to divide through by a negative, I had to flip the inequality signs.
Advertisement
Note also that you might (as I do) find the above answer to be more easily understood if it's written the other way around, with "less than" inequalities.
And, because this is a (sort of) real world problem, my working should show the fractions, but my answer should probably be converted to decimal form, because it's more natural to say "one and a half seconds" than it is to say "three-halves seconds". So I convert the last line above to the following:
0.5 ≤ t ≤ 1.5
Looking back at the original question, it did not ask for the value of the variable " t ", but asked for the times when the velocity was between certain values. So the actual answer is:
The velocity will be between 32 and 64 feet per second between 0.5 seconds after launch and 1.5 seconds after launch.
Okay; my answer above was *extremely* verbose and "complete"; you don't likely need to be so extreme. You can probably safely get away with saying something simpler like, "between 0.5 seconds and 1.5 seconds". Just make sure that you do indeed include the approprioate units (in this case, "seconds").
Always remember when doing word problems, that, once you've found the value for the variable, you need to go back and re-read the problem to make sure that you're answering the actual question. The inequality 0.5 ≤ t ≤ 1.5 did not answer the actual question regarding time. I had to interpret the inequality and express the values in terms of the original question.
- Solve 5 x + 7 < 3( x + 1) .
First I'll multiply through on the right-hand side, and then solve as usual:
5 x + 7 < 3( x + 1)
5 x + 7 < 3 x + 3
2 x + 7 < 3
2 x < −4
x < −2
In solving this inequality, I divided through by a positive 2 to get the final answer; as a result (that is, because I did *not* divide through by a minus), I didn't have to flip the inequality sign.
- You want to invest $30,000 . Part of this will be invested in a stable 5% -simple-interest account. The remainder will be "invested" in your father's business, and he says that he'll pay you back with 7% interest. Your father knows that you're making these investments in order to pay your child's college tuition with the interest income. What is the least you can "invest" with your father, and still (assuming he really pays you back) get at least $1900 in interest?
First, I have to set up equations for this. The interest formula for simple interest is I = Prt , where I is the interest, P is the beginning principal, r is the interest rate expressed as a decimal, and t is the time in years.
Since no time-frame is specified for this problem, I'll assume that t = 1 ; that is, I'll assume (hope) that he's promising to pay me at the end of one year. I'll let x be the amount that I'm going to "invest" with my father. Then the rest of my money, being however much is left after whatever I give to him, will be represented by "the total, less what I've already given him", so 30000 − x will be left to invest in the safe account.
Then the interest on the business investment, assuming that I get paid back, will be:
I = ( x )(0.07)(1) = 0.07 x
The interest on the safe investment will be:
(30 000 − x )(0.05)(1) = 1500 − 0.05 x
The total interest is the sum of what is earned on each of the two separate investments, so my expression for the total interest is:
0.07 x + (1500 − 0.05 x ) = 0.02 x + 1500
I need to get at least $1900 ; that is, the sum of the two investments' interest must be greater than, or at least equal to, $1,900 . This allows me to create my inequality:
0.02 x + 1500 ≥ 1900
0.02 x ≥ 400
x ≥ 20 000
That is, I will need to "invest" at least $20,000 with my father in order to get $1,900 in interest income. Since I want to give him as little money as possible, I will give him the minimum amount:
I will invest $20,000 at 7% .

- An alloy needs to contain between 46% copper and 50% copper. Find the least and greatest amounts of a 60% copper alloy that should be mixed with a 40% copper alloy in order to end up with thirty pounds of an alloy containing an allowable percentage of copper.
This is similar to a mixture word problem , except that this will involve inequality symbols rather than "equals" signs. I'll set it up the same way, though, starting with picking a variable for the unknown that I'm seeking. I will use x to stand for the pounds of 60% copper alloy that I need to use. Then 30 − x will be the number of pounds, out of total of thirty pounds needed, that will come from the 40% alloy.
Of course, I'll remember to convert the percentages to decimal form for doing the algebra.
| pounds | % copper | pounds copper | |
|---|---|---|---|
| 60% alloy | 0.6 | 0.6 | |
| 40% alloy | 30 − | 0.4 | 0.4(30 − ) = 12 − 0.4 |
| mixture | 30 | between 0.46 and 0.5 | between 13.8 and 15 |
How did I get those values in the bottom right-hand box? I multiplied the total number of pounds in the mixture ( 30 ) by the minimum and maximum percentages ( 46% and 50% , respectively). That is, I multiplied across the bottom row, just as I did in the " 60% alloy" row and the " 40% alloy" row, to get the right-hand column's value.
The total amount of copper in the mixture will be the sum of the copper contributed by each of the two alloys that are being put into the mixture. So I'll add the expressions for the amount of copper from each of the alloys, and place the expression for the total amount of copper in the mixture as being between the minimum and the maximum allowable amounts of copper:
13.8 ≤ 0.6 x + (12 − 0.4 x ) ≤ 15
13.8 ≤ 0.2 x + 12 ≤ 15
1.8 ≤ 0.2 x ≤ 3
9 ≤ x ≤ 15
Checking back to my set-up, I see that I chose my variable to stand for the number of pounds that I need to use of the 60% copper alloy. And they'd only asked me for this amount, so I can ignore the other alloy in my answer.
I will need to use between 9 and 15 pounds of the 60% alloy.
Per yoozh, I'm verbose in my answer. You can answer simply as " between 9 and 15 pounds ".
- Solve 3( x − 2) + 4 ≥ 2(2 x − 3)
First I'll multiply through and simplify; then I'll solve:
3( x − 2) + 4 ≥ 2(2 x − 3)
3 x − 6 + 4 ≥ 4 x − 6
3 x − 2 ≥ 4 x − 6
−2 ≥ x − 6 (*)
Why did I move the 3 x over to the right-hand side (to get to the line marked with a star), instead of moving the 4 x to the left-hand side? Because by moving the smaller term, I was able to avoid having a negative coefficient on the variable, and therefore I was able to avoid having to remember to flip the inequality when I divided through by that negative coefficient. I find it simpler to work this way; I make fewer errors. But it's just a matter of taste; you do what works for you.
Why did I switch the inequality in the last line and put the variable on the left? Because I'm more comfortable with inequalities when the answers are formatted this way. Again, it's only a matter of taste. The form of the answer in the previous line, 4 ≥ x , is perfectly acceptable.
As long as you remember to flip the inequality sign when you multiply or divide through by a negative, you shouldn't have any trouble with solving linear inequalities.
URL: https://www.purplemath.com/modules/ineqlin3.htm
Page 1 Page 2 Page 3
Standardized Test Prep
College math, homeschool math, share this page.
- Terms of Use
- Privacy / Cookies
- About Purplemath
- About the Author
- Tutoring from PM
- Advertising
- Linking to PM
- Site licencing
Visit Our Profiles
Linear Inequalities
Solving linear inequalities.
Most of the rules or techniques involved in solving multi-step equations should easily translate to solving inequalities.
The only big difference is how the inequality symbol switches direction when a negative number is multiplied or divided to both sides of an equation.
In this lesson, I will go over seven (7) worked examples with different levels of difficulty to provide enough practice.
Inequality Symbols with Examples and Illustrations on Number Lines
GREATER THAN

GREATER THAN OR EQUAL TO

LESS THAN OR EQUAL TO

Examples of How to Solve and Graph Linear Inequalities
Example 1: Solve and graph the solution of the inequality
To solve this inequality, we want to find all values of [latex]x[/latex] that can satisfy it. This means there are almost infinite values of [latex]x[/latex] which when substituted, would yield true statements.
Check the values [latex]x = 0[/latex], [latex]x = 1[/latex], [latex]x = 2[/latex], [latex]x = 3[/latex], [latex]x = 5[/latex], [latex]x = 6[/latex] and [latex]x = 7[/latex].
Which of these [latex]x[/latex]-values give back a true statement?
You should agree after performing some back substitutions that only [latex]5[/latex], [latex]6[/latex], and [latex]7[/latex] work; and the rest fail. But the question is, are there more values of [latex]x[/latex] other than the ones mentioned? The answer is yes! Now, let us solve the inequality to figure out the entire set of values that can make it true.
- Write the original problem.
- Add [latex]17[/latex] on both sides to keep the variables on the left side and the constant on the right.
- The inequality is reduced to this after simplifying.
- Divide both sides of the inequality by the coefficient of [latex]x[/latex].
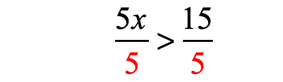
- Final answer:
- Use an open hole to indicate that [latex]3[/latex] is not part of the solution. The solution to the inequality [latex]x > 3[/latex] includes all values to the right of [latex]3[/latex] but excluding [latex]3[/latex] itself. Do you see now why all numbers greater than [latex]3[/latex] are solutions?
Example 2: Solve and graph the solution of the inequality
This example illustrates what happens to the inequality symbol when divided by a negative number.
- To isolate variable [latex]x[/latex] to the left of the inequality, I will add both sides by [latex]2[/latex].
- This is how it looks after I simplify using the above step.
- Now, to solve for [latex]x[/latex], I will divide both sides by [latex] – \,3[/latex].
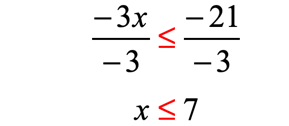
ALWAYS switch the direction of the inequality whenever you divide or multiply a negative number to both sides of the inequality.
Use a close or shaded hole to indicate that [latex]7[/latex] is part of the solution. The solution of the inequality [latex]x \le 7[/latex] includes [latex]7[/latex] and everything to its left.
Example 3: Solve and graph the solution of the inequality
In this problem, I have variables on both sides of the inequality. Although it doesn’t matter where we keep the variable, left or right, it makes sense to be consistent all the time by isolating it on the left side. It’s just a “standard” way, I think.
However, if you try to keep the variable on the right, make sure that you’re aware of their subtleties. For instance, the answer to this problem is [latex]x < – \,6[/latex], which is the same as [latex] – \,6 > x[/latex]. They are equivalent because the opening of the inequality is also pointing towards [latex] – \,6[/latex]. Therefore, this means that if I switch the variable and the constant in my final answer, I must also change the direction of the symbol to keep the meaning the same.
- I want to keep [latex]x[/latex] on the left. I will do that by adding [latex]6x[/latex] to both sides by
- After the step above, I need to move the constant to the right side.
- Subtract both sides by [latex]7[/latex].
- To finally isolate [latex]x[/latex] on the left, divide both sides by the coefficient of [latex]x[/latex] which is [latex]2[/latex].
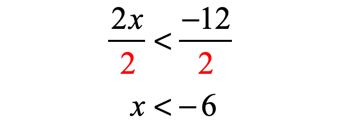
Notice that I did not switch the direction of the inequality because I divided both sides by a positive number.
- Use an open hole to indicate that [latex] – \,6[/latex] is not part of the solution. The solution to the inequality [latex]x < – \,6[/latex] includes all values to the left of [latex] – \,6[/latex] but excluding [latex] – \,6[/latex] itself.
Example 4: Solve and graph the solution of the inequality
I constructed this problem to emphasize the step required in dealing with the parenthesis symbol . I know that this won’t throw you off because you’ve seen it before when solving linear equations, right? The step required to get rid of the parenthesis is to apply the distributive property of multiplication over addition. However, I must caution you to be careful in dealing with the signs during the multiplication process. Remember, the product of two terms with the same signs is positive and when signs are unlike, the product is negative.
- Write the original problem. I will remove the parenthesis first by distributing that [latex] – \,4[/latex] into the binomial [latex]\left( {x – 5} \right)[/latex].
- Simplify and be careful when you distribute. Remember, you get a positive product if the signs are the same and negative if the signs are different.
- In solving inequalities, I make it a habit to “always” keep the variable to the left side. Although, keeping it on the right is also correct. This is just a matter of preference. To keep [latex]x[/latex] to the left, subtract both sides by [latex]3x[/latex].
- Since I want the constant to stay on the right, it becomes clear that my next step is to eliminate the [latex]20[/latex] on the left.
- Subtract both sides by [latex]20[/latex].
- Obviously, I will divide both sides by the negative coefficient and switch the inequality.
- To solve for [latex]x[/latex], divide both sides by [latex] – \,7[/latex] which leaves us the final answer.
- Use a close or shaded hole to indicate that [latex]5[/latex] is part of the solution. The solution of the inequality [latex]x \ge 5[/latex] includes [latex]5[/latex] and everything to its right.
Example 5: Solve and graph the solution of the inequality
My general approach here is to immediately eliminate the parentheses using the distributive property, combine similar terms on both sides, and finally keep [latex]x[/latex] on the left and the constant to the opposite side.
- Write the original problem. I will apply the distributive property twice on the left side for the two parentheses.
For the right side, they are similar terms so I will simply combine them.
- Simplify. At this point, I will further combine like terms on the left. Combine the [latex]x[/latex]’s and the constants together.
- This is what I got after doing the above step.
- Move the constants to the right by adding both sides by [latex]6[/latex].
- Now, move all variables to the left by adding both sides by [latex]4x[/latex].
- Divide both sides by [latex] – \,3[/latex] to isolate [latex]x[/latex]. However, I must change the orientation of the inequality symbol since I divided both sides by a negative number.
- Use an open hole to indicate that [latex] – \,2[/latex] is not part of the solution. The solution of the inequality [latex]x > – 2[/latex] implies all the values to the right of [latex] – \,2[/latex] but excluding [latex] – \,2[/latex].
Example 6: Solve and graph the solution of the inequality
The “complexity” of this problem should not bother you. The key to successfully solving this is to apply all the techniques you have learned so far from our previous examples. If you need a review, please feel free to take a look back.
Try to solve this problem without looking at the detailed solution. Whenever you think you’re done, compare what you have on paper with the answer below.
- Write the original problem. Get rid of the parentheses on both sides of the inequality by applying the distributive property.
- Simplify. Combine similar terms on both sides.
- This is how it looks after combining like terms.
- Subtract both sides by [latex]12[/latex] to keep [latex]x[/latex] on the left.
- Subtract both sides by [latex]5x[/latex] to keep the constant on the right.
- Solve [latex]x[/latex] by dividing both sides by [latex] – 10[/latex], however, don’t forget to switch the direction of the inequality as well.
- Use an open hole to indicate that [latex]2[/latex] is not part of the solution. The solution of the inequality includes all values above [latex]2[/latex] but excluding [latex]2[/latex].
Example 7: Solve and graph the solution of the inequality
Let’s finish strong by doing one final example for mastery! Again, do this yourself first on paper and then compare your solution with the answer below.
- Write the original problem. Combine the [latex]x[/latex] terms on the left side and then apply the distributive property twice on the right side of the inequality.
- This is what we got after doing the step above.
Next, simplify the right side by combing like terms that came out after distribution.
- To isolate [latex]x[/latex] on the left, subtract both sides by [latex]5[/latex].
- Get rid of any variables on the right by subtracting [latex]7x[/latex].
- Finally, divide both sides by [latex] – \,3[/latex] to isolate [latex]x[/latex]. Make sure that we change the direction of the inequality symbol to compensate for the division of a negative number.
- Use a close or shaded hole to indicate that [latex] – \,1[/latex] is part of the solution. The solution to the inequality [latex]x \ge – 1[/latex] includes [latex] – \,1[/latex] and all values to its right as shown by the direction of the arrow.
You might also like these tutorials:
- Steps on How to Graph Linear Inequalities
- Graphing Linear Inequalities Examples
- Graphing Systems of Linear Inequalities
- Solving Compound Inequalities

Linear Inequalities – Examples and Practice Problems
Inequality problems and exercises can be solved with a process similar to the one we use to solve equations. The main difference regarding inequalities is that we have to change the side of the inequality sign when we multiply or divide by negative numbers.
Here, we will look at a summary of how to solve inequalities. In addition, we will look at several examples with answers to master the process of solving inequalities.
Relevant for …
Learning to solve inequalities with solved examples.
See examples
Process used to solve inequalities
Inequalities – examples with answers, inequalities – practice problems.
Remember that inequalities are relationships that compare two values using the signs greater than (>), less than (<), greater than or equal to (≥), and less than or equal to (≤). For example, $latex 3x<6$ and $latex 2x+2>3$ are inequalities.
To solve inequalities, we can follow the following steps:
Step 1: We simplify the inequality if possible. This includes removing grouping signs such as parentheses, combining like terms, and removing fractions.
Step 2: Solve for the variable. We have to do addition and subtraction so that all the variables are located on one side of the inequality and the constants are located on the other side.
Step 3: Solve. We use division or multiplication to find the answer. Note: When we multiply or divide an inequality by a negative number, we must switch sides to the inequality sign.
Step 4: If we have to graph, we have to remember that we use an empty point to indicate that the limiting number is not part of the solution and we use a filled point to indicate that the limiting number is part of the solution.
For example, if the solution is $latex x>2$, the 2 is not part of the solution, so we use an empty point and if the solution is $latex x \ge 2$, the 2 is part of the solution, so we use a filled point.
Solve and graph the inequality $latex 3x-5>1$.
- We start by writing the original problem:
$latex 3x-5>1$
- To solve for the variable, we add 5 to both sides of the inequality:
$latex 3x-5+5>1+5$
- After simplifying, the expression reduces to:
$latex 3x>6$
- To solve, we divide both sides by 3:
$latex \frac{3}{3}x> \frac{6}{3}$
$latex x> 2$
- We graph the inequality with an open point since 2 is not included in the solution. The solution is all the numbers to the right of 2:

Solve and graph the inequality $latex 5x-10<15$.
Step 1: Here, we have nothing to simplify, so we start with:
$latex 5x-10<15$
Step 2: To solve for the variable, we add 10 from both sides and simplify:
$latex 5x-10+10<15+10$
$latex 5x<25$
Step 3: To solve, we divide both sides by 5:
$latex \frac{5}{5}x<\frac{25}{5}$
$latex x<5$
Step 4: To graph, we note that the solutions to the inequality are all real numbers to the left of 5. The 5 is not included, so we use an empty point to indicate this:

Solve and graph the inequality $latex -4x-5\leq 3$.
Step 1: We have nothing to simplify, so we start with:
$latex -4x-5\leq 3$
Step 2: We add 5 to both sides to solve for the variable:
$latex -4x-5+5\leq 3+5$
$latex -4x\leq 8$
Step 3: We divide both sides by -4 to get:
$latex \frac{-4}{-4}x\leq\frac{8}{-4}$
$latex x\geq -2$
| Don’t forget to change the inequality sign when multiplying or dividing by a negative number. |
Step 4: In this case, -2 is part of the solution. Therefore, we use a solid point to indicate that the solutions are all numbers to the right of -2, including -2:

Solve and graph the inequality $latex 4x+2\geq 2x+10$.
In this case, we have variables on both sides. We have to move the variables to one side and the constants to the other. It doesn’t matter which side contains the variables, but it is common to move the variables to the left:
- We start with the original problem:
$latex 4x+2\geq 2x+10$
- We subtract 2 and 2x from both sides to solve for the variable:
$$4x+2-2-2x\geq 2x+10-2-2x$$
- Simplifying the inequality, we have:
$latex 2x\geq 8$
- We divide both sides by 2 and simplify to get the answer:
$latex \frac{2}{2}x\geq \frac{8}{2}$
$latex x\geq 4$
- Here, the 4 is part of the solution, so we use a closed point to indicate this:

Solve the inequality $latex 5x+3>3x-3$.
Step 1: We have nothing to simplify. We start with the inequality:
$latex 5x+3>3x-3$
Step 2: We subtract 3 and 3x from both sides to solve for the variable:
$latex 5x+3-3-3x>3x-3-3-3x$
$latex 2x>-6$
Step 3: We divide both sides by 2 to solve:
$latex \frac{2}{2}x>\frac{-6}{2}$
$latex x>-3$
Solve the inequality $latex 3(x+2)>-9$.
Step 1: We have parentheses, so we apply the distributive property to eliminate them:
$latex 3(x+2)>-9$
$latex 3x+6>-9$
Step 2: To solve for the variable, we subtract 6 from both sides:
$latex 3x+6-6>-9-6$
$latex 3x>-15$
Step 3: To solve, we divide both sides by 3:
$latex \frac{3}{3}x>\frac{-15}{3}$
$latex x>-5$
Solve the inequality $latex 2(3x-3)>4x$.
In this case, we have parentheses, so we use the distributive property to remove parentheses and simplify:
- We write the original problem:
$latex 2(3x-3)>4x$
- We apply the distributive property:
$latex 2(3x)+2(-3)>4x$
$latex 6x-6>4x$
- We add 6 from both sides and subtract 4x to solve for the variable:
$$6x-6+6-4x>4x+6-4x$$
$latex 2x>6$
- By dividing both sides by 2, we have:
$latex \frac{2}{2}x> \frac{6}{2}$
$latex x> 3$
Solve the inequality $latex 2(2x+4)+5>1$.
Step 1: We simplify the parentheses and combine like terms:
$latex 2(2x+4)+5>1$
$latex 4x+8+5>1$
$latex 4x+13>1$
Step 2: We isolate the variable by subtracting 13 from both sides:
$latex 4x+13-13>1-13$
$latex 4x>-12$
Step 3: We have to divide by 4:
$latex \frac{4}{4}x>\frac{-12}{4}$
Solve the inequality $latex 4(2x+4)-3\leq 2(3x+4)+3$.
Step 1: We simplify the parentheses on both sides and combine like terms:
$latex 4(2x+4)-3\leq 2(3x+4)+3$
$latex 8x+16-3\leq 6x+8+3$
$latex 8x+13\leq 6x+11$
Step 2: We subtract 13 and 6x from both sides to solve for the variable:
$$8x+13-13-6x\leq 6x+11-13-6x$$
$latex 2x\leq -2$
Step 3: To solve, we divide both sides by 2:
$latex \frac{2}{2}x\leq \frac{-2}{2}$
$latex x\leq -1$
Solve the inequality $latex 2(x+5)-10\geq 4(2x+6)$.
$latex 2(x+5)-10\geq 4(2x+6)$
$latex 2x+10-10\geq 8x+24$
$latex 2x\geq 8x+24$
Step 2: We subtract both sides by 8x to solve for x :
$latex 2x-8x\geq 8x+24-8x$
$latex -6x\geq 24$
Step 3: Now, we divide by -6:
$latex \frac{-6}{-6}x\geq\frac{24}{-6}$
$latex x\leq -4$

Solve the inequality $latex (-3x-2)+2>-x-2(-2x+6)$
Write the answer in the input box.
Interested in learning more about inequalities? Take a look at these pages:
- How to Solve Linear Inequalities?
- Properties of Inequalities
- 10 Examples of Quadratic Inequalities with Answers

Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.

Learn mathematics with our additional resources in different topics

Copyright © 2024 Neurochispas
All rights reserved.
INFORMATION
Terms and Conditions
Privacy Policy
About Neurochispas
About the Author
Solving Inequalities
Sometimes we need to solve Inequalities like these:
| > | 2 | |
| < | 28 | |
| ≥ | x − 1 | |
| ≤ | 7 |
Our aim is to have x (or whatever the variable is) on its own on the left of the inequality sign:
| Something like: | x < 5 | |
| or: | y ≥ 11 |
We call that "solved".
Example: x + 2 > 12
Subtract 2 from both sides:
x + 2 − 2 > 12 − 2
x > 10
How to Solve
Solving inequalities is very like solving equations , we do most of the same things ...
... but we must also pay attention to the direction of the inequality .
Some things can change the direction !
< becomes >
> becomes <
≤ becomes ≥
≥ becomes ≤
Safe Things To Do
These things do not affect the direction of the inequality:
- Add (or subtract) a number from both sides
- Multiply (or divide) both sides by a positive number
- Simplify a side
Example: 3x < 7+3
We can simplify 7+3 without affecting the inequality:
But these things do change the direction of the inequality ("<" becomes ">" for example):
- Multiply (or divide) both sides by a negative number
- Swapping left and right hand sides
Example: 2y+7 < 12
When we swap the left and right hand sides, we must also change the direction of the inequality :
12 > 2y+7
Here are the details:
Adding or Subtracting a Value
We can often solve inequalities by adding (or subtracting) a number from both sides (just as in Introduction to Algebra ), like this:
Example: x + 3 < 7
If we subtract 3 from both sides, we get:
x + 3 − 3 < 7 − 3
And that is our solution: x < 4
In other words, x can be any value less than 4.
What did we do?
| We went from this:
To this: | x+3 < 7
x < 4 | |||
And that works well for adding and subtracting , because if we add (or subtract) the same amount from both sides, it does not affect the inequality
Example: Alex has more coins than Billy. If both Alex and Billy get three more coins each, Alex will still have more coins than Billy.

What If I Solve It, But "x" Is On The Right?
No matter, just swap sides, but reverse the sign so it still "points at" the correct value!
Example: 12 < x + 5
If we subtract 5 from both sides, we get:
12 − 5 < x + 5 − 5
That is a solution!
But it is normal to put "x" on the left hand side ...
... so let us flip sides (and the inequality sign!):
Do you see how the inequality sign still "points at" the smaller value (7) ?
And that is our solution: x > 7
Note: "x" can be on the right, but people usually like to see it on the left hand side.
Multiplying or Dividing by a Value
Another thing we do is multiply or divide both sides by a value (just as in Algebra - Multiplying ).
But we need to be a bit more careful (as you will see).
Positive Values
Everything is fine if we want to multiply or divide by a positive number :
Example: 3y < 15
If we divide both sides by 3 we get:
3y /3 < 15 /3
And that is our solution: y < 5
Negative Values
| When we multiply or divide by a we must the inequality. |
Well, just look at the number line!
For example, from 3 to 7 is an increase , but from −3 to −7 is a decrease.
| −7 < −3 | 7 > 3 |
See how the inequality sign reverses (from < to >) ?
Let us try an example:
Example: −2y < −8
Let us divide both sides by −2 ... and reverse the inequality !
−2y < −8
−2y /−2 > −8 /−2
And that is the correct solution: y > 4
(Note that I reversed the inequality on the same line I divided by the negative number.)
So, just remember:
When multiplying or dividing by a negative number, reverse the inequality
Multiplying or Dividing by Variables
Here is another (tricky!) example:
Example: bx < 3b
It seems easy just to divide both sides by b , which gives us:
... but wait ... if b is negative we need to reverse the inequality like this:
But we don't know if b is positive or negative, so we can't answer this one !
To help you understand, imagine replacing b with 1 or −1 in the example of bx < 3b :
- if b is 1 , then the answer is x < 3
- but if b is −1 , then we are solving −x < −3 , and the answer is x > 3
The answer could be x < 3 or x > 3 and we can't choose because we don't know b .
Do not try dividing by a variable to solve an inequality (unless you know the variable is always positive, or always negative).
A Bigger Example
Example: x−3 2 < −5.
First, let us clear out the "/2" by multiplying both sides by 2.
Because we are multiplying by a positive number, the inequalities will not change.
x−3 2 ×2 < −5 ×2
x−3 < −10
Now add 3 to both sides:
x−3 + 3 < −10 + 3
And that is our solution: x < −7
Two Inequalities At Once!
How do we solve something with two inequalities at once?
Example: −2 < 6−2x 3 < 4
First, let us clear out the "/3" by multiplying each part by 3.
Because we are multiplying by a positive number, the inequalities don't change:
−6 < 6−2x < 12
−12 < −2x < 6
Now divide each part by 2 (a positive number, so again the inequalities don't change):
−6 < −x < 3
Now multiply each part by −1. Because we are multiplying by a negative number, the inequalities change direction .
6 > x > −3
And that is the solution!
But to be neat it is better to have the smaller number on the left, larger on the right. So let us swap them over (and make sure the inequalities point correctly):
−3 < x < 6
- Many simple inequalities can be solved by adding, subtracting, multiplying or dividing both sides until you are left with the variable on its own.
- Multiplying or dividing both sides by a negative number
- Don't multiply or divide by a variable (unless you know it is always positive or always negative)
Systems of Linear Inequalities, Word Problems - Examples - Expii
SOLVING LINEAR INEQUALITIES IN ONE VARIABLE WORD PROBLEMS
In this section, you will learn how to solve word problems using linear inequalities.
To solve word problems using linear inequalities, we have to model the information given in the question as linear inequalities and solve for unknown.
Problem 1 :
Find all pairs of consecutive odd positive integers, both of which are smaller than 18, such that their sum is more than 20.
Let x be the smaller of the two consecutive odd positive integers.
Then, the other odd integer is (x + 2).
Given : Both the integers are smaller than 18.
In solving this kind of problems, when both the smaller and larger integers are less than 18, always we have to take the larger integer to form inequality.
Then, we have
x + 2 < 18
Subtract 2 from each side.
x < 16 -----(1)
Given : Sum of the integers is more than 20.
x + (x + 2) > 20
x + x + 2 > 20
2x + 2 > 20
Subtract 2 from each side.
Divide each side by 2.
9 < x -----(2)
Combine (1) and (2).
9 < x < 16
So, the value of x is any odd integer between 9 and 16.
The possible values of x are
When x = 11, 12, 13, the possibles values of (x + 2) are
Therefore, the required pairs of odd integers are
(11, 13), (13, 15) and (15, 17)
Problem 2 :
Find all pairs of consecutive even positive integers, both of which are larger than 8, such that their sum is less than 25.
Given : Both the integers are larger than 8.
In solving this kind of problems, when both the smaller and larger integers are larger than 18, always we have to take the smaller integer to form inequality.
8 < x -----(1)
Given : Sum of the integers is less than 25.
x + (x + 2) < 25
x + x + 2 < 25
2x + 2 < 25
x < 11.5 -----(2)
8 < x < 11.5
So, the value of x is any even integer between 8 and 11.5.
There is only one even integer between 8 and 11.5
So, the possible value of x is
When x = 10, the possibles value of (x + 2) is
Therefore, the required pair of even integers is
Problem 3 :
In the first four papers each of 100 marks, John got 95, 72, 73, 83 marks. If he wants an average of greater than or equal to 75 marks and less than 80 marks, find the range of marks he should score in the fifth paper.
Let x be the marks scored by John in fifth paper.
75 ≤ [(95 + 72 + 73 + 83 + x)/5] < 80
75 ≤ (323 + x) / 5 < 80
Multiply each side by 5.
375 ≤ (323 + x) < 400
Subtract 323 from each side.
52 ≤ x < 77
So, John should score between 51 and 77 marks in his fifth paper.
Problem 4 :
A man wants to cut three lengths from a single piece of board of length 91 cm. The second length is to be 3 cm longer than the shortest and third length is to be twice as the shortest. What are the possible lengths for the shortest piece, if third piece is to be at least 5 cm longer than the second ?
Let x be the length of the shortest piece
Then, the lengths of the second and third piece are
x + 3 and 2x
Given : The total length of the board is 91 cm.
x + (x + 3) + 2x ≤ 91
4x + 3 ≤ 91
Subtract 3 from each side.
4x ≤ 88
x ≤ 22 -----(1)
Given : The third piece has to be at least 5 cm longer than the second.
2x ≥ (x + 3) + 5
2x ≥ x + 8
Subtract x from each side.
8 ≤ x -----(2)
Combine (1) and (2).
8 ≤ x ≤ 22
So, the shortest piece must be at least 8 cm long but not more than 22 cm long.
Kindly mail your feedback to [email protected]
We always appreciate your feedback.
© All rights reserved. onlinemath4all.com
- Sat Math Practice
- SAT Math Worksheets
- PEMDAS Rule
- BODMAS rule
- GEMDAS Order of Operations
- Math Calculators
- Transformations of Functions
- Order of rotational symmetry
- Lines of symmetry
- Compound Angles
- Quantitative Aptitude Tricks
- Trigonometric ratio table
- Word Problems
- Times Table Shortcuts
- 10th CBSE solution
- PSAT Math Preparation
- Privacy Policy
- Laws of Exponents
Recent Articles
Solving exponential equations problems and solutions (part - 4).
Aug 31, 24 06:48 PM
Geometry Problems with Solutions (Part - 7)
Aug 31, 24 07:14 AM
Digital SAT Math Problems and Solutions (part - 12)
Aug 30, 24 08:45 PM
- School Guide
- Mathematics
- Number System and Arithmetic
- Trigonometry
- Probability
- Mensuration
- Maths Formulas
- Class 8 Maths Notes
- Class 9 Maths Notes
- Class 10 Maths Notes
- Class 11 Maths Notes
- Class 12 Maths Notes
Solving Linear Inequalities Word Problems
We are well versed with equations in multiple variables. Linear Equations represent a point in a single dimension, a line in a two-dimensional, and a plane in a three-dimensional world. Solutions to linear inequalities represent a region of the Cartesian plane. It becomes essential for us to know how to translate real-life problems into linear inequalities.
Linear Inequalities
Before defining the linear inequalities formally, let’s see them through a real-life situation and observe why their need arises in the first place. Let’s say Albert went to buy some novels for himself at the book fair. He has a total of Rs 200 with him. The book fair has a special sale policy which offers any book at Rs 70. Now he knows that he may not be able to spend the full amount on the books. Let’s say x is the number of books he bought. This situation can be represented mathematically by the following equation,
70x < 200
Since he can’t spend all the amount on books, and also the amount spent by him will always be less than Rs 200. The present situation can only be represented by the equation given above. Now let’s study the linear inequalities with a formal description,
Two real numbers or two algebraic expressions which are related by symbols such as ‘>’, ‘<‘, ‘≥’ and’≤’ form the inequalities. Linear inequalities are formed by linear equations which are connected with these symbols. These inequalities can be further classified into two parts: Strict Inequalities: The inequalities with the symbols such as ‘>’ or ‘<‘. Slack Inequalities: The inequalities with the symbols such as ‘≥’ or ‘≤’.
Rules of Solving Linear Inequalities
There are certain rules which we should keep in mind while solving linear inequalities.
- Equal numbers can be added or subtracted from both sides of the inequality without affecting its sign.
- Both sides of Inequality can be divided or multiplied by any positive number but when they are multiplied or divided by a negative number, the sign of the linear inequality is reversed.
Now with this brief introduction to linear inequalities, let’s see some word problems on this concept.
Sample Problems
Question 1: Considering the problem given in the beginning. Albert went to buy some novels for himself at the book fair. He has a total of Rs 200 with him. The book fair has a special sale policy which offers any book at Rs 70. Now he knows that he may not be able to spend the full amount on the books. Let’s say x is the number of books he bought. Represent this situation mathematically and graphically.
We know that Albert cannot buy books for all the money he has. So, let’s say the number of books he buys is “x”. Then, 70x < 200 ⇒ x < [Tex]\frac{20}{7}[/Tex] To plot the graph of this inequality, put x = 0. 0 < [Tex]\frac{20}{7} [/Tex] Thus, x = 0 satisfies the inequality. So, the graph for the following inequality will look like,
Question 2: Consider the performance of the strikers of the football club Real Madrid in the last 3 matches. Ronaldo and Benzema together scored less than 9 goals in the last three matches. It is also known that Ronaldo scored three more goals than Benzema. What can be the possible number of goals Ronaldo scored?
Let’s say the number of goals scored by Benzema and Ronaldo are y and x respectively. x = y + 3 …..(1) x + y < 9 …..(2) Substituting the value of x from equation (1) in equation (2). y + 3 + y < 9 ⇒2y < 6 ⇒y < 3 Possible values of y: 0,1,2 Possible values of x: 3,4,5
Question 3: A classroom can fit at least 9 tables with an area of a one-meter square. We know that the perimeter of the classroom is 12m. Find the bounds on the length and breadth of the classroom.
It can fit 9 tables, that means the area of the classroom is atleast 9m 2 . Let’s say the length of the classroom is x and breadth is y meters. 2(x + y) = 12 {Perimeter of the classroom} ⇒ x + y = 6 Area of the rectangle is given by, xy > 9 ⇒x(6 – x) > 9 ⇒6x – x 2 > 9 ⇒ 0 > x 2 – 6x + 9 ⇒ 0 > (x – 3) 2 ⇒ 0 > x – 3 ⇒ x < 3 Thus, length of the classroom must be less than 3 m. So, then the breadth of the classroom will be greater than 3 m.
Question 4: Formulate the linear inequality for the following situation and plot its graph.
Let’s say Aman and Akhil went to a stationery shop. Aman bought 3 notebooks and Akhil bought 4 books. Let’s say cost of each notebook was “x” and each book was “y”. The total expenditure was less than Rs 500.
Cost of each notebook was “x” and for each book, it was “y”. Then the inequality can be described as, 3x + 4y < 500 Putting (x,y) → (0,0) 3(0) + 4(0) < 500 Origin satisfies the inequality. Thus, the graph of its solutions will look like, x.
Question 5: Formulate the linear inequality for the following situation and plot its graph.
A music store sells its guitars at five times their cost price. Find the shopkeeper’s minimum cost price if his profit is more than Rs 3000.
Let’s say the selling price of the guitar is y, and the cost price is x. y – x > 3000 ….(1) It is also given that, y = 5x ….(2) Substituting the value of y from equation (2) to equation (1). 5x – x > 3000 ⇒ 4x > 3000 ⇒ x > [Tex]\frac{3000}{4}[/Tex] ⇒ x> 750 Thus, the cost price must be greater than Rs 750.
Question 6: The length of the rectangle is 4 times its breadth. The perimeter of the rectangle is less than 20. Formulate a linear inequality in two variables for the given situation, plot its graph and calculate the bounds for both length and breadth.
Let’s say the length is “x” and breadth is “y”. Perimeter = 2(x + y) < 20 ….(1) ⇒ x + y < 10 Given : x = 4y Substituting the value of x in equation (1). x + y < 10 ⇒ 5y < 10 ⇒ y < 2 So, x < 8 and y < 2.
Question 7: Rahul and Rinkesh play in the same football team. In the previous game, Rahul scored 2 more goals than Rinkesh, but together they scored less than 8 goals. Solve the linear inequality and plot this on a graph.
The equations obtained from the given information in the question, Suppose Rahul scored x Number of goals and Rinkesh scored y number of goals, Equations obtained will be, x = y+2 ⇢ (1) x+y< 8 ⇢ (2) Solving both the equations, y+2 + y < 8 2y < 6 y< 3 Putting this value in equation (2), x< 5
Question 8: In a class of 100 students, there are more girls than boys, Can it be concluded that how many girls would be there?
Let’s suppose that B is denoted for boys and G is denoted for girls. Now, since Girls present in the class are more than boys, it can be written in equation form as, G > B The total number of students present in class is 100 (given), It can be written as, G+ B= 100 B = 100- G Substitute G> B in the equation formed, G> 100 – G 2G > 100 G> 50 Hence, it is fixed that the number of girls has to be more than 50 in class, it can be 60, 65, etc. Basically any number greater than 50 and less than 100.
Question 9: In the previous question, is it possible for the number of girls to be exactly 50 or exactly 100? If No, then why?
No, It is not possible for the Number of girls to be exactly 50 since while solving, it was obtained that, G> 50 In any case if G= 50 is a possibility, from equation G+ B= 100, B = 50 will be obtained. This simply means that the number of boys is equal to the number of girls which contradicts to what is given in the question. No, it is not possible for G to be exactly 100 as well, as this proves that there are 0 boys in the class.
Question 10: Solve the linear inequality and plot the graph for the same,
7x+ 8y < 30
The linear inequality is given as, 7x+ 8y< 30 At x= 0, y= 30/8= 3.75 At y= 0, x= 30/7= 4.28 These values are the intercepts. The graph for the above shall look like, Putting x= y/2, that is, y= 2x in the linear inequality, 7x + 16x < 30 x = 1.304 y = 2.609
Related Articles:
- Linear Equations Formula
- Linear Equations
- Linear Algebra
Solving Linear Inequalities Word Practice Problems
Problem 1: A company produces widgets and sells them for $20 each. They have a fixed cost of $500 and a variable cost of $5 per widget. If the company wants to make a profit of at least $1000, how many widgets must they sell?
Problem 2: Sarah is planning a party and wants to spend no more than $150 on food. If each sandwich costs $3 and each drink costs $2 how many sandwiches and drinks can she buy if she wants to spend her entire budget?
Problem 3: A student has a maximum of 3 hours per day to study. If he spends 45 minutes on math homework and 30 minutes on science homework how much time does he have left for history homework each day?
Problem 4: A theater has a maximum seating capacity of 200 people. If the theater sells tickets for $15 each. how many tickets can they sell if they want to make at least $1500 in revenue?
Problem 5: John is saving money to buy a new laptop. He saves $50 per week and has already saved $200. If the laptop costs $600 how many more weeks will he need to save to afford the laptop?
Problem 6: A car rental company charges a base fee of $30 per day plus $0.25 per mile driven. If a customer’s budget is $100. what is the maximum number of miles they can drive?
Problem 7: A gardener has 10 meters of fencing and wants to enclose a rectangular garden. If the length of the garden is to be at least 2 meters. what is the maximum width of the garden he can have?
Problem 8: A student needs to complete at least 120 hours of community service. If she has already completed 45 hours. how many more hours does she need to complete?
Problem 9: A local grocery store offers a discount of 10% on all purchases over $50. If a customer wants to spend no more than $60 including tax what is the maximum amount they can spend before the discount?
Problem 10: An online course charges a monthly fee of $25 and $5 for each additional module. If a student has a budget of $75. how many additional modules can they purchase?
FAQs – Solving Linear Inequalities Word Problems
What is the difference between linear equations and linear inequalities.
The Linear equations represent a straight line and have an equal sign (=). The Linear inequalities represent a range of the solutions and use inequality signs (>, <, ≥, ≤).
Can I graph linear inequalities?
Yes, the linear inequalities can be graphed on the coordinate plane. The solution set is usually represented by a shaded region that satisfies the inequality.
How do I interpret word problems involving linear inequalities?
The Identify the variables write the inequality that models the problem and solve the inequality to find the range of the solutions that satisfy the conditions.
What if the inequality involves more than one variable?
For inequalities involving the more than one variable solve for one variable in the terms of the others and graph the solution region in the coordinate plane.
Can linear inequalities have no solution?
Yes, if the inequality represents a situation that cannot be satisfied by the any real number the solution set is empty.
Please Login to comment...
Similar reads.
- School Learning
- Maths-Class-11
- Best 10 IPTV Service Providers in Germany
- Python 3.13 Releases | Enhanced REPL for Developers
- IPTV Anbieter in Deutschland - Top IPTV Anbieter Abonnements
- Best SSL Certificate Providers in 2024 (Free & Paid)
- Content Improvement League 2024: From Good To A Great Article
Improve your Coding Skills with Practice
What kind of Experience do you want to share?
SOLVING LINEAR INEQUALITIES WORD PROBLEMS IN TWO VARIABLES
A statement involving the symbols ‘>’, ‘<’, ‘ ≥’, ‘≤’ is called an inequality.
By understanding the real situation, we have to use two variables to represent each quantities
Problem 1 :
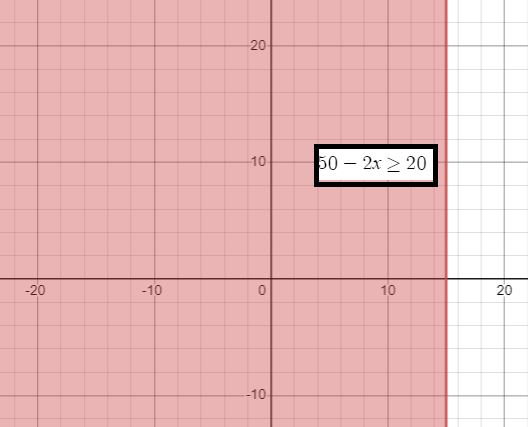
Katie has $50 in a savings account at the beginning of the summer. She wants to have at least $20 in the account by the end of the summer. She withdraws $2 each week for food, clothes, and movie tickets. Write an inequality that expresses Katie’s situation and display it on the graph below. For how many weeks can Katie withdraw money?
Let x be the number of weeks
50 - 2x ≥ 20
2x ≤ 30
x ≤ 15 weeks
Problem 2 :
Skate Land charges a $50 flat fee for a birthday party rental and $4 for each person. Joann has no more than $100 to budget for her party. Write an inequality that models her situation and display it on the graph below. How many people can attend Joann's party.
Assume x people can attend the party.
y = 50 + 4x
50 + 4x ≤ 100
So, 12 people can attend Joan’s party.
Problem 3 :
Sarah is selling bracelets and earrings to make money for summer vacation. The bracelets cost $2 and the earrings cost $3. She needs to make at least $60. Sarah knows she will sell more than 10 bracelets. Write inequalities to represent the income from jewelry sold and number of bracelets sold. Find two possible solutions.
Let x be the number of bracelets sold.
Let y be the number of earrings sold.
2x + 3y ≥ 60
If x = 11, then 2(11) + 3y ≥ 60
3y ≥ 60 - 22
3y ≥ 38
Since y is the number of earrings, x = 11 is not possible.
| If x = 12 2(12) + 3y = 60 24 + 3y = 60 3y = 60 - 24 3y = 36 y = 12 x = 12 and y = 12 | If x = 15 2(15) + 3y = 60 30 + 3y = 60 3y = 60 - 30 3y = 30 y = 10 x = 15 and y = 10 |
- Variables and Expressions
- Variables and Expressions Worksheet
- Place Value of Number
- Formation of Large Numbers
- Laws of Exponents
- Angle Bisector Theorem
- Pre Algebra
- SAT Practice Topic Wise
- Geometry Topics
- SMO Past papers
- Parallel Lines and Angles
- Properties of Quadrilaterals
- Circles and Theorems
- Transformations of 2D Shapes
- Quadratic Equations and Functions
- Composition of Functions
- Polynomials
- Fractions Decimals and Percentage
- Customary Unit and Metric Unit
- Honors Geometry
- 8th grade worksheets
- Linear Equations
- Precalculus Worksheets
- 7th Grade Math Worksheets
- Vocabulary of Triangles and Special right triangles
- 6th Grade Math Topics
- STAAR Math Practice
- Math 1 EOC Review Worksheets
- 11 Plus Math Papers
- CA Foundation Papers
- Algebra 1 Worksheets
Recent Articles
Finding range of values inequality problems.
May 21, 24 08:51 PM
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
© All rights reserved. intellectualmath.com
- AI Math Solver Graphing Calculator Popular Problems Worksheets Study Guides Cheat Sheets Calculators Verify Solution
- Solutions Integral Calculator Derivative Calculator Algebra Calculator Matrix Calculator More...
- Graphing Line Graph Exponential Graph Quadratic Graph Sine Graph More...
- Calculators BMI Calculator Compound Interest Calculator Percentage Calculator Acceleration Calculator More...
- Geometry Pythagorean Theorem Calculator Circle Area Calculator Isosceles Triangle Calculator Triangles Calculator More...
- Tools Notebook Groups Cheat Sheets Worksheets Study Guides Practice Verify Solution
| x^{\msquare} | \log_{\msquare} | \sqrt{\square} | \nthroot[\msquare]{\square} | \le | \ge | \frac{\msquare}{\msquare} | \cdot | \div | x^{\circ} | \pi | |||||||||||
| \left(\square\right)^{'} | \frac{d}{dx} | \frac{\partial}{\partial x} | \int | \int_{\msquare}^{\msquare} | \lim | \sum | \infty | \theta | (f\:\circ\:g) | f(x) | |||||||||||
| ▭\:\longdivision{▭} | \times \twostack{▭}{▭} | + \twostack{▭}{▭} | - \twostack{▭}{▭} | \left( | \right) | \times | \square\frac{\square}{\square} |
- Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
- Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Prove That Logical Sets Word Problems
- Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Coterminal Angle Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
- Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
- Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
- Linear Algebra Matrices Vectors
- Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
- Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
- Physics Mechanics
- Chemistry Chemical Reactions Chemical Properties
- Finance Simple Interest Compound Interest Present Value Future Value
- Economics Point of Diminishing Return
- Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
- Pre Algebra
- One-Step Addition
- One-Step Subtraction
- One-Step Multiplication
- One-Step Division
- One-Step Decimals
- Two-Step Integers
- Two-Step Add/Subtract
- Two-Step Multiply/Divide
- Two-Step Fractions
- Two-Step Decimals
- Multi-Step Integers
- Multi-Step with Parentheses
- Multi-Step Rational
- Multi-Step Fractions
- Multi-Step Decimals
- Solve by Factoring
- Completing the Square
- Quadratic Formula
- Biquadratic
- Logarithmic
- Exponential
- Rational Roots
- Floor/Ceiling
- Equation Given Roots
- Equation Given Points
- Newton Raphson
- Substitution
- Elimination
- Cramer's Rule
- Gaussian Elimination
- System of Inequalities
- Perfect Squares
- Difference of Squares
- Difference of Cubes
- Sum of Cubes
- Polynomials
- Distributive Property
- FOIL method
- Perfect Cubes
- Binomial Expansion
- Negative Rule
- Product Rule
- Quotient Rule
- Expand Power Rule
- Fraction Exponent
- Exponent Rules
- Exponential Form
- Logarithmic Form
- Absolute Value
- Rational Number
- Powers of i
- Complex Form
- Partial Fractions
- Is Polynomial
- Leading Coefficient
- Leading Term
- Standard Form
- Complete the Square
- Synthetic Division
- Linear Factors
- Rationalize Denominator
- Rationalize Numerator
- Identify Type
- Convergence
- Interval Notation
- Pi (Product) Notation
- Boolean Algebra
- Truth Table
- Mutual Exclusive
- Cardinality
- Caretesian Product
- Age Problems
- Distance Problems
- Cost Problems
- Investment Problems
- Number Problems
- Percent Problems
- Addition/Subtraction
- Multiplication/Division
- Dice Problems
- Coin Problems
- Card Problems
- Pre Calculus
- Linear Algebra
- Trigonometry
- Conversions
| x^{\msquare} | \log_{\msquare} | \sqrt{\square} | \nthroot[\msquare]{\square} | \le | \ge | \frac{\msquare}{\msquare} | \cdot | \div | x^{\circ} | \pi | |||||||||||
| \left(\square\right)^{'} | \frac{d}{dx} | \frac{\partial}{\partial x} | \int | \int_{\msquare}^{\msquare} | \lim | \sum | \infty | \theta | (f\:\circ\:g) | f(x) | |||||||||||
| - \twostack{▭}{▭} | \lt | 7 | 8 | 9 | \div | AC |
| + \twostack{▭}{▭} | \gt | 4 | 5 | 6 | \times | \square\frac{\square}{\square} |
| \times \twostack{▭}{▭} | \left( | 1 | 2 | 3 | - | x |
| ▭\:\longdivision{▭} | \right) | . | 0 | = | + | y |
Number Line
- -x+3\gt 2x+1
- (x+5)(x-5)\gt 0
- 2x^2-x\gt 0
- (x+3)^2\le 10x+6
- \left|3+2x\right|\le 7
- \frac{\left|3x+2\right|}{\left|x-1\right|}>2
- What are the 4 inequalities?
- There are four types of inequalities: greater than, less than, greater than or equal to, and less than or equal to.
- What is a inequality in math?
- In math, inequality represents the relative size or order of two values.
- How do you solve inequalities?
- To solve inequalities, isolate the variable on one side of the inequality, If you multiply or divide both sides by a negative number, flip the direction of the inequality.
- What are the 2 rules of inequalities?
- The two rules of inequalities are: If the same quantity is added to or subtracted from both sides of an inequality, the inequality remains true. If both sides of an inequality are multiplied or divided by the same positive quantity, the inequality remains true. If we multiply or divide both sides of an inequality by the same negative number, we must flip the direction of the inequality to maintain its truth.
inequalities-calculator
- High School Math Solutions – Inequalities Calculator, Radical Inequalities Last post, we went over how to solve absolute value inequalities. For today’s post, we will talk about how to solve...
- Solve Inequalities Learning Outcomes Describe solutions to inequalities Represent inequalities on a number line Represent inequalities using interval notation Solve single-step inequalities Use the addition and multiplication properties to solve algebraic inequalities and express their solutions graphically and with...
- 3A.2 Solve Compound Inequalities 3A.2 Learning Objectives Use interval notation to describe intersections and unions Use graphs to describe intersections and unions Solve compound inequalities in the form of or and express the solution graphically and with an interval Express solutions to inequalities graphically and with interval...
- Linear Inequalities and Systems of Linear Inequalities in Two Variables Learning Objectives Define solutions to a linear inequality in two variables Identify and follow steps for graphing a linear inequality in two variables Identify whether an ordered pair is in the solution set of a linear inequality Define solutions to systems of linear inequalities Graph a system o...
- Compound Inequalities Learning Objectives Describe sets as intersections or unions Use interval notation to describe intersections and unions Use graphs to describe intersections and unions Solve compound inequalities—OR Solve compound inequalities in the form of or and express the solution graphically and with an inter...
- Inequalities Introduction to Inequalities Inequalities are used to demonstrate relationships between numbers or expressions. Learning Objectives Explain what inequalities represent and how they are used Key Takeaways Key Points An inequality describes a relationship between two different values. The notation me...
- Systems of Linear Inequalities 6.3 Learning Objectives Define solutions to systems of linear inequalities Graph a system of linear inequalities and define the solutions region Verify whether a point is a solution to a system of inequalities Identify when a system of inequalities has no solution Solutions from graphs of linear in...
- 3A.1 Single- and Multi-Step Inequalities 3A.1 Learning Objectives Represent inequalities on a number line Represent inequalities using interval notation Use the addition and multiplication properties to solve algebraic inequalities Express solutions to inequalities graphically, with interval notation, and as an inequality Sometimes there...
- Reading: Solving One-Step Inequalities Inequalities are similar to equations in that they show a relationship between two expressions. We solve and graph inequalities in a similar way to equations. However, there are some differences that we will talk about in this chapter. The main difference is that for linear inequalities the answer i...
- Linear Inequalities and Absolute Value Inequalities It is not easy to make the honor role at most top universities. Suppose students were required to carry a course load of at least 12 credit hours and maintain a grade point average of 3.5 or above. How could these honor roll requirements be expressed mathematically? In this section, we will explore...
- Poverty and Economic Inequality Figure 1. Occupying Wall StreetOn September 17, 2011, Occupy Wall Street began in New York City’s Wall Street financial district. (Credit: modification of work by David Shankbone/Flickr Creative Commons) Occupy Wall Street In September 2011, a group of protesters gathered in Zuccotti Park in New Yo...
We want your feedback
Please add a message.
Message received. Thanks for the feedback.
- ML Aggarwal Solutions
- ML Aggarwal Class 10 Solutions
- Chapter 4 Linear Inequations

ML Aggarwal Solutions for Class 10 Maths Chapter 4 Linear Inequations
ML Aggarwal Solutions for Class 10 Maths Chapter 4 Linear Inequations can be utilised by the students to comprehend the concepts and solve problems in an effective way. The solutions are clearly briefed in a step-by-step manner in order to help students understand easily. Further, these solutions are in accordance with the latest ICSE board guidelines. To learn more about these concepts, students can access the ML Aggarwal Solutions for Class 10 Maths Chapter 4 Linear Inequations PDF from the link provided below.
The main topics covered in this chapter are inequalities among real numbers, linear inequations and solving linear inequations in one variable using the two permissible rules. Students can start solving the problems on a regular basis so that their conceptual knowledge becomes stronger and their problem-solving skills are also improved, which is important from the examination perspective. Moreover, the ML Aggarwal Solutions can be used as a reference to answers and to learn the other methods of solving problems effortlessly.
ML Aggarwal Solutions for Class 10 Maths Chapter 4 Linear Inequations:
carouselExampleControls111

Previous Next
Access ML Aggarwal Solutions for Class 10 Maths Chapter 4 Linear Inequations
1. Solve the inequation, 3x – 11 < 3 where x ∈ {1, 2, 3, ……, 10}. Also, represent its solution on a number line.
Given inequation, 3x – 11 < 3
3x < 3 + 11
⇒ x < 14/3
But, x ∈ {1, 2, 3,……, 10}
Hence, the solution set is {1, 2, 3, 4}.
Representing the solution on a number line:
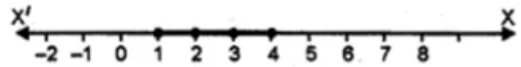
2. Solve 2(x – 3) < 1, x ∈ {1, 2, 3, …. 10}
Given inequation, 2(x – 3) < 1
2x – 6 < 1
⇒ x < 7/2
But, x ∈ {1, 2, 3, …. 10}
Hence, the solution set is {1, 2, 3}
3. Solve 5 – 4x > 2 – 3x, x ∈ W. Also represent its solution on the number line.
Given inequation, 5 – 4x > 2 – 3x
– 4x + 3x > 2 – 5
On multiplying both sides by -1, the inequality reverses
⇒ x < 3
Since, x ∈ W
The solution set is {0, 1, 2}

4. List the solution set of 30 – 4 (2x – 1) < 30, given that x is a positive integer. Solution:
Given inequation, 30 – 4 (2x – 1) < 30
30 – 8x + 4 < 30
34 – 8x < 30
-8x < 30 – 34
-8x < -4 [On multiplying both sides by -1, the inequality reverses]
⇒ x > 1/2
As x is a positive integer
The solution set is {1, 2, 3, … }
5. Solve: 2 (x – 2) < 3x – 2, x ∈ {– 3, – 2, – 1, 0, 1, 2, 3}. Solution:
Given inequation, 2 (x – 2) < 3x – 2
2x – 4 < 3x – 2
2x – 3x < -2 + 4
⇒ x > -2
But, x ∈ {– 3, – 2, – 1, 0, 1, 2, 3}
Hence, the solution set is {– 1, 0, 1, 2, 3}.
6. If x is a negative integer, find the solution set of 2/3 + 1/3 (x + 1) > 0. Solution:
Given inequation, 2/3 + 1/3 (x + 1) > 0.
2/3 + x/3 + 1/3 > 0
x/3 + 1 > 0
x/3 > -1
⇒ x > -3
As x is a negative integer
The solution set is {-1, -2}.
7. Solve x – 3 (2 + x) > 2 (3x – 1), x ∈ { – 3, – 2, – 1, 0, 1, 2, 3}. Also represent its solution on the number line. Solution:
Given inequation, x – 3 (2 + x) > 2 (3x – 1)
x – 6 – 3x > 6x – 2
-2x – 6 > 6x – 2
-6x – 2x > -2 + 6
x < -4/8
⇒ x < -1/2
But, x ∈ { – 3, – 2, – 1, 0, 1, 2, 3}
Hence, the solution set is {-3, -2, -1}
8. Given x ∈ {1, 2, 3, 4, 5, 6, 7, 9} solve x – 3 < 2x – 1.
Given inequation, x – 3 < 2x – 1
x – 2x < – 1 + 3
But, x ∈ {1, 2, 3, 4, 5, 6, 7, 9}
Hence, the solution set is {1, 2, 3, 4, 5, 6, 7, 9}.
9. List the solution set of the inequation ½ + 8x > 5x – 3/2, x ∈ Z Solution:
Given inequation, ½ + 8x > 5x – 3/2
8x – 5x > -3/2 – ½
3x > -4/2
⇒ x > -2/3
As x ∈ Z
The solution set is {0, 1, 2, 3, 4, 5, …}
10. List the solution set of (11 – 2x)/5 ≥ (9 – 3x)/8 + 3/4, x ∈ N
Given inequation, (11 – 2x)/5 ≥ (9 – 3x)/8 + ¾
(11 – 2x)/5 ≥ (9 – 3x + 6)/8
8 (11 – 2x) ≥ 5 (15 – 3x)
88 – 16x ≥ 75 – 15x
15x – 16x ≥ 75 – 88
-x ≥ -13
⇒ x ≤ 13
As x ∈ N
Hence, the solution set is {1, 2, 3, 4, …, 13}.

-2 ≤ (3 – 4x)/ 6 ≤ 11/6
-12 ≤ 3 – 4x ≤ 11
-12 – 3 ≤ -4x ≤ 11 – 3
-15 ≤ -4x ≤ 8
-15/4 ≤ -x ≤ 8/4
⇒ 15/4 ≥ x ≥ -2
As x ∈ N,
The solution set is {1, 2, 3}.

12. If x ∈ W, find the solution set of 3/5 x – (2x – 1)/3 > 1. Also graph the solution set on the number line, if possible. Solution:
Given inequation, 3/5 x – (2x – 1)/3 > 1
9/15 x – 5(2x – 1)/15 > 1 [Taking L.C.M]
9x – 5(2x – 1) > 15 [Multiplying by 15 on both sides]
9x – 10x + 5 > 15
-x > 15 – 5
⇒ x < -10
But, x ∈ W
Hence, the solution set is a null set.
Thus, it can’t be represented on number line.
(i) x/2 + 5 ≤ x/3 + 6, where x is a positive odd integer.
(ii) (2x + 3)/3 ≥ (3x – 1)/4, where x is positive even integer. Solution:
(i) Given inequation, x/2 + 5 ≤ x/3 + 6
(x + 10)/2 ≤ (x + 18)/3 [Taking L.C.M on both sides]
3 (x + 10) ≤ 2 (x + 18) [On cross-multiplying]
3x + 30 ≤ 2x + 36
3x – 2x ≤ 36 – 30
⇒ x ≤ 6
As x is a positive odd integer.
Hence, the solution set is {1, 3, 5}.
(ii) Given inequation, (2x + 3)/3 ≥ (3x – 1)/4
4 (2x + 3) ≥ 3 (3x – 1) [On cross-multiplying]
8x + 12 ≥ 9x – 3
-9x + 8x ≥ -12 – 3
-x ≥ -15
⇒ x ≤ 15
As x is a positive even integer.
Hence, the solution set is {2, 4, 6, 8, 10, 12, 14}.
14. Given that x ∈ I, solve the inequation and graph the solution on the number line:
3 ≥ (x – 4)/2 + x/3 ≥ 2
Given inequation, 3 ≥ (x – 4)/2 + x/3 ≥ 2
Now, let’s take
3 ≥ (x – 4)/2 + x/3, we have
3 ≥ (3x – 12 + 2x)/6 [Taking L.C.M]
18 ≥ 5x – 12
⇒ x ≤ 6 …. (i)
(x – 4)/2 + x/3 ≥ 2
(3x – 12 + 2x)/6 ≥ 2
5x – 12 ≥ 12
x ≥ 24/5 ⇒ x ≥ 4.8 … (ii)
Hence, from (i) and (ii) we have
Solution of x = {5, 6}
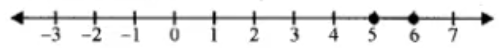
15. Solve: 1 ≥ 15 – 7x > 2x – 27, x ∈ N Solution:
Given inequation, 1 ≥ 15 – 7x > 2x – 27,
So, we have
1 ≥ 15 – 7x and 15 – 7x > 2x – 27
7x ≥ 15 – 1 and -2x – 7x > -27 – 15
7x ≥ 14 and -9x > -42
x ≥ 2 and -x > -42/9
x ≥ 2 and x < 14/3
⇒ 2 ≤ x < 14/3
But as x ∈ N
The solution set is {2, 3, 4}.
16. If x ∈ Z, solve 2 + 4x < 2x – 5 ≤ 3x. Also represent its solution on the number line. Solution
Given inequation, 2 + 4x < 2x – 5 ≤ 3x
2 + 4x < 2x – 5 and 2x – 5 ≤ 3x
4x – 2x < -5 – 2 and 2x – 3x ≤ 5
2x < -7 and -x ≤ 5
x < -7/2 and x ≥ -5
⇒ -5 ≤ x < -7/2
The solution set is {-5, -4}.
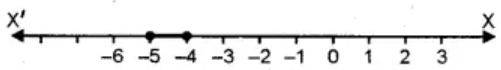
17. Solve: (4x – 10)/3 ≤ (5x – 7)/2, x ∈ R and represent the solution set on the number line. Solution:
Given inequation, (4x – 10)/3 ≤ (5x – 7)/2
2 (4x – 10) ≤ 3 (5x – 7) [On cross-multiplying]
8x – 20 ≤ 15x – 21
8x – 15x ≤ -21 + 20
-7x ≤ -1
-x ≤ -1/7
As x ∈ R
Hence, the solution set is {x: x ∈ R, x ≥ 1/7}

18. Solve 3x/5 – (2x – 1)/3 > 1, x ∈ R and represent the solution set on the number line. Solution:
Given inequation, 3x/5 – (2x – 1)/3 > 1
(9x – 10x + 5)/15 > 1 [Taking L.C.M]
-x + 5 > 15
Hence, the solution set is {x: x ∈ R, x < -10}

19. Given that x ∈ R, solve the following inequation and graph the solution on the number line: -1 ≤ 3 + 4x < 23.
Given inequation, -1 ≤ 3 + 4x < 23
-1 – 3 ≤ 4x < 23 – 3
-4 ≤ 4x < 20
-4/4 ≤ x < 20/4
-1 ≤ x < 5
Hence, the solution set is {-1 ≤ x < 5; x ∈ R}

Given inequation,
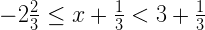
-8/3 ≤ (3x + 1)/3 < 10/3
-8 ≤ 3x + 1 < 10 [Multiplying by 3]
-8 – 1 ≤ 3x < 10 – 1
-9 ≤ 3x < 9
-3 ≤ x < 3 [Dividing by 5]
Thus, the solution set is {x: x ∈ R, -3 ≤ x < 3}
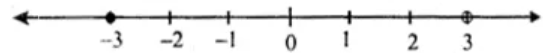
Given in equation,
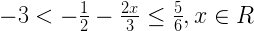
-3 < -(3 + 4x)/6 ≤ 5/6 [Taking L.C.M]
-18 < -3 – 4x ≤ 5 [Multiplying by 6]
-18 + 3 < -4x ≤ 5 + 3
-15 < -4x ≤ 8
-15/4 < -x ≤ 8/4
-2 ≤ x < 15/4
Hence, the solution set is {x : x ∈ R, -2 ≤ x < 15/4}
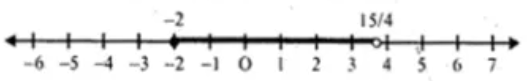
22. Solving the following inequation, write the solution set and represent it on the number line
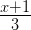
–3x + 21 ≥ 15 – 7x > (x + 1)/3
-3x + 21 ≥ 15 – 7x
7x – 3x ≥ 15 – 21
x ≥ -6/4
x ≥ -3/2
15 – 7x > (x + 1)/3
3(15 – 7x) > x + 1
45 – 21x > x + 1
-21x – x > 1 – 45
-22x > -44
-x > -44/22
Hence, the solution set is {x : x ∈ R , -3/2 ≤ x < 2}

23. Solve the following inequation, write down the solution set and represent it on the real number line:
-2 + 10x ≤ 13x + 10 ≤ 24 + 10x, x ∈ Z
Given inequation, -2 + 10x ≤ 13x + 10 ≤ 24 + 10x
-2 + 10x ≤ 13x + 10 and 13x + 10 ≤ 24 + 10x
10x – 13x ≤ 10 + 2 and 13x – 10x ≤ 24 – 10
-3x ≤ 12 and 3x ≤ 14
x ≥ -12/3 and x ≤ 14/3
x ≥ -4 and x ≤ 14/3
So, -4 ≤ x ≤ 14/3
Thus, the solution set is {-4, -3, -2, -1, 0, 1, 2, 3, 4}

24. Solve the inequation 2x – 5 ≤ 5x + 4 < 11, where x ∈ I. Also represent the solution set on the number line.
Given inequation, 2x – 5 ≤ 5x + 4 < 11
2x – 5 ≤ 5x + 4 and 5x + 4 < 11
2x – 5x ≤ 4 + 5 and 5x < 11 – 4
-3x ≤ 9 and 5x < 7
-x ≤ 9/3 and x < 7/5
x ≥ -3 and x < 7/5
-3 ≤ x < 7/5
As x ∈ I
Thus, the solutions set is {-3, -2, -1, 0, 1}

25. If x ∈ I, A is the solution set of 2 (x – 1) < 3x – 1 and B is the solution set of 4x – 3 ≤ 8 + x, find A ∩ B. Solution:
Given inequations,
2 (x – 1) < 3x – 1 and 4x – 3 ≤ 8 + x for x ∈ I
Solving for both, we have
2x – 3x < 2 – 1 and 4x – x ≤ 8 + 3
-x < 1 and 3x ≤ 11
x > -1 and x ≤ 11/3
Solution set A = {0, 1, 2, 3, …}
Solution set B = {3, 2, 1, 0, -1, … }
Thus, A ⋂ B = {0, 1, 2, 3}
26. If P is the solution set of -3x + 4 < 2x – 3, x ∈ N and Q is the solution set of 4x – 5 < 12, x ∈ W, find (i) P ∩ Q (ii) Q – P. Solution:
-3x + 4 < 2x – 3 where x ∈ N and 4x – 5 < 12 where x ∈ W
So, solving
-3x + 4 < 2x – 3 where x ∈ N
-3x – 2x < -3 – 4
-5x < -7
Hence, the solution set P is {2, 3, 4, 5, …}
And, solving
4x – 5 < 12 where x ∈ W
4x < 12 + 5
x < 17/4
Hence, the solution set Q is {0, 1, 2, 3, 4}
(i) P ∩ Q = {2, 3, 4}
(ii) Q – P = {0, 1}
27. A = {x : 11x – 5 > 7x + 3, x ∈ R} and
B = {x : 18x – 9 ≥ 15 + 12x, x ∈ R} Find the range of set A ∩ B and represent it on a number line Solution:
Given, A = {x : 11x – 5 > 7x + 3, x ∈ R} and B = {x : 18x – 9 ≥ 15 + 12x, x ∈ R}
Solving for A,
11x – 5 > 7x + 3
11x – 7x > 3 + 5
Hence, A = {x : x > 2, x ∈ R}
Next, solving for B
18x – 9 ≥ 15 + 12x
18x – 12x ≥ 15 + 9
Hence, B = {x : x ≥ 4, x ∈ R}
Thus, A ∩ B = x ≥ 4

28. Given: P {x : 5 < 2x – 1 ≤ 11, x ∈ R} Q {x : – 1 ≤ 3 + 4x < 23, x ∈ I} where R = (real numbers), I = (integers) Represent P and Q on number line. Write down the elements of P ∩ Q. Solution:
Given, P {x : 5 < 2x – 1 ≤ 11, x ∈ R} and Q {x : – 1 ≤ 3 + 4x < 23, x ∈ I}
Solving for P,
5 < 2x – 1 ≤ 11
5 + 1 < 2x ≤ 11 + 1
6 < 2x ≤ 12
3 < x ≤ 6
Hence, P = P {x : 3 < x ≤ 6, x ∈ R}

Next, solving for Q
– 1 ≤ 3 + 4x < 23
Hence, solution Q = {-1, 0, 1, 2, 3, 4}

Therefore, P ∩ Q = {4}
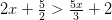
(4x + 5)/2 > (5x + 6)/3 [Taking L.C.M]
3 (4x + 5) > 2 (5x + 6) [On cross-multiplication]
12x + 15 > 10x + 12
12x – 10x > 12 – 15
x > -3/2
Hence, for x ∈ I the smallest value of x is -1.
30. Given 20 – 5 x < 5 (x + 8), find the smallest value of x, when (i) x ∈ I (ii) x ∈ W (iii) x ∈ N. Solution:
Given inequation, 20 – 5 x < 5 (x + 8)
20 – 5x < 5x + 40
-5x – 5x < 40 – 20
-10x < 20
-x < 20/10
(i) For x ∈ I, the smallest value = -1
(ii) For x ∈ W, the smallest value = 0
(iii) For x ∈ N, the smallest value = 1
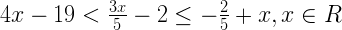
4x – 19 < 3x/5 – 2 and 3x/5 – 2 ≤ -2/5 + x
4x – 3x/5 < 19 – 2 and 3x/5 – x ≤ 2 – 2/5
(20x – 3x)/5 < 17 and (3x – 5x)/5 ≤ (10 – 2)/5
17x < 35 and -2x ≤ 8 [Multiplying by 5]
x < 5 and -x ≤ 4
x < 5 and x ≥ 4
-4 ≤ x < 5, x ∈ R
Hence, the solution set is {x : -4 ≤ x < 5, x ∈ R}
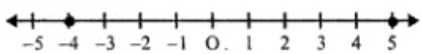
32. Solve the given inequation and graph the solution on the number line: 2y – 3 < y + 1 ≤ 4y + 7; y ∈ R. Solution:
Given inequation, 2y – 3 < y + 1 ≤ 4y + 7
2y – 3 < y + 1 and y + 1 ≤ 4y + 7
2y – y < 1 + 3 and y – 4y ≤ 7 – 1
y < 4 and -3y ≤ 6
y < 4 and -y ≤ 2 ⇒ y ≥ -2
Thus, -2 ≤ y < 4
The solution set is {y : -2 ≤ y < 4, y ∈ R}
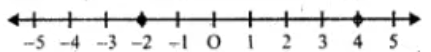
-3 + x ≤ 8x/3 + 2 and 8x/3 + 2 ≤ 14/3 + 2x
x – 8x/3 ≤ 2 + 3 and 8x/3 – 2x ≤ 14/3 – 2
(3x – 8x)/3 ≤ 5 and (8x – 6x)/3 ≤ (14 – 6)/3 [Taking L.C.M]
-5x/3 ≤ 5 and 2x ≤ 8
-5x ≤ 15 and x ≤ 8/2
-x ≤ 3 and x ≤ 4
x ≥ -3 and x ≤ 4
⇒ -3 ≤ x ≤ 4
Thus, the solution set is {-3, -2, -1, 0, 1, 2, 3, 4}
34. Find the greatest integer which is such that if 7 is added to its double, the resulting number becomes greater than three times the integer. Solution:
Let’s consider the greatest integer to be x
Then according to the given condition, we have
2x + 7 > 3x
2x – 3x > -7
x < 7 , x ∈ R
Hence, the greatest integer value is 6.
35. One-third of a bamboo pole is buried in mud, one-sixth of it is in water and the part above the water is greater than or equal to 3 metres. Find the length of the shortest pole. Solution:
Let’s assume the length of the shortest pole = x metre
Length of the pole which is buried in mud = x/3
Length of the pole which is in the water = x/6
x – [x/3 + x/6] ≥ 3
x – [(2x + x)/6] ≥ 3
x – 3x/6 ≥ 3
x – x/2 ≥ 3
x ≥ 6 [Multiplying by 6]
Therefore, the length of the shortest pole is 6 metres.
Chapter Test
1. Solve the inequation: 5x – 2 ≤ 3 (3 – x) where x ∈ {-2, -1, 0, 1, 2, 3, 4}. Also represent its solution on the number line.
Given inequation, 5x – 2 ≤ 3 (3 – x)
5x – 2 ≤ 9 – 3x
5x + 3x ≤ 9 + 2
x ≤ 11/8
As x ∈ {-2, -1, 0, 1, 2, 3, 4}
The solution set is {-2, -1, 0, 1}

2. Solve the inequation: 6x – 5 < 3x + 4, x ∈ I
Given inequation, 6x – 5 < 3x + 4
6x – 3x < 4 + 5
The solution set is {2, 1, 0, -1, -2, …}
3. Find the solution set of the inequation x + 5 ≤ 2x + 3; x ∈ R
Graph the solution set on the number line.
Given inequation, x + 5 ≤ 2x + 3
x – 2x ≤ 3 – 5
Thus, the solution set is {2, 3, 4, 5, …}

4. If x ∈ R (real numbers) and -1 < 3 – 2x ≤ 7, find solution set and present it on a number line.
Given inequation, -1 < 3 – 2x ≤ 7
-1 – 3 < -2x ≤ 7 – 3
-4 < -2x ≤ 4
-4/2 < -x ≤ 4/2
-2 < -x ≤ 2
Thus, -2 ≤ x < 2
The solution set is {x : x ∈ R, -2 ≤ x < 2}

5. Solve the inequation:
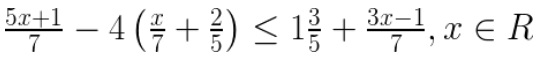
(5x + 1)/7 – 4 (5x + 14)/35 ≤ 8/5 + (3x – 1)/7
(25x + 5 – 20x – 56) ≤ 56 + 15x – 5
5x – 51 ≤ 51 + 15x
5x – 15x ≤ 51 + 51
-10x ≤ 102
-x ≤ 102/10
x ≥ – 51/5
Hence, the solution set is {x : x ∈ R , x ≥ – 51/5}
6. Find the range of values of a, which satisfy 7 ≤ – 4x + 2 < 12, x ∈ R. Graph these values of a on the real number line.
7 < – 4x + 2 < 12
7 < – 4x + 2 and – 4x + 2 < 12
7. If x ∈ R, solve 2x – 3 ≥ x + (1 – x)/3 > 2x/5
Given inequation, 2x – 3 ≥ x + (1 – x)/3 > 2x/5
2x – 3 ≥ x + (1 – x)/3 and x + (1 – x)/3 > 2x/5
2x – 3 ≥ (3x + 1 – x)/3 and (3x + 1 – x)/3 > 2x/5 [On taking L.C.M]
3(2x – 3) ≥ 2x + 1 and (2x + 1) × 5 > 2x × 3 [Upon cross multiplication]
6x – 9 ≥ 2x + 1 and 10x + 5 > 6x
6x – 2x ≥ 1 + 9 and 10x – 6x > -5
4x ≥ 10 and 4x > -5
x ≥ 10/4 and x > -5/4
Thus, the solution set is {x: x ∈ R, x ≥ 5/2}

7. If x ∈ R, solve 2x – 3 ≥ x + (1 – x)/3 > 2x/5. Also represent the solution on the number line.
3 (2x – 3) ≥ 2x + 1 and 5 × (2x + 1) > 3 × 2x
The solution set = {x: x ∈ R, x ≥ 5/2}

8. Find positive integers which are such that if 6 is subtracted from five times the integer then the resulting number cannot be greater than four times the integer.
Let’s consider the positive integer be x
Then according to the problem, we have
5a – 6 < 4x
5a – 4x < 6
⇒ x < 6
Hence, the solution set = {x : x < 6}
= { 1, 2, 3, 4, 5, 6}
9. Find three smallest consecutive natural numbers such that the difference between one-third of the largest and one-fifth of the smallest is at least 3.
Let’s consider the first least natural number as x
Then, second number = x + 1
And third number = x + 2
So, according the conditions given in the problem, we have
1/3 × (x + 2) – x/5 ≥ 3
5x + 10 – 3x ≥ 3 × 15
2x ≥ 45 – 10
x ≥ 35/2
x ≥ 17.5
As x is a natural least number
Thus, first least natural number = 18
Second number = 18 + 1 = 19
And, third number = 18 + 2 = 20
Hence, the least natural numbers are 18, 19 and 20
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.

IMAGES
VIDEO
COMMENTS
Graph Inequalities on the Number Line Do you remember what it means for a number to be a solution to an equation? A solution of an equation is a value of a variable that makes a true statement when substituted into the equation. What about the solution of an inequality? What number would make the inequality x > 3 true?
The method we will use to solve applications with linear inequalities is very much like the one we used when we solved applications with equations. We will read the problem and make sure all the words are understood.
This worksheet contains two-step inequalities as well as some more difficult multi-step linear inequality problems! This worksheet is also provided in PDF format for ease of access. Remember to check the answer key to confirm your understanding of solving more complex linear inequalities.
To solve linear inequalities, isolate the variable on one side of the inequality, keeping track of the sign of the inequality when multiplying or dividing by a negative number, and express the solution as an interval. A linear inequality is a first degree equation with an inequality sign.
What are linear inequalities. Learn how to solve and graph them on a number line with examples.
As long as you remember to flip the inequality sign when you multiply or divide through by a negative, you shouldn't have any trouble with solving linear inequalities. Linear inequalities can be simple (x<3) or complex (3x+2≤½−14x), and can arise naturally in the real world so — you guessed it — word problems!
Learn the rules and techniques for solving multi-step linear inequalities using the different signs: GREATER THAN, GREATER THAN OR EQUAL TO, LESS THAN, and LESS THAN OR EQUAL TO.
Linear inequalities questions and solutions help the students to solve various problems on inequalities in mathematics. In this article, you will get solved questions on linear inequalities, and additional questions for practice.
Linear Inequalities - Examples and Practice Problems Inequality problems and exercises can be solved with a process similar to the one we use to solve equations. The main difference regarding inequalities is that we have to change the side of the inequality sign when we multiply or divide by negative numbers.
Solutions to a system of linear inequalities are the ordered pairs that solve all the inequalities in the system. Therefore, to solve these systems, graph the solution sets of the inequalities on the same set of axes and determine where they intersect.
Many simple inequalities can be solved by adding, subtracting, multiplying or dividing both sides until you are left with the variable on its own. But these things will change direction of the inequality: Multiplying or dividing both sides by a negative number. Swapping left and right hand sides.
Systems of Linear Equations word problems are the same as any other. Translate the problem into a system of inequalities, then solve.
System of Linear Inequalities A system of linear inequalities in two variables includes at least two linear inequalities in the identical variables. When we solve linear inequality then we get an ordered pair. So basically, in a system, the solution to all inequalities and the graph of the linear inequality is the graph displaying all solutions of the system. Let us see an example to ...
To solve word problems using linear inequalities, we have to model the information given in the question as linear inequalities and solve for unknown. Problem 1 : Find all pairs of consecutive odd positive integers, both of which are smaller than 18, such that their sum is more than 20. Solution :
Linear Equations represent a point in a single dimension, a line in a two-dimensional, and a plane in a three-dimensional world. Solutions to linear inequalities represent a region of the Cartesian plane. It becomes essential for us to know how to translate real-life problems into linear inequalities.
Linear Inequalities are used in many real-life applications such as income and expenditure problems, to find the proportion of the amount spent on various things. Two types of linear inequalities are explained in NCERT Solutions for Class 11 Maths of Chapter 6, i.e., linear inequalities in one variable and linear inequalities in two variables.
The solution to a system of linear equations in two variables is any ordered pair that satisfies each equation independently. Systems of equations are classified as independent with one solution, dependent with an infinite number of solutions, or inconsistent with no solution. 7.2: Systems of Linear Equations with Three Variables
SOLVING LINEAR INEQUALITIES WORD PROBLEMS IN TWO VARIABLES A statement involving the symbols '>', '<', ' ≥', '≤' is called an inequality. By understanding the real situation, we have to use two variables to represent each quantities Problem 1 : Katie has $50 in a savings account at the beginning of the summer.
An equation is a statement indicating that two algebraic expressions are equal. A linear equation with one variable, x , is an equation that can be written in the standard form ax+b=0 where a …
Solve linear, quadratic and absolute inequalities, step-by-step. There are four types of inequalities: greater than, less than, greater than or equal to, and less than or equal to. In math, inequality represents the relative size or order of two values. To solve inequalities, isolate the variable on one side of the inequality, If you multiply ...
The main topics covered in this chapter are inequalities among real numbers, linear inequations and solving linear inequations in one variable using the two permissible rules. Students can start solving the problems on a regular basis so that their conceptual knowledge becomes stronger and their problem-solving skills are also improved, which is important from the examination perspective ...
We will now re-visit this problem using some of the techniques developed in this section not only to reinforce our solution in Section 2.3, but to also help formulate a general analytic procedure for solving all quadratic inequalities. If we consider \(f(x) = x^2-x-6\) and \(g(x)=0\), then solving \(x^2 - x -6 < 0\) corresponds graphically to ...
The solution to a system of linear equations in two variables is any ordered pair that satisfies each equation independently. In this example, the ordered pair \((4,7)\) is the solution to the system of linear equations. We can verify the solution by substituting the values into each equation to see if the ordered pair satisfies both equations.
Representing a Linear Function in Function Notation. Another approach to representing linear functions is by using function notation. One example of function notation is an equation written in the form known as the slope-intercept form of a line, where \(x\) is the input value, \(m\) is the rate of change, and \(b\) is the initial value of the dependent variable.