how to find p value hypothesis test

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

Knowledge Base
Understanding P values | Definition and Examples

Understanding P-values | Definition and Examples

Published on July 16, 2020 by Rebecca Bevans . Revised on June 22, 2023.

The p value is a number, calculated from a statistical test, that describes how likely you are to have found a particular set of observations if the null hypothesis were true.

P values are used in hypothesis testing to help decide whether to reject the null hypothesis. The smaller the p value, the more likely you are to reject the null hypothesis.

What is a null hypothesis, what exactly is a p value, how do you calculate the p value, p values and statistical significance, reporting p values, caution when using p values, other interesting articles, frequently asked questions about p-values.

All statistical tests have a null hypothesis. For most tests, the null hypothesis is that there is no relationship between your variables of interest or that there is no difference among groups.

For example, in a two-tailed t test , the null hypothesis is that the difference between two groups is zero.

Null hypothesis ( H 0 ): there is no difference in longevity between the two groups.
Alternative hypothesis ( H A or H 1 ): there is a difference in longevity between the two groups.

Prevent plagiarism. Run a free check.

The p value , or probability value, tells you how likely it is that your data could have occurred under the null hypothesis. It does this by calculating the likelihood of your test statistic , which is the number calculated by a statistical test using your data.

The p value tells you how often you would expect to see a test statistic as extreme or more extreme than the one calculated by your statistical test if the null hypothesis of that test was true. The p value gets smaller as the test statistic calculated from your data gets further away from the range of test statistics predicted by the null hypothesis.

The p value is a proportion: if your p value is 0.05, that means that 5% of the time you would see a test statistic at least as extreme as the one you found if the null hypothesis was true.

P values are usually automatically calculated by your statistical program (R, SPSS, etc.).

You can also find tables for estimating the p value of your test statistic online. These tables show, based on the test statistic and degrees of freedom (number of observations minus number of independent variables) of your test, how frequently you would expect to see that test statistic under the null hypothesis.

The calculation of the p value depends on the statistical test you are using to test your hypothesis :

Different statistical tests have different assumptions and generate different test statistics. You should choose the statistical test that best fits your data and matches the effect or relationship you want to test.
The number of independent variables you include in your test changes how large or small the test statistic needs to be to generate the same p value.

No matter what test you use, the p value always describes the same thing: how often you can expect to see a test statistic as extreme or more extreme than the one calculated from your test.

P values are most often used by researchers to say whether a certain pattern they have measured is statistically significant.

Statistical significance is another way of saying that the p value of a statistical test is small enough to reject the null hypothesis of the test.

How small is small enough? The most common threshold is p < 0.05; that is, when you would expect to find a test statistic as extreme as the one calculated by your test only 5% of the time. But the threshold depends on your field of study – some fields prefer thresholds of 0.01, or even 0.001.

The threshold value for determining statistical significance is also known as the alpha value.

P values of statistical tests are usually reported in the results section of a research paper , along with the key information needed for readers to put the p values in context – for example, correlation coefficient in a linear regression , or the average difference between treatment groups in a t -test.

P values are often interpreted as your risk of rejecting the null hypothesis of your test when the null hypothesis is actually true.

In reality, the risk of rejecting the null hypothesis is often higher than the p value, especially when looking at a single study or when using small sample sizes. This is because the smaller your frame of reference, the greater the chance that you stumble across a statistically significant pattern completely by accident.

P values are also often interpreted as supporting or refuting the alternative hypothesis. This is not the case. The p value can only tell you whether or not the null hypothesis is supported. It cannot tell you whether your alternative hypothesis is true, or why.

If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.

Normal distribution
Descriptive statistics
Measures of central tendency
Correlation coefficient
Null hypothesis

Methodology

Cluster sampling
Stratified sampling
Types of interviews
Cohort study
Thematic analysis

Research bias

Implicit bias
Cognitive bias
Survivorship bias
Availability heuristic
Nonresponse bias
Regression to the mean

A p -value , or probability value, is a number describing how likely it is that your data would have occurred under the null hypothesis of your statistical test .

P -values are usually automatically calculated by the program you use to perform your statistical test. They can also be estimated using p -value tables for the relevant test statistic .

P -values are calculated from the null distribution of the test statistic. They tell you how often a test statistic is expected to occur under the null hypothesis of the statistical test, based on where it falls in the null distribution.

If the test statistic is far from the mean of the null distribution, then the p -value will be small, showing that the test statistic is not likely to have occurred under the null hypothesis.

Statistical significance is a term used by researchers to state that it is unlikely their observations could have occurred under the null hypothesis of a statistical test . Significance is usually denoted by a p -value , or probability value.

Statistical significance is arbitrary – it depends on the threshold, or alpha value, chosen by the researcher. The most common threshold is p < 0.05, which means that the data is likely to occur less than 5% of the time under the null hypothesis .

When the p -value falls below the chosen alpha value, then we say the result of the test is statistically significant.

No. The p -value only tells you how likely the data you have observed is to have occurred under the null hypothesis .

If the p -value is below your threshold of significance (typically p < 0.05), then you can reject the null hypothesis, but this does not necessarily mean that your alternative hypothesis is true.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

Bevans, R. (2023, June 22). Understanding P-values | Definition and Examples. Scribbr. Retrieved September 5, 2024, from https://www.scribbr.com/statistics/p-value/

Is this article helpful?

Rebecca Bevans

Other students also liked, an easy introduction to statistical significance (with examples), test statistics | definition, interpretation, and examples, what is effect size and why does it matter (examples), what is your plagiarism score.

Hypothesis Testing Calculator

$H_o$:
$H_a$:	μ	≠	μ₀

$n$

$\bar{x}$

$\text{Test Statistic: }$

$\text{Degrees of Freedom: } $

$df$

$ \text{Level of Significance: } $

$\alpha$

Type II Error

$H_o$:	$\mu$
$H_a$:	$\mu$	≠	$\mu_0$

$n$

$\mu$

$\text{Level of Significance: }$

$\alpha$

The first step in hypothesis testing is to calculate the test statistic. The formula for the test statistic depends on whether the population standard deviation (σ) is known or unknown. If σ is known, our hypothesis test is known as a z test and we use the z distribution. If σ is unknown, our hypothesis test is known as a t test and we use the t distribution. Use of the t distribution relies on the degrees of freedom, which is equal to the sample size minus one. Furthermore, if the population standard deviation σ is unknown, the sample standard deviation s is used instead. To switch from σ known to σ unknown, click on $\boxed{\sigma}$ and select $\boxed{s}$ in the Hypothesis Testing Calculator.

	$\sigma$ Known	$\sigma$ Unknown
Test Statistic	$ z = \dfrac{\bar{x}-\mu_0}{\sigma/\sqrt{{\color{Black} n}}} $	$ t = \dfrac{\bar{x}-\mu_0}{s/\sqrt{n}} $

Next, the test statistic is used to conduct the test using either the p-value approach or critical value approach. The particular steps taken in each approach largely depend on the form of the hypothesis test: lower tail, upper tail or two-tailed. The form can easily be identified by looking at the alternative hypothesis (H a ). If there is a less than sign in the alternative hypothesis then it is a lower tail test, greater than sign is an upper tail test and inequality is a two-tailed test. To switch from a lower tail test to an upper tail or two-tailed test, click on $\boxed{\geq}$ and select $\boxed{\leq}$ or $\boxed{=}$, respectively.

Lower Tail Test	Upper Tail Test	Two-Tailed Test
$H_0 \colon \mu \geq \mu_0$	$H_0 \colon \mu \leq \mu_0$	$H_0 \colon \mu = \mu_0$
$H_a \colon \mu	$H_a \colon \mu \neq \mu_0$

In the p-value approach, the test statistic is used to calculate a p-value. If the test is a lower tail test, the p-value is the probability of getting a value for the test statistic at least as small as the value from the sample. If the test is an upper tail test, the p-value is the probability of getting a value for the test statistic at least as large as the value from the sample. In a two-tailed test, the p-value is the probability of getting a value for the test statistic at least as unlikely as the value from the sample.

To test the hypothesis in the p-value approach, compare the p-value to the level of significance. If the p-value is less than or equal to the level of signifance, reject the null hypothesis. If the p-value is greater than the level of significance, do not reject the null hypothesis. This method remains unchanged regardless of whether it's a lower tail, upper tail or two-tailed test. To change the level of significance, click on $\boxed{.05}$. Note that if the test statistic is given, you can calculate the p-value from the test statistic by clicking on the switch symbol twice.

In the critical value approach, the level of significance ($\alpha$) is used to calculate the critical value. In a lower tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the lower tail of the sampling distribution of the test statistic. In an upper tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the upper tail of the sampling distribution of the test statistic. In a two-tailed test, the critical values are the values of the test statistic providing areas of $\alpha / 2$ in the lower and upper tail of the sampling distribution of the test statistic.

To test the hypothesis in the critical value approach, compare the critical value to the test statistic. Unlike the p-value approach, the method we use to decide whether to reject the null hypothesis depends on the form of the hypothesis test. In a lower tail test, if the test statistic is less than or equal to the critical value, reject the null hypothesis. In an upper tail test, if the test statistic is greater than or equal to the critical value, reject the null hypothesis. In a two-tailed test, if the test statistic is less than or equal the lower critical value or greater than or equal to the upper critical value, reject the null hypothesis.

Lower Tail Test	Upper Tail Test	Two-Tailed Test
If $z \leq -z_\alpha$, reject $H_0$.	If $z \geq z_\alpha$, reject $H_0$.	If $z \leq -z_{\alpha/2}$ or $z \geq z_{\alpha/2}$, reject $H_0$.
If $t \leq -t_\alpha$, reject $H_0$.	If $t \geq t_\alpha$, reject $H_0$.	If $t \leq -t_{\alpha/2}$ or $t \geq t_{\alpha/2}$, reject $H_0$.

When conducting a hypothesis test, there is always a chance that you come to the wrong conclusion. There are two types of errors you can make: Type I Error and Type II Error. A Type I Error is committed if you reject the null hypothesis when the null hypothesis is true. Ideally, we'd like to accept the null hypothesis when the null hypothesis is true. A Type II Error is committed if you accept the null hypothesis when the alternative hypothesis is true. Ideally, we'd like to reject the null hypothesis when the alternative hypothesis is true.

		Condition
		$H_0$ True	$H_a$ True
Conclusion	Accept $H_0$	Correct	Type II Error
Conclusion	Reject $H_0$	Type I Error	Correct

Hypothesis testing is closely related to the statistical area of confidence intervals. If the hypothesized value of the population mean is outside of the confidence interval, we can reject the null hypothesis. Confidence intervals can be found using the Confidence Interval Calculator . The calculator on this page does hypothesis tests for one population mean. Sometimes we're interest in hypothesis tests about two population means. These can be solved using the Two Population Calculator . The probability of a Type II Error can be calculated by clicking on the link at the bottom of the page.

Step-by-step guide to hypothesis testing in statistics

Hypothesis testing in statistics helps us use data to make informed decisions. It starts with an assumption or guess about a group or population—something we believe might be true. We then collect sample data to check if there is enough evidence to support or reject that guess. This method is useful in many fields, like science, business, and healthcare, where decisions need to be based on facts.

Learning how to do hypothesis testing in statistics step-by-step can help you better understand data and make smarter choices, even when things are uncertain. This guide will take you through each step, from creating your hypothesis to making sense of the results, so you can see how it works in practical situations.

What is Hypothesis Testing?

Table of Contents

Hypothesis testing is a method for determining whether data supports a certain idea or assumption about a larger group. It starts by making a guess, like an average or a proportion, and then uses a small sample of data to see if that guess seems true or not.

For example, if a company wants to know if its new product is more popular than its old one, it can use hypothesis testing. They start with a statement like “The new product is not more popular than the old one” (this is the null hypothesis) and compare it with “The new product is more popular” (this is the alternative hypothesis). Then, they look at customer feedback to see if there’s enough evidence to reject the first statement and support the second one.

Simply put, hypothesis testing is a way to use data to help make decisions and understand what the data is really telling us, even when we don’t have all the answers.

Importance Of Hypothesis Testing In Decision-Making And Data Analysis

Hypothesis testing is important because it helps us make smart choices and understand data better. Here’s why it’s useful:

Reduces Guesswork : It helps us see if our guesses or ideas are likely correct, even when we don’t have all the details.
Uses Real Data : Instead of just guessing, it checks if our ideas match up with real data, which makes our decisions more reliable.
Avoids Errors : It helps us avoid mistakes by carefully checking if our ideas are right so we don’t make costly errors.
Shows What to Do Next : It tells us if our ideas work or not, helping us decide whether to keep, change, or drop something. For example, a company might test a new ad and decide what to do based on the results.
Confirms Research Findings : It makes sure that research results are accurate and not just random chance so that we can trust the findings.

Here’s a simple guide to understanding hypothesis testing, with an example:

1. Set Up Your Hypotheses

Explanation: Start by defining two statements:

Null Hypothesis (H0): This is the idea that there is no change or effect. It’s what you assume is true.
Alternative Hypothesis (H1): This is what you want to test. It suggests there is a change or effect.

Example: Suppose a company says their new batteries last an average of 500 hours. To check this:

Null Hypothesis (H0): The average battery life is 500 hours.
Alternative Hypothesis (H1): The average battery life is not 500 hours.

2. Choose the Test

Explanation: Pick a statistical test that fits your data and your hypotheses. Different tests are used for various kinds of data.

Example: Since you’re comparing the average battery life, you use a one-sample t-test .

3. Set the Significance Level

Explanation: Decide how much risk you’re willing to take if you make a wrong decision. This is called the significance level, often set at 0.05 or 5%.

Example: You choose a significance level of 0.05, meaning you’re okay with a 5% chance of being wrong.

4. Gather and Analyze Data

Explanation: Collect your data and perform the test. Calculate the test statistic to see how far your sample result is from what you assumed.

Example: You test 30 batteries and find they last an average of 485 hours. You then calculate how this average compares to the claimed 500 hours using the t-test.

5. Find the p-Value

Explanation: The p-value tells you the probability of getting a result as extreme as yours if the null hypothesis is true.

Example: You find a p-value of 0.0001. This means there’s a very small chance (0.01%) of getting an average battery life of 485 hours or less if the true average is 500 hours.

6. Make Your Decision

Explanation: Compare the p-value to your significance level. If the p-value is smaller, you reject the null hypothesis. If it’s larger, you do not reject it.

Example: Since 0.0001 is much less than 0.05, you reject the null hypothesis. This means the data suggests the average battery life is different from 500 hours.

7. Report Your Findings

Explanation: Summarize what the results mean. State whether you rejected the null hypothesis and what that implies.

Example: You conclude that the average battery life is likely different from 500 hours. This suggests the company’s claim might not be accurate.

Hypothesis testing is a way to use data to check if your guesses or assumptions are likely true. By following these steps—setting up your hypotheses, choosing the right test, deciding on a significance level, analyzing your data, finding the p-value, making a decision, and reporting results—you can determine if your data supports or challenges your initial idea.

Understanding Hypothesis Testing: A Simple Explanation

Hypothesis testing is a way to use data to make decisions. Here’s a straightforward guide:

1. What is the Null and Alternative Hypotheses?

Null Hypothesis (H0): This is your starting assumption. It says that nothing has changed or that there is no effect. It’s what you assume to be true until your data shows otherwise. Example: If a company says their batteries last 500 hours, the null hypothesis is: “The average battery life is 500 hours.” This means you think the claim is correct unless you find evidence to prove otherwise.
Alternative Hypothesis (H1): This is what you want to find out. It suggests that there is an effect or a difference. It’s what you are testing to see if it might be true. Example: To test the company’s claim, you might say: “The average battery life is not 500 hours.” This means you think the average battery life might be different from what the company says.

2. One-Tailed vs. Two-Tailed Tests

One-Tailed Test: This test checks for an effect in only one direction. You use it when you’re only interested in finding out if something is either more or less than a specific value. Example: If you think the battery lasts longer than 500 hours, you would use a one-tailed test to see if the battery life is significantly more than 500 hours.
Two-Tailed Test: This test checks for an effect in both directions. Use this when you want to see if something is different from a specific value, whether it’s more or less. Example: If you want to see if the battery life is different from 500 hours, whether it’s more or less, you would use a two-tailed test. This checks for any significant difference, regardless of the direction.

3. Common Misunderstandings

Clarification: Hypothesis testing doesn’t prove that the null hypothesis is true. It just helps you decide if you should reject it. If there isn’t enough evidence against it, you don’t reject it, but that doesn’t mean it’s definitely true.
Clarification: A small p-value shows that your data is unlikely if the null hypothesis is true. It suggests that the alternative hypothesis might be right, but it doesn’t prove the null hypothesis is false.
Clarification: The significance level (alpha) is a set threshold, like 0.05, that helps you decide how much risk you’re willing to take for making a wrong decision. It should be chosen carefully, not randomly.
Clarification: Hypothesis testing helps you make decisions based on data, but it doesn’t guarantee your results are correct. The quality of your data and the right choice of test affect how reliable your results are.

Benefits and Limitations of Hypothesis Testing

Clear Decisions: Hypothesis testing helps you make clear decisions based on data. It shows whether the evidence supports or goes against your initial idea.
Objective Analysis: It relies on data rather than personal opinions, so your decisions are based on facts rather than feelings.
Concrete Numbers: You get specific numbers, like p-values, to understand how strong the evidence is against your idea.
Control Risk: You can set a risk level (alpha level) to manage the chance of making an error, which helps avoid incorrect conclusions.
Widely Used: It can be used in many areas, from science and business to social studies and engineering, making it a versatile tool.

Limitations

Sample Size Matters: The results can be affected by the size of the sample. Small samples might give unreliable results, while large samples might find differences that aren’t meaningful in real life.
Risk of Misinterpretation: A small p-value means the results are unlikely if the null hypothesis is true, but it doesn’t show how important the effect is.
Needs Assumptions: Hypothesis testing requires certain conditions, like data being normally distributed . If these aren’t met, the results might not be accurate.
Simple Decisions: It often results in a basic yes or no decision without giving detailed information about the size or impact of the effect.
Can Be Misused: Sometimes, people misuse hypothesis testing, tweaking data to get a desired result or focusing only on whether the result is statistically significant.
No Absolute Proof: Hypothesis testing doesn’t prove that your hypothesis is true. It only helps you decide if there’s enough evidence to reject the null hypothesis, so the conclusions are based on likelihood, not certainty.

Final Thoughts

Hypothesis testing helps you make decisions based on data. It involves setting up your initial idea, picking a significance level, doing the test, and looking at the results. By following these steps, you can make sure your conclusions are based on solid information, not just guesses.

This approach lets you see if the evidence supports or contradicts your initial idea, helping you make better decisions. But remember that hypothesis testing isn’t perfect. Things like sample size and assumptions can affect the results, so it’s important to be aware of these limitations.

In simple terms, using a step-by-step guide for hypothesis testing is a great way to better understand your data. Follow the steps carefully and keep in mind the method’s limits.

What is the difference between one-tailed and two-tailed tests?

A one-tailed test assesses the probability of the observed data in one direction (either greater than or less than a certain value). In contrast, a two-tailed test looks at both directions (greater than and less than) to detect any significant deviation from the null hypothesis.

How do you choose the appropriate test for hypothesis testing?

The choice of test depends on the type of data you have and the hypotheses you are testing. Common tests include t-tests, chi-square tests, and ANOVA. You get more details about ANOVA, you may read Complete Details on What is ANOVA in Statistics ? It’s important to match the test to the data characteristics and the research question.

What is the role of sample size in hypothesis testing?

Sample size affects the reliability of hypothesis testing. Larger samples provide more reliable estimates and can detect smaller effects, while smaller samples may lead to less accurate results and reduced power.

Can hypothesis testing prove that a hypothesis is true?

Hypothesis testing cannot prove that a hypothesis is true. It can only provide evidence to support or reject the null hypothesis. A result can indicate whether the data is consistent with the null hypothesis or not, but it does not prove the alternative hypothesis with certainty.

How to Find the Best Online Statistics Homework Help

why-spss-homework-help-is-an-important-aspects-for-students

Why SPSS Homework Help Is An Important aspect for Students?

StatPearls [Internet].

Hypothesis testing, p values, confidence intervals, and significance.

Jacob Shreffler ; Martin R. Huecker .

Affiliations

Last Update: March 13, 2023 .

Definition/Introduction

Medical providers often rely on evidence-based medicine to guide decision-making in practice. Often a research hypothesis is tested with results provided, typically with p values, confidence intervals, or both. Additionally, statistical or research significance is estimated or determined by the investigators. Unfortunately, healthcare providers may have different comfort levels in interpreting these findings, which may affect the adequate application of the data.

Issues of Concern

Without a foundational understanding of hypothesis testing, p values, confidence intervals, and the difference between statistical and clinical significance, it may affect healthcare providers' ability to make clinical decisions without relying purely on the research investigators deemed level of significance. Therefore, an overview of these concepts is provided to allow medical professionals to use their expertise to determine if results are reported sufficiently and if the study outcomes are clinically appropriate to be applied in healthcare practice.

Hypothesis Testing

Investigators conducting studies need research questions and hypotheses to guide analyses. Starting with broad research questions (RQs), investigators then identify a gap in current clinical practice or research. Any research problem or statement is grounded in a better understanding of relationships between two or more variables. For this article, we will use the following research question example:

Research Question: Is Drug 23 an effective treatment for Disease A?

Research questions do not directly imply specific guesses or predictions; we must formulate research hypotheses. A hypothesis is a predetermined declaration regarding the research question in which the investigator(s) makes a precise, educated guess about a study outcome. This is sometimes called the alternative hypothesis and ultimately allows the researcher to take a stance based on experience or insight from medical literature. An example of a hypothesis is below.

Research Hypothesis: Drug 23 will significantly reduce symptoms associated with Disease A compared to Drug 22.

The null hypothesis states that there is no statistical difference between groups based on the stated research hypothesis.

Researchers should be aware of journal recommendations when considering how to report p values, and manuscripts should remain internally consistent.

Regarding p values, as the number of individuals enrolled in a study (the sample size) increases, the likelihood of finding a statistically significant effect increases. With very large sample sizes, the p-value can be very low significant differences in the reduction of symptoms for Disease A between Drug 23 and Drug 22. The null hypothesis is deemed true until a study presents significant data to support rejecting the null hypothesis. Based on the results, the investigators will either reject the null hypothesis (if they found significant differences or associations) or fail to reject the null hypothesis (they could not provide proof that there were significant differences or associations).

To test a hypothesis, researchers obtain data on a representative sample to determine whether to reject or fail to reject a null hypothesis. In most research studies, it is not feasible to obtain data for an entire population. Using a sampling procedure allows for statistical inference, though this involves a certain possibility of error. [1] When determining whether to reject or fail to reject the null hypothesis, mistakes can be made: Type I and Type II errors. Though it is impossible to ensure that these errors have not occurred, researchers should limit the possibilities of these faults. [2]

Significance

Significance is a term to describe the substantive importance of medical research. Statistical significance is the likelihood of results due to chance. [3] Healthcare providers should always delineate statistical significance from clinical significance, a common error when reviewing biomedical research. [4] When conceptualizing findings reported as either significant or not significant, healthcare providers should not simply accept researchers' results or conclusions without considering the clinical significance. Healthcare professionals should consider the clinical importance of findings and understand both p values and confidence intervals so they do not have to rely on the researchers to determine the level of significance. [5] One criterion often used to determine statistical significance is the utilization of p values.

P values are used in research to determine whether the sample estimate is significantly different from a hypothesized value. The p-value is the probability that the observed effect within the study would have occurred by chance if, in reality, there was no true effect. Conventionally, data yielding a p<0.05 or p<0.01 is considered statistically significant. While some have debated that the 0.05 level should be lowered, it is still universally practiced. [6] Hypothesis testing allows us to determine the size of the effect.

An example of findings reported with p values are below:

Statement: Drug 23 reduced patients' symptoms compared to Drug 22. Patients who received Drug 23 (n=100) were 2.1 times less likely than patients who received Drug 22 (n = 100) to experience symptoms of Disease A, p<0.05.

Statement:Individuals who were prescribed Drug 23 experienced fewer symptoms (M = 1.3, SD = 0.7) compared to individuals who were prescribed Drug 22 (M = 5.3, SD = 1.9). This finding was statistically significant, p= 0.02.

For either statement, if the threshold had been set at 0.05, the null hypothesis (that there was no relationship) should be rejected, and we should conclude significant differences. Noticeably, as can be seen in the two statements above, some researchers will report findings with < or > and others will provide an exact p-value (0.000001) but never zero [6] . When examining research, readers should understand how p values are reported. The best practice is to report all p values for all variables within a study design, rather than only providing p values for variables with significant findings. [7] The inclusion of all p values provides evidence for study validity and limits suspicion for selective reporting/data mining.

While researchers have historically used p values, experts who find p values problematic encourage the use of confidence intervals. [8] . P-values alone do not allow us to understand the size or the extent of the differences or associations. [3] In March 2016, the American Statistical Association (ASA) released a statement on p values, noting that scientific decision-making and conclusions should not be based on a fixed p-value threshold (e.g., 0.05). They recommend focusing on the significance of results in the context of study design, quality of measurements, and validity of data. Ultimately, the ASA statement noted that in isolation, a p-value does not provide strong evidence. [9]

When conceptualizing clinical work, healthcare professionals should consider p values with a concurrent appraisal study design validity. For example, a p-value from a double-blinded randomized clinical trial (designed to minimize bias) should be weighted higher than one from a retrospective observational study [7] . The p-value debate has smoldered since the 1950s [10] , and replacement with confidence intervals has been suggested since the 1980s. [11]

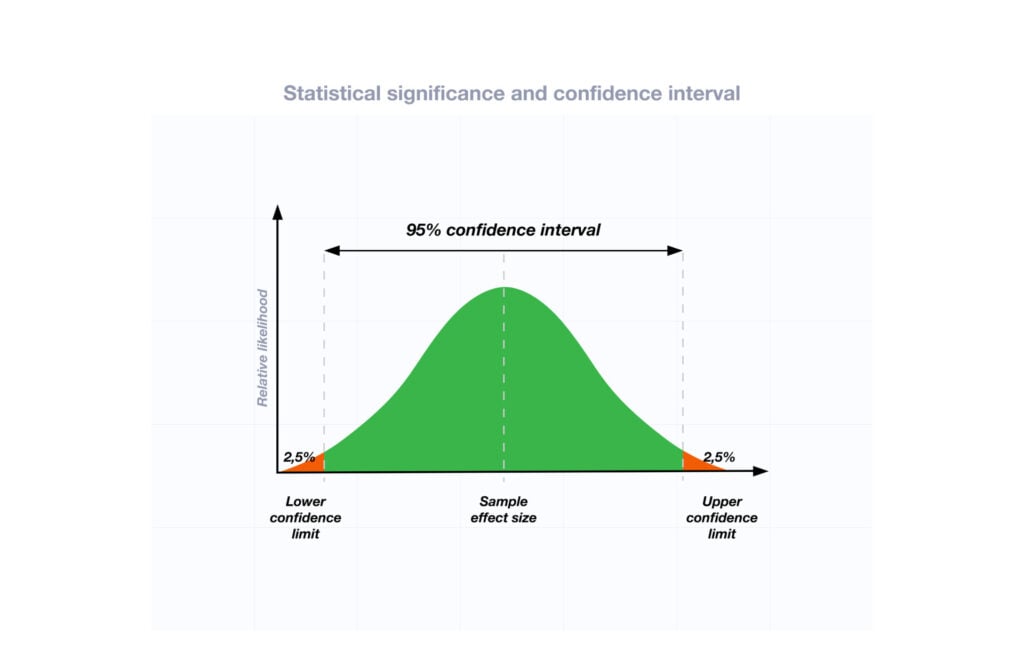
Confidence Intervals

A confidence interval provides a range of values within given confidence (e.g., 95%), including the accurate value of the statistical constraint within a targeted population. [12] Most research uses a 95% CI, but investigators can set any level (e.g., 90% CI, 99% CI). [13] A CI provides a range with the lower bound and upper bound limits of a difference or association that would be plausible for a population. [14] Therefore, a CI of 95% indicates that if a study were to be carried out 100 times, the range would contain the true value in 95, [15] confidence intervals provide more evidence regarding the precision of an estimate compared to p-values. [6]

In consideration of the similar research example provided above, one could make the following statement with 95% CI:

Statement: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22; there was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).

It is important to note that the width of the CI is affected by the standard error and the sample size; reducing a study sample number will result in less precision of the CI (increase the width). [14] A larger width indicates a smaller sample size or a larger variability. [16] A researcher would want to increase the precision of the CI. For example, a 95% CI of 1.43 – 1.47 is much more precise than the one provided in the example above. In research and clinical practice, CIs provide valuable information on whether the interval includes or excludes any clinically significant values. [14]

Null values are sometimes used for differences with CI (zero for differential comparisons and 1 for ratios). However, CIs provide more information than that. [15] Consider this example: A hospital implements a new protocol that reduced wait time for patients in the emergency department by an average of 25 minutes (95% CI: -2.5 – 41 minutes). Because the range crosses zero, implementing this protocol in different populations could result in longer wait times; however, the range is much higher on the positive side. Thus, while the p-value used to detect statistical significance for this may result in "not significant" findings, individuals should examine this range, consider the study design, and weigh whether or not it is still worth piloting in their workplace.

Similarly to p-values, 95% CIs cannot control for researchers' errors (e.g., study bias or improper data analysis). [14] In consideration of whether to report p-values or CIs, researchers should examine journal preferences. When in doubt, reporting both may be beneficial. [13] An example is below:

Reporting both: Individuals who were prescribed Drug 23 had no symptoms after three days, which was significantly faster than those prescribed Drug 22, p = 0.009. There was a mean difference between the two groups of days to the recovery of 4.2 days (95% CI: 1.9 – 7.8).

Clinical Significance

Recall that clinical significance and statistical significance are two different concepts. Healthcare providers should remember that a study with statistically significant differences and large sample size may be of no interest to clinicians, whereas a study with smaller sample size and statistically non-significant results could impact clinical practice. [14] Additionally, as previously mentioned, a non-significant finding may reflect the study design itself rather than relationships between variables.

Healthcare providers using evidence-based medicine to inform practice should use clinical judgment to determine the practical importance of studies through careful evaluation of the design, sample size, power, likelihood of type I and type II errors, data analysis, and reporting of statistical findings (p values, 95% CI or both). [4] Interestingly, some experts have called for "statistically significant" or "not significant" to be excluded from work as statistical significance never has and will never be equivalent to clinical significance. [17]

The decision on what is clinically significant can be challenging, depending on the providers' experience and especially the severity of the disease. Providers should use their knowledge and experiences to determine the meaningfulness of study results and make inferences based not only on significant or insignificant results by researchers but through their understanding of study limitations and practical implications.

Nursing, Allied Health, and Interprofessional Team Interventions

All physicians, nurses, pharmacists, and other healthcare professionals should strive to understand the concepts in this chapter. These individuals should maintain the ability to review and incorporate new literature for evidence-based and safe care.

Review Questions
Access free multiple choice questions on this topic.
Comment on this article.

Disclosure: Jacob Shreffler declares no relevant financial relationships with ineligible companies.

Disclosure: Martin Huecker declares no relevant financial relationships with ineligible companies.

This book is distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) ( http://creativecommons.org/licenses/by-nc-nd/4.0/ ), which permits others to distribute the work, provided that the article is not altered or used commercially. You are not required to obtain permission to distribute this article, provided that you credit the author and journal.

Cite this Page Shreffler J, Huecker MR. Hypothesis Testing, P Values, Confidence Intervals, and Significance. [Updated 2023 Mar 13]. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

In this Page

Bulk download.

Bulk download StatPearls data from FTP

Related information

PMC PubMed Central citations
PubMed Links to PubMed

Recent Activity

Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearl... Hypothesis Testing, P Values, Confidence Intervals, and Significance - StatPearls

Your browsing activity is empty.

Activity recording is turned off.

Turn recording back on

Connect with NLM

National Library of Medicine 8600 Rockville Pike Bethesda, MD 20894

Web Policies FOIA HHS Vulnerability Disclosure

Help Accessibility Careers

P-Value And Statistical Significance: What It Is & Why It Matters

Saul McLeod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul McLeod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Learn about our Editorial Process

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

The p-value in statistics quantifies the evidence against a null hypothesis. A low p-value suggests data is inconsistent with the null, potentially favoring an alternative hypothesis. Common significance thresholds are 0.05 or 0.01.

P-Value Explained in Normal Distribution

Hypothesis testing

When you perform a statistical test, a p-value helps you determine the significance of your results in relation to the null hypothesis.

The null hypothesis (H0) states no relationship exists between the two variables being studied (one variable does not affect the other). It states the results are due to chance and are not significant in supporting the idea being investigated. Thus, the null hypothesis assumes that whatever you try to prove did not happen.

The alternative hypothesis (Ha or H1) is the one you would believe if the null hypothesis is concluded to be untrue.

The alternative hypothesis states that the independent variable affected the dependent variable, and the results are significant in supporting the theory being investigated (i.e., the results are not due to random chance).

What a p-value tells you

A p-value, or probability value, is a number describing how likely it is that your data would have occurred by random chance (i.e., that the null hypothesis is true).

The level of statistical significance is often expressed as a p-value between 0 and 1.

The smaller the p -value, the less likely the results occurred by random chance, and the stronger the evidence that you should reject the null hypothesis.

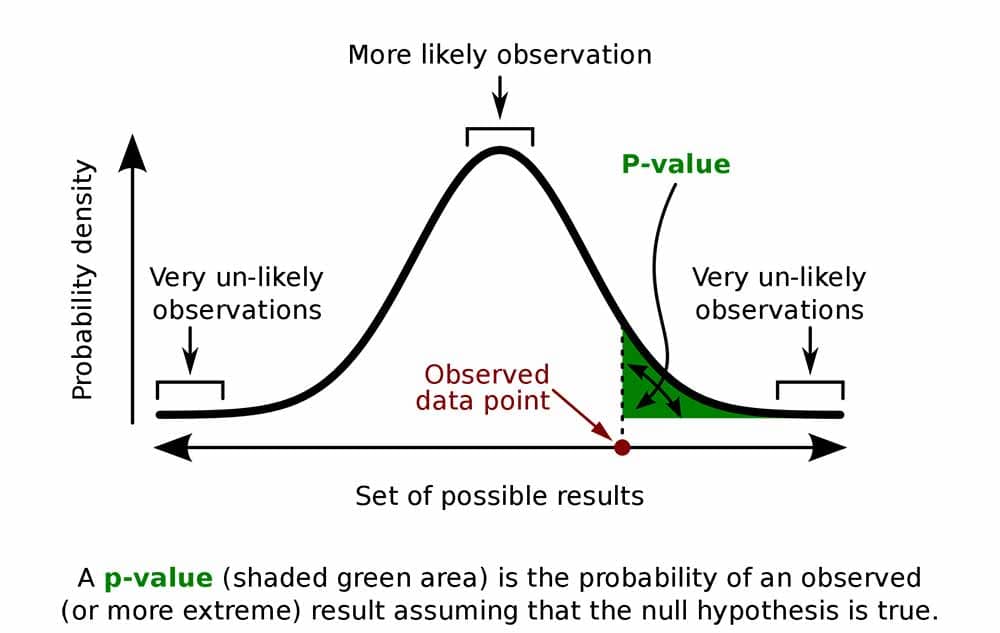
Remember, a p-value doesn’t tell you if the null hypothesis is true or false. It just tells you how likely you’d see the data you observed (or more extreme data) if the null hypothesis was true. It’s a piece of evidence, not a definitive proof.

Example: Test Statistic and p-Value

Suppose you’re conducting a study to determine whether a new drug has an effect on pain relief compared to a placebo. If the new drug has no impact, your test statistic will be close to the one predicted by the null hypothesis (no difference between the drug and placebo groups), and the resulting p-value will be close to 1. It may not be precisely 1 because real-world variations may exist. Conversely, if the new drug indeed reduces pain significantly, your test statistic will diverge further from what’s expected under the null hypothesis, and the p-value will decrease. The p-value will never reach zero because there’s always a slim possibility, though highly improbable, that the observed results occurred by random chance.

P-value interpretation

The significance level (alpha) is a set probability threshold (often 0.05), while the p-value is the probability you calculate based on your study or analysis.

A p-value less than or equal to your significance level (typically ≤ 0.05) is statistically significant.

A p-value less than or equal to a predetermined significance level (often 0.05 or 0.01) indicates a statistically significant result, meaning the observed data provide strong evidence against the null hypothesis.

This suggests the effect under study likely represents a real relationship rather than just random chance.

For instance, if you set α = 0.05, you would reject the null hypothesis if your p -value ≤ 0.05.

It indicates strong evidence against the null hypothesis, as there is less than a 5% probability the null is correct (and the results are random).

Therefore, we reject the null hypothesis and accept the alternative hypothesis.

Example: Statistical Significance

Upon analyzing the pain relief effects of the new drug compared to the placebo, the computed p-value is less than 0.01, which falls well below the predetermined alpha value of 0.05. Consequently, you conclude that there is a statistically significant difference in pain relief between the new drug and the placebo.

What does a p-value of 0.001 mean?

A p-value of 0.001 is highly statistically significant beyond the commonly used 0.05 threshold. It indicates strong evidence of a real effect or difference, rather than just random variation.

Specifically, a p-value of 0.001 means there is only a 0.1% chance of obtaining a result at least as extreme as the one observed, assuming the null hypothesis is correct.

Such a small p-value provides strong evidence against the null hypothesis, leading to rejecting the null in favor of the alternative hypothesis.

A p-value more than the significance level (typically p > 0.05) is not statistically significant and indicates strong evidence for the null hypothesis.

This means we retain the null hypothesis and reject the alternative hypothesis. You should note that you cannot accept the null hypothesis; we can only reject it or fail to reject it.

Note : when the p-value is above your threshold of significance, it does not mean that there is a 95% probability that the alternative hypothesis is true.

One-Tailed Test

Probability and statistical significance in ab testing. Statistical significance in a b experiments

Two-Tailed Test

How do you calculate the p-value ?

Most statistical software packages like R, SPSS, and others automatically calculate your p-value. This is the easiest and most common way.

Online resources and tables are available to estimate the p-value based on your test statistic and degrees of freedom.

These tables help you understand how often you would expect to see your test statistic under the null hypothesis.

Understanding the Statistical Test:

Different statistical tests are designed to answer specific research questions or hypotheses. Each test has its own underlying assumptions and characteristics.

For example, you might use a t-test to compare means, a chi-squared test for categorical data, or a correlation test to measure the strength of a relationship between variables.

Be aware that the number of independent variables you include in your analysis can influence the magnitude of the test statistic needed to produce the same p-value.

This factor is particularly important to consider when comparing results across different analyses.

Example: Choosing a Statistical Test

If you’re comparing the effectiveness of just two different drugs in pain relief, a two-sample t-test is a suitable choice for comparing these two groups. However, when you’re examining the impact of three or more drugs, it’s more appropriate to employ an Analysis of Variance ( ANOVA) . Utilizing multiple pairwise comparisons in such cases can lead to artificially low p-values and an overestimation of the significance of differences between the drug groups.

How to report

A statistically significant result cannot prove that a research hypothesis is correct (which implies 100% certainty).

Instead, we may state our results “provide support for” or “give evidence for” our research hypothesis (as there is still a slight probability that the results occurred by chance and the null hypothesis was correct – e.g., less than 5%).

Example: Reporting the results

In our comparison of the pain relief effects of the new drug and the placebo, we observed that participants in the drug group experienced a significant reduction in pain ( M = 3.5; SD = 0.8) compared to those in the placebo group ( M = 5.2; SD = 0.7), resulting in an average difference of 1.7 points on the pain scale (t(98) = -9.36; p < 0.001).

The 6th edition of the APA style manual (American Psychological Association, 2010) states the following on the topic of reporting p-values:

“When reporting p values, report exact p values (e.g., p = .031) to two or three decimal places. However, report p values less than .001 as p < .001.

The tradition of reporting p values in the form p < .10, p < .05, p < .01, and so forth, was appropriate in a time when only limited tables of critical values were available.” (p. 114)

Do not use 0 before the decimal point for the statistical value p as it cannot equal 1. In other words, write p = .001 instead of p = 0.001.
Please pay attention to issues of italics ( p is always italicized) and spacing (either side of the = sign).
p = .000 (as outputted by some statistical packages such as SPSS) is impossible and should be written as p < .001.
The opposite of significant is “nonsignificant,” not “insignificant.”

Why is the p -value not enough?

A lower p-value is sometimes interpreted as meaning there is a stronger relationship between two variables.

However, statistical significance means that it is unlikely that the null hypothesis is true (less than 5%).

To understand the strength of the difference between the two groups (control vs. experimental) a researcher needs to calculate the effect size .

When do you reject the null hypothesis?

In statistical hypothesis testing, you reject the null hypothesis when the p-value is less than or equal to the significance level (α) you set before conducting your test. The significance level is the probability of rejecting the null hypothesis when it is true. Commonly used significance levels are 0.01, 0.05, and 0.10.

Remember, rejecting the null hypothesis doesn’t prove the alternative hypothesis; it just suggests that the alternative hypothesis may be plausible given the observed data.

The p -value is conditional upon the null hypothesis being true but is unrelated to the truth or falsity of the alternative hypothesis.

What does p-value of 0.05 mean?

If your p-value is less than or equal to 0.05 (the significance level), you would conclude that your result is statistically significant. This means the evidence is strong enough to reject the null hypothesis in favor of the alternative hypothesis.

Are all p-values below 0.05 considered statistically significant?

No, not all p-values below 0.05 are considered statistically significant. The threshold of 0.05 is commonly used, but it’s just a convention. Statistical significance depends on factors like the study design, sample size, and the magnitude of the observed effect.

A p-value below 0.05 means there is evidence against the null hypothesis, suggesting a real effect. However, it’s essential to consider the context and other factors when interpreting results.

Researchers also look at effect size and confidence intervals to determine the practical significance and reliability of findings.

How does sample size affect the interpretation of p-values?

Sample size can impact the interpretation of p-values. A larger sample size provides more reliable and precise estimates of the population, leading to narrower confidence intervals.

With a larger sample, even small differences between groups or effects can become statistically significant, yielding lower p-values. In contrast, smaller sample sizes may not have enough statistical power to detect smaller effects, resulting in higher p-values.

Therefore, a larger sample size increases the chances of finding statistically significant results when there is a genuine effect, making the findings more trustworthy and robust.

Can a non-significant p-value indicate that there is no effect or difference in the data?

No, a non-significant p-value does not necessarily indicate that there is no effect or difference in the data. It means that the observed data do not provide strong enough evidence to reject the null hypothesis.

There could still be a real effect or difference, but it might be smaller or more variable than the study was able to detect.

Other factors like sample size, study design, and measurement precision can influence the p-value. It’s important to consider the entire body of evidence and not rely solely on p-values when interpreting research findings.

Can P values be exactly zero?

While a p-value can be extremely small, it cannot technically be absolute zero. When a p-value is reported as p = 0.000, the actual p-value is too small for the software to display. This is often interpreted as strong evidence against the null hypothesis. For p values less than 0.001, report as p < .001

Further Information

P Value Calculator From T Score
P-Value Calculator For Chi-Square
P-values and significance tests (Kahn Academy)
Hypothesis testing and p-values (Kahn Academy)
Wasserstein, R. L., Schirm, A. L., & Lazar, N. A. (2019). Moving to a world beyond “ p “< 0.05”.
Criticism of using the “ p “< 0.05”.
Publication manual of the American Psychological Association
Statistics for Psychology Book Download

Bland, J. M., & Altman, D. G. (1994). One and two sided tests of significance: Authors’ reply. BMJ: British Medical Journal , 309 (6958), 874.

Goodman, S. N., & Royall, R. (1988). Evidence and scientific research. American Journal of Public Health , 78 (12), 1568-1574.

Goodman, S. (2008, July). A dirty dozen: twelve p-value misconceptions . In Seminars in hematology (Vol. 45, No. 3, pp. 135-140). WB Saunders.

Lang, J. M., Rothman, K. J., & Cann, C. I. (1998). That confounded P-value. Epidemiology (Cambridge, Mass.) , 9 (1), 7-8.

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

Chapter 5: Hypothesis Testing and P-Values

Last updated
Save as PDF
Page ID 99725

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

Here you can find a series of pre-recorded lecture videos that cover this content: https://youtube.com/playlist?list=PL...I4vAR1y-lP1Ees

Hypothesis Testing for a Single Mean for a Small Sample Size

The reason we are using these statistical tools is to make certain decisions regarding a measurand. One of the most common methods for doing this is hypothesis testing .

Typically we deal with two hypotheses:

• Null Hypothesis

– First step in hypothesis testing

– H 0 : µ = µ 0 where µ 0 is some constant specific value

• Alternative Hypothesis

– Second step

– Choice should reflect on what we are attempting to show

∗ Two-tailed test: concerned with whether a population mean, µ is different from specific value µ 0 , i.e. $H_{a}: \mu \neq \mu_{0}$

∗ Left-tailed test: concerned with whether a population mean is less than a specific value, $H_{a}: \mu < \mu_{0}$

∗ Right-tailed test: concerned with whether a population mean is greater than a specific value, $H_{a}: \mu > \mu_{0}$

Procedure for Hypothesis Testing

(1) Define null hypothesis, H 0

(2) Define alternative hypothesis, H a

(3) Define c% interval

(4) Calculate the value of t exp from the data

(5) Determine proper value of $t_{\alpha, \nu}$ or $t_{\frac{\alpha}{2}, \nu}$ using the degrees of freedom ν

(6) If t exp falls in the reject H 0 region, we reject H 0 and accept the alternative hypothesis H a

(7) If t exp falls in the do not reject H 0 region, we conclude that we do not have sufficient data to reject H 0 at the level of confidence specified

Figure $\PageIndex{1}$: Rejecting null hypothesis for two, right, and left tailed test.

Let’s start with a two-tailed test and ask ourselves the following question, does the PCM data from the example last lecture come from a population with a true mean of 2mg assuming a confidence level of 95%.

\begin{eqnarray} H_{0}: \mu = 2.00 mg \\ H_{a}: \mu \neq 2.00 mg \\ t_{exp} = \frac{\overline{x} - \mu_{0}}{\frac{S_{x}}{\sqrt{n}}} = 0.99011 \\ t_{\alpha, \nu} = t_{0.025,17} = 2.11 \end{eqnarray}

We can look at our figure and we see that our t-value falls within the do-not reject Ho region. Does this match with result from R???

I don’t see any result only some mysterious thing called the P-value, but no worries we actually already intuitively know what this mysterious value is.

Often if you have read scientific articles or if you have taken other statistics courses you may have heard of the term P-Value . This term is ubiquitous and is used much much more often than z or t-values. Simply put, the P-value is the probability of getting a result that is more extreme than the value that is actually observed . Let’s see how it is used in the context of our previous hypothesis tests, starting with a two-tailed test.

Our P-value effectively gives us the probability of measuring a value greater than the observed, i.e. the tail ends. The way that we interpret the P-value is if we are running a two-tailed confidence interval at 5% confidence if the P-value is greater than 2.5% or 0.025 then we fall in the Do-Not Reject H o regime and if it less than that value then we fall in the Reject H o regime.

So we have previously found that we fall in the Do Not Reject region and looking at our calculated P-value of 0.336 that falls in the Do Not Reject region which matches our result!!!

Another PCM Application

Using the data from the previous example does the sample come from a population whose true mean weight is greater than 1.99mg, assuming a confidence level of 99%?

\begin{eqnarray} H_{0}: \mu = 1.99 mg \\ H_{a}: \mu > 1.99 mg \\ t_{exp} = \frac{\overline{x} - \mu_{0}}{\frac{S_{x}}{\sqrt{n}}} = 2.025 \\ t_{\alpha, \nu} = t_{0.01,17} = 2.567 \end{eqnarray}

Clearly since it is a right tailed test it does not fall in the do not reject H 0 region. So we conclude with 99% confidence that the population mean was not significantly different than 1.99mg. Note the subtle distinction of the phrase was not significantly different than 1.99mg or we do not have sufficient data to reject H 0 with 99% confidence. We are not saying that the population mean is 1.99mg.

If we examine this from a P-value perspective we find that our P-value is 0.02943 and that also falls in the Do Not Reject Region as well!!

Yet Another PCM Application

Using the data from the previous example does the sample come from a population whose true mean weight is less than 2.01mg, assuming a confidence level of 90%?

\begin{eqnarray} H_{0}: \mu = 2.01 mg \\ H_{a}: \mu < 2.01 mg \\ t_{exp} = \frac{\overline{x} - \mu_{0}}{\frac{S_{x}}{\sqrt{n}}} = -0.0448035 \\ t_{\alpha, \nu} = t_{0.01,17} = -2.567 \end{eqnarray}

Clearly since it is a left tailed test it does not fall in the do not reject H 0 region. So we conclude with 90% confidence that the population mean was not significantly different than 2.01mg.

If we examine this from a P-value perspective we find that our P-value is 0.4824 and that also falls in the Do Not Reject Region as well!!

Hypothesis Testing Single Mean for Large Sample Size

For larger sample sizes we follow the exact same procedure but we replace t α ,ν by z α and t exp by:

\begin{equation} z_{exp} = \frac{\overline{x} - \mu_{0}}{\frac{S_{x}}{\sqrt{n}}} \end{equation}

However, we can just use the t-table and use the value for degrees of freedom that corresponds to the n > 30 scenario i.e. ν ≈∞.

Looking Back at Rolling Velocity

Does the sample of our rolling magnetic beads come from a population with a velocity less than 3.1 $\frac{\mu m}{s}$ at a confidence level of 99%.

\begin{eqnarray} H_{0}: \mu = 3.1 \frac{\mu m}{s} \\ H_{a}: \mu < 3.1 \frac{\mu m}{s} \\ t_{exp} = \frac{\overline{x} - \mu_{0}}{\frac{S_{x}}{\sqrt{n}}} = -1.3383\\ t_{0.01,|Inf} = -2.362 \end{eqnarray}

We can see we are in the Do Not Reject H 0 and we see that the P-Value is 0.09151 so we can confirm that we are in the Do Not Reject H 0 .

t-Test Comparison of Sample Means

To compare two samples solely based on their means:

\begin{equation} t = \frac{\overline{x}_{1} - \overline{x}_{2}}{\sqrt{\bigg(\frac{S_{1}^{2}}{n_{1}}\bigg) + \bigg(\frac{S_{2}^{2}}{n_{2}}\bigg)}} \end{equation}

where x 1 ,S 1 , and n 1 and x 2 , S 2 , and n 2 are the mean, standard deviations,and sizes of the two samples. and the degrees of freedom can be approximated by:

\begin{equation} \nu = \frac{[(\frac{S_{1}^{2}}{n_{1}}) + (\frac{S_{2}^{2}}{n_{2}}) ] ^{2}}{\frac{(\frac{S_{1}^{2}}{n_{1}})^{2}}{n_{1} - 1} + \frac{(\frac{S_{2}^{2}}{n_{2}})^{2}}{n_{2}-1}} \end{equation}

and ν is rounded to nearest integer. If the value t falls into the interval $\pm t_{\frac{\alpha}{2}, \nu}$ then the two means are not significantly difference at the chosen confidence level. One of the great things about this technique is that this equation is applicable for any combination comparing large and small samples sizes.

Are these Materials Significantly Stiffer

Conisder Material A with a Young's Modulus average of 302.6 GPa, measured 12 times, and a sample standard deviation of 1.27 GPa and Material B with a Young's Modulus average of 302.3 GPa, measured 15 times, and a sample standard deviation of 1.7 GPa.

\begin{eqnarray} H_{0} = \overline{x}_{A} = \overline{x}_{B}\\ H_{a} = \overline{x}_{A} \neq \overline{x}_{B}\\ \nu \approx 25\\ t_{exp} = 0.547\\ t_{0.025,25} = 2.060 \end{eqnarray}

The value falls in the do not reject region so there is not a significant difference in the stiffness of Material A and B.

We can also perform a P-value analysis to a t-Test comparison of different samples as well you will see the R code can be simply adapted to examine different samples. Let’s simulate the example here and we find a P-value of 0.02194 so for this simulated example that would be a reject finding, again the difference here would be due to the simulated number values, as we can confirm the means and standard deviation values are slightly different. In fact if we were to re-run the analysis using our method by hand we can achieve the same result. Let’s try that really quickly.

Skip to secondary menu
Skip to main content
Skip to primary sidebar

Statistics By Jim

Making statistics intuitive

How Hypothesis Tests Work: Significance Levels (Alpha) and P values

By Jim Frost 45 Comments

Hypothesis testing is a vital process in inferential statistics where the goal is to use sample data to draw conclusions about an entire population . In the testing process, you use significance levels and p-values to determine whether the test results are statistically significant.

You hear about results being statistically significant all of the time. But, what do significance levels, P values, and statistical significance actually represent? Why do we even need to use hypothesis tests in statistics?

In this post, I answer all of these questions. I use graphs and concepts to explain how hypothesis tests function in order to provide a more intuitive explanation. This helps you move on to understanding your statistical results.

Hypothesis Test Example Scenario

To start, I’ll demonstrate why we need to use hypothesis tests using an example.

A researcher is studying fuel expenditures for families and wants to determine if the monthly cost has changed since last year when the average was $260 per month. The researcher draws a random sample of 25 families and enters their monthly costs for this year into statistical software. You can download the CSV data file: FuelsCosts . Below are the descriptive statistics for this year.

Table of descriptive statistics for our fuel cost example.

We’ll build on this example to answer the research question and show how hypothesis tests work.

Descriptive Statistics Alone Won’t Answer the Question

The researcher collected a random sample and found that this year’s sample mean (330.6) is greater than last year’s mean (260). Why perform a hypothesis test at all? We can see that this year’s mean is higher by $70! Isn’t that different?

Regrettably, the situation isn’t as clear as you might think because we’re analyzing a sample instead of the full population. There are huge benefits when working with samples because it is usually impossible to collect data from an entire population. However, the tradeoff for working with a manageable sample is that we need to account for sample error.

The sampling error is the gap between the sample statistic and the population parameter. For our example, the sample statistic is the sample mean, which is 330.6. The population parameter is μ, or mu, which is the average of the entire population. Unfortunately, the value of the population parameter is not only unknown but usually unknowable. Learn more about Sampling Error .

We obtained a sample mean of 330.6. However, it’s conceivable that, due to sampling error, the mean of the population might be only 260. If the researcher drew another random sample, the next sample mean might be closer to 260. It’s impossible to assess this possibility by looking at only the sample mean. Hypothesis testing is a form of inferential statistics that allows us to draw conclusions about an entire population based on a representative sample. We need to use a hypothesis test to determine the likelihood of obtaining our sample mean if the population mean is 260.

Background information : The Difference between Descriptive and Inferential Statistics and Populations, Parameters, and Samples in Inferential Statistics

A Sampling Distribution Determines Whether Our Sample Mean is Unlikely

It is very unlikely for any sample mean to equal the population mean because of sample error. In our case, the sample mean of 330.6 is almost definitely not equal to the population mean for fuel expenditures.

If we could obtain a substantial number of random samples and calculate the sample mean for each sample, we’d observe a broad spectrum of sample means. We’d even be able to graph the distribution of sample means from this process.

This type of distribution is called a sampling distribution. You obtain a sampling distribution by drawing many random samples of the same size from the same population. Why the heck would we do this?

Because sampling distributions allow you to determine the likelihood of obtaining your sample statistic and they’re crucial for performing hypothesis tests.

Luckily, we don’t need to go to the trouble of collecting numerous random samples! We can estimate the sampling distribution using the t-distribution, our sample size, and the variability in our sample.

We want to find out if the average fuel expenditure this year (330.6) is different from last year (260). To answer this question, we’ll graph the sampling distribution based on the assumption that the mean fuel cost for the entire population has not changed and is still 260. In statistics, we call this lack of effect, or no change, the null hypothesis . We use the null hypothesis value as the basis of comparison for our observed sample value.

Sampling distributions and t-distributions are types of probability distributions.

Related posts : Sampling Distributions and Understanding Probability Distributions

Graphing our Sample Mean in the Context of the Sampling Distribution

The graph below shows which sample means are more likely and less likely if the population mean is 260. We can place our sample mean in this distribution. This larger context helps us see how unlikely our sample mean is if the null hypothesis is true (μ = 260).

Sampling distribution of means for our fuel cost data.

The graph displays the estimated distribution of sample means. The most likely values are near 260 because the plot assumes that this is the true population mean. However, given random sampling error, it would not be surprising to observe sample means ranging from 167 to 352. If the population mean is still 260, our observed sample mean (330.6) isn’t the most likely value, but it’s not completely implausible either.

The Role of Hypothesis Tests

The sampling distribution shows us that we are relatively unlikely to obtain a sample of 330.6 if the population mean is 260. Is our sample mean so unlikely that we can reject the notion that the population mean is 260?

In statistics, we call this rejecting the null hypothesis. If we reject the null for our example, the difference between the sample mean (330.6) and 260 is statistically significant. In other words, the sample data favor the hypothesis that the population average does not equal 260.

However, look at the sampling distribution chart again. Notice that there is no special location on the curve where you can definitively draw this conclusion. There is only a consistent decrease in the likelihood of observing sample means that are farther from the null hypothesis value. Where do we decide a sample mean is far away enough?

To answer this question, we’ll need more tools—hypothesis tests! The hypothesis testing procedure quantifies the unusualness of our sample with a probability and then compares it to an evidentiary standard. This process allows you to make an objective decision about the strength of the evidence.

We’re going to add the tools we need to make this decision to the graph—significance levels and p-values!

These tools allow us to test these two hypotheses:

Null hypothesis: The population mean equals the null hypothesis mean (260).
Alternative hypothesis: The population mean does not equal the null hypothesis mean (260).

Related post : Hypothesis Testing Overview

What are Significance Levels (Alpha)?

A significance level, also known as alpha or α, is an evidentiary standard that a researcher sets before the study. It defines how strongly the sample evidence must contradict the null hypothesis before you can reject the null hypothesis for the entire population. The strength of the evidence is defined by the probability of rejecting a null hypothesis that is true. In other words, it is the probability that you say there is an effect when there is no effect.

For instance, a significance level of 0.05 signifies a 5% risk of deciding that an effect exists when it does not exist.

Lower significance levels require stronger sample evidence to be able to reject the null hypothesis. For example, to be statistically significant at the 0.01 significance level requires more substantial evidence than the 0.05 significance level. However, there is a tradeoff in hypothesis tests. Lower significance levels also reduce the power of a hypothesis test to detect a difference that does exist.

The technical nature of these types of questions can make your head spin. A picture can bring these ideas to life!

To learn a more conceptual approach to significance levels, see my post about Understanding Significance Levels .

Graphing Significance Levels as Critical Regions

On the probability distribution plot, the significance level defines how far the sample value must be from the null value before we can reject the null. The percentage of the area under the curve that is shaded equals the probability that the sample value will fall in those regions if the null hypothesis is correct.

To represent a significance level of 0.05, I’ll shade 5% of the distribution furthest from the null value.

Graph that displays a two-tailed critical region for a significance level of 0.05.

The two shaded regions in the graph are equidistant from the central value of the null hypothesis. Each region has a probability of 0.025, which sums to our desired total of 0.05. These shaded areas are called the critical region for a two-tailed hypothesis test.

The critical region defines sample values that are improbable enough to warrant rejecting the null hypothesis. If the null hypothesis is correct and the population mean is 260, random samples (n=25) from this population have means that fall in the critical region 5% of the time.

Our sample mean is statistically significant at the 0.05 level because it falls in the critical region.

Related posts : One-Tailed and Two-Tailed Tests Explained , What Are Critical Values? , and T-distribution Table of Critical Values

Comparing Significance Levels

Let’s redo this hypothesis test using the other common significance level of 0.01 to see how it compares.

Chart that shows a two-tailed critical region for a significance level of 0.01.

This time the sum of the two shaded regions equals our new significance level of 0.01. The mean of our sample does not fall within with the critical region. Consequently, we fail to reject the null hypothesis. We have the same exact sample data, the same difference between the sample mean and the null hypothesis value, but a different test result.

What happened? By specifying a lower significance level, we set a higher bar for the sample evidence. As the graph shows, lower significance levels move the critical regions further away from the null value. Consequently, lower significance levels require more extreme sample means to be statistically significant.

You must set the significance level before conducting a study. You don’t want the temptation of choosing a level after the study that yields significant results. The only reason I compared the two significance levels was to illustrate the effects and explain the differing results.

The graphical version of the 1-sample t-test we created allows us to determine statistical significance without assessing the P value. Typically, you need to compare the P value to the significance level to make this determination.

Related post : Step-by-Step Instructions for How to Do t-Tests in Excel

What Are P values?

P values are the probability that a sample will have an effect at least as extreme as the effect observed in your sample if the null hypothesis is correct.

This tortuous, technical definition for P values can make your head spin. Let’s graph it!

First, we need to calculate the effect that is present in our sample. The effect is the distance between the sample value and null value: 330.6 – 260 = 70.6. Next, I’ll shade the regions on both sides of the distribution that are at least as far away as 70.6 from the null (260 +/- 70.6). This process graphs the probability of observing a sample mean at least as extreme as our sample mean.

Probability distribution plot shows how our sample mean has a p-value of 0.031.

The total probability of the two shaded regions is 0.03112. If the null hypothesis value (260) is true and you drew many random samples, you’d expect sample means to fall in the shaded regions about 3.1% of the time. In other words, you will observe sample effects at least as large as 70.6 about 3.1% of the time if the null is true. That’s the P value!

Learn more about How to Find the P Value .

Using P values and Significance Levels Together

If your P value is less than or equal to your alpha level, reject the null hypothesis.

The P value results are consistent with our graphical representation. The P value of 0.03112 is significant at the alpha level of 0.05 but not 0.01. Again, in practice, you pick one significance level before the experiment and stick with it!

Using the significance level of 0.05, the sample effect is statistically significant. Our data support the alternative hypothesis, which states that the population mean doesn’t equal 260. We can conclude that mean fuel expenditures have increased since last year.

P values are very frequently misinterpreted as the probability of rejecting a null hypothesis that is actually true. This interpretation is wrong! To understand why, please read my post: How to Interpret P-values Correctly .

Discussion about Statistically Significant Results

Hypothesis tests determine whether your sample data provide sufficient evidence to reject the null hypothesis for the entire population. To perform this test, the procedure compares your sample statistic to the null value and determines whether it is sufficiently rare. “Sufficiently rare” is defined in a hypothesis test by:

Assuming that the null hypothesis is true—the graphs center on the null value.
The significance (alpha) level—how far out from the null value is the critical region?
The sample statistic—is it within the critical region?

There is no special significance level that correctly determines which studies have real population effects 100% of the time. The traditional significance levels of 0.05 and 0.01 are attempts to manage the tradeoff between having a low probability of rejecting a true null hypothesis and having adequate power to detect an effect if one actually exists.

The significance level is the rate at which you incorrectly reject null hypotheses that are actually true ( type I error ). For example, for all studies that use a significance level of 0.05 and the null hypothesis is correct, you can expect 5% of them to have sample statistics that fall in the critical region. When this error occurs, you aren’t aware that the null hypothesis is correct, but you’ll reject it because the p-value is less than 0.05.

This error does not indicate that the researcher made a mistake. As the graphs show, you can observe extreme sample statistics due to sample error alone. It’s the luck of the draw!

Related posts : Statistical Significance: Definition & Meaning and Types of Errors in Hypothesis Testing

Hypothesis tests are crucial when you want to use sample data to make conclusions about a population because these tests account for sample error. Using significance levels and P values to determine when to reject the null hypothesis improves the probability that you will draw the correct conclusion.

Keep in mind that statistical significance doesn’t necessarily mean that the effect is important in a practical, real-world sense. For more information, read my post about Practical vs. Statistical Significance .

If you like this post, read the companion post: How Hypothesis Tests Work: Confidence Intervals and Confidence Levels .

You can also read my other posts that describe how other tests work:

How t-Tests Work
How the F-test works in ANOVA
How Chi-Squared Tests of Independence Work

To see an alternative approach to traditional hypothesis testing that does not use probability distributions and test statistics, learn about bootstrapping in statistics !

Reader Interactions

December 11, 2022 at 10:56 am

For very easy concept about level of significance & p-value 1.Teacher has given a one assignment to student & asked how many error you have doing this assignment? Student reply, he can has error ≤ 5% (it is level of significance). After completion of assignment, teacher checked his error which is ≤ 5% (may be 4% or 3% or 2% even less, it is p-value) it means his results are significant. Otherwise he has error > 5% (may be 6% or 7% or 8% even more, it is p-value) it means his results are non-significant. 2. Teacher has given a one assignment to student & asked how many error you have doing this assignment? Student reply, he can has error ≤ 1% (it is level of significance). After completion of assignment, teacher checked his error which is ≤ 1% (may be 0.9% or 0.8% or 0.7% even less, it is p-value) it means his results are significant. Otherwise he has error > 1% (may be 1.1% or 1.5% or 2% even more, it is p-value) it means his results are non-significant. p-value is significant or not mainly dependent upon the level of significance.

December 11, 2022 at 7:50 pm

I think that approach helps explain how to determine statistical significance–is the p-value less than or equal to the significance level. However, it doesn’t really explain what statistical significance means. I find that comparing the p-value to the significance level is the easy part. Knowing what it means and how to choose your significance level is the harder part!

December 3, 2022 at 5:54 pm

What would you say to someone who believes that a p-value higher than the level of significance (alpha) means the null hypothesis has been proven? Should you support that statement or deny it?

December 3, 2022 at 10:18 pm

Hi Emmanuel,

When the p-value is greater than the significance level, you fail to reject the null hypothesis . That is different than proving it. To learn why and what it means, click the link to read a post that I’ve written that will answer your question!

April 19, 2021 at 12:27 am

Thank you so much Sir

April 18, 2021 at 2:37 pm

Hi sir, your blogs are much more helpful for clearing the concepts of statistics, as a researcher I find them much more useful. I have some quarries:

1. In many research papers I have seen authors using the statement ” means or values are statically at par at p = 0.05″ when they do some pair wise comparison between the treatments (a kind of post hoc) using some value of CD (critical difference) or we can say LSD which is calculated using alpha not using p. So with this article I think this should be alpha =0.05 or 5%, not p = 0.05 earlier I thought p and alpha are same. p it self is compared with alpha 0.05. Correct me if I am wrong.

2. When we can draw a conclusion using critical value based on critical values (CV) which is based on alpha values in different tests (e.g. in F test CV is at F (0.05, t-1, error df) when alpha is 0.05 which is table value of F and is compared with F calculated for drawing the conclusion); then why we go for p values, and draw a conclusion based on p values, even many online software do not give p value, they just mention CD (LSD)

3. can you please help me in interpreting interaction in two factor analysis (Factor A X Factor b) in Anova.

Thank You so much!

(Commenting again as I have not seen my comment in comment list; don’t know why)

April 18, 2021 at 10:57 pm

Hi Himanshu,

I manually approve comments so there will be some time lag involved before they show up.

Regarding your first question, yes, you’re correct. Test results are significant at particular significance levels or alpha. They should not use p to define the significance level. You’re also correct in that you compare p to alpha.

Critical values are a different (but related) approach for determining significance. It was more common before computer analysis took off because it reduced the calculations. Using this approach in its simplest form, you only know whether a result is significant or not at the given alpha. You just determine whether the test statistic falls within a critical region to determine statistical significance or not significant. However, it is ok to supplement this type of result with the actual p-value. Knowing the precise p-value provides additional information that significant/not significant does not provide. The critical value and p-value approaches will always agree too. For more information about why the exact p-value is useful, read my post about Five Tips for Interpreting P-values .

Finally, I’ve written about two-way ANOVA in my post, How to do Two-Way ANOVA in Excel . Additionally, I write about it in my Hypothesis Testing ebook .

January 28, 2021 at 3:12 pm

Thank you for your answer, Jim, I really appreciate it. I’m taking a Coursera stats course and online learning without being able to ask questions of a real teacher is not my forte!

You’re right, I don’t think I’m ready for that calculation! However, I think I’m struggling with something far more basic, perhaps even the interpretation of the t-table? I’m just not sure how you came up with the p-value as .03112, with the 24 degrees of freedom. When I pull up a t-table and look at the 24-degrees of freedom row, I’m not sure how any of those numbers correspond with your answer? Either the single tail of 0.01556 or the combined of 0.03112. What am I not getting? (which, frankly, could be a lot!!) Again, thank you SO much for your time.

January 28, 2021 at 11:19 pm

Ah ok, I see! First, let me point you to several posts I’ve written about t-values and the t-distribution. I don’t cover those in this post because I wanted to present a simplified version that just uses the data in its regular units. The basic idea is that the hypothesis tests actually convert all your raw data down into one value for a test statistic, such as the t-value. And then it uses that test statistic to determine whether your results are statistically significant. To be significant, the t-value must exceed a critical value, which is what you lookup in the table. Although, nowadays you’d typically let your software just tell you.

So, read the following two posts, which covers several aspects of t-values and distributions. And then if you have more questions after that, you can post them. But, you’ll have a lot more information about them and probably some of your questions will be answered! T-values T-distributions

January 27, 2021 at 3:10 pm

Jim, just found your website and really appreciate your thoughtful, thorough way of explaining things. I feel very dumb, but I’m struggling with p-values and was hoping you could help me.

Here’s the section that’s getting me confused:

“First, we need to calculate the effect that is present in our sample. The effect is the distance between the sample value and null value: 330.6 – 260 = 70.6. Next, I’ll shade the regions on both sides of the distribution that are at least as far away as 70.6 from the null (260 +/- 70.6). This process graphs the probability of observing a sample mean at least as extreme as our sample mean.

** I’m good up to this point. Draw the picture, do the subtraction, shade the regions. BUT, I’m not sure how to figure out the area of the shaded region — even with a T-table. When I look at the T-table on 24 df, I’m not sure what to do with those numbers, as none of them seem to correspond in any way to what I’m looking at in the problem. In the end, I have no idea how you calculated each shaded area being 0.01556.

I feel like there’s a (very simple) step that everyone else knows how to do, but for some reason I’m missing it.

Again, dumb question, but I’d love your help clarifying that.

thank you, Sara

January 27, 2021 at 9:51 pm

That’s not a dumb question at all. I actually don’t show or explain the calculations for figuring out the area. The reason for that is the same reason why students never calculate the critical t-values for their test, instead you look them up in tables or use statistical software. The common reason for all that is because calculating these values is extremely complicated! It’s best to let software do that for you or, when looking critical values, use the tables!

The principal though is that percentage of the area under the curve equals the probability that values will fall within that range.

And then, for this example, you’d need to figure out the area under the curve for particular ranges!

January 15, 2021 at 10:57 am

HI Jim, I have a question related to Hypothesis test.. in Medical imaging, there are different way to measure signal intensity (from a tumor lesion for example). I tested for the same 100 patients 4 different ways to measure tumor captation to a injected dose. So for the 100 patients, i got 4 linear regression (relation between injected dose and measured quantity at tumor sites) = so an output of 4 equations Condition A output = -0,034308 + 0,0006602*input Condition B output = 0,0117631 + 0,0005425*input Condition C output = 0,0087871 + 0,0005563*input Condition D output = 0,001911 + 0,0006255*input

My question : i want to compare the 4 methods to find the best one (compared to others) : do Hypothesis test good to me… and if Yes, i do not find test to perform it. Can you suggest me a software. I uselly used JMP for my stats… but open to other softwares…

THank for your time G

November 16, 2020 at 5:42 am

Thank you very much for writing about this topic!

Your explanation made more sense to me about: Why we reject Null Hypothesis when p value < significance level

Kind greetings, Jalal

September 25, 2020 at 1:04 pm

Hi Jim, Your explanations are so helpful! Thank you. I wondered about your first graph. I see that the mean of the graph is 260 from the null hypothesis, and it looks like the standard deviation of the graph is about 31. Where did you get 31 from? Thank you

September 25, 2020 at 4:08 pm

Hi Michelle,

That is a great question. Very observant. And it gets to how these tests work. The hypothesis test that I’m illustrating here is the one-sample t-test. And this graph illustrates the sampling distribution for the t-test. T-tests use the t-distribution to determine the sampling distribution. For the t-distribution, you need to specify the degrees of freedom, which entirely defines the distribution (i.e., it’s the only parameter). For 1-sample t-tests, the degrees of freedom equal the number of observations minus 1. This dataset has 25 observations. Hence, the 24 DF you see in the graph.

Unlike the normal distribution, there is no standard deviation parameter. Instead, the degrees of freedom determines the spread of the curve. Typically, with t-tests, you’ll see results discussed in terms of t-values, both for your sample and for defining the critical regions. However, for this introductory example, I’ve converted the t-values into the raw data units (t-value * SE mean).

So, the standard deviation you’re seeing in the graph is a result of the spread of the underlying t-distribution that has 24 degrees of freedom and then applying the conversion from t-values to raw values.

September 10, 2020 at 8:19 am

Your blog is incredible.

I am having difficulty understanding why the phrase ‘as extreme as’ is required in the definition of p-value (“P values are the probability that a sample will have an effect at least as extreme as the effect observed in your sample if the null hypothesis is correct.”)

Why can’t P-Values simply be defined as “The probability of sample observation if the null hypothesis is correct?”

In your other blog titled ‘Interpreting P values’ you have explained p-values as “P-values indicate the believability of the devil’s advocate case that the null hypothesis is correct given the sample data”. I understand (or accept) this explanation. How does one move from this definition to one that contains the phrase ‘as extreme as’?

September 11, 2020 at 5:05 pm

Thanks so much for your kind words! I’m glad that my website has been helpful!

The key to understanding the “at least as extreme” wording lies in the probability plots for p-values. Using probability plots for continuous data, you can calculate probabilities, but only for ranges of values. I discuss this in my post about understanding probability distributions . In a nutshell, we need a range of values for these probabilities because the probabilities are derived from the area under a distribution curve. A single value just produces a line on these graphs rather than an area. Those ranges are the shaded regions in the probability plots. For p-values, the range corresponds to the “at least as extreme” wording. That’s where it comes from. We need a range to calculate a probability. We can’t use the single value of the observed effect because it doesn’t produce an area under the curve.

I hope that helps! I think this is a particularly confusing part of understanding p-values that most people don’t understand.

August 7, 2020 at 5:45 pm

Hi Jim, thanks for the post.

Could you please clarify the following excerpt from ‘Graphing Significance Levels as Critical Regions’:

“The percentage of the area under the curve that is shaded equals the probability that the sample value will fall in those regions if the null hypothesis is correct.”

I’m not sure if I understood this correctly. If the sample value fall in one of the shaded regions, doesn’t mean that the null hypothesis can be rejected, hence that is not correct?

August 7, 2020 at 10:23 pm

Think of it this way. There are two basic reasons for why a sample value could fall in a critical region:

The null hypothesis is correct and random chance caused the sample value to be unusual.
The null hypothesis is not correct.

You don’t know which one is true. Remember, just because you reject the null hypothesis it doesn’t mean the null is false. However, by using hypothesis tests to determine statistical significance, you control the chances of #1 occurring. The rate at which #1 occurs equals your significance level. On the hand, you don’t know the probability of the sample value falling in a critical region if the alternative hypothesis is correct (#2). It depends on the precise distribution for the alternative hypothesis and you usually don’t know that, which is why you’re testing the hypotheses in the first place!

I hope I answered the question you were asking. If not, feel free to ask follow up questions. Also, this ties into how to interpret p-values . It’s not exactly straightforward. Click the link to learn more.

June 4, 2020 at 6:17 am

Hi Jim, thank you very much for your answer. You helped me a lot!

June 3, 2020 at 5:23 pm

Hi, Thanks for this post. I’ve been learning a lot with you. My question is regarding to lack of fit. The p-value of my lack of fit is really low, making my lack of fit significant, meaning my model does not fit well. Is my case a “false negative”? given that my pure error is really low, making the computation of the lack of fit low. So it means my model is good. Below I show some information, that I hope helps to clarify my question.

SumSq DF MeanSq F pValue ________ __ ________ ______ __________

Total 1246.5 18 69.25 Model 1241.7 6 206.94 514.43 9.3841e-14 . Linear 1196.6 3 398.87 991.53 1.2318e-14 . Nonlinear 45.046 3 15.015 37.326 2.3092e-06 Residual 4.8274 12 0.40228 . Lack of fit 4.7388 7 0.67698 38.238 0.0004787 . Pure error 0.088521 5 0.017704

June 3, 2020 at 7:53 pm

As you say, a low p-value for a lack of fit test indicates that the model doesn’t fit your data adequately. This is a positive result for the test, which means it can’t be a “false negative.” At best, it could be a false positive, meaning that your data actually fit model well despite the low p-value.

I’d recommend graphing the residuals and looking for patterns . There is probably a relationship between variables that you’re not modeling correctly, such as curvature or interaction effects. There’s no way to diagnose the specific nature of the lack-of-fit problem by using the statistical output. You’ll need the graphs.

If there are no patterns in the residual plots, then your lack-of-fit results might be a false positive.

I hope this helps!

May 30, 2020 at 6:23 am

First of all, I have to say there are not many resources that explain a complicated topic in an easier manner.

My question is, how do we arrive at “if p value is less than alpha, we reject the null hypothesis.”

Is this covered in a separate article I could read?

Thanks Shekhar

May 25, 2020 at 12:21 pm

Hi Jim, terrific website, blog, and after this I’m ordering your book. One of my biggest challenges is nomenclature, definitions, context, and formulating the hypotheses. Here’s one I want to double-be-sure I understand: From above you write: ” These tools allow us to test these two hypotheses:

Null hypothesis: The population mean equals the null hypothesis mean (260). Alternative hypothesis: The population mean does not equal the null hypothesis mean (260). ” I keep thinking that 260 is the population mean mu, the underlying population (that we never really know exactly) and that the Null Hypothesis is comparing mu to x-bar (the sample mean of the 25 families randomly sampled w mean = sample mean = x-bar = 330.6).

So is the following incorrect, and if so, why? Null hypothesis: The population mean mu=260 equals the null hypothesis mean x-bar (330.6). Alternative hypothesis: The population mean mu=269 does not equal the null hypothesis mean x-bar (330.6).

And my thinking is that usually the formulation of null and alternative hypotheses is “test value” = “mu current of underlying population”, whereas I read the formulation on the webpage above to be the reverse.

Any comments appreciated. Many Thanks,

May 26, 2020 at 8:56 pm

The null hypothesis states that population value equals the null value. Now, I know that’s not particularly helpful! But, the null value varies based on test and context. So, in this example, we’re setting the null value aa $260, which was the mean from the previous year. So, our null hypothesis states:

Null: the population mean (mu) = 260. Alternative: the population mean ≠ 260.

These hypothesis statements are about the population parameter. For this type of one-sample analysis, the target or reference value you specify is the null hypothesis value. Additionally, you don’t include the sample estimate in these statements, which is the X-bar portion you tacked on at the end. It’s strictly about the value of the population parameter you’re testing. You don’t know the value of the underlying distribution. However, given the mutually exclusive nature of the null and alternative hypothesis, you know one or the other is correct. The null states that mu equals 260 while the alternative states that it doesn’t equal 260. The data help you decide, which brings us to . . .

However, the procedure does compare our sample data to the null hypothesis value, which is how it determines how strong our evidence is against the null hypothesis.

I hope I answered your question. If not, please let me know!

May 8, 2020 at 6:00 pm

Really using the interpretation “In other words, you will observe sample effects at least as large as 70.6 about 3.1% of the time if the null is true”, our head seems to tie a knot. However, doing the reverse interpretation, it is much more intuitive and easier. That is, we will observe the sample effect of at least 70.6 in about 96.9% of the time, if the null is false (that is, our hypothesis is true).

May 8, 2020 at 7:25 pm

Your phrasing really isn’t any simpler. And it has the additional misfortune of being incorrect.

What you’re essentially doing is creating a one-sided confidence interval by using the p-value from a two-sided test. That’s incorrect in two ways.

Don’t mix and match one-sided and two-sided test results.
Confidence levels are determine by the significance level, not p-values.

So, what you need is a two-sided 95% CI (1-alpha). You could then state the results are statistically significant and you have 95% confidence that the population effect is between X and Y. If you want a lower bound as you propose, then you’ll need to use a one-sided hypothesis test with a 95% Lower Bound. That’ll give you a different value for the lower bound than the one you use.

I like confidence intervals. As I write elsewhere, I think they’re easier to understand and provide more information than a binary test result. But, you need to use them correctly!

One other point. When you are talking about p-values, it’s always under the assumption that the null hypothesis is correct. You *never* state anything about the p-value in relation to the null being false (i.e. alternative is true). But, if you want to use the type of phrasing you suggest, use it in the context of CIs and incorporate the points I cover above.

February 10, 2020 at 11:13 am

Muchas gracias profesor por compartir sus conocimientos. Un saliud especial desde Colombia.

August 6, 2019 at 11:46 pm

i found this really helpful . also can you help me out ?

I’m a little confused Can you tell me if level of significance and pvalue are comparable or not and if they are what does it mean if pvalue < LS . Do we reject the null hypothesis or do we accept the null hypothesis ?

August 7, 2019 at 12:49 am

Hi Divyanshu,

Yes, you compare the p-value to the significance level. When the p-value is less than the significance level (alpha), your results are statistically significant and you reject the null hypothesis.

I’d suggest re-reading the “Using P values and Significance Levels Together” section near the end of this post more closely. That describes the process. The next section describes what it all means.

July 1, 2019 at 4:19 am

sure.. I will use only in my class rooms that too offline with due credits to your orginal page. I will encourage my students to visit your blog . I have purchased your eBook on Regressions….immensely useful.

July 1, 2019 at 9:52 am

Hi Narasimha, that sounds perfect. Thanks for buying my ebook as well. I’m thrilled to hear that you’ve found it to be helpful!

June 28, 2019 at 6:22 am

I have benefited a lot by your writings….Can I share the same with my students in the classroom?

June 30, 2019 at 8:44 pm

Hi Narasimha,

Yes, you can certainly share with your students. Please attribute my original page. And please don’t copy whole sections of my posts onto another webpage as that can be bad with Google! Thanks!

February 11, 2019 at 7:46 pm

Hello, great site and my apologies if the answer to the following question exists already.

I’ve always wondered why we put the sampling distribution about the null hypothesis rather than simply leave it about the observed mean. I can see mathematically we are measuring the same distance from the null and basically can draw the same conclusions.

For example we take a sample (say 50 people) we gather an observation (mean wage) estimate the standard error in that observation and so can build a sampling distribution about the observed mean. That sampling distribution contains a confidence interval, where say, i am 95% confident the true mean lies (i.e. in repeated sampling the true mean would reside within this interval 95% of the time).

When i use this for a hyp-test, am i right in saying that we place the sampling dist over the reference level simply because it’s mathematically equivalent and it just seems easier to gauge how far the observation is from 0 via t-stats or its likelihood via p-values?

It seems more natural to me to look at it the other way around. leave the sampling distribution on the observed value, and then look where the null sits…if it’s too far left or right then it is unlikely the true population parameter is what we believed it to be, because if the null were true it would only occur ~ 5% of the time in repeated samples…so perhaps we need to change our opinion.

Can i interpret a hyp-test that way? Or do i have a misconception?

February 12, 2019 at 8:25 pm

The short answer is that, yes, you can draw the interval around the sample mean instead. And, that is, in fact, how you construct confidence intervals. The distance around the null hypothesis for hypothesis tests and the distance around the sample for confidence intervals are the same distance, which is why the results will always agree as long as you use corresponding alpha levels and confidence levels (e.g., alpha 0.05 with a 95% confidence level). I write about how this works in a post about confidence intervals .

I prefer confidence intervals for a number of reasons. They’ll indicate whether you have significant results if they exclude the null value and they indicate the precision of the effect size estimate. Corresponding with what you’re saying, it’s easier to gauge how far a confidence interval is from the null value (often zero) whereas a p-value doesn’t provide that information. See Practical versus Statistical Significance .

So, you don’t have any misconception at all! Just refer to it as a confidence interval rather than a hypothesis test, but, of course, they are very closely related.

January 9, 2019 at 10:37 pm

Hi Jim, Nice Article.. I have a question… I read the Central limit theorem article before this article…

Coming to this article, During almost every hypothesis test, we draw a normal distribution curve assuming there is a sampling distribution (and then we go for test statistic, p value etc…). Do we draw a normal distribution curve for hypo tests because of the central limit theorem…

Thanks in advance, Surya

January 10, 2019 at 1:57 am

These distributions are actually the t-distribution which are different from the normal distribution. T-distributions only have one parameter–the degrees of freedom. As the DF of increases, the t-distribution tightens up. Around 25 degrees of freedom, the t-distribution approximates the normal distribution. Depending on the type of t-test, this corresponds to a sample size of 26 or 27. Similarly, the sampling distribution of the means also approximate the normal distribution at around these sample sizes. With a large enough sample size, both the t-distribution and the sample distribution converge to a normal distribution regardless (largely) of the underlying population distribution. So, yes, the central limit theorem plays a strong role in this.

It’s more accurate to say that central limit theorem causes the sampling distribution of the means to converge on the same distribution that the t-test uses, which allows you to assume that the test produces valid results. But, technically, the t-test is based on the t-distribution.

Problems can occur if the underlying distribution is non-normal and you have a small sample size. In that case, the sampling distribution of the means won’t approximate the t-distribution that the t-test uses. However, the test results will assume that it does and produce results based on that–which is why it causes problems!

November 19, 2018 at 9:15 am

Dear Jim! Thank you very much for your explanation. I need your help to understand my data. I have two samples (about 300 observations) with biased distributions. I did the ttest and obtained the p-value, which is quite small. Can I draw the conclusion that the effect size is small even when the distribution of my data is not normal? Thank you

November 19, 2018 at 9:34 am

Hi Tetyana,

First, when you say that your p-value is small and that you want to “draw the conclusion that the effect size is small,” I assume that you mean statistically significant. When the p-value is low, the null hypothesis must go! In other words, you reject the null and conclude that there is a statistically significant effect–not a small effect.

Now, back to the question at hand! Yes, When you have a sufficiently large sample-size, t-tests are robust to departures from normality. For a 2-sample t-test, you should have at least 15 samples per group, which you exceed by quite a bit. So, yes, you can reliably conclude that your results are statistically significant!

You can thank the central limit theorem! 🙂

September 10, 2018 at 12:18 am

Hello Jim, I am very sorry; I have very elementary of knowledge of stats. So, would you please explain how you got a p- value of 0.03112 in the above calculation/t-test? By looking at a chart? Would you also explain how you got the information that “you will observe sample effects at least as large as 70.6 about 3.1% of the time if the null is true”?

July 6, 2018 at 7:02 am

A quick question regarding your use of two-tailed critical regions in the article above: why? I mean, what is a real-world scenario that would warrant a two-tailed test of any kind (z, t, etc.)? And if there are none, why keep using the two-tailed scenario as an example, instead of the one-tailed which is both more intuitive and applicable to most if not all practical situations. Just curious, as one person attempting to educate people on stats to another (my take on the one vs. two-tailed tests can be seen here: http://blog.analytics-toolkit.com/2017/one-tailed-two-tailed-tests-significance-ab-testing/ )

Thanks, Georgi

July 6, 2018 at 12:05 pm

There’s the appropriate time and place for both one-tailed and two-tailed tests. I plan to write a post on this issue specifically, so I’ll keep my comments here brief.

So much of statistics is context sensitive. People often want concrete rules for how to do things in statistics but that’s often hard to provide because the answer depends on the context, goals, etc. The question of whether to use a one-tailed or two-tailed test falls firmly in this category of it depends.

I did read the article you wrote. I’ll say that I can see how in the context of A/B testing specifically there might be a propensity to use one-tailed tests. You only care about improvements. There’s probably not too much downside in only caring about one direction. In fact, in a post where I compare different tests and different options , I suggest using a one-tailed test for a similar type of casing involving defects. So, I’m onboard with the idea of using one-tailed tests when they’re appropriate. However, I do think that two-tailed tests should be considered the default choice and that you need good reasons to move to a one-tailed test. Again, your A/B testing area might supply those reasons on a regular basis, but I can’t make that a blanket statement for all research areas.

I think your article mischaracterizes some of the pros and cons of both types of tests. Just a couple of for instances. In a two-tailed test, you don’t have to take the same action regardless of which direction the results are significant (example below). And, yes, you can determine the direction of the effect in a two-tailed test. You simply look at the estimated effect. Is it positive or negative?

On the other hand, I do agree that one-tailed tests don’t increase the overall Type I error. However, there is a big caveat for that. In a two-tailed test, the Type I error rate is evenly split in both tails. For a one-tailed test, the overall Type I error rate does not change, but the Type I errors are redistributed so they all occur in the direction that you are interested in rather than being split between the positive and negative directions. In other words, you’ll have twice as many Type I errors in the specific direction that you’re interested in. That’s not good.

My big concerns with one-tailed tests are that it makes it easier to obtain the results that you want to obtain. And, all of the Type I errors (false positives) are in that direction too. It’s just not a good combination.

To answer your question about when you might want to use two-tailed tests, there are plenty of reasons. For one, you might want to avoid the situation I describe above. Additionally, in a lot of scientific research, the researchers truly are interested in detecting effects in either direction for the sake of science. Even in cases with a practical application, you might want to learn about effects in either direction.

For example, I was involved in a research study that looked at the effects of an exercise intervention on bone density. The idea was that it might be a good way to prevent osteoporosis. I used a two-tailed test. Obviously, we’re hoping that there was positive effect. However, we’d be very interested in knowing whether there was a negative effect too. And, this illustrates how you can have different actions based on both directions. If there was a positive effect, you can recommend that as a good approach and try to promote its use. If there’s a negative effect, you’d issue a warning to not do that intervention. You have the potential for learning both what is good and what is bad. The extra false-positives would’ve cause problems because we’d think that there’d be health benefits for participants when those benefits don’t actually exist. Also, if we had performed only a one-tailed test and didn’t obtain significant results, we’d learn that it wasn’t a positive effect, but we would not know whether it was actually detrimental or not.

Here’s when I’d say it’s OK to use a one-tailed test. Consider a one-tailed test when you’re in situation where you truly only need to know whether an effect exists in one direction, and the extra Type I errors in that direction are an acceptable risk (false positives don’t cause problems), and there’s no benefit in determining whether an effect exists in the other direction. Those conditions really restrict when one-tailed tests are the best choice. Again, those restrictions might not be relevant for your specific field, but as for the usage of statistics as a whole, they’re absolutely crucial to consider.

On the other hand, according to this article, two-tailed tests might be important in A/B testing !

March 30, 2018 at 5:29 am

Dear Sir, please confirm if there is an inadvertent mistake in interpretation as, “We can conclude that mean fuel expenditures have increased since last year.” Our null hypothesis is =260. If found significant, it implies two possibilities – both increase and decrease. Please let us know if we are mistaken here. Many Thanks!

March 30, 2018 at 9:59 am

Hi Khalid, the null hypothesis as it is defined for this test represents the mean monthly expenditure for the previous year (260). The mean expenditure for the current year is 330.6 whereas it was 260 for the previous year. Consequently, the mean has increased from 260 to 330.7 over the course of a year. The p-value indicates that this increase is statistically significant. This finding does not suggest both an increase and a decrease–just an increase. Keep in mind that a significant result prompts us to reject the null hypothesis. So, we reject the null that the mean equals 260.

Let’s explore the other possible findings to be sure that this makes sense. Suppose the sample mean had been closer to 260 and the p-value was greater than the significance level, those results would indicate that the results were not statistically significant. The conclusion that we’d draw is that we have insufficient evidence to conclude that mean fuel expenditures have changed since the previous year.

If the sample mean was less than the null hypothesis (260) and if the p-value is statistically significant, we’d concluded that mean fuel expenditures have decreased and that this decrease is statistically significant.

When you interpret the results, you have to be sure to understand what the null hypothesis represents. In this case, it represents the mean monthly expenditure for the previous year and we’re comparing this year’s mean to it–hence our sample suggests an increase.

Comments and Questions Cancel reply

P-Value Method for Hypothesis Testing

The p-value method is a method that is commonly used in hypothesis testing to validate the hypothesis. in this article, i will be explaining this method with a solved example..

Ameya Shukla

Towards Data Science

Why Hypothesis Testing is done

Usually, we get Sample Datasets to work on and perform data analysis and visualization and find insights. Through that analysis, we make inferences on the whole population. The population is the entire dataset, whereas Sample Datasets are chunks from the Population Dataset. Similar to population, these sample datasets also have some mean and standard deviation associated.

These samples mean values usually vary from the population mean by different ranges. These ranges can deviate from very close to very far from the population mean. For making correct inferences, our sample datasets need to resemble the properties of the population dataset. So, these samples and the sample means are validated through various hypothesis testing methods like the P-value method, Critical Value method, T-test, ANOVA test, etc.

For example, consider a store that sells electronic devices. They launched a new laptop a while back and held a marketing campaign to promote the product. The campaign ran for 100 days. They claim that, on average, 500 of those laptops were sold per day across all branches during the campaign. This claim value (500) is the population mean, which says about the laptops sold per day in that campaign of 100 days. Now, we take out multiple samples, each of which has 20 days of data, and check the mean laptop sales of each sample. We know that each sample will have a mean value that might vary from other samples’ mean. These sample means can differ from the population mean (500). If the sample mean value is close to 500, such as if we get the sample mean of laptops sold as 490 or 498 or 505, we are more likely to believe the claim made by the store. But if the sample means are extreme values, such as 200 or 150 or 710, we are less likely to believe the claim. In such cases, the p-value method helps in validating the hypothesis statistically.

What is the P-value method in Hypothesis Testing? The P-value method is used in Hypothesis Testing to check the significance of the given Null Hypothesis. Then, deciding to reject or support it is based upon the specified significance level or threshold.

A P-value is calculated in this method which is a test statistic. This statistic can give us the probability of finding a value (Sample Mean) that is as far away as the population mean.

The P in P-value stands for Probability .

Based on that probability and a significance level, we Reject or Fail to Reject the Null Hypothesis.

Generally, the lower the p-value, the higher the chances are for Rejecting the Null Hypothesis and vice versa.

Also, we make use of the Z-table to perform this process.

How to perform hypothesis testing through p-value method ?

To perform this method, we first formulate the Null and Alternate Hypotheses.

Then, we have the following given inputs:

Alpha or the Significance level is the probability of making an error in Hypothesis Testing when the Null Hypothesis is true. It also specifies the critical region or the rejection region of the Null Hypothesis in the distribution. If the Sample Mean lies in that critical region, we reject Null Hypothesis and accept the Alternate Hypothesis.

The commonly used alpha is 0.05 (5 %), but it can vary depending on the business requirements. If the test is a 2-tailed test, we divide the alpha by 2 to equally distribute the significance level on the lower and upper cut-off. In the case of a 1-tailed test, we keep the alpha as it is.

You can read more on the two types of tests here .

Then, we calculate the Standard Error of the sample, which is the Population Standard Deviation divided by the square root of sample size (n).

After finding the Standard Error, we take a sample and the mean of that sample and then find the Z-score associated with that mean value.

Now, we find the p-value associated with the Z-score we calculated. Then we refer the Z-table to find the probability of the Z-score calculated. Then, to find the p-value, we subtract that probability from 1.

Finally, we check if the calculated p-value is greater than the significance level or not.

If the P-value > Significance Level , then we Fail To Reject The Null Hypothesis . Or else, if the P-value < Significance Level , we Reject the Null Hypothesis .

Let’s understand the method better through an example

Let’s take the previous example of the electronic store. The store launched a new laptop a while back. They had run a marketing campaign for 100 days to promote the product. The store claimed that the average number of laptops sold was 500 units per day during the 100 days of the marketing campaign. It means that, on average, the store sold 500 laptop units per day during the campaign across all of their stores. So, the population mean is 500.

So, the Null and Alternate hypotheses would be :

So, looking at the Null and the Alternate Hypothesis, we notice that this is a 2-tailed test.

Now, we take around 5 sample datasets from the entire dataset of the campaign. Each sample has data of 15 days (Also, the data in these samples might overlap).

We observe the average of the laptop units sold in each of the samples. We obtain the mean of the 5 samples as follows:

Now, let’s validate Sample 1 using the p-value method. We will take the threshold or the significance level of 0.05 (5%) to validate this hypothesis. Because this is a 2-tailed test, we divide the significance level by 2 for distributing equally on the Upper and Lower critical points.

We assume that the Standard deviation of the population is 45. But the Standard Deviation of the Population is usually known.

We know the condition that if the calculated p-value for any sample is higher than the significance level, we Fail to Reject the Null Hypothesis. Else, we Reject the Null Hypothesis.

Here, we are validating for the 1st Sample ( Sample_1 ).

So, the given inputs we have are as follows:

We now calculate the Standard Error

The 2nd step is to calculate the Z-score

We got the Z-Score as 3.05 . Now, we will refer the Z-table for finding the probability of the Z-score obtained.

The Z-Score we got was 3.05. Now, in the Z-table, we need to go look for the value in the first column vertically (+3). After that, we need to look for the next decimal value horizontally (0.05). So, we find the probability of the Z-score by going at +3 vertically and 0.05 horizontally. The probability of Z-score comes out to be 0.99886

Now, to calculate the p-value :

Since, this is a 2-tailed test, we will multiply the the p-value by 2

We got the P-value = 0.002

Finally, we will compare this now with the significance level

We notice that, P-value < Significance Level

This means that, in this problem statement and the hypothesis, finding a sample mean value of 535.5 has a probability of 0.002 or 0.2%, which is extremely less than the significance level (0.05 or 5%) and is considered too far away from the population mean (500).

Thus, we Reject The Null Hypothesis.

This also means that our sample mean value of 535.5 lies outside the acceptance region and we cannot expect such variance in the value of claim made by the store (Average Laptops sold = 500 per day).

The sample mean value of 535.5 is thus not an accepted mean value for this hypothesis and thus the status quo (Null Hypothesis) needs to be verified and changed.

Similarly, the same process is repeated for all the samples with their sample means and their p-value is calculated and compared with the significance level.

In this way, a hypothesis is validated using the P-value method approach.

In this article, I explained how Hypothesis Testing is done using one of the most common methods called as P-value method by solving a practical example. I would be more than happy to hear your comments and reviews on this article here in the comments. Also, feel free to message me on LinkedIn .

Written by Ameya Shukla

I write articles about on Data Science concepts and Statistics linkedin.com/in/ameyashukla1999

Text to speech

If you could change one thing about college, what would it be?

Graduate faster

Better quality online classes

Flexible schedule

Access to top-rated instructors

Calculating p-Value in Hypothesis Testing

10.15.2021 • 9 min read

Sarah Thomas

Subject Matter Expert

In this article, we'll take a deep dive on p-values, beginning with a description and definition of this key component of statistical hypothesis testing, before moving on to look at how to calculate it for different types of variables.

In a hypothesis test, you have two competing hypotheses: a null (or starting) hypothesis, H 0 H_0 H 0 and an alternative hypothesis, H a H_a H a . The goal of a hypothesis test is to use statistical evidence from a sample or multiple samples to determine which of the hypotheses is more likely to be true. The p-value can be used in the final stage of the test to make this determination.

Interpreting a p-value

Because it is a probability, the p-value can be expressed as a decimal or a percentage ranging from 0 to 1 or 0% to 100%. The closer the p-value is to zero, the stronger the evidence is in support of the alternative hypothesis, H a H_a H a .

Reject or Fail to Reject the Null Hypothesis?

When the p-value is below a certain threshold, the null hypothesis is rejected in favor of the alternative hypothesis. This threshold is known as the significance level (or alpha level) of the test.

The most commonly used significance level is 0.05 or 5%, but the choice of the significance level is up to the researcher. You could just as easily use a significance level of 0.1 or 0.01, for example. Remember, however, that the lower the p-value, the stronger the evidence is in support of the alternative hypothesis. For this reason, choosing a lower significance level means that you can have more confidence in your decision to reject a null hypothesis.

When the p-value is greater than the significance level, the evidence favors the null hypothesis, and the researcher or statistician must fail to reject the null hypothesis.

As mentioned earlier, the p-value is the probability of observing sample data that’s at least as extreme as the observed sample data, assuming that the null hypothesis is true.

If your data consists of a discrete random variable, you can map out the entire set of possible outcomes and their respective probabilities in order to calculate the p-value.

The p-value will then be the sum of three things:

the probability of the observed outcome

the probability of all outcomes that are just as likely as the observed outcome

and the probability of any outcome that is less likely than the observed outcome

Here is an example.

A stranger invites you to play a game of dice, and claims her dice are fair. The rules of the game are as follows: You roll a single die. If you roll an even number, you count that as a win (or success) and earn $1. If you roll an odd number, you count that as a loss (or failure) and lose $0.80. You can play the game for as many rounds as you like.

Let’s say you play four rounds of the game, and you lose all four rounds. This leaves you $3.20 poorer than before you started playing.

Given your losses, you may be interested in conducting a hypothesis test. The null hypothesis will be that the dice used in the game are indeed fair and that there is an equal chance of rolling an even or odd number with each roll. Your alternative hypothesis is that the dice are weighted towards landing on odd numbers.

To calculate the p-value, we map all of the possible outcomes of playing four rounds of the game. In each round, there are only two possible outcomes (odd or even), and after four rounds, there are a total of 2 4 2^4 2 4 , or 16, outcomes. If we assume the null hypothesis is true—that the dice are fair)—each of these outcomes is equally likely, with a probability of 1/16.

Since we are only concerned about the total number of wins and losses, and not concerned at all with their order, the outcomes and probabilities we care about are the following:

the probability of getting 4 wins and 0 losses = 1/16

the probability of getting 3 wins and 1 loss = 4/16

the probability of getting 2 wins and 2 losses = 6/16

the probability of getting 1 win and 3 losses = 4/16

the probability of getting 0 wins and 4 losses = 1/16

To calculate the p-value, we sum up the following:

the probability of the observed outcome (0 wins and 4 losses)

the probability of any outcome that is just as likely as the observed outcome (4 wins and 0 losses)

the probability of any outcome that is less likely than the observed outcome (in this example, there are no outcomes that are less likely than the observed outcome, so this value is zero)

p-Value = 1/16 + 1/16 = 1/8 or 0.125

The p-value we found is 0.125. Surprisingly, this is still well above a 0.05 significance level. It is even above a 0.10 (or 10%) significance level. Regardless of which of these thresholds you choose, you must fail to reject the null hypothesis. In other words, despite four losses in a row, the evidence still favors the hypothesis that the dice are fair! It may be a different story if you experience 10 or even 5 losses in a row. Calculate the p-value to find out!

When the hypothesis test involves a continuous random variable, we use a test statistic and the area under the probability density function to determine the p-value. The intuition behind the p-value is the same as in the discrete case. Assuming that the null hypothesis is true, we are calculating the probability of observing sample data that is at least as extreme as the sample data we have observed.

Let’s take a look at another example.

Say you have an orange grove, and you’re convinced that your oranges now grow larger than when you first started growing citrus. You happen to know that the standard deviation of the weights of your oranges, σ \sigma σ , is equal to 0.8 oz. This is the perfect opportunity to conduct a hypothesis test.

Your null hypothesis, in this case, is that the mean weight of your oranges has remained unchanged over the years and is equal to 5 oz (the null hypothesis typically represents the hypothesis that you are trying to move away from). Your alternative hypothesis is that the average weight of your oranges is now greater than 5 oz.

Because you can’t weigh every orange in your grove, you pick a large random sample of oranges (with a sample size of 100), weigh those, and observe that the average weight in your sample, x ‾ \overline x x , is equal to 5.2 oz.

Does this result support the null hypothesis or the alternative hypothesis? It’s not immediately clear. By pure chance, you could have had a handful of extra-large oranges in your sample, and this could have pushed your sample mean above a population mean of 5 oz. Alternatively, the sample mean could indicate that the population mean is, in fact, greater than 5 oz.

Here is where we begin the hypothesis test. We’ll conduct the test at a 0.05 significance level.

We start by asking the following question: Assuming that the null hypothesis is true, how likely or unlikely is it to observe a sample mean x ‾ \overline x x = 5.2 oz?

From the central limit theorem, we know that if our sample is randomly drawn and large enough, we can assume that the sampling distribution of the sample means is normally distributed with a mean equal to the true population mean, μ \mu μ , and a standard error equal to σ n \frac\sigma{\sqrt n} n σ . This means that if the null hypothesis is true, the sampling distribution for the sample mean of our orange weights will be normally distributed, with a mean equal to 5 and a standard error equal to 0.08.

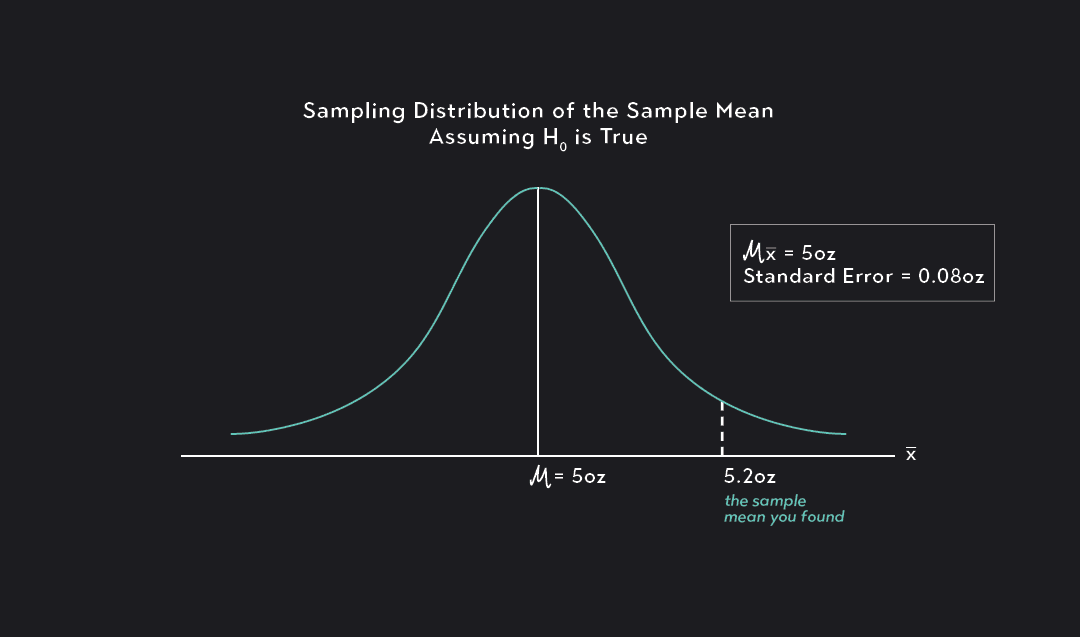
From here, we can convert our sample mean of 5.2 into what is known as a test statistic. To do this we use the exact same process we use when calculating standardized units such as z-scores or t-scores. Since we know the sampling distribution is approximately normal, and since we know the population standard deviation σ \sigma σ and the standard error σ n \frac\sigma{\sqrt n} n σ of the sampling distribution, we can calculate a Z-test statistic in the same way that we would calculate a z-score (if we did not know σ \sigma σ , we would use the sample standard deviation, s, to calculate a t-test statistic in the same way that we calculate t-scores).

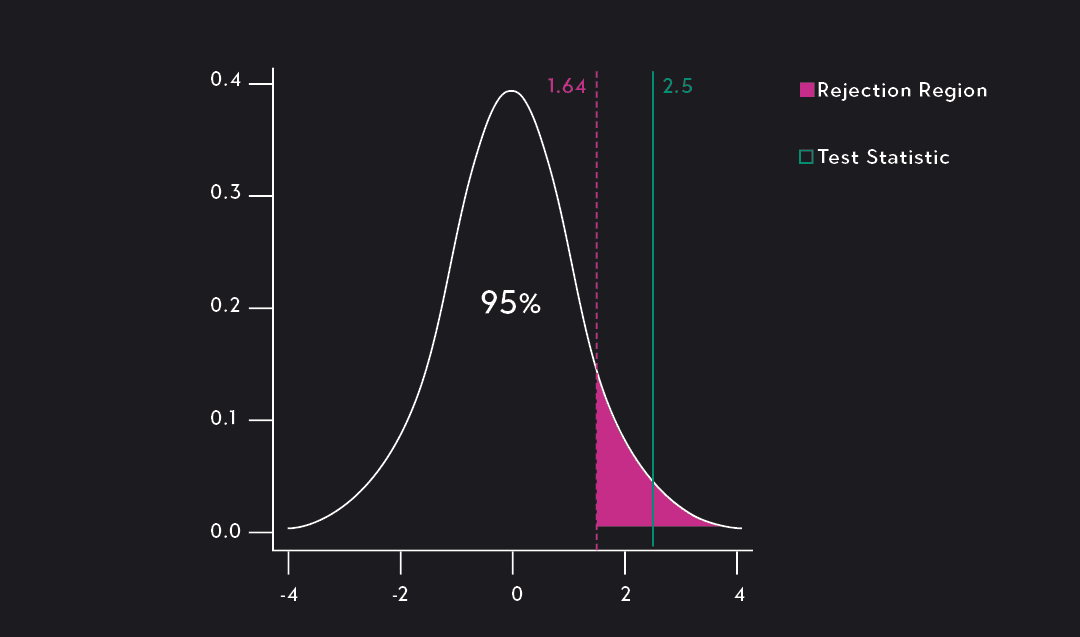
The test statistic is telling us that if our null hypothesis is true, then our observed sample mean, x ‾ \overline x x , is 2.5 standard deviations above the mean of the sampling distribution. To put the p-value to work we can do one of two things.

1. We can calculate the p-value associated with the test statistic. This can be done by finding the area under the standard normal distribution that lies to the right of 2.5. This gives us a p-value of 0.0062. The p-value is telling us that if the null hypothesis is true, we would only observe a sample mean of 5.2 or greater 0.0062 (or 0.62%) of the time. Because this probability is so low, it’s likely that the null hypothesis is false.

Since the p-value of 0.0062 is less than the significance level of 0.05, we can reject the null hypothesis at the 0.05 significance level. We can even reject it at the 0.01 significance level! You’re likely to be right about your oranges: the average weights have likely increased over time.

2. If you are familiar with standard normal distributions you may have realized that the significance level of our test (alpha = 0.05) is associated with the 95th percentile of the standard normal distribution. You may also know that the 95th percentile of a standard normal distribution is associated with a Z-score of 1.64. Since the test statistic 2.5 lies to the right of the Z-score, we can assume that the p-value will be less than 0.05. This is another way to complete the hypothesis test without having to do additional calculations.

Two-sided, upper-tailed, and lower-tailed hypothesis tests

In the orange grove example above, we conducted an upper-tailed hypothesis test, because the alternative hypothesis H a H_a H a was of the form μ > μ 0 \mu>\mu_0 μ > μ 0 . It’s important to know, however, how the calculation of p-values differs when you have a two-tailed or a lower-tailed hypothesis test.

For a two-tailed test (when the alternative hypothesis, H a H_a H a , stipulates that a population parameter is ≠ to some number), the p-value is equal to twice the probability associated with the test statistic. If we had conducted a two-tailed test in the orange grove example ( H a H_a H a : μ ≠ 5 \mu\neq5 μ  = 5 ), the p-value would be equal to the probability that x ‾ \overline x x was greater than 2.5 plus the probability that x ‾ \overline x x is less than -2.5. Because the standard normal is symmetric about the mean, this is equal to (0.0062 * 2 = 0.0124).

For a lower-tailed test (when the alternative hypothesis, H a H_a H a , stipulates that a population parameter is ≤ to some number) the process is similar to the upper-tailed test, but the p-value will be the probability of getting a sample statistic that lies to the left of the test-statistic, rather than to the right of it.

Explore Outlier's Award-Winning For-Credit Courses

Outlier (from the co-founder of MasterClass) has brought together some of the world's best instructors, game designers, and filmmakers to create the future of online college.

Check out these related courses:

Intro to Statistics

How data describes our world.

Intro to Microeconomics

Why small choices have big impact.

Intro to Macroeconomics

How money moves our world.

Intro to Psychology

The science of the mind.

Mound of letters and numbers that represent the use of sets and subsets

What Do Subsets Mean in Statistics?

This article explains what subsets are in statistics and why they are important. You’ll learn about different types of subsets with formulas and examples for each.

Set Operations: Formulas, Properties, Examples & Exercises

Here is an overview of set operations, what they are, properties, examples, and exercises.

Definite Integrals: What Are They and How to Calculate Them

Knowing how to find definite integrals is an essential skill in calculus. In this article, we’ll learn the definition of definite integrals, how to evaluate definite integrals, and practice with some examples.

Rachel McLean

P-Value in Statistical Hypothesis Tests: What is it?

P value definition.

A p value is used in hypothesis testing to help you support or reject the null hypothesis . The p value is the evidence against a null hypothesis . The smaller the p-value, the stronger the evidence that you should reject the null hypothesis.

P values are expressed as decimals although it may be easier to understand what they are if you convert them to a percentage . For example, a p value of 0.0254 is 2.54%. This means there is a 2.54% chance your results could be random (i.e. happened by chance). That’s pretty tiny. On the other hand, a large p-value of .9(90%) means your results have a 90% probability of being completely random and not due to anything in your experiment. Therefore, the smaller the p-value, the more important (“ significant “) your results.

When you run a hypothesis test , you compare the p value from your test to the alpha level you selected when you ran the test. Alpha levels can also be written as percentages.

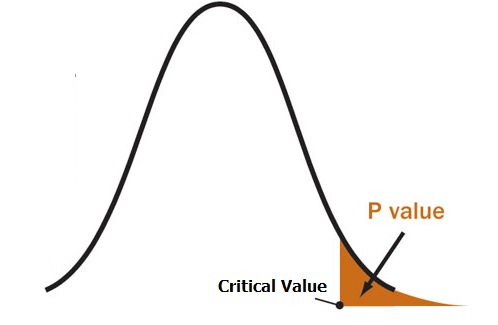
P Value vs Alpha level

Alpha levels are controlled by the researcher and are related to confidence levels . You get an alpha level by subtracting your confidence level from 100%. For example, if you want to be 98 percent confident in your research, the alpha level would be 2% (100% – 98%). When you run the hypothesis test, the test will give you a value for p. Compare that value to your chosen alpha level. For example, let’s say you chose an alpha level of 5% (0.05). If the results from the test give you:

A small p (≤ 0.05), reject the null hypothesis . This is strong evidence that the null hypothesis is invalid.
A large p (> 0.05) means the alternate hypothesis is weak, so you do not reject the null.

P Values and Critical Values

What if I Don’t Have an Alpha Level?

In an ideal world, you’ll have an alpha level. But if you do not, you can still use the following rough guidelines in deciding whether to support or reject the null hypothesis:

If p > .10 → “not significant”
If p ≤ .10 → “marginally significant”
If p ≤ .05 → “significant”
If p ≤ .01 → “highly significant.”

How to Calculate a P Value on the TI 83

Example question: The average wait time to see an E.R. doctor is said to be 150 minutes. You think the wait time is actually less. You take a random sample of 30 people and find their average wait is 148 minutes with a standard deviation of 5 minutes. Assume the distribution is normal. Find the p value for this test.

Press STAT then arrow over to TESTS.
Press ENTER for Z-Test .
Arrow over to Stats. Press ENTER.
Arrow down to μ0 and type 150. This is our null hypothesis mean.
Arrow down to σ. Type in your std dev: 5.
Arrow down to xbar. Type in your sample mean : 148.
Arrow down to n. Type in your sample size : 30.
Arrow to <μ0 for a left tail test . Press ENTER.
Arrow down to Calculate. Press ENTER. P is given as .014, or about 1%.

The probability that you would get a sample mean of 148 minutes is tiny, so you should reject the null hypothesis.

Note : If you don’t want to run a test, you could also use the TI 83 NormCDF function to get the area (which is the same thing as the probability value).

Dodge, Y. (2008). The Concise Encyclopedia of Statistics . Springer. Gonick, L. (1993). The Cartoon Guide to Statistics . HarperPerennial.

Search Search Please fill out this field.

What Is P-Value?

Understanding p-value.

P-Value in Hypothesis Testing

The Bottom Line

Corporate Finance
Financial Analysis

P-Value: What It Is, How to Calculate It, and Why It Matters

Yarilet Perez is an experienced multimedia journalist and fact-checker with a Master of Science in Journalism. She has worked in multiple cities covering breaking news, politics, education, and more. Her expertise is in personal finance and investing, and real estate.

In statistics, a p-value is defined as In statistics, a p-value indicates the likelihood of obtaining a value equal to or greater than the observed result if the null hypothesis is true.

The p-value serves as an alternative to rejection points to provide the smallest level of significance at which the null hypothesis would be rejected. A smaller p-value means stronger evidence in favor of the alternative hypothesis.

P-value is often used to promote credibility for studies or reports by government agencies. For example, the U.S. Census Bureau stipulates that any analysis with a p-value greater than 0.10 must be accompanied by a statement that the difference is not statistically different from zero. The Census Bureau also has standards in place stipulating which p-values are acceptable for various publications.

Key Takeaways

A p-value is a statistical measurement used to validate a hypothesis against observed data.
A p-value measures the probability of obtaining the observed results, assuming that the null hypothesis is true.
The lower the p-value, the greater the statistical significance of the observed difference.
A p-value of 0.05 or lower is generally considered statistically significant.
P-value can serve as an alternative to—or in addition to—preselected confidence levels for hypothesis testing.

Jessica Olah / Investopedia

P-values are usually calculated using statistical software or p-value tables based on the assumed or known probability distribution of the specific statistic tested. While the sample size influences the reliability of the observed data, the p-value approach to hypothesis testing specifically involves calculating the p-value based on the deviation between the observed value and a chosen reference value, given the probability distribution of the statistic. A greater difference between the two values corresponds to a lower p-value.

Mathematically, the p-value is calculated using integral calculus from the area under the probability distribution curve for all values of statistics that are at least as far from the reference value as the observed value is, relative to the total area under the probability distribution curve. Standard deviations, which quantify the dispersion of data points from the mean, are instrumental in this calculation.

The calculation for a p-value varies based on the type of test performed. The three test types describe the location on the probability distribution curve: lower-tailed test, upper-tailed test, or two-tailed test . In each case, the degrees of freedom play a crucial role in determining the shape of the distribution and thus, the calculation of the p-value.

In a nutshell, the greater the difference between two observed values, the less likely it is that the difference is due to simple random chance, and this is reflected by a lower p-value.

The P-Value Approach to Hypothesis Testing

The p-value approach to hypothesis testing uses the calculated probability to determine whether there is evidence to reject the null hypothesis. This determination relies heavily on the test statistic, which summarizes the information from the sample relevant to the hypothesis being tested. The null hypothesis, also known as the conjecture, is the initial claim about a population (or data-generating process). The alternative hypothesis states whether the population parameter differs from the value of the population parameter stated in the conjecture.

In practice, the significance level is stated in advance to determine how small the p-value must be to reject the null hypothesis. Because different researchers use different levels of significance when examining a question, a reader may sometimes have difficulty comparing results from two different tests. P-values provide a solution to this problem.

Even a low p-value is not necessarily proof of statistical significance, since there is still a possibility that the observed data are the result of chance. Only repeated experiments or studies can confirm if a relationship is statistically significant.

For example, suppose a study comparing returns from two particular assets was undertaken by different researchers who used the same data but different significance levels. The researchers might come to opposite conclusions regarding whether the assets differ.

If one researcher used a confidence level of 90% and the other required a confidence level of 95% to reject the null hypothesis, and if the p-value of the observed difference between the two returns was 0.08 (corresponding to a confidence level of 92%), then the first researcher would find that the two assets have a difference that is statistically significant , while the second would find no statistically significant difference between the returns.

To avoid this problem, the researchers could report the p-value of the hypothesis test and allow readers to interpret the statistical significance themselves. This is called a p-value approach to hypothesis testing. Independent observers could note the p-value and decide for themselves whether that represents a statistically significant difference or not.

Example of P-Value

An investor claims that their investment portfolio’s performance is equivalent to that of the Standard & Poor’s (S&P) 500 Index . To determine this, the investor conducts a two-tailed test.

The null hypothesis states that the portfolio’s returns are equivalent to the S&P 500’s returns over a specified period, while the alternative hypothesis states that the portfolio’s returns and the S&P 500’s returns are not equivalent—if the investor conducted a one-tailed test , the alternative hypothesis would state that the portfolio’s returns are either less than or greater than the S&P 500’s returns.

The p-value hypothesis test does not necessarily make use of a preselected confidence level at which the investor should reset the null hypothesis that the returns are equivalent. Instead, it provides a measure of how much evidence there is to reject the null hypothesis. The smaller the p-value, the greater the evidence against the null hypothesis.

Thus, if the investor finds that the p-value is 0.001, there is strong evidence against the null hypothesis, and the investor can confidently conclude that the portfolio’s returns and the S&P 500’s returns are not equivalent.

Although this does not provide an exact threshold as to when the investor should accept or reject the null hypothesis, it does have another very practical advantage. P-value hypothesis testing offers a direct way to compare the relative confidence that the investor can have when choosing among multiple different types of investments or portfolios relative to a benchmark such as the S&P 500.

For example, for two portfolios, A and B, whose performance differs from the S&P 500 with p-values of 0.10 and 0.01, respectively, the investor can be much more confident that portfolio B, with a lower p-value, will actually show consistently different results.

Is a 0.05 P-Value Significant?

A p-value less than 0.05 is typically considered to be statistically significant, in which case the null hypothesis should be rejected. A p-value greater than 0.05 means that deviation from the null hypothesis is not statistically significant, and the null hypothesis is not rejected.

What Does a P-Value of 0.001 Mean?

A p-value of 0.001 indicates that if the null hypothesis tested were indeed true, then there would be a one-in-1,000 chance of observing results at least as extreme. This leads the observer to reject the null hypothesis because either a highly rare data result has been observed or the null hypothesis is incorrect.

How Can You Use P-Value to Compare 2 Different Results of a Hypothesis Test?

If you have two different results, one with a p-value of 0.04 and one with a p-value of 0.06, the result with a p-value of 0.04 will be considered more statistically significant than the p-value of 0.06. Beyond this simplified example, you could compare a 0.04 p-value to a 0.001 p-value. Both are statistically significant, but the 0.001 example provides an even stronger case against the null hypothesis than the 0.04.

The p-value is used to measure the significance of observational data. When researchers identify an apparent relationship between two variables, there is always a possibility that this correlation might be a coincidence. A p-value calculation helps determine if the observed relationship could arise as a result of chance.

U.S. Census Bureau. “ Statistical Quality Standard E1: Analyzing Data .”

Terms of Service
Editorial Policy
Privacy Policy
Your Privacy Choices

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
Duis aute irure dolor in reprehenderit in voluptate
Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

9.3 - the p-value approach, example 9-4 section .

Up until now, we have used the critical region approach in conducting our hypothesis tests. Now, let's take a look at an example in which we use what is called the P -value approach .

Among patients with lung cancer, usually, 90% or more die within three years. As a result of new forms of treatment, it is felt that this rate has been reduced. In a recent study of n = 150 lung cancer patients, y = 128 died within three years. Is there sufficient evidence at the $\alpha = 0.05$ level, say, to conclude that the death rate due to lung cancer has been reduced?

The sample proportion is:

$\hat{p}=\dfrac{128}{150}=0.853$

The null and alternative hypotheses are:

$H_0 \colon p = 0.90$ and $H_A \colon p < 0.90$

The test statistic is, therefore:

$Z=\dfrac{\hat{p}-p_0}{\sqrt{\dfrac{p_0(1-p_0)}{n}}}=\dfrac{0.853-0.90}{\sqrt{\dfrac{0.90(0.10)}{150}}}=-1.92$

And, the rejection region is:

Since the test statistic Z = −1.92 < −1.645, we reject the null hypothesis. There is sufficient evidence at the $\alpha = 0.05$ level to conclude that the rate has been reduced.

Example 9-4 (continued) Section

What if we set the significance level $\alpha$ = P (Type I Error) to 0.01? Is there still sufficient evidence to conclude that the death rate due to lung cancer has been reduced?

In this case, with $\alpha = 0.01$, the rejection region is Z ≤ −2.33. That is, we reject if the test statistic falls in the rejection region defined by Z ≤ −2.33:

Because the test statistic Z = −1.92 > −2.33, we do not reject the null hypothesis. There is insufficient evidence at the $\alpha = 0.01$ level to conclude that the rate has been reduced.

In the first part of this example, we rejected the null hypothesis when $\alpha = 0.05$. And, in the second part of this example, we failed to reject the null hypothesis when $\alpha = 0.01$. There must be some level of $\alpha$, then, in which we cross the threshold from rejecting to not rejecting the null hypothesis. What is the smallest $\alpha \text{ -level}$ that would still cause us to reject the null hypothesis?

We would, of course, reject any time the critical value was smaller than our test statistic −1.92:

That is, we would reject if the critical value were −1.645, −1.83, and −1.92. But, we wouldn't reject if the critical value were −1.93. The $\alpha \text{ -level}$ associated with the test statistic −1.92 is called the P -value . It is the smallest $\alpha \text{ -level}$ that would lead to rejection. In this case, the P -value is:

P ( Z < −1.92) = 0.0274

So far, all of the examples we've considered have involved a one-tailed hypothesis test in which the alternative hypothesis involved either a less than (<) or a greater than (>) sign. What happens if we weren't sure of the direction in which the proportion could deviate from the hypothesized null value? That is, what if the alternative hypothesis involved a not-equal sign (≠)? Let's take a look at an example.

What if we wanted to perform a " two-tailed " test? That is, what if we wanted to test:

$H_0 \colon p = 0.90$ versus $H_A \colon p \ne 0.90$

at the $\alpha = 0.05$ level?

Let's first consider the critical value approach . If we allow for the possibility that the sample proportion could either prove to be too large or too small, then we need to specify a threshold value, that is, a critical value, in each tail of the distribution. In this case, we divide the " significance level " $\alpha$ by 2 to get $\alpha/2$:

That is, our rejection rule is that we should reject the null hypothesis $H_0 \text{ if } Z ≥ 1.96$ or we should reject the null hypothesis $H_0 \text{ if } Z ≤ −1.96$. Alternatively, we can write that we should reject the null hypothesis $H_0 \text{ if } |Z| ≥ 1.96$. Because our test statistic is −1.92, we just barely fail to reject the null hypothesis, because 1.92 < 1.96. In this case, we would say that there is insufficient evidence at the $\alpha = 0.05$ level to conclude that the sample proportion differs significantly from 0.90.

Now for the P -value approach . Again, needing to allow for the possibility that the sample proportion is either too large or too small, we multiply the P -value we obtain for the one-tailed test by 2:

That is, the P -value is:

$P=P(|Z|\geq 1.92)=P(Z>1.92 \text{ or } Z<-1.92)=2 \times 0.0274=0.055$

Because the P -value 0.055 is (just barely) greater than the significance level $\alpha = 0.05$, we barely fail to reject the null hypothesis. Again, we would say that there is insufficient evidence at the $\alpha = 0.05$ level to conclude that the sample proportion differs significantly from 0.90.

Let's close this example by formalizing the definition of a P -value, as well as summarizing the P -value approach to conducting a hypothesis test.

The P -value is the smallest significance level $\alpha$ that leads us to reject the null hypothesis.

Alternatively (and the way I prefer to think of P -values), the P -value is the probability that we'd observe a more extreme statistic than we did if the null hypothesis were true.

If the P -value is small, that is, if $P ≤ \alpha$, then we reject the null hypothesis $H_0$.

Note! Section

By the way, to test $H_0 \colon p = p_0$, some statisticians will use the test statistic:

$Z=\dfrac{\hat{p}-p_0}{\sqrt{\dfrac{\hat{p}(1-\hat{p})}{n}}}$

rather than the one we've been using:

$Z=\dfrac{\hat{p}-p_0}{\sqrt{\dfrac{p_0(1-p_0)}{n}}}$

One advantage of doing so is that the interpretation of the confidence interval — does it contain $p_0$? — is always consistent with the hypothesis test decision, as illustrated here:

For the sake of ease, let:

$se(\hat{p})=\sqrt{\dfrac{\hat{p}(1-\hat{p})}{n}}$

Two-tailed test. In this case, the critical region approach tells us to reject the null hypothesis $H_0 \colon p = p_0$ against the alternative hypothesis $H_A \colon p \ne p_0$:

if $Z=\dfrac{\hat{p}-p_0}{se(\hat{p})} \geq z_{\alpha/2}$ or if $Z=\dfrac{\hat{p}-p_0}{se(\hat{p})} \leq -z_{\alpha/2}$

which is equivalent to rejecting the null hypothesis:

if $\hat{p}-p_0 \geq z_{\alpha/2}se(\hat{p})$ or if $\hat{p}-p_0 \leq -z_{\alpha/2}se(\hat{p})$

if $p_0 \geq \hat{p}+z_{\alpha/2}se(\hat{p})$ or if $p_0 \leq \hat{p}-z_{\alpha/2}se(\hat{p})$

That's the same as saying that we should reject the null hypothesis $H_0 \text{ if } p_0$ is not in the $\left(1-\alpha\right)100\%$ confidence interval!

Left-tailed test. In this case, the critical region approach tells us to reject the null hypothesis $H_0 \colon p = p_0$ against the alternative hypothesis $H_A \colon p < p_0$:

if $Z=\dfrac{\hat{p}-p_0}{se(\hat{p})} \leq -z_{\alpha}$

if $\hat{p}-p_0 \leq -z_{\alpha}se(\hat{p})$

if $p_0 \geq \hat{p}+z_{\alpha}se(\hat{p})$

That's the same as saying that we should reject the null hypothesis $H_0 \text{ if } p_0$ is not in the upper $\left(1-\alpha\right)100\%$ confidence interval:

$(0,\hat{p}+z_{\alpha}se(\hat{p}))$

Data Science
Data Analysis
Data Visualization
Machine Learning
Deep Learning
Computer Vision
Artificial Intelligence
AI ML DS Interview Series
AI ML DS Projects series
Data Engineering
Web Scrapping

P-Value: Comprehensive Guide to Understand, Apply, and Interpret

A p-value is a statistical metric used to assess a hypothesis by comparing it with observed data.

This article delves into the concept of p-value, its calculation, interpretation, and significance. It also explores the factors that influence p-value and highlights its limitations.

Table of Content

What is P-value?

How P-value is calculated?

How to interpret p-value, p-value in hypothesis testing, implementing p-value in python, applications of p-value, what is the p-value.

The p-value, or probability value, is a statistical measure used in hypothesis testing to assess the strength of evidence against a null hypothesis. It represents the probability of obtaining results as extreme as, or more extreme than, the observed results under the assumption that the null hypothesis is true.

In simpler words, it is used to reject or support the null hypothesis during hypothesis testing. In data science, it gives valuable insights on the statistical significance of an independent variable in predicting the dependent variable.

Calculating the p-value typically involves the following steps:

Formulate the Null Hypothesis (H0) : Clearly state the null hypothesis, which typically states that there is no significant relationship or effect between the variables.
Choose an Alternative Hypothesis (H1) : Define the alternative hypothesis, which proposes the existence of a significant relationship or effect between the variables.
Determine the Test Statistic : Calculate the test statistic, which is a measure of the discrepancy between the observed data and the expected values under the null hypothesis. The choice of test statistic depends on the type of data and the specific research question.
Identify the Distribution of the Test Statistic : Determine the appropriate sampling distribution for the test statistic under the null hypothesis. This distribution represents the expected values of the test statistic if the null hypothesis is true.
Calculate the Critical-value : Based on the observed test statistic and the sampling distribution, find the probability of obtaining the observed test statistic or a more extreme one, assuming the null hypothesis is true.
Interpret the results: Compare the critical-value with t-statistic. If the t-statistic is larger than the critical value, it provides evidence to reject the null hypothesis, and vice-versa.

Its interpretation depends on the specific test and the context of the analysis. Several popular methods for calculating test statistics that are utilized in p-value calculations.

Test	Scenario	Interpretation
	Used when dealing with large sample sizes or when the population standard deviation is known.	A small p-value (smaller than 0.05) indicates strong evidence against the null hypothesis, leading to its rejection.
	Appropriate for small sample sizes or when the population standard deviation is unknown.	Similar to the Z-test
	Used for tests of independence or goodness-of-fit.	A small p-value indicates that there is a significant association between the categorical variables, leading to the rejection of the null hypothesis.
	Commonly used in Analysis of Variance (ANOVA) to compare variances between groups.	A small p-value suggests that at least one group mean is different from the others, leading to the rejection of the null hypothesis.
	Measures the strength and direction of a linear relationship between two continuous variables.	A small p-value indicates that there is a significant linear relationship between the variables, leading to rejection of the null hypothesis that there is no correlation.

In general, a small p-value indicates that the observed data is unlikely to have occurred by random chance alone, which leads to the rejection of the null hypothesis. However, it’s crucial to choose the appropriate test based on the nature of the data and the research question, as well as to interpret the p-value in the context of the specific test being used.

The table given below shows the importance of p-value and shows the various kinds of errors that occur during hypothesis testing.


	Correct decision based on the given p-value	Type I error
	Type II error	Incorrect decision based on the given p-value

Type I error: Incorrect rejection of the null hypothesis. It is denoted by α (significance level). Type II error: Incorrect acceptance of the null hypothesis. It is denoted by β (power level)

Let’s consider an example to illustrate the process of calculating a p-value for Two Sample T-Test:

A researcher wants to investigate whether there is a significant difference in mean height between males and females in a population of university students.

Suppose we have the following data:

$\overline{x_1} = 175$

Starting with interpreting the process of calculating p-value

Step 1 : Formulate the Null Hypothesis (H0):

H0: There is no significant difference in mean height between males and females.

Step 2 : Choose an Alternative Hypothesis (H1):

H1: There is a significant difference in mean height between males and females.

Step 3 : Determine the Test Statistic:

The appropriate test statistic for this scenario is the two-sample t-test, which compares the means of two independent groups.

The t-statistic is a measure of the difference between the means of two groups relative to the variability within each group. It is calculated as the difference between the sample means divided by the standard error of the difference. It is also known as the t-value or t-score.

$t = \frac{\overline{x_1} - \overline{x_2}}{ \sqrt{\frac{(s_1)^2}{n_1} + \frac{(s_2)^2}{n_2}}}$

s1 = First sample’s standard deviation
s2 = Second sample’s standard deviation
n1 = First sample’s sample size
n2 = Second sample’s sample size

$\begin{aligned}t &= \frac{175 - 168}{\sqrt{\frac{5^2}{30} + \frac{6^2}{35}}}\\&= \frac{7}{\sqrt{0.8333 + 1.0286}}\\&= \frac{7}{\sqrt{1.8619}}\\& \approx \frac{7}{1.364}\\& \approx 5.13\end{aligned}$

So, the calculated two-sample t-test statistic (t) is approximately 5.13.

Step 4 : Identify the Distribution of the Test Statistic:

The t-distribution is used for the two-sample t-test . The degrees of freedom for the t-distribution are determined by the sample sizes of the two groups.

The t-distribution is a probability distribution with tails that are thicker than those of the normal distribution.

where, n1 is total number of values for 1st category.
n2 is total number of values for 2nd category.

The degrees of freedom (63) represent the variability available in the data to estimate the population parameters. In the context of the two-sample t-test, higher degrees of freedom provide a more precise estimate of the population variance, influencing the shape and characteristics of the t-distribution.

T-Statistic

The t-distribution is symmetric and bell-shaped, similar to the normal distribution. As the degrees of freedom increase, the t-distribution approaches the shape of the standard normal distribution. Practically, it affects the critical values used to determine statistical significance and confidence intervals.

Step 5 : Calculate Critical Value.

To find the critical t-value with a t-statistic of 5.13 and 63 degrees of freedom, we can either consult a t-table or use statistical software.

We can use scipy.stats module in Python to find the critical t-value using below code.

Comparing with T-Statistic:

The larger t-statistic suggests that the observed difference between the sample means is unlikely to have occurred by random chance alone. Therefore, we reject the null hypothesis.

$(\alpha)$

p ≤ (α = 0.05) : Reject the null hypothesis. There is sufficient evidence to conclude that the observed effect or relationship is statistically significant, meaning it is unlikely to have occurred by chance alone.
p > (α = 0.05) : reject alternate hypothesis (or accept null hypothesis). The observed effect or relationship does not provide enough evidence to reject the null hypothesis. This does not necessarily mean there is no effect; it simply means the sample data does not provide strong enough evidence to rule out the possibility that the effect is due to chance.

In case the significance level is not specified, consider the below general inferences while interpreting your results.

If p > .10: not significant
If p ≤ .10: slightly significant
If p ≤ .05: significant
If p ≤ .001: highly significant

Graphically, the p-value is located at the tails of any confidence interval. [As shown in fig 1]

Fig 1: Graphical Representation

What influences p-value?

The p-value in hypothesis testing is influenced by several factors:

Sample Size : Larger sample sizes tend to yield smaller p-values, increasing the likelihood of detecting significant effects.
Effect Size: A larger effect size results in smaller p-values, making it easier to detect a significant relationship.
Variability in the Data : Greater variability often leads to larger p-values, making it harder to identify significant effects.
Significance Level : A lower chosen significance level increases the threshold for considering p-values as significant.
Choice of Test: Different statistical tests may yield different p-values for the same data.
Assumptions of the Test : Violations of test assumptions can impact p-values.

Understanding these factors is crucial for interpreting p-values accurately and making informed decisions in hypothesis testing.

Significance of P-value

The p-value provides a quantitative measure of the strength of the evidence against the null hypothesis.
Decision-Making in Hypothesis Testing
P-value serves as a guide for interpreting the results of a statistical test. A small p-value suggests that the observed effect or relationship is statistically significant, but it does not necessarily mean that it is practically or clinically meaningful.

Limitations of P-value

The p-value is not a direct measure of the effect size, which represents the magnitude of the observed relationship or difference between variables. A small p-value does not necessarily mean that the effect size is large or practically meaningful.
Influenced by Various Factors

The p-value is a crucial concept in statistical hypothesis testing, serving as a guide for making decisions about the significance of the observed relationship or effect between variables.

Let’s consider a scenario where a tutor believes that the average exam score of their students is equal to the national average (85). The tutor collects a sample of exam scores from their students and performs a one-sample t-test to compare it to the population mean (85).

The code performs a one-sample t-test to compare the mean of a sample data set to a hypothesized population mean.
It utilizes the scipy.stats library to calculate the t-statistic and p-value. SciPy is a Python library that provides efficient numerical routines for scientific computing.
The p-value is compared to a significance level (alpha) to determine whether to reject the null hypothesis.

Since, 0.7059>0.05 , we would conclude to fail to reject the null hypothesis. This means that, based on the sample data, there isn’t enough evidence to claim a significant difference in the exam scores of the tutor’s students compared to the national average. The tutor would accept the null hypothesis, suggesting that the average exam score of their students is statistically consistent with the national average.

During Forward and Backward propagation: When fitting a model (say a Multiple Linear Regression model), we use the p-value in order to find the most significant variables that contribute significantly in predicting the output.
Effects of various drug medicines: It is highly used in the field of medical research in determining whether the constituents of any drug will have the desired effect on humans or not. P-value is a very strong statistical tool used in hypothesis testing. It provides a plethora of valuable information while making an important decision like making a business intelligence inference or determining whether a drug should be used on humans or not, etc. For any doubt/query, comment below.

The p-value is a crucial concept in statistical hypothesis testing, providing a quantitative measure of the strength of evidence against the null hypothesis. It guides decision-making by comparing the p-value to a chosen significance level, typically 0.05. A small p-value indicates strong evidence against the null hypothesis, suggesting a statistically significant relationship or effect. However, the p-value is influenced by various factors and should be interpreted alongside other considerations, such as effect size and context.

Frequently Based Questions (FAQs)

Why is p-value greater than 1.

A p-value is a probability, and probabilities must be between 0 and 1. Therefore, a p-value greater than 1 is not possible.

What does P 0.01 mean?

It means that the observed test statistic is unlikely to occur by chance if the null hypothesis is true. It represents a 1% chance of observing the test statistic or a more extreme one under the null hypothesis.

Is 0.9 a good p-value?

A good p-value is typically less than or equal to 0.05, indicating that the null hypothesis is likely false and the observed relationship or effect is statistically significant.

What is p-value in a model?

It is a measure of the statistical significance of a parameter in the model. It represents the probability of obtaining the observed value of the parameter or a more extreme one, assuming the null hypothesis is true.

Why is p-value so low?

A low p-value means that the observed test statistic is unlikely to occur by chance if the null hypothesis is true. It suggests that the observed relationship or effect is statistically significant and not due to random sampling variation.

How Can You Use P-value to Compare Two Different Results of a Hypothesis Test?

Compare p-values: Lower p-value indicates stronger evidence against null hypothesis, favoring results with smaller p-values in hypothesis testing.

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

The p-value and rejecting the null (for one- and two-tail tests)

The p-value and rejecting the null blog post.jpeg

What is the p-value?

The ???p??? -value (or the observed level of significance) is the smallest level of significance at which you can reject the null hypothesis, assuming the null hypothesis is true.

You can also think about the ???p???-value as the total area of the region of rejection. Remember that in a one-tailed test, the region of rejection is consolidated into one tail, whereas in a two-tailed test, the rejection region is split between two tails.

$Krista King Math.jpg$

Hi! I'm krista.

I create online courses to help you rock your math class. Read more.

So, as you might expect, calculating the ???p???-value as the area of the rejection region will be slightly different depending on whether we’re using a two-tailed test or a one-tailed test, and whether the one-tailed test is an upper-tail test or lower-tail test.

Calculating the ???p???-value

For a one-tailed, lower-tail test

For a one-tailed test, first calculate your ???z???-test statistic. For a lower-tail test, ???z??? will be negative. Look up the ???z???-value in a ???z???-table, and the value you find in the body of the table represents the area under the probability distribution curve to the left of your negative ???z???-value.

For instance, assume you found ???z=-1.46???. In a ???z???-table, you find

So ???0.0721??? is the area under the curve to the left of ???z=-1.46???, and this is the ???p???-value also. So ???p=0.0721???.

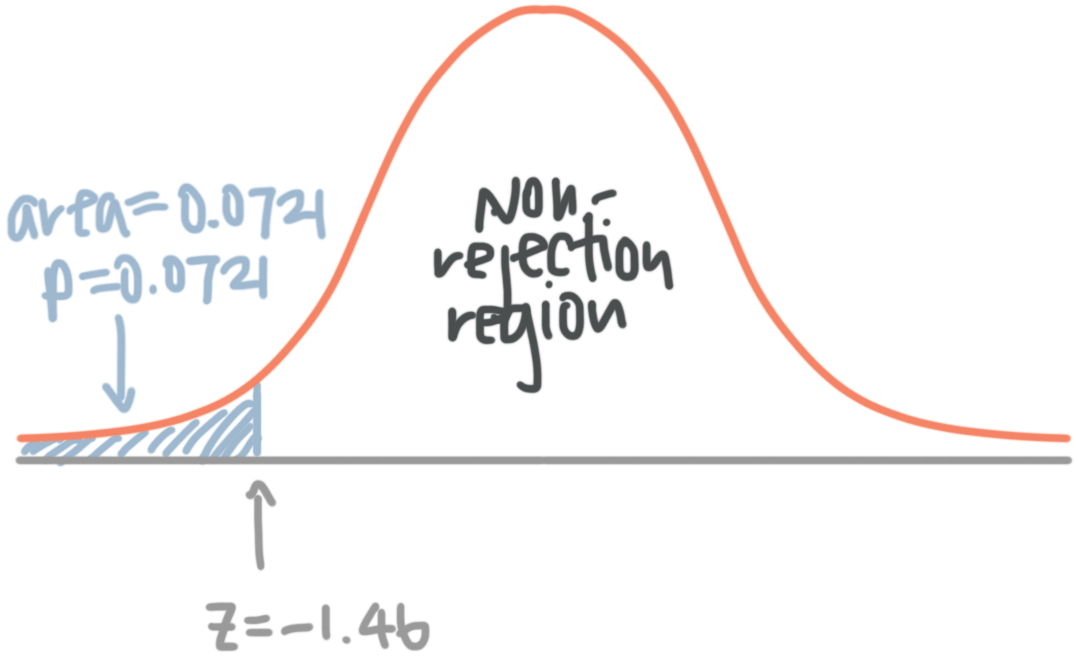
For a one-tailed, upper-tail test

For a one-tailed test, first calculate your ???z???-test statistic. For an upper-tail test, ???z??? will be positive. Look up the ???z???-value in a ???z???-table, and the value you find in the body of the table represents the area under the probability distribution curve to the left of your positive ???z???-value.

For instance, assume you found ???z=1.46???. In a ???z???-table, you find

But in an upper-tail test, you’re interested in the area to the right of the ???z???-value, not the area to the left. To find the area to the right, you need to subtract the value in the ???z???-table from ???1???.

???1-0.9279=0.0721???

So ???0.0721??? is the area under the curve to the right of ???z=1.46???, and this is the ???p???-value also. So ???p=0.0721???.

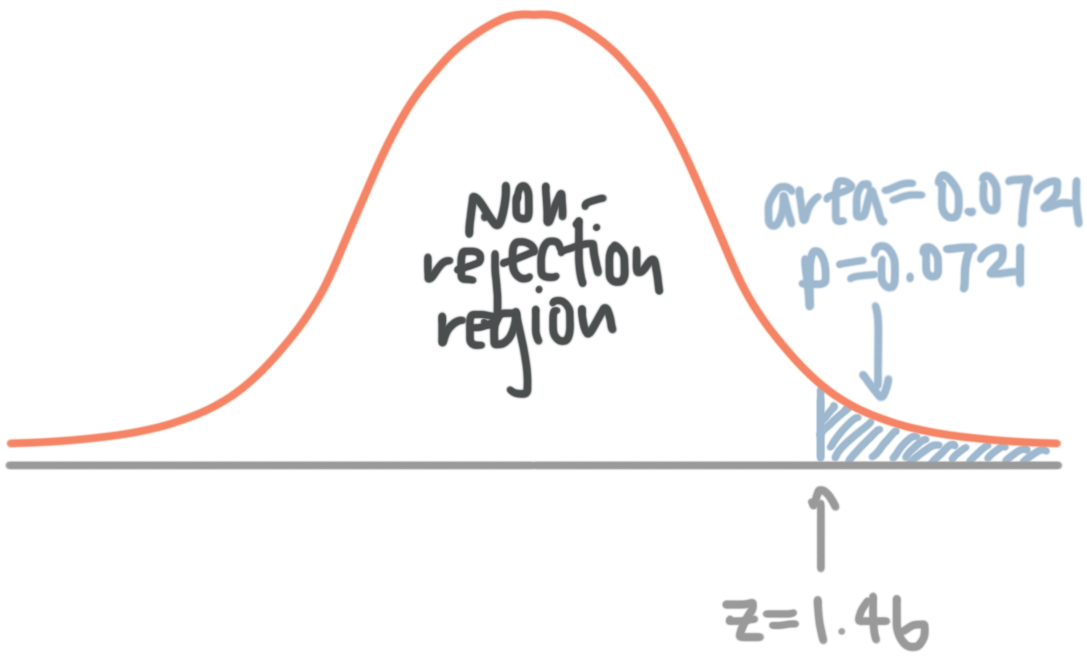
For a two-tailed test

For a two-tailed test, first calculate your ???z???-test statistic. For an two-tail test, ???z??? could be either positive or negative. Look up the ???z???-value in a -table, and the value you find in the body of the table represents the area under the probability distribution curve to the left of your ???z???-value.

For instance, assume you found ???z=1.23???. In a ???z???-table, you find

But for a positive ???z???-value, you’re interested in the area to the right of the ???z???-value, not the area to the left. To find the area to the right, you need to subtract the value in the ???z???-table from ???1???.

???1-0.8907=0.1093???

So ???0.1093??? is the area under the curve to the right of ???z=1.23???. Because this is a two-tail test, the region of rejection is not only the ???10.93\%??? of area under the upper tail, but also the symmetrical ???10.93\%??? of area under the lower tail. So we’ll double ???0.1093??? to get ???2(0.1093)=0.2186???, and this is the ???p???-value also. So ???p=0.2186???.

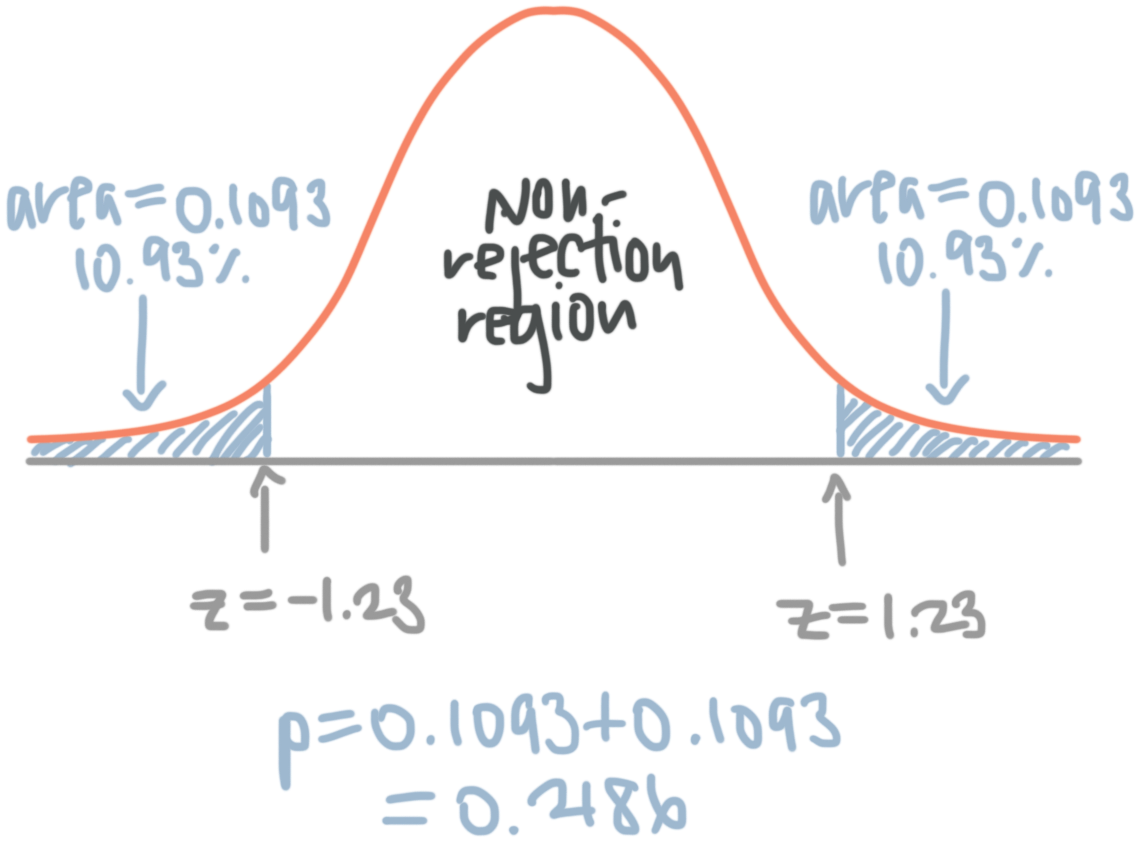
How to reject the null hypothesis

The reason we’ve gone through all this work to understand the ???p???-value is because using a ???p???-value is a really quick way to decide whether or not to reject the null hypothesis.

Whether or not you should reject ???H_0??? can be determined by the relationship between the ???\alpha??? level and the ???p???-value.

If ???p\leq \alpha???, reject the null hypothesis

If ???p>\alpha???, do not reject the null hypothesis

In our earlier examples, we found

???p=0.0721??? for the lower-tail one-tailed test

???p=0.0721??? for the upper-tail one-tailed test

???p=0.2186??? for the two-tailed test

With these in mind, let’s say for instance you set the confidence level of your hypothesis test at ???90\%???, which is the same as setting the ???\alpha??? level at ???\alpha=0.10???. In that case,

???p=0.0721\leq\alpha=0.10???

???p=0.2186>\alpha=0.10???

So we would have rejected the null hypothesis for both one-tailed tests, but we would have failed to reject the null in the two-tailed test. If, however, we’d picked a more rigorous ???\alpha=0.05??? or ???\alpha=0.01???, we would have failed to reject the null hypothesis every time.

Significance

The significance (or statistical significance ) of a test is the probability of obtaining your result by chance. The less likely it is that we obtained a result by chance, the more significant our results.

Hopefully by now it’s not too surprising by now that all of these are equivalent statements:

The finding is significant at the ???0.01??? level

The confidence level is ???99\%???

The Type I error rate is ???0.01???

The alpha level is ???0.01???, ???\alpha=0.01???

The area of the rejection region is ???0.01???

The ???p???-value is ???0.01???, ???p=0.01???

There’s a ???1??? in ???100??? chance of getting a result as, or more, extreme as this one

The smaller the ???p???-value, or the smaller the alpha value, or the lower the Type I error rate, and the smaller the region of rejection, the higher the confidence level, and the less likely it is that you got your result by chance.

In other words, an alpha level of ???0.10??? (or a ???p???-value of ???0.10???, or a confidence level of ???90\%???) is a lower bar to clear. At that significance level, there’s a ???1??? in ???10??? chance that the result we got was just by chance. And therefore there’s a ???1??? in ???10??? chance that we’ll reject the null hypothesis when we really shouldn’t have, thinking that we provided support for the alternative hypothesis when we shouldn’t have.

But a stricter alpha level of ???0.01??? (or a ???p???-value of ???0.01???, or a confidence level of ???99\%???) is a higher bar to clear. At that significance level, there’s only a ???1??? in ???100??? chance that the result we got was just by chance. And therefore there’s only a ???1??? in ???100??? chance that we’ll reject the null hypothesis when we really shouldn’t have, thinking that we provided support for the alternative hypothesis when we shouldn’t have.

If we find a result that clears the bar we’ve set for ourselves, then we reject the null hypothesis and we say that the finding is significant at the ???p???-value that we find. Otherwise, we fail to reject the null.

How to use the p-value to determine whether or not you can reject the null hypothesis

$Krista King Math Signup.png$

Take the course

Want to learn more about probability & statistics i have a step-by-step course for that. :).

Solutions Integral Calculator Derivative Calculator Algebra Calculator Matrix Calculator More...
Graphing Line Graph Exponential Graph Quadratic Graph Sine Graph More...
Calculators BMI Calculator Compound Interest Calculator Percentage Calculator Acceleration Calculator More...
Geometry Pythagorean Theorem Calculator Circle Area Calculator Isosceles Triangle Calculator Triangles Calculator More...
Tools Notebook Groups Cheat Sheets Worksheets Study Guides Practice Verify Solution
A P-value calculator is used to determine the statistical significance of an observed result in hypothesis testing. It takes as input the observed test statistic, the null hypothesis, and the relevant parameters of the statistical test (such as degrees of freedom), and computes the p-value. The p-value represents the probability of obtaining results as extreme as, or more extreme than, the observed data, assuming the null hypothesis is true. A lower p-value suggests stronger evidence against the null hypothesis, indicating that the observed result is unlikely to have occurred by random chance alone. The calculated p-value is used in comparison with a predefined significance level (alpha) to make decisions about the null hypothesis. If the p-value is less than or equal to alpha, typically 0.05, the results are considered statistically significant, leading to the rejection of the null hypothesis in favor of the alternative hypothesis. If the p-value is greater than alpha, there is insufficient evidence to reject the null hypothesis.
How do I calculate p-value?
The p-value is calculated by determining the probability of observing a test statistic as extreme as, or more extreme than, the observed one under the assumption of the null hypothesis.
What is p-value in Z test?
In a Z-test, the p-value is the probability of observing a Z-statistic as extreme as, or more extreme than, the calculated one, assuming a normal distribution and under the null hypothesis.
What is the p-value?
The p-value, or probability value, is a measure in statistics that quantifies the strength of evidence against a null hypothesis. It indicates the likelihood of observing a test statistic as extreme as, or more extreme than, the one obtained from the data, assuming the null hypothesis is true.
What is the alpha for p-value?
The alpha (α) for a p-value is the chosen level of significance that determines the threshold for rejecting the null hypothesis. It represents the maximum probability of making a Type I error (incorrectly rejecting a true null hypothesis) and is typically set at common values such as 0.05 or 0.01.
What does p-value under 0.05 mean?
A p-value under 0.05 typically suggests that there is statistically significant evidence to reject the null hypothesis in favor of an alternative hypothesis.

We want your feedback

Please add a message.

Message received. Thanks for the feedback.

P-value Calculator

Statistical significance calculator to easily calculate the p-value and determine whether the difference between two proportions or means (independent groups) is statistically significant. T-test calculator & z-test calculator to compute the Z-score or T-score for inference about absolute or relative difference (percentage change, percent effect). Suitable for analysis of simple A/B tests.

Related calculators

Using the p-value calculator
What is "p-value" and "significance level"
P-value formula
Why do we need a p-value?
How to interpret a statistically significant result / low p-value
P-value and significance for relative difference in means or proportions

Using the p-value calculator

This statistical significance calculator allows you to perform a post-hoc statistical evaluation of a set of data when the outcome of interest is difference of two proportions (binomial data, e.g. conversion rate or event rate) or difference of two means (continuous data, e.g. height, weight, speed, time, revenue, etc.). You can use a Z-test (recommended) or a T-test to find the observed significance level (p-value statistic). The Student's T-test is recommended mostly for very small sample sizes, e.g. n < 30. In order to avoid type I error inflation which might occur with unequal variances the calculator automatically applies the Welch's T-test instead of Student's T-test if the sample sizes differ significantly or if one of them is less than 30 and the sampling ratio is different than one.

If entering proportions data, you need to know the sample sizes of the two groups as well as the number or rate of events. These can be entered as proportions (e.g. 0.10), percentages (e.g. 10%) or just raw numbers of events (e.g. 50).

If entering means data, simply copy/paste or type in the raw data, each observation separated by comma, space, new line or tab. Copy-pasting from a Google or Excel spreadsheet works fine.

The p-value calculator will output : p-value, significance level, T-score or Z-score (depending on the choice of statistical hypothesis test), degrees of freedom, and the observed difference. For means data it will also output the sample sizes, means, and pooled standard error of the mean. The p-value is for a one-sided hypothesis (one-tailed test), allowing you to infer the direction of the effect (more on one vs. two-tailed tests ). However, the probability value for the two-sided hypothesis (two-tailed p-value) is also calculated and displayed, although it should see little to no practical applications.

Warning: You must have fixed the sample size / stopping time of your experiment in advance, otherwise you will be guilty of optional stopping (fishing for significance) which will inflate the type I error of the test rendering the statistical significance level unusable. Also, you should not use this significance calculator for comparisons of more than two means or proportions, or for comparisons of two groups based on more than one metric. If a test involves more than one treatment group or more than one outcome variable you need a more advanced tool which corrects for multiple comparisons and multiple testing. This statistical calculator might help.

What is "p-value" and "significance level"

The p-value is a heavily used test statistic that quantifies the uncertainty of a given measurement, usually as a part of an experiment, medical trial, as well as in observational studies. By definition, it is inseparable from inference through a Null-Hypothesis Statistical Test (NHST) . In it we pose a null hypothesis reflecting the currently established theory or a model of the world we don't want to dismiss without solid evidence (the tested hypothesis), and an alternative hypothesis: an alternative model of the world. For example, the statistical null hypothesis could be that exposure to ultraviolet light for prolonged periods of time has positive or neutral effects regarding developing skin cancer, while the alternative hypothesis can be that it has a negative effect on development of skin cancer.

In this framework a p-value is defined as the probability of observing the result which was observed, or a more extreme one, assuming the null hypothesis is true . In notation this is expressed as:

p(x 0 ) = Pr(d(X) > d(x 0 ); H 0 )

where x 0 is the observed data (x 1 ,x 2 ...x n ), d is a special function (statistic, e.g. calculating a Z-score), X is a random sample (X 1 ,X 2 ...X n ) from the sampling distribution of the null hypothesis. This equation is used in this p-value calculator and can be visualized as such:

p value statistical significance explained

Therefore the p-value expresses the probability of committing a type I error : rejecting the null hypothesis if it is in fact true. See below for a full proper interpretation of the p-value statistic .

Another way to think of the p-value is as a more user-friendly expression of how many standard deviations away from the normal a given observation is. For example, in a one-tailed test of significance for a normally-distributed variable like the difference of two means, a result which is 1.6448 standard deviations away (1.6448σ) results in a p-value of 0.05.

The term "statistical significance" or "significance level" is often used in conjunction to the p-value, either to say that a result is "statistically significant", which has a specific meaning in statistical inference ( see interpretation below ), or to refer to the percentage representation the level of significance: (1 - p value), e.g. a p-value of 0.05 is equivalent to significance level of 95% (1 - 0.05 * 100). A significance level can also be expressed as a T-score or Z-score, e.g. a result would be considered significant only if the Z-score is in the critical region above 1.96 (equivalent to a p-value of 0.025).

P-value formula

There are different ways to arrive at a p-value depending on the assumption about the underlying distribution. This tool supports two such distributions: the Student's T-distribution and the normal Z-distribution (Gaussian) resulting in a T test and a Z test, respectively.

In both cases, to find the p-value start by estimating the variance and standard deviation, then derive the standard error of the mean, after which a standard score is found using the formula [2] :

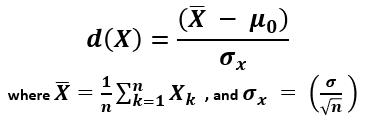
X (read "X bar") is the arithmetic mean of the population baseline or the control, μ 0 is the observed mean / treatment group mean, while σ x is the standard error of the mean (SEM, or standard deviation of the error of the mean).

When calculating a p-value using the Z-distribution the formula is Φ(Z) or Φ(-Z) for lower and upper-tailed tests, respectively. Φ is the standard normal cumulative distribution function and a Z-score is computed. In this mode the tool functions as a Z score calculator.

When using the T-distribution the formula is T n (Z) or T n (-Z) for lower and upper-tailed tests, respectively. T n is the cumulative distribution function for a T-distribution with n degrees of freedom and so a T-score is computed. Selecting this mode makes the tool behave as a T test calculator.

The population standard deviation is often unknown and is thus estimated from the samples, usually from the pooled samples variance. Knowing or estimating the standard deviation is a prerequisite for using a significance calculator. Note that differences in means or proportions are normally distributed according to the Central Limit Theorem (CLT) hence a Z-score is the relevant statistic for such a test.

Why do we need a p-value?

If you are in the sciences, it is often a requirement by scientific journals. If you apply in business experiments (e.g. A/B testing) it is reported alongside confidence intervals and other estimates. However, what is the utility of p-values and by extension that of significance levels?

First, let us define the problem the p-value is intended to solve. People need to share information about the evidential strength of data that can be easily understood and easily compared between experiments. The picture below represents, albeit imperfectly, the results of two simple experiments, each ending up with the control with 10% event rate treatment group at 12% event rate.

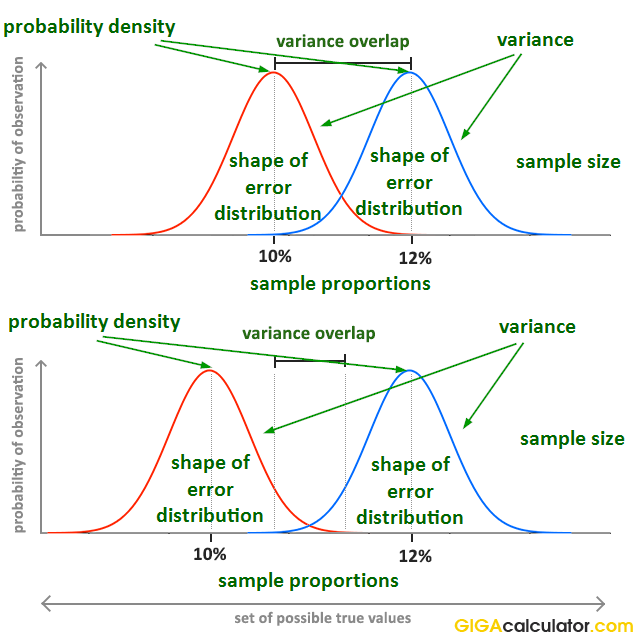
However, it is obvious that the evidential input of the data is not the same, demonstrating that communicating just the observed proportions or their difference (effect size) is not enough to estimate and communicate the evidential strength of the experiment. In order to fully describe the evidence and associated uncertainty , several statistics need to be communicated, for example, the sample size, sample proportions and the shape of the error distribution. Their interaction is not trivial to understand, so communicating them separately makes it very difficult for one to grasp what information is present in the data. What would you infer if told that the observed proportions are 0.1 and 0.12 (e.g. conversion rate of 10% and 12%), the sample sizes are 10,000 users each, and the error distribution is binomial?

Instead of communicating several statistics, a single statistic was developed that communicates all the necessary information in one piece: the p-value . A p-value was first derived in the late 18-th century by Pierre-Simon Laplace, when he observed data about a million births that showed an excess of boys, compared to girls. Using the calculation of significance he argued that the effect was real but unexplained at the time. We know this now to be true and there are several explanations for the phenomena coming from evolutionary biology. Statistical significance calculations were formally introduced in the early 20-th century by Pearson and popularized by Sir Ronald Fisher in his work, most notably "The Design of Experiments" (1935) [1] in which p-values were featured extensively. In business settings significance levels and p-values see widespread use in process control and various business experiments (such as online A/B tests, i.e. as part of conversion rate optimization, marketing optimization, etc.).

How to interpret a statistically significant result / low p-value

Saying that a result is statistically significant means that the p-value is below the evidential threshold (significance level) decided for the statistical test before it was conducted. For example, if observing something which would only happen 1 out of 20 times if the null hypothesis is true is considered sufficient evidence to reject the null hypothesis, the threshold will be 0.05. In such case, observing a p-value of 0.025 would mean that the result is interpreted as statistically significant.

But what does that really mean? What inference can we make from seeing a result which was quite improbable if the null was true?

Observing any given low p-value can mean one of three things [3] :

There is a true effect from the tested treatment or intervention.
There is no true effect, but we happened to observe a rare outcome. The lower the p-value, the rarer (less likely, less probable) the outcome.
The statistical model is invalid (does not reflect reality).

Obviously, one can't simply jump to conclusion 1.) and claim it with one hundred percent certainty, as this would go against the whole idea of the p-value and statistical significance. In order to use p-values as a part of a decision process external factors part of the experimental design process need to be considered which includes deciding on the significance level (threshold), sample size and power (power analysis), and the expected effect size, among other things. If you are happy going forward with this much (or this little) uncertainty as is indicated by the p-value calculation suggests, then you have some quantifiable guarantees related to the effect and future performance of whatever you are testing, e.g. the efficacy of a vaccine or the conversion rate of an online shopping cart.

Note that it is incorrect to state that a Z-score or a p-value obtained from any statistical significance calculator tells how likely it is that the observation is "due to chance" or conversely - how unlikely it is to observe such an outcome due to "chance alone". P-values are calculated under specified statistical models hence 'chance' can be used only in reference to that specific data generating mechanism and has a technical meaning quite different from the colloquial one. For a deeper take on the p-value meaning and interpretation, including common misinterpretations, see: definition and interpretation of the p-value in statistics .

P-value and significance for relative difference in means or proportions

When comparing two independent groups and the variable of interest is the relative (a.k.a. relative change, relative difference, percent change, percentage difference), as opposed to the absolute difference between the two means or proportions, the standard deviation of the variable is different which compels a different way of calculating p-values [5] . The need for a different statistical test is due to the fact that in calculating relative difference involves performing an additional division by a random variable: the event rate of the control during the experiment which adds more variance to the estimation and the resulting statistical significance is usually higher (the result will be less statistically significant). What this means is that p-values from a statistical hypothesis test for absolute difference in means would nominally meet the significance level, but they will be inadequate given the statistical inference for the hypothesis at hand.

In simulations I performed the difference in p-values was about 50% of nominal: a 0.05 p-value for absolute difference corresponded to probability of about 0.075 of observing the relative difference corresponding to the observed absolute difference. Therefore, if you are using p-values calculated for absolute difference when making an inference about percentage difference, you are likely reporting error rates which are about 50% of the actual, thus significantly overstating the statistical significance of your results and underestimating the uncertainty attached to them.

In short - switching from absolute to relative difference requires a different statistical hypothesis test. With this calculator you can avoid the mistake of using the wrong test simply by indicating the inference you want to make.

References

1 Fisher R.A. (1935) – "The Design of Experiments", Edinburgh: Oliver & Boyd

2 Mayo D.G., Spanos A. (2010) – "Error Statistics", in P. S. Bandyopadhyay & M. R. Forster (Eds.), Philosophy of Statistics, (7, 152–198). Handbook of the Philosophy of Science . The Netherlands: Elsevier.

3 Georgiev G.Z. (2017) "Statistical Significance in A/B Testing – a Complete Guide", [online] https://blog.analytics-toolkit.com/2017/statistical-significance-ab-testing-complete-guide/ (accessed Apr 27, 2018)

4 Mayo D.G., Spanos A. (2006) – "Severe Testing as a Basic Concept in a Neyman–Pearson Philosophy of Induction", British Society for the Philosophy of Science , 57:323-357

5 Georgiev G.Z. (2018) "Confidence Intervals & P-values for Percent Change / Relative Difference", [online] https://blog.analytics-toolkit.com/2018/confidence-intervals-p-values-percent-change-relative-difference/ (accessed May 20, 2018)

Cite this calculator & page

If you'd like to cite this online calculator resource and information as provided on the page, you can use the following citation: Georgiev G.Z., "P-value Calculator" , [online] Available at: https://www.gigacalculator.com/calculators/p-value-significance-calculator.php URL [Accessed Date: 08 Sep, 2024].

Our statistical calculators have been featured in scientific papers and articles published in high-profile science journals by:

The author of this tool

Statistical calculators

Three Ways to Find a P-Value from a t Statistic

A hypothesis test is a formal statistical test we use to reject or fail to reject a statistical hypothesis.

Whether we conduct a hypothesis test for a mean, a proportion, a difference in means, or a difference in proportions, we often end up with a t statistic for our test.

Once we have a t statistic, we can then find a corresponding p-value that we can use to reject or fail to reject the null hypothesis of our test.

This tutorial explains three different ways to find a p-value from a t statistic.

In each of the following examples, we’ll find the p-value for a right-tailed test with a t statistic of 1.441 and 13 degrees of freedom.

Technique 1: t Score to P Value Calculator

The first way to find a p-value from a t statistic is to use an online calculator like the T Score to P Value Calculator . We can simply enter the value for t and the degrees of freedom, then select “one-tailed”, then click the “Calculate” button:

The corresponding p-value is 0.08662 .

Technique 2: t Distribution Table

Another way to find the p-value for a given t statistic is to use the t distribution table .

Using the table, look up the row that has degrees of freedom (DF) = 13, then find the values that 1.441 lies between. It turns out to be 1.35 and 1.771. Next, look up at the top of the table for “one-tail” and you’ll notice that these values correspond with 0.1 and 0.05. This tells us that the corresponding p-value is somewhere between 0.05 and 0.1.

Notice the drawback of using the t distribution table: it does not tell us the exact p-value; it only gives us a range of values.

Technique 3: TI-83 or TI-84 Calculator

Another way to find the p-value for a given t statistic is to use a graphing calculator like a TI-83 or TI-84.

On your calculator, click 2ND VARS (to get to DISTR ), scroll down, and click the tcdf function. The syntax to use this function to find the p-value for a right-tailed test is as follows:

tcdf(smaller value, larger value, degrees of freedom)

Since we are conducting a right-tailed test, we can use 1.441 as the smaller value, 9999 as the larger value, and 13 as the degrees of freedom:

tcdf(1.441, 9999, 13)

This returns a value of 0 .08662 , which matches the p-value that we got from the online calculator.

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike. My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

One Reply to “Three Ways to Find a P-Value from a t Statistic”

This is great!!! What values would you put for the lower and smaller value if it was a lower tail test ? What values for a 2-tailed test?

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

t-test Calculator

Table of contents

Welcome to our t-test calculator! Here you can not only easily perform one-sample t-tests , but also two-sample t-tests , as well as paired t-tests .

Do you prefer to find the p-value from t-test, or would you rather find the t-test critical values? Well, this t-test calculator can do both! 😊

What does a t-test tell you? Take a look at the text below, where we explain what actually gets tested when various types of t-tests are performed. Also, we explain when to use t-tests (in particular, whether to use the z-test vs. t-test) and what assumptions your data should satisfy for the results of a t-test to be valid. If you've ever wanted to know how to do a t-test by hand, we provide the necessary t-test formula, as well as tell you how to determine the number of degrees of freedom in a t-test.

When to use a t-test?

A t-test is one of the most popular statistical tests for location , i.e., it deals with the population(s) mean value(s).

There are different types of t-tests that you can perform:

A one-sample t-test;
A two-sample t-test; and
A paired t-test.

In the next section , we explain when to use which. Remember that a t-test can only be used for one or two groups . If you need to compare three (or more) means, use the analysis of variance ( ANOVA ) method.

The t-test is a parametric test, meaning that your data has to fulfill some assumptions :

The data points are independent; AND
The data, at least approximately, follow a normal distribution .

If your sample doesn't fit these assumptions, you can resort to nonparametric alternatives. Visit our Mann–Whitney U test calculator or the Wilcoxon rank-sum test calculator to learn more. Other possibilities include the Wilcoxon signed-rank test or the sign test.

Which t-test?

Your choice of t-test depends on whether you are studying one group or two groups:

One sample t-test

Choose the one-sample t-test to check if the mean of a population is equal to some pre-set hypothesized value .

The average volume of a drink sold in 0.33 l cans — is it really equal to 330 ml?

The average weight of people from a specific city — is it different from the national average?

Two-sample t-test

Choose the two-sample t-test to check if the difference between the means of two populations is equal to some pre-determined value when the two samples have been chosen independently of each other.

In particular, you can use this test to check whether the two groups are different from one another .

The average difference in weight gain in two groups of people: one group was on a high-carb diet and the other on a high-fat diet.

The average difference in the results of a math test from students at two different universities.

This test is sometimes referred to as an independent samples t-test , or an unpaired samples t-test .

Paired t-test

A paired t-test is used to investigate the change in the mean of a population before and after some experimental intervention , based on a paired sample, i.e., when each subject has been measured twice: before and after treatment.

In particular, you can use this test to check whether, on average, the treatment has had any effect on the population .

The change in student test performance before and after taking a course.

The change in blood pressure in patients before and after administering some drug.

How to do a t-test?

So, you've decided which t-test to perform. These next steps will tell you how to calculate the p-value from t-test or its critical values, and then which decision to make about the null hypothesis.

Decide on the alternative hypothesis :

Use a two-tailed t-test if you only care whether the population's mean (or, in the case of two populations, the difference between the populations' means) agrees or disagrees with the pre-set value.

Use a one-tailed t-test if you want to test whether this mean (or difference in means) is greater/less than the pre-set value.

Compute your T-score value :

Formulas for the test statistic in t-tests include the sample size , as well as its mean and standard deviation . The exact formula depends on the t-test type — check the sections dedicated to each particular test for more details.

Determine the degrees of freedom for the t-test:

The degrees of freedom are the number of observations in a sample that are free to vary as we estimate statistical parameters. In the simplest case, the number of degrees of freedom equals your sample size minus the number of parameters you need to estimate . Again, the exact formula depends on the t-test you want to perform — check the sections below for details.

The degrees of freedom are essential, as they determine the distribution followed by your T-score (under the null hypothesis). If there are d degrees of freedom, then the distribution of the test statistics is the t-Student distribution with d degrees of freedom . This distribution has a shape similar to N(0,1) (bell-shaped and symmetric) but has heavier tails . If the number of degrees of freedom is large (>30), which generically happens for large samples, the t-Student distribution is practically indistinguishable from N(0,1).

💡 The t-Student distribution owes its name to William Sealy Gosset, who, in 1908, published his paper on the t-test under the pseudonym "Student". Gosset worked at the famous Guinness Brewery in Dublin, Ireland, and devised the t-test as an economical way to monitor the quality of beer. Cheers! 🍺🍺🍺

p-value from t-test

Recall that the p-value is the probability (calculated under the assumption that the null hypothesis is true) that the test statistic will produce values at least as extreme as the T-score produced for your sample . As probabilities correspond to areas under the density function, p-value from t-test can be nicely illustrated with the help of the following pictures:

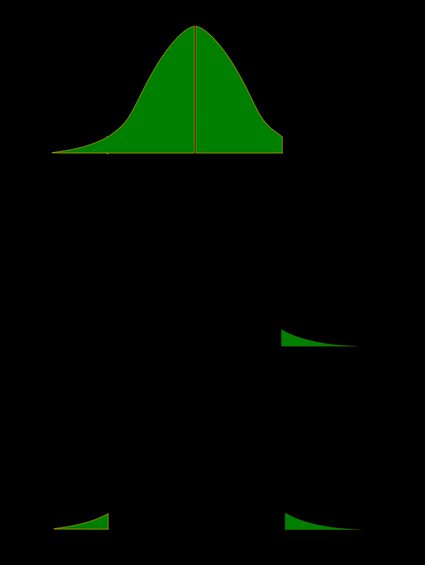
The following formulae say how to calculate p-value from t-test. By cdf t,d we denote the cumulative distribution function of the t-Student distribution with d degrees of freedom:

p-value from left-tailed t-test:

p-value = cdf t,d (t score )

p-value from right-tailed t-test:

p-value = 1 − cdf t,d (t score )

p-value from two-tailed t-test:

p-value = 2 × cdf t,d (−|t score |)

or, equivalently: p-value = 2 − 2 × cdf t,d (|t score |)

However, the cdf of the t-distribution is given by a somewhat complicated formula. To find the p-value by hand, you would need to resort to statistical tables, where approximate cdf values are collected, or to specialized statistical software. Fortunately, our t-test calculator determines the p-value from t-test for you in the blink of an eye!

t-test critical values

Recall, that in the critical values approach to hypothesis testing, you need to set a significance level, α, before computing the critical values , which in turn give rise to critical regions (a.k.a. rejection regions).

Formulas for critical values employ the quantile function of t-distribution, i.e., the inverse of the cdf :

Critical value for left-tailed t-test: cdf t,d -1 (α)

critical region:

(-∞, cdf t,d -1 (α)]

Critical value for right-tailed t-test: cdf t,d -1 (1-α)

[cdf t,d -1 (1-α), ∞)

Critical values for two-tailed t-test: ±cdf t,d -1 (1-α/2)

(-∞, -cdf t,d -1 (1-α/2)] ∪ [cdf t,d -1 (1-α/2), ∞)

To decide the fate of the null hypothesis, just check if your T-score lies within the critical region:

If your T-score belongs to the critical region , reject the null hypothesis and accept the alternative hypothesis.

If your T-score is outside the critical region , then you don't have enough evidence to reject the null hypothesis.

How to use our t-test calculator

Choose the type of t-test you wish to perform:

A one-sample t-test (to test the mean of a single group against a hypothesized mean);

A two-sample t-test (to compare the means for two groups); or

A paired t-test (to check how the mean from the same group changes after some intervention).

Two-tailed;

Left-tailed; or

Right-tailed.

This t-test calculator allows you to use either the p-value approach or the critical regions approach to hypothesis testing!

Enter your T-score and the number of degrees of freedom . If you don't know them, provide some data about your sample(s): sample size, mean, and standard deviation, and our t-test calculator will compute the T-score and degrees of freedom for you .

Once all the parameters are present, the p-value, or critical region, will immediately appear underneath the t-test calculator, along with an interpretation!

One-sample t-test

The null hypothesis is that the population mean is equal to some value μ 0 \mu_0 μ 0 .

The alternative hypothesis is that the population mean is:

different from μ 0 \mu_0 μ 0 ;
smaller than μ 0 \mu_0 μ 0 ; or
greater than μ 0 \mu_0 μ 0 .

One-sample t-test formula :

μ 0 \mu_0 μ 0 — Mean postulated in the null hypothesis;
n n n — Sample size;
x ˉ \bar{x} x ˉ — Sample mean; and
s s s — Sample standard deviation.

Number of degrees of freedom in t-test (one-sample) = n − 1 n-1 n − 1 .

The null hypothesis is that the actual difference between these groups' means, μ 1 \mu_1 μ 1 , and μ 2 \mu_2 μ 2 , is equal to some pre-set value, Δ \Delta Δ .

The alternative hypothesis is that the difference μ 1 − μ 2 \mu_1 - \mu_2 μ 1 − μ 2 is:

Different from Δ \Delta Δ ;
Smaller than Δ \Delta Δ ; or
Greater than Δ \Delta Δ .

In particular, if this pre-determined difference is zero ( Δ = 0 \Delta = 0 Δ = 0 ):

The null hypothesis is that the population means are equal.

The alternate hypothesis is that the population means are:

μ 1 \mu_1 μ 1 and μ 2 \mu_2 μ 2 are different from one another;
μ 1 \mu_1 μ 1 is smaller than μ 2 \mu_2 μ 2 ; and
μ 1 \mu_1 μ 1 is greater than μ 2 \mu_2 μ 2 .

Formally, to perform a t-test, we should additionally assume that the variances of the two populations are equal (this assumption is called the homogeneity of variance ).

There is a version of a t-test that can be applied without the assumption of homogeneity of variance: it is called a Welch's t-test . For your convenience, we describe both versions.

Two-sample t-test if variances are equal

Use this test if you know that the two populations' variances are the same (or very similar).

Two-sample t-test formula (with equal variances) :

where s p s_p s p is the so-called pooled standard deviation , which we compute as:

Δ \Delta Δ — Mean difference postulated in the null hypothesis;
n 1 n_1 n 1 — First sample size;
x ˉ 1 \bar{x}_1 x ˉ 1 — Mean for the first sample;
s 1 s_1 s 1 — Standard deviation in the first sample;
n 2 n_2 n 2 — Second sample size;
x ˉ 2 \bar{x}_2 x ˉ 2 — Mean for the second sample; and
s 2 s_2 s 2 — Standard deviation in the second sample.

Number of degrees of freedom in t-test (two samples, equal variances) = n 1 + n 2 − 2 n_1 + n_2 - 2 n 1 + n 2 − 2 .

Two-sample t-test if variances are unequal (Welch's t-test)

Use this test if the variances of your populations are different.

Two-sample Welch's t-test formula if variances are unequal:

s 1 s_1 s 1 — Standard deviation in the first sample;
s 2 s_2 s 2 — Standard deviation in the second sample.

The number of degrees of freedom in a Welch's t-test (two-sample t-test with unequal variances) is very difficult to count. We can approximate it with the help of the following Satterthwaite formula :

Alternatively, you can take the smaller of n 1 − 1 n_1 - 1 n 1 − 1 and n 2 − 1 n_2 - 1 n 2 − 1 as a conservative estimate for the number of degrees of freedom.

🔎 The Satterthwaite formula for the degrees of freedom can be rewritten as a scaled weighted harmonic mean of the degrees of freedom of the respective samples: n 1 − 1 n_1 - 1 n 1 − 1 and n 2 − 1 n_2 - 1 n 2 − 1 , and the weights are proportional to the standard deviations of the corresponding samples.

As we commonly perform a paired t-test when we have data about the same subjects measured twice (before and after some treatment), let us adopt the convention of referring to the samples as the pre-group and post-group.

The null hypothesis is that the true difference between the means of pre- and post-populations is equal to some pre-set value, Δ \Delta Δ .

The alternative hypothesis is that the actual difference between these means is:

Typically, this pre-determined difference is zero. We can then reformulate the hypotheses as follows:

The null hypothesis is that the pre- and post-means are the same, i.e., the treatment has no impact on the population .

The alternative hypothesis:

The pre- and post-means are different from one another (treatment has some effect);
The pre-mean is smaller than the post-mean (treatment increases the result); or
The pre-mean is greater than the post-mean (treatment decreases the result).

Paired t-test formula

In fact, a paired t-test is technically the same as a one-sample t-test! Let us see why it is so. Let x 1 , . . . , x n x_1, ... , x_n x 1 , ... , x n be the pre observations and y 1 , . . . , y n y_1, ... , y_n y 1 , ... , y n the respective post observations. That is, x i , y i x_i, y_i x i , y i are the before and after measurements of the i -th subject.

For each subject, compute the difference, d i : = x i − y i d_i := x_i - y_i d i := x i − y i . All that happens next is just a one-sample t-test performed on the sample of differences d 1 , . . . , d n d_1, ... , d_n d 1 , ... , d n . Take a look at the formula for the T-score :

Δ \Delta Δ — Mean difference postulated in the null hypothesis;

n n n — Size of the sample of differences, i.e., the number of pairs;

x ˉ \bar{x} x ˉ — Mean of the sample of differences; and

s s s — Standard deviation of the sample of differences.

Number of degrees of freedom in t-test (paired): n − 1 n - 1 n − 1

t-test vs Z-test

We use a Z-test when we want to test the population mean of a normally distributed dataset, which has a known population variance . If the number of degrees of freedom is large, then the t-Student distribution is very close to N(0,1).

Hence, if there are many data points (at least 30), you may swap a t-test for a Z-test, and the results will be almost identical. However, for small samples with unknown variance, remember to use the t-test because, in such cases, the t-Student distribution differs significantly from the N(0,1)!

🙋 Have you concluded you need to perform the z-test? Head straight to our z-test calculator !

What is a t-test?

A t-test is a widely used statistical test that analyzes the means of one or two groups of data. For instance, a t-test is performed on medical data to determine whether a new drug really helps.

What are different types of t-tests?

Different types of t-tests are:

One-sample t-test;
Two-sample t-test; and
Paired t-test.

How to find the t value in a one sample t-test?

To find the t-value:

Subtract the null hypothesis mean from the sample mean value.
Divide the difference by the standard deviation of the sample.
Multiply the resultant with the square root of the sample size.

.css-m482sy.css-m482sy{color:#2B3148;background-color:transparent;font-family:var(--calculator-ui-font-family),Verdana,sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-m482sy.css-m482sy:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-m482sy .js-external-link-button.link-like,.css-m482sy .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-m482sy .js-external-link-button.link-like:hover,.css-m482sy .js-external-link-anchor:hover,.css-m482sy .js-external-link-button.link-like:active,.css-m482sy .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-m482sy .js-external-link-button.link-like:focus-visible,.css-m482sy .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-m482sy p,.css-m482sy div{margin:0;display:block;}.css-m482sy pre{margin:0;display:block;}.css-m482sy pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-m482sy pre:not(:first-child){padding-top:8px;}.css-m482sy ul,.css-m482sy ol{display:block margin:0;padding-left:20px;}.css-m482sy ul li,.css-m482sy ol li{padding-top:8px;}.css-m482sy ul ul,.css-m482sy ol ul,.css-m482sy ul ol,.css-m482sy ol ol{padding-top:0;}.css-m482sy ul:not(:first-child),.css-m482sy ol:not(:first-child){padding-top:4px;} .css-63uqft{margin:auto;background-color:white;overflow:auto;overflow-wrap:break-word;word-break:break-word;}.css-63uqft code,.css-63uqft kbd,.css-63uqft pre,.css-63uqft samp{font-family:monospace;}.css-63uqft code{padding:2px 4px;color:#444;background:#ddd;border-radius:4px;}.css-63uqft figcaption,.css-63uqft caption{text-align:center;}.css-63uqft figcaption{font-size:12px;font-style:italic;overflow:hidden;}.css-63uqft h3{font-size:1.75rem;}.css-63uqft h4{font-size:1.5rem;}.css-63uqft .mathBlock{font-size:24px;-webkit-padding-start:4px;padding-inline-start:4px;}.css-63uqft .mathBlock .katex{font-size:24px;text-align:left;}.css-63uqft .math-inline{background-color:#f0f0f0;display:inline-block;font-size:inherit;padding:0 3px;}.css-63uqft .videoBlock,.css-63uqft .imageBlock{margin-bottom:16px;}.css-63uqft .imageBlockimage-align--left,.css-63uqft .videoBlockvideo-align--left{float:left;}.css-63uqft .imageBlockimage-align--right,.css-63uqft .videoBlockvideo-align--right{float:right;}.css-63uqft .imageBlockimage-align--center,.css-63uqft .videoBlockvideo-align--center{display:block;margin-left:auto;margin-right:auto;clear:both;}.css-63uqft .imageBlockimage-align--none,.css-63uqft .videoBlockvideo-align--none{clear:both;margin-left:0;margin-right:0;}.css-63uqft .videoBlockvideo--wrapper{position:relative;padding-bottom:56.25%;height:0;}.css-63uqft .videoBlockvideo--wrapper iframe{position:absolute;top:0;left:0;width:100%;height:100%;}.css-63uqft .videoBlock__caption{text-align:left;}@font-face{font-family:'KaTeX_AMS';src:url(/katex-fonts/KaTeX_AMS-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_AMS-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_AMS-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Caligraphic';src:url(/katex-fonts/KaTeX_Caligraphic-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Caligraphic-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Caligraphic-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Fraktur';src:url(/katex-fonts/KaTeX_Fraktur-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Fraktur-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Fraktur-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_Main';src:url(/katex-fonts/KaTeX_Main-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Main-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Main-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-BoldItalic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-BoldItalic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-BoldItalic.ttf) format('truetype');font-weight:bold;font-style:italic;}@font-face{font-family:'KaTeX_Math';src:url(/katex-fonts/KaTeX_Math-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_Math-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_Math-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Bold.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Bold.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Bold.ttf) format('truetype');font-weight:bold;font-style:normal;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Italic.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Italic.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Italic.ttf) format('truetype');font-weight:normal;font-style:italic;}@font-face{font-family:'KaTeX_SansSerif';src:url(/katex-fonts/KaTeX_SansSerif-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_SansSerif-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_SansSerif-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Script';src:url(/katex-fonts/KaTeX_Script-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Script-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Script-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size1';src:url(/katex-fonts/KaTeX_Size1-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size1-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size1-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size2';src:url(/katex-fonts/KaTeX_Size2-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size2-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size2-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size3';src:url(/katex-fonts/KaTeX_Size3-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size3-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size3-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Size4';src:url(/katex-fonts/KaTeX_Size4-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Size4-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Size4-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}@font-face{font-family:'KaTeX_Typewriter';src:url(/katex-fonts/KaTeX_Typewriter-Regular.woff2) format('woff2'),url(/katex-fonts/KaTeX_Typewriter-Regular.woff) format('woff'),url(/katex-fonts/KaTeX_Typewriter-Regular.ttf) format('truetype');font-weight:normal;font-style:normal;}.css-63uqft .katex{font:normal 1.21em KaTeX_Main,Times New Roman,serif;line-height:1.2;text-indent:0;text-rendering:auto;}.css-63uqft .katex *{-ms-high-contrast-adjust:none!important;border-color:currentColor;}.css-63uqft .katex .katex-version::after{content:'0.13.13';}.css-63uqft .katex .katex-mathml{position:absolute;clip:rect(1px,1px,1px,1px);padding:0;border:0;height:1px;width:1px;overflow:hidden;}.css-63uqft .katex .katex-html>.newline{display:block;}.css-63uqft .katex .base{position:relative;display:inline-block;white-space:nowrap;width:-webkit-min-content;width:-moz-min-content;width:-webkit-min-content;width:-moz-min-content;width:min-content;}.css-63uqft .katex .strut{display:inline-block;}.css-63uqft .katex .textbf{font-weight:bold;}.css-63uqft .katex .textit{font-style:italic;}.css-63uqft .katex .textrm{font-family:KaTeX_Main;}.css-63uqft .katex .textsf{font-family:KaTeX_SansSerif;}.css-63uqft .katex .texttt{font-family:KaTeX_Typewriter;}.css-63uqft .katex .mathnormal{font-family:KaTeX_Math;font-style:italic;}.css-63uqft .katex .mathit{font-family:KaTeX_Main;font-style:italic;}.css-63uqft .katex .mathrm{font-style:normal;}.css-63uqft .katex .mathbf{font-family:KaTeX_Main;font-weight:bold;}.css-63uqft .katex .boldsymbol{font-family:KaTeX_Math;font-weight:bold;font-style:italic;}.css-63uqft .katex .amsrm{font-family:KaTeX_AMS;}.css-63uqft .katex .mathbb,.css-63uqft .katex .textbb{font-family:KaTeX_AMS;}.css-63uqft .katex .mathcal{font-family:KaTeX_Caligraphic;}.css-63uqft .katex .mathfrak,.css-63uqft .katex .textfrak{font-family:KaTeX_Fraktur;}.css-63uqft .katex .mathtt{font-family:KaTeX_Typewriter;}.css-63uqft .katex .mathscr,.css-63uqft .katex .textscr{font-family:KaTeX_Script;}.css-63uqft .katex .mathsf,.css-63uqft .katex .textsf{font-family:KaTeX_SansSerif;}.css-63uqft .katex .mathboldsf,.css-63uqft .katex .textboldsf{font-family:KaTeX_SansSerif;font-weight:bold;}.css-63uqft .katex .mathitsf,.css-63uqft .katex .textitsf{font-family:KaTeX_SansSerif;font-style:italic;}.css-63uqft .katex .mainrm{font-family:KaTeX_Main;font-style:normal;}.css-63uqft .katex .vlist-t{display:inline-table;table-layout:fixed;border-collapse:collapse;}.css-63uqft .katex .vlist-r{display:table-row;}.css-63uqft .katex .vlist{display:table-cell;vertical-align:bottom;position:relative;}.css-63uqft .katex .vlist>span{display:block;height:0;position:relative;}.css-63uqft .katex .vlist>span>span{display:inline-block;}.css-63uqft .katex .vlist>span>.pstrut{overflow:hidden;width:0;}.css-63uqft .katex .vlist-t2{margin-right:-2px;}.css-63uqft .katex .vlist-s{display:table-cell;vertical-align:bottom;font-size:1px;width:2px;min-width:2px;}.css-63uqft .katex .vbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:column;-ms-flex-direction:column;flex-direction:column;-webkit-align-items:baseline;-webkit-box-align:baseline;-ms-flex-align:baseline;align-items:baseline;}.css-63uqft .katex .hbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:100%;}.css-63uqft .katex .thinbox{display:-webkit-inline-box;display:-webkit-inline-flex;display:-ms-inline-flexbox;display:inline-flex;-webkit-flex-direction:row;-ms-flex-direction:row;flex-direction:row;width:0;max-width:0;}.css-63uqft .katex .msupsub{text-align:left;}.css-63uqft .katex .mfrac>span>span{text-align:center;}.css-63uqft .katex .mfrac .frac-line{display:inline-block;width:100%;border-bottom-style:solid;}.css-63uqft .katex .mfrac .frac-line,.css-63uqft .katex .overline .overline-line,.css-63uqft .katex .underline .underline-line,.css-63uqft .katex .hline,.css-63uqft .katex .hdashline,.css-63uqft .katex .rule{min-height:1px;}.css-63uqft .katex .mspace{display:inline-block;}.css-63uqft .katex .llap,.css-63uqft .katex .rlap,.css-63uqft .katex .clap{width:0;position:relative;}.css-63uqft .katex .llap>.inner,.css-63uqft .katex .rlap>.inner,.css-63uqft .katex .clap>.inner{position:absolute;}.css-63uqft .katex .llap>.fix,.css-63uqft .katex .rlap>.fix,.css-63uqft .katex .clap>.fix{display:inline-block;}.css-63uqft .katex .llap>.inner{right:0;}.css-63uqft .katex .rlap>.inner,.css-63uqft .katex .clap>.inner{left:0;}.css-63uqft .katex .clap>.inner>span{margin-left:-50%;margin-right:50%;}.css-63uqft .katex .rule{display:inline-block;border:solid 0;position:relative;}.css-63uqft .katex .overline .overline-line,.css-63uqft .katex .underline .underline-line,.css-63uqft .katex .hline{display:inline-block;width:100%;border-bottom-style:solid;}.css-63uqft .katex .hdashline{display:inline-block;width:100%;border-bottom-style:dashed;}.css-63uqft .katex .sqrt>.root{margin-left:0.27777778em;margin-right:-0.55555556em;}.css-63uqft .katex .sizing.reset-size1.size1,.css-63uqft .katex .fontsize-ensurer.reset-size1.size1{font-size:1em;}.css-63uqft .katex .sizing.reset-size1.size2,.css-63uqft .katex .fontsize-ensurer.reset-size1.size2{font-size:1.2em;}.css-63uqft .katex .sizing.reset-size1.size3,.css-63uqft .katex .fontsize-ensurer.reset-size1.size3{font-size:1.4em;}.css-63uqft .katex .sizing.reset-size1.size4,.css-63uqft .katex .fontsize-ensurer.reset-size1.size4{font-size:1.6em;}.css-63uqft .katex .sizing.reset-size1.size5,.css-63uqft .katex .fontsize-ensurer.reset-size1.size5{font-size:1.8em;}.css-63uqft .katex .sizing.reset-size1.size6,.css-63uqft .katex .fontsize-ensurer.reset-size1.size6{font-size:2em;}.css-63uqft .katex .sizing.reset-size1.size7,.css-63uqft .katex .fontsize-ensurer.reset-size1.size7{font-size:2.4em;}.css-63uqft .katex .sizing.reset-size1.size8,.css-63uqft .katex .fontsize-ensurer.reset-size1.size8{font-size:2.88em;}.css-63uqft .katex .sizing.reset-size1.size9,.css-63uqft .katex .fontsize-ensurer.reset-size1.size9{font-size:3.456em;}.css-63uqft .katex .sizing.reset-size1.size10,.css-63uqft .katex .fontsize-ensurer.reset-size1.size10{font-size:4.148em;}.css-63uqft .katex .sizing.reset-size1.size11,.css-63uqft .katex .fontsize-ensurer.reset-size1.size11{font-size:4.976em;}.css-63uqft .katex .sizing.reset-size2.size1,.css-63uqft .katex .fontsize-ensurer.reset-size2.size1{font-size:0.83333333em;}.css-63uqft .katex .sizing.reset-size2.size2,.css-63uqft .katex .fontsize-ensurer.reset-size2.size2{font-size:1em;}.css-63uqft .katex .sizing.reset-size2.size3,.css-63uqft .katex .fontsize-ensurer.reset-size2.size3{font-size:1.16666667em;}.css-63uqft .katex .sizing.reset-size2.size4,.css-63uqft .katex .fontsize-ensurer.reset-size2.size4{font-size:1.33333333em;}.css-63uqft .katex .sizing.reset-size2.size5,.css-63uqft .katex .fontsize-ensurer.reset-size2.size5{font-size:1.5em;}.css-63uqft .katex .sizing.reset-size2.size6,.css-63uqft .katex .fontsize-ensurer.reset-size2.size6{font-size:1.66666667em;}.css-63uqft .katex .sizing.reset-size2.size7,.css-63uqft .katex .fontsize-ensurer.reset-size2.size7{font-size:2em;}.css-63uqft .katex .sizing.reset-size2.size8,.css-63uqft .katex .fontsize-ensurer.reset-size2.size8{font-size:2.4em;}.css-63uqft .katex .sizing.reset-size2.size9,.css-63uqft .katex .fontsize-ensurer.reset-size2.size9{font-size:2.88em;}.css-63uqft .katex .sizing.reset-size2.size10,.css-63uqft .katex .fontsize-ensurer.reset-size2.size10{font-size:3.45666667em;}.css-63uqft .katex .sizing.reset-size2.size11,.css-63uqft .katex .fontsize-ensurer.reset-size2.size11{font-size:4.14666667em;}.css-63uqft .katex .sizing.reset-size3.size1,.css-63uqft .katex .fontsize-ensurer.reset-size3.size1{font-size:0.71428571em;}.css-63uqft .katex .sizing.reset-size3.size2,.css-63uqft .katex .fontsize-ensurer.reset-size3.size2{font-size:0.85714286em;}.css-63uqft .katex .sizing.reset-size3.size3,.css-63uqft .katex .fontsize-ensurer.reset-size3.size3{font-size:1em;}.css-63uqft .katex .sizing.reset-size3.size4,.css-63uqft .katex .fontsize-ensurer.reset-size3.size4{font-size:1.14285714em;}.css-63uqft .katex .sizing.reset-size3.size5,.css-63uqft .katex .fontsize-ensurer.reset-size3.size5{font-size:1.28571429em;}.css-63uqft .katex .sizing.reset-size3.size6,.css-63uqft .katex .fontsize-ensurer.reset-size3.size6{font-size:1.42857143em;}.css-63uqft .katex .sizing.reset-size3.size7,.css-63uqft .katex .fontsize-ensurer.reset-size3.size7{font-size:1.71428571em;}.css-63uqft .katex .sizing.reset-size3.size8,.css-63uqft .katex .fontsize-ensurer.reset-size3.size8{font-size:2.05714286em;}.css-63uqft .katex .sizing.reset-size3.size9,.css-63uqft .katex .fontsize-ensurer.reset-size3.size9{font-size:2.46857143em;}.css-63uqft .katex .sizing.reset-size3.size10,.css-63uqft .katex .fontsize-ensurer.reset-size3.size10{font-size:2.96285714em;}.css-63uqft .katex .sizing.reset-size3.size11,.css-63uqft .katex .fontsize-ensurer.reset-size3.size11{font-size:3.55428571em;}.css-63uqft .katex .sizing.reset-size4.size1,.css-63uqft .katex .fontsize-ensurer.reset-size4.size1{font-size:0.625em;}.css-63uqft .katex .sizing.reset-size4.size2,.css-63uqft .katex .fontsize-ensurer.reset-size4.size2{font-size:0.75em;}.css-63uqft .katex .sizing.reset-size4.size3,.css-63uqft .katex .fontsize-ensurer.reset-size4.size3{font-size:0.875em;}.css-63uqft .katex .sizing.reset-size4.size4,.css-63uqft .katex .fontsize-ensurer.reset-size4.size4{font-size:1em;}.css-63uqft .katex .sizing.reset-size4.size5,.css-63uqft .katex .fontsize-ensurer.reset-size4.size5{font-size:1.125em;}.css-63uqft .katex .sizing.reset-size4.size6,.css-63uqft .katex .fontsize-ensurer.reset-size4.size6{font-size:1.25em;}.css-63uqft .katex .sizing.reset-size4.size7,.css-63uqft .katex .fontsize-ensurer.reset-size4.size7{font-size:1.5em;}.css-63uqft .katex .sizing.reset-size4.size8,.css-63uqft .katex .fontsize-ensurer.reset-size4.size8{font-size:1.8em;}.css-63uqft .katex .sizing.reset-size4.size9,.css-63uqft .katex .fontsize-ensurer.reset-size4.size9{font-size:2.16em;}.css-63uqft .katex .sizing.reset-size4.size10,.css-63uqft .katex .fontsize-ensurer.reset-size4.size10{font-size:2.5925em;}.css-63uqft .katex .sizing.reset-size4.size11,.css-63uqft .katex .fontsize-ensurer.reset-size4.size11{font-size:3.11em;}.css-63uqft .katex .sizing.reset-size5.size1,.css-63uqft .katex .fontsize-ensurer.reset-size5.size1{font-size:0.55555556em;}.css-63uqft .katex .sizing.reset-size5.size2,.css-63uqft .katex .fontsize-ensurer.reset-size5.size2{font-size:0.66666667em;}.css-63uqft .katex .sizing.reset-size5.size3,.css-63uqft .katex .fontsize-ensurer.reset-size5.size3{font-size:0.77777778em;}.css-63uqft .katex .sizing.reset-size5.size4,.css-63uqft .katex .fontsize-ensurer.reset-size5.size4{font-size:0.88888889em;}.css-63uqft .katex .sizing.reset-size5.size5,.css-63uqft .katex .fontsize-ensurer.reset-size5.size5{font-size:1em;}.css-63uqft .katex .sizing.reset-size5.size6,.css-63uqft .katex .fontsize-ensurer.reset-size5.size6{font-size:1.11111111em;}.css-63uqft .katex .sizing.reset-size5.size7,.css-63uqft .katex .fontsize-ensurer.reset-size5.size7{font-size:1.33333333em;}.css-63uqft .katex .sizing.reset-size5.size8,.css-63uqft .katex .fontsize-ensurer.reset-size5.size8{font-size:1.6em;}.css-63uqft .katex .sizing.reset-size5.size9,.css-63uqft .katex .fontsize-ensurer.reset-size5.size9{font-size:1.92em;}.css-63uqft .katex .sizing.reset-size5.size10,.css-63uqft .katex .fontsize-ensurer.reset-size5.size10{font-size:2.30444444em;}.css-63uqft .katex .sizing.reset-size5.size11,.css-63uqft .katex .fontsize-ensurer.reset-size5.size11{font-size:2.76444444em;}.css-63uqft .katex .sizing.reset-size6.size1,.css-63uqft .katex .fontsize-ensurer.reset-size6.size1{font-size:0.5em;}.css-63uqft .katex .sizing.reset-size6.size2,.css-63uqft .katex .fontsize-ensurer.reset-size6.size2{font-size:0.6em;}.css-63uqft .katex .sizing.reset-size6.size3,.css-63uqft .katex .fontsize-ensurer.reset-size6.size3{font-size:0.7em;}.css-63uqft .katex .sizing.reset-size6.size4,.css-63uqft .katex .fontsize-ensurer.reset-size6.size4{font-size:0.8em;}.css-63uqft .katex .sizing.reset-size6.size5,.css-63uqft .katex .fontsize-ensurer.reset-size6.size5{font-size:0.9em;}.css-63uqft .katex .sizing.reset-size6.size6,.css-63uqft .katex .fontsize-ensurer.reset-size6.size6{font-size:1em;}.css-63uqft .katex .sizing.reset-size6.size7,.css-63uqft .katex .fontsize-ensurer.reset-size6.size7{font-size:1.2em;}.css-63uqft .katex .sizing.reset-size6.size8,.css-63uqft .katex .fontsize-ensurer.reset-size6.size8{font-size:1.44em;}.css-63uqft .katex .sizing.reset-size6.size9,.css-63uqft .katex .fontsize-ensurer.reset-size6.size9{font-size:1.728em;}.css-63uqft .katex .sizing.reset-size6.size10,.css-63uqft .katex .fontsize-ensurer.reset-size6.size10{font-size:2.074em;}.css-63uqft .katex .sizing.reset-size6.size11,.css-63uqft .katex .fontsize-ensurer.reset-size6.size11{font-size:2.488em;}.css-63uqft .katex .sizing.reset-size7.size1,.css-63uqft .katex .fontsize-ensurer.reset-size7.size1{font-size:0.41666667em;}.css-63uqft .katex .sizing.reset-size7.size2,.css-63uqft .katex .fontsize-ensurer.reset-size7.size2{font-size:0.5em;}.css-63uqft .katex .sizing.reset-size7.size3,.css-63uqft .katex .fontsize-ensurer.reset-size7.size3{font-size:0.58333333em;}.css-63uqft .katex .sizing.reset-size7.size4,.css-63uqft .katex .fontsize-ensurer.reset-size7.size4{font-size:0.66666667em;}.css-63uqft .katex .sizing.reset-size7.size5,.css-63uqft .katex .fontsize-ensurer.reset-size7.size5{font-size:0.75em;}.css-63uqft .katex .sizing.reset-size7.size6,.css-63uqft .katex .fontsize-ensurer.reset-size7.size6{font-size:0.83333333em;}.css-63uqft .katex .sizing.reset-size7.size7,.css-63uqft .katex .fontsize-ensurer.reset-size7.size7{font-size:1em;}.css-63uqft .katex .sizing.reset-size7.size8,.css-63uqft .katex .fontsize-ensurer.reset-size7.size8{font-size:1.2em;}.css-63uqft .katex .sizing.reset-size7.size9,.css-63uqft .katex .fontsize-ensurer.reset-size7.size9{font-size:1.44em;}.css-63uqft .katex .sizing.reset-size7.size10,.css-63uqft .katex .fontsize-ensurer.reset-size7.size10{font-size:1.72833333em;}.css-63uqft .katex .sizing.reset-size7.size11,.css-63uqft .katex .fontsize-ensurer.reset-size7.size11{font-size:2.07333333em;}.css-63uqft .katex .sizing.reset-size8.size1,.css-63uqft .katex .fontsize-ensurer.reset-size8.size1{font-size:0.34722222em;}.css-63uqft .katex .sizing.reset-size8.size2,.css-63uqft .katex .fontsize-ensurer.reset-size8.size2{font-size:0.41666667em;}.css-63uqft .katex .sizing.reset-size8.size3,.css-63uqft .katex .fontsize-ensurer.reset-size8.size3{font-size:0.48611111em;}.css-63uqft .katex .sizing.reset-size8.size4,.css-63uqft .katex .fontsize-ensurer.reset-size8.size4{font-size:0.55555556em;}.css-63uqft .katex .sizing.reset-size8.size5,.css-63uqft .katex .fontsize-ensurer.reset-size8.size5{font-size:0.625em;}.css-63uqft .katex .sizing.reset-size8.size6,.css-63uqft .katex .fontsize-ensurer.reset-size8.size6{font-size:0.69444444em;}.css-63uqft .katex .sizing.reset-size8.size7,.css-63uqft .katex .fontsize-ensurer.reset-size8.size7{font-size:0.83333333em;}.css-63uqft .katex .sizing.reset-size8.size8,.css-63uqft .katex .fontsize-ensurer.reset-size8.size8{font-size:1em;}.css-63uqft .katex .sizing.reset-size8.size9,.css-63uqft .katex .fontsize-ensurer.reset-size8.size9{font-size:1.2em;}.css-63uqft .katex .sizing.reset-size8.size10,.css-63uqft .katex .fontsize-ensurer.reset-size8.size10{font-size:1.44027778em;}.css-63uqft .katex .sizing.reset-size8.size11,.css-63uqft .katex .fontsize-ensurer.reset-size8.size11{font-size:1.72777778em;}.css-63uqft .katex .sizing.reset-size9.size1,.css-63uqft .katex .fontsize-ensurer.reset-size9.size1{font-size:0.28935185em;}.css-63uqft .katex .sizing.reset-size9.size2,.css-63uqft .katex .fontsize-ensurer.reset-size9.size2{font-size:0.34722222em;}.css-63uqft .katex .sizing.reset-size9.size3,.css-63uqft .katex .fontsize-ensurer.reset-size9.size3{font-size:0.40509259em;}.css-63uqft .katex .sizing.reset-size9.size4,.css-63uqft .katex .fontsize-ensurer.reset-size9.size4{font-size:0.46296296em;}.css-63uqft .katex .sizing.reset-size9.size5,.css-63uqft .katex .fontsize-ensurer.reset-size9.size5{font-size:0.52083333em;}.css-63uqft .katex .sizing.reset-size9.size6,.css-63uqft .katex .fontsize-ensurer.reset-size9.size6{font-size:0.5787037em;}.css-63uqft .katex .sizing.reset-size9.size7,.css-63uqft .katex .fontsize-ensurer.reset-size9.size7{font-size:0.69444444em;}.css-63uqft .katex .sizing.reset-size9.size8,.css-63uqft .katex .fontsize-ensurer.reset-size9.size8{font-size:0.83333333em;}.css-63uqft .katex .sizing.reset-size9.size9,.css-63uqft .katex .fontsize-ensurer.reset-size9.size9{font-size:1em;}.css-63uqft .katex .sizing.reset-size9.size10,.css-63uqft .katex .fontsize-ensurer.reset-size9.size10{font-size:1.20023148em;}.css-63uqft .katex .sizing.reset-size9.size11,.css-63uqft .katex .fontsize-ensurer.reset-size9.size11{font-size:1.43981481em;}.css-63uqft .katex .sizing.reset-size10.size1,.css-63uqft .katex .fontsize-ensurer.reset-size10.size1{font-size:0.24108004em;}.css-63uqft .katex .sizing.reset-size10.size2,.css-63uqft .katex .fontsize-ensurer.reset-size10.size2{font-size:0.28929605em;}.css-63uqft .katex .sizing.reset-size10.size3,.css-63uqft .katex .fontsize-ensurer.reset-size10.size3{font-size:0.33751205em;}.css-63uqft .katex .sizing.reset-size10.size4,.css-63uqft .katex .fontsize-ensurer.reset-size10.size4{font-size:0.38572806em;}.css-63uqft .katex .sizing.reset-size10.size5,.css-63uqft .katex .fontsize-ensurer.reset-size10.size5{font-size:0.43394407em;}.css-63uqft .katex .sizing.reset-size10.size6,.css-63uqft .katex .fontsize-ensurer.reset-size10.size6{font-size:0.48216008em;}.css-63uqft .katex .sizing.reset-size10.size7,.css-63uqft .katex .fontsize-ensurer.reset-size10.size7{font-size:0.57859209em;}.css-63uqft .katex .sizing.reset-size10.size8,.css-63uqft .katex .fontsize-ensurer.reset-size10.size8{font-size:0.69431051em;}.css-63uqft .katex .sizing.reset-size10.size9,.css-63uqft .katex .fontsize-ensurer.reset-size10.size9{font-size:0.83317261em;}.css-63uqft .katex .sizing.reset-size10.size10,.css-63uqft .katex .fontsize-ensurer.reset-size10.size10{font-size:1em;}.css-63uqft .katex .sizing.reset-size10.size11,.css-63uqft .katex .fontsize-ensurer.reset-size10.size11{font-size:1.19961427em;}.css-63uqft .katex .sizing.reset-size11.size1,.css-63uqft .katex .fontsize-ensurer.reset-size11.size1{font-size:0.20096463em;}.css-63uqft .katex .sizing.reset-size11.size2,.css-63uqft .katex .fontsize-ensurer.reset-size11.size2{font-size:0.24115756em;}.css-63uqft .katex .sizing.reset-size11.size3,.css-63uqft .katex .fontsize-ensurer.reset-size11.size3{font-size:0.28135048em;}.css-63uqft .katex .sizing.reset-size11.size4,.css-63uqft .katex .fontsize-ensurer.reset-size11.size4{font-size:0.32154341em;}.css-63uqft .katex .sizing.reset-size11.size5,.css-63uqft .katex .fontsize-ensurer.reset-size11.size5{font-size:0.36173633em;}.css-63uqft .katex .sizing.reset-size11.size6,.css-63uqft .katex .fontsize-ensurer.reset-size11.size6{font-size:0.40192926em;}.css-63uqft .katex .sizing.reset-size11.size7,.css-63uqft .katex .fontsize-ensurer.reset-size11.size7{font-size:0.48231511em;}.css-63uqft .katex .sizing.reset-size11.size8,.css-63uqft .katex .fontsize-ensurer.reset-size11.size8{font-size:0.57877814em;}.css-63uqft .katex .sizing.reset-size11.size9,.css-63uqft .katex .fontsize-ensurer.reset-size11.size9{font-size:0.69453376em;}.css-63uqft .katex .sizing.reset-size11.size10,.css-63uqft .katex .fontsize-ensurer.reset-size11.size10{font-size:0.83360129em;}.css-63uqft .katex .sizing.reset-size11.size11,.css-63uqft .katex .fontsize-ensurer.reset-size11.size11{font-size:1em;}.css-63uqft .katex .delimsizing.size1{font-family:KaTeX_Size1;}.css-63uqft .katex .delimsizing.size2{font-family:KaTeX_Size2;}.css-63uqft .katex .delimsizing.size3{font-family:KaTeX_Size3;}.css-63uqft .katex .delimsizing.size4{font-family:KaTeX_Size4;}.css-63uqft .katex .delimsizing.mult .delim-size1>span{font-family:KaTeX_Size1;}.css-63uqft .katex .delimsizing.mult .delim-size4>span{font-family:KaTeX_Size4;}.css-63uqft .katex .nulldelimiter{display:inline-block;width:0.12em;}.css-63uqft .katex .delimcenter{position:relative;}.css-63uqft .katex .op-symbol{position:relative;}.css-63uqft .katex .op-symbol.small-op{font-family:KaTeX_Size1;}.css-63uqft .katex .op-symbol.large-op{font-family:KaTeX_Size2;}.css-63uqft .katex .op-limits>.vlist-t{text-align:center;}.css-63uqft .katex .accent>.vlist-t{text-align:center;}.css-63uqft .katex .accent .accent-body{position:relative;}.css-63uqft .katex .accent .accent-body:not(.accent-full){width:0;}.css-63uqft .katex .overlay{display:block;}.css-63uqft .katex .mtable .vertical-separator{display:inline-block;min-width:1px;}.css-63uqft .katex .mtable .arraycolsep{display:inline-block;}.css-63uqft .katex .mtable .col-align-c>.vlist-t{text-align:center;}.css-63uqft .katex .mtable .col-align-l>.vlist-t{text-align:left;}.css-63uqft .katex .mtable .col-align-r>.vlist-t{text-align:right;}.css-63uqft .katex .svg-align{text-align:left;}.css-63uqft .katex svg{display:block;position:absolute;width:100%;height:inherit;fill:currentColor;stroke:currentColor;fill-rule:nonzero;fill-opacity:1;stroke-width:1;stroke-linecap:butt;stroke-linejoin:miter;stroke-miterlimit:4;stroke-dasharray:none;stroke-dashoffset:0;stroke-opacity:1;}.css-63uqft .katex svg path{stroke:none;}.css-63uqft .katex img{border-style:none;min-width:0;min-height:0;max-width:none;max-height:none;}.css-63uqft .katex .stretchy{width:100%;display:block;position:relative;overflow:hidden;}.css-63uqft .katex .stretchy::before,.css-63uqft .katex .stretchy::after{content:'';}.css-63uqft .katex .hide-tail{width:100%;position:relative;overflow:hidden;}.css-63uqft .katex .halfarrow-left{position:absolute;left:0;width:50.2%;overflow:hidden;}.css-63uqft .katex .halfarrow-right{position:absolute;right:0;width:50.2%;overflow:hidden;}.css-63uqft .katex .brace-left{position:absolute;left:0;width:25.1%;overflow:hidden;}.css-63uqft .katex .brace-center{position:absolute;left:25%;width:50%;overflow:hidden;}.css-63uqft .katex .brace-right{position:absolute;right:0;width:25.1%;overflow:hidden;}.css-63uqft .katex .x-arrow-pad{padding:0 0.5em;}.css-63uqft .katex .cd-arrow-pad{padding:0 0.55556em 0 0.27778em;}.css-63uqft .katex .x-arrow,.css-63uqft .katex .mover,.css-63uqft .katex .munder{text-align:center;}.css-63uqft .katex .boxpad{padding:0 0.3em 0 0.3em;}.css-63uqft .katex .fbox,.css-63uqft .katex .fcolorbox{box-sizing:border-box;border:0.04em solid;}.css-63uqft .katex .cancel-pad{padding:0 0.2em 0 0.2em;}.css-63uqft .katex .cancel-lap{margin-left:-0.2em;margin-right:-0.2em;}.css-63uqft .katex .sout{border-bottom-style:solid;border-bottom-width:0.08em;}.css-63uqft .katex .angl{box-sizing:border-box;border-top:0.049em solid;border-right:0.049em solid;margin-right:0.03889em;}.css-63uqft .katex .anglpad{padding:0 0.03889em 0 0.03889em;}.css-63uqft .katex .eqn-num::before{counter-increment:katexEqnNo;content:'(' counter(katexEqnNo) ')';}.css-63uqft .katex .mml-eqn-num::before{counter-increment:mmlEqnNo;content:'(' counter(mmlEqnNo) ')';}.css-63uqft .katex .mtr-glue{width:50%;}.css-63uqft .katex .cd-vert-arrow{display:inline-block;position:relative;}.css-63uqft .katex .cd-label-left{display:inline-block;position:absolute;right:calc(50% + 0.3em);text-align:left;}.css-63uqft .katex .cd-label-right{display:inline-block;position:absolute;left:calc(50% + 0.3em);text-align:right;}.css-63uqft .katex-display{display:block;margin:1em 0;text-align:center;}.css-63uqft .katex-display>.katex{display:block;white-space:nowrap;}.css-63uqft .katex-display>.katex>.katex-html{display:block;position:relative;}.css-63uqft .katex-display>.katex>.katex-html>.tag{position:absolute;right:0;}.css-63uqft .katex-display.leqno>.katex>.katex-html>.tag{left:0;right:auto;}.css-63uqft .katex-display.fleqn>.katex{text-align:left;padding-left:2em;}.css-63uqft body{counter-reset:katexEqnNo mmlEqnNo;}.css-63uqft table{width:-webkit-max-content;width:-moz-max-content;width:max-content;}.css-63uqft .tableBlock{max-width:100%;margin-bottom:1rem;overflow-y:scroll;}.css-63uqft .tableBlock thead,.css-63uqft .tableBlock thead th{border-bottom:1px solid #333!important;}.css-63uqft .tableBlock th,.css-63uqft .tableBlock td{padding:10px;text-align:left;}.css-63uqft .tableBlock th{font-weight:bold!important;}.css-63uqft .tableBlock caption{caption-side:bottom;color:#555;font-size:12px;font-style:italic;text-align:center;}.css-63uqft .tableBlock caption>p{margin:0;}.css-63uqft .tableBlock th>p,.css-63uqft .tableBlock td>p{margin:0;}.css-63uqft .tableBlock [data-background-color='aliceblue']{background-color:#f0f8ff;color:#000;}.css-63uqft .tableBlock [data-background-color='black']{background-color:#000;color:#fff;}.css-63uqft .tableBlock [data-background-color='chocolate']{background-color:#d2691e;color:#fff;}.css-63uqft .tableBlock [data-background-color='cornflowerblue']{background-color:#6495ed;color:#fff;}.css-63uqft .tableBlock [data-background-color='crimson']{background-color:#dc143c;color:#fff;}.css-63uqft .tableBlock [data-background-color='darkblue']{background-color:#00008b;color:#fff;}.css-63uqft .tableBlock [data-background-color='darkseagreen']{background-color:#8fbc8f;color:#000;}.css-63uqft .tableBlock [data-background-color='deepskyblue']{background-color:#00bfff;color:#000;}.css-63uqft .tableBlock [data-background-color='gainsboro']{background-color:#dcdcdc;color:#000;}.css-63uqft .tableBlock [data-background-color='grey']{background-color:#808080;color:#fff;}.css-63uqft .tableBlock [data-background-color='lemonchiffon']{background-color:#fffacd;color:#000;}.css-63uqft .tableBlock [data-background-color='lightpink']{background-color:#ffb6c1;color:#000;}.css-63uqft .tableBlock [data-background-color='lightsalmon']{background-color:#ffa07a;color:#000;}.css-63uqft .tableBlock [data-background-color='lightskyblue']{background-color:#87cefa;color:#000;}.css-63uqft .tableBlock [data-background-color='mediumblue']{background-color:#0000cd;color:#fff;}.css-63uqft .tableBlock [data-background-color='omnigrey']{background-color:#f0f0f0;color:#000;}.css-63uqft .tableBlock [data-background-color='white']{background-color:#fff;color:#000;}.css-63uqft .tableBlock [data-text-align='center']{text-align:center;}.css-63uqft .tableBlock [data-text-align='left']{text-align:left;}.css-63uqft .tableBlock [data-text-align='right']{text-align:right;}.css-63uqft .tableBlock [data-vertical-align='bottom']{vertical-align:bottom;}.css-63uqft .tableBlock [data-vertical-align='middle']{vertical-align:middle;}.css-63uqft .tableBlock [data-vertical-align='top']{vertical-align:top;}.css-63uqft .tableBlockfont-size--xxsmall{font-size:10px;}.css-63uqft .tableBlockfont-size--xsmall{font-size:12px;}.css-63uqft .tableBlockfont-size--small{font-size:14px;}.css-63uqft .tableBlockfont-size--large{font-size:18px;}.css-63uqft .tableBlockborder--some tbody tr:not(:last-child){border-bottom:1px solid #e2e5e7;}.css-63uqft .tableBlockborder--bordered td,.css-63uqft .tableBlockborder--bordered th{border:1px solid #e2e5e7;}.css-63uqft .tableBlockborder--borderless tbody+tbody,.css-63uqft .tableBlockborder--borderless td,.css-63uqft .tableBlockborder--borderless th,.css-63uqft .tableBlockborder--borderless tr,.css-63uqft .tableBlockborder--borderless thead,.css-63uqft .tableBlockborder--borderless thead th{border:0!important;}.css-63uqft .tableBlock:not(.tableBlocktable-striped) tbody tr{background-color:unset!important;}.css-63uqft .tableBlocktable-striped tbody tr:nth-of-type(odd){background-color:#f9fafc!important;}.css-63uqft .tableBlocktable-compactl th,.css-63uqft .tableBlocktable-compact td{padding:3px!important;}.css-63uqft .tableBlockfull-size{width:100%;}.css-63uqft .textBlock{margin-bottom:16px;}.css-63uqft .textBlocktext-formatting--finePrint{font-size:12px;}.css-63uqft .textBlocktext-infoBox{padding:0.75rem 1.25rem;margin-bottom:1rem;border:1px solid transparent;border-radius:0.25rem;}.css-63uqft .textBlocktext-infoBox p{margin:0;}.css-63uqft .textBlocktext-infoBox--primary{background-color:#cce5ff;border-color:#b8daff;color:#004085;}.css-63uqft .textBlocktext-infoBox--secondary{background-color:#e2e3e5;border-color:#d6d8db;color:#383d41;}.css-63uqft .textBlocktext-infoBox--success{background-color:#d4edda;border-color:#c3e6cb;color:#155724;}.css-63uqft .textBlocktext-infoBox--danger{background-color:#f8d7da;border-color:#f5c6cb;color:#721c24;}.css-63uqft .textBlocktext-infoBox--warning{background-color:#fff3cd;border-color:#ffeeba;color:#856404;}.css-63uqft .textBlocktext-infoBox--info{background-color:#d1ecf1;border-color:#bee5eb;color:#0c5460;}.css-63uqft .textBlocktext-infoBox--dark{background-color:#d6d8d9;border-color:#c6c8ca;color:#1b1e21;}.css-63uqft .text-overline{-webkit-text-decoration:overline;text-decoration:overline;}.css-63uqft.css-63uqft{color:#2B3148;background-color:transparent;font-family:var(--calculator-ui-font-family),Verdana,sans-serif;font-size:20px;line-height:24px;overflow:visible;padding-top:0px;position:relative;}.css-63uqft.css-63uqft:after{content:'';-webkit-transform:scale(0);-moz-transform:scale(0);-ms-transform:scale(0);transform:scale(0);position:absolute;border:2px solid #EA9430;border-radius:2px;inset:-8px;z-index:1;}.css-63uqft .js-external-link-button.link-like,.css-63uqft .js-external-link-anchor{color:inherit;border-radius:1px;-webkit-text-decoration:underline;text-decoration:underline;}.css-63uqft .js-external-link-button.link-like:hover,.css-63uqft .js-external-link-anchor:hover,.css-63uqft .js-external-link-button.link-like:active,.css-63uqft .js-external-link-anchor:active{text-decoration-thickness:2px;text-shadow:1px 0 0;}.css-63uqft .js-external-link-button.link-like:focus-visible,.css-63uqft .js-external-link-anchor:focus-visible{outline:transparent 2px dotted;box-shadow:0 0 0 2px #6314E6;}.css-63uqft p,.css-63uqft div{margin:0;display:block;}.css-63uqft pre{margin:0;display:block;}.css-63uqft pre code{display:block;width:-webkit-fit-content;width:-moz-fit-content;width:fit-content;}.css-63uqft pre:not(:first-child){padding-top:8px;}.css-63uqft ul,.css-63uqft ol{display:block margin:0;padding-left:20px;}.css-63uqft ul li,.css-63uqft ol li{padding-top:8px;}.css-63uqft ul ul,.css-63uqft ol ul,.css-63uqft ul ol,.css-63uqft ol ol{padding-top:0;}.css-63uqft ul:not(:first-child),.css-63uqft ol:not(:first-child){padding-top:4px;} Test setup

Choose test type

t-test for the population mean, μ, based on one independent sample . Null hypothesis H 0 : μ = μ 0

Alternative hypothesis H 1

Test details

Significance level α

The probability that we reject a true H 0 (type I error).

Degrees of freedom

Calculated as sample size minus one.

Test results

What is p-value , p value vs alpha level, p values and critical values, how is p-value calculated, p-value in hypothesis testing, p-values and statistical significance, reporting p-values, our learners also ask, what is p-value in statistical hypothesis.

Few statistical estimates are as significant as the p-value. The p-value or probability value is a number, calculated from a statistical test , that describes how likely your results would have occurred if the null hypothesis were true. A P-value less than 0.5 is statistically significant, while a value higher than 0.5 indicates the null hypothesis is true; hence it is not statistically significant. So, what is P-Value exactly, and why is it so important?

In statistical hypothesis testing , P-Value or probability value can be defined as the measure of the probability that a real-valued test statistic is at least as extreme as the value actually obtained. P-value shows how likely it is that your set of observations could have occurred under the null hypothesis. P-Values are used in statistical hypothesis testing to determine whether to reject the null hypothesis. The smaller the p-value, the stronger the likelihood that you should reject the null hypothesis.

Your Data Analytics Career is Around The Corner!

P-values are expressed as decimals and can be converted into percentage. For example, a p-value of 0.0237 is 2.37%, which means there's a 2.37% chance of your results being random or having happened by chance. The smaller the P-value, the more significant your results are.

In a hypothesis test, you can compare the p value from your test with the alpha level selected while running the test. Now, let’s try to understand what is P-Value vs Alpha level.

A P-value indicates the probability of getting an effect no less than that actually observed in the sample data.

An alpha level will tell you the probability of wrongly rejecting a true null hypothesis. The level is selected by the researcher and obtained by subtracting your confidence level from 100%. For instance, if you are 95% confident in your research, the alpha level will be 5% (0.05).

When you run the hypothesis test, if you get:

A small p value (<=0.05), you should reject the null hypothesis
A large p value (>0.05), you should not reject the null hypothesis

In addition to the P-value, you can use other values given by your test to determine if your null hypothesis is true.

For example, if you run an F-test to compare two variances in Excel, you will obtain a p-value, an f-critical value, and a f-value. Compare the f-value with f-critical value. If f-critical value is lower, you should reject the null hypothesis.

P-Values are usually calculated using p-value tables or spreadsheets, or calculated automatically using statistical software like R, SPSS, etc.

Depending on the test statistic and degrees of freedom (subtracting no. of independent variables from no. of observations) of your test, you can find out from the tables how frequently you can expect the test statistic to be under the null hypothesis.

How to calculate P-value depends on which statistical test you’re using to test your hypothesis.

Every statistical test uses different assumptions and generates different statistics. Select the test method that best suits your data and matches the effect or relationship being tested.
The number of independent variables included in your test determines how big or small the test statistic should be in order to generate the same p-value.

Regardless of what statistical test you are using, the p-value will always denote the same thing – how frequently you can expect to get a test statistic as extreme or even more extreme than the one given by your test.

In the P-Value approach to hypothesis testing, a calculated probability is used to decide if there’s evidence to reject the null hypothesis, also known as the conjecture. The conjecture is the initial claim about a data population, while the alternative hypothesis ascertains if the observed population parameter differs from the population parameter value according to the conjecture.

Effectively, the significance level is declared in advance to determine how small the P-value needs to be such that the null hypothesis is rejected. The levels of significance vary from one researcher to another; so it can get difficult for readers to compare results from two different tests. That is when P-value makes things easier.

Readers could interpret the statistical significance by referring to the reported P-value of the hypothesis test. This is known as the P-value approach to hypothesis testing. Using this, readers could decide for themselves whether the p value represents a statistically significant difference.

The level of statistical significance is usually represented as a P-value between 0 and 1. The smaller the p-value, the more likely it is that you would reject the null hypothesis.

A P-Value < or = 0.05 is considered statistically significant. It denotes strong evidence against the null hypothesis, since there is below 5% probability of the null being correct. So, we reject the null hypothesis and accept the alternative hypothesis.
But if P-Value is lower than your threshold of significance, though the null hypothesis can be rejected, it does not mean that there is 95% probability of the alternative hypothesis being true.
A P-Value >0.05 is not statistically significant. It denotes strong evidence for the null hypothesis being true. Thus, we retain the null hypothesis and reject the alternative hypothesis. We cannot accept null hypothesis; we can only reject or not reject it.

A statistically significant result does not prove a research hypothesis to be correct. Instead, it provides support for or provides evidence for the hypothesis.

You should report exact P-Values upto two or three decimal places.
For P-values less than .001, report as p < .001.
Do not use 0 before the decimal point as it cannot equal1. Write p = .001, and not p = 0.001
Make sure p is always italicized and there is space on either side of the = sign.
It is impossible to get P = .000, and should be written as p < .001

An investor says that the performance of their investment portfolio is equivalent to that of the Standard & Poor’s (S&P) 500 Index. He performs a two-tailed test to determine this.

The null hypothesis here says that the portfolio’s returns are equivalent to the returns of S&P 500, while the alternative hypothesis says that the returns of the portfolio and the returns of the S&P 500 are not equivalent.

The p-value hypothesis test gives a measure of how much evidence is present to reject the null hypothesis. The smaller the p value, the higher the evidence against null hypothesis.

Therefore, if the investor gets a P value of .001, it indicates strong evidence against null hypothesis. So he confidently deduces that the portfolio’s returns and the S&P 500’s returns are not equivalent.

1. What does P-value mean?

P-Value or probability value is a number that denotes the likelihood of your data having occurred under the null hypothesis of your statistical test.

2. What does p 0.05 mean?

A P-value less than 0.05 is deemed to be statistically significant, meaning the null hypothesis should be rejected in such a case. A P-Value greater than 0.05 is not considered to be statistically significant, meaning the null hypothesis should not be rejected.

3. What is P-value and how is it calculated?

The p-value or probability value is a number, calculated from a statistical test, that tells how likely it is that your results would have occurred under the null hypothesis of the test.

P-values are usually automatically calculated using statistical software. They can also be calculated using p-value tables for the relevant statistical test. P values are calculated based on the null distribution of the test statistic. In case the test statistic is far from the mean of the null distribution, the p-value obtained is small. It indicates that the test statistic is unlikely to have occurred under the null hypothesis.

4. What is p-value in research?

P values are used in hypothesis testing to help determine whether the null hypothesis should be rejected. It plays a major role when results of research are discussed. Hypothesis testing is a statistical methodology frequently used in medical and clinical research studies.

5. Why is the p-value significant?

Statistical significance is a term that researchers use to say that it is not likely that their observations could have occurred if the null hypothesis were true. The level of statistical significance is usually represented as a P-value or probability value between 0 and 1. The smaller the p-value, the more likely it is that you would reject the null hypothesis.

6. What is null hypothesis and what is p-value?

A null hypothesis is a kind of statistical hypothesis that suggests that there is no statistical significance in a set of given observations. It says there is no relationship between your variables.

P-value or probability value is a number, calculated from a statistical test, that tells how likely it is that your results would have occurred under the null hypothesis of the test.

P-Value is used to determine the significance of observational data. Whenever researchers notice an apparent relation between two variables, a P-Value calculation helps ascertain if the observed relationship happened as a result of chance. Learn more about statistical analysis and data analytics and fast track your career with our Professional Certificate Program In Data Analytics .

Data Science & Business Analytics Courses Duration and Fees

Data Science & Business Analytics programs typically range from a few weeks to several months, with fees varying based on program and institution.

Program Name	Duration	Fees
Cohort Starts:	6 Months	$ 8,500
Cohort Starts:	8 months	$ 3,500
Cohort Starts:	11 months	$ 3,800
Cohort Starts:	14 weeks	$ 2,624
Cohort Starts:	32 weeks	$ 3,850
Cohort Starts:	11 Months	$ 4,500
	11 months	$ 1,449
	11 months	$ 1,449

Get Affiliated Certifications with Live Class programs

Post graduate program in data analytics.

Post Graduate Program certificate and Alumni Association membership
Exclusive hackathons and Ask me Anything sessions by IBM

Data Analyst

Industry-recognized Data Analyst Master’s certificate from Simplilearn
Dedicated live sessions by faculty of industry experts
PMP, PMI, PMBOK, CAPM, PgMP, PfMP, ACP, PBA, RMP, SP, and OPM3 are registered marks of the Project Management Institute, Inc.

IMAGES

P-Value Method For Hypothesis Testing
What is P-value in hypothesis testing
P-Value
Calculate the P-Value in Statistics
Hypothesis Test for Proportion
Hypothesis testing tutorial using p value method

VIDEO

Using P-value: Hypothesis Test for Mean. (Large sample)
24. p-Value in Hypothesis Testing
How to Calculate Probability Value (P-Value) in Excel
P Value: Get Complete Clarity With Practical Examples
Hypothesis Testing Part 2
Hypothesis Test

COMMENTS

How to Find the P value: Process and Calculations
How to Find the P value: Process and Calculations
S.3.2 Hypothesis Testing (P-Value Approach)
S.3.2 Hypothesis Testing (P-Value Approach) - STAT ONLINE
p-value Calculator
p-value Calculator | Formula | Interpretation
Understanding P-values
Understanding P-values | Definition and Examples
Hypothesis Testing Calculator with Steps
To test the hypothesis in the p-value approach, compare the p-value to the level of significance. ... To change the level of significance, click on $\boxed{.05}$. Note that if the test statistic is given, you can calculate the p-value from the test statistic by clicking on the switch symbol twice. In the critical value approach, the level of ...
Step-by-step guide to hypothesis testing in statistics
You then calculate how this average compares to the claimed 500 hours using the t-test. 5. Find the p-Value. Explanation: The p-value tells you the probability of getting a result as extreme as yours if the null hypothesis is true. Example: You find a p-value of 0.0001. This means there's a very small chance (0.01%) of getting an average ...
Hypothesis Testing, P Values, Confidence Intervals, and Significance
Hypothesis Testing, P Values, Confidence Intervals, and ...
Interpreting P values
Interpreting P values
Understanding P-Values and Statistical Significance
What a p-value tells you. A p-value, or probability value, is a number describing how likely it is that your data would have occurred by random chance (i.e., that the null hypothesis is true). The level of statistical significance is often expressed as a p-value between 0 and 1. The smaller the p -value, the less likely the results occurred by ...
Chapter 5: Hypothesis Testing and P-Values
Simply put, the P-value is the probability of getting a result that is more extreme than the value that is actually observed. Let's see how it is used in the context of our previous hypothesis tests, starting with a two-tailed test. Our P-value effectively gives us the probability of measuring a value greater than the observed, i.e. the tail ...
How Hypothesis Tests Work: Significance Levels (Alpha) and P values
Hypothesis testing is a vital process in inferential statistics where the goal is to use sample data to draw conclusions about an entire population. In the testing process, you use significance levels and p-values to determine whether the test results are statistically significant. You hear about results being statistically significant all of ...
P-Value Method for Hypothesis Testing
The P-value method is used in Hypothesis Testing to check the significance of the given Null Hypothesis. Then, deciding to reject or support it is based upon the specified significance level or threshold. A P-value is calculated in this method which is a test statistic. This statistic can give us the probability of finding a value (Sample Mean ...
Hypothesis Testing
Using the p-value to make the decision. The p-value represents how likely we would be to observe such an extreme sample if the null hypothesis were true. The p-value is a probability computed assuming the null hypothesis is true, that the test statistic would take a value as extreme or more extreme than that actually observed. Since it's a probability, it is a number between 0 and 1.
Calculating p-Value in Hypothesis Testing
The p-value can be used in the final stage of the test to make this determination. Interpreting a p-value. Because it is a probability, the p-value can be expressed as a decimal or a percentage ranging from 0 to 1 or 0% to 100%. The closer the p-value is to zero, the stronger the evidence is in support of the alternative hypothesis, H a H_a H a .
P-Value in Statistical Hypothesis Tests: What is it?
P-Value in Statistical Hypothesis Tests: What is it? - ...
P-Value: What It Is, How to Calculate It, and Why It Matters
P-Value: What It Is, How to Calculate It, and Why It Matters
9.3
9.3 - The P-Value Approach | STAT 415
8.1: The null and alternative hypotheses
a probability value or p-value which is associated with the test statistic, assuming a null hypothesis is "true" in the population from which we sample. Note that as discussed in (Chapter 8.2) , this is not strictly the interpretation of p-value, but a shorthand for how likely the data is to fit the null hypothesis.
P-Value: Comprehensive Guide to Understand, Apply, and Interpret
P-Value: Comprehensive Guide to Understand, Apply, and ...
The p-value and rejecting the null (for one- and two-tail tests)
The p-value (or the observed level of significance) is the smallest level of significance at which you can reject the null hypothesis, assuming the null hypothesis is true. You can also think about the p-value as the total area of the region of rejection. Remember that in a one-tailed test, the regi
P-value Calculator
P-value Calculator
P-value Calculator & Statistical Significance Calculator
P-value Calculator & Statistical Significance Calculator
Three Ways to Find a P-Value from a t Statistic
In each of the following examples, we'll find the p-value for a right-tailed test with a t statistic of 1.441 and 13 degrees of freedom. Technique 1: t Score to P Value Calculator. The first way to find a p-value from a t statistic is to use an online calculator like the T Score to P Value Calculator. We can simply enter the value for t and ...
t-test Calculator
t-test Calculator | Formula | p-value
What Is P-Value in Statistical Hypothesis?
The p-value or probability value is a number, calculated from a statistical test, that describes how likely your results would have occurred if the null hypothesis were true. A P-value less than 0.5 is statistically significant, while a value higher than 0.5 indicates the null hypothesis is true; hence it is not statistically significant.