ORIGINAL RESEARCH article
Mathematical problem-solving through cooperative learning—the importance of peer acceptance and friendships.

- 1 Department of Education, Uppsala University, Uppsala, Sweden
- 2 Department of Education, Culture and Communication, Malardalen University, Vasteras, Sweden
- 3 School of Natural Sciences, Technology and Environmental Studies, Sodertorn University, Huddinge, Sweden
- 4 Faculty of Education, Gothenburg University, Gothenburg, Sweden
Mathematical problem-solving constitutes an important area of mathematics instruction, and there is a need for research on instructional approaches supporting student learning in this area. This study aims to contribute to previous research by studying the effects of an instructional approach of cooperative learning on students’ mathematical problem-solving in heterogeneous classrooms in grade five, in which students with special needs are educated alongside with their peers. The intervention combined a cooperative learning approach with instruction in problem-solving strategies including mathematical models of multiplication/division, proportionality, and geometry. The teachers in the experimental group received training in cooperative learning and mathematical problem-solving, and implemented the intervention for 15 weeks. The teachers in the control group received training in mathematical problem-solving and provided instruction as they would usually. Students (269 in the intervention and 312 in the control group) participated in tests of mathematical problem-solving in the areas of multiplication/division, proportionality, and geometry before and after the intervention. The results revealed significant effects of the intervention on student performance in overall problem-solving and problem-solving in geometry. The students who received higher scores on social acceptance and friendships for the pre-test also received higher scores on the selected tests of mathematical problem-solving. Thus, the cooperative learning approach may lead to gains in mathematical problem-solving in heterogeneous classrooms, but social acceptance and friendships may also greatly impact students’ results.

Introduction
The research on instruction in mathematical problem-solving has progressed considerably during recent decades. Yet, there is still a need to advance our knowledge on how teachers can support their students in carrying out this complex activity ( Lester and Cai, 2016 ). Results from the Program for International Student Assessment (PISA) show that only 53% of students from the participating countries could solve problems requiring more than direct inference and using representations from different information sources ( OECD, 2019 ). In addition, OECD (2019) reported a large variation in achievement with regard to students’ diverse backgrounds. Thus, there is a need for instructional approaches to promote students’ problem-solving in mathematics, especially in heterogeneous classrooms in which students with diverse backgrounds and needs are educated together. Small group instructional approaches have been suggested as important to promote learning of low-achieving students and students with special needs ( Kunsch et al., 2007 ). One such approach is cooperative learning (CL), which involves structured collaboration in heterogeneous groups, guided by five principles to enhance group cohesion ( Johnson et al., 1993 ; Johnson et al., 2009 ; Gillies, 2016 ). While CL has been well-researched in whole classroom approaches ( Capar and Tarim, 2015 ), few studies of the approach exist with regard to students with special educational needs (SEN; McMaster and Fuchs, 2002 ). This study contributes to previous research by studying the effects of the CL approach on students’ mathematical problem-solving in heterogeneous classrooms, in which students with special needs are educated alongside with their peers.
Group collaboration through the CL approach is structured in accordance with five principles of collaboration: positive interdependence, individual accountability, explicit instruction in social skills, promotive interaction, and group processing ( Johnson et al., 1993 ). First, the group tasks need to be structured so that all group members feel dependent on each other in the completion of the task, thus promoting positive interdependence. Second, for individual accountability, the teacher needs to assure that each group member feels responsible for his or her share of work, by providing opportunities for individual reports or evaluations. Third, the students need explicit instruction in social skills that are necessary for collaboration. Fourth, the tasks and seat arrangements should be designed to promote interaction among group members. Fifth, time needs to be allocated to group processing, through which group members can evaluate their collaborative work to plan future actions. Using these principles for cooperation leads to gains in mathematics, according to Capar and Tarim (2015) , who conducted a meta-analysis on studies of cooperative learning and mathematics, and found an increase of .59 on students’ mathematics achievement scores in general. However, the number of reviewed studies was limited, and researchers suggested a need for more research. In the current study, we focused on the effect of CL approach in a specific area of mathematics: problem-solving.
Mathematical problem-solving is a central area of mathematics instruction, constituting an important part of preparing students to function in modern society ( Gravemeijer et al., 2017 ). In fact, problem-solving instruction creates opportunities for students to apply their knowledge of mathematical concepts, integrate and connect isolated pieces of mathematical knowledge, and attain a deeper conceptual understanding of mathematics as a subject ( Lester and Cai, 2016 ). Some researchers suggest that mathematics itself is a science of problem-solving and of developing theories and methods for problem-solving ( Hamilton, 2007 ; Davydov, 2008 ).
Problem-solving processes have been studied from different perspectives ( Lesh and Zawojewski, 2007 ). Problem-solving heuristics Pólya, (1948) has largely influenced our perceptions of problem-solving, including four principles: understanding the problem, devising a plan, carrying out the plan, and looking back and reflecting upon the suggested solution. Schoenfield, (2016) suggested the use of specific problem-solving strategies for different types of problems, which take into consideration metacognitive processes and students’ beliefs about problem-solving. Further, models and modelling perspectives on mathematics ( Lesh and Doerr, 2003 ; Lesh and Zawojewski, 2007 ) emphasize the importance of engaging students in model-eliciting activities in which problem situations are interpreted mathematically, as students make connections between problem information and knowledge of mathematical operations, patterns, and rules ( Mousoulides et al., 2010 ; Stohlmann and Albarracín, 2016 ).
Not all students, however, find it easy to solve complex mathematical problems. Students may experience difficulties in identifying solution-relevant elements in a problem or visualizing appropriate solution to a problem situation. Furthermore, students may need help recognizing the underlying model in problems. For example, in two studies by Degrande et al. (2016) , students in grades four to six were presented with mathematical problems in the context of proportional reasoning. The authors found that the students, when presented with a word problem, could not identify an underlying model, but rather focused on superficial characteristics of the problem. Although the students in the study showed more success when presented with a problem formulated in symbols, the authors pointed out a need for activities that help students distinguish between different proportional problem types. Furthermore, students exhibiting specific learning difficulties may need additional support in both general problem-solving strategies ( Lein et al., 2020 ; Montague et al., 2014 ) and specific strategies pertaining to underlying models in problems. The CL intervention in the present study focused on supporting students in problem-solving, through instruction in problem-solving principles ( Pólya, 1948 ), specifically applied to three models of mathematical problem-solving—multiplication/division, geometry, and proportionality.
Students’ problem-solving may be enhanced through participation in small group discussions. In a small group setting, all the students have the opportunity to explain their solutions, clarify their thinking, and enhance understanding of a problem at hand ( Yackel et al., 1991 ; Webb and Mastergeorge, 2003 ). In fact, small group instruction promotes students’ learning in mathematics by providing students with opportunities to use language for reasoning and conceptual understanding ( Mercer and Sams, 2006 ), to exchange different representations of the problem at hand ( Fujita et al., 2019 ), and to become aware of and understand groupmates’ perspectives in thinking ( Kazak et al., 2015 ). These opportunities for learning are created through dialogic spaces characterized by openness to each other’s perspectives and solutions to mathematical problems ( Wegerif, 2011 ).
However, group collaboration is not only associated with positive experiences. In fact, studies show that some students may not be given equal opportunities to voice their opinions, due to academic status differences ( Langer-Osuna, 2016 ). Indeed, problem-solvers struggling with complex tasks may experience negative emotions, leading to uncertainty of not knowing the definite answer, which places demands on peer support ( Jordan and McDaniel, 2014 ; Hannula, 2015 ). Thus, especially in heterogeneous groups, students may need additional support to promote group interaction. Therefore, in this study, we used a cooperative learning approach, which, in contrast to collaborative learning approaches, puts greater focus on supporting group cohesion through instruction in social skills and time for reflection on group work ( Davidson and Major, 2014 ).
Although cooperative learning approach is intended to promote cohesion and peer acceptance in heterogeneous groups ( Rzoska and Ward, 1991 ), previous studies indicate that challenges in group dynamics may lead to unequal participation ( Mulryan, 1992 ; Cohen, 1994 ). Peer-learning behaviours may impact students’ problem-solving ( Hwang and Hu, 2013 ) and working in groups with peers who are seen as friends may enhance students’ motivation to learn mathematics ( Deacon and Edwards, 2012 ). With the importance of peer support in mind, this study set out to investigate whether the results of the intervention using the CL approach are associated with students’ peer acceptance and friendships.
The Present Study
In previous research, the CL approach has shown to be a promising approach in teaching and learning mathematics ( Capar and Tarim, 2015 ), but fewer studies have been conducted in whole-class approaches in general and students with SEN in particular ( McMaster and Fuchs, 2002 ). This study aims to contribute to previous research by investigating the effect of CL intervention on students’ mathematical problem-solving in grade 5. With regard to the complexity of mathematical problem-solving ( Lesh and Zawojewski, 2007 ; Degrande et al., 2016 ; Stohlmann and Albarracín, 2016 ), the CL approach in this study was combined with problem-solving principles pertaining to three underlying models of problem-solving—multiplication/division, geometry, and proportionality. Furthermore, considering the importance of peer support in problem-solving in small groups ( Mulryan, 1992 ; Cohen, 1994 ; Hwang and Hu, 2013 ), the study investigated how peer acceptance and friendships were associated with the effect of the CL approach on students’ problem-solving abilities. The study aimed to find answers to the following research questions:
a) What is the effect of CL approach on students’ problem-solving in mathematics?
b) Are social acceptance and friendship associated with the effect of CL on students’ problem-solving in mathematics?
Participants
The participants were 958 students in grade 5 and their teachers. According to power analyses prior to the start of the study, 1,020 students and 51 classes were required, with an expected effect size of 0.30 and power of 80%, provided that there are 20 students per class and intraclass correlation is 0.10. An invitation to participate in the project was sent to teachers in five municipalities via e-mail. Furthermore, the information was posted on the website of Uppsala university and distributed via Facebook interest groups. As shown in Figure 1 , teachers of 1,165 students agreed to participate in the study, but informed consent was obtained only for 958 students (463 in the intervention and 495 in the control group). Further attrition occurred at pre- and post-measurement, resulting in 581 students’ tests as a basis for analyses (269 in the intervention and 312 in the control group). Fewer students (n = 493) were finally included in the analyses of the association of students’ social acceptance and friendships and the effect of CL on students’ mathematical problem-solving (219 in the intervention and 274 in the control group). The reasons for attrition included teacher drop out due to sick leave or personal circumstances (two teachers in the control group and five teachers in the intervention group). Furthermore, some students were sick on the day of data collection and some teachers did not send the test results to the researchers.
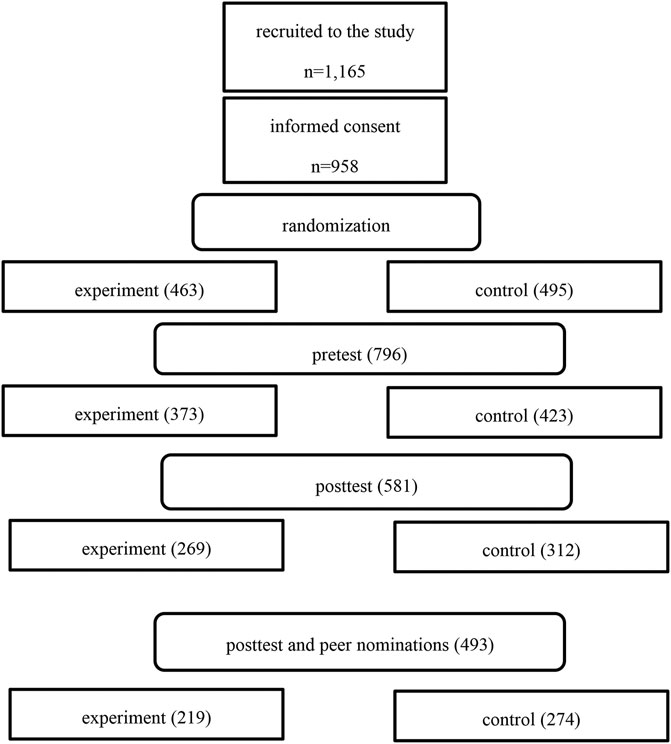
FIGURE 1 . Flow chart for participants included in data collection and data analysis.
As seen in Table 1 , classes in both intervention and control groups included 27 students on average. For 75% of the classes, there were 33–36% of students with SEN. In Sweden, no formal medical diagnosis is required for the identification of students with SEN. It is teachers and school welfare teams who decide students’ need for extra adaptations or special support ( Swedish National Educational Agency, 2014 ). The information on individual students’ type of SEN could not be obtained due to regulations on the protection of information about individuals ( SFS 2009 ). Therefore, the information on the number of students with SEN on class level was obtained through teacher reports.

TABLE 1 . Background characteristics of classes and teachers in intervention and control groups.
Intervention
The intervention using the CL approach lasted for 15 weeks and the teachers worked with the CL approach three to four lessons per week. First, the teachers participated in two-days training on the CL approach, using an especially elaborated CL manual ( Klang et al., 2018 ). The training focused on the five principles of the CL approach (positive interdependence, individual accountability, explicit instruction in social skills, promotive interaction, and group processing). Following the training, the teachers introduced the CL approach in their classes and focused on group-building activities for 7 weeks. Then, 2 days of training were provided to teachers, in which the CL approach was embedded in activities in mathematical problem-solving and reading comprehension. Educational materials containing mathematical problems in the areas of multiplication and division, geometry, and proportionality were distributed to the teachers ( Karlsson and Kilborn, 2018a ). In addition to the specific problems, adapted for the CL approach, the educational materials contained guidance for the teachers, in which problem-solving principles ( Pólya, 1948 ) were presented as steps in problem-solving. Following the training, the teachers applied the CL approach in mathematical problem-solving lessons for 8 weeks.
Solving a problem is a matter of goal-oriented reasoning, starting from the understanding of the problem to devising its solution by using known mathematical models. This presupposes that the current problem is chosen from a known context ( Stillman et al., 2008 ; Zawojewski, 2010 ). This differs from the problem-solving of the textbooks, which is based on an aim to train already known formulas and procedures ( Hamilton, 2007 ). Moreover, it is important that students learn modelling according to their current abilities and conditions ( Russel, 1991 ).
In order to create similar conditions in the experiment group and the control group, the teachers were supposed to use the same educational material ( Karlsson and Kilborn, 2018a ; Karlsson and Kilborn, 2018b ), written in light of the specified view of problem-solving. The educational material is divided into three areas—multiplication/division, geometry, and proportionality—and begins with a short teachers’ guide, where a view of problem solving is presented, which is based on the work of Polya (1948) and Lester and Cai (2016) . The tasks are constructed in such a way that conceptual knowledge was in focus, not formulas and procedural knowledge.
Implementation of the Intervention
To ensure the implementation of the intervention, the researchers visited each teachers’ classroom twice during the two phases of the intervention period, as described above. During each visit, the researchers observed the lesson, using a checklist comprising the five principles of the CL approach. After the lesson, the researchers gave written and oral feedback to each teacher. As seen in Table 1 , in 18 of the 23 classes, the teachers implemented the intervention in accordance with the principles of CL. In addition, the teachers were asked to report on the use of the CL approach in their teaching and the use of problem-solving activities embedding CL during the intervention period. As shown in Table 1 , teachers in only 11 of 23 classes reported using the CL approach and problem-solving activities embedded in the CL approach at least once a week.
Control Group
The teachers in the control group received 2 days of instruction in enhancing students’ problem-solving and reading comprehension. The teachers were also supported with educational materials including mathematical problems Karlsson and Kilborn (2018b) and problem-solving principles ( Pólya, 1948 ). However, none of the activities during training or in educational materials included the CL approach. As seen in Table 1 , only 10 of 25 teachers reported devoting at least one lesson per week to mathematical problem-solving.
Tests of Mathematical Problem-Solving
Tests of mathematical problem-solving were administered before and after the intervention, which lasted for 15 weeks. The tests were focused on the models of multiplication/division, geometry, and proportionality. The three models were chosen based on the syllabus of the subject of mathematics in grades 4 to 6 in the Swedish National Curriculum ( Swedish National Educational Agency, 2018 ). In addition, the intention was to create a variation of types of problems to solve. For each of these three models, there were two tests, a pre-test and a post-test. Each test contained three tasks with increasing difficulty ( Supplementary Appendix SA ).
The tests of multiplication and division (Ma1) were chosen from different contexts and began with a one-step problem, while the following two tasks were multi-step problems. Concerning multiplication, many students in grade 5 still understand multiplication as repeated addition, causing significant problems, as this conception is not applicable to multiplication beyond natural numbers ( Verschaffel et al., 2007 ). This might be a hindrance in developing multiplicative reasoning ( Barmby et al., 2009 ). The multi-step problems in this study were constructed to support the students in multiplicative reasoning.
Concerning the geometry tests (Ma2), it was important to consider a paradigm shift concerning geometry in education that occurred in the mid-20th century, when strict Euclidean geometry gave way to other aspects of geometry like symmetry, transformation, and patterns. van Hiele (1986) prepared a new taxonomy for geometry in five steps, from a visual to a logical level. Therefore, in the tests there was a focus on properties of quadrangles and triangles, and how to determine areas by reorganising figures into new patterns. This means that structure was more important than formulas.
The construction of tests of proportionality (M3) was more complicated. Firstly, tasks on proportionality can be found in many different contexts, such as prescriptions, scales, speeds, discounts, interest, etc. Secondly, the mathematical model is complex and requires good knowledge of rational numbers and ratios ( Lesh et al., 1988 ). It also requires a developed view of multiplication, useful in operations with real numbers, not only as repeated addition, an operation limited to natural numbers ( Lybeck, 1981 ; Degrande et al., 2016 ). A linear structure of multiplication as repeated addition leads to limitations in terms of generalization and development of the concept of multiplication. This became evident in a study carried out in a Swedish context ( Karlsson and Kilborn, 2018c ). Proportionality can be expressed as a/b = c/d or as a/b = k. The latter can also be expressed as a = b∙k, where k is a constant that determines the relationship between a and b. Common examples of k are speed (km/h), scale, and interest (%). An important pre-knowledge in order to deal with proportions is to master fractions as equivalence classes like 1/3 = 2/6 = 3/9 = 4/12 = 5/15 = 6/18 = 7/21 = 8/24 … ( Karlsson and Kilborn, 2020 ). It was important to take all these aspects into account when constructing and assessing the solutions of the tasks.
The tests were graded by an experienced teacher of mathematics (4 th author) and two students in their final year of teacher training. Prior to grading, acceptable levels of inter-rater reliability were achieved by independent rating of students’ solutions and discussions in which differences between the graders were resolved. Each student response was to be assigned one point when it contained a correct answer and two points when the student provided argumentation for the correct answer and elaborated on explanation of his or her solution. The assessment was thus based on quality aspects with a focus on conceptual knowledge. As each subtest contained three questions, it generated three student solutions. So, scores for each subtest ranged from 0 to 6 points and for the total scores from 0 to 18 points. To ascertain that pre- and post-tests were equivalent in degree of difficulty, the tests were administered to an additional sample of 169 students in grade 5. Test for each model was conducted separately, as students participated in pre- and post-test for each model during the same lesson. The order of tests was switched for half of the students in order to avoid the effect of the order in which the pre- and post-tests were presented. Correlation between students’ performance on pre- and post-test was .39 ( p < 0.000) for tests of multiplication/division; .48 ( p < 0.000) for tests of geometry; and .56 ( p < 0.000) for tests of proportionality. Thus, the degree of difficulty may have differed between pre- and post-test.
Measures of Peer Acceptance and Friendships
To investigate students’ peer acceptance and friendships, peer nominations rated pre- and post-intervention were used. Students were asked to nominate peers who they preferred to work in groups with and who they preferred to be friends with. Negative peer nominations were avoided due to ethical considerations raised by teachers and parents ( Child and Nind, 2013 ). Unlimited nominations were used, as these are considered to have high ecological validity ( Cillessen and Marks, 2017 ). Peer nominations were used as a measure of social acceptance, and reciprocated nominations were used as a measure of friendship. The number of nominations for each student were aggregated and divided by the number of nominators to create a proportion of nominations for each student ( Velásquez et al., 2013 ).
Statistical Analyses
Multilevel regression analyses were conducted in R, lme4 package Bates et al. (2015) to account for nestedness in the data. Students’ classroom belonging was considered as a level 2 variable. First, we used a model in which students’ results on tests of problem-solving were studied as a function of time (pre- and post) and group belonging (intervention and control group). Second, the same model was applied to subgroups of students who performed above and below median at pre-test, to explore whether the CL intervention had a differential effect on student performance. In this second model, the results for subgroups of students could not be obtained for geometry tests for subgroup below median and for tests of proportionality for subgroup above median. A possible reason for this must have been the skewed distribution of the students in these subgroups. Therefore, another model was applied that investigated students’ performances in math at both pre- and post-test as a function of group belonging. Third, the students’ scores on social acceptance and friendships were added as an interaction term to the first model. In our previous study, students’ social acceptance changed as a result of the same CL intervention ( Klang et al., 2020 ).
The assumptions for the multilevel regression were assured during the analyses ( Snijders and Bosker, 2012 ). The assumption of normality of residuals were met, as controlled by visual inspection of quantile-quantile plots. For subgroups, however, the plotted residuals deviated somewhat from the straight line. The number of outliers, which had a studentized residual value greater than ±3, varied from 0 to 5, but none of the outliers had a Cook’s distance value larger than 1. The assumption of multicollinearity was met, as the variance inflation factors (VIF) did not exceed a value of 10. Before the analyses, the cases with missing data were deleted listwise.
What Is the Effect of the CL Approach on Students’ Problem-Solving in Mathematics?
As seen in the regression coefficients in Table 2 , the CL intervention had a significant effect on students’ mathematical problem-solving total scores and students’ scores in problem solving in geometry (Ma2). Judging by mean values, students in the intervention group appeared to have low scores on problem-solving in geometry but reached the levels of problem-solving of the control group by the end of the intervention. The intervention did not have a significant effect on students’ performance in problem-solving related to models of multiplication/division and proportionality.
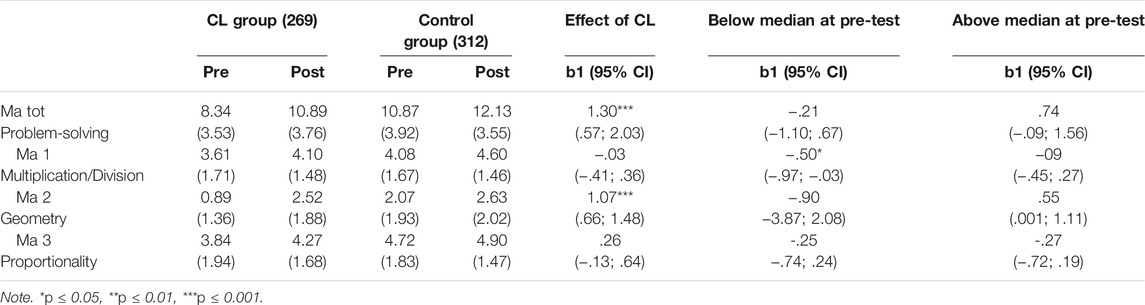
TABLE 2 . Mean scores (standard deviation in parentheses) and unstandardized multilevel regression estimates for tests of mathematical problem-solving.
The question is, however, whether CL intervention affected students with different pre-test scores differently. Table 2 includes the regression coefficients for subgroups of students who performed below and above median at pre-test. As seen in the table, the CL approach did not have a significant effect on students’ problem-solving, when the sample was divided into these subgroups. A small negative effect was found for intervention group in comparison to control group, but confidence intervals (CI) for the effect indicate that it was not significant.
Is Social Acceptance and Friendships Associated With the Effect of CL on Students’ Problem-Solving in Mathematics?
As seen in Table 3 , students’ peer acceptance and friendship at pre-test were significantly associated with the effect of the CL approach on students’ mathematical problem-solving scores. Changes in students’ peer acceptance and friendships were not significantly associated with the effect of the CL approach on students’ mathematical problem-solving. Consequently, it can be concluded that being nominated by one’s peers and having friends at the start of the intervention may be an important factor when participation in group work, structured in accordance with the CL approach, leads to gains in mathematical problem-solving.
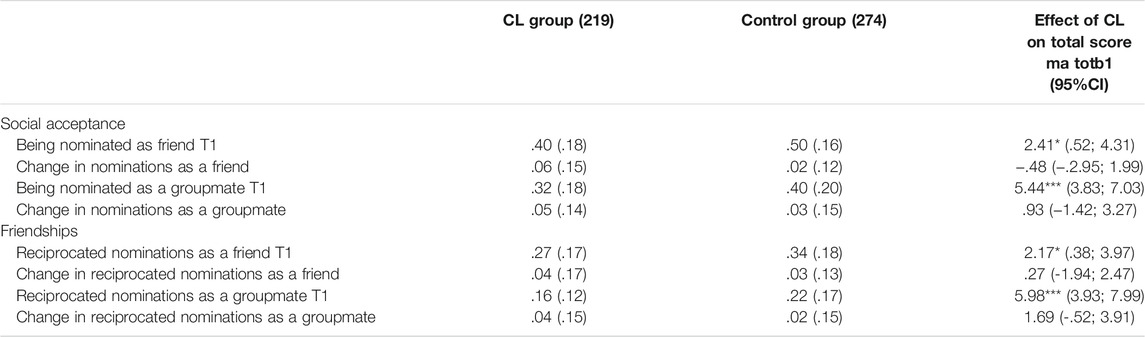
TABLE 3 . Mean scores (standard deviation in parentheses) and unstandardized multilevel regression estimates for tests of mathematical problem-solving, including scores of social acceptance and friendship in the model.
In light of the limited number of studies on the effects of CL on students’ problem-solving in whole classrooms ( Capar and Tarim, 2015 ), and for students with SEN in particular ( McMaster and Fuchs, 2002 ), this study sought to investigate whether the CL approach embedded in problem-solving activities has an effect on students’ problem-solving in heterogeneous classrooms. The need for the study was justified by the challenge of providing equitable mathematics instruction to heterogeneous student populations ( OECD, 2019 ). Small group instructional approaches as CL are considered as promising approaches in this regard ( Kunsch et al., 2007 ). The results showed a significant effect of the CL approach on students’ problem-solving in geometry and total problem-solving scores. In addition, with regard to the importance of peer support in problem-solving ( Deacon and Edwards, 2012 ; Hwang and Hu, 2013 ), the study explored whether the effect of CL on students’ problem-solving was associated with students’ social acceptance and friendships. The results showed that students’ peer acceptance and friendships at pre-test were significantly associated with the effect of the CL approach, while change in students’ peer acceptance and friendships from pre- to post-test was not.
The results of the study confirm previous research on the effect of the CL approach on students’ mathematical achievement ( Capar and Tarim, 2015 ). The specific contribution of the study is that it was conducted in classrooms, 75% of which were composed of 33–36% of students with SEN. Thus, while a previous review revealed inconclusive findings on the effects of CL on student achievement ( McMaster and Fuchs, 2002 ), the current study adds to the evidence of the effect of the CL approach in heterogeneous classrooms, in which students with special needs are educated alongside with their peers. In a small group setting, the students have opportunities to discuss their ideas of solutions to the problem at hand, providing explanations and clarifications, thus enhancing their understanding of problem-solving ( Yackel et al., 1991 ; Webb and Mastergeorge, 2003 ).
In this study, in accordance with previous research on mathematical problem-solving ( Lesh and Zawojewski, 2007 ; Degrande et al., 2016 ; Stohlmann and Albarracín, 2016 ), the CL approach was combined with training in problem-solving principles Pólya (1948) and educational materials, providing support in instruction in underlying mathematical models. The intention of the study was to provide evidence for the effectiveness of the CL approach above instruction in problem-solving, as problem-solving materials were accessible to teachers of both the intervention and control groups. However, due to implementation challenges, not all teachers in the intervention and control groups reported using educational materials and training as expected. Thus, it is not possible to draw conclusions of the effectiveness of the CL approach alone. However, in everyday classroom instruction it may be difficult to separate the content of instruction from the activities that are used to mediate this content ( Doerr and Tripp, 1999 ; Gravemeijer, 1999 ).
Furthermore, for successful instruction in mathematical problem-solving, scaffolding for content needs to be combined with scaffolding for dialogue ( Kazak et al., 2015 ). From a dialogical perspective ( Wegerif, 2011 ), students may need scaffolding in new ways of thinking, involving questioning their understandings and providing arguments for their solutions, in order to create dialogic spaces in which different solutions are voiced and negotiated. In this study, small group instruction through CL approach aimed to support discussions in small groups, but the study relies solely on quantitative measures of students’ mathematical performance. Video-recordings of students’ discussions may have yielded important insights into the dialogic relationships that arose in group discussions.
Despite the positive findings of the CL approach on students’ problem-solving, it is important to note that the intervention did not have an effect on students’ problem-solving pertaining to models of multiplication/division and proportionality. Although CL is assumed to be a promising instructional approach, the number of studies on its effect on students’ mathematical achievement is still limited ( Capar and Tarim, 2015 ). Thus, further research is needed on how CL intervention can be designed to promote students’ problem-solving in other areas of mathematics.
The results of this study show that the effect of the CL intervention on students’ problem-solving was associated with students’ initial scores of social acceptance and friendships. Thus, it is possible to assume that students who were popular among their classmates and had friends at the start of the intervention also made greater gains in mathematical problem-solving as a result of the CL intervention. This finding is in line with Deacon and Edwards’ study of the importance of friendships for students’ motivation to learn mathematics in small groups ( Deacon and Edwards, 2012 ). However, the effect of the CL intervention was not associated with change in students’ social acceptance and friendship scores. These results indicate that students who were nominated by a greater number of students and who received a greater number of friends did not benefit to a great extent from the CL intervention. With regard to previously reported inequalities in cooperation in heterogeneous groups ( Cohen, 1994 ; Mulryan, 1992 ; Langer Osuna, 2016 ) and the importance of peer behaviours for problem-solving ( Hwang and Hu, 2013 ), teachers should consider creating inclusive norms and supportive peer relationships when using the CL approach. The demands of solving complex problems may create negative emotions and uncertainty ( Hannula, 2015 ; Jordan and McDaniel, 2014 ), and peer support may be essential in such situations.
Limitations
The conclusions from the study must be interpreted with caution, due to a number of limitations. First, due to the regulation of protection of individuals ( SFS 2009 ), the researchers could not get information on type of SEN for individual students, which limited the possibilities of the study for investigating the effects of the CL approach for these students. Second, not all teachers in the intervention group implemented the CL approach embedded in problem-solving activities and not all teachers in the control group reported using educational materials on problem-solving. The insufficient levels of implementation pose a significant challenge to the internal validity of the study. Third, the additional investigation to explore the equivalence in difficulty between pre- and post-test, including 169 students, revealed weak to moderate correlation in students’ performance scores, which may indicate challenges to the internal validity of the study.
Implications
The results of the study have some implications for practice. Based on the results of the significant effect of the CL intervention on students’ problem-solving, the CL approach appears to be a promising instructional approach in promoting students’ problem-solving. However, as the results of the CL approach were not significant for all subtests of problem-solving, and due to insufficient levels of implementation, it is not possible to conclude on the importance of the CL intervention for students’ problem-solving. Furthermore, it appears to be important to create opportunities for peer contacts and friendships when the CL approach is used in mathematical problem-solving activities.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics Statement
The studies involving human participants were reviewed and approved by the Uppsala Ethical Regional Committee, Dnr. 2017/372. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.
Author Contributions
NiK was responsible for the project, and participated in data collection and data analyses. NaK and WK were responsible for intervention with special focus on the educational materials and tests in mathematical problem-solving. PE participated in the planning of the study and the data analyses, including coordinating analyses of students’ tests. MK participated in the designing and planning the study as well as data collection and data analyses.
The project was funded by the Swedish Research Council under Grant 2016-04,679.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We would like to express our gratitude to teachers who participated in the project.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2021.710296/full#supplementary-material
Barmby, P., Harries, T., Higgins, S., and Suggate, J. (2009). The array representation and primary children's understanding and reasoning in multiplication. Educ. Stud. Math. 70 (3), 217–241. doi:10.1007/s10649-008-914510.1007/s10649-008-9145-1
CrossRef Full Text | Google Scholar
Bates, D., Mächler, M., Bolker, B., and Walker, S. (2015). Fitting Linear Mixed-Effects Models Usinglme4. J. Stat. Soft. 67 (1), 1–48. doi:10.18637/jss.v067.i01
Capar, G., and Tarim, K. (2015). Efficacy of the cooperative learning method on mathematics achievement and attitude: A meta-analysis research. Educ. Sci-theor Pract. 15 (2), 553–559. doi:10.12738/estp.2015.2.2098
Child, S., and Nind, M. (2013). Sociometric methods and difference: A force for good - or yet more harm. Disabil. Soc. 28 (7), 1012–1023. doi:10.1080/09687599.2012.741517
Cillessen, A. H. N., and Marks, P. E. L. (2017). Methodological choices in peer nomination research. New Dir. Child Adolesc. Dev. 2017, 21–44. doi:10.1002/cad.20206
PubMed Abstract | CrossRef Full Text | Google Scholar
Clarke, B., Cheeseman, J., and Clarke, D. (2006). The mathematical knowledge and understanding young children bring to school. Math. Ed. Res. J. 18 (1), 78–102. doi:10.1007/bf03217430
Cohen, E. G. (1994). Restructuring the classroom: Conditions for productive small groups. Rev. Educ. Res. 64 (1), 1–35. doi:10.3102/00346543064001001
Davidson, N., and Major, C. H. (2014). Boundary crossings: Cooperative learning, collaborative learning, and problem-based learning. J. Excell. Coll. Teach. 25 (3-4), 7.
Google Scholar
Davydov, V. V. (2008). Problems of developmental instructions. A Theoretical and experimental psychological study . New York: Nova Science Publishers, Inc .
Deacon, D., and Edwards, J. (2012). Influences of friendship groupings on motivation for mathematics learning in secondary classrooms. Proc. Br. Soc. Res. into Learn. Math. 32 (2), 22–27.
Degrande, T., Verschaffel, L., and van Dooren, W. (2016). “Proportional word problem solving through a modeling lens: a half-empty or half-full glass?,” in Posing and Solving Mathematical Problems, Research in Mathematics Education . Editor P. Felmer.
Doerr, H. M., and Tripp, J. S. (1999). Understanding how students develop mathematical models. Math. Thinking Learn. 1 (3), 231–254. doi:10.1207/s15327833mtl0103_3
Fujita, T., Doney, J., and Wegerif, R. (2019). Students' collaborative decision-making processes in defining and classifying quadrilaterals: a semiotic/dialogic approach. Educ. Stud. Math. 101 (3), 341–356. doi:10.1007/s10649-019-09892-9
Gillies, R. (2016). Cooperative learning: Review of research and practice. Ajte 41 (3), 39–54. doi:10.14221/ajte.2016v41n3.3
Gravemeijer, K. (1999). How Emergent Models May Foster the Constitution of Formal Mathematics. Math. Thinking Learn. 1 (2), 155–177. doi:10.1207/s15327833mtl0102_4
Gravemeijer, K., Stephan, M., Julie, C., Lin, F.-L., and Ohtani, M. (2017). What mathematics education may prepare students for the society of the future? Int. J. Sci. Math. Educ. 15 (S1), 105–123. doi:10.1007/s10763-017-9814-6
Hamilton, E. (2007). “What changes are needed in the kind of problem-solving situations where mathematical thinking is needed beyond school?,” in Foundations for the Future in Mathematics Education . Editors R. Lesh, E. Hamilton, and Kaput (Mahwah, NJ: Lawrence Erlbaum ), 1–6.
Hannula, M. S. (2015). “Emotions in problem solving,” in Selected Regular Lectures from the 12 th International Congress on Mathematical Education . Editor S. J. Cho. doi:10.1007/978-3-319-17187-6_16
Hwang, W.-Y., and Hu, S.-S. (2013). Analysis of peer learning behaviors using multiple representations in virtual reality and their impacts on geometry problem solving. Comput. Edu. 62, 308–319. doi:10.1016/j.compedu.2012.10.005
Johnson, D. W., Johnson, R. T., and Johnson Holubec, E. (2009). Circle of Learning: Cooperation in the Classroom . Gurgaon: Interaction Book Company .
Johnson, D. W., Johnson, R. T., and Johnson Holubec, E. (1993). Cooperation in the Classroom . Gurgaon: Interaction Book Company .
Jordan, M. E., and McDaniel, R. R. (2014). Managing uncertainty during collaborative problem solving in elementary school teams: The role of peer influence in robotics engineering activity. J. Learn. Sci. 23 (4), 490–536. doi:10.1080/10508406.2014.896254
Karlsson, N., and Kilborn, W. (2018a). Inclusion through learning in group: tasks for problem-solving. [Inkludering genom lärande i grupp: uppgifter för problemlösning] . Uppsala: Uppsala University .
Karlsson, N., and Kilborn, W. (2018c). It's enough if they understand it. A study of teachers 'and students' perceptions of multiplication and the multiplication table [Det räcker om de förstår den. En studie av lärares och elevers uppfattningar om multiplikation och multiplikationstabellen]. Södertörn Stud. Higher Educ. , 175.
Karlsson, N., and Kilborn, W. (2018b). Tasks for problem-solving in mathematics. [Uppgifter för problemlösning i matematik] . Uppsala: Uppsala University .
Karlsson, N., and Kilborn, W. (2020). “Teacher’s and student’s perception of rational numbers,” in Interim Proceedings of the 44 th Conference of the International Group for the Psychology of Mathematics Education , Interim Vol., Research Reports . Editors M. Inprasitha, N. Changsri, and N. Boonsena (Khon Kaen, Thailand: PME ), 291–297.
Kazak, S., Wegerif, R., and Fujita, T. (2015). Combining scaffolding for content and scaffolding for dialogue to support conceptual breakthroughs in understanding probability. ZDM Math. Edu. 47 (7), 1269–1283. doi:10.1007/s11858-015-0720-5
Klang, N., Olsson, I., Wilder, J., Lindqvist, G., Fohlin, N., and Nilholm, C. (2020). A cooperative learning intervention to promote social inclusion in heterogeneous classrooms. Front. Psychol. 11, 586489. doi:10.3389/fpsyg.2020.586489
Klang, N., Fohlin, N., and Stoddard, M. (2018). Inclusion through learning in group: cooperative learning [Inkludering genom lärande i grupp: kooperativt lärande] . Uppsala: Uppsala University .
Kunsch, C. A., Jitendra, A. K., and Sood, S. (2007). The effects of peer-mediated instruction in mathematics for students with learning problems: A research synthesis. Learn. Disabil Res Pract 22 (1), 1–12. doi:10.1111/j.1540-5826.2007.00226.x
Langer-Osuna, J. M. (2016). The social construction of authority among peers and its implications for collaborative mathematics problem solving. Math. Thinking Learn. 18 (2), 107–124. doi:10.1080/10986065.2016.1148529
Lein, A. E., Jitendra, A. K., and Harwell, M. R. (2020). Effectiveness of mathematical word problem solving interventions for students with learning disabilities and/or mathematics difficulties: A meta-analysis. J. Educ. Psychol. 112 (7), 1388–1408. doi:10.1037/edu0000453
Lesh, R., and Doerr, H. (2003). Beyond Constructivism: Models and Modeling Perspectives on Mathematics Problem Solving, Learning and Teaching . Mahwah, NJ: Erlbaum .
Lesh, R., Post, T., and Behr, M. (1988). “Proportional reasoning,” in Number Concepts and Operations in the Middle Grades . Editors J. Hiebert, and M. Behr (Hillsdale, N.J.: Lawrence Erlbaum Associates ), 93–118.
Lesh, R., and Zawojewski, (2007). “Problem solving and modeling,” in Second Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics . Editor L. F. K. Lester (Charlotte, NC: Information Age Pub ), vol. 2.
Lester, F. K., and Cai, J. (2016). “Can mathematical problem solving be taught? Preliminary answers from 30 years of research,” in Posing and Solving Mathematical Problems. Research in Mathematics Education .
Lybeck, L. (1981). “Archimedes in the classroom. [Arkimedes i klassen],” in Göteborg Studies in Educational Sciences (Göteborg: Acta Universitatis Gotoburgensis ), 37.
McMaster, K. N., and Fuchs, D. (2002). Effects of Cooperative Learning on the Academic Achievement of Students with Learning Disabilities: An Update of Tateyama-Sniezek's Review. Learn. Disabil Res Pract 17 (2), 107–117. doi:10.1111/1540-5826.00037
Mercer, N., and Sams, C. (2006). Teaching children how to use language to solve maths problems. Lang. Edu. 20 (6), 507–528. doi:10.2167/le678.0
Montague, M., Krawec, J., Enders, C., and Dietz, S. (2014). The effects of cognitive strategy instruction on math problem solving of middle-school students of varying ability. J. Educ. Psychol. 106 (2), 469–481. doi:10.1037/a0035176
Mousoulides, N., Pittalis, M., Christou, C., and Stiraman, B. (2010). “Tracing students’ modeling processes in school,” in Modeling Students’ Mathematical Modeling Competencies . Editor R. Lesh (Berlin, Germany: Springer Science+Business Media ). doi:10.1007/978-1-4419-0561-1_10
Mulryan, C. M. (1992). Student passivity during cooperative small groups in mathematics. J. Educ. Res. 85 (5), 261–273. doi:10.1080/00220671.1992.9941126
OECD (2019). PISA 2018 Results (Volume I): What Students Know and Can Do . Paris: OECD Publishing . doi:10.1787/5f07c754-en
CrossRef Full Text
Pólya, G. (1948). How to Solve it: A New Aspect of Mathematical Method . Princeton, N.J.: Princeton University Press .
Russel, S. J. (1991). “Counting noses and scary things: Children construct their ideas about data,” in Proceedings of the Third International Conference on the Teaching of Statistics . Editor I. D. Vere-Jones (Dunedin, NZ: University of Otago ), 141–164., s.
Rzoska, K. M., and Ward, C. (1991). The effects of cooperative and competitive learning methods on the mathematics achievement, attitudes toward school, self-concepts and friendship choices of Maori, Pakeha and Samoan Children. New Zealand J. Psychol. 20 (1), 17–24.
Schoenfeld, A. H. (2016). Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics (reprint). J. Edu. 196 (2), 1–38. doi:10.1177/002205741619600202
SFS 2009:400. Offentlighets- och sekretesslag. [Law on Publicity and confidentiality] . Retrieved from https://www.riksdagen.se/sv/dokument-lagar/dokument/svensk-forfattningssamling/offentlighets--och-sekretesslag-2009400_sfs-2009-400 on the 14th of October .
Snijders, T. A. B., and Bosker, R. J. (2012). Multilevel Analysis. An Introduction to Basic and Advanced Multilevel Modeling . 2nd Ed. London: SAGE .
Stillman, G., Brown, J., and Galbraith, P. (2008). Research into the teaching and learning of applications and modelling in Australasia. In H. Forgasz, A. Barkatas, A. Bishop, B. Clarke, S. Keast, W. Seah, and P. Sullivan (red.), Research in Mathematics Education in Australasiae , 2004-2007 , p.141–164. Rotterdam: Sense Publishers .doi:10.1163/9789087905019_009
Stohlmann, M. S., and Albarracín, L. (2016). What is known about elementary grades mathematical modelling. Edu. Res. Int. 2016, 1–9. doi:10.1155/2016/5240683
Swedish National Educational Agency (2014). Support measures in education – on leadership and incentives, extra adaptations and special support [Stödinsatser I utbildningen – om ledning och stimulans, extra anpassningar och särskilt stöd] . Stockholm: Swedish National Agency of Education .
Swedish National Educational Agency (2018). Syllabus for the subject of mathematics in compulsory school . Retrieved from https://www.skolverket.se/undervisning/grundskolan/laroplan-och-kursplaner-for-grundskolan/laroplan-lgr11-for-grundskolan-samt-for-forskoleklassen-och-fritidshemmet?url=-996270488%2Fcompulsorycw%2Fjsp%2Fsubject.htm%3FsubjectCode%3DGRGRMAT01%26tos%3Dgr&sv.url=12.5dfee44715d35a5cdfa219f ( on the 32nd of July, 2021).
van Hiele, P. (1986). Structure and Insight. A Theory of Mathematics Education . London: Academic Press .
Velásquez, A. M., Bukowski, W. M., and Saldarriaga, L. M. (2013). Adjusting for Group Size Effects in Peer Nomination Data. Soc. Dev. 22 (4), a–n. doi:10.1111/sode.12029
Verschaffel, L., Greer, B., and De Corte, E. (2007). “Whole number concepts and operations,” in Second Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics . Editor F. K. Lester (Charlotte, NC: Information Age Pub ), 557–628.
Webb, N. M., and Mastergeorge, A. (2003). Promoting effective helping behavior in peer-directed groups. Int. J. Educ. Res. 39 (1), 73–97. doi:10.1016/S0883-0355(03)00074-0
Wegerif, R. (2011). “Theories of Learning and Studies of Instructional Practice,” in Theories of learning and studies of instructional Practice. Explorations in the learning sciences, instructional systems and Performance technologies . Editor T. Koschmann (Berlin, Germany: Springer ). doi:10.1007/978-1-4419-7582-9
Yackel, E., Cobb, P., and Wood, T. (1991). Small-group interactions as a source of learning opportunities in second-grade mathematics. J. Res. Math. Edu. 22 (5), 390–408. doi:10.2307/749187
Zawojewski, J. (2010). Problem Solving versus Modeling. In R. Lesch, P. Galbraith, C. R. Haines, and A. Hurford (red.), Modelling student’s mathematical modelling competencies: ICTMA , p. 237–243. New York, NY: Springer .doi:10.1007/978-1-4419-0561-1_20
Keywords: cooperative learning, mathematical problem-solving, intervention, heterogeneous classrooms, hierarchical linear regression analysis
Citation: Klang N, Karlsson N, Kilborn W, Eriksson P and Karlberg M (2021) Mathematical Problem-Solving Through Cooperative Learning—The Importance of Peer Acceptance and Friendships. Front. Educ. 6:710296. doi: 10.3389/feduc.2021.710296
Received: 15 May 2021; Accepted: 09 August 2021; Published: 24 August 2021.
Reviewed by:
Copyright © 2021 Klang, Karlsson, Kilborn, Eriksson and Karlberg. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nina Klang, [email protected]
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Click through the PLOS taxonomy to find articles in your field.
For more information about PLOS Subject Areas, click here .
Loading metrics
Open Access
Peer-reviewed
Research Article
Effects of Mathematics Anxiety and Mathematical Metacognition on Word Problem Solving in Children with and without Mathematical Learning Difficulties
Affiliation Institute of Developmental Psychology, Beijing Normal University, Beijing, P. R. China
* E-mail: [email protected]
- Yinghui Lai,
- Xiaoshuang Zhu,
- Yinghe Chen,

- Published: June 19, 2015
- https://doi.org/10.1371/journal.pone.0130570
- Reader Comments
Mathematics is one of the most objective, logical, and practical academic disciplines. Yet, in addition to cognitive skills, mathematical problem solving also involves affective factors. In the current study, we first investigated effects of mathematics anxiety (MA) and mathematical metacognition on word problem solving (WPS). We tested 224 children (116 boys, M = 10.15 years old, SD = 0.56) with the Mathematics Anxiety Scale for Children, the Chinese Revised-edition Questionnaire of Pupil’s Metacognitive Ability in Mathematics, and WPS tasks. The results indicated that mathematical metacognition mediated the effect of MA on WPS after controlling for IQ. Second, we divided the children into four mathematics achievement groups including high achieving (HA), typical achieving (TA), low achieving (LA), and mathematical learning difficulty (MLD). Because mathematical metacognition and MA predicted mathematics achievement, we compared group differences in metacognition and MA with IQ partialled out. The results showed that children with MLD scored lower in self-image and higher in learning mathematics anxiety (LMA) than the TA and HA children, but not in mathematical evaluation anxiety (MEA). MLD children’s LMA was also higher than that of their LA counterparts. These results provide insight into factors that may mediate poor WPS performance which emerges under pressure in mathematics. These results also suggest that the anxiety during learning mathematics should be taken into account in mathematical learning difficulty interventions.
Citation: Lai Y, Zhu X, Chen Y, Li Y (2015) Effects of Mathematics Anxiety and Mathematical Metacognition on Word Problem Solving in Children with and without Mathematical Learning Difficulties. PLoS ONE 10(6): e0130570. https://doi.org/10.1371/journal.pone.0130570
Editor: Bert De Smedt, University of Leuven, BELGIUM
Received: July 8, 2014; Accepted: May 22, 2015; Published: June 19, 2015
Copyright: © 2015 Lai et al. This is an open access article distributed under the terms of the Creative Commons Attribution License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited
Data Availability: The data of the current manuscript is deposited on Figshare, and may be accessed through the following link: http://dx.doi.org/10.6084/m9.figshare.1344805 .
Funding: The work described in this paper was supported by grants from National Natural Science Foundation of China (31271106) ( http://www.nsfc.gov.cn/nsfc/cen/2014sqsl/index.html ).
Competing interests: The authors have declared that no competing interests exist.
Introduction
Problem solving is “cognitive processing directed at achieving a goal when no solution method is obvious to the problem solver” (p. 287) [ 1 ]. As an important component of mathematical problem solving, Word problem solving (WPS) “involves knowledge about semantic construction and mathematical relations as well as knowledge of basic numerical skills and strategies” (p. 1) [ 2 ]. For example, a word problem often presents a story (e.g. “Xiaoming bought five pencils, and Xiaohong took three of them. How many pencils does Xiaoming have now?”). Learning how to solve word problems has long been difficult for students and has gained attention in the field of mathematical development [ 3 ].
Mathematical problem solving is shaped by affective and cognitive factors [ 4 – 6 ]. Mathematics anxiety (MA) was one of the first affective features which were systematically investigated in the mathematics learning domain [ 7 ]. Richardson and Suinn (p. 551) [ 8 ] define MA as “involving feelings of tension and anxiety that interfere with the manipulating of numbers and the solving of mathematical problems in a wide variety of ordinary life and academic situations.” The Mathematics Anxiety Rating Scale (MARS) measures MA in adults and is popular among educators [ 9 ]. The Mathematics Anxiety Scale for Children (MASC) [ 10 ] is developed based on the MARS, and used to measure MA in children. MA is an important factor that impedes one’s mathematical problem solving success [ 11 ]. High levels of anxiety were found to be related to less efficient mathematical problem solving [ 6 ].
In recent years, researchers have made concerted efforts to identify and understand the cognitive mechanisms that underlie children’s word problem solving. Such mechanisms include working memory, processing speed, executive functioning, etc. (e.g. [ 12 – 14 ]) Among various cognitive resources which have been theoretically and empirically investigated in relation to WPS, early research findings have highlighted that metacognition develops alongside general cognitive ability and might be even more effective than general aptitude in predicting mathematics performance [ 15 – 17 ].
The classical concept of metacognition consists of three primary components, i.e. metacognitive knowledge, metacognitive experience, and metacognitive skills [ 18 ]. Here, we used Panaoura and Philippou’s concepts [ 19 ]. These concepts were consistent with the scale that used to measure mathematical metacognition in the present study. They [ 19 , 20 ] considered metacognition as mainly indicative of awareness (e.g. self-image) and the monitoring of one’s own cognitive system and its functioning (e.g. self-regulation). As a component of metacognitive knowledge, self-image concerns personal strengths and limitations relative to the abilities of others. Self-image-related terms include self-consciousness and self-evaluation (e.g. pupils’ beliefs about, and self-efficacy with respect to, their abilities) [ 19 , 20 ]. Characterized by the processes of coordinating and steering cognition, self-regulation reflects the ability to strategically use cognitive knowledge to achieve cognitive goals, particularly when cognitive obstacles need to be overcome [ 19 , 21 ]. They also suggested that strategies and motivation are two more dimensions of metacognitive ability, although self-image and self-regulation had a relatively strong relationship with metacognitive performance [ 19 ]. Strategies concerned the approaches pupils used in order to monitor the problem solving process. Using strategies is an important metacognitive skill. Finally, motivation refers to eliciting pupils’ beliefs about their efforts, about their will on their performance, and about the impact of their parents and teachers. Motivation is an important energizing factor of metacognition and can activate the self-regulation process.
A number of studies (e.g. [ 22 – 24 ]) have explored the effect of metacognition on mathematical problem solving. The meta-skills of children in grades 3 and 4 are strongly related to their numerical and geometrical problem solving abilities [ 22 ], and metacognitive ability also predicts performance in a WPS task [ 21 , 24 ]. Moreover, metacognition can be trained to improve WPS ability [ 25 , 26 ].
In summary, metacognition and MA are important cognitive and affective variables that are related to students’ mathematical performances and mathematical problem solving. What is not so clear is how MA and metacognition to be related to mathematics problem solving performance. Some research supports the conclusion that MA may impede mathematics performance by affecting cognitive process [ 27 – 29 ], but only a few studies have explored the relationship between MA and metacognition in learning: Students who experienced lower anxiety used more metacognitive regulation [ 30 , 31 ]. Children with positive beliefs about social support experienced much less math anxiety than those who did not [ 32 ]. The attribution of failure or success may also be correlated to test anxiety [ 33 ].
Additional research examined the influences of test anxiety and metacognitive word knowledge on reading comprehension performance [ 34 ]. This study found that test anxiety exerts a negative influence on students' metacognitive performances [ 34 ]. Although that experiment focused on the reading domain, its results suggest that metacognition and anxiety are related to performance in other learning domains. Recently, Legg and Locker [ 35 ] measured metacognitive awareness and mathematics anxiety in adults. They hypothesized that individuals with high metacognition and high mathematics anxiety would tend to display poorer mathematics performance. However, the results showed that at high anxiety levels, individuals performed increasingly worse as their metacognition scores decreased, but the performance did not differ at low anxiety levels regardless of the level of metacognition. However, this study did not investigate the holistic relationship between MA, mathematical metacognition, and mathematical problem solving in children.
The relationship between MA, metacognition, and mathematical performance may be multi-directional. For example, MA may lead to poor mathematical performance and vice versa in the longitudinal view. For example, Ma and Xu [ 36 ] used longitudinal panel analysis throughout junior and senior high school. They found prior mathematics achievement to be negatively related to later mathematics anxiety. Jansen et al. [ 37 ] used a computer-adaptive program that adjusted the difficulty of each problem to the individual’s ability level to manipulate children’s experience of success in mathematics. They did not find that experiencing mathematical success affected the level of mathematics anxiety.
In the current study, our purpose was to determine whether (a) mathematics anxiety was negatively related to word problem solving; (b) metacognition could counter this negative relation; or (c) a potential compensatory relationship between metacognition and mathematics anxiety on WPS might exist in children. We tested the path model of “MA-> metacognition-> WPS”, and predicted that metacognition would mediate the relationship between MA and children’s WPS performance.
This path model was to some extent inspired by Kulm’s model for attitude-behavior relationships [ 38 ]. Kulm developed the model as a source of hypotheses for research on attitudes toward mathematics. Hypotheses generated from the model have a general form: “Hypothesis: Given attitude factor A (+ or-), mediating factor B (+ or-), and learning situation C (+ or-), the subject's response will be (positive or negative)” (p. 380) [ 39 ]. Although attitude is not the same as emotional factors, and although aspects of the learning situation, such as children’s perception of the importance of the task were not measured, this model inspired the current investigation of the relationship among negative attitudes and emotion (anxiety about mathematics), mediating factors such as mathematical metacognition, and specific behavioral responses (word problem solving performance).
After investigating the relationship between MA, mathematical metacognition, and WPS, we examined MA and metacognitions of the children at four mathematical learning achievement levels, i.e. high achieving (HA), typical achieving (TA), low achieving (LA), and exhibiting mathematical learning difficulty (MLD).
Mathematical learning difficulty refers to a specific learning deficit that affects the normal acquisition of mathematical skills [ 40 ], and a preponderance of researchers have relied on standardized achievement tests often in combination with measures of intelligence (IQ), to identify MLD [ 41 ]. Although the criteria for identifying children with MLD remain unresolved, researchers commonly use cutoff scores on standardized achievement tests for grouping [ 42 , 43 ]. The current study used standardized mathematics achievement scores to define the four mathematics achievement groups.
A number of studies have shown that MLD children exhibit poorer WPS abilities than do their typical peers [ 23 , 44 , 45 ], and that they are typically poor mathematical problem solvers with restricted cognitive and metacognitive knowledge [ 17 , 46 , 47 ]. MLD children tend to overestimate their mathematics abilities [ 48 , 49 ], to respond impulsively, to fail to verify or evaluate answers, and to settle for the first answer in mathematics tasks [ 45 ]. Moreover, these children use fewer metacognitive strategies and exhibit more nonproductive behaviors than do high achievers, when solving mathematics problems [ 17 , 47 ]. Desoete, Roeyers, and Buysse [ 50 ] argued that above-average mathematical problem solvers did better on metacognitive knowledge (declarative, procedural, and conditional knowledge), skill (prediction, planning, monitoring, and evaluation skills), and attribution to effort than average performers, yet only prediction and evaluation skills can differentiate children with MLD from their average performing peers. Prediction skill was measured by asking children to look at exercises without solving them and to predict whether they would be successful in this task, and evaluation skill refers to self-judging the answers and to the process of arriving at these answers. In some reports [ 50 , 51 ], the majority of children with MLD in Grade 3 made inaccurate predictions and exhibited evaluation skills insufficient for word problems that involve language-related and mental representation tasks.
Furthermore, Rosenzweig et al. [ 17 ] found that the students with learning difficulties (LD) had significantly more nonproductive metacognitive verbalizations than both the low and average achievers on difficult problems. This suggests that students with LD might not have the metacognitive resources (ability to self-monitor, self-instruct, self-question, and self-correct statements/questions directly related to solving the problem) available to apply to the tasks that their low achieving peers have, when confronted with problems that are difficult or that they perceive to be difficult.
In the current study, we distinguished LA from MLD for the following reasons. In some studies, the children in the lowest 25% (the highest cutoff criterion was the 46 th percentile) were placed in the MLD group [ 44 , 52 ]. Some researchers [ 53 ] believe that studies with high cutoffs may actually measure causes of low math achievement rather than causes of MLD. In the longitudinal view, the growth rate of mathematical and math-related skills in these two groups may differ [ 43 ]. Although the current study did not investigate the rate of development of mathematical ability in the two groups, the existence of any difference between the LA group (children who typically scored between the 11 th and 25 th percentiles on mathematical achievement performance) and the MLD group (children who scored at or below the 10 th percentile) related to metacognitive and affective features. We also hoped that these data may offer information on the selection of children for special education or related interventions.
Additional studies have examined the relationship between anxiety and learning difficulty. A meta-analysis of 58 empirical studies on school-aged students revealed that the learning disabled individuals suffered more trait anxiety (defined as general anxiety that is stable over time and across settings) than did their typical peers and that their level of test anxiety was significantly related to reading and mathematics achievement scores [ 54 , 55 ]. According to the definition of mathematical anxiety, MA may both reflect the anxiety aroused in an assumed test situation and the anxiety of children’s ordinary life related to mathematics. Early research [ 38 ] suggested that mathematics anxiety may be positively related to test anxiety and this correlation seemed to be stronger than that of mathematical anxiety and trait anxiety. Recently, Wu et al. [ 56 ] conducted a study in which they did not find any relationship between mathematics anxiety and trait anxiety in second and third graders.
Test anxiety should be measured in certain test situations, and the level of test anxiety may vary with the interval between the time of the test anxiety measurement and the tests. Trait anxiety may be harder to mediate over the short term via metacognition on word problem solving than the other two types of anxiety. Considering these reasons, we focused on mathematical anxiety. Because MLD is likely to show some of the same characteristics as other forms of LD, we therefore expected that the MLD children would experience higher levels of MA and lower levels of mathematical metacognition compared to their typical peers.
Accordingly, the goal of the present research was to answer two specific research questions. First, we investigated the mediating role of mathematical metacognition between the relationship of mathematics anxiety and word problem solving. Second, we divided the children into four mathematical achievement groups, and investigated group differences in mathematical metacognition and mathematics anxiety.
Ethics Statement
This research was approved by the local ethical committee of Beijing Normal University. We obtained informed written consent from the next of kin, caretakers, or guardians on behalf of the minors/children participants involved in the study according to the institutional guidelines of Beijing Normal University.
Participants
We tested 224 10-year-old Chinese children (116 boys, M = 10.15 years old, SD = 0.56) in the fourth grade from three elementary schools. All of the children were of medium socioeconomic status, and their monthly family incomes near or slightly above national averages. We used this sample to test the mediating effect of metacognition. Because the definition of MLD emphasized children of normal intelligence [ 57 ], we excluded 7 children of extremely low non-verbal intelligence score (see below), leaving a sample of 217 for grouping.
The present study focused on the children who met the following criteria across two successive semesters. We considered a child’s standardized mathematical achievement scores consistent, if those scores fell within the same range (specified below) over one year and fell within the 95% confidence intervals for that range throughout the year. We used the consistent mathematical achievement scores across the year for grouping for the following reasons. Some studies [ 52 ] used a single mathematical achievement score to identify the children with MLD, but some others [ 58 ] suggested that these criteria may lead to false positives. In these cases, children will be classified as MLD who in fact typically show improved achievement scores in later grades. More recently, while some studies [ 59 ] still use one mathematical achievement score to identify children with MLD, others [ 60 ] have begun to use longitudinal analysis to collect children’s mathematical achievement scores for two or more years. If children consistently fell into the same range, they were classified into the same group. In this way, although the present study was not a longitudinal study, in order to reduce the possible biases that one mathematical achievement score might have, we used two mathematical achievement scores to classify children.
We used cut-off scores on standardized mathematics achievement tests as a proxy classification. Eighteen children (12 boys) met the criteria for MLD due to mathematical achievement scores that fell at or below the 10 th percentile. We selected this percentile to align with the reported prevalence of MLD (~6–11%) [ 61 , 62 ], and this same cut-off point has been used in many previous investigations [ 51 , 61 , 62 ]. Further, 28 children (11 boys) met the low achieving (LA) criteria, with scores between the 11 th and 25 th percentiles. This range for LA children was used in some research (e.g. [ 63 ]). Although the 25 th percentile was used in some earlier research as the criterion for MLD [ 52 ], that value is inconsistent with reported MLD prevalence and may obscure underlying differences. Additionally, 151 children (78 boys) met typically achieving (TA) criteria, with scores between the 25 th and 95 th percentiles, and 18 children (10 boys) met the high achieving (HA) criteria, with scores above the 95 th percentile. The 95 th percentile was selected for subgrouping HA children because it is a commonly used criterion for school placement in gifted and talented programs, and has been used in earlier studies of HA students [ 64 , 65 ].
Materials and procedure
In January, we first measured children’s verbal intelligence individually. Then, two days later, we assessed children’s non-verbal intelligence in six different classes from three primary schools (the number of children in each class ranged from 33 to 47). We also recorded the pupils’ first final mathematics test performances. One month after the first final mathematics test, their metacognitive abilities in mathematics and their MA scores were recorded. One day later, we administered the WPS test. This time interval may help reduce the possible influence of math achievement task on children’s mathematical metacognition and MA scores. Finally, we collected the second final mathematics test scores in July. All tests except the verbal intelligence test were administered collectively in children’s classrooms. Materials were all presented in Chinese and that quotes from them in this paper are translations.
Intelligence measures.
The present study utilized the Chinese revised edition of Raven’s Standard Progressive Matrices (RPM-CR) [ 66 ] to measure the participants’ non-verbal intelligence. We administered the verbal comprehension subtests of the Wechsler Intelligence Scale for Children-Fourth Edition (WISC-IV; Chinese Version) [ 67 ] to screen the children’s verbal intelligence. The verbal and non-verbal intelligence scores were significantly correlated ( r = .22, p < .01). We excluded 7 children (5 boys, M = 10.19 years old, SD = 0.74) from the initial pool when grouping children into different mathematical achievement levels, because their Raven's matrices scores were in the bottom 5% based on Chinese National Raven’s age-appropriate norms. This exclusion was based on the definition of MLD, which emphasized that those children have normal intelligence [ 57 ]. In addition, we compared both verbal and non-verbal IQ in the four achievement groups using multivariate analysis of variance (Manova). Group differences were significant for both verbal and non-verbal IQ, F (3, 213) = 72.42, p < .001, ƞ p 2 = .51, 1 - β = .98; F (3, 213) = 2.86, p < .05, ƞ p 2 = .04, 1 - β = .68. Because the results showed that these groups were not equivalent in general intelligence, it was necessary to control for IQ score.
Mathematical achievement measures.
We used the scores from the final mathematics examinations over the two previous semesters to evaluate the students’ mathematical achievement. These two tests were developed by the Education Committee of the Haidian District of Beijing, and followed the Chinese mathematics curriculum standards for full-time compulsory education [ 68 ]. Total scores could range from 0 to 100 and examined numerical abilities (30 items, 60 points), visual-spatial abilities (10 items, 10 points) and mathematics application abilities (5 items, 30 points). The internal consistency reliabilities were high (Cronbach’s α = .90, .92, and .88; respectively). The correlation of numerical abilities and visual-spatial abilities was non-significant ( r = .11, p = .13), the correlation of numerical ability and mathematics application abilities was significant ( r = .24, p < .01), and the correlation of visual-spatial abilities and mathematical application abilities was also significant ( r = .47, p < .01). Because the visual-spatial abilities did not reflect the pure mathematical ability, we removed these scores before analysis and used the mean score of the two mathematical achievement scores in the data analyses (see Results ). Both of the tests were conducted in the schools and administered by two teachers and one experimenter.
Mathematical metacognition.
We assessed mathematical metacognition using the Chinese revised-edition Questionnaire of Pupil’s Metacognitive Ability in Mathematics, which was developed by Panaoura and Philippou [ 19 ] and revised by Hao et al. [ 69 ] This questionnaire contains 30 5-point Likert-type items (1 = never, 5 = always). Items evaluate the following four factors: Self-Image (Cronbach’s α = .81), 7 items that examine the pupils’ beliefs and self-efficacies about their abilities (e.g. “I know how to remember the knowledge of mathematics that I have learned”); Self-Regulation in Mathematics (α = .82), 7 items that examine the pupils’ abilities to clarify the targets of problems, understand mathematical concepts, apply knowledge to generate solution strategies and monitor their progress toward solutions (e.g. “To solve the math problem, I'll try a variety of methods and then determine the final method”); Strategies (α = .90), 12 items that examine the strategies that the pupils use to solve problems and overcome cognitive obstacles (e.g. “I'll draw pictures to help myself to better understand difficult mathematical questions”); and Motivations (α = .68), 4 items that elicit the pupils’ beliefs about the effects of their efforts and those of their parents and teachers on their performances (e.g. “Parents believe that I can learn math well”). Participants rate themselves with respect to each of the statements. The ratings for the items which made up each factor were averaged to give factor scores used in the statistical analyses. A confirmatory factor analysis (CFA) for the present data set indicated a good fit for a four-factor solution ( χ 2 = 711.25, df = 399, χ 2 / df = 1.78, RMSEA = 0.07, CFI = 0.97).
Mathematics anxiety.
We revised the Mathematics Anxiety Scale for Children (MASC) [ 10 ]. This scale contains 22 4-point Likert-type items (1 = never anxious, 4 = very anxious). An exploratory factor analysis on our revision yielded two factors consistent with Plake and Parker [ 70 ]. The first factor was labeled Learning Mathematics Anxiety ( LMA ). It was related to activities during learning or in the process of studying mathematics (e.g. watching a teacher solve an algebraic equation on the blackboard or listening to a lecture in a mathematics class). Cronbach’s α for this factor was .84. The second factor was labeled Mathematics Evaluation Anxiety ( MEA ). It was related to evaluations of mathematic or statistical learning (e.g. being given a surprise quiz in a mathematics class). Cronbach’s α for the second factor was .89. The ratings for items making up each factor were averaged to allow comparison. A confirmatory factor analysis indicated a good fit for a two-factor solution ( χ 2 = 413.01, df = 208, χ 2 / df = 2.04, RMSEA = 0.07, CFI = 0.94).
Word problems.
The children attempted to solve 10 word problems that required them to incorporate their knowledge of mathematics involved in scenarios that would have been familiar from their daily lives, and that depend on their knowledge about magnitude relationships. The word problem measures in the present study are a part of a standardized battery that measures children’s mathematical abilities [ 71 ]. The problems included addition, subtraction, multiplication and division (for the full set of problems, Cronbach’s α = .69), and all the problems were similar in size (e.g. 2-digit + 2-digit addition, etc.) An example of these questions is shown in Fig 1 . Three elementary mathematics teachers who each had extensive teaching experience evaluated the difficulties of the problems based on a 5-point Likert scale (1 = quite easy, 5 = quite hard) and agreed that the average degree of difficulty was moderate ( M = 2.67, SD = 0.24). The Kendall coefficient of concordance ( W ) among the teachers was .93. Participants were asked to compute each problem. Each participant was given two pieces of scratch paper, and they had free access to scratch paper. If the answer was correct, it earned one score point; otherwise, no point was awarded. Scores, therefore, could range from 0 (no problems solved correctly) to 10 (all problems solved correctly). The students had 45 minutes to solve the problems.
- PPT PowerPoint slide
- PNG larger image
- TIFF original image
How high is the table?
https://doi.org/10.1371/journal.pone.0130570.g001
Effects of MA and mathematical metacognition on WPS
We applied structural equation modeling using Mplus 7.0 to examine the hypothesized models. In the models, mathematical metacognition partially mediated the effect of MA on WPS after controlling for IQ. Because the correlation between the verbal IQ score and WPS was not significant ( r = .12, p = .07), we only controlled for the non-verbal IQ score ( r = .41, p < .01).
We first evaluated the measurement model to assess whether latent variables were well represented by indicator variables. The confirmatory factor analysis was conducted with four latent factors and eight observed variables. The latent variable Metacognition was indexed by 4 indicators (Self-Image, Self-Regulation, Strategies, and Motivation). The latent variable MA was indexed by 2 indicators (Learning mathematics anxiety and Mathematics evaluation anxiety). WPS and non-verbal IQ were each represented by a single indicator with the error variance fixed to zero. The estimation of the measurement model revealed a satisfactory fit to the data: χ 2 = 36.18, df = 16, χ 2 /df = 2.26, RMSEA = 0.075, TLI = 0.96, SRMR = 0.039, CFI = 0.98. All the factor loadings for the indicators on the latent variables were significant ( ps < .001) and the standardized factor loadings ranged from 0.70 to 0.95, indicating that all the latent factors were well represented by their respective indicators.
To test meant to assess the mediating role of mathematical metacognition between MA and WPS, we constructed a partially mediated model (Model 1) for all 224 participants (the partial correlation matrix is shown in Table 1 ). In this model, mathematical metacognition partially mediated the effect of MA on WPS after controlling for the non-verbal IQ (see Fig 2 ).
MA = mathematics anxiety, LMA = learning mathematics anxiety, MEA = mathematical evaluation anxiety, WPS = word problem solving. * p < .05. ** p < .01. *** p < .001.
https://doi.org/10.1371/journal.pone.0130570.g002
https://doi.org/10.1371/journal.pone.0130570.t001
Model 1 revealed a good fit to the data ( χ 2 = 37.54, df = 18, χ 2 /df = 2.08, RMSEA = 0.07, TLI = 0.97, SRMR = 0.05, CFI = 0.98). However, the standardized path coefficient from mathematics anxiety (MA) to word problem solving (WPS) was non-significant ( ß = -0.04, p = .71), as was the path from Metacognition to word problem solving ( ß = 0.13, p = .12). Consequently, a fully mediated model (Model 2) was tested (see Fig 3 ), which also exhibited a good fit to the data ( χ 2 = 37.72, df = 19, χ 2 / df = 1.99, RMSEA = 0.07, TLI = 0.97, SRMR = 0.05, CFI = 0.98). No significant Chi-square difference existed between Model 1 and Model 2, Δ χ 2 = 0.18, Δ df = 1, Δ χ 2 /Δ df = 0.18, p > .05. Because there was no significant difference between the models according to the fit indices, the parsimony of Model 2 suggested that its fit was more satisfactory.
https://doi.org/10.1371/journal.pone.0130570.g003
The results of Model 2 revealed a significant negative path from the latent MA variable to the latent variable Metacognition ( ß = -0.51, p = .001) and a significant positive path from Metacognition to WPS ( ß = 0.15, p = .02).
We generated 1,000 bootstrapping samples from the original data via random sampling. The indirect effect of metacognition from MA to WPS was -0.08, and the associated 95% confidence intervals were -0.14 to -0.012. The intervals did not overlap with zero; thus, Metacognition exerted a significant indirect effect on WPS via MA.
We also ran both the partially mediated model and fully mediated model with MA as a mediator, and these results are given in the Supporting Information ( S1 Table , S1 Fig and S2 Fig ). The Supporting Information shows that, in model 3 (the partially mediated model), the paths from the latent MA variable and Metacognition variable to WPS were non-significant. In model 4 (the fully mediated model), the path from MA to WPS was also non-significant. MA was not found to have any mediating effect.
Group differences in mathematical metacognition and MA
First, we used Hierarchical Regression Analyses to explore the prediction of mathematics achievement scores from mathematical metacognition and MA, when the effect of IQ was partialled out (see Table 2 ). For the purity of the mathematics measure, the visual-spatial question scores were excluded. All the scores in the regression were standardized. Based on the fact that the prediction was significant, we employed analysis of covariance (ANCOVA) to compare the differences related to mathematical metacognition and MA among the MLD, LA, TA, and HA groups. In order to avoid bias due to the grossly larger number of TA participants, while maintaining a sample size adequate to insure statistical stability, we randomly selected 30 individuals from the TA group. We did this using the Rand (random number) function of the 2010 edition of Microsoft Excel to randomly select 30 subjects (14 boys, M age = 10.22 years) from the 151 participants in the TA group. Table 3 displays the means and standard deviations of the variable measures for the four groups.
https://doi.org/10.1371/journal.pone.0130570.t002
https://doi.org/10.1371/journal.pone.0130570.t003
Group differences in mathematical metacognition.
The regression analysis above ( Table 2 ) showed that Self-image significantly predicted mathematics achievement. Based on these results, we conducted an ANCOVA, using the mathematics achievement groups as the independent variable and the self-image scores as the dependent variable. When controlling for IQ, the main effect of mathematics achievement group was significant, F (3, 211) = 3.84, p < .05, ƞ p 2 = .11, 1 - β = .81. Post hoc comparisons using the least significant differences (LSD) procedure with an alpha value of .05 revealed that the self-image in children with MLD ( M = 3.21) was significantly lower than TA and HA groups ( M TA = 3.76, p = .005; M HA = 3.98, p = .001). The difference between the MLD and LA groups was approaching significance ( M LA = 3.54, p = .05). Fig 4 shows these outcomes. We also used the entire TA group ( n = 151) to run the ANCOVA, and the results showed that the group differences in self-image were significant, F (3, 211) = 3.77, p < .05, ƞ p 2 = .05, 1 - β = .81.
MLD = mathematical learning difficulty, LA = low achieving, TA = typical achieving, HA = high achieving. LMA = learning mathematics anxiety, MEA = mathematical evaluation anxiety.
https://doi.org/10.1371/journal.pone.0130570.g004
Group differences in Mathematics Anxiety (MA).
The regression analysis above ( Table 2 ) also showed that learning mathematics anxiety (LMA) can significantly predict mathematics achievement. So we conducted an ANCOVA using the mathematics achievement groups as the independent variable and LMA score as the dependent variables, IQ as a covariate. The main effect of group was approaching significance, F (3,90) = 2.67, p = .05, ƞ p 2 = .08, 1 - β = .63. On average, the MLD group ( M = 1.97) showed significantly higher LMA scores than did the LA group ( M = 1.66, p = .018), the TA group ( M = 1.55, p = .009), and the HA groups ( M = 1.54, p = .015). The other groups were not significantly different from each other ( ps > .05). Fig 5 shows those results graphically. We also conducted the ANCOVA using the entire TA group, and the results showed the significant main effect of mathematics achievement groups in LMA, F (3, 211) = 3.10, p < .05, ƞ p 2 = .04, 1 - β = .72.
https://doi.org/10.1371/journal.pone.0130570.g005
Zan et al. have argued that “the most important problem for research on affect in mathematics is the understanding of the interrelationship between affect and cognition” (p.117) [ 72 ]. The current study revealed that mathematical metacognition mediated the relationship between children’s MA and word problem solving (WPS), after controlling for IQ. Regarding the group differences in mathematical metacognition and MA, the LA children exhibited lower levels of LMA than the MLD children with IQ partialled out. Moreover, the MLD children exhibited deficits in self-image, and LMA, but not MEA, compared to the TA and HA students.
Research in the domain of reading has revealed that test anxiety has a harmful effect on metacognitive word knowledge and influences performance in reading comprehension tasks [ 34 ]. Research in the mathematical domain has also found that individuals with higher anxiety benefit from having higher levels of metacognition when performing mathematical tasks [ 35 ]. Our results showed MA to be negatively related to the mathematical metacognition of 10-year-old children and subsequently related to WPS performance. This finding provides insight into factors that may mediate poor WPS performance which emerged under pressure in mathematics. This mediation effect also suggests that metacognition can counter the negative or stressful perceptions in mathematical performance.
It is worthy to note that the relationship among mathematics anxiety, metacognition, and word problem solving is complicated. First, in the longitudinal view, prior mathematical performance may be related to later mathematics anxiety [ 36 ]. However, there is also the possibility that mathematics anxiety may exist when children begin to learn mathematics in a formal academic setting [ 56 ]. In the present study, the mathematics anxiety measured here was a general fear or tension associated with anxiety-provoking situations that involve interaction with math in a wide variety of ordinary situations. The development of such anxiety may be related more globally to poor math performance instead of only word problem solving performance. It is here proposed that testing the “WPS-> MA-> metacognition” or “WPS-> metacognition-> MA” or “metacognition-> WPS—> MA” direction path models may be more valuable in longitudinal studies.
Second, the relationship “MA-> WPS-> metacognition” may also exist. Mathematics anxiety may be negatively related to WPS and may impact children’s mathematical metacognition. However, the mathematical metacognition we measured was a self-assessment on general metacognition about mathematical learning, and we measured it before WPS. Both MA and metacognition may have deep developmental origins (perhaps construed as trait variables) and short term origins (perhaps construed as state variables). Note that testing word problem solving may have only short-term effects, and the prediction that WPS would lead to metacognition could not be explained.
Third, even though the arrows in Kulm’s model mentioned in the introduction started from attitude, we acknowledged that attitudes are important both as independent and dependent variables. Similarly, metacognition might predict mathematics anxiety, and it might be related to WPS. However, only a few previous works have reviewed metacognition as it is related specifically to mathematics anxiety, and research about these three variables is sparse.
Jain and Dowson used structural equation modeling and found self-efficacy to be a mediating variable between self-regulation and mathematics anxiety [ 31 ]. That study was cross-sectional, although the aim was to find causal ordering. Consequently, the conclusion should be interpreted cautiously. As previously mentioned, Legg and Locker found that metacognition appeared to reduce the impact of anxiety on performance [ 35 ]. This work did not offer a holistic statistical analysis of the three variables. Another cross-cultural study [ 73 ] also showed a relationship between test anxiety and mathematical self-concept. Participants from Korea and Japan demonstrated low mathematical self-concept and high mathematics anxiety despite their high mathematical performance scores.
Past research includes investigations of the relationship between metacognition and anxiety, but existing studies have come to conflicting conclusions regarding the relationship among the three variables evaluated here. The purpose of the present study was to offer information regarding the role of metacognition in the relationship of MA and WPS. Considering the possibility of prediction from metacognition to anxiety, we ran the path models of “metacognition-> MA-> WPS” (see S1 Table , S1 Fig and S2 Fig ), but the results did not show any mediating effect of MA on the relationship between metacognition and WPS.
In addition, many investigations have focused on cognitive deficits in children with MLD and their LA peers (e.g. [ 74 , 75 ]), but there has been little or if any progress toward elaborating emotional functioning in these two groups [ 44 ]. Comparisons between MLD and LA students in the present study showed some intriguing differences. The children with MLD showed higher LMA and lower self-image than did those in the LA group. Because the difference in self-image between MLD and LA group was almost significant, caution should be used when generalizing the result. These results indicated that these two groups should not be conflated [ 42 ]. The present findings also suggest that one benefit of mathematical metacognition may be related to promoting beliefs about, and feelings of self-efficacy with respect to, the MLD children’s mathematical abilities. Moreover, helping MLD children reduce anxiety during the mathematics learning process should be incorporated into future interventions.
Results in the children with MLD also showed that MA and metacognition related to mathematical performance. They exhibited lower self-image, but higher levels of LMA, than did their TA and HA peers. Children classified with mathematical learning difficulty at some point experienced considerable failure and negative competence feedback at school. These experiences would likely be internalized and represented in a more negative view of self [ 76 ]. Our results showed self-image to be a powerful variable related to children’s mathematics performance. Self-image may reflect a wide range of related variables. Some studies have suggested that self-image is related to extended effort and persistence [ 77 ]. Individuals with higher mathematical self-image may interact with their teachers more frequently and may spend more time on tasks than students with lower self-concepts [ 38 ]. Because these variables behind self-image, such as interaction with teachers, may also be related to children’s performance, further research is needed to control these variables and explore the relationship between self-image and mathematical performance.
In the present study, no group differences were observed with respect to self-regulation, strategies, or motivation. We did not measure children’s strategies and self-regulation when they were doing mathematics tasks. Instead, we measured their general mathematical metacognitive strategies and self-regulation ability. For example, children had to evaluate situations in which “after I finish mathematics assignments, I review the main points in order to make sure I did learn the new knowledge.” Such strategies represented the basic strategies children used when facing similar supposed situations. It is possible that the basic strategies in children with MLD were sufficient, but when they were performing real mathematical tasks, the tasks may require more detailed and flexible strategies to monitor, adjust, and reflect upon the problem-solving process. These specific strategies may show differences among four mathematics achievement groups. The results suggested that determining the specificity of the metacognitive strategies used (general/specific) may be a useful way to identify children with MLD in the future.
Meanwhile, in the present study, children’s motivation to engage in mathematical learning reflected the impacts of their parents and teachers. For example, children were asked to rate the statement “my parents asked me to learn mathematics thoroughly.” Chinese parents and teachers tend to push children hard [ 78 , 79 ], and this might be one of the reasons why the levels of motivation in the four achievement groups showed little difference. However, more research is needed.
Higher LMA in the MLD group indicates that the students might worry about their mathematics learning processes. LMA is a type of dynamic anxiety that involves children applying cognitive resources to ruminating on anxious thoughts and thus limiting the cognitive capacities available to organize WPS strategies. The data also point to the conclusion that MLD children might feel more nervous and anxious due to the process of learning mathematics rather than due to other people’s evaluations of them. Both the surroundings that are rich in mathematical information and mathematics problem solving settings may increase their anxious thoughts and then lower their performance. Indeed, recent research [ 80 ] has begun to focus on the early signs of LMA in young children in kindergarten, when these children view pictures of natural mathematics information in daily life and in situations involving simple mathematics. All of these findings are informative for schools in terms of the means by which to respond to the learning challenges of children, particularly children with MLD.
The results of the present study suggest a variety of avenues for potentially productive research, with additional possible practical applications. The present study used Chinese students. A few studies have shown that Confucian Asian students experience higher levels of mathematics anxiety and mathematics self-doubt than do students from other parts of the world [ 73 , 81 ]. Because mathematics is a major key to success in so many fields, it is therefore easily conceivable that those affective elements impact mathematics learning, and possibly subsequent achievement in areas which rely on mathematics skills (e.g. traditional sciences, economics, and accounting). Even though the present study did not specifically test for cultural differences, there is a possibility that behavioral and psychosocial outcomes may differ across cultures, with special emphasis on Chinese vs. western culture. This possibility will need to be investigated in the future.
Another limitation warrant cautious consideration of these results. The present study was a cross-sectional study, and we did not experimentally manipulate anxiety and metacognition. It is important to recognize that the use of structural equation modeling does not automatically warrant creditability to any knowledge claim on a causal relationship. Longitudinal data would enable an estimation of the causal effects of metacognition and mathematics anxiety on word problem solving taking into account previous levels of each of these variables. We suggest that future studies could incorporate more diverse samples, providing longitudinal data, in order to verify the results of the study under more robust sampling and statistical conditions.
We also emphasize that this study only examined the structural relationship between metacognition, operationalized using a particular scale, and a particular (albeit important) form of mathematics performance, WPS. Further studies should record specific metacognitive behaviors, such as the types of strategies employed, during the solving of word problems to extend these results [ 82 ]. Other types of mathematics problems remain to be explored.
In that same vein, many of the correlations with WPS and with mathematics achievement scores are relatively small (see Table 1 ), none exceeding .28 (about 8% variance accounted for). While significant, those values strongly suggest that additional variables—likely including cognitive, metacognitive, and affective elements—play important roles in mathematics learning and performance. Those additional variables remain to be identified.
In the present study, working memory was not tested and the study only controlled for children’s intelligence score, because general intelligence is a critical control variable used for screening children with MLD, and because general intelligence here believed to represent individuals’ ability to process information. General intelligence indicates a variety of cognitive variables (e.g. reasoning ability, comprehension), and many researchers have suggested that general intelligence and working memory may share common variance [ 83 – 85 ]. Future studies that control for working memory or investigate the relationship among working memory, metacognition, mathematical anxiety, and word problem solving are planned. Besides, we acknowledge that reading ability is likely to be a covariate in predicting the degree of success with word problems, beyond general intelligence. While we did account for verbal IQ, reading ability was not assessed directly. Although pictorial illustrations were supplied for each word problem to help students interpret the text, future research should either include a control group without pictorial illustrations or directly measure reading ability. Those approaches were not feasible in the present study due to constraints on access to the children.
Additionally, the scales we used to measure metacognition and mathematics anxiety are only two possible ways to evaluate the relevant variables. Other convergent measures clearly would be highly desirable. Moreover, the measures we used are ordinal, and the range of ratings available is typically limited, even though such measures are widely used in behavioral studies. Future research should attempt to explore the fine gradations of the underlying variable that are impossible to discern with the measures we employed.
We tested fourth-grade children, all around 10 years of age and found affective and metacognitive correlates of mathematics performance. Mathematics education in China begins before that age and continues through all educational levels. It seems reasonable to propose that the patterns of affective and metacognitive influences seen across school ages might vary. It would therefore be advantageous to evaluate such patterns, and developmental changes in them, in students both younger and older than those we tested.
Finally, the small number of MLD students calls for caution in interpreting the path diagram of the three variables to examine the mediating effects in MLD children. Future research will need to test those relationships with larger samples of MLD children.
This study examined effects of two important affective and cognitive variables (i.e. mathematical anxiety and mathematical metacognition) on children’s word problem solving abilities and explored the differences between four mathematics achievement groups. The results help identify the critical roles of, and relationships between, the two categories of variables in relation to children’s mathematical learning. Application of these outcomes has the potential to positively influence the formulation of targeted education and intervention plans for different groups. The present study also provides theoretical support for teachers seeking to decrease the effect of student mathematics anxiety on WPS from the new perspective of metacognitive intervention training.
Supporting Information
S1 fig. model 3: partially mediated model with ma as a mediator and iq partialled out..
LMA = learning mathematics anxiety, MEA = mathematical evaluation anxiety. WPS = word problem solving. *** p < .001, ** p < .01.
https://doi.org/10.1371/journal.pone.0130570.s001
S2 Fig. Model 4: Fully mediated model with MA as a mediator and IQ partialled out.
https://doi.org/10.1371/journal.pone.0130570.s002
S1 Table. Fit indices for the structural equation modeling of mathematical metacognition, mathematics anxiety, and word problem solving with MA as a mediator.
https://doi.org/10.1371/journal.pone.0130570.s003
Author Contributions
Conceived and designed the experiments: YHL XSZ YHC. Performed the experiments: YHL XSZ YHC YJL. Analyzed the data: YHL XSZ. Contributed reagents/materials/analysis tools: YHL XSZ. Wrote the paper: YHL XSZ.
- 1. Mayer RE, Wittrock MC. Problem solving. In: Alexander PA, Winne PH, editors. Handbook of educational psychology (2nd ed). Mahwah, New Jersey: Erlbaum; 2006. pp. 287–303.
- View Article
- Google Scholar
- 7. Hannula MS. Affect in mathematics education. In: Lerman S, editor. Encyclopedia of Mathematics Education. Dordrecht: Springer; 2014. pp. 23–27.
- PubMed/NCBI
- 38. Kulm G. Research on mathematics attitude. In: Shumway RJ, editors. Research in mathematics education. Reston: National Council of Teachers of Mathematics; 1980. p.380.
- 40. American Psychiatric Association. Diagnostic and statistical manual of mental disorders, text revision (DSM-IV-TR). Washington, DC: American Psychiatric Association; 2000.
- 41. Swanson HL, Harris KR, Graham S. Handbook of learning disabilities. New York: Guilford Press; 2013.
- 58. Geary DC. Learning disabilities in arithmetic: Problem-solving differences and cognitive deficits. In Swanson HL, Harris KR, Graham S, editors. Handbook of learning disabilities. New York: The Guilford Press; 2003. pp. 199–212.
- 68. Liu J, Sun XT. Chinese mathematics curriculum standards of Full-time compulsory education reading. Beijing: Beijing Normal University Publishing Group; 2002.
Peer tutoring models in collaborative learning of mathematical problem solving and their effect on group achievement
- Published: 19 November 2022
- Volume 28 , pages 6595–6618, ( 2023 )
Cite this article

- Yangyang Li ORCID: orcid.org/0000-0001-5361-5058 1 , 2 ,
- Chunlian Jiang ORCID: orcid.org/0000-0002-2740-1870 3 ,
- Zengzhao Chen ORCID: orcid.org/0000-0002-4022-9139 1 , 2 ,
- Jing Fang ORCID: orcid.org/0000-0002-9244-5896 1 , 2 ,
- Chenyang Wang ORCID: orcid.org/0000-0002-2753-6505 1 , 2 &
- Xiuling He ORCID: orcid.org/0000-0001-7880-8710 1 , 2
847 Accesses
2 Citations
Explore all metrics
This article has been updated
This study was conducted to examine peer tutoring models in collaborative learning of mathematical problem solving (MPS) in flipped classrooms and their effect on group achievement. Quantitative data collected include 32 videos of eight groups of students in four MPS periods that were designed based on a simplified version of Polya’s four-stage model, and their worksheets completed in each period. The video data were coded based on a framework with low-level and high-level cognitive behaviors as well as management behaviors and were analyzed using lag sequence analysis from which three types of peer tutoring models were determined: organization-oriented, cognitive-supported, and cognitive-guided. ANOVA analysis showed that the groups with cognitive-guided tutors performed significantly better than the groups guided by cognitive-supported and organization-oriented tutors, between which the performance difference did not reach a significant level. The results of this study suggest that training provided to peer tutors should focus more on how to stimulate high-level cognitive thinking skills than on organization skills.
This is a preview of subscription content, log in via an institution to check access.
Access this article
Subscribe and save.
- Get 10 units per month
- Download Article/Chapter or eBook
- 1 Unit = 1 Article or 1 Chapter
- Cancel anytime
Price includes VAT (Russian Federation)
Instant access to the full article PDF.
Rent this article via DeepDyve
Institutional subscriptions
Similar content being viewed by others

Research on Student Interaction in Peer Collaborative Problem Solving in Mathematics
Examining evolutions in the adoption of metacognitive regulation in reciprocal peer tutoring groups.
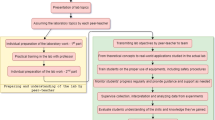
Students’ perception of peer teaching in engineering education: a mixed–method case study
Explore related subjects.
- Digital Education and Educational Technology
Data availability
The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.
Change history
26 november 2022.
Springer Nature’s version of this paper was updated: In PDF version, Figure 6 has been moved under “Appendix. A worksheet for group discussion” heading.
Al-Zahrani, A. M. (2015). From passive to active: The impact of the flipped classroom through social learning platforms on higher education students’ creative thinking. British Journal of Educational Technology, 46 (6), 1133–1148. https://doi.org/10.1111/bjet.12353
Article Google Scholar
Anderson, J. R. (1993). Problem Solving and Learning. American Psychologist , 48 (1), 35–44. https://doi.org/10.1037/0003-066X.48.1.35
Bakeman, R., & Quera, V. (2011). Sequential Analysis and Observational Methods for the Behavioral Sciences. Cambridge University Press . https://doi.org/10.1017/CBO9781139017343
Article MATH Google Scholar
Berghmans, I., Michiels, L., Salmon, S., Dochy, F., & Struyven, K. (2014). Directive versus facilitative peer tutoring? A view on students’ appraisal, reported learning gains and experiences within two differently-tutored learning environments. Learning Environments Research, 17 (3), 437–459. https://doi.org/10.1007/s10984-014-9168-8
Berghmans, I., Neckebroeck, F., Dochy, F., & Struyven, K. (2013). A typology of approaches to peer tutoring. Unraveling peer tutors’ behavioural strategies. European Journal of Psychology of Education, 28 (3), 703–723. https://doi.org/10.1007/s10212-012-0136-3
Bergmann, J., & Sams, A. (2012). Flip your classroom: Reach every student in every class every day . International society for technology in education.
Google Scholar
Bhagat, K. K., Chang, C. N., & Chang, C. Y. (2016). The impact of the flipped classroom on mathematics concept learning in high school. Journal of Educational Technology & Society, 19 (3), 134–142. https://www.jstor.org/stable/jeductechsoci.19.3.134 .
Bishop, J. L., & Verleger, M. A. (2013). The flipped classroom: A survey of the research . Paper presented at 2013 ASEE Annual Conference & Exposition, Atlanta, Georgia.
Capstick, S., & Fleming, H. (2004). The learning environment of peer assisted learning. In: Peer Assisted Learning Conference, Bournemouth.
Chiang, T. H. C. (2017). Analysis of learning behavior in a flipped programing classroom adopting problem-solving strategies. Interactive Learning Environments, 25 (2), 189–202. https://doi.org/10.1080/10494820.2016.1276084
Chu, H. C., Chen, J. M., & Tsai, C. L. (2017). Effects of an online formative peer-tutoring approach on students’ learning behaviors, performance and cognitive load in mathematics. Interactive Learning Environments, 25 (2), 203–219. https://doi.org/10.1080/10494820.2016.1276085
Colvin, J. W., & Ashman, M. (2010). Roles, risks, and benefits of peer mentoring relationships in higher education. Mentoring & Tutoring: Partnership in Learning, 18 (2), 121–134. https://doi.org/10.1080/13611261003678879
Curriculum Planning and Development Division (CPDD). (2019). Mathematics syllabuses secondary one to four express course, normal (academic) course . Singapore: Ministry of Education. Retrieved May 20, 2022, from https://www.moe.gov.sg/-/media/files/secondary/syllabuses/maths/2020-express_na-maths_syllabuses.ashx?la=en&hash=E79043503E0EE64FA579D7514760663151459ED9
Curriculum Planning and Development Division (CPDD). (2020). Mathematics syllabus primary one to six . Singapore: Ministry of Education. Retrieved May 20, 2022, from https://www.moe.gov.sg/-/media/files/primary/mathematics_syllabus_primary_1_to_6.pdf
Dalkin, S., Forster, N., Hodgson, P., Lhussier, M., & Carr, S. M. (2021). Using computer assisted qualitative data analysis software (CAQDAS; NVivo) to assist in the complex process of realist theory generation, refinement and testing. International Journal of Social Research Methodology, 24 (1), 123–134. https://doi.org/10.1080/13645579.2020.1803528
De Smet, M., Van Keer, H., & Valcke, M. (2008). Blending asynchronous discussion groups and peer tutoring in higher education: An exploratory study of online peer tutoring behaviour. Computers in Education, 50 , 207–223. https://doi.org/10.1016/j.compedu.2006.05.001
Erbil, D. G. (2020). A review of flipped classroom and cooperative learning method within the context of Vygotsky theory. Frontiers in Psychology, 11 , 1–9. https://doi.org/10.3389/fpsyg.2020.01157
Foldnes, N. (2016). The flipped classroom and cooperative learning: Evidence from a randomised experiment. Active Learning in Higher Education, 17 (1), 39–49. https://doi.org/10.1177/1469787415616726
Galway, L. P., Corbett, K. K., Takaro, T. K., Tairyan, K., & Frank, E. (2014). A novel integration of online and flipped classroom instructional models in public health higher education. BMC Medical Education, 14 (1), 1–9. https://doi.org/10.1186/1472-6920-14-181
Gong, D., Yang, H. H., & Cai, J. (2020). Exploring the key influencing factors on college students’ computational thinking skills through flipped-classroom instruction. International Journal of Educational Technology in Higher Education, 17 , 1–13. https://doi.org/10.1186/s41239-020-00196-0
González-Gómez, D., Jeong, J. S., & Rodríguez, D. A. (2016). Performance and perception in the flipped learning model: An initial approach to evaluate the effectiveness of a new teaching methodology in a general science classroom. Journal of Science Education and Technology, 25 (3), 450–459. https://doi.org/10.1007/s10956-016-9605-9
Goodrich, A. (2018). Peer mentoring and peer tutoring among K–12 students: A literature review. Update: Applications of Research in Music Education , 36 (2), 13–21. https://doi.org/10.1177/8755123317708765
Hembree, R. (1992). Experiments and relational studies in problem solving: A meta-analysis. Journal for Research in Mathematics Education, 23 (2), 242–273. https://doi.org/10.2307/749120
Hwang, G. J., & Chen, P. Y. (2019). Effects of a collective problem-solving promotion-based flipped classroom on students’ learning performances and interactive patterns. Interactive Learning Environments, 1–16 ,. https://doi.org/10.1080/10494820.2019.1568263
Jdaitawi, M. (2020). Does Flipped Learning Promote Positive Emotions in Science Education? A Comparison between Traditional and Flipped Classroom Approaches. Electronic Journal of e-Learning , 18 (6), 516–524. https://doi.org/10.34190/JEL.18.6.004
Jiang, C., & Chua, B. L. (2010). Strategies for solving three fraction-related word problems on speed: A comparative study between Chinese and Singapore students. International Journal of Science and Mathematics Education, 8 (1), 73–96. https://doi.org/10.1007/s10763-009-9163-1
Johnson, D. W., Johnson, R. T., & Stanne, M. B. (2000). Cooperative learning methods: A meta-analysis. Retrieved March 5, 2022, from https://www.researchgate.net/profile/David-Johnson-113/publication/220040324_Cooperative_learning_methods_A_meta-analysis/links/00b4952b39d258145c000000/Cooperative-learning-methods-A-meta-analysis.pdf
Lai, C. L., & Hwang, G. J. (2016). A self-regulated flipped classroom approach to improving students’ learning performance in a mathematics course. Computers & Education, 100 , 126–140. https://doi.org/10.1016/j.compedu.2016.05.006
Madaio, M., Cassell, J., & Ogan, A. (2017). “I think you just got mixed up”: Confident peer tutors hedge to support partners’ face needs. International Journal of Computer-Supported Collaborative Learning, 12 (4), 401–421. https://doi.org/10.1007/s11412-017-9266-6
McComas, J. J., Moore, T., Dahl, N., Hartman, E., Hoch, J., & Symons, F. (2009). Calculating contingencies in natural environments: Issues in the application of sequential analysis. Journal of Applied Behavior Analysis, 42 (2), 413–423. https://doi.org/10.1901/jaba.2009.42-413
McLaughlin, J. E., Griffin, L. M., Esserman, D. A., Davidson, C. A., Glatt, D. M., Roth, M. T., … & Mumper, R. J. (2013). Pharmacy student engagement, performance, and perception in a flipped satellite classroom. American Journal of Pharmaceutical Education, 77 (9), 1–8. https://doi.org/10.5688/ajpe779196
Munir, M. T., Baroutian, S., Young, B. R., & Carter, S. (2018). Flipped classroom with cooperative learning as a cornerstone. Education for Chemical Engineers, 23 , 25–33. https://doi.org/10.1016/j.ece.2018.05.001
National Council of Teachers of Mathematics (NCTM). (2000). Principles and standards for school mathematics . Reston, VA, NCTM. Retrieved May 20, 2022, from https://www.rainierchristian.org/NCTM_principles-and-standards-for-school-mathematics.pdf
Nawaz, A., & Rehman, Z. U. (2017). Strategy of peer tutoring and students success in mathematics: An analysis. Journal of Research and Reflections in Education, 11 (1), 15–30. https://ue.edu.pk/jrre/articles/1101002.pdf .
Nguyen, B., Yu, X., Japutra, A., & Chen, C. H. S. (2016). Reverse teaching: Exploring student perceptions of “flip teaching.” Active Learning in Higher Education, 17 (1), 51–61. https://doi.org/10.1177/1469787415616727
Organization for Economic Co-operation and Development (OECD). (2018). PISA 2021 Mathematics Framework (first draft). Retrieved May 15, 2022, from https://www.mokykla2030.lt/wp-content/uploads/2018/12/GB-2018-4-PISA-2021-Mathematics-Framework-First-Draft.pdf
Qiang, J. (2018). Effects of digital flipped classroom teaching method integrated cooperative learning model on learning motivation and outcome. EURASIA Journal of Mathematics, Science and Technology Education , 14 (6), 2213–2220. https://doi.org/10.29333/ejmste/102356
Sahin, A., Cavlazoglu, B., & Zeytuncu, Y. E. (2015). Flipping a college calculus course: A case study. Journal of Educational Technology & Society, 18 (3), 142–152. https://www.jstor.org/stable/jeductechsoci.18.3.142 .
Shi, Y., Ma, Y., MacLeod, J., & Yang, H. H. (2020). College students’ cognitive learning outcomes in flipped classroom instruction: A meta-analysis of the empirical literature. Journal of Computers in Education, 7 (1), 79–103. https://doi.org/10.1007/s40692-019-00142-8
Sun, J. C. Y., & Wu, Y. T. (2016). Analysis of learning achievement and teacher–student interactions in flipped and conventional classrooms. International Review of Research in Open and Distributed Learning , 17 (1), 79–99. https://doi.org/10.19173/irrodl.v17i1.2116
Sun, Z., Lin, C. H., Lv, K., & Song, J. (2021). Knowledge-construction behaviors in a mobile learning environment: A lag-sequential analysis of group differences. Educational Technology Research and Development, 69 (2), 533–551. https://doi.org/10.1007/s11423-021-09938-x
Tong, H. (2017). 混合学习环境中协作知识建构策略研究 [Research on cooperative knowledge construction strategy in mixed learning environment](pp. 65–66). Publishing house of electronics industry .
Tucker, B. (2012). The flipped classroom. Education Next, 12 (1), 82–83. https://lists.tki.org.nz/sympa/arc/ictenglish/2014-02/msg00032/ednext_20121_BTucker_flippedclassroom.pdf .
Wang, C., Fang, T., & Gu, Y. (2020). Learning performance and behavioral patterns of online collaborative learning: Impact of cognitive load and affordances of different multimedia. Computers & Education, 143 , 1–14. https://doi.org/10.1016/j.compedu.2019.103683
Wang, K., & Zhu, C. (2019). MOOC-based flipped learning in higher education: Students’ participation, experience and learning performance. International Journal of Educational Technology in Higher Education, 16 (1), 1–18. https://doi.org/10.1186/s41239-019-0163-0
Wang, Y. L., Cheng, Y., Wang, F., Tong, S. H., & Huang, K. B. (2016). 技术支持下的课堂教学行为观察方法探究 [Research on the observation method of classroom teaching behavior supported by technology]. Modern Educational Technology, 26 (09), 39–45.
Wei, X., Cheng, I., Chen, N. S., Yang, X., Liu, Y., Dong, Y., & Zhai, X. (2020). Effect of the flipped classroom on the mathematics performance of middle school students. Educational Technology Research and Development, 68 (3), 1461–1484. https://doi.org/10.1007/s11423-020-09752-x
Zheng, L., Bhagat, K. K., Zhen, Y., & Zhang, X. (2020). The Effectiveness of the Flipped Classroom on Students’ Learning Achievement and Learning Motivation: A Meta-Analysis. Journal of Educational Technology & Society, 23 (1), 1–15. https://www.jstor.org/stable/26915403 .
Zulaiha, Z., Bharata, H., & Dahlan, S. (2020). Developing Discovery Learning Assisted Peer Tutors to Improve Problem Solving. International Journal of Trends in Mathematics Education Research, 3 (2), 106–111. https://ijtmer.saintispub.com/index.php/ijtmer/article/view/79 .
Download references
Author information
Authors and affiliations.
Faculty of Artificial Intelligence in Education, Central China Normal University, Wuhan, China
Yangyang Li, Zengzhao Chen, Jing Fang, Chenyang Wang & Xiuling He
National Engineering Research Center for Educational Big Data, Central China Normal University, Wuhan, China
Faculty of Education, University of Macau, Macao, China
Chunlian Jiang
You can also search for this author in PubMed Google Scholar
Contributions
All authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by Yangyang Li, Zengzhao Chen, Jing Fang, and Chenyang Wang. The first draft of the manuscript was written by Yangyang Li. The review and editing of the manuscript was done by Xiuling He and Chunlian Jiang. All authors read and approved the final manuscript. This research was supported by National Natural Science Foundation of China (NSFC) for the Project “A Study on the Perception and Attribution Analysis of Learners' Higher-Order Thinking Activities” (No.: 61807012). We are grateful for the support from NSFC, National Intelligent Society Governance Experiment Base (Education), and Central China Normal University. Any opinions expressed herein are those of the authors and do not necessarily represent the funds' views.
Corresponding author
Correspondence to Xiuling He .
Ethics declarations
Conflict of interests.
The authors declare that they have no conflict of interest.
Additional information
Publisher's note.
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix. A worksheet for group discussion

A worksheet for group discussion
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
Reprints and permissions
About this article
Li, Y., Jiang, C., Chen, Z. et al. Peer tutoring models in collaborative learning of mathematical problem solving and their effect on group achievement. Educ Inf Technol 28 , 6595–6618 (2023). https://doi.org/10.1007/s10639-022-11429-2
Download citation
Received : 03 August 2022
Accepted : 24 October 2022
Published : 19 November 2022
Issue Date : June 2023
DOI : https://doi.org/10.1007/s10639-022-11429-2
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Collaborative Learning
- Flipped Classroom
- Lag Sequence Analysis
- Mathematical Problem Solving
- Peer Tutoring Models
- Find a journal
- Publish with us
- Track your research
Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.
- View all journals
- Explore content
- About the journal
- Publish with us
- Sign up for alerts
- Open access
- Published: 07 September 2024
Interplay between music and mathematics in the eyes of the beholder: focusing on differing types of expertise
- Libby Azaryahu 1 , 2 ,
- Ido Ariel 3 &
- Roza Leikin 4
Humanities and Social Sciences Communications volume 11 , Article number: 1153 ( 2024 ) Cite this article
1 Altmetric
Metrics details
- Development studies
This study explored the unique connections between music and mathematics as perceived by four groups of experts: professional mathematicians and musicians, as well as teacher educators in these two fields. Using 2 × 2 study design, we studied four groups of participants, comprising theorists and educators from various Israeli universities. During semi-structured interviews, the study participants were asked about their views on the connections between mathematics and music. This study proposes a model of experts’ conceptions of the connection between mathematics and music, which is of descriptive and explanatory power. that reveals differences between the four groups of experts. Theoreticians in both disciplines highlighted Mathematics as a key tool for music analysis and creation . Musical educators emphasized the role of music as a tool for learning mathematics . All the study participants, independently of the field of their expertise, value structure, beauty, sense of wonder, freedom and creative thinking as characteristics of both fields. Additionally, all the experts hold conceptions of the importance of integrating music and mathematics into various discipline . This study opened new doors for future research wherein utilization of experts’ insights to craft integrated study modules of music and mathematics can be explored, a pursuit that carries substantial significance.
Similar content being viewed by others
Examining students’ music listening willingness and engagement to foster their musical achievement and development in higher educational institutions
Mathematics in the Spanish press: a case study of the 18th century journal Semanario de Salamanca
Exploring the foundations of tonality: statistical cognitive modeling of modes in the history of Western classical music
Introduction.
The connection between Western music and mathematics has been recognized since the days of Pythagoras, Plato and Aristotle, who wrote about the overlap and parallels between the two disciplines. Both disciplines – music and mathematics – are expressed through the use of representative language and symbolic notation (Papadopoulos 2002 ). Mathematical concepts such as symmetry, patterns, ratio, and division are expressed in music. In music, intervals, rhythm, duration, speed, and many musical concepts are naturally represented by numbers (Bamberger and Disessa 2003 ). For example, the intervals between harmonic notes in music are determined by ratios of small whole numbers. When plucking two strings of the same length, the ratio between their lengths is 1:1, resulting in identical and harmonious sounds (sounds that blend well together). Moreover, differing ratios of string lengths will produce various harmonic intervals, such as the octave (string ratio of 1:2), the fifth (2:3), and the fourth (3:4).
Music was a subject of research among mathematicians such as Descartes, Kepler, and Euler, and on the other hand musicians were attracted to the possibilities inherent in the science of mathematics for analyzing works and composing (Wollenberg 2003 ). Compositional methods that draw inspiration from mathematical ideas included, among others, counterpoint (a second voice that appears simultaneously with the first voice in a polyphonic texture), a crab canon (the second voice is an imitation of the first voice in reverse), or a palindrome (a section that can be played from beginning to end and from end to beginning, in mathematics y = −x), and geometric designs of musical melodies (for example reflective symmetry, where a melody repeats itself in a mirrored fashion). In addition, mathematical images in Western music are expressed musically in the theory of harmony, the theory of rhythm, and the theory of forms. The theory of harmony reveals a fundamental regularity in how sounds are combined simultaneously, how they relate to one another, and how they are distributed over time. The theory of rhythm refers to how the sounds are organized in time and the continuation relationships between them. And finally, the theory of forms addresses how musical events are organized and the proportions created between musical parts (Douthett 2008 ; Johnson 2008 ; Rothstein 2006 ). In light thereof, the current study aims to uncover the profound interconnections between the disciplines, as perceived by mathematicians, musicians, and educators in teacher training programs. By adopting a wholistic perspective, this research seeks to highlight the practical relevance of these interdisciplinary connections both in training teachers and instructing students.

The connections between mathematics and music in teaching and learning
Recent studies that cited the explicit connections between the knowledge embodied in music and mathematics indicated positive transfer effects (Akın 2023 ; Azaryahu et al. 2024 ; Azaryahu et al. 2023 ; Wang et al. 2024 ). These studies used symbolic notation to create an explicit parallel between musical concepts and mathematical concepts among elementary school students. For example, two studies conducted with 84 third graders and 86 fourth graders found that the experimental groups increased their mathematical and musical achievements over the control group following participation in a multidisciplinary program combining music and mathematics regarding patterns and symmetry (Azaryahu et al. 2023 ) and fractions (Azaryahu et al. 2024 ). The methodologies employed in these studies used symbolic notations to create an explicit parallel between temporal music concepts and numerical and spatial math concepts, such as fractions, symmetry, ratios, and patterns, demonstrating the natural alignment between these disciplines (Courey et al. 2012 ; Hallam and Himonides 2022 ; Wang et al. 2024 ).
A recent meta-analysis by Wang et al. ( 2024 ) supports previous research, showing a significant positive impact of integrating music into mathematics instruction. It highlights critical factors such as incorporating music instruction within math interventions, the use of calming and math-related music, and exposure at early grade levels that significantly enhance the effectiveness of music in improving mathematical learning outcomes compared to other moderating categories. Music as a pedagogical tool facilitates the connection of mathematical concepts to real-world contexts, thereby making lessons more meaningful and relevant (Erickson 2002 ; Nagisetty 2014 ). This multidisciplinary approach has the potential to enhance students’ interest and motivation in mathematics (An 2012 ).
In the current study, we explore the content areas that can be effectively paralleled in the classroom learning process, as perceived by musical experts and mathematicians who are actively engaged in teaching at universities and teacher training colleges.
Professional identity of theorists and educators in music and mathematics
The dynamic between theorists and educators lies in the clear distinction between the two separate realms of knowledge and practice. The academic community specializes in crafting and disseminating theoretically framed, universally applicable knowledge derived from research. In contrast, educational practitioners cultivate and enhance their knowledge while actively addressing challenges and solving problems to achieve specific objectives within a particular educational context (Bressler 1999 ).
Professional identity is a key underlying concept in our behavior. The development of professional identity is shaped by interactions and embedded connections with colleagues, occurring within the contexts of culture, profession, and personal experience (Hargreaves 2001 ). Beijaard et al. decomposed teacher identity into three categories based on a personal knowledge perspective: teacher as subject matter expert, teacher as pedagogical expert, and teacher as didactical expert (Beijaard et al. 2000 ). Subject matter mastery involves comprehension of the material to be taught. Didactical proficiency encompasses crafting and imparting a learning encounter, as well as evaluating the results of teaching methods. Pedagogical adeptness involves addressing students’ emotional and social needs, and customizing instruction to suit individual learning needs. Teachers are positioned within this framework according to the priority that they attribute to each form of expertise.
Pedagogical content knowledge (PCK), first introduced by Shulman in 1986, aligns closely with this framework of teacher identity. Described as the combination of teachers’ subject matter expertise with their pedagogical skills, PCK represents the integration of content knowledge and pedagogical knowledge, enabling teachers to effectively deliver subject matter tailored to the abilities and interests of learners (Shulman 1987 ). Some studies further define PCK as encompassing content knowledge (CK), pedagogical knowledge (PK), and knowledge of learners (Gess-Newsome et al. 2019 ; Liu 2013 ). Consequently, PCK equips teachers to address and correct students’ misconceptions about the subject matter they are learning.
According to Palmer’s ( 2017 ) perspective, adopting a comprehensive method for becoming a teacher involves intertwining the roles of teacher, student, subject, and life. He claimed that constructing a teacher identity involves recognizing one’s “inner landscapes,” which includes intellectual, emotional, and spiritual self-awareness. Therein, educators’ objectives in music/mathematics should revolve around aiding students in discovering avenues to knowing, comprehending, and enhancing their own selves.
In addition, it is widely recognized that emotions interact with and affect the learning process (Baker et al. 2010 ; D’Mello et al. 2014 ). Although it is commonly assumed that emotions play a role in musicians’ and music educators’ creative and educational endeavors (Smith 2021 ), the same holds true for mathematicians and mathematics educators (Bishop 2008 ; DeBellis & Goldin 2006 ; Resnick 1988 ; Schoenfeld 2016 ; Zan et al. 2006 ). Researchers accordingly discuss the influence of affect on “mathematical thinking” (Schoenfeld 2016 ), “problem solving” (Resnick 1988 ) and “mathematical capability” (DeBellis and Goldin 2006 ) among other related aspects.
Compared to educators, theorists typically present a set of propositions and theorems that are logically related to one another, providing an integrated and comprehensive way of thinking about the target phenomena (Bruscia 2005 ). A theory, as defined by Bruscia ( 2012b ), is a supposition based on logically and comprehensively integrated principles derived from extensive high-quality research. Music theorists grapple with how individuals acquire the ability to derive significance from sounds. Ultimately, the responsibility falls upon the teacher to make pivotal choices regarding the optimal methods for addressing the diverse needs of students in the music classroom (Isbell 2012 ). In mathematics, teachers with limited mathematical knowledge might find their professional capabilities restricted, although possessing such expertise doesn’t necessarily ensure effective teaching of mathematics (Da Ponte and Chapman 2015 ).
In the current study, we focus on investigating the convictions held by professionals in the realms of mathematics and music who specialize in theory and education. We aim to explore their viewpoints concerning the interrelation between these two disciplines.
Integrating music and mathematics
Integrated instruction involves the presentation of varied perspectives, each with distinct aims and objectives, within a shared educational context (Park and Son 2010 ). The integration of various disciplines brings about numerous benefits, including fostering innovation, literacy, motivation, teamwork, creativity, and actively engaging students in the learning process while promoting essential problem-solving skills (Liao 2016 ; NAEA 2016 ; Root-Bernstein 2015 ). Although multidisciplinary learning is highlighted in discussions concerning 21st-century skills, its practical implementation in educational settings tends to be relatively limited as students progress through K-12 education (Boice et al. 2021 ).
Special attention has been paid in recent years to music’s contribution to STEM in promoting creative thinking, for example in the fields of computing (e.g., Engelman et al. 2017 ) and math (e.g., Azaryahu et al. 2023 ; Azaryahu et al. 2024 ). The bulk of research focusing on the music learning’s effect on mathematical achievement centers around elementary students. The primary objective of this research is to explore how music can positively influence aspects such as memory, motivation, learning, and creativity in these students (Akın 2023 ; Azaryahu et al. 2023 ; Azaryahu et al. 2020 ; Azaryahu and Adi‐Japha 2022 ; Hallam and Himonides 2022 ). However, few researchers have examined the effect of music on mathematical learning among high school students and at the university level (Crowther, 2012 ; Lesser, 2014 , 2015 ).
This study aims to broaden the scope of integrating disciplines by focusing on middle school, high school, and music and mathematics teacher trainees at universities and colleges. Therethrough, we seek to examine the interconnections between these disciplines from the perspectives of experienced teachers and lecturers in these disciplines. The ultimate goal is to lay the foundation for developing multidisciplinary content units suitable for upper-division and university-level students.
Teachers’ perceptions of multidisciplinary education
The development of multidisciplinary curricula raises numerous questions, such as determining which content should be combined, and for which age groups or grade levels. Additionally, there is a need to explore how the integration will be applied in the classroom. Developing integrative curricula requires extensive knowledge and massive investment of both human and financial resources. As noted by Humes ( 2013 ), a teacher who undertakes the blending of two disciplines must possess a comprehensive mastery of both subjects. Moreover, blending two disciplines necessitates the respective teachers having excellent and effective didactic and pedagogic skills.
Research exploring teachers’ perceptions of multidisciplinary education is still in its early stages. However, recent studies in China, Korea, and Indonesia have shed light on the positive views of teachers regarding the future benefits to students pursuing careers that demand integrated skills (Kang 2019 ; Kartini and Widodo 2020 ; Kim et al. 2019 ; Rosikhoh et al. 2019 ). On the other hand, the obstacles to implementing such learning lie in two main areas: 1. The teachers’ sense of self-efficacy and knowledge; and 2. The teachers both being prepared for and open to the process.
Initially, it was found that teachers faced challenges in implementing multidisciplinary learning due to insufficient skills resulting from a lack of knowledge, comprehension, supportive resources, and adequate training. In many cases, teachers perceived multidisciplinary teaching merely as a series of isolated activities rather than embracing it as a wholistic approach to learning that emphasizes exploration and project-based learning (Boice et al. 2021 ). In the context of teaching math specifically, teachers report that there are a limited number of math areas that are appropriate for implementation in a multidisciplinary framework (Kim et al. 2019 ). According to their perspectives, educators believe that math is better suited as a supporting component in multidisciplinary learning rather than being the central focus. While this approach has the potential to facilitate progressive teaching and learning methods, its implementation is not fully realized to the extent it could be.
The literature presented in this section supports multidisciplinary teaching. However, it also cites significant challenges hindering its implementation, particularly concerning applications and consistent integration. These challenges stem from factors such as limited preparation time, inadequate educational resources, and the need for extensive knowledge in both music and mathematics. Moreover, it is essential to acknowledge that a deep understanding of the connections between music and mathematics often requires expertise in both disciplines. Mathematics teachers lacking familiarity and knowledge of basic music theory may encounter difficulties when attempting to establish meaningful connections between the two disciplines.
The study goal and questions
The main goal of the current study is to identify the perspectives of various kinds of experts on the interplay between music and mathematics. The study’s questions are:
What are the main categories of perceptions about the connection between music and mathematics?
How do the distinctions between these categories manifest among musicians, mathematicians, and lecturers in teacher training programs?
The study participants
The study’s participants consisted of 16 experts (4 musicians, 4 mathematicians, 4 music education lecturers, and 4 mathematic education lecturers) who participated voluntarily in this study (see Fig. 1 ).
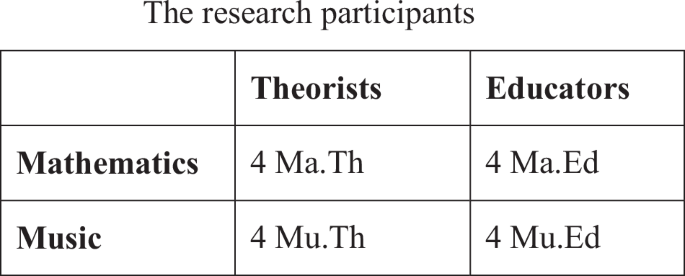
Includes groups of 4 musicians, 4 mathematicians, 4 music education lecturers, and 4 mathematics education lecturers.
Data collection
The data were collected by means of a qualitative research paradigm, through semi-structured interviews. The first author of this paper carried out all data collection. The experts were asked to think about and express their perceptions regarding the connections between music and mathematics in a general sense and from an applied pedagogical perspective during the interview. During interviews, the researcher kept a neutral attitude and did not provide any evaluative remarks. She asked the experts to clarify their ideas when they were not entirely clear and to contemplate the interconnection between their respective disciplines as it manifests in their work. Altogether 16 interviews were conducted, which were video- and audio-recorded, and all the recordings were transcribed.
Data analysis
In this study, we set out to explore the diverse perspectives of experts through three distinct lenses: theory, affect, and learning opportunities. These three distinct lenses emerged directly from the research participants – comprised of theorists and educators – and from the general literature on theory and practice (Bressler 1999 ). The research participants’ professional identities – whether rooted in theoretical frameworks (theory) or practical applications (learning opportunities) – can significantly shape their perspectives on the interconnection between music and mathematics (Bruscia 2005 ; Da Ponte and Chapman 2015 ; Palmer 2017). The third lens, affect, is shared by both participant types in the study – theorists and educators – given that emotions are inherent in any process of investigation, creation, or learning (Baker et al. 2010 ; D’Mello et al. 2014 ). Development of the subcategories was based on the grounded theory approach (Strauss and Corbin 1990 ), using content analysis of teachers’ discourse by repeated viewings of the videos of the interviews, and repeated readings of the transcripts.
First, experts’ statements about the relationship between music and mathematics were classified as fitting into one of the three categories: theory, affect, and learning opportunities. The category of theory included talk related to structures recognition, formal systems, abstract concepts and symbolic representations, and mathematical and musical creations. The category of affect included statements related to emotional engagement and enjoyment regarding aesthetic and beauty and their emotional effect on learning. The category of learning opportunities comprised statements related to educational approaches that integrate music and mathematics that enhance learning in both subjects.
Next, all of the data classified as belonging to a particular category – theory, affect, and/or learning opportunities – were categorized to create subcategories that reflect experts’ perceptions of the relationship between music and mathematics. The data analysis was inductive, first identifying the initial subcategories based on some of the data collected for a particular participant, then refining and extending the initial subcategories based on more data collected with the same participant, and finally, to refining the devised sub-categories by the analysis of data collected from all of the participating experts. Furthermore, all of the subcategories devised for the various categories of theory, affect, and learning opportunities were analyzed for commonalities and differences across the categories.
We performed inter-coder validation of the transcripts’ categorization buy the first and the third authors of this paper. We attained agreement on about 90% of utterances, while the remaining utterances were discussed by the authors and categorized based their agreement.
In this paper we present examples that illustrate experts’ perspectives on the connection between music and mathematics. The examples are borrowed mainly from the data collected from four content experts (indicated by pseudonyms) from the field of musical and mathematical theory and education, as their views were fairly common and corroborated those of many others who participated in the study: (1) a mathematics educator named Dan, (2) a music educator named Mika, (3) a mathematician named Adam and (4) a music theorist named Lisa. When any of the subcategories of theory, affect, and learning opportunities were missing in their talk, we used examples from other experts. The next section will present the outcomes derived from the insights of esteemed experts in the theoretical and educational domains of mathematics and music.
As presented in data analysis sections through directed analysis toward theory, affect, and learning opportunities, we developed various sub-categories that characterize experts’ perspectives on connections between music and mathematics. In what follows, we present excerpts from the interviews that exemplify various types of perspectives.
Theory perspectives
Abstract languages and structure.
Dan and Mika are experts in their respective fields of mathematics education (Dan) and music education (Mika). When asked how they view the connecting lines between music and mathematics, they replied:
1Ma_Ed - Dan – “Both mathematics and music are semantic systems [1-1] therefore they both allow formalization [1-2]. In other words, if there is some agreement on certain rules [1-3], a musical work and a mathematical work can be combined [1-4]. Both music and mathematics in a certain sense are a means of communication between people [1-5] … It seems to me that there is some element here that is related to the transmission of messages one way or another [1-6] … In terms of the structure of these systems, they are quite similar. My point is that there is some basic structure [1-7] from which you can grow and develop [1-8]. There are patterns in both music and mathematics, and this can be represented with the help of numbers and notes” [1-9].
2Mu_Ed - Mika – “The mystical aspect in me shows that music and mathematics are two embodiments and two languages of the same principle [2-1]. The principle is the divine order in which the world was created [2-2]. It is a way of communication [2-3]. I think it is very beautiful and important to link musical theory to the structures from which it is created. Symmetry, proportions and geometry [2-4].
The excerpts contain clear indicators of Dan and Mika’s conceptions of the connection between music and mathematics as two abstract languages with common semantic systems [1-1, 2-1, later 3-1] that are expressed by musical notes and numbers [1-9]. We consider this an indicator of their views on the Theory of music and mathematics. Both disciplines allow formalization [1-2] and behave according to certain rules and order [1-3, 2-2]. Dan’s view of the connection between music and mathematics, as it relates to form and structure, including natural structures and patterns [1-4, 1-7, 2-4, later 3-3], is a clear indicator of his connecting the theory of both disciplines. In Dan’s view, the basic structures and order enables growing and developing [1-8]. It is interesting to note that the experts in the field of musical and mathematical education viewed the commonality between the two languages as a means of communication [1-5, 2-3] and transmission of messages from a pedagogical perspective [1-6].
The same question about the connection between music and mathematics was posed to the theoreticians well. Adam and Lisa, experts in mathematics and music theory respectively, replied:
3Ma_Th - Adam – “Both languages are abstract [3-1]. Numbers are connected to both of them [3-2] …When the music is good, you discover the order there. Regularity [3-3] … The first name that comes up is Pythagoras. There is the Pythagorean theorem on one side and the Pythagorean scale on the other [3-4]. The Pythagoreans viewed numbers as something musical” [3-5].
4Mu_Th – Jack – “Math is numbers and music is numbers… you could just as well replace every sound with a number and it would work just as well [4-1] … I can give a numerical representation of almost any musical element [4-2]. All music and the history of music is deeply connected and inseparable from numbers and calculations” [4-3].
While both these theoreticians view both disciplines as abstract languages, just as the educational experts do, their emphasis lies on the central foundations of these disciplines. Adam and Jack’s descriptions focus on numerical representation as a unifier between music and mathematics [3-2, 3-5, 4-1, 4-2). Also, their theoretical explanation relies on historical context [4-3] for example, the Pythagorean theorem and the Pythagorean scale [3-4].
These excerpts (1Ma_Ed Dan, 2Mu_Ed Mika, 3Ma_Th Adam and 4Mus_Th Jack) reveal that the professors’ conceptions of the connection between music and mathematics includes the fundamentals of both disciplines as abstract languages adhering to strict form and structure. We found that the direction of talk about the connection between music and math is typical for most of those who participated in this study. However, while theoreticians in both disciplines referred to the representation of music through numbers from a historical perspective and stressed the language and structure as core elements, educational experts in both fields emphasized the commonality between the languages regarding communication and the transmission of messages from a pedagogical perspective.
Freedom and creative thinking
Along with the orderly structure that characterizes the two languages, music and mathematics, the need for breaching conventions, freedom, and creativity arose in the experts’ talk. In the following excerpt, Jack described how he uses the format to compose music:
5Mu_Th – Jack – “In my composition I leave myself the freedom to do what I want [5-1]. I don’t limit myself to a certain format [5-2]. What I pour into the pattern is my business and is taken from many considerations: what instruments I write for, the tempo, the atmosphere I want to create, the harmony, the dynamic, all these elements affect what I’m going to write [5-3] … I looked, for example, at how an architect designs a house [5-4]. First of all, s/he starts drawing the outline of the house, and little by little goes into the details [5-5]. So, I create the same thing, only in music [5-6].”
Like other music theorists, Jack expands upon the structural connection between music and mathematics for the purposes of composition, and emphasizes the ability to create original music by using an ordered pattern. In the above excerpt [5Mu_Th – Jack], he describes the composition process as being analogous to an architectural work [5-4]. The structure and form, which were mentioned earlier, serve as an excellent foundation for planning his musical work [5-5, 5-6]. Creative and original content can be poured into this structure [5-3], so there is a lot of freedom within the framework [5-1, 5-2]. Lisa expands upon Jack’s line of thinking, discussing the concept of freedom in the historical context of democracy:
6Mu_Th - Lisa – “In music there’s a lot of freedom [6-1], but the Greek philosophers said that if you change things in music, then society will change too [6-2]. Music would not have developed without the development of democracy and individualism [6-3] …The existence of the individual within a society that on the one hand has very regulated structures and on the other hand allows for the individual’s personal existence [6-4]”.
In Lisa’s view, as a musical theorist, there is a lot of freedom in music, which connects to the development of democracy and individualism in ancient Greece. While in the above excerpt [6Mu_Th_Lisa], she cites a parallel line of thinking to Jack’s regarding musical freedom [6-1], her reply contains an extension connecting freedom to concepts of individualism and democracy [6-2, 6-3].
The educational experts from both disciplines also referred to the transitions between defined musical or mathematical structures and liberating departures therefrom. Emma, a mathematics education professor, and Sue, a music education professor, had this to say:
7Ma_Ed - Emma – “Both the realms of mathematics and music offer opportunities for creativity, freedom, and flexibility for our students [1] - I also find liberty of invention in mathematics [2]. [after watching the video]: Elevation! It’s charming and amazing [3] because what appears symmetrical and beautiful – an elaborate polygon blocked inside a circle – also sounds very pleasant [4]. Equal peripheral angles that rest on equal strings creating harmony [5]. As soon as you break the rules, then you have something a little more interesting; it creates dissonance [6]”.
8Mu_Ed- Sue - “In general, I see maybe something related to order at the deeper level [1]. A musical analysis that needs some sort of order in it, some kind of thinking of derivatives [2]. [after watching the video]: I saw that when there’s something symmetrical, then the sounds are also harmonious [3], and when there’s something disharmonic, then the shapes are neither completely symmetrical nor different [4]. I think it’s very beautiful and important [5]. Symmetry, proportions, and geometry are also seen as shapes, and as movement, and as color [6]. Very illustrative and helpful [7]”.
Like all of the experts who participated in the study, Emma and Sue watched a short video presenting connection between geometrical shapes and sound. After doing so, they mentioned in the above excerpts [7Ma_Ed_Emma and 8Mu_Ed_Sue] the idea that there is a visual-aural connection between the disciplines [8-6, 8-7]. Most of the participants agreed that on the one hand, symmetrical shapes were demonstrated to represent harmonized sounds [7-4, 7-5, 8-1, 8-2, 8-3], while breaking the rules of symmetry resulted in dissonant or disharmonious sounds [7-6, 8-4]. In addition, not only do both music and mathematics enable creative thinking and breaching conventions, but both disciplines offer opportunities for creativity, freedom, and flexibility [7-1], and encourage new inventions [7-2].
In addition to the theoretical aspect discussed in the above excerpts [7Ma_Ed_Emma and 8Mu_Ed_Sue], the relationship between music and mathematics and its profound impact emerged. The interplay of patterns and rules, their manifestation in geometrical forms and sounds, and the freedom that they grant for creative expression and thinking all directly contribute to the affect , which is manifested by aesthetics, beauty, and evocation of emotion [7-3, 7-5].
Affect perspectives
Beauty and aesthetics.
The majority of research participants from both the theoretical and educational domains in music and mathematics cited the significance of beauty and aesthetics as a central theme:
9Ma_Ed - Dan – “Both fields are influenced by aesthetic beauty [9-1]. There’s no mathematics without aesthetic beauty, and there’s no music without aesthetic beauty [9-2]. The whole concept of aesthetics and harmony is related to both mathematics and music [9-3]. It’s very beautiful to see what you hear [9-4]. It’s visual, clear, and beautiful [9-5]. It’s interesting to explore the structure of a polygon with all the diagonals there and to hear the visual representation of all these symmetries [9-6]”.
10Mu_Ed – Sue - “Music and math are neat and beautiful! [10-1]. Patterns and connections [10-2]. If you connect a terraza and a quarta (i.e., musical intervals), you see how it also connects beautifully in geometrical space [10-3]. Mathematics is a beautiful thing [10-4]. I don’t understand it exactly [10-5] … But maybe if you find out the patterns that exists, it’s probably beautiful and they’ll understand the aesthetics better [10-6]”.
When prompted to reflect on the intersections between music and mathematics, the notion of affect arose unanimously among all the interviewees. The educational experts talked about beauty and aesthetics as tools for thinking about and understanding the disciplines. In the above excerpts [9Ma_Ed - Dan and 10Mu_Ed – Sue], the educational experts discussed the implementation of aesthetics and beauty within each discipline [9-2, 10-1, 10-4], as well as the interconnection between these disciplines [9-1, 9-3]. In addition, they cited the audio-visual connection, aforementioned in Emma’s and Lisa’s responses, which they described as giving rise to this beauty in the musical and mathematical space [9-4, 9-5, 10-3].
The theory experts approached the question of the origin of beauty and aesthetics from another aspect, citing the structural context:
11Ma_Th - Adam – “What makes beauty in music? The structure [11-1]. We cannot interpret it. You can hear a Beethoven symphony endless time. Why? Because you never get to the bottom of the guy’s mind [11-2]! That’s the complexity, that you unconsciously grasp the structure” [11-3].
12Mu_Th - Lisa – “When Beethoven writes a symphony in a way that is very regulated on the one hand and on the other hand finds his personal expression, it’s beautiful” [12-1].
Adam and Lisa argue that beauty rests on musical or mathematical form and structure [11-1, 11-3, 10-2]. In the above quotes [11Ma_Th – Adam, and 12Mu_Th – Lisa] they cited how both music and mathematics possess distinct boundaries that can be transcended or breached, and thus are difficult to understand [11-2, 11-3, 12-1, 10-5, 10-6]. In many cases, it is possible to discover the beauty and aesthetics in music and mathematics, which is accompanied by wonder and often evokes diverse emotions.
Discovery, wonder, and emotions
Beyond the sense of beauty and aesthetics associated with the musical or mathematical structure, experts from all fields linked music and mathematics to the sense of wonder when discovering a musical or mathematical phenomenon.
13Ma_Ed - Dan – “What is beauty? That’s a good question. [It’s] when we say ‘wow’ about some idea, or about something that was not clear to us and was not familiar [13-1], and suddenly it worked out so well [13-2]. I believe that both in music and in mathematics, there are such wonderful moments of discovery [13-3]”.
14Mu_Ed - Mika – “I’ve had cases where I derive aesthetic pleasure from musical structures [14-1]. Suddenly there’s a harmonious movement, and you say ‘wow, what beauty [14-2]’, and you get excited [14-3] …. I wish math teachers would try to find moments for students to experience the aesthetics of math [14-4]”.
15Ma_Ed - Emma – “The spiritual connection in my view is the main connection [15-1]. Mathematics was born, created, and developed thanks to the human spirit [15-2]. Owing to the people, the minds [15-3]. Objects with symmetrical and visually appealing qualities, such as an intricate polygon enclosed within a circle, possess an inherent pleasantness when translated into sound [15-4]”.
16Ma_Th - Adam – “A mathematical idea and a poem can affect us in the same way [16-1]. It’s a wonderful thing about music as well [16-2]. I can know that Brahms was a genius without understanding what he did [16-3]. One perceives it unconsciously as in poetry [16-4]”.
From an affect perspective, experts from all fields acknowledged the profound aesthetic connection shared by both music and mathematics. In the above excerpts [13Ma_Ed – Dan, 14Mu_Ed – Mika, 15Ma_Ed – Emma and 16Ma_Th – Adam], the participants stressed the sense of wonder [13-1,14-2, 16-2, 16-3, 16-4] and emotional experience when encountering the inherent beauty within these disciplines. Dan mentions the moment of discovery [13-2, 13-3] that evokes powerful emotions, such as pleasure or enthusiasm, and a deep appreciation for the interplay between music and mathematics [14-1, 14-3, 15-4, 16-1]. Moreover, the experts addressed the spiritual as the main connection between the disciplines [15-1]. From an affect perspective, Emma said that mathematics was born, created, and developed owing to the humans spirit and mind [15-1, 15-2, 15-3], which enable us to appreciate beauty and aesthetics, leading us to discover and be deeply moved by moments of wonder. Finally, Mika, with a music education expert’s view, mentioned her wish that mathematic instruction would enable students to learn about the aesthetics of math [14-4].
Learning opportunities
Integrating mathematics and music into various disciplines.
As aforementioned, the affect perspectives inherent in music and mathematics have the power to evoke emotions, thereby facilitating deep learning experiences. Moreover, this emotional spark serves as a catalyst for meaningful multidisciplinary learning, opening up new paths for wholistic and impactful learning.
17Mu_Th – Jack - “Music doesn’t develop in a vacuum. It’s connected to nature in a wholistic way [17-1]. I would combine music and art, music and literature, and philosophy to expand thinking [17-2]. Anything that opens the mind to new things is welcome [17-3], but you have to remember that it can also scare students [17-4]”.
18Mu_Ed - Mika – “In my opinion, there’s great value in multidisciplinary learning in schools [18-1]. It can broaden students’ horizons by encouraging them to explore phenomena or objects from various perspectives and angles [18-2]. I built a lesson plan once on the subject of longing, related to infinity and the path of infinity, i.e., does a number represent what it is? And when you reach the destination? [18-3] … the entire issue of intervals and difference also relates to longing and musical, physical, and emotional distance [18-4].
19Ma_Th – Tom – “Sound is a physical phenomenon, and as we know, physics is a field where the main tool is mathematics, and there is mathematics at a very deep level that can analyze sounds [19-1], for example how musical instruments work, how waves propagate… architectural acoustics with mathematical analyses… scales, intervals, regularities [19-2]. Sound is cyclical, a wave that repeats. And it happens so fast – thousands of vibrations per second – so you don’t hear each one separately, but the pitch is the frequency [19-3]”.
From a learning opportunities perspective, most of the participants supported multidisciplinary learning in schools [17-2, 17-3, 18-1]. In the above excerpts [17Mu_Th – Jack, 18Mu_Ed – Mika and 19Ma_Th – Tom], they engaged in talk regarding the intersections of music, mathematics, and other subjects such as literature, philosophy, art, or science, and cited their potential for broadening horizons, skills, and knowledge [17-1, 18-2]. Tom expanded in his talk upon the connection between music, mathematics, and acoustics [19-1]. Beyond the physical properties of sound, he described how combining the disciplines can contribute to our knowledge of how musical instruments work, how waves propagate, etc. [19-2, 19-3]. Mika also linked a concept such as infinity to both fields, and connected it to numbers and emotions (i.e., longing) [18-3, 18-4]. This is an excellent example of the connection of music and mathematics in a theory perspective and from an affect perspective implemented in an integrated curriculum.
Only one mathematical theory expert expressed reservations about multidisciplinary learning:
20Ma_Th – Adam – I don’t think it’s necessary to combine the fields [20-1]. Mathematics is mathematics and music is music. You need to understand the Pythagorean theorem; you won’t learn something that will teach you the Pythagorean theorem [21-2]. But yes, in my opinion, music should be introduced into schools in general. It is important. It will make us better people [21-3].
From his own experience, Adam describes his resistance to the combining of music and mathematics in school [20Ma_Th – Adam]. He voiced concerns that the fusion of subjects could lead to disruption [21-2], and consequently, he believes that there is no place for such an approach [21-1]. Another professor, a musician theorist, expressed earlier that while multidisciplinary learning is welcome, it might potentially intimidate or frighten the students [17-4]. Nonetheless, Adam concluded with the notion that music is an important subject to be learned, separately, in order to “become better people” [21-3].
Music as a tool for learning mathematics
A common thread was identified only among the music education experts, who drew a connection between music and mathematics vis-a-vis teaching mathematics through the use of musical tools.
21Mu_Ed - Mika – “Only when they started working with me on rhythms, did I start to understand fractions [21-1]”.
22Mu_Ed - Sue – “Fractions and rhythms. How can one explain that twice the speed can end up reaching the same finish line as a slower speed? Division of time [22-1]. Rhythm exercises in general are a very successful way to explain topics in mathematics [22-2]. Pythagoras, the harmonic smith, divided the octave into intervals that are smaller and smaller, and the distances are mathematical. So you see the division of the musical space, which is very similar to a geometric space [22-3]”.
The music education experts recognized the potential of combining music and mathematics to enhance students’ comprehension of fractions. In the above excerpts [21Mu_Ed – Mika and 21Mu_Ed – Sue], Sue shared successful experiences in her work with children, using music as a tool to facilitate the understanding of concepts such as rhythm, division of time, and simple fractions [22-1, 22-2, 22-3]. According to Sue, there is a potential in utilizing music as a vehicle for learning fractions. In addition, Mika talked about her personal experience of understanding fractions by rhythm [21-1]. Note that except for the music education experts, none of the other participants referred to this issue.
Mathematics as a key tool for music analysis and creation
The final common thread was identified only among the music theory experts, who described mathematics as a key tool for music analysis and creation.
23Mu_Th – Jack – “I compose with a fractal method that refers to durations, proportions, and structure, and thus the micro and macro are the same as in the fractal [23-1] … I’ve been exploring this in my musical works for 20 years [23-2]. It’s a whole world, because there’s no limit to how many things you can do with it [23-3]. I wrote dozens of works using this method [23-4]”.
24Mu_Th – Zak – “Mathematics is a tool for composition [24-1]. Counterpoint, for example, is a completely mathematical matter [24-2]. Mathematical thinking is always integrated into music [24-3] … Analyzing musical works is done logically [24-4] … it reminds me that I wrote works with geometric thinking, like playing, increasing, decreasing, rotating, reflecting [24-5]”.
25Ma_Th – Adam – “Musicians think like mathematicians [25-1]. To write music or understand music, you need to understand mathematical rules and understand abstract thinking [25-2].
The theoreticians in both disciplines discussed the role of mathematical thinking in understanding and composing music. In the above excepts [23Mu_Th – Jack, 24Mu_Th – Zak and 25Ma_Th - Adam], Jack and Zak shared their own composition process resting on mathematical concepts [23-1, 24-5]. Zak cited the strong connection between composing and analyzing music using mathematical thinking and logic [24-2, 24-3, 24-4], and stated that mathematics is a tool for composing music [24-1]. Jack delved deeper into this topic, sharing his two-decade journey in composition, marked by the application of mathematical thinking [23-2, 23-3], a journey that has yielded a diverse body of musical work [23-4]. Note that only the theoreticians in both disciplines referred to this issue. In addition, Adam, a mathematical theorist who is not a composer and has no musical expertise, corroborated the others’ claims and drew a direct line between composition and mathematical thinking and understanding [25-1, 25-2].
This paper seeks to characterize mathematical and musical experts’ perceptions of the connection between music and mathematics. Interviews with musicians, mathematicians, and educators in both disciplines were analyzed. To illustrate the main findings of this study, we chose several examples, mostly from the material generated by four particular experts (Dan, Mika, Adam, and Lisa), and added other examples to help us draw a more complete picture of experts’ perceptions of the connection between music and mathematics. The paper focuses on theory, affect, and learning opportunities as main indicators of this connection. We analyzed the experts’ discourse in light of these three categories. Based on this analysis, we devised specific characteristics of the connection between music and mathematics that reflect the experts’ perceptions. In this section, we summarize our findings, propose a model of the connection between music and mathematics, and discuss this model.
We found that experts’ perceptions of the connection between music and mathematics consist of seven main categories: (1) abstract language and structure , i.e., perceiving the core foundational structure on one hand, and their pedagogical perspective on the other, (2) freedom and creative thinking , i.e., thinking outside the box and breaching conventions, (3) beauty and aesthetics , i.e., connecting the musical and mathematical space aesthetically and structurally on one hand, and as tools for thinking and understanding on the other hand, (4) discovery, wonder, and emotions , i.e., citing the added value inherent in each discipline in expressive aspects, (5) integrating mathematics and music into various disciplines , i.e., combining the shared areas from each discipline into wholistic learning, (6) music as a tool for learning mathematics , i.e., using music to enhance mathematics, and finally (7) mathematics as a tool for music analysis and creation , i.e., using mathematics to analyze and create music. Figure 2 presents a word cloud highlighting the main words used by all participants. (Fig. 2 ) Fig. 3 presents a word cloud showing the main words used by different types of experts: theorists and educators from various disciplines. (Fig. 3 ).

The word cloud emphasizes the most frequently used words by all participants, illustrating key themes and terms.

The word clouds illustrate the main words used by different types of experts: A . Mathematicians, B . Math Educators, C . Musicians, D . Music Educators, highlighting unique and common themes within each group.
We found that musicians and mathematicians (theoreticians) recognize the connection between the two disciplines through concepts such as abstract languages and structure as core foundation . The educators in both disciplines referred to language and structure from a pedagogical perspective. The recognition of structure and language fosters an understanding of the beauty and aesthetics inherent in these domains in a structural context for the theorists, or as tools for thinking and understanding for the educators, cultivating a profound sense of exploration and wonder , while also enabling creative thinking . The conceptual combination of these four components leads to the possibility of integrating mathematics and music into various disciplines , using music as a tool for learning mathematics or using mathematics as a tool for music analysis and creation . (Fig. 4 ).
This model depicts experts' conceptions of the interrelationships between mathematics and music, highlighting key connections and themes identified in the study.
Two main issues that emerged unanimously among participants – both theorists and educators from the disciplines of music and mathematics through differing prisms – were abstract languages and structure and beauty and aesthetics . Similar to numerous researchers (Papadopoulos 2002 ; Douthett 2008 ; Johnson 2008 ), both the musicians and mathematicians discussed the historical dimension of representing music through numerical elements and expressing mathematical concepts in music. Compared to them, educational experts in both disciplines cited these languages’ shared attributes in terms of facilitating communication and conveying messages. All participants related the form and structure component in both disciplines to beauty and aesthetics. Whereas discussions among musicians and mathematicians delved into the concepts of beauty and aesthetics stemming from structured arrangements and innovative rule-breaking, educational experts from both disciplines underscored the pedagogical significance of audio-visual associations with beauty and aesthetics. They all expressed a strong urge to nurture an appreciation for these aspects in their students. These findings corroborate the research conclusions of Beijaard et al. ( 2000 ) concerning the self-identity of educators. Therein, they highlighted the shared aspects of enriching subject expertise (in terms of form and structure), devising engaging didactical approaches (including visual-auditory integration), and fostering pedagogic perspectives that facilitate the comprehension of beauty and aesthetics in both disciplines.
Two other topics that arose among the majority of participants to varying degrees were freedom and creative thinking and discovery, wonder, and emotions . In contrast to the two previous topics, the discussion thereon was not contingent upon the discipline of either music or mathematics; rather, it was shaped by theoretical or educational perspectives. Many educational experts in both disciplines cited the sense of wonder and the profound emotional journey that accompanies the experience of teaching music or mathematics, where the inherent beauty of these subjects is discovered. Liao ( 2016 ) and Root-Bernstein ( 2015 ) claimed that the integration of several disciplines brings about numerous benefits, including fostering innovation, motivation, teamwork, creativity, and actively engaging students in the learning process. From the perspective of experts in music and mathematics education, the process of learning, which encompasses understanding structural aspects on the one hand and recognizing aesthetic elements on the other, demands the cultivation of a mindset centered around exploration, discovery, and appreciation among both educators and students in these fields. Discovering the wonder inherent in both disciplines enables freedom and develops creative thinking, both significant 21st-century skills (OECD, 2019).
It is interesting that musical theorists, unlike mathematical theorists, stressed freedom and creative thinking . Most of them talked about the structural connection between music and mathematics particularly in the realm of composition, citing the ability to generate innovative musical compositions through the deliberate utilization of structured patterns. The structure and format provide a solid foundation for planning musical pieces. Therein, innovative and authentic content can be incorporated, thereby enabling substantial creative liberty. Note also that while theoretical musicians emphasized this matter, theoretical mathematicians chose not to engage in its discussion.
The examination of the four categories in this chapter (i.e., abstract languages and structure , beauty and aesthetics , discovery, wonder, and emotions , and freedom and creative thinking ) paves the way to several learning opportunities. Educational experts extensively mentioned the concept of integrating mathematics and music into various disciplines , while theoreticians mentioned it to a lesser extent. Educational experts from both disciplines cited the power of wholistic pedagogy in education. They underscored this approach to education, wherein one subject can be comprehended from various perspectives. Thus, according to the experts in this study, music and mathematics can be taught along with science, literature, philosophy, or art. This kind of broad connection combines the structure of the languages, the aesthetics and beauty therein, the process of discovering the wonder of the wholistic connection, and consequently eliciting the liberty of creative thinking from each discipline.
The concept of combining music and mathematics sparked the potential for music educators to employ music as a teaching tool for mathematics, and to utilize mathematical thinking for the analysis and composition of music. Music educators acknowledged the capacity to synergize music and mathematics to enrich students’ grasp of fractions. They reported productive instances from their interactions with children when utilizing music as a tool to simplify comprehension of concepts like rhythm, temporal division, and basic fractions. While this integrated approach to learning simple fraction concepts via rhythm corroborates previous studies (Azaryahu et al. 2020 ; Courey et al. 2012 ), the educational challenge is to provide interesting and stimulating integrated lessons that could lead students to discover the wonder and beauty of these disciplines. Finally, theoretical musicians and mathematicians cited mathematics’ role in composing and analyzing music. The musicians recounted their personal experiences in employing mathematical tools and logic in the process of music composition.
Conclusions
In conclusion, when examining the intriguing relationship between music and mathematics from the perspectives of theoreticians and educators, we found that while theorists engage directly with issues related to structure, creative thinking, beauty, and the sense of wonder in discovering phenomena; educators leverage these shared aspects to enhance students’ comprehension, provide experiential learning opportunities, and deepen students’ theoretical knowledge.
The conclusions reported herein should be considered within the limitations of the study. The current study was limited by a relatively small sample size. Future research should involve a larger population of mathematicians, musicians, and education experts in both fields, and employ mixed methods to thoroughly test the model.
This study opened new doors for future research wherein utilization of experts’ insights to craft integrated study modules of music and mathematics can be explored, a pursuit that carries substantial significance. We hope to have shed light on the pivotal facets of the unique interrelation between these disciplines, a revelation poised to catalyze deep and fascinating integrated learning inspection in the times ahead.
Data availability
The datasets generated and analyzed during the current study are not publicly available due to individual privacy but are available from the corresponding author upon reasonable request.
Akin, A. (2024). Let me make mathematics and music together: A meta-analysis of the causal role of music interventions on mathematics achievement. Educational Studies. https://doi.org/10.1080/03055698.2023.2216826
An, S (2012). The effects of music-mathematics integrated curriculum and instruction on elementary students’ mathematics achievement and dispositions. Texas A&M University
Azaryahu L, Courey SJ, Elkoshi R, Adi‐Japha E (2020) ‘MusiMath’ and ‘Academic Music’: two music‐based intervention programs for fractions learning in fourth grade students. Dev Sci 23(4):e12882
Article PubMed Google Scholar
Azaryahu L, Adi-Japha E (2022) “MusiMath”: a music-based intervention program for learning patterns and symmetry. J Exp Educ 90(2):319–343
Article Google Scholar
Azaryahu L, Broza O, Cohen S, Hershkovitz S, Adi-Japha E (2023) Development of creative thinking patterns via math and music. Think Ski Creat 47(1):101196. https://doi.org/10.1016/j.tsc.2022.101196
Azaryahu L, Broza O, Cohen S, Hershkovitz S, Adi-Japha E (2024) Development of creative thinking via fractions and rhythm. Think Skills Creat 52:101514
Baker R. S, D’Mello S. K, Rodrigo M. M. T, Graesser A. C (2010) Better to be frustrated than bored: The incidence, persistence, and impact of learners’ cognitive–affective states during interactions with three different computer-based learning environments. Int J Hum-Comput Stud 68(4):223–241
Bamberger J, Disessa A (2003) Music as embodied mathematics: a study of a mutually informing affinity. Int J Comput Math Educ 8:123–160
Google Scholar
Beijaard D, Verloop N, Vermunt JD (2000) Teachers’ perceptions of professional identity: an exploratory study from a personal knowledge perspective. Teach Teach Educ 16(7):749–764
Bishop AJ (2008) Teachers’ mathematical values for developing mathematical thinking in classrooms: theory, research, and policy. Math Educ 11(1/2):79–88
Boice KL, Jackson JR, Alemdar M, Rao AE, Grossman S, Usselman M (2021) Supporting teachers on their STEAM journey: a collaborative STEAM teacher training program. Educ Sci 11(3):105
Bressler CE (1999) An Introduction to Theory and Practice. Prentice-Hall, Upper Saddle River, NJ
Bruscia KE (2005) Developing theory. Music Ther Res 2:540–551
Bruscia, KE (ed.). (2012b). “Developing theory” in Readings on Music Therapy Theory (pp. 67–153). Gilsum, NH: Barcelona Publishers
Courey S. J, Balogh E, Siker J. R, Paik J (2012) Academic music: Music instruction to engage third-grade students in learning basic fraction concepts. Edu Stud Math 81:251–278
Crowther G (2012) Using science songs to enhance learning: An interdisciplinary approach. CBE—Life Sci Educ 11(1):26–30
Article PubMed PubMed Central Google Scholar
Da Ponte JP, Chapman O (2015) “Prospective mathematics teachers’ learning and knowledge for teaching” in Handbook of International Research in Mathematics Education (pp. 275–296). Routledge
DeBellis VA, Goldin GA (2006) Affect and meta-affect in mathematical problem solving: a representational perspective. Educ Stud Math 63(2):131–147
Douthett JM (2008) Music theory and mathematics: Chords, collections, and transformations (Vol. 50). University of Rochester Press
D’Mello S, Lehman B, Pekrun R, Graesser A (2014) Confusion can be beneficial for learning. Learn Instr 29:153–170
Engelman S, Magerko B, McKlin T, Miller M, Edwards D, Freeman J (2017) “Creativity in authentic STEAM education with EarSketch” in Proceedings of the 2017 ACM SIGCSE Technical Symposium on Computer Science Education, Seattle, pp. 183–188
Erickson HL (2002) Concept-based curriculum and instruction: teaching beyond the facts. Corwin Press
Gess-Newsome J, Taylor JA, Carlson J, Gardner AL, Wilson CD, Stuhlsatz MA (2019) Teacher pedagogical content knowledge, practice, and student achievement. Int J Sci Educ 41(7):944–963
Hargreaves A (2001) Emotional geographies of teaching. Teach Coll Rec 103(6):1056–1080
Hallam S, Himonides E (2022) The power of music: an exploration of the evidence. Open Book Publishers
Humes W (2013) Curriculum for excellence and interdisciplinary learning. Scott Educ Rev 45(1):82–93
Isbell D (2012) Learning theories: insights for music educators. Gen Music Today 25(2):19–23
Johnson TA (2008) Foundations of diatonic theory: a mathematically based approach to music fundamentals. Scarecrow Press, Lanham, MD
Kang NH (2019) A review of the effect of integrated STEM or STEAM (science, technology, engineering, arts, and mathematics) education in South Korea. Asia-Pac Sci Educ 5(1):1–22
Kartini D, Widodo A (2020) Exploring elementary teachers’ and students’ beliefs and readiness toward STEAM education. Elem Sch Forum 7(1):58–69
Kim MK, Lee JY, Yang H, Lee J, Jang JN, Kim SJ (2019) Analysis of elementary school teachers’ perceptions of mathematics-focused STEAM education in Korea. EURASIA J Math Sci Technol Educ 15(9):em1746
Lesser, L. (2014) “Mathematical Lyrics: Noteworthy Endeavours in Education,” J Arts, 8(1–2), 46–53. https://www.tandfonline.com/doi/abs/10.1080/17513472.2014.950833
Lesser, L. (2015) “ ‘American Pi’: The Story of a Song about Pi,” J Math Educ, 8(2), 158–168. https://educationforatoz.com/images/2015_Larry_Lesser.pdf
Liu S (2013) Pedagogical content knowledge: a case study of ESL teacher educator. Engl Lang Teach 6(7):128–138
Liao C (2016) From interdisciplinary to transdisciplinary: An arts-integrated approach to STEAM education. ART educ 69(6):44–49
Nagisetty V (2014) Using music-related concepts to teach high school math (Doctoral dissertation, Portland State University)
National Art Education Association [NAEA]. (2016) Using art education to build a stronger workforce (Accessed 10 December 2017) at https://arteducators-prod.s3.amazonaws.com/documents/535/ff8bfae5-6b4f-4352-b900-4fc1182ad2b1.pdf?1455134278
OECD. (2019) An OECD Learning Framework 2030. The Future of Education and Labor, 23-35
Palmer, P. J. (2017). The courage to teach guide for reflection and renewal. John Wiley & Sons
Papadopoulos A (2002) Mathematics and music theory: from Pythagoras to Rameau. Math Intell 24(1):65–73
Article MathSciNet Google Scholar
Park JY, Son JB (2010) Transitioning toward transdisciplinary learning in a multidisciplinary environment. Int J Pedagogies Learn 6(1):82–93
Resnick LB (1988) Treating mathematics as an ill-structured discipline. Learning Research and Development Center, Pittsburgh Univ., PA
Rosikhoh D, Mardhiyatirrahmah L, Abdussakir A, Abtokhi A, Rofiki I (2019) Experienced teachers’ perceptions: math-focused STEAM learning. Abjadia: Int J Educ 4(2):118–128
Rothstein E (2006) Emblems of mind: the inner life of music and mathematics. University of Chicago Press
Root-Bernstein R (2015) Arts and crafts as adjuncts to STEM education to foster creativity in gifted and talented students. Asia Pac Educ Rev 16:203–212. https://doi.org/10.1007/s12564-015-9362
Schoenfeld AH (2016) Learning to think mathematically: problem solving, metacognition, and sense making in mathematics [reprint]. J Educ 196(2):1–38
Shulman L (1987) Knowledge and teaching: foundations of the new reform. Harv Educ Rev 57(1):1–23
Article ADS Google Scholar
Smith TD (2021) Music education for surviving and thriving: cultivating children’s wonder, senses, emotional wellbeing, and wild nature as a means to discover and fulfill their life’s purpose. Front Educ 6:648799. AprilLausanne, CH: Frontiers Media
Strauss, A., & Corbin, J. (1990) Basics of qualitative research (Vol. 15). Newbury Park, CA: sage
Wang Y, Zhang J, Mao Y (2024) Harmonizing mathematics: unveiling the impact of music integration on academic performance–a meta-analysis. Think Skills Creativity 52:101554
Wollenberg S (2003) “Music and mathematics: an overview”. In: Fauvel J, Flood R, Wilson R (eds.) Music and mathematics: From Pythagoras to fractals. Oxford University Press, Oxford, UK, p 1–9
Zan R, Brown L, Evans J, Hannula M. S(2006) Affect in mathematics education: An introduction. Educ Stud Math 63:113–121. https://doi.org/10.1007/s10649-006-9028-2
Download references
Acknowledgements
The research was supported by the MOFET institute.
Author information
Authors and affiliations.
The MOFET Institute, Tel-Aviv, Israel
Libby Azaryahu
The Academic College Levinsky - Wingate, Tel-Aviv, Israel
The Jerusalem Academy of Music and Dance Israel, Jerusalem, Israel
University of Haifa, Haifa, Israel
Roza Leikin
You can also search for this author in PubMed Google Scholar
Contributions
IA contributed to the conception of the study. RL contributed to the design of the study, interpretation of data, data analysis and substantively revising it. LA conducted the study and contributed to the analysis of the data, interpretation of data, and substantively revised it. All authors read and approved the final manuscript.
Corresponding author
Correspondence to Libby Azaryahu .
Ethics declarations
Ethical statements.
The study was approved by the ethics committee of the MOFET Institute’s Review Board for the Protection of Human Participants in Research number RB2302PD.
Informed consent
An informed consent was obtained from all participants.
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/ .
Reprints and permissions
About this article
Cite this article.
Azaryahu, L., Ariel, I. & Leikin, R. Interplay between music and mathematics in the eyes of the beholder: focusing on differing types of expertise. Humanit Soc Sci Commun 11 , 1153 (2024). https://doi.org/10.1057/s41599-024-03631-z
Download citation
Received : 24 February 2024
Accepted : 21 August 2024
Published : 07 September 2024
DOI : https://doi.org/10.1057/s41599-024-03631-z
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
Quick links
- Explore articles by subject
- Guide to authors
- Editorial policies
An official website of the United States government
The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.
The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.
- Publications
- Account settings
Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .
- Advanced Search
- Journal List
- Front Psychol
Gaining Mathematical Understanding: The Effects of Creative Mathematical Reasoning and Cognitive Proficiency
Bert jonsson.
1 Department of Applied Educational Science, Umeå University, Umeå, Sweden
2 Umeå Mathematics Education Research Center, Umeå, Sweden
Carina Granberg
Johan lithner.
3 Department of Science and Mathematics Education, Umeå University, Umeå, Sweden
Associated Data
The datasets are available on request to the corresponding author.
In the field of mathematics education, one of the main questions remaining under debate is whether students’ development of mathematical reasoning and problem-solving is aided more by solving tasks with given instructions or by solving them without instructions. It has been argued, that providing little or no instruction for a mathematical task generates a mathematical struggle, which can facilitate learning. This view in contrast, tasks in which routine procedures can be applied can lead to mechanical repetition with little or no conceptual understanding. This study contrasts Creative Mathematical Reasoning (CMR), in which students must construct the mathematical method, with Algorithmic Reasoning (AR), in which predetermined methods and procedures on how to solve the task are given. Moreover, measures of fluid intelligence and working memory capacity are included in the analyses alongside the students’ math tracks. The results show that practicing with CMR tasks was superior to practicing with AR tasks in terms of students’ performance on practiced test tasks and transfer test tasks . Cognitive proficiency was shown to have an effect on students’ learning for both CMR and AR learning conditions. However, math tracks (advanced versus a more basic level) showed no significant effect. It is argued that going beyond step-by-step textbook solutions is essential and that students need to be presented with mathematical activities involving a struggle. In the CMR approach, students must focus on the relevant information in order to solve the task, and the characteristics of CMR tasks can guide students to the structural features that are critical for aiding comprehension.
Introduction
Supporting students’ mathematical reasoning and problem-solving has been pointed out as important by the National Council of Teachers of Mathematics (NCTM; 26T 1 ). This philosophy is reflected in the wide range of mathematics education research focusing on the impact different teaching designs might have on students’ reasoning, problem-solving ability, and conceptual understanding (e.g., Coles and Brown, 2016 ; Lithner, 2017 ). One of the recurrent questions in this field is whether students learn more by solving tasks with given instructions or without them: “The contrast between the two positions is best understood as a continuum, and both ends appear to have their own strengths and weaknesses” ( Lee and Anderson, 2013 , p. 446).
It has been argued that providing students with instructions for solving tasks lowers the cognitive demand and frees up resources that students can use to develop a conceptual understanding (e.g., worked example design; Sweller et al., 2011 ). In contrast, other approaches argue that students should not be given instructions for solving tasks; one example is Kapur (2008 , 2010) suggestion of “ill-structured” task design. With respect to the latter approach, Hiebert and Grouws (2007) and Niss (2007) emphasize that providing students with little or no instruction generates a struggle (in a positive sense) with important mathematics, which in turn facilitates learning. According to Hiebert (2003) and Lithner (2008 , 2017) , one of the most challenging aspects of mathematical education is that the teaching models used in schools are commonly based on mechanical repetition, following step-by-step methods, and using predefined algorithms—methods that are commonly viewed as rote learning. Rote learning (i.e., learning facts and procedures) can be positive, as it can reduce the load on the working memory and free up cognitive resources, which can be used for more cognitively demanding activities ( Wirebring et al., 2015 ). A typical example of rote learning is knowledge of the multiplication table, which involves the ability to immediately retrieve “7 × 9 = 63” from the long-term memory; this is much less cognitively demanding than calculating 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7. However, if teaching and/or learning strategies are solely based on rote learning, students will be prevented from developing their ability to struggle with important mathematics, forming an interest in such struggles, gaining conceptual understanding, and finding their own solution methods.
Indeed, several studies have shown that students are mainly given tasks that promote the use of predetermined algorithms, procedures, and/or examples of how to solve the task rather than opportunities to engage in a problem-solving struggle without instruction ( Stacey and Vincent, 2009 ; Denisse et al., 2012 ; Boesen et al., 2014 ; Jäder et al., 2019 ). For example, Jäder et al. (2019) examined mathematics textbooks from 12 countries and found that 79% of the textbook tasks could be solved by merely following provided procedures, 13% could be solved by minor adjustments of the procedure, and only 9% required students to create (parts of) their own methods (for similar findings, also see Pointon and Sangwin, 2003 ; Bergqvist, 2007 ; Mac an Bhaird et al., 2017 ). In response to these findings, Lithner (2008 , 2017) developed a framework arguing that the use of instructions in terms of predefined algorithms has negative long-term consequences for the development of students’ conceptual understanding. To develop their conceptual understanding, students must instead engage in creating (parts of) the methods by themselves. This framework, which addresses algorithmic and creative reasoning, guides the present study.
Research Framework: Algorithmic and Creative Mathematical Reasoning
In the Lithner (2008) framework, task design, students’ reasoning, and students’ learning opportunities are related. When students solve tasks using provided methods/algorithms, their reasoning is likely to become imitative (i.e., using the provided method/algorithm without any reflection). Lithner (2008) defines this kind of reasoning as Algorithmic Reasoning (AR), and argues that AR is likely to lead to rote learning. In contrast, when students solve tasks without a provided method or algorithm, they are “forced” to struggle, and their reasoning needs to be—and will become—more creative. Lithner denotes this way of reasoning as Creative Mathematical Reasoning (CMR) and suggests that CMR is beneficial for the development of conceptual understanding. It is important to note that creativity in this context is neither “genius” nor “exceptional novelty;” rather, creativity is defined as “the creation of mathematical task solutions that are original to the individual who creates them, though the solutions can be modest” ( Jonsson et al., 2014 , p. 22; see also Silver, 1997 ; Lithner, 2008 ; for similar reasoning). Lithner (2008) argues that the reasoning inherent in CMR must fulfill three criteria: (i) creativity , as the learner creates a previously unexperienced reasoning sequence or recreates a forgotten one; (ii) plausibility , as there are predictive arguments supporting strategy choice and verification arguments explaining why the strategy implementation and conclusions are true or plausible; and (iii) anchoring , as the learner’s arguments are anchored in the intrinsic mathematical properties of the reasoning components.
Previous studies have shown that students practicing with CMR outperform students practicing with AR on test tasks ( Jonsson et al., 2014 ; Jonsson et al., 2016 ; Norqvist, 2017 ; Norqvist et al., 2019 ). Jonsson et al. (2016) investigated whether the effects of effortful struggle or overlapping processes based on task similarity (denoted as transfer appropriate processing, or TAP; Franks et al., 2000 ) underlie the effects of using CMR and AR. The results did reveal effects of TAP for both CMR and AR tasks, with an average effect size (Cohens d ; Cohen, 1992 ) of d = 0.27. While for effortful struggle, which characterizes CMR, the average effect size was d = 1.34. It was concluded that effortful struggle is a more likely explanation for the positive effects of using CMR than TAP.
In sum, the use of instructions in terms of predefined algorithms (AR) is argued to have negative long-term consequences on students’ development of conceptual understanding and to deteriorate students’ interest in struggling with important mathematics (e.g., Jäder et al., 2019 ). In contrast, the CMR approach requires students to engage in a effortful and productive struggle when performing CMR (e.g., Lithner, 2017 ). However, since the students that participated in previous studies were only given practiced test tasks (albeit with different numbers), the results may “merely” reflect memory consolidation without a corresponding conceptual understanding. If, after practice, students can apply their acquired reasoning to tasks not previously practiced, this would indicate a conceptual understanding.
In the present study, we investigate the effects of using AR and CMR tasks during practice, on subsequent test tasks, including both practiced test tasks and transfer test tasks . We are familiar with the large amount of transfer research in the literature and are aware that a distinction has been made between near transfer and far transfer tasks (e.g., Barnett and Ceci, 2002 ; Butler et al., 2017 ). In the present study, no attempt to distinguish between transfer and near transfer is made, we define transfer tasks as tasks that require a new reasoning sequence in order to be solved (see Mac an Bhaird et al., 2017 for a similar argument). These tasks are further described in the Methods section in conjunction with examples of tasks.
Mathematics and Individual Differences in Cognition
Domain-general abilities, such as general intelligence, influence learning across many academic domains, with mathematics being no exception ( Carroll, 1993 ). General intelligence, which is commonly denoted as the ability to think logically and systematically, was explored in a prospective study of 70,000 students. Overall, it was found that general intelligence could explain 58.6% of the variation in performance on national tests at 16 years of age ( Deary et al., 2007 ). Others have found slightly lower correlations. In a survey by Mackintosh and Mackintosh (2011) , the correlations between intelligence quotient (IQ) scores and school grades were between 0.4 and 0.7. Fluid intelligence is both part of and closely related to general intelligence ( Primi et al., 2010 ), and is recognized as a causal factor in an individual’s response when encountering new situations ( Watkins et al., 2007 ; Valentin Kvist and Gustafsson, 2008 ) and solving mathematical tasks ( Floyd et al., 2003 ; Taub et al., 2008 ). Moreover, there is a high degree of similarity between the mathematics problems used in schools and those commonly administered during intelligence tests that measure fluid cognitive skills ( Blair et al., 2005 ).
Solving arithmetic task places demands on our working memory because of the multiple steps that often characterize math. When doing math, we use our working memory to retrieve the information needed to solve the math task, keep relevant information about the problem salient, and inhibit irrelevant information. Baddeley (2000 , 2010) multicomponent working memory model is a common model used to describe the working memory. This model consists of the phonological loop and the visuospatial sketchpad, which, respectively, handle visuospatial and phonological information. These two sub-systems are controlled by the central executive and its executive components, updating, shifting, and inhibition ( Miyake et al., 2000 ). In his model, Baddeley (2000) added the episodic buffer, which is alleged to be responsible for the temporary storage of information from the two sub-systems and the long-term memory. Individual differences in the performance of complex working memory tasks, which are commonly defined as measures of the working memory capacity (WMC), arise from differences in an individual’s cognitive ability to actively store, actively process, and selectively consider the information required to produce an output in a setting with potentially interfering distractions ( Shah and Miyake, 1996 ; Wiklund-Hörnqvist et al., 2016 ).
There is a wealth of evidence and a general consensus in the field that working memory directly influences math performance ( Passolunghi et al., 2008 ; De Smedt et al., 2009 ; Raghubar et al., 2010 ; Passolunghi and Costa, 2019 ). In addition, many studies have shown that children with low WMC have more difficulty doing math ( Adam and Hitch, 1997 ; McLean and Hitch, 1999 ; Andersson and Lyxell, 2007 ; Szücs et al., 2014 ). Moreover, children with low WMC are overrepresented among students with various other problems, including problems with reading and writing ( Adam and Hitch, 1997 ; Gathercole et al., 2003 ; Alloway, 2009 ). Raghubar et al. (2010) concluded that “Research on working memory and math across experimental, disability, and cross-sectional and longitudinal developmental studies reveal that working memory is indeed related to mathematical performance in adults and in typically developing children and in children with difficulties in math” (p. 119; for similar reasoning, also see Geary et al., 2017 ).
Math Tracks
A math track is a specific series of courses students follow in their mathematics studies. Examples might include a basic or low-level math track in comparison with an advanced math track. In Sweden, there are five levels of math, each of which is subdivided into parts a--c, ranging from basic (a) to advanced (c). That is, course 1c is more advanced than course 1b, and course 1b is more advanced than course 1a. In comparison with social science students, natural science students study math on a higher level and move through the curriculum at a faster pace. At the end of year one, natural science students have gone through courses 1c and 2c, while social science students have gone through course 1b. Moreover, natural science students that are starting upper secondary school typically have higher grades from lower secondary school than social science students 2 . Therefore, in the present study, it is reasonable to assume that natural science students as a group have better, more advanced mathematical pre-knowledge than social science students.
In the present study, we acknowledge the importance of both fluid intelligence and working memory and thus include a complex working task and a general fluid intelligence task as measures of cognitive proficiency. Furthermore, based on their curriculum, the students in this study were divided according to their mathematical tracks (basic and advanced), with the aim of capturing differences in mathematical skills.
This study’s hypotheses were guided by previous theoretical arguments ( Lithner, 2008 , 2017 ) and empirical findings ( Jonsson et al., 2014 , 2016 ; Norqvist et al., 2019 ). On this basis, we hypothesized that:
- 1. Practicing with CMR tasks would to a greater extent facilitate performance on practiced tests tasks than practicing with AR tasks.
- 2. Practice with CMR tasks would to a greater extent facilitate performance on transfer test tasks than practice with AR tasks.
- 3. Students that are more cognitively proficient would outperform those who are less cognitively proficient on both practiced test tasks and transfer test tasks
- 4. Students enrolled in advanced math tracks are likely to outperform those enrolled in basic math tracks on both practiced test tasks and transfer test tasks .
Rationales for the Experiments
The three separate experiments presented below were conducted over a period of 2 years and encompassed 270 students. The overall aim was to contrast CMR with AR with respect to mathematical understanding. An additional aim was to contrast more cognitively proficient students with less cognitively proficient students and investigate potential interactions. The experiments progressed as a function of the experimental finding obtained in each experiment and were as such, not fully planned ahead. Experiment 1 was designed to replicate a previous study on practiced test tasks ( Jonsson et al., 2014 ), and also introduced transfer test tasks with the aim of better capturing conceptual understanding. However, when running a between-subject design, as in experiment 1, there is a risk of non-equivalent group bias when compared with using a within-subject design. It was also hypothesized that the findings (CMR > AR) could be challenged if the students were provided with an easier response mode. It was therefore decided that experiment 2 should employ a within-subject design and use multiple-choice (MC) questions as the test format. After experiment 2, it was discussed whether the eight transfer test tasks used in experiment 2 were too few to build appropriate statistics and whether the MC test format did not fully capture students’ conceptual understanding because of the possibility of students using response elimination and/or guessing. Moreover, the total number of test tasks was 32 (24 practiced test tasks and eight transfer test tasks ), and some students complained that there were too many test tasks, which may have affected their performance. It was therefore decided that experiment 3 should focus solely on transfer test tasks , thereby decreasing the total number of test tasks but increase the number of transfer test tasks without introducing fatigue. In experiment 3, we returned to short answers as a test format, thus restricting the possibility of students using response elimination and/or guessing.
Materials and Methods
Practice tasks.
A set of 35 tasks were pilot tested by 50 upper secondary school students. The aim was to establish a set of novel and challenging tasks that were not so complex that the students would have difficulty understanding what was requested. Twenty-eight of the 35 tasks fulfilled the criteria and were selected for the interventions. Each of the 28 tasks was then written as an AR task and as a CMR task, respectively ( Figures 1A,B ). The AR tasks were designed to resemble the design of everyday mathematical textbook tasks. Hence, each AR task provided the student with a method (a formula) for solving the task, an example of how to apply the formula, and a numerical test question ( Figure 1A ). The CMR tasks did not include any formulas, examples, or explanations, and the students were only asked to solve the numerical test questions ( Figure 1B ). Each of the 2 × 28 task sets (AR and CMR) included 10 subtasks, which only differed with respect to the numerical value used for the calculation. Although the number of task sets differed between the three experiments, there were 10 subtasks in each task set in all three experiments. Moreover, in each CMR task set, the third subtask asked students to construct a formula ( Figure 1C ). If the students completed all 10 subtasks, the software randomly resampled new numerical tasks until the session ended. This resampling ensured that the CMR and AR practice conditions lasted for the same length of time in all three experiments.

(A–C) Examples of AR and CMR practice tasks and how they were presented to the students on their laptop screen. (A) AR practice task ; (B) CMR practice task ; (C) CMR task asking for the formula.
Test tasks that were the same as the practice tasks (albeit with different numbers) are denoted as “ practiced test tasks ” while the tasks that were different from the practice tasks are denoted as “ transfer test tasks .”
Practiced Test Tasks
The layout of the practiced test tasks consisting of numerical- and formula tasks and can be seen in Figures 2A,C . The similarities between practice tasks and practiced test tasks may promote overlapping processing activities ( Franks et al., 2000 ) or, according to the encoding specificity principle, provide contextual cues during practice that can aid later test performance ( Tulving and Thomson, 1973 ). Transfer test tasks were therefore developed.

(A–D) Examples of test tasks and how they were presented to the students on their laptop screen. (A,C) Practiced test tasks and (B,D) transfer test task .
Transfer Test Tasks
The layout of the transfer test tasks consisting of numerical- and formula tasks can be seen in Figures 2B,D . The rationale underlying why transfer test tasks constitute a more valid measure of exploring students’ conceptual understanding of mathematics is that the solution algorithm (e.g., y = 3 x + 1) could have been memorized without any conceptual understanding. For a transfer test tasks the same algorithm cannot be used again, but the same general solution idea (e.g., multiplying the number of squares or rectangles with the number of matches needed for each new square/rectangle, and then adding the number of matches needed to complete the first square/rectangle) can be employed. We argue that knowing this idea of a general solution constitutes a local conceptual understanding of the task.
The Supplementary Material provides more examples of tasks.
Practice and Test Settings
In all three experiments, the practice sessions and test sessions were conducted in the students’ classroom. Both sets of tasks were presented to the students on their laptops. All tasks were solved individually; hence, no teacher or peer support was provided. The students were offered the use of a simple virtual calculator, which was displayed on their laptop screen. After submitting each answer during a practice session, the correct answer was shown to the students. However, no correct answers were provided to tasks that asked the students to construct formulas (i.e., the third CMR task). This was done to prevent students from using a provided formula instead of constructing a method/formula.
The software that was used for presenting practice and test tasks also checked and saved the answers automatically. All students received the same elements of the intervention, which due to the computer presentations, were delivered in the same manner to all the students, ensuring high fidelity ( Horner et al., 2006 ). The Supplementary Material provides additional examples and descriptions of the tasks employed in this study. The three experiments did not include a pre-test due to the risk of an interaction between the pre-test and the learning conditions, making the students more or less responsive to manipulation (for a discussion, see Pasnak, 2018 ). Moreover, the students were unfamiliar with the mathematical tasks.
Cognitive Measurement
The cognitive measures included cognitive testing of a complex working memory task (operation span; Unsworth et al., 2005 ) and general fluid intelligence (Raven’s Advanced Progressive Matrices; Raven et al., 2003 ). Raven’s APM consists of 48 items, including 12 practice items. To capture individual differences and to prevent both ceiling and floor effects, we used the 12 practice items as well as the 36 original test items. The 12 practice items were validated against Raven’s Standard Progressive Matrices ( Chiesi et al., 2012 ). These 48 test items were divided into 24 odd-numbered and 24 even-numbered items. Half of the students were randomly assigned to the odd-numbered items and half were assigned the even-numbered items. The total number of correct solutions was summed, providing a maximum score of 24. The task was self-paced over a maximum of 25 min. The countdown from 25 min was displayed in the upper-right corner of the screen. Initially, the students practiced on three items derived from Raven’s Standard Progressive Matrices. A measure of internal consistency (Cronbach’s alpha) was extracted from a larger pool of data, which encompassed the data obtained from the students in experiments 1 and 2, and was found to be 0.84.
In the operation span task students were asked to perform mathematical operations while retaining specific letters in their memory. After a sequence of mathematical operations and letters, they were asked to recall these letters in the same order as they were presented. The mathematical operations were self-paced (with an upper limit of 2.5 standard deviations above each individual average response time, extracted from an initial practice session). Each letter was presented after each mathematical operation and displayed for 800 ms. The letters to recall were presented in three sets of each set size. Every set size contained three to seven letters. The sum of all entirely recalled sets was used as the student’s WMC score. The measure of internal consistency revealed a Cronbach’s alpha of 0.83. Operation span was also self-paced, but without any time limit.
The operation span task and Raven’s matrices were combined into a composite score denoted as the cognitive proficiency (CP) index. The CP index score was based on a z -transformation of the operation span task performance and Raven’s matrices, thus forming the CP composite scores. These CP composite scores were then used to split (median split) students into lower and higher CP groups, and were used as a factor in the subsequent analyses across all three experiments. The students conducted the cognitive tests in their classrooms approximately 1 week before each of the three experiments.
Experiment 1
Participants.
A priori power analysis with effect sizes ( d = 0.73) from Jonsson et al. (2014) indicated that with an alpha of 0.05 and a statistical power of 0.80, a sample size of 61 students would obtain a statistical group difference. The students attended a large upper secondary school located in a municipality in a northern region of Sweden. Recruitment of students was conducted in class by the authors. One hundred and forty-four students were included in the experiment. Within each math track (basic, advanced) students were randomly assigned to engage in either the AR or CMR 3 groups. Out of those, 137 students (63 boys, 74 girls) with a mean age of 17.13 years ( SD = 0.62) were included and subsequently analyzed according to their natural science (advanced level), social science (basic level) math tracks and CP. All students spoke Swedish. Written informed consent was obtained from the students in accordance with the Helsinki declaration. The Regional Ethics Committee at Umeå University, Sweden, approved the study.
Cognitive Measures
The cognitive testing included measures of the working memory task (operation span; Unsworth et al., 2005 ) and general fluid intelligence (Raven’s matrices; Raven et al., 2003 ). The mean value for the operation span task was 31.52 ( SD = 16.35) and 12.63 ( SD = 5.10) for Raven’s matrices, respectively. The correlation between the operation span and the Raven’s matrices was found to be significant, r = 0.42, p < 0.001. A CP composite score was formed based on the operation span and Raven’s matrices scores, and was used to split the students into low and high CP groups; it was also used as a factor in the subsequent analyses.
From the 28 designed tasks (see above), 14 practice tasks were randomly chosen for the practice session. The corresponding 14 practiced test tasks together with seven transfer test tasks were used during the test.
In a between-group design, the students engaged in either the AR practice ( N = 72), which involved solving 14 AR task sets ( Figure 1A ), or the CMR ( N = 65) practice, which involved solving 14 CMR task sets ( Figure 1B ). The students had 4 min to conclude each of the 14 task sets.
One week later, a test was conducted in which students were asked to solve 14 practiced test tasks , formula and numerical tasks ( Figures 2A,C ) and seven transfer test tasks , formula and numerical tasks ( Figures 2B,D ). The first test task for both the practiced test tasks and the transfer test tasks was to write down the formula corresponding to the practice task with a time limit of 30 s. The second test task for both the practiced test tas ks and the transfer test tasks was comprised of solving a numerical test task. The students were given 4 min to solve each task. The practiced test tasks were always presented before the transfer test tasks .
Statistical Analysis
A 2 (CP; low, high) × 2 (group; AR, CMR) × 2 (math tracks; basic, advanced) multivariate analysis of variance (MANOVA) was followed by univariate analyses of variance (ANOVAs). The proportions of correct responses on numerical (practiced, transfer) and formula (practiced, transfer) tasks were entered as the dependent variables. Cohens d , and partial eta square (η p 2 ) were used as index of effect sizes.
Table 1A displays mean values, standard deviations, skewness, kurtosis, and Cronbach’s alpha of proportion correct responses for the test tasks for both AR and CMR learning conditions. Separate independent t -tests revealed that there were no significant differences between students in the AR and CMR learning conditions for operation span, t (135) = 0.48, p = 63, d = 0.08 and for the Raven’s matrices, t (135) = 0.12, p = 0.90, d = 0.02, respectively, showing that these groups were equal with respect to both complex working memory and fluid intelligence. Moreover, a subsequent analysis (independent t -test) of the CP composite score dividing the students into high and low CP groups showed that they could be considered to be cognitively separated, t (135) = 15.71, p < 0.001, d = 2.68.
Mean proportion correct response ( M ) and standard deviations ( SD ), skewness, kurtosis and Cronbach’s alpha for the AR and CMR learning conditions, respectively.
| Learning condition (AR/CMR) | M | SD | Skewness | Kurtosis | Cronbach’s alpha |
| Practiced test task formula | 0.08 | 0.13 | 2.13 | 3.50 | 0.86 |
| Practiced test task numerical | 0.26 | 0.26 | 0.95 | 0.25 | 0.83 |
| Transfer test task formula | 0.12 | 0.18 | 1.72 | 3.07 | 0.61 |
| Transfer test task numerical | 0.27 | 0.26 | 0.87 | –0.11 | 0.71 |
| Practiced test task formula | 0.20 | 0.22 | 0.97 | –0.11 | 0.86 |
| Practiced test task numerical | 0.42 | 0.25 | 0.06 | 1.06 | 0.88 |
| Transfer test task formula | 0.19 | 0.22 | 1.40 | 1.58 | 0.62 |
| Transfer test task numerical | 0.35 | 0.30 | 0.59 | –0.68 | 0.76 |
Table 1B display proportion correct responses for the test tasks divided according to their CP level. The statistical analyses confirmed that the students in the CMR learning condition outperformed those in the AR learning condition, F (4,126) = 4.42, p = 0.002, Wilk’s Λ = 0.40, η p 2 = 0.12. Follow-up ANOVAs for each dependent variable were significant, practiced test task formula , F (1,129) = 15.83, p < 0.001, η p 2 = 0.10; practiced test task numerical , F (1,129) = 12.35, p = 0.001, η p 2 = 0.09; transfer test task formula , F (1,129) = 8.83, p = 0.04, η p 2 = 0.06; and transfer test task numerical , F (1,129) = 5.05, p = 0.03, η p 2 = 0.04. An effect of CP was also obtained, F (4,126) = 7.71, p < 0.001, Wilk’s Λ = 0.80, η p 2 = 0.20, showing that the more cognitively proficient students outperformed those who were less proficient. Follow-up ANOVAs for each dependent variable revealed significant univariate effects of CP for the practiced test task formula , F (1,129) = 12.35, p < 0.001, η p 2 = 0.09; the practiced test task numerical , F (1,129) = 25.72, p < 0.001, η p 2 = 0.17; the transfer test task formula, F (1,129) = 22.63, p < 0.001, η p 2 = 0.15; and the transfer test task numerical , F (1,129) = 22.46, p < 0.01, η p 2 = 0.15. However, no multivariate main effects of math tracks and no multivariate interactions were obtained, with all p’s > 0.10.
Mean proportion correct response ( M ) and standard deviations ( SD ) for AR and CMR learning conditions across low and high CP groups.
| CP group (low/high) | ||||
| Practiced test task formula | 0.04 | 0.11 | 0.11 | 0.15 |
| Practiced test task numerical | 0.14 | 0.19 | 0.29 | 0.21 |
| Transfer test task formula | 0.05 | 0.10 | 0.08 | 0.14 |
| Transfer test task Numerical | 0.13 | 0.16 | 0.22 | 0.27 |
| Practiced test task formula | 0.11 | 0.15 | 0.29 | 0.24 |
| Practiced test task numerical | 0.38 | 0.26 | 0.54 | 0.23 |
| Transfer test task formula | 0.19 | 0.21 | 0.30 | 0.25 |
| Transfer test task Numerical | 0.41 | 0.27 | 0.48 | 0.27 |
With respect to all four dependent variables, the analyses showed that students practicing with CMR had superior results on the subsequent test 1 week later than students practicing with AR (confirming hypotheses 1 and 2) and that the more cognitively proficient students outperformed their less cognitively proficient counterparts, independent of group (confirming hypothesis 3). Although the natural science students performed, on average, better than social science students on all four dependent variables, no significant main effect was observed for math tracks (disconfirming hypothesis 4).
Experiment 2
The same hypotheses as in experiment 1 were posed in experiment 2. However, as pointed out above, there is a higher risk of non-equivalent group bias when using a between-subject design, and a simpler test format could challenge the differential effects found in experiment 1 (CMR > AR). It was therefore decided that experiment 2 should employ a within-subject design and use MC questions as a test format instead of short answers.
A priori power analysis based on a within-subjects pilot study ( N = 20) indicated that with an alpha of 0.05 and a statistical power of 0.80, a sample size of 50 students would obtain a statistical group difference. The students were from a larger pool of students, of which 82 students were randomly allocated to a functional Magnetic Resonance Imaging (fMRI) study, and the remaining 51 students participated in experiment 2. An independent t -test revealed no differences concerning age, general fluid intelligence (Raven’s matrices), or WMC (operation span), with p -values > 0.37. The separate fMRI experiment is not reported here. Experiment 2 included 51 students (27 girls, 24 boys) from natural science and social science programs in three upper secondary schools located in a municipality in a northern region of Sweden with a mean age of 18.13 years ( SD = 0.24). Recruitment of students was conducted in class by the authors, at each school. The natural science students were enrolled in more advanced math track compared with the Social science students; as in experiment 1, math tracks (basic, advanced) were subsequently entered as a factor in the analyses.
As in experiment 1, the cognitive testing included operation span and Raven’s matrices. The mean values and standard deviations of the operation span and Raven’s matrices were similar to those in experiment 1, for the operation span task ( M = 38.27, SD = 19.10) and Ravens matrices ( M = 14.47, SD = 5.34), respectively. The correlation between operation span and Raven’s matrices was found to be significant, with r = 0.52 and p < 0.001. A CP composite score was formed based on the operation span and Raven’s matrices scores. The CP score was used to split the students into a low CP group and a high CP group, and was also used as a factor in the subsequent analyses.
In a within-subject design, each student practice with 12 AR task sets and 12 CMR task sets. The corresponding 24 practice test tasks , together with eight transfer test tasks , were used as test tasks.
In this within-subject design, the students first practiced with 12 AR task sets. After a break of a few hours, they then practiced with 12 CMR task sets. This order was chosen to avoid carry-over effects from CMR tasks to AR tasks. The rationale was that starting with CMR tasks would reveal the underlying manipulation, which the students could then use to solve the AR tasks. Hence, constructing the solution without using the provided formula is the critical factor in the manipulation. To prevent item effects in which some tasks were more suitable to be designed as AR or CMR tasks, the tasks that were, respectively, assigned to be CMR and AR tasks were counterbalanced. The students were given 4 min to conclude each of the 12 task sets.
One week later, the students were asked to solve 24 randomly presented practiced test tasks (albeit with different numbers than before), of which 12 had been practiced as CMR tasks and 12 as AR tasks. These tasks were followed by eight transfer test tasks .
Statistical Analyses
A mixed-design ANOVA was conducted with learning condition (AR and CMR) and task type (practiced and transfer) as the within-subject factors and CP (low and high) and math tracks (basic and advanced) as the between-subject factors. The proportions of correct responses on practiced test tasks and transfer test tasks were entered as the dependent variables. Cohens d and partial eta square (η p 2 ) were used as index of effect sizes. Although a within-subject design was used, the more cognitively proficient students, who are likely to have better metacognitive ability (see Desoete and De Craene, 2019 for an overview), could potentially make use of constructive matching by comparing a possible solution with the response alternatives, response elimination by determining which answer is more likely, or of guessing ( Arendasy and Sommer, 2013 ; see also Gonthier and Roulin, 2020 ). Therefore, the analysis was corrected using the formula FS = R – W/C – 1, where FS = formula score; R = number of items/questions answered correctly; W = number of items/questions answered incorrectly; and C = number of choices per item/question (e.g., Diamond and Evans, 1973 ; Stenlund et al., 2014 ).
Table 2A displays the mean values of proportion correct response (not corrected for guessing), standard errors, and psychometric properties of skewness, kurtosis, and Cronbach’s alpha for the test tasks. An independent t -test of the CP composite score dividing the students into high CP groups and low CP groups showed that the students could be considered to be cognitively separated, t (49) = 12.14, p < 0.001. d = 3.40. The table shows that the mean values for CMR are higher than the corresponding values for AR learning condition for both the practiced test tasks and transfer test tasks . Table 2B display proportion correct responses (not corrected for guessing) for the test tasks divided according to their CP level. The statistical analysis corrected for guessing revealed significant within-subject effects of learning condition, with the CMR condition being superior to the AR condition, F (1,47) = 9.36, p = 0.004, Wilk’s Λ = 0.83, η p 2 = 0.17. However, there was no significant within-subject effect of task type, F (1,47) = 0.77, p = 0.38, Wilk’s Λ = 0.98, η p 2 = 0.012. Moreover, there was no significant between-subject effects of CP, F (1,47) = 0.23, p = 0.64, η p 2 = 0.004, or of math tracks, F (1,47) = 0.84, p = 0.36, η p 22 = 0.005, and there were no interaction effects ( p’s > 0.67).
| Learning condition (AR/CMR) | M | SD | Skewness | Kurtosis | Cronbach’s alpha |
| Practiced test task | 0.48 | 0.25 | 0.27 | −0.84 | 0.80 |
| Transfer test task | 0.46 | 0.33 | 0.35 | −0.99 | 0.69 |
| Practiced test task | 0.55 | 0.27 | 0.00 | −1.40 | 0.82 |
| Transfer test task | 0.53 | 0.35 | 0.00 | 1.40 | 0.63 |
| CP group (low/high) | AR | CMR | ||
| Practiced test task | 0.35 | 0.17 | 0.40 | 0.21 |
| Transfer test task | 0.33 | 0.28 | 0.29 | 0.22 |
| Practiced test task | 0.61 | 0.24 | 0.76 | 0.24 |
| Transfer test task | 0.58 | 0.33 | 0.69 | 0.30 |
The non-significant effect of CP was rather surprising; therefore, it was decided to re-run the analyses without the correction formula. The analyses again revealed a significant within-subject effect of learning condition, with the CMR condition being superior to the AR condition, F (1,47) = 7.80, p = 0.008, Wilk’s Λ = 0.85, η p 2 = 0.14. Again no significant within-subject effects from task type, F (1,47) = 2.3, p = 0.13, Wilk’s Λ = 0.95, η p 2 = 0.02 or between-subject effect of math tracks, F (1,47) = 3.45, p = 0.07, η p 2 = 0.07 were detected. However, the between-subject effect of CP was now clearly significant, F (1,47) = 18.74, p < 0.001, η p 2 = 0.28. Moreover, a learning condition × CP interaction F (1,47) = 9.05, p = 0.004, Wilk’s Λ = 0.83 η p 2 = 0.16 was qualified by a learning condition × task type × CP interaction, F (1,47) = 8.10, p = 0.005, Wilk’s Λ = 0.84, η p 2 = 0.16. The three-way interaction was driven by students with a high CP performing better in the CMR learning condition than in the AR learning condition especially pronounced for the transfer test tasks. No other interaction effects were detected ( p’s > 0.70).
With respect to both practiced test tasks and transfer test tasks , the analyses showed, as expected, that students who practiced with CMR had superior results on the subsequent tests 1 week later compared to the students who practiced with AR (confirming hypothesis 1 and 2). In comparison with experiment 1, experiment 2 showed notably higher performance levels, which most likely reflected the MC test format. Viewed in relation to previous studies of CMR (e.g., Jonsson et al., 2014 ) and the significant number of studies showing that educational attainments in math are intimately related to cognitive abilities (e.g., Adam and Hitch, 1997 ; Andersson and Lyxell, 2007 ), the non-significant effect of CP was unexpected. The finding that task type was non-significant, albeit in the direction of the practiced test task being easier than the transfer test tasks was also somewhat unexpected. It is possible that the eight transfer test tasks (four AR and four CMR) may have been too few to build reliable statistics. Although no significant effect was obtained for math tracks, the natural science students (advanced math track) performed better than the social science students (basic math track) on average; however, this trend did not reach statistical significance (disconfirming hypothesis 4). After the unexpected non-significant effect of CP, the analysis was re-run without the correction formula. The analysis revealed a main effect of CP (confirming hypothesis 3) and a learning condition × CP interaction that was qualified by a learning condition × task type × CP interaction. The three-way interaction indicates that cognitively stronger students could utilize response elimination or successful guessing in subsequent MC tests more effectively than their lower CP counterparts, especially for the transfer test tasks.
This design, in which the CMR practice tasks were presented shortly after the AR tasks, may have introduced a recency effect and thus facilitated the test performance more for CMR than for AR tasks. However, the CMR practice session contained 12 different task sets, and each new task set was a potential distractor for the previous task sets. Moreover, between the learning session and subsequent test 1 week later, the students attended their regular classes. These activities, viewed in conjunction with the well-known fact that the recency effect is rather transitory ( Koppenaal and Glanzer, 1990 ) and that recall is severely disrupted even by unrelated in-between cognitive activities ( Glanzer and Cunitz, 1966 ; Kuhn et al., 2018 ), probably eliminated the risk of recency effects. In experiment 2, the total number of test tasks was 32 (24 practiced test tasks and eight transfer test tasks ), and some students complained that there were too many tasks, which may have affected their performance, potentially the cognitively more proficient students were less affected by the large number test tasks.
Experiment 3
In experiment 3, the same hypotheses were posed as in experiments 1 and 2. However, as pointed out above, the more cognitively proficient students were potentially less affected by fatigue and gained more from using MC questions as a test format. Therefore, it was decided that experiment 3 should retain the within-subject design but use only transfer test tasks . Moreover, we reintroduced written answers as a response mode to prevent processes of constructive matching and response elimination. To reduce a potential, but unlikely, recency effect, the presentation order for a subsample was reversed, with CMR tasks being presented before AR tasks.
Experiment 3 included 82 students. The average age of participants was 17.35 years ( SD = 0.66), whereof 35 were girls, and 47 boys. The participants were from two upper secondary schools located in a municipality in a northern region of Sweden. Recruitment of students was conducted in class by the authors, at each school. The students were divided into two math tracks. The first was a mathematical track that included year 3 technical students and year 2 natural science students (advanced math tracks); these students were regarded by their schoolteachers as approximately equal in math skill background. The second math track consisted of year 1 natural science students and year 2 social science students (basic math track); these students were also regarded as approximately equal in math skill background. The students were subsequently analyzed according to their math tracks.
The cognitive tests were the same as in experiments 1 and 2. The mean values and standard deviations of the operation span ( M = 36.78, SD = 16.07) and Raven’s matrices ( M = 14.33, SD = 4.35) were similar to those from experiments 1 and 2. The correlation between operation span and Raven’s matrices was found to be significant, with r = 0.40 and p < 0.001, and a CP composite score based on operation span and Raven’s matrices scores was again formed, used to split the students into a low CP group and a high CP group, and used as a factor in the subsequent analyses.
The same practice tasks were used, as in experiment 2. In a within-subject design, the students practiced with 12 AR task sets and 12 CMR task sets, and 24 transfer test tasks were used during the test.
The students practiced with the same tasks and setup as in experiment 2, with the exception that the order of presentation was reversed for a subset of students, with AR tasks being practiced before CMR tasks. The students had 4 min to conclude each of the 12 task sets during practice. One week later, the students were asked to solve 24 transfer test tasks . The students were given 130 s to solve each test task.
The initial mixed-design ANOVA analysis, with learning condition (AR and CMR) as the within-subject factor and order of presentation as the between-subject variable and the proportion correct response as the dependent variable, investigated the potential presentation order × learning condition interaction. The analysis revealed that this interaction was non-significant, with F (1,80) = 0.22, p = 0.88, Wilk’s Λ = 0.10, η p 2 = 0.0004. Therefore, the presentation order was excluded from further analyses. Considering that the students differed in age (by approximately 1 year), we controlled for age by conducting a mixed-design analysis of covariance (ANCOVA) with learning condition (AR and CMR) as a within-subject factor and with CP (low and high) and math track (basic and advanced) as the between-subject factors. The proportion of correct responses on the transfer test tasks was entered as the dependent variable, and age was used as a covariate. Cohens d and partial eta square (η p 2 ) were used as index of effect sizes.
Table 3A displays the mean values, standard deviations, skewness, kurtosis, and Cronbach’s alpha for the test tasks. An independent t -test of the CP composite score used to divide the students into a high CP group and a low CP group showed that the students could be considered as cognitively separated, t (80) = 12.88, p < 0.001, d = 2.84. The table shows that practicing with the CMR tasks was superior to practicing with the AR tasks. Table 3B display proportion correct responses for the transfer test tasks divided according to their CP level. The statistical analysis confirmed a within-subject effect of learning condition, F (1,77) = 20.88, p < 0.001, Wilk’s Λ = 0.78, η p 2 = 0.21. The analysis also revealed a between-subject effect of CP, F (1,76) = 21.50, p < 0.001, η p 2 = 0.22. However, no between-subject effect of math tracks and no interaction effects were obtained, p’s > 0.15.
| Learning condition (AR/CMR) | M | SD | Skewness | Kurtosis | Cronbach’s alpha |
| Transfer test task | 0.26 | 0.21 | 0.78 | −0.12 | 0.78 |
| Transfer test task | 0.36 | 0.23 | 0.37 | −0.33 | 0.75 |
| CP group (low/high) | AR | CMR | ||
| Transfer test task | 0.19 | 0.15 | 0.26 | 0.18 |
| Transfer test task | 0.34 | 0.24 | 0.47 | 0.22 |
The findings from experiment 3 were in line with those from the previous experiments, providing evidence that practicing with CMR tasks was superior to practicing with AR tasks (confirming hypotheses 1 and 2). As expected, the analyses showed that the more cognitively proficient students outperformed those who were less cognitively proficient (confirming hypothesis 3). Again, no significant effect was obtained for math tracks (again disconfirming hypothesis 4).
General Discussion
This study contrasted CMR with AR across three experiments encompassing 270 students. It was hypothesized that practicing with CMR leads to better performances than practicing with AR on practiced test tasks and transfer test tasks (hypotheses 1 and 2). Experiments 1 and 2 included both practiced test tasks and transfer test tasks , while experiment 3 focused exclusively on transfer test tasks . The practiced test tasks were identical to the tasks that the students had practiced (albeit with different numbers). The transfer test tasks were different from the practice tasks , but they shared an underlying solution idea. To solve the transfer test tasks , the students had to rely on relevant knowledge (a solution idea) acquired during their practice, which is critical in mathematics. If a student has no solution idea to rely on, the transfer test tasks required the student to construct the method from scratch.
Moreover, this study hypothesized that the more cognitively proficient students would outperform those who were less cognitively proficient (hypothesis 3), independent of learning conditions. The upper secondary students were from different student programs with different mathematical backgrounds (i.e., basic and advanced math tracks), which was entered as a factor in the analyses. It was expected that those enrolled in a more advanced math track would outperform those enrolled in a basic math track (hypothesis 4).
Overall, the results confirmed hypotheses 1–3. However, no effects of math tracks were obtained, disconfirming hypothesis 4. Below, these hypotheses are discussed in detail.
Hypotheses 1 and 2
The analysis of both the practiced test tasks in experiment 1 followed the setup of Jonsson et al. (2014) , in which the dependent variables included trying to remember specific formulas and solving numerical practiced test tasks . Moreover, experiment 1 also went beyond Jonsson et al. (2014) and added transfer test tasks . The results of experiment 1 were in line with those of Jonsson et al. (2014) : Practicing with CMR tasks lead to significantly better performance on the practiced test tasks than practicing with AR tasks. Experiment 1 also found that practicing with CMR lead to significantly better performance on transfer test tasks . In experiment 2, we turned to a within-subject design, with the aim of removing potential non-equivalent group bias, and introduced MC questions as a test format, thereby challenging hypotheses 1 and 2 by using an easier test format. Again, significant CMR > AR effects were detected for both practiced test tasks and transfer test tasks . However, the fact that only four AR and four CMR transfer test tasks were used in experiment 2, the results could be questioned in terms of building adequate statistics. Therefore, using a within-subject design, experiment 3 focused solely on transfer test tasks , which increased the number of transfer test tasks and reduced the total number of tasks and, thus, the risk of fatigue. We also reintroduced written answers as a response mode to prevent processes of response elimination and guessing. The analysis of experiment 3 revealed that practicing with CMR tasks had a more beneficial effect than practicing with AR tasks on the transfer test tasks , again confirming hypothesis 2.
Hypothesis 3
When a short answer format was used, as in experiments 1 and 3, the effects of CP were clear, confirming previous studies and hypothesis 3. The second analysis in experiment 2 also confirmed hypothesis 3. The analysis showed that all participants improved their performance; hence the proportion correct was higher in experiment 2 than in experiments 1 and 3 ( Tables 1 – 3 ). This performance was most likely due to the MC response mode. The second analysis indicates that the cognitively more proficient students could in addition, use response elimination or successful guessing more effective ( Desoete and De Craene, 2019 ), thereby outperforming the cognitively less proficient. However, when the analysis was corrected for guessing (the first analysis), the benefits of using response elimination or guessing were removed, but the effects of the easier MC response mode remained, which even out the difference between the CP groups and thereby also removed the effect of CP.
Hypothesis 4
The non-significant effect of mathematical track was somewhat surprising, and disconfirmed hypothesis 4. A plausible interpretation is that the students enrolled in more advanced math tracks, which involve (according to the curriculum) better mathematical training, could not make use of their acquired mathematical knowledge when solving the novel experimental test tasks; if this interpretation is correct, it would indicate that the assumption of task novelty was also correct.
Overall, this study provides support for the argument that CMR facilitates learning to a greater degree than AR and confirms the results of previous studies ( Jonsson et al., 2014 , 2016 ; Norqvist et al., 2019 ). Although the effect sizes were rather small, they must be viewed in relation to the short interventions that the students went through. We argue that when students are practicing with CMR tasks, they are “forced” to pay attention to the intrinsic and relevant mathematical components, which develops their conceptual understanding. The effects on transfer test tasks indicate that practicing with CMR tasks—in comparison with practicing with AR tasks—facilitates students’ ability to transfer their knowledge to a greater extent; that is, they can better transfer their solution idea from the practice task to a different task sharing the same underlying solution idea (transfer test tasks ). This argument is in line with the findings of the Norqvist et al. (2019) eye-tracking study: When students practiced with AR tasks, they disregarded critical information that could be used to build a more in-depth understanding; in contrast, students that practiced with CMR tasks focused on critical information more frequently. Practice with CMR is most likely associated with more effortful struggle—an argument that shares similarities with the framework of “ill-structured tasks” ( Kapur, 2008 , 2010 ). In the ill-structured task approach, students are provided with tasks for which no method or procedure on how to solve the task is available and for which multiple solution paths may exist. Students are required to (try to) solve the ill-structured task by constructing their own methods before the teacher provides instructions on the mathematics to be learned ( VanLehn et al., 2003 ; Kapur, 2010 ). Those studies showed that the struggle of creating methods was especially beneficial for developing a conceptual understanding of the task, as demonstrated by significantly better performance on transfer test tasks (e.g., Kapur, 2010 , 2011 ). It is argued that the task complexity inherent in the ill-defined tasks was a key factor that helped students to create structures that facilitated their conceptual understanding of mathematics. Furthermore, studies have shown that the more solutions students generate on their own, the better the students’ test performance becomes, even when their methods do not fully solve the practice task ( Kapur, 2014 ). In the CMR tasks used in the present study, no instructions were given. Similar to the ill-structured approach, such tasks may identify knowledge gaps and enable (or “force”) students to search for and perceive in-depth structural problem features ( Newman and DeCaro, 2019 ). Although an excessively high cognitive load may hamper learning, a desirable amount of cognitive load in terms of struggle (in a positive sense) with mathematics may be beneficial for developing conceptual understanding ( Hiebert and Grouws, 2007 ). In the present study, such development of students’ conceptual understanding was seen in the form of better performance on the later test as a function of practicing with CMR tasks relative to AR tasks.
This study provides support for the theoretical link between the learning process using CMR, performance, and conceptual understanding. The results also underscore that although CP was associated with better performance, it did not interact with the learning condition. Hence, both cognitively stronger and cognitively weaker students benefited from using CMR relative to using AR. The theoretical framework ( Lithner, 2008 , 2017 ) could potentially be updated with an individual differences perspective with respect to cognitive prerequisites and their implication for the learning process. With respect to the non-significant effect of math tracks, the assumption of task novelty seems to be correct. Moreover, the non-significant effect of math tracks also indicates that students can gain conceptual understanding by using CMR even with tasks for which the students lack or have negligible pre-knowledge, and among students with “only” basic mathematical background.
The results from this study could be discussed from a self-explanation perspective (for an overview, see Rittle-Johnson et al., 2017 ). According to Rittle-Johnson et al. (2017) , the mechanism underlying self-explanation is the integration of new information with previous knowledge. This involves guiding students’ attention to the structural features—rather than the surface features—of the to-be-learned material, and can aid comprehension and transfer. In the CMR assumption, predictive arguments supporting strategy choice and verification arguments explaining why the strategy implementation and conclusions are “true or plausible” are regarded as critical features.
In sum, in the CMR/AR, ill-structured tasks, and self-explanation approaches, the critical aspects are how tasks are designed and how mathematical reasoning is supported. Moreover, in order to move beyond textbooks’ step-by-step solutions and understand the underlying ideas, students need to face (in a positive sense) mathematical struggle activities. Nevertheless, it is not likely that students will take on such effort by themselves. The framework of CMR and ill-structured tasks removes the task-solving methods and requires students to find an underlying idea and to create solutions on their own. Although CMR task solving is more cognitively demanding during practice than AR task solving, it helps the learner to focus on relevant information for solving the task. Moreover, similar to the self-explanation approach, the CMR approach guides students to the structural features that are critical for aiding comprehension.
Limitations
A limitation in the present study is that experiment 3 did not include any practiced test tasks . However, the results from experiments 1 and 2 indicate that using practiced test tasks in experiment 3 would have yielded the same conclusions as in experiments 1 and 2. A further potential limitation is that the presentation format differed in experiment 2 in comparison with experiments 1 and 3. However, it could in fact be argued that this is a strength of the study: Despite the different response formats for the test tasks, the experiments yielded similar results, with CMR consistently outperforming AR. Although the experiments were based on convenience samples, which could potentially narrow the external validity, the students were from four different upper secondary schools, which provided some heterogeneity. The results can also be discussed from the perspective of Hawthorne effects: The awareness of knowing that they were part of a study may have affected the students’ performance, and—although this is unlikely—the findings may not generalize to a regular setting when the researcher is not present.
Moreover, there were no pre-test measures in any of the experiments, as it was argued that a pre-test could make the students more or less responsive to the manipulation (see Pasnak, 2018 , for a discussion). On the other hand, pre-tests could have provided insight into how comprehension increased from the pre- to a post-test. In experiment 1, pre-tests would have provided a baseline of student performance, which could have been used to evaluate initial group differences.
Implications and Future Research
The results from the present and previous studies (e.g., Jonsson et al., 2014 , 2016 ; Norqvist et al., 2019 ) have implications for school settings, as AR tasks (as opposed to CMR tasks) are commonly used in teaching approaches and textbooks ( Stacey and Vincent, 2009 ; Denisse et al., 2012 ; Shield and Dole, 2013 ; Boesen et al., 2014 ; Jäder et al., 2019 ), but as argued do not promote optimal student learning. We argue that an eclectic perspective in which validated methods that emphasize mathematical struggles—such as task solving using CMR, ill-structured tasks, and self-explanations—should be a part of the mathematical curriculum, in conjunction with approaches that reduce cognitive load, such as worked examples. In future studies, it would be interesting not only to contrast CMR with other approaches, but also to investigate how to combine the CMR approach with, for example, self-explanation ( Rittle-Johnson et al., 2017 ) and, potentially, with worked examples as well ( Sweller et al., 2011 ). Another potential combination could involve retrieval practice, which is a cognitive-based learning strategy based on self-testing. At first glance, retrieval practice is very different from using CMR. Using CMR emphasizes the construction of solutions, while retrieval practice strengthens memory consolidation through the process of retrieving information from long-term memory. For example, retrieving the definition of working memory without the support of written text will enhance one’s ability to remember the definition across long-term retention intervals ( Wiklund-Hörnqvist et al., 2014 ). The performance difference between retrieval practice and other ways of attaining information—most commonly re-reading—is denoted as the “testing effect.” The testing effect is supported by both behavioral and functional fMRI evidence (for overviews, see Dunlosky et al., 2013 ; van den Broek et al., 2016 ; Adesope et al., 2017 ; Antony et al., 2017 ; Moreira et al., 2019 ; Jonsson et al., 2020 ). Research that currently underway shows that measures of brain activity following the testing effect (retrieval practice > study) and the “CMR effect” (CMR > AR) indicate that the same brain areas are activated. It is possible that by adding retrieval practice after formulas or procedures have been established by using CMR, the memory strength of specific formulas may be enhanced. Future studies are planned to pursue this reasoning.
Moreover, as stated in the limitation, the experiments in the present study were based on convenience samples. A purely randomized sampling or a stratified sampling would be preferable in future studies. It is also unclear whether the CMR approach is potent among students with special needs, although the non-significant effects of math tracks found in the present study were encouraging; future studies should pursue this question.
Data Availability Statement
Ethics statement.
The studies involving human participants were reviewed and approved by The Regional Ethics Committee at Umeå University, Sweden approved the study at University. Written informed consent from the participants’ legal guardian/next of kin was not required to participate in this study in accordance with the national legislation and the institutional requirements.
Author Contributions
BJ, CG, and JL came up with the idea for the study and jointly contributed to the conceptualization and design of the study and revised the manuscript for important intellectual content. CG and BJ conducted the data collection. BJ performed the statistical analysis and wrote the first draft of the manuscript. All authors contributed to manuscript revision and read and approved the submitted version.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Tony Qwillbard for data management and computer support, the students who took part in the experiments, and the teacher who allowed access to the schools.
Funding. Funding was received from the Swedish Research Council VR, Grant 2014–2099.
1 https://www.nctm.org/26T
2 www.skolverket.se
3 In the CMR group data from six participants were lost due to administrative error.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fpsyg.2020.574366/full#supplementary-material
- Adam J., Hitch G. (1997). Working memory and ‘children’s mental addition. Working memory and arithmetic. J. Exp. Child Psychol. 67 21–38. 10.1006/jecp.1997.2397 [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Adesope O. O., Trevisan D. A., Sundararajan N. (2017). Rethinking the Use of Tests: A Meta-Analysis of Practice Testing. Rev. Educ. Res. 87 659–701. 10.3102/0034654316689306 [ CrossRef ] [ Google Scholar ]
- Alloway T. P. (2009). Working memory, but not IQ, predicts subsequent learning in children with learning difficulties. Eur. J. Psychol. Assess. 25 92–98. 10.1027/1015-5759.25.2.92 [ CrossRef ] [ Google Scholar ]
- Andersson U., Lyxell B. (2007). Working memory deficit in children with mathematical difficulties: A general or specific deficit? J. Exp. Child Psychol. 96 197–228. 10.1016/j.jecp.2006.10.001 [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Antony J. W., Ferreira C. S., Norman K. A., Wimber M. (2017). Retrieval as a Fast Route to Memory Consolidation. Trends Cognit. Sci. 21 573–576. 10.1016/j.tics.2017.05.001 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Arendasy M. E., Sommer M. (2013). Reducing response elimination strategies enhances the construct validity of figural matrices. Intelligence 41 234–243. 10.1016/j.intell.2013.03.006 [ CrossRef ] [ Google Scholar ]
- Baddeley A. (2000). The episodic buffer: a new component of working memory? Trends Cognit. Sci. 4 417–423. 10.1016/s1364-6613(00)01538-2 [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Baddeley A. (2010). Working memory. Curr. Biol. 20 R136–R140. 10.1016/j.cub.2009.12.014 [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Barnett S. M., Ceci S. J. (2002). When and where do we apply what we learn: A taxonomy for far transfer. Psychol. Bull. 128 612–637. 10.1037/0033-2909.128.4.612 [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Bergqvist E. (2007). Types of reasoning required in university exams in mathematics. J. Math. Behav. 26 348–370. 10.1016/j.jmathb.2007.11.001 [ CrossRef ] [ Google Scholar ]
- Blair C., Gamson D., Thorne S., Baker D. (2005). Rising mean IQ: Cognitive demand of mathematics education for young children, population exposure to formal schooling, and the neurobiology of the prefrontal cortex. Intelligence 33 93–106. 10.1016/j.intell.2004.07.00826T [ CrossRef ] [ Google Scholar ]
- Boesen J., Helenius O., Bergqvist E., Bergqvist T., Lithner J., Palm T., et al. (2014). Developing mathematical competence: From the intended to the enacted curriculum. J. Math. Behav. 33 72–87. 10.1016/j.jmathb.2013.10.001 [ CrossRef ] [ Google Scholar ]
- Butler A. C., Black-Maier A. C., Raley N. D., Marsh E. J. (2017). Retrieving and applying knowledge to different examples promotes transfer of learning. J. Exp. Psychol. 23 433–446. 10.1037/xap0000142 [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Carroll J. B. (1993). Human cognitive abilities: A survey of factor-analytic studies. Cambridge:Cambridge University Press. [ Google Scholar ]
- Chiesi F., Ciancaleoni M., Galli S., Primi C. (2012). Using the Advanced Progressive Matrices (Set I) to assess fluid ability in a short time frame: An item response theory–based analysis. Psychol. Assess. 24 892–900. 10.1037/a0027830 [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Cohen J. (1992). A power primer. Psychol. Bull. 112 155–159. 10.1037/0033-2909.112.1.155 [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Coles A., Brown L. (2016). Task design for ways of working: making distinctions in teaching and learning mathematics. J. Math. Teacher Educ. 19 149–168. 10.1007/s10857-015-9337-4 [ CrossRef ] [ Google Scholar ]
- De Smedt B., Janssen R., Bouwens K., Verschaffel L., Boets B., Ghesquière P. (2009). Working memory and individual differences in mathematics achievement: A longitudinal study from first grade to second grade. J. Exp. Child Psychol. 103 186–201. 10.1016/j.jecp.2009.01.004 [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Deary I. J., Strand S., Smith P., Fernandes C. (2007). Intelligence and educational achievement. Intelligence 35 13–21. 10.1016/j.intell.2006.02.001 [ CrossRef ] [ Google Scholar ]
- Denisse R. T., Sharon L. S., Gwendolyn J. J. (2012). Opportunities to Learn Reasoning and Proof in High School Mathematics Textbooks. J. Res. Math. Educ. 43 253–295. 10.5951/jresematheduc.43.3.0253 [ CrossRef ] [ Google Scholar ]
- Desoete A., De Craene B. (2019). Metacognition and mathematics education: an overview. ZDM 51 565–575. 10.1007/s11858-019-01060-w [ CrossRef ] [ Google Scholar ]
- Diamond J., Evans W. (1973). The Correction for Guessing. Rev. Educ. Res. 43 181–191. 10.3102/00346543043002181 [ CrossRef ] [ Google Scholar ]
- Dunlosky J., Rawson K. A., Marsh E. J., Nathan M. J., Willingham D. T. (2013). Improving Students’ Learning With Effective Learning Techniques: Promising Directions From Cognitive and Educational Psychology. Psychol. Sci. Public Interest 14 4–58. 10.1177/1529100612453266 [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Floyd R. G., Evans J. J., McGrew K. S. (2003). Relations between measures of cattell-horn-carroll (CHC) cognitive abilities and mathematics achievement across the school-age years [Review]. Psychol. Schools 40 155–171. 10.1002/pits.10083 [ CrossRef ] [ Google Scholar ]
- Franks J. J., Bilbrey C. W., Lien K. G., McNamara T. P. (2000). Transfer-appropriate processing (TAP). Memory Cognit. 28 1140–1151. 10.3758/bf03211815 [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Gathercole S. E., Brown L., Pickering S. J. (2003). Working memory assessments at school entry as longitudinal predictors of National Curriculum attainment levels. Educat. Child Psychol. 20 109–122. [ Google Scholar ]
- Geary D. C., Nicholas A., Li Y., Sun J. (2017). Developmental change in the influence of domain-general abilities and domain-specific knowledge on mathematics achievement: An eight-year longitudinal study. J. Educat. Psychol. 109 680–693. 10.1037/edu0000159 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Glanzer M., Cunitz A. R. (1966). Two storage mechanisms in free recall. J. Verb. Learning Verb. Behav. 5 351–360. 10.1016/S0022-5371(66)80044-0 [ CrossRef ] [ Google Scholar ]
- Gonthier C., Roulin J.-L. (2020). Intraindividual strategy shifts in ‘Raven’s matrices, and their dependence on working memory capacity and need for cognition. J. Exp. Psychol. General 149 564–579. 10.1037/xge0000660 [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Hiebert J. (2003). “ What research says about the NCTM Standards ,” in A research companion to principles andstandards for school mathematics , eds Kilpatrick J., Martin G., Schifter D. (Reston, VA:National Council of Teachers of Mathematics; ), 5–26. [ Google Scholar ]
- Hiebert J., Grouws D. A. (2007). The effects of classroom mathematics teaching on ‘students’ learning. Second Handbook Res. Math. Teaching Learning 1 371–404. [ Google Scholar ]
- Horner S., Rew L., Torres R. (2006). Enhancing intervention fidelity: a means of strengthening study impact. J. Spec. Pediatr. Nurs. 11 80–89. 10.1111/j.1744-6155.2006.00050.x [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Jäder J., Lithner J., Sidenvall J. (2019). Mathematical problem solving in textbooks from twelve countries. Int. J. Math. Educ. Sci. Technol. 51 1–17. 10.1080/0020739X.2019.1656826 [ CrossRef ] [ Google Scholar ]
- Jonsson B., Kulaksiz Y. C., Lithner J. (2016). Creative and algorithmic mathematical reasoning: effects of transfer-appropriate processing and effortful struggle. Int. J. Math. Educat. Sci. Technol. 47 1206–1225. 10.1080/0020739x.2016.1192232 [ CrossRef ] [ Google Scholar ]
- Jonsson B., Norqvist M., Liljekvist Y., Lithner J. (2014). Learning mathematics through algorithmic and creative reasoning. J. Math. Behav. 36 20–32. 10.1016/j.jmathb.2014.08.003 [ CrossRef ] [ Google Scholar ]
- Jonsson B., Wiklund-Hörnqvist C., Stenlund T., Andersson M., Nyberg L. (2020). A learning method for all: The testing effect is independent of cognitive ability. J. Educ. Psychol. 2020 :edu0000627 10.1037/edu0000627 [ CrossRef ] [ Google Scholar ]
- Kapur M. (2008). Productive failure. Cognit. Instruct. 26 379–424. [ Google Scholar ]
- Kapur M. (2010). Productive failure in mathematical problem solving. Instruct. Sci. 38 523–550. 10.1007/s11251-009-9093-x [ CrossRef ] [ Google Scholar ]
- Kapur M. (2011). A further study of productive failure in mathematical problem solving: unpacking the design components. Instr. Sci. 39 561–579. 10.1007/s11251-010-9144-3 [ CrossRef ] [ Google Scholar ]
- Kapur M. (2014). Productive Failure in Learning Math. Cognit. Sci. 38 1008–1022. 10.1111/cogs.12107 [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Koppenaal L., Glanzer M. (1990). An examination of the continuous distractor task and the “long-term recency effect”. Memory Cognit. 18 183–195. 10.3758/BF03197094 [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Kuhn J. R., Lohnas L. J., Kahana M. J. (2018). A spacing account of negative recency in final free recall. J. Exp. Psychol. 44 1180–1185. 10.1037/xlm0000491 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Lee H. S., Anderson J. R. (2013). Student Learning: What Has Instruction Got to Do With It? Annu. Rev. Psychol. 64 445–469. 10.1146/annurev-psych-113011-143833 [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Lithner J. (2008). A research framework for creative and imitative reasoning. Educat. Stud. Math. 67 255–276. 10.1007/s10649-007-9104-2 [ CrossRef ] [ Google Scholar ]
- Lithner J. (2017). Principles for designing mathematical tasks that enhance imitative and creative reasoning. ZDM 49 937–949. 10.1007/s11858-017-0867-3 [ CrossRef ] [ Google Scholar ]
- Mac an Bhaird C., Nolan B. C., O’Shea A., Pfeiffer K. (2017). A study of creative reasoning opportunities in assessments in undergraduate calculus courses. Res. Math. Educ. 19 147–162. 10.1080/14794802.2017.1318084 [ CrossRef ] [ Google Scholar ]
- Mackintosh N., Mackintosh N. J. (2011). IQ and human intelligence. Oxford:Oxford University Press. [ Google Scholar ]
- McLean J. F., Hitch G. J. (1999). Working Memory Impairments in Children with Specific Arithmetic Learning Difficulties. J. Exp. Child Psychol. 74 240–260. 10.1006/jecp.1999.2516 [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Miyake A., Friedman N. P., Emerson M. J., Witzki A. H., Howerter A., Wager T. D. (2000). The Unity and Diversity of Executive Functions and Their Contributions to Complex “Frontal Lobe” Tasks: A Latent Variable Analysis. Cognit. Psychol. 41 49–100. 10.1006/cogp.1999.0734 [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Moreira B. F. T., Pinto T. S. S., Starling D. S. V., Jaeger A. (2019). Retrieval Practice in Classroom Settings: A Review of Applied Research. Front. Educ. 4 :005 10.3389/feduc.2019.00005 [ CrossRef ] [ Google Scholar ]
- Newman P. M., DeCaro M. S. (2019). 2019/08/01/). Learning by exploring: How much guidance is optimal? Learning Instruct. 62 49–63. 10.1016/j.learninstruc.2019.05.005 [ CrossRef ] [ Google Scholar ]
- Niss M. (2007). “ Reactions on the state and trends in research on mathematics teaching and learning ,” in Second handbook of research on mathematics teaching and learning ed. Lester I. F. (Mumbai:IAP; ). [ Google Scholar ]
- Norqvist M. (2017). The effect of explanations on mathematical reasoning tasks. Int. J. Math. Educ. 49 1–16. 10.1080/0020739X.2017.1340679 [ CrossRef ] [ Google Scholar ]
- Norqvist M., Jonsson B., Lithner J., Qwillbard T., Holm L. (2019). Investigating algorithmic and creative reasoning strategies by eye tracking. J. Math. Behav. 55 :008 10.1016/j.jmathb.2019.03.008 [ CrossRef ] [ Google Scholar ]
- Pasnak R. (2018). To Pretest or Not to Pretest. Biomed. J. Sci. Technical Res. 5 :1185 10.26717/bjstr.2018.05.001185 [ CrossRef ] [ Google Scholar ]
- Passolunghi M. C., Costa H. M. (2019). “ Working Memory and Mathematical Learning ,” in International Handbook of Mathematical Learning Difficulties: From the Laboratory to the Classroom , eds Fritz A., Haase V. G., Räsänen P. (Cham:Springer International Publishing; ). [ Google Scholar ]
- Passolunghi M. C., Mammarella I. C., Altoè G. (2008). Cognitive Abilities as Precursors of the Early Acquisition of Mathematical Skills During First Through Second Grades. Dev. Neuropsychol. 33 229–250. 10.1080/87565640801982320 [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Pointon A., Sangwin C. J. (2003). An analysis of undergraduate core material in the light of hand-held computer algebra systems. Int. J. Math. Educ. Sci. Technol. 34 671–686. 10.1080/0020739031000148930 [ CrossRef ] [ Google Scholar ]
- Primi R., Ferrão M. E., Almeida L. S. (2010). Fluid intelligence as a predictor of learning: A longitudinal multilevel approach applied to math. Learning Individu. Differ. 20 446–451. 10.1016/j.lindif.2010.05.001 [ CrossRef ] [ Google Scholar ]
- Raghubar K. P., Barnes M. A., Hecht S. A. (2010). Working memory and mathematics: A review of developmental, individual difference, and cognitive approaches. Learning Individ. Differ. 20 110–122. 10.1016/j.lindif.2009.10.005 [ CrossRef ] [ Google Scholar ]
- Raven J., Raven J. C., Court J. H. (2003). Manual for Raven’s Progressive Matrices and Vocabulary Scales . San Antonio, TX:Harcourt Assessment. [ Google Scholar ]
- Rittle-Johnson B., Loehr A. M., Durkin K. (2017). Promoting self-explanation to improve mathematics learning: A meta-analysis and instructional design principles. ZDM 49 599–611. 10.1007/s11858-017-0834-z [ CrossRef ] [ Google Scholar ]
- Shah P., Miyake A. (1996). The separability of working memory resources for spatial thinking and language processing: An individual differences approach. J. Exp. Psychol. 125 4–27. 10.1037/0096-3445.125.1.426T26T [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Shield M., Dole S. (2013). Assessing the potential of mathematics textbooks to promote deep learning. Educat. Stud. Math. 82 183–199. 10.1007/s10649-012-9415-9 [ CrossRef ] [ Google Scholar ]
- Silver E. (1997). Fostering creativity through instruction rich in mathematical problem solving and problem posing. ZDM 29 75–80. 10.1007/s11858-997-0003-x [ CrossRef ] [ Google Scholar ]
- Stacey K., Vincent J. (2009). Modes of reasoning in explanations in Australian eighth-grade mathematics textbooks. Educat. Stud. Math. 72 271 10.1007/s10649-009-9193-1 [ CrossRef ] [ Google Scholar ]
- Stenlund T., Sundström A., Jonsson B. (2014). Effects of repeated testing on short- and long-term memory performance across different test formats. Educat. Psychol. 36 1–18. 10.1080/01443410.2014.953037 [ CrossRef ] [ Google Scholar ]
- Sweller J., Ayres P., Kalyuga S. (2011). “ Measuring Cognitive Load ,” in Cognitive Load Theory , ed. Sweller J. (New York, NY:Springer New York; ), 71–85. 10.1007/978-1-4419-8126-4_6 [ CrossRef ] [ Google Scholar ]
- Szücs D., Devine A., Soltesz F., Nobes A., Gabriel F. (2014). Cognitive components of a mathematical processing network in 9-year-old children. Dev. Sci. 17 506–524. 10.1111/desc.12144 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Taub G. E., Floyd R. G., Keith T. Z., McGrew K. S. (2008). Effects of General and Broad Cognitive Abilities on Mathematics Achievement [Article]. School Psychol. Quart. 23 187–198. 10.1037/1045-3830.23.2.187 [ CrossRef ] [ Google Scholar ]
- Tulving E., Thomson D. M. (1973). Encoding specificity and retrieval processes in episodic memory. Psychol. Rev. 80 352–373. 10.1037/h0020071 [ CrossRef ] [ Google Scholar ]
- Unsworth N., Heitz R., Schrock J., Engle R. (2005). An automated version of the operation span task. Behav. Res. Methods 37 498–505. 10.3758/BF03192720 [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Valentin Kvist A., Gustafsson J.-E. (2008). The relation between fluid intelligence and the general factor as a function of cultural background: A test of Cattell’s Investment theory. Intelligence 36 422–436. 10.1016/j.intell.2007.08.004 [ CrossRef ] [ Google Scholar ]
- van den Broek G., Takashima A., Wiklund-Hörnqvist C., Karlsson Wirebring L., Segers E., Verhoeven L., et al. (2016). Neurocognitive mechanisms of the “testing effect”: A review. Trends Neurosci. Educ. 5 52–66. 10.1016/j.tine.2016.05.001 [ CrossRef ] [ Google Scholar ]
- VanLehn K., Siler S., Murray C., Yamauchi T., Baggett W. B. (2003). Why Do Only Some Events Cause Learning During Human Tutoring? Cognit. Instruct. 21 209–249. 10.1207/S1532690XCI2103_01 [ CrossRef ] [ Google Scholar ]
- Watkins M. W., Lei P. W., Canivez G. L. (2007). Psychometric intelligence and achievement: A cross-lagged panel analysis. Intelligence 35 59–68. 10.1016/j.intell.2006.04.00526T [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Wiklund-Hörnqvist C., Jonsson B., Nyberg L. (2014). Strengthening concept learning by repeated testing. Scand. J. Psychol. 55 10–16. 10.1111/sjop.12093 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Wiklund-Hörnqvist C., Jonsson B., Korhonen J., Eklöf H., Nyroos M. (2016). Untangling the Contribution of the Subcomponents of Working Memory to Mathematical Proficiency as Measured by the National Tests: A Study among Swedish Third Graders. Front. Psychol. 7 :1062. 10.3389/fpsyg.2016.01062 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Wirebring L. K., Wiklund-Hörnqvist C., Eriksson J., Andersson M., Jonsson B., Nyberg L. (2015). Lesser Neural Pattern Similarity across Repeated Tests Is Associated with Better Long-Term Memory Retention. J. Neurosci. 35 9595–9602. 10.1523/jneurosci.3550-14.2015 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Mathematics Education
- Problem Solving
Multiple Representation Skills and Creativity Effects on Mathematical Problem Solving using a Multimedia Whiteboard System
- Educational Technology & Society 10(2):191-212
- 10(2):191-212

- National Dong-Hwa University; National Central University

- National Taiwan Normal University

- National FengYuan Senior High School
- This person is not on ResearchGate, or hasn't claimed this research yet.
Abstract and Figures

Discover the world's research
- 25+ million members
- 160+ million publication pages
- 2.3+ billion citations

- Lia Yuliati

- Muhammad Hilmi Fadhlurrahman
- Samsul Maarif
- Remilda Agustina

- Lasmita Sari

- Rizqi Amaliyakh Sholikhakh
- Sri Yulianti
- Sani Sahara
- Nurjanah Nurjanah
- Ahmad Fajri Lutfi

- Agus Muliadi

- Aliefman Hakim

- Milanda Viona Delfiza

- Ahmad Nizar Rangkuti
- Sinar Devi Harahap
- Ilma Masrawati Siregar

- Douglas J. Hacker

- Thomas R. Post
- Merlyn J. Behr
- National Council Teachers Mathematics
- PSYCHOL INQ
- Robert J. Sternberg

- Graham Wallas
- Mayer R. E.
- M. C. Wittrock
- APPL MATH MODEL

- David Hough
- Carol S. Parke
- Sylvia M. Truman

- Milton Keynes
- Clement A. Stone
- Robert D. Ankenmann
- Recruit researchers
- Join for free
- Login Email Tip: Most researchers use their institutional email address as their ResearchGate login Password Forgot password? Keep me logged in Log in or Continue with Google Welcome back! Please log in. Email · Hint Tip: Most researchers use their institutional email address as their ResearchGate login Password Forgot password? Keep me logged in Log in or Continue with Google No account? Sign up

IMAGES
VIDEO
COMMENTS
In tracing recent research trends and directions in mathematical problem-solving, it is argued that advances in mathematics practices occur and take place around two intertwined activities, mathematics problem formulation and ways to approach and solve those problems. In this context, a problematizing principle emerges as central activity to organize mathematics curriculum proposals and ways ...
For the teaching and learning of problem solving in regular mathematics classes, the current view according to which cognitive, heuristic aspects were paramount, was expanded by certain student-specific aspects, such as attitudes, emotions and self-regulated behaviour (c.f. Kretschmer 1983; Schoenfeld 1985, 1987, 1992).
In the current study, we focused on the effect of CL approach in a specific area of mathematics: problem-solving. Mathematical problem-solving is a central area of mathematics instruction, constituting an important part of preparing students to function in modern society (Gravemeijer et al., 2017).
Experimental studies (n = 17) demonstrating the effects of interventions designed to enhance mathematical problem solving for secondary students with or at risk of learning disabilities were analyzed. Findings indicate that the efficacy of the three intervention approaches varies, and that the real‐world connections differ. ...
The problem solving approach or teaching through problem solving focuses on "teaching mathematical topics through problem-solving contexts and inquiry oriented environments which are characterized by the teacher "helping students construct a deep understanding of mathematical ideas and processes by engaging them in doing mathematics ...
The effects of cognitive and metacognitive strategy instruction on mathematical problem solving of middle school students with learning disabilities. Journal of Learning Disabilities , 25, 230-248. Google Scholar
Mathematics is one of the most objective, logical, and practical academic disciplines. Yet, in addition to cognitive skills, mathematical problem solving also involves affective factors. In the current study, we first investigated effects of mathematics anxiety (MA) and mathematical metacognition on word problem solving (WPS). We tested 224 children (116 boys, M = 10.15 years old, SD = 0.56 ...
The effects of a mathematical problem-solving intervention on students' problem-solving performance and math achievement were measured in a randomized control trial with 1,059 7th-grade students. The intervention, Solve It!, is a research-based cognitive strategy instructional intervention that was shown to improve the problem-solving performance of 8th-grade students with and without ...
The positive effects of peer tutors have been found in a variety of subjects including mathematics (Chu et al., 2017) and, in particular, mathematical problem solving (MPS; Zulaiha et al., 2020). Chu et al. ( 2017 ) proposed a formative peer-tutoring approach in which a student whose performance is better on one learning activity can take the ...
Although mathematical problem solving involves utilising mathematical concepts, including skills, strategies, and the application of concepts like recognising repeating patterns, to tackle and solve a specific problem (Klang et al., 2021; Li & Disney, 2023). Research indicates the importance of mathematical reasoning and problem-solving skills.
The study aimed to analyze the interaction effect teaching models and cognitive style field dependent (FD)-field independent (FI) to students' mathematical problem-solving ability (MPSA), as well as students' MPSA ... Mathematical problem-solving ability (MPSA) of students can be seen from several dimensions, one of .
ctly addresses the effects of different types of representations on mathematics performance. Theories offer differing pe. spectives about how visual representations such as illustrations influence student learning. Here, we inves. igated the effects of diagrams and contextual illustrations on trigonometry problem solving. Diagrams helped.
Enhancing Problem-Solving Skills for Word Problems: Impact of Diagram and Learner Expertise ... Hegarty, M., & Kozhevnikov, M. (1999). Types of visual-spatial representations and mathematical problem solving. Journal of Educational Psychology, 91, 684-689. https: ... Effects of worked examples, example-problem, and problem-example pairs on ...
Researchers accordingly discuss the influence of affect on "mathematical thinking" (Schoenfeld 2016), "problem solving" (Resnick 1988) and "mathematical capability" (DeBellis and ...
In order to solve COGNITIVE LOAD DURING PROBLEM SOLVING 279 C 49` 4 35' D A B Figure 3. Example Trigonometry Problem (If the goal of the problem is to find the length of CB, the solution is CA=sine 35/4.4; CB=CA/cosine 49.) this problem the sine ratio needs to be used followed by the cosine ratio.
while dealing with the mathematical problem-solving task. In this study, problem-solving refers to the common situational problems in mathematics in a form of problem set or worded problems. The problems are composed of items in arithmetic and algebra, trigonometry, geometry, sets, probability, number
Introduction. Supporting students' mathematical reasoning and problem-solving has been pointed out as important by the National Council of Teachers of Mathematics (NCTM; 26T 1).This philosophy is reflected in the wide range of mathematics education research focusing on the impact different teaching designs might have on students' reasoning, problem-solving ability, and conceptual ...
rather than giving complex problem solving. Therefore, most students are trained to acquire knowledge through the first and second steps in problem solving proposed by Lesh (1987). They seldom have the chance to explain their solutions using verbal or written problem solving. However, without the final step, teachers cannot truly determine if
Taking into consideration the aforementioned different theories of leaning embedded on mathematical modeling, this study attempted to determine the effects of integrating mathematical modeling to the problem solving performance and math anxiety of Grade 9 students. In this study, much is given importance to the process rather than the product.
the problems, mathematical problem-solving skills often involve a focused mindset in perfecting the strategies that have been studied in mathematics directly to find specific solutions (Mawaddah & Anisah, 2015 ò Widjajanti, 2009). There are four main steps in the math problem-solving activity. It means
The purpose of this study was to explore methods to enhance mathematical problem solving for students with mathematics disabilities (MD). A small-group problem-solving tutoring treatment incorporated explicit instruction on problem-solution rules and on transfer.
For example, Hembree's (1992) meta-analysis showed that problem solving strategies and mathematical problem solving were significantly positively correlated (r = .31 for drawing a diagram and r = .20 for using equations, Etc.). Among the various problem solving strategies, backward reasoning is an effective strategy for the provision of
This study determined the effects of the integration of mathematical modeling on the. problem solving performance and m ath anxiety level of Grade 9 students. Two groups of students. were exposed ...
To explore the effects of multiple repr esentation skills and creativity on mathematical problem solving, the studen ts were classified into different groups according to t heir solution ...
the standard of learning mathematics, it is necessary to develop a program of teaching mathematics by problem-solving. The art of problem-solving is the heart and essence of mathematics, because problem-solving can serve as a vehicle for learning new mathematical ideas and skills. Therefore, it was necessary to conduct a study for improving