Quadratic assignment problem
Author: Thomas Kueny, Eric Miller, Natasha Rice, Joseph Szczerba, David Wittmann (SysEn 5800 Fall 2020)
- 1 Introduction
- 2.1 Koopmans-Beckman Mathematical Formulation
- 2.2.1 Parameters
- 2.3.1 Optimization Problem
- 2.4 Computational Complexity
- 2.5 Algorithmic Discussions
- 2.6 Branch and Bound Procedures
- 2.7 Linearizations
- 3.1 QAP with 3 Facilities
- 4.1 Inter-plant Transportation Problem
- 4.2 The Backboard Wiring Problem
- 4.3 Hospital Layout
- 4.4 Exam Scheduling System
- 5 Conclusion
- 6 References

Introduction
The Quadratic Assignment Problem (QAP), discovered by Koopmans and Beckmann in 1957 [1] , is a mathematical optimization module created to describe the location of invisible economic activities. An NP-Complete problem, this model can be applied to many other optimization problems outside of the field of economics. It has been used to optimize backboards, inter-plant transportation, hospital transportation, exam scheduling, along with many other applications not described within this page.
Theory, Methodology, and/or Algorithmic Discussions
Koopmans-beckman mathematical formulation.
Economists Koopmans and Beckman began their investigation of the QAP to ascertain the optimal method of locating important economic resources in a given area. The Koopmans-Beckman formulation of the QAP aims to achieve the objective of assigning facilities to locations in order to minimize the overall cost. Below is the Koopmans-Beckman formulation of the QAP as described by neos-guide.org.
Quadratic Assignment Problem Formulation

Inner Product

Note: The true objective cost function only requires summing entries above the diagonal in the matrix comprised of elements

Since this matrix is symmetric with zeroes on the diagonal, dividing by 2 removes the double count of each element to give the correct cost value. See the Numerical Example section for an example of this note.
Optimization Problem
With all of this information, the QAP can be summarized as:

Computational Complexity
QAP belongs to the classification of problems known as NP-complete, thus being a computationally complex problem. QAP’s NP-completeness was proven by Sahni and Gonzalez in 1976, who states that of all combinatorial optimization problems, QAP is the “hardest of the hard”. [2]
Algorithmic Discussions
While an algorithm that can solve QAP in polynomial time is unlikely to exist, there are three primary methods for acquiring the optimal solution to a QAP problem:
- Dynamic Program
- Cutting Plane
Branch and Bound Procedures
The third method has been proven to be the most effective in solving QAP, although when n > 15, QAP begins to become virtually unsolvable.
The Branch and Bound method was first proposed by Ailsa Land and Alison Doig in 1960 and is the most commonly used tool for solving NP-hard optimization problems.
A branch-and-bound algorithm consists of a systematic enumeration of candidate solutions by means of state space search: the set of candidate solutions is thought of as forming a rooted tree with the full set at the root. The algorithm explores branches of this tree, which represent subsets of the solution set. Before one lists all of the candidate solutions of a branch, the branch is checked against upper and lower estimated bounds on the optimal solution, and the branch is eliminated if it cannot produce a better solution than the best one found so far by the algorithm.
Linearizations
The first attempts to solve the QAP eliminated the quadratic term in the objective function of

in order to transform the problem into a (mixed) 0-1 linear program. The objective function is usually linearized by introducing new variables and new linear (and binary) constraints. Then existing methods for (mixed) linear integer programming (MILP) can be applied. The very large number of new variables and constraints, however, usually poses an obstacle for efficiently solving the resulting linear integer programs. MILP formulations provide LP relaxations of the problem which can be used to compute lower bounds.
Numerical Example
Qap with 3 facilities.

| Permutation | Cost |
| (123) | 91.4 |
| 99.8 | |
| 98.4 | |
| 86.5 | |
| 103.3 | |
| 90 |

Applications
Inter-plant transportation problem.
The QAP was first introduced by Koopmans and Beckmann to address how economic decisions could be made to optimize the transportation costs of goods between both manufacturing plants and locations. [1] Factoring in the location of each of the manufacturing plants as well as the volume of goods between locations to maximize revenue is what distinguishes this from other linear programming assignment problems like the Knapsack Problem.
The Backboard Wiring Problem
As the QAP is focused on minimizing the cost of traveling from one location to another, it is an ideal approach to determining the placement of components in many modern electronics. Leon Steinberg proposed a QAP solution to optimize the layout of elements on a blackboard by minimizing the total amount of wiring required. [4]
When defining the problem Steinberg states that we have a set of n elements

as well as a set of r points

In his paper he derives the below formula:

In his paper Steinberg a backboard with a 9 by 4 array, allowing for 36 potential positions for the 34 components that needed to be placed on the backboard. For the calculation, he selected a random initial placement of s1 and chose a random family of 25 unconnected sets.
The initial placement of components is shown below:

After the initial placement of elements, it took an additional 35 iterations to get us to our final optimized backboard layout. Leading to a total of 59 iterations and a final wire length of 4,969.440.
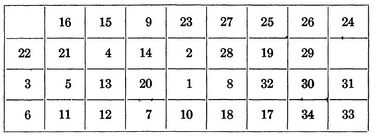
Hospital Layout
Building new hospitals was a common event in 1977 when Alealid N Elshafei wrote his paper on "Hospital Layouts as a Quadratic Assignment Problem". [5] With the high initial cost to construct the hospital and to staff it, it is important to ensure that it is operating as efficiently as possible. Elshafei's paper was commissioned to create an optimization formula to locate clinics within a building in such a way that minimizes the total distance that a patient travels within the hospital throughout the year. When doing a study of a major hospital in Cairo he determined that the Outpatient ward was acting as a bottleneck in the hospital and focused his efforts on optimizing the 17 departments there.
Elshafei identified the following QAP to determine where clinics should be placed:

For the Cairo hospital with 17 clinics, and one receiving and recording room bringing us to a total of 18 facilities. By running the above optimization Elshafei was able to get the total distance per year down to 11,281,887 from a distance of 13,973,298 based on the original hospital layout.
Exam Scheduling System
The scheduling system uses matrices for Exams, Time Slots, and Rooms with the goal of reducing the rate of schedule conflicts. To accomplish this goal, the “examination with the highest cross faculty student is been prioritized in the schedule after which the examination with the highest number of cross-program is considered and finally with the highest number of repeating student, at each stage group with the highest number of student are prioritized.” [6]

- ↑ 1.0 1.1 1.2 Koopmans, T., & Beckmann, M. (1957). Assignment Problems and the Location of Economic Activities. Econometrica, 25(1), 53-76. doi:10.2307/1907742
- ↑ 2.0 2.1 Quadratic Assignment Problem. (2020). Retrieved December 14, 2020, from https://neos-guide.org/content/quadratic-assignment-problem
- ↑ 3.0 3.1 3.2 Burkard, R. E., Çela, E., Pardalos, P. M., & Pitsoulis, L. S. (2013). The Quadratic Assignment Problem. https://www.opt.math.tugraz.at/~cela/papers/qap_bericht.pdf .
- ↑ 4.0 4.1 Leon Steinberg. The Backboard Wiring Problem: A Placement Algorithm. SIAM Review . 1961;3(1):37.
- ↑ 5.0 5.1 Alwalid N. Elshafei. Hospital Layout as a Quadratic Assignment Problem. Operational Research Quarterly (1970-1977) . 1977;28(1):167. doi:10.2307/300878
- ↑ 6.0 6.1 Muktar, D., & Ahmad, Z.M. (2014). Examination Scheduling System Based On Quadratic Assignment.
Navigation menu
- Analysis of Algorithms
- Backtracking
- Dynamic Programming
- Divide and Conquer
- Geometric Algorithms
- Mathematical Algorithms
- Pattern Searching
- Bitwise Algorithms
- Branch & Bound
- Randomized Algorithms
Quadratic Assignment Problem (QAP)
The Quadratic Assignment Problem (QAP) is an optimization problem that deals with assigning a set of facilities to a set of locations, considering the pairwise distances and flows between them.
The problem is to find the assignment that minimizes the total cost or distance, taking into account both the distances and the flows.
The distance matrix and flow matrix, as well as restrictions to ensure each facility is assigned to exactly one location and each location is assigned to exactly one facility, can be used to formulate the QAP as a quadratic objective function.
The QAP is a well-known example of an NP-hard problem , which means that for larger cases, computing the best solution might be difficult. As a result, many algorithms and heuristics have been created to quickly identify approximations of answers.
There are various types of algorithms for different problem structures, such as:
- Precise algorithms
- Approximation algorithms
- Metaheuristics like genetic algorithms and simulated annealing
- Specialized algorithms
Example: Given four facilities (F1, F2, F3, F4) and four locations (L1, L2, L3, L4). We have a cost matrix that represents the pairwise distances or costs between facilities. Additionally, we have a flow matrix that represents the interaction or flow between locations. Find the assignment that minimizes the total cost based on the interactions between facilities and locations. Each facility must be assigned to exactly one location, and each location can only accommodate one facility.
Facilities cost matrix:
| L1 | L2 | L3 | L4 | |
|---|---|---|---|---|
| F1 | 0 | 2 | 3 | 1 |
| F2 | 2 | 0 | 1 | 4 |
| F3 | 3 | 1 | 0 | 2 |
| F4 | 1 | 4 | 2 | 0 |
Flow matrix:
| F1 | F2 | F3 | F4 | |
|---|---|---|---|---|
| L1 | 0 | 1 | 2 | 3 |
| L2 | 1 | 0 | 4 | 2 |
| L3 | 2 | 4 | 0 | 1 |
| L4 | 3 | 2 | 1 | 0 |
To solve the QAP, various optimization techniques can be used, such as mathematical programming, heuristics, or metaheuristics. These techniques aim to explore the search space and find the optimal or near-optimal solution.
The solution to the QAP will provide an assignment of facilities to locations that minimizes the overall cost.
The solution generates all possible permutations of the assignment and calculates the total cost for each assignment. The optimal assignment is the one that results in the minimum total cost.
To calculate the total cost, we look at each pair of facilities in (i, j) and their respective locations (location1, location2). We then multiply the cost of assigning facility1 to facility2 (facilities[facility1][facility2]) with the flow from location1 to location2 (locations[location1][location2]). This process is done for all pairs of facilities in the assignment, and the costs are summed up.
Overall, the output tells us that assigning facilities to locations as F1->L1, F3->L2, F2->L3, and F4->L4 results in the minimum total cost of 44. This means that Facility 1 is assigned to Location 1, Facility 3 is assigned to Location 2, Facility 2 is assigned to Location 3, and Facility 4 is assigned to Location 4, yielding the lowest cost based on the given cost and flow matrices.This example demonstrates the process of finding the optimal assignment by considering the costs and flows associated with each facility and location. The objective is to find the assignment that minimizes the total cost, taking into account the interactions between facilities and locations.
Applications of the QAP include facility location, logistics, scheduling, and network architecture, all of which require effective resource allocation and arrangement.
Please Login to comment...
Similar reads.
- 105 Funny Things to Do to Make Someone Laugh
- Best PS5 SSDs in 2024: Top Picks for Expanding Your Storage
- Best Nintendo Switch Controllers in 2024
- Xbox Game Pass Ultimate: Features, Benefits, and Pricing in 2024
- #geekstreak2024 – 21 Days POTD Challenge Powered By Deutsche Bank
Improve your Coding Skills with Practice
The Quadratic Assignment Problem : Theory and Algorithms
Available online.
- SpringerLink
More options
- Find it at other libraries via WorldCat
- Contributors
Description
Creators/contributors, contents/summary.
- Preface. List of Figures. List of Tables.
- 1. Problem Statement and Complexity Aspects.
- 2. Exact Algorithms and Lower Bounds.
- 3. Heuristics and Asymptotic Behavior.
- 4. QAPs on Specially Structured Matrices.
- 5. Two More Restricted Versions of the QAP.
- 6. QAPs Arising as Optimization Problems in Graphs.
- 7. On the Biquadratic Assignment Problem (BIQAP). References. Notation Index. Subject Index.
- (source: Nielsen Book Data)
Bibliographic information
- Stanford Home
- Maps & Directions
- Search Stanford
- Emergency Info
- Terms of Use
- Non-Discrimination
- Accessibility
© Stanford University , Stanford , California 94305 .
Academia.edu no longer supports Internet Explorer.
To browse Academia.edu and the wider internet faster and more securely, please take a few seconds to upgrade your browser .
Enter the email address you signed up with and we'll email you a reset link.
- We're Hiring!
- Help Center


The Quadratic Assignment Problem

Related Papers
Encyclopedia of Optimization
Panos Pardalos
Panos M Pardalos
Abstract This paper aims at describing the state of the art on quadratic assignment problems (QAPs). It discusses the most important developments in all aspects of the QAP such as linearizations, QAP polyhedra, algorithms to solve the problem to optimality, heuristics, polynomially solvable special cases, and asymptotic behavior.
Güneş Erdoğan
The Quadratic Assignment Problem (QAP) is one of the hardest combinatorial optimization problems known. Exact solution attempts proposed for instances of size larger than 15 have been generally unsuccessful even though successful implementations have been reported on some test problems from the QAPLIB up to size 36. In this dissertation, we analyze the binary structure of the QAP and present new IP formulations. We focus on “flow-based” formulations, strengthen the formulations with valid inequalities, and report computational experience with a branch-and-cut algorithm. Next, we present new classes of instances of the QAP that can be completely or partially reduced to the Linear Assignment Problem and give procedures to check whether or not an instance is an element of one of these classes. We also identify classes of instances of the Koopmans-Beckmann form of the QAP that are solvable in polynomial time. Lastly, we present a strong lower bound based on Bender’s decomposition.
Cesar Beltran-Royo
Pesquisa Operacional
Paulo Boaventura Netto
We investigate the classical Gilmore-Lawler lower bound for the quadratic assignment problem. We provide evidence of the difficulty of improving the Gilmore-Lawler bound and develop new bounds by means of optimal reduction schemes. Computational results are reported indicating that the new lower bounds have advantages over previous bounds and can be used in a branch-and-bound type algorithm for the quadratic assignment problem.
Computers & Operations Research
Ricardo P M Ferreira
Ilyes Beltaef
Loading Preview
Sorry, preview is currently unavailable. You can download the paper by clicking the button above.
RELATED PAPERS
Paulo Gonçalves
Dennis Heffley
Franz Rendl
Vittorio Maniezzo
New ideas in optimization
Marco Dorigo
Álvaro M. Valdebenito B.
Journal of Combinatorial Optimization
Madalina Drugan
Ali Safari Mamaghani
Informs Journal on Computing
Dushyant Sharma
Mathematics of Operations Research
Discrete Applied Mathematics
catherine roucairol
IEEE Transactions on Knowledge and Data Engineering
Cut Latifah
European Journal of Operational Research
Bernard Mans
Teodor Crainic
Applied Mathematical Sciences
Hassan Mishmast Nehi
Panos M Pardalos , John Mitchell
Paulo Boaventura-Netto
Ajay Bidyarthy
Yugoslav Journal of …
Journal of Industrial Engineering International
Hossein Karimi
NURDIYANA JAMIL
Ajith Abraham
IEEE Transactions on Information Theory
David Malah
Tansel Dökeroğlu
Matteo Fischetti
Sunderesh Heragu
RELATED TOPICS
- We're Hiring!
- Help Center
- Find new research papers in:
- Health Sciences
- Earth Sciences
- Cognitive Science
- Mathematics
- Computer Science
- Academia ©2024
Help | Advanced Search
Quantum Physics
Title: an encoding of argumentation problems using quadratic unconstrained binary optimization.
Abstract: In this paper, we develop a way to encode several NP-Complete problems in Abstract Argumentation to Quadratic Unconstrained Binary Optimization (QUBO) problems. In this form, a solution for a QUBO problem involves minimizing a quadratic function over binary variables (0/1), where the coefficients can be represented by a symmetric square matrix (or an equivalent upper triangular version). With the QUBO formulation, exploiting new computing architectures, such as Quantum and Digital Annealers, is possible. A more conventional approach consists of developing approximate solvers, which, in this case, are used to tackle the intrinsic complexity. We performed tests to prove the correctness and applicability of classical problems in Argumentation and enforcement of argument sets. We compared our approach to two other approximate solvers in the literature during tests. In the final experimentation, we used a Simulated Annealing algorithm on a local machine. Also, we tested a Quantum Annealer from the D-Wave Ocean SDK and the Leap Quantum Cloud Service.
| Subjects: | Quantum Physics (quant-ph); Artificial Intelligence (cs.AI) |
| Cite as: | [quant-ph] |
| (or [quant-ph] for this version) | |
| Focus to learn more arXiv-issued DOI via DataCite (pending registration) | |
| Journal reference: | Quantum Mach. Intell. 6(2): 51 (2024) |
| : | Focus to learn more DOI(s) linking to related resources |
Submission history
Access paper:.
- HTML (experimental)
- Other Formats
References & Citations
- INSPIRE HEP
- Google Scholar
- Semantic Scholar
BibTeX formatted citation
Bibliographic and Citation Tools
Code, data and media associated with this article, recommenders and search tools.
- Institution
arXivLabs: experimental projects with community collaborators
arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.
Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.
Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .
The Quadratic Assignment Problem: A Brief Review
- Conference paper
- Cite this conference paper

- E. L. Lawler 3
Part of the book series: NATO Advanced Study Institutes Series ((ASIC,volume 19))
285 Accesses
1 Citations
The quadratic assignment problem, its applications, and various exact and inexact procedures for its solution are briefly reviewed. Certain special cases of the one-dimensional module placement problem, itself a special case of the quadratic assignment problem, are surveyed.
The preparation of this paper was supported in part by the U.S. Air Force Office of Scientific Research, Grant AFOSR-71–2076.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Subscribe and save.
- Get 10 units per month
- Download Article/Chapter or eBook
- 1 Unit = 1 Article or 1 Chapter
- Cancel anytime
- Available as PDF
- Read on any device
- Instant download
- Own it forever
- Compact, lightweight edition
- Dispatched in 3 to 5 business days
- Free shipping worldwide - see info
Tax calculation will be finalised at checkout
Purchases are for personal use only
Institutional subscriptions
Unable to display preview. Download preview PDF.
Similar content being viewed by others

The Quadratic Assignment Problem

Optimization Theory

Quadratic equations
D. Adolphson and T.C. Hu, “Optimal Linear Ordering,” SIAM J. Appl. Math. 25 (1973), 403–423.
Article MathSciNet MATH Google Scholar
P.S. Davis and T.L. Ray, “A Branch-Bound Algorithm for the Capacitated Facilities Location Problem,” Naval Res. Logistics Qtrly 16 (1969), 331–344.
MATH Google Scholar
M.A. Efroymson and T.L. Ray, “A Branch-Bound Algorithm for Plant Location,” Opns. Res. 14 (1966), 361–368.
Article Google Scholar
J.N. Gavert and N.V. Plyter, “The Optimal Assignment of Facilities to Locations by Branch and Bound,” Opns.Res. 14 (1966), 210–232.
P.C. Gilmore, “Optimal and Sub-optimal Algorithms for the Quadratic Assignment Problem,” SIAM J. Appl. Math. 10 (1962), 305–313.
R.H. Glaser, “A Quasi-Simplex Method for Designing Suboptimal Packages for Electronic Building Blocks,” Proc. 1959 Computer Applic. Symp. , Armour Res. Found., Ill. Inst. Tech., 100–111.
Google Scholar
R.E. Gomory and T.C. Hu, “Multi-Terminal Network Flows,” SIAM J. Appl. Math. 9 (1961), 551–570.
G.W. Graves and A.B. Whinston, “An Algorithm for the Quadratic Assignment Problem,” Mgt. Sci. 16 (1970), 453–471.
Article MATH Google Scholar
S.A. Graciano, “Branch and Bound Solutions to the Capacitated Plant Location Problem,” Opns. Res. 17 (1969), 1005–1016.
M. Hanan and J.M. Kurtzberg, “A Review of the Placement and Quadratic Assignment Problems,” SIAM Rev. 14 (1972), 324–342.
G. Henry, “Recherche d’un Reseau de Depots Optimum,” Reuve Francaise d’informatique et de Recherche Operationnelle 2 (1968), 61–70.
F.S. Hillier and M.M. Connors, “Quadratic Assignment Problem Algorithms and the Location of Indivisible Facilities,” Mgt. Sci. 13 (1966), 42–57.
W.A. Horn, “Single Machine Job Sequencing with Treelike Precedence Ordering and Linear Delay Penalties,” SIAM J. Appl. Math. 23 (1972), 189–202.
R.M. Karp, “Reducibility Among Combinatorial Problems,” in Complexity of Computer Computations , R.E. Miller and J.W. Thatcher, eds., Plenum Press, N.Y., 1972, 85–104.
R.M. Karp, A.C. McKellar, C.K. Wong, “Near-Optimal Solutions to a 2-Dimensional Placement Problem,” IBM Research Tech. Report RC4740, February 1974.
U.R. Kodres, “Geometrical Positioning of Circuit Elements in a Computer,” Conf. Paper 1172 , AIEE Fall General Mtg., Oct. 1959.
T.C. Koopmans and M.J. Beckmann, “Assignment Problems and the Location of Economic Activities,” Econometrica 25 (1957), 52–75.
Article MathSciNet Google Scholar
A.H. Land, “A Problem of Assignment with Inter-related Costs,” Opnl. Res. Qtrly 14 (1963), 185–199.
E.L. Lawler, “The Quadratic Assignment Problem,” Mgt. Sci. 9 (1963), 586–589.
P.M. Morse, “Optimal Linear Ordering of Information Items,” Opns. Res. 20 (1972), 741–751.
C.E. Nugent, T.E. Vollman and J. Ruml, “An Experimental Comparison of Techniques for the Assignment of Facilities to Locations,” Opns. Res. 16 (1968), 150–173.
V.R. Pratt, “An N log N Algorithm to Distribute N Records Optimally in a Sequential Access File,” in Complexity of Computer Computations , R.E. Miller and J.W. Thatcher, eds., Plenum Press, N.Y., 1972, 111–118.
T.C. Raymond, “A Method for Optimizing Circuit Module Placement,” IBM Tech. Disclosure Bull. 13 (1970), 274–276.
J. Sidney, Ph.D. dissertation, University of Michigan, Ann Arbor, 1971.
K. Spielberg, “Plant Location with Generalized Search Origin,” Mgt. Sci. 16 (1969), 165–178.
L. Steinberg, “The Backboard Wiring Problem: A Placement Algorithm,” SIAM Rev. 3 (1961), 37–50.
Download references
Author information
Authors and affiliations.
Department of Electrical Engineering and Computer Sciences, The University of California, Berkeley, CA, USA
E. L. Lawler
You can also search for this author in PubMed Google Scholar
Editor information
Editors and affiliations.
Université de Paris, France
B. Roy ( Professeur et Conseiller Scientifique ) ( Professeur et Conseiller Scientifique )
SEMA, France
Rights and permissions
Reprints and permissions
Copyright information
© 1995 D. Reidel Publishing Company, Dordrecht-Holland
About this paper
Cite this paper.
Lawler, E.L. (1995). The Quadratic Assignment Problem: A Brief Review. In: Roy, B. (eds) Combinatorial Programming: Methods and Applications. NATO Advanced Study Institutes Series, vol 19. Springer, Dordrecht. https://doi.org/10.1007/978-94-011-7557-9_20
Download citation
DOI : https://doi.org/10.1007/978-94-011-7557-9_20
Publisher Name : Springer, Dordrecht
Print ISBN : 978-94-011-7559-3
Online ISBN : 978-94-011-7557-9
eBook Packages : Springer Book Archive
Share this paper
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Publish with us
Policies and ethics
- Find a journal
- Track your research

COMMENTS
The quadratic assignment problem (QAP) is one of the fundamental combinatorial optimization problems in the branch of optimization or operations research in mathematics, from the category of the facilities location problems first introduced by Koopmans and Beckmann. [1]The problem models the following real-life problem: There are a set of n facilities and a set of n locations.
The Quadratic Assignment ProblemThe. eonidas S. Pitsoulis‡AbstractThis paper aims at describing the state of the art on quad. atic assignment problems (QAPs). It discusses the most important developments in all aspects of the QAP such as linearizations, QAP polyhedra, algorithms to solve the problem to optimality, heuristics, polynomially ...
The Quadratic Assignment Problem (QAP), discovered by Koopmans and Beckmann in 1957, is a mathematical optimization module created to describe the location of invisible economic activities. An NP-Complete problem, this model can be applied to many other optimization problems outside of the field of economics. It has been used to optimize ...
The Quadratic Assignment Problem (QAP) is an optimization problem that deals with assigning a set of facilities to a set of locations, considering the pairwise distances and flows between them.. The problem is to find the assignment that minimizes the total cost or distance, taking into account both the distances and the flows. The distance matrix and flow matrix, as well as restrictions to ...
Abstract. The quadratic assignment problem (QAP) was introduced by Koopmans and Beckmann in 1957 as a mathematical model for the location of a set of indivisible economical activities [113]. Consider the problem of allocating a set of facilities to a set of locations, with the cost being a function of the distance and flow between the ...
The quadratic assignment problem (QAP) is a combinatorial optimization problem, that although there is a substantial amount of research devoted to it, it is still, up to this date, not well solvable in the sense that no exact algorithm can solve problems of size n > 20 in reasonable computational time.The QAP can be viewed as a natural extension of the linear assignment problem (LAP; cf. also ...
The quadratic assignment problem (QAP) was introduced in 1957 by Koopmans and Beckmann to model a plant location problem. Since then the QAP has been object of numerous investigations by mathematicians, computers scientists, ope- tions researchers and practitioners. Nowadays the QAP is widely considered as a classical combinatorial optimization problem which is (still) attractive from many ...
The quadratic assignment problem (QAP), one of the most difficult problems in the NP-hard class, models many real-life problems in several areas such as facilities location, parallel and distributed computing, and combinatorial data analysis. Combinatorial optimization problems, such as the traveling salesman problem, maximal clique and graph ...
The quadratic assignment problem (QAP) is arguably one of the hardest NP-hard discrete optimization problems. Problems of dimension greater than 25 are still considered to be large scale. Current successful solution techniques use branch-and-bound methods, which rely on obtaining strong and inexpensive bounds.
THE QUADRATIC ASSIGNMENT PROBLEM 21 (A further attempt to avoid taking the sum of two minima obtained by treating the quadratic and linear parts separately is given in the paper by Karisch, Rendl, and Wolkowicz in these proceedings.) 5.2.3. Reformulation Based Bounds. There are also other types of lower bounds for the QAP.
The quadratic assignment problem (QAP) was introduced in 1957 by Koopmans and Beckmann to model a plant location problem. Since then the QAP has been object of numerous investigations by mathematicians, computers scientists, ope- tions researchers and practitioners. Nowadays the QAP is widely considered as a classical combinatorial optimization ...
The quadratic assignment problem (QAP) is considered one of the most difficult optimization problems to solve optimally. The QAP is a combinatorial optimization problem stated for the first time by Koopmans and Beckmann ().Early papers on the subject include Gilmore (), Pierce and Crowston (), Lawler (), and Love and Wong ().The problem is defined as follows.
The quadratic assignment problem (QAP) was originally introduced in 1957 by Tjalling C. Koopmans and Martin Beckman [26] who were trying to 1. model a facilities location problem [10]. Since then, it has been among the most studied problems in all of combinatorial optimization. Many scientists
The Quadratic Assignment Problem (QAP) is one of the most inter-esting and most challenging combinatorial optimization problems in exis-tence. This paper will be a survey of the QAP. An introduction discussing the origins of the problem will be provided ̄rst. Next, formal problem descriptions and mathematical formulations will be given.
The Quadratic Assignment Problem (QAP) is one of the hardest combinatorial optimization problems known. Exact solution attempts proposed for instances of size larger than 15 have been generally unsuccessful even though successful implementations have been reported on some test problems from the QAPLIB up to size 36. In this dissertation, we ...
The quadratic assignment problem (QAP) was introduced by Koopmans and Beckmann in 1957 as a mathematical model for the location of a set of indivisible economical activities [113]. Consider the ...
The quadratic assignment problem (QAP) was introduced in 1957 by Koopmans and Beckmann to model a plant location problem. Since then the QAP has been object of numerous investigations by mathematicians, computers scientists, ope- tions researchers and practitioners. Nowadays the QAP is widely considered as a classical combinatorial optimization ...
the quadratic assignment problem. It will also be demonstrated, by example, that the optimal solution to this problem may entail integral assignments, contrary to the findings of K-B. The following LP problem is formulated as in the K-B paper; however, here it is not reduced to a cost minimization procedure; in general, aki varies with location.
The quadratic assignment problem (QAP) is a combinatorial optimization problem, that although there is a substantial amount of research devoted to it, it is still, up to this date, not well solvable in the sense that no exact algorithm can solve problems of size n > 20 in reasonable computational time. The QAP can be ...
The quadratic assignment problem (QAP) has considered one of the most significant combinatorial optimization problems due to its variant and significant applications in real life such as scheduling, production, computer manufacture, chemistry, facility location, communication, and other fields. QAP is NP-hard problem that is impossible to be solved in polynomial time when the problem size ...
Correlation of Problem Hardness and Fitness Landscapes in the Quadratic Assignment Problem. An approach based on simulated annealing to optimize the performance of extraction of the flower region using mean-shift segmentation. A non-greedy systematic neighbourhood search heuristic for solving facility layout problem.
In this paper, we develop a way to encode several NP-Complete problems in Abstract Argumentation to Quadratic Unconstrained Binary Optimization (QUBO) problems. In this form, a solution for a QUBO problem involves minimizing a quadratic function over binary variables (0/1), where the coefficients can be represented by a symmetric square matrix (or an equivalent upper triangular version). With ...
The quadratic assignment problem, its applications, and various exact and inexact procedures for its solution are briefly reviewed. Certain special cases of the one-dimensional module placement problem, itself a special case of the quadratic assignment problem, are surveyed.