Hypothesis tests about the variance
by Marco Taboga , PhD
This page explains how to perform hypothesis tests about the variance of a normal distribution, called Chi-square tests.
We analyze two different situations:
when the mean of the distribution is known;
when it is unknown.
Depending on the situation, the Chi-square statistic used in the test has a different distribution.
At the end of the page, we propose some solved exercises.
Table of contents

Normal distribution with known mean
The null hypothesis, the test statistic, the critical region, the decision, the power function, the size of the test, how to choose the critical value, normal distribution with unknown mean, solved exercises.
The assumptions are the same previously made in the lecture on confidence intervals for the variance .
The sample is drawn from a normal distribution .
A test of hypothesis based on it is called a Chi-square test .
Otherwise the null is not rejected.
![hypothesis testing for population variance [eq8]](https://www.statlect.com/images/hypothesis-testing-variance__21.png)
We explain how to do this in the page on critical values .
We now relax the assumption that the mean of the distribution is known.
![hypothesis testing for population variance [eq29]](https://www.statlect.com/images/hypothesis-testing-variance__74.png)
See the comments on the choice of the critical value made for the case of known mean.
Below you can find some exercises with explained solutions.
Suppose that we observe 40 independent realizations of a normal random variable.
we run a Chi-square test of the null hypothesis that the variance is equal to 1;
Make the same assumptions of Exercise 1 above.
If the unadjusted sample variance is equal to 0.9, is the null hypothesis rejected?
How to cite
Please cite as:
Taboga, Marco (2021). "Hypothesis tests about the variance", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/fundamentals-of-statistics/hypothesis-testing-variance.
Most of the learning materials found on this website are now available in a traditional textbook format.
- Convergence in probability
- Multivariate normal distribution
- Characteristic function
- Moment generating function
- Chi-square distribution
- Beta function
- Bernoulli distribution
- Mathematical tools
- Fundamentals of probability
- Probability distributions
- Asymptotic theory
- Fundamentals of statistics
- About Statlect
- Cookies, privacy and terms of use
- Posterior probability
- IID sequence
- Probability space
- Probability density function
- Continuous mapping theorem
- To enhance your privacy,
- we removed the social buttons,
- but don't forget to share .
Hypothesis Testing - Analysis of Variance (ANOVA)
Lisa Sullivan, PhD
Professor of Biostatistics
Boston University School of Public Health

Introduction
This module will continue the discussion of hypothesis testing, where a specific statement or hypothesis is generated about a population parameter, and sample statistics are used to assess the likelihood that the hypothesis is true. The hypothesis is based on available information and the investigator's belief about the population parameters. The specific test considered here is called analysis of variance (ANOVA) and is a test of hypothesis that is appropriate to compare means of a continuous variable in two or more independent comparison groups. For example, in some clinical trials there are more than two comparison groups. In a clinical trial to evaluate a new medication for asthma, investigators might compare an experimental medication to a placebo and to a standard treatment (i.e., a medication currently being used). In an observational study such as the Framingham Heart Study, it might be of interest to compare mean blood pressure or mean cholesterol levels in persons who are underweight, normal weight, overweight and obese.
The technique to test for a difference in more than two independent means is an extension of the two independent samples procedure discussed previously which applies when there are exactly two independent comparison groups. The ANOVA technique applies when there are two or more than two independent groups. The ANOVA procedure is used to compare the means of the comparison groups and is conducted using the same five step approach used in the scenarios discussed in previous sections. Because there are more than two groups, however, the computation of the test statistic is more involved. The test statistic must take into account the sample sizes, sample means and sample standard deviations in each of the comparison groups.
If one is examining the means observed among, say three groups, it might be tempting to perform three separate group to group comparisons, but this approach is incorrect because each of these comparisons fails to take into account the total data, and it increases the likelihood of incorrectly concluding that there are statistically significate differences, since each comparison adds to the probability of a type I error. Analysis of variance avoids these problemss by asking a more global question, i.e., whether there are significant differences among the groups, without addressing differences between any two groups in particular (although there are additional tests that can do this if the analysis of variance indicates that there are differences among the groups).
The fundamental strategy of ANOVA is to systematically examine variability within groups being compared and also examine variability among the groups being compared.
Learning Objectives
After completing this module, the student will be able to:
- Perform analysis of variance by hand
- Appropriately interpret results of analysis of variance tests
- Distinguish between one and two factor analysis of variance tests
- Identify the appropriate hypothesis testing procedure based on type of outcome variable and number of samples
The ANOVA Approach
Consider an example with four independent groups and a continuous outcome measure. The independent groups might be defined by a particular characteristic of the participants such as BMI (e.g., underweight, normal weight, overweight, obese) or by the investigator (e.g., randomizing participants to one of four competing treatments, call them A, B, C and D). Suppose that the outcome is systolic blood pressure, and we wish to test whether there is a statistically significant difference in mean systolic blood pressures among the four groups. The sample data are organized as follows:
|
|
|
|
|
|
|---|---|---|---|---|
|
| n | n | n | n |
|
|
|
|
|
|
|
| s | s | s | s |
The hypotheses of interest in an ANOVA are as follows:
- H 0 : μ 1 = μ 2 = μ 3 ... = μ k
- H 1 : Means are not all equal.
where k = the number of independent comparison groups.
In this example, the hypotheses are:
- H 0 : μ 1 = μ 2 = μ 3 = μ 4
- H 1 : The means are not all equal.
The null hypothesis in ANOVA is always that there is no difference in means. The research or alternative hypothesis is always that the means are not all equal and is usually written in words rather than in mathematical symbols. The research hypothesis captures any difference in means and includes, for example, the situation where all four means are unequal, where one is different from the other three, where two are different, and so on. The alternative hypothesis, as shown above, capture all possible situations other than equality of all means specified in the null hypothesis.
Test Statistic for ANOVA
The test statistic for testing H 0 : μ 1 = μ 2 = ... = μ k is:
and the critical value is found in a table of probability values for the F distribution with (degrees of freedom) df 1 = k-1, df 2 =N-k. The table can be found in "Other Resources" on the left side of the pages.
NOTE: The test statistic F assumes equal variability in the k populations (i.e., the population variances are equal, or s 1 2 = s 2 2 = ... = s k 2 ). This means that the outcome is equally variable in each of the comparison populations. This assumption is the same as that assumed for appropriate use of the test statistic to test equality of two independent means. It is possible to assess the likelihood that the assumption of equal variances is true and the test can be conducted in most statistical computing packages. If the variability in the k comparison groups is not similar, then alternative techniques must be used.
The F statistic is computed by taking the ratio of what is called the "between treatment" variability to the "residual or error" variability. This is where the name of the procedure originates. In analysis of variance we are testing for a difference in means (H 0 : means are all equal versus H 1 : means are not all equal) by evaluating variability in the data. The numerator captures between treatment variability (i.e., differences among the sample means) and the denominator contains an estimate of the variability in the outcome. The test statistic is a measure that allows us to assess whether the differences among the sample means (numerator) are more than would be expected by chance if the null hypothesis is true. Recall in the two independent sample test, the test statistic was computed by taking the ratio of the difference in sample means (numerator) to the variability in the outcome (estimated by Sp).
The decision rule for the F test in ANOVA is set up in a similar way to decision rules we established for t tests. The decision rule again depends on the level of significance and the degrees of freedom. The F statistic has two degrees of freedom. These are denoted df 1 and df 2 , and called the numerator and denominator degrees of freedom, respectively. The degrees of freedom are defined as follows:
df 1 = k-1 and df 2 =N-k,
where k is the number of comparison groups and N is the total number of observations in the analysis. If the null hypothesis is true, the between treatment variation (numerator) will not exceed the residual or error variation (denominator) and the F statistic will small. If the null hypothesis is false, then the F statistic will be large. The rejection region for the F test is always in the upper (right-hand) tail of the distribution as shown below.
Rejection Region for F Test with a =0.05, df 1 =3 and df 2 =36 (k=4, N=40)

For the scenario depicted here, the decision rule is: Reject H 0 if F > 2.87.
The ANOVA Procedure
We will next illustrate the ANOVA procedure using the five step approach. Because the computation of the test statistic is involved, the computations are often organized in an ANOVA table. The ANOVA table breaks down the components of variation in the data into variation between treatments and error or residual variation. Statistical computing packages also produce ANOVA tables as part of their standard output for ANOVA, and the ANOVA table is set up as follows:
| Source of Variation | Sums of Squares (SS) | Degrees of Freedom (df) | Mean Squares (MS) | F |
|---|---|---|---|---|
| Between Treatments |
| k-1 |
|
|
| Error (or Residual) |
| N-k |
| |
| Total |
| N-1 |
where
- X = individual observation,
- k = the number of treatments or independent comparison groups, and
- N = total number of observations or total sample size.
The ANOVA table above is organized as follows.
- The first column is entitled "Source of Variation" and delineates the between treatment and error or residual variation. The total variation is the sum of the between treatment and error variation.
- The second column is entitled "Sums of Squares (SS)" . The between treatment sums of squares is
and is computed by summing the squared differences between each treatment (or group) mean and the overall mean. The squared differences are weighted by the sample sizes per group (n j ). The error sums of squares is:
and is computed by summing the squared differences between each observation and its group mean (i.e., the squared differences between each observation in group 1 and the group 1 mean, the squared differences between each observation in group 2 and the group 2 mean, and so on). The double summation ( SS ) indicates summation of the squared differences within each treatment and then summation of these totals across treatments to produce a single value. (This will be illustrated in the following examples). The total sums of squares is:
and is computed by summing the squared differences between each observation and the overall sample mean. In an ANOVA, data are organized by comparison or treatment groups. If all of the data were pooled into a single sample, SST would reflect the numerator of the sample variance computed on the pooled or total sample. SST does not figure into the F statistic directly. However, SST = SSB + SSE, thus if two sums of squares are known, the third can be computed from the other two.
- The third column contains degrees of freedom . The between treatment degrees of freedom is df 1 = k-1. The error degrees of freedom is df 2 = N - k. The total degrees of freedom is N-1 (and it is also true that (k-1) + (N-k) = N-1).
- The fourth column contains "Mean Squares (MS)" which are computed by dividing sums of squares (SS) by degrees of freedom (df), row by row. Specifically, MSB=SSB/(k-1) and MSE=SSE/(N-k). Dividing SST/(N-1) produces the variance of the total sample. The F statistic is in the rightmost column of the ANOVA table and is computed by taking the ratio of MSB/MSE.
A clinical trial is run to compare weight loss programs and participants are randomly assigned to one of the comparison programs and are counseled on the details of the assigned program. Participants follow the assigned program for 8 weeks. The outcome of interest is weight loss, defined as the difference in weight measured at the start of the study (baseline) and weight measured at the end of the study (8 weeks), measured in pounds.
Three popular weight loss programs are considered. The first is a low calorie diet. The second is a low fat diet and the third is a low carbohydrate diet. For comparison purposes, a fourth group is considered as a control group. Participants in the fourth group are told that they are participating in a study of healthy behaviors with weight loss only one component of interest. The control group is included here to assess the placebo effect (i.e., weight loss due to simply participating in the study). A total of twenty patients agree to participate in the study and are randomly assigned to one of the four diet groups. Weights are measured at baseline and patients are counseled on the proper implementation of the assigned diet (with the exception of the control group). After 8 weeks, each patient's weight is again measured and the difference in weights is computed by subtracting the 8 week weight from the baseline weight. Positive differences indicate weight losses and negative differences indicate weight gains. For interpretation purposes, we refer to the differences in weights as weight losses and the observed weight losses are shown below.
| Low Calorie | Low Fat | Low Carbohydrate | Control |
|---|---|---|---|
| 8 | 2 | 3 | 2 |
| 9 | 4 | 5 | 2 |
| 6 | 3 | 4 | -1 |
| 7 | 5 | 2 | 0 |
| 3 | 1 | 3 | 3 |
Is there a statistically significant difference in the mean weight loss among the four diets? We will run the ANOVA using the five-step approach.
- Step 1. Set up hypotheses and determine level of significance
H 0 : μ 1 = μ 2 = μ 3 = μ 4 H 1 : Means are not all equal α=0.05
- Step 2. Select the appropriate test statistic.
The test statistic is the F statistic for ANOVA, F=MSB/MSE.
- Step 3. Set up decision rule.
The appropriate critical value can be found in a table of probabilities for the F distribution(see "Other Resources"). In order to determine the critical value of F we need degrees of freedom, df 1 =k-1 and df 2 =N-k. In this example, df 1 =k-1=4-1=3 and df 2 =N-k=20-4=16. The critical value is 3.24 and the decision rule is as follows: Reject H 0 if F > 3.24.
- Step 4. Compute the test statistic.
To organize our computations we complete the ANOVA table. In order to compute the sums of squares we must first compute the sample means for each group and the overall mean based on the total sample.
|
| Low Calorie | Low Fat | Low Carbohydrate | Control |
|---|---|---|---|---|
| n | 5 | 5 | 5 | 5 |
| Group mean | 6.6 | 3.0 | 3.4 | 1.2 |
We can now compute
So, in this case:
Next we compute,
SSE requires computing the squared differences between each observation and its group mean. We will compute SSE in parts. For the participants in the low calorie diet:
|
| 6.6 |
|
|---|---|---|
| 8 | 1.4 | 2.0 |
| 9 | 2.4 | 5.8 |
| 6 | -0.6 | 0.4 |
| 7 | 0.4 | 0.2 |
| 3 | -3.6 | 13.0 |
| Totals | 0 | 21.4 |
For the participants in the low fat diet:
|
| 3.0 |
|
|---|---|---|
| 2 | -1.0 | 1.0 |
| 4 | 1.0 | 1.0 |
| 3 | 0.0 | 0.0 |
| 5 | 2.0 | 4.0 |
| 1 | -2.0 | 4.0 |
| Totals | 0 | 10.0 |
For the participants in the low carbohydrate diet:
|
|
|
|
|---|---|---|
| 3 | -0.4 | 0.2 |
| 5 | 1.6 | 2.6 |
| 4 | 0.6 | 0.4 |
| 2 | -1.4 | 2.0 |
| 3 | -0.4 | 0.2 |
| Totals | 0 | 5.4 |
For the participants in the control group:
|
|
|
|
|---|---|---|
| 2 | 0.8 | 0.6 |
| 2 | 0.8 | 0.6 |
| -1 | -2.2 | 4.8 |
| 0 | -1.2 | 1.4 |
| 3 | 1.8 | 3.2 |
| Totals | 0 | 10.6 |
We can now construct the ANOVA table .
| Source of Variation | Sums of Squares (SS) | Degrees of Freedom (df) | Means Squares (MS) | F |
|---|---|---|---|---|
| Between Treatmenst | 75.8 | 4-1=3 | 75.8/3=25.3 | 25.3/3.0=8.43 |
| Error (or Residual) | 47.4 | 20-4=16 | 47.4/16=3.0 | |
| Total | 123.2 | 20-1=19 |
- Step 5. Conclusion.
We reject H 0 because 8.43 > 3.24. We have statistically significant evidence at α=0.05 to show that there is a difference in mean weight loss among the four diets.
ANOVA is a test that provides a global assessment of a statistical difference in more than two independent means. In this example, we find that there is a statistically significant difference in mean weight loss among the four diets considered. In addition to reporting the results of the statistical test of hypothesis (i.e., that there is a statistically significant difference in mean weight losses at α=0.05), investigators should also report the observed sample means to facilitate interpretation of the results. In this example, participants in the low calorie diet lost an average of 6.6 pounds over 8 weeks, as compared to 3.0 and 3.4 pounds in the low fat and low carbohydrate groups, respectively. Participants in the control group lost an average of 1.2 pounds which could be called the placebo effect because these participants were not participating in an active arm of the trial specifically targeted for weight loss. Are the observed weight losses clinically meaningful?
Another ANOVA Example
Calcium is an essential mineral that regulates the heart, is important for blood clotting and for building healthy bones. The National Osteoporosis Foundation recommends a daily calcium intake of 1000-1200 mg/day for adult men and women. While calcium is contained in some foods, most adults do not get enough calcium in their diets and take supplements. Unfortunately some of the supplements have side effects such as gastric distress, making them difficult for some patients to take on a regular basis.
A study is designed to test whether there is a difference in mean daily calcium intake in adults with normal bone density, adults with osteopenia (a low bone density which may lead to osteoporosis) and adults with osteoporosis. Adults 60 years of age with normal bone density, osteopenia and osteoporosis are selected at random from hospital records and invited to participate in the study. Each participant's daily calcium intake is measured based on reported food intake and supplements. The data are shown below.
|
|
|
|
|---|---|---|
| 1200 | 1000 | 890 |
| 1000 | 1100 | 650 |
| 980 | 700 | 1100 |
| 900 | 800 | 900 |
| 750 | 500 | 400 |
| 800 | 700 | 350 |
Is there a statistically significant difference in mean calcium intake in patients with normal bone density as compared to patients with osteopenia and osteoporosis? We will run the ANOVA using the five-step approach.
H 0 : μ 1 = μ 2 = μ 3 H 1 : Means are not all equal α=0.05
In order to determine the critical value of F we need degrees of freedom, df 1 =k-1 and df 2 =N-k. In this example, df 1 =k-1=3-1=2 and df 2 =N-k=18-3=15. The critical value is 3.68 and the decision rule is as follows: Reject H 0 if F > 3.68.
To organize our computations we will complete the ANOVA table. In order to compute the sums of squares we must first compute the sample means for each group and the overall mean.
| Normal Bone Density |
|
|
|---|---|---|
| n =6 | n =6 | n =6 |
|
|
|
|
If we pool all N=18 observations, the overall mean is 817.8.
We can now compute:
Substituting:
SSE requires computing the squared differences between each observation and its group mean. We will compute SSE in parts. For the participants with normal bone density:
|
|
|
|
|---|---|---|
| 1200 | 261.6667 | 68,486.9 |
| 1000 | 61.6667 | 3,806.9 |
| 980 | 41.6667 | 1,738.9 |
| 900 | -38.3333 | 1,466.9 |
| 750 | -188.333 | 35,456.9 |
| 800 | -138.333 | 19,126.9 |
| Total | 0 | 130,083.3 |
For participants with osteopenia:
|
|
|
|
|---|---|---|
| 1000 | 200 | 40,000 |
| 1100 | 300 | 90,000 |
| 700 | -100 | 10,000 |
| 800 | 0 | 0 |
| 500 | -300 | 90,000 |
| 700 | -100 | 10,000 |
| Total | 0 | 240,000 |
For participants with osteoporosis:
|
|
|
|
|---|---|---|
| 890 | 175 | 30,625 |
| 650 | -65 | 4,225 |
| 1100 | 385 | 148,225 |
| 900 | 185 | 34,225 |
| 400 | -315 | 99,225 |
| 350 | -365 | 133,225 |
| Total | 0 | 449,750 |
|
|
|
|
|
|
|---|---|---|---|---|
| Between Treatments | 152,477.7 | 2 | 76,238.6 | 1.395 |
| Error or Residual | 819,833.3 | 15 | 54,655.5 | |
| Total | 972,311.0 | 17 |
We do not reject H 0 because 1.395 < 3.68. We do not have statistically significant evidence at a =0.05 to show that there is a difference in mean calcium intake in patients with normal bone density as compared to osteopenia and osterporosis. Are the differences in mean calcium intake clinically meaningful? If so, what might account for the lack of statistical significance?
One-Way ANOVA in R
The video below by Mike Marin demonstrates how to perform analysis of variance in R. It also covers some other statistical issues, but the initial part of the video will be useful to you.
Two-Factor ANOVA
The ANOVA tests described above are called one-factor ANOVAs. There is one treatment or grouping factor with k > 2 levels and we wish to compare the means across the different categories of this factor. The factor might represent different diets, different classifications of risk for disease (e.g., osteoporosis), different medical treatments, different age groups, or different racial/ethnic groups. There are situations where it may be of interest to compare means of a continuous outcome across two or more factors. For example, suppose a clinical trial is designed to compare five different treatments for joint pain in patients with osteoarthritis. Investigators might also hypothesize that there are differences in the outcome by sex. This is an example of a two-factor ANOVA where the factors are treatment (with 5 levels) and sex (with 2 levels). In the two-factor ANOVA, investigators can assess whether there are differences in means due to the treatment, by sex or whether there is a difference in outcomes by the combination or interaction of treatment and sex. Higher order ANOVAs are conducted in the same way as one-factor ANOVAs presented here and the computations are again organized in ANOVA tables with more rows to distinguish the different sources of variation (e.g., between treatments, between men and women). The following example illustrates the approach.
Consider the clinical trial outlined above in which three competing treatments for joint pain are compared in terms of their mean time to pain relief in patients with osteoarthritis. Because investigators hypothesize that there may be a difference in time to pain relief in men versus women, they randomly assign 15 participating men to one of the three competing treatments and randomly assign 15 participating women to one of the three competing treatments (i.e., stratified randomization). Participating men and women do not know to which treatment they are assigned. They are instructed to take the assigned medication when they experience joint pain and to record the time, in minutes, until the pain subsides. The data (times to pain relief) are shown below and are organized by the assigned treatment and sex of the participant.
Table of Time to Pain Relief by Treatment and Sex
|
|
|
|
|---|---|---|
|
| 12 | 21 |
| 15 | 19 | |
| 16 | 18 | |
| 17 | 24 | |
| 14 | 25 | |
|
| 14 | 21 |
| 17 | 20 | |
| 19 | 23 | |
| 20 | 27 | |
| 17 | 25 | |
|
| 25 | 37 |
| 27 | 34 | |
| 29 | 36 | |
| 24 | 26 | |
| 22 | 29 |
The analysis in two-factor ANOVA is similar to that illustrated above for one-factor ANOVA. The computations are again organized in an ANOVA table, but the total variation is partitioned into that due to the main effect of treatment, the main effect of sex and the interaction effect. The results of the analysis are shown below (and were generated with a statistical computing package - here we focus on interpretation).
ANOVA Table for Two-Factor ANOVA
|
|
|
|
|
|
|
|---|---|---|---|---|---|
| Model | 967.0 | 5 | 193.4 | 20.7 | 0.0001 |
| Treatment | 651.5 | 2 | 325.7 | 34.8 | 0.0001 |
| Sex | 313.6 | 1 | 313.6 | 33.5 | 0.0001 |
| Treatment * Sex | 1.9 | 2 | 0.9 | 0.1 | 0.9054 |
| Error or Residual | 224.4 | 24 | 9.4 | ||
| Total | 1191.4 | 29 |
There are 4 statistical tests in the ANOVA table above. The first test is an overall test to assess whether there is a difference among the 6 cell means (cells are defined by treatment and sex). The F statistic is 20.7 and is highly statistically significant with p=0.0001. When the overall test is significant, focus then turns to the factors that may be driving the significance (in this example, treatment, sex or the interaction between the two). The next three statistical tests assess the significance of the main effect of treatment, the main effect of sex and the interaction effect. In this example, there is a highly significant main effect of treatment (p=0.0001) and a highly significant main effect of sex (p=0.0001). The interaction between the two does not reach statistical significance (p=0.91). The table below contains the mean times to pain relief in each of the treatments for men and women (Note that each sample mean is computed on the 5 observations measured under that experimental condition).
Mean Time to Pain Relief by Treatment and Gender
|
|
|
|
|---|---|---|
| A | 14.8 | 21.4 |
| B | 17.4 | 23.2 |
| C | 25.4 | 32.4 |
Treatment A appears to be the most efficacious treatment for both men and women. The mean times to relief are lower in Treatment A for both men and women and highest in Treatment C for both men and women. Across all treatments, women report longer times to pain relief (See below).

Notice that there is the same pattern of time to pain relief across treatments in both men and women (treatment effect). There is also a sex effect - specifically, time to pain relief is longer in women in every treatment.
Suppose that the same clinical trial is replicated in a second clinical site and the following data are observed.
Table - Time to Pain Relief by Treatment and Sex - Clinical Site 2
|
|
|
|
|---|---|---|
|
| 22 | 21 |
| 25 | 19 | |
| 26 | 18 | |
| 27 | 24 | |
| 24 | 25 | |
|
| 14 | 21 |
| 17 | 20 | |
| 19 | 23 | |
| 20 | 27 | |
| 17 | 25 | |
|
| 15 | 37 |
| 17 | 34 | |
| 19 | 36 | |
| 14 | 26 | |
| 12 | 29 |
The ANOVA table for the data measured in clinical site 2 is shown below.
Table - Summary of Two-Factor ANOVA - Clinical Site 2
| Source of Variation | Sums of Squares (SS) | Degrees of freedom (df) | Mean Squares (MS) | F | P-Value |
|---|---|---|---|---|---|
| Model | 907.0 | 5 | 181.4 | 19.4 | 0.0001 |
| Treatment | 71.5 | 2 | 35.7 | 3.8 | 0.0362 |
| Sex | 313.6 | 1 | 313.6 | 33.5 | 0.0001 |
| Treatment * Sex | 521.9 | 2 | 260.9 | 27.9 | 0.0001 |
| Error or Residual | 224.4 | 24 | 9.4 | ||
| Total | 1131.4 | 29 |
Notice that the overall test is significant (F=19.4, p=0.0001), there is a significant treatment effect, sex effect and a highly significant interaction effect. The table below contains the mean times to relief in each of the treatments for men and women.
Table - Mean Time to Pain Relief by Treatment and Gender - Clinical Site 2
|
|
|
|
|---|---|---|
|
| 24.8 | 21.4 |
|
| 17.4 | 23.2 |
|
| 15.4 | 32.4 |
Notice that now the differences in mean time to pain relief among the treatments depend on sex. Among men, the mean time to pain relief is highest in Treatment A and lowest in Treatment C. Among women, the reverse is true. This is an interaction effect (see below).

Notice above that the treatment effect varies depending on sex. Thus, we cannot summarize an overall treatment effect (in men, treatment C is best, in women, treatment A is best).
When interaction effects are present, some investigators do not examine main effects (i.e., do not test for treatment effect because the effect of treatment depends on sex). This issue is complex and is discussed in more detail in a later module.
11.6 Test of a Single Variance
A test of a single variance assumes that the underlying distribution is normal . The null and alternative hypotheses are stated in terms of the population variance (or population standard deviation). The test statistic is:
- n = the total number of data
- s 2 = sample variance
- σ 2 = population variance
You may think of s as the random variable in this test. The number of degrees of freedom is df = n - 1. A test of a single variance may be right-tailed, left-tailed, or two-tailed. Example 11.10 will show you how to set up the null and alternative hypotheses. The null and alternative hypotheses contain statements about the population variance.
Example 11.10
Math instructors are not only interested in how their students do on exams, on average, but how the exam scores vary. To many instructors, the variance (or standard deviation) may be more important than the average.
Suppose a math instructor believes that the standard deviation for his final exam is five points. One of his best students thinks otherwise. The student claims that the standard deviation is more than five points. If the student were to conduct a hypothesis test, what would the null and alternative hypotheses be?
Even though we are given the population standard deviation, we can set up the test using the population variance as follows.
- H 0 : σ 2 = 5 2
- H a : σ 2 > 5 2
Try It 11.10
A SCUBA instructor wants to record the collective depths each of his students dives during their checkout. He is interested in how the depths vary, even though everyone should have been at the same depth. He believes the standard deviation is three feet. His assistant thinks the standard deviation is less than three feet. If the instructor were to conduct a test, what would the null and alternative hypotheses be?
Example 11.11
With individual lines at its various windows, a post office finds that the standard deviation for normally distributed waiting times for customers on Friday afternoon is 7.2 minutes. The post office experiments with a single, main waiting line and finds that for a random sample of 25 customers, the waiting times for customers have a standard deviation of 3.5 minutes.
With a significance level of 5%, test the claim that a single line causes lower variation among waiting times (shorter waiting times) for customers .
Since the claim is that a single line causes less variation, this is a test of a single variance. The parameter is the population variance, σ 2 , or the population standard deviation, σ .
Random Variable: The sample standard deviation, s , is the random variable. Let s = standard deviation for the waiting times.
- H 0 : σ 2 = 7.2 2
- H a : σ 2 < 7.2 2
The word "less" tells you this is a left-tailed test.
Distribution for the test: χ 24 2 χ 24 2 , where:
- n = the number of customers sampled
- df = n – 1 = 25 – 1 = 24
Calculate the test statistic:
χ 2 = ( n − 1 ) s 2 σ 2 = ( 25 − 1 ) ( 3.5 ) 2 7.2 2 = 5.67 χ 2 = ( n − 1 ) s 2 σ 2 = ( 25 − 1 ) ( 3.5 ) 2 7.2 2 = 5.67
where n = 25, s = 3.5, and σ = 7.2.
Probability statement: p -value = P ( χ 2 < 5.67) = 0.000042
Compare α and the p -value: α = 0.05 ; p -value = 0.000042 ; α > p -value
Make a decision: Since α > p -value, reject H 0 . This means that you reject σ 2 = 7.2 2 . In other words, you do not think the variation in waiting times is 7.2 minutes; you think the variation in waiting times is less.
Conclusion: At a 5% level of significance, from the data, there is sufficient evidence to conclude that a single line causes a lower variation among the waiting times or with a single line, the customer waiting times vary less than 7.2 minutes.
Using the TI-83, 83+, 84, 84+ Calculator
In 2nd DISTR , use 7:χ2cdf . The syntax is (lower, upper, df) for the parameter list. For Example 11.11 , χ2cdf(-1E99,5.67,24) . The p -value = 0.000042.
Try It 11.11
The FCC conducts broadband speed tests to measure how much data per second passes between a consumer’s computer and the internet. As of August of 2012, the standard deviation of Internet speeds across Internet Service Providers (ISPs) was 12.2 percent. Suppose a sample of 15 ISPs is taken, and the standard deviation is 13.2. An analyst claims that the standard deviation of speeds is more than what was reported. State the null and alternative hypotheses, compute the degrees of freedom, the test statistic, sketch the graph of the p -value, and draw a conclusion. Test at the 1% significance level.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/introductory-statistics/pages/1-introduction
- Authors: Barbara Illowsky, Susan Dean
- Publisher/website: OpenStax
- Book title: Introductory Statistics
- Publication date: Sep 19, 2013
- Location: Houston, Texas
- Book URL: https://openstax.org/books/introductory-statistics/pages/1-introduction
- Section URL: https://openstax.org/books/introductory-statistics/pages/11-6-test-of-a-single-variance
© Jun 23, 2022 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
| H : | |||
| H : | for a lower one-tailed test | ||
| \( \sigma^2 > \sigma_0^2 \) | for an upper one-tailed test | ||
| \( \sigma^2 \ne \sigma_0^2 \) | for a two-tailed test |
| \( T > \chi^2_{1-\alpha, \, N-1} \) | for an upper one-tailed alternative | |
| \( T | for a lower one-tailed alternative | |
| \( T | for a two-tailed alternative |
Section 10.4: Hypothesis Tests for a Population Standard Deviation
- 10.1 The Language of Hypothesis Testing
- 10.2 Hypothesis Tests for a Population Proportion
- 10.3 Hypothesis Tests for a Population Mean
- 10.4 Hypothesis Tests for a Population Standard Deviation
- 10.5 Putting It Together: Which Method Do I Use?
By the end of this lesson, you will be able to...
- test hypotheses about a population standard deviation
For a quick overview of this section, watch this short video summary:
Before we begin this section, we need a quick refresher of the Χ 2 distribution.
The Chi-Square ( Χ 2 ) distribution
Reminder: "chi-square" is pronounced "kai" as in sky, not "chai" like the tea .
If a random sample size n is obtained from a normally distributed population with mean μ and standard deviation σ , then
has a chi-square distribution with n-1 degrees of freedom.
Properties of the Χ 2 distribution
- It is not symmetric.
- The shape depends on the degrees of freedom.
- As the number of degrees of freedom increases, the distribution becomes more symmetric.
- Χ 2 ≥0
Finding Probabilities Using StatCrunch
Click on > > Enter the degrees of freedom, the direction of the inequality, and X. Then press . |
We again have some conditions that need to be true in order to perform the test
- the sample was randomly selected, and
- the population from which the sample is drawn is normally distributed
Note that in the second requirement, the population must be normally distributed. The steps in performing the hypothesis test should be familiar by now.
Performing a Hypothesis Test Regarding Ï
Step 1 : State the null and alternative hypotheses.
| H : = H : ≠ | H : = H : < | H : = H : > |
Step 2 : Decide on a level of significance, α .
Step 4 : Determine the P -value.
Step 5 : Reject the null hypothesis if the P -value is less than the level of significance, α.
Step 6 : State the conclusion.
In Example 2 , in Section 10.2, we assumed that the standard deviation for the resting heart rates of ECC students was 12 bpm. Later, in Example 2 in Section 10.3, we considered the actual sample data below.
| 61 | 63 | 64 | 65 | 65 |
| 67 | 71 | 72 | 73 | 74 |
| 75 | 77 | 79 | 80 | 81 |
| 82 | 83 | 83 | 84 | 85 |
| 86 | 86 | 89 | 95 | 95 |
( Click here to view the data in a format more easily copied.)
Based on this sample, is there enough evidence to say that the standard deviation of the resting heart rates for students in this class is different from 12 bpm?
Note: Be sure to check that the conditions for performing the hypothesis test are met.
[ reveal answer ]
From the earlier examples, we know that the resting heart rates could come from a normally distributed population and there are no outliers.
Step 1 : H 0 : σ = 12 H 1 : σ ≠ 12
Step 2 : α = 0.05
Step 4 : P -value = 2P( Χ 2 > 15.89) ≈ 0.2159
Step 5 : Since P -value > α , we do not reject H 0 .
Step 6 : There is not enough evidence at the 5% level of significance to support the claim that the standard deviation of the resting heart rates for students in this class is different from 12 bpm.
Hypothesis Testing Regarding σ Using StatCrunch
| > > if you have the data, or if you only have the summary statistics. , then click . |
Let's look at Example 1 again, and try the hypothesis test with technology.
Using DDXL:
Using StatCrunch:
<< previous section | next section >>


Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
How can we ever know the population variance?
In hypothesis testing, a common question is what is the population variance? My question is how can we ever know the population variance? If we knew the entire distribution, we might as well know the mean of the entire population. Then what is the point of hypothesis testing?
- hypothesis-testing
- $\begingroup$ Some relevant literature: nber.org/papers/w20325 $\endgroup$ – dv_bn Commented May 25, 2016 at 11:47
- $\begingroup$ One can know the variance without knowing anything about the mean. For instance, the variance can be recovered from the squares of all differences of values in the population, but those differences give no information about the mean. Regardless, I do not see how the statements and questions in this post lead up to the question itself about the point of hypothesis testing. $\endgroup$ – whuber ♦ Commented May 25, 2016 at 20:14
6 Answers 6
I'm not sure that this issue really comes up "often" outside of Stats 101 (introduction to statistics). I'm not sure I've ever seen it. On the other hand, we do present the material that way when teaching introductory courses, because it provides a logical progression: You start with a simple situation where there is only one group and you know the variance, then progress to where you don't know the variance, then progress to where there are two groups (but with equal variance), etc.
To address a slightly different point, you ask why we would bother with hypothesis testing if we knew the variance, since we must therefore also know the mean. The latter part is reasonable, but the first part is a misunderstanding: The mean we would know would be the mean under the null hypothesis. That's what we're testing. Consider @StephanKolassa's example of IQ scores. We know the mean is 100 and the standard deviation is 15; what we're testing is if our group (say, left-handed redheads, or perhaps introductory statistics students) differs from that.
- 2 $\begingroup$ (+1) Perhaps it comes up more when "sampling from a population" is a way of thinking about the data-generating process, rather than something to be taken literally. Knowing the precision of a measuring instrument for example. $\endgroup$ – Scortchi - Reinstate Monica ♦ Commented May 25, 2016 at 13:37
- $\begingroup$ Gung, as a practitioner with a 20+ year career, this issue came up in my experience more frequently than you imply. I'm not suggesting that it came up "frequently," just that the debates occurred. However, and to your point about Stats 101, more times than not the discussions were red herrings that resolved little or nothing regarding the particulars of a study or project -- somebody just wanted to create the appearance of intelligence in asking the question. $\endgroup$ – user78229 Commented May 25, 2016 at 15:34
- 1 $\begingroup$ @DJohnson, I suppose it depends on the topics you work on. $\endgroup$ – gung - Reinstate Monica Commented May 25, 2016 at 15:44
Often we don't know the population variance as such - but we have a very reliable estimate from a different sample. For instance, here is an example on assessing whether average weight of penguins has gone down, where we use the mean from a small-ish sample, but the variance from a larger independent sample. Of course, this presupposes that the variance is the same in both populations.
A different example might be classical IQ scales. These are normalized to have a mean of 100 and a standard deviation of 15, using really large samples. We might then take a specific sample (say, 50 left-handed redheads) and ask whether their mean IQ is significantly larger than 100, using 15^2 as a "known" variance. Of course, once again, this begs the question whether the variance is really equal between the two samples - after all, we are already testing whether means are different, so why should variances be equal?
Bottom line: your concerns are valid, and usually tests with known moments only serve didactic purposes. In statistics courses, they are usually immediately followed with tests using estimated moments.
The only way to know the population variance is to measure the entire population.
However, measuring an entire population is often not feasible; it requires resources including money, tools, personnel, and access. For this reason we sample populations; that is measuring a subset of the population. The sampling process should be designed carefully and with the objective of creating a sample population which is representative of the population; giving two key considerations - sample size and sampling technique.
Toy example: You wish to estimate the variance in weight for the adult population of Sweden. There are some 9.5 million Swedes so it is not likely that you can go out and measure them all. Therefore you need to measure a sample population from which you can estimate the true within-population variance.
You head out to sample the Swedish population. To do this you go and stand in Stockholm city centre, and just so happen to stand right outside the popular fictitious Swedish burger chain Burger Kungen . In fact, it's raining and cold (it must be summer) so you stand inside the restaurant. Here you weigh four people.
The chances are, your sample will not reflect the population of Sweden very well. What you have is a sample of people in Stockholm, who are in a burger restaurant. This is a poor sampling technique because it is likely to bias the result by not giving a fair representation of the population which you are trying to estimate. Furthermore, you have a small sample size , so you have a high risk of picking four people that are in the extremes of the population; either very light or very heavy. If you sampled 1000 people you are less likely to cause a sampling bias; it is far less likely to pick 1000 people that are unusual than it is to pick four that are unusual. A larger sample size would at least give you a more accurate estimate of the mean and variance in weight among the customers of Burger Kungen.

The histogram illustrates the effect of sampling technique, the grey distribution could represent the population of Sweden that doesn't eat at Burger Kungen (mean 85 kg), while the red could represent the population of the customers of Burger Kungen (mean 100 kg), and the blue dashes could be the four people you sample. Correct sampling technique would need to weigh the population fairly, and in this case ~75% of the population, thus 75% of the samples that are measured, should not be customers of Burger Kungen.
This is a major issue with a lot of surveys. For example, people likely to respond to surveys of customer satisfaction, or opinion polls in elections, tend to be disproportionately represented by those with extreme views; people with less strong opinions tend to be more reserved in expressing them.
The point of hypothesis testing is ( not always ), for example, to test whether two populations differ from one another. E.g. Do customers of Burger Kungen weigh more than Swedes that do not eat at Burger Kungen? The ability to test this accurately is reliant on proper sampling technique and sufficient sample size.
R code to test make all this happen:
Sometimes the population variance is set a priori . For example, SAT scores are scaled so that the standard deviation is 110 and IQ tests are scaled to have a standard deviation of 15 .
- $\begingroup$ Yes, that's true, but in those cases there is also scaling to a fixed mean, so it does not yield a situation where there is an unknown mean and known variance. Also, the scaling is done after all values are known. $\endgroup$ – Ben Commented Feb 19, 2019 at 9:25
The only realistic example I can think of when the mean is unknown but the variance is known is when there is random sampling of points on a hypersphere (in whatever dimension) with a fixed radius and an unknown centre. This problem has an unknown mean (centre of the sphere) but a fixed variance (squared-radius of the sphere). I am unaware of any other realistic examples where there is an unknown mean but known variance. (And to be clear: merely having an outside variance estimate from other data is not an example of a known variance. Also, if you have this variance estimate from other data, why don't you also have a corresponding mean estimate from that same data?)
In my view, introductory statistical courses that teach tests with an unknown mean and known variance are an anachronism, and they are misguided as a modern teaching tool. Pedagogically, it is far better to start directly with the T-test for the case of an unknown mean and variance, and treat the z-test as an asymptotic approximation to this that holds when the degrees-of-freedom is large (or not even bother to teach the z-test at all). The number of situations where there would be a known variance but unknown mean is vanishingly small, and it is generally misleading to students to introduce this (insanely rare) case.
Sometimes in applied problems, there are reasons presented by physics, economics, etc that tell us about variance and have no uncertainty. Other times, the population may be finite and we may happen to know some things about everyone, but need to sample and perform statistics to learn the rest.
Generally, your concern is pretty valid.
- 5 $\begingroup$ I have a hard time picturing an example from physics or economics where we would know the variance, but not the mean. Similar for discrete distributions. Could you give a concrete example or two? $\endgroup$ – Stephan Kolassa Commented May 25, 2016 at 11:40
- 1 $\begingroup$ @StephanKolassa I believe that physics experimental measurements would be an example - we may have a process or device of measurement that has a well known variance (measurement error), so when measuring a particular event then you can assume that variance is the same but you can only estimate the true mean. $\endgroup$ – Peteris Commented May 25, 2016 at 14:27
- 2 $\begingroup$ @Peteris: that makes sense - but it sounds more like the case I note , of the variance (of your instrument) having been estimated on previous "calibration samples". I'd expect a theoretically derived variance with no uncertainty (!) to be a different thing. $\endgroup$ – Stephan Kolassa Commented May 25, 2016 at 14:34
Your Answer
Sign up or log in, post as a guest.
Required, but never shown
By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .
Not the answer you're looking for? Browse other questions tagged hypothesis-testing variance t-test z-test or ask your own question .
- Featured on Meta
- We've made changes to our Terms of Service & Privacy Policy - July 2024
- Bringing clarity to status tag usage on meta sites
Hot Network Questions
- What does it mean to have a truth value of a 'nothing' type instance?
- Does the Ghost achievement require no kills?
- Unknown tool. Not sure what this tool is, found it in a tin of odds and ends
- Word to classify what powers a god is associated with?
- Who became an oligarch after the collapse of the USSR
- Using illustrations and comics in dissertations
- Does the First Amendment protect deliberately publicizing the incorrect date for an election?
- Giant War-Marbles of Doom: What's the Biggest possible Spherical Vehicle we could Build?
- Do "Whenever X becomes the target of a spell" abilities get triggered by counterspell?
- What is the connection between a regular language's pumping number, and the number of states of an equivalent deterministic automaton?
- Age is just a number!
- Has technology regressed in the Alien universe?
- Sulphur smell in Hot water only
- Can I use "Member, IEEE" as my affiliation for publishing papers?
- Polar coordinate plot incorrectly plotting with PGF Plots
- Can I use the Chi-square statistic to evaluate theoretical PDFs against an empirical dataset of 60,000 values?
- Why is たってよ used in this sentence to denote a request?
- What is a transition of point man in French?
- Sci-fi book about humanity warring against aliens that eliminate all species in the galaxy
- What is the meaning of these Greek words ἵπποπείρην and ἐπεμβάτην?
- Has anybody replaced a LM723 for a ua723 and experienced problems with drift and oscillations
- How to cite a book if only its chapters have DOIs?
- Unexpected behaviour during implicit conversion in C
- ambobus? (a morphologically peculiar adjective with a peculiar syntax here)

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
8.7 Hypothesis Tests for a Population Mean with Unknown Population Standard Deviation
Learning objectives.
- Conduct and interpret hypothesis tests for a population mean with unknown population standard deviation.
Some notes about conducting a hypothesis test:
- The null hypothesis [latex]H_0[/latex] is always an “equal to.” The null hypothesis is the original claim about the population parameter.
- The alternative hypothesis [latex]H_a[/latex] is a “less than,” “greater than,” or “not equal to.” The form of the alternative hypothesis depends on the context of the question.
- If the alternative hypothesis is a “less than”, then the test is left-tail. The p -value is the area in the left-tail of the distribution.
- If the alternative hypothesis is a “greater than”, then the test is right-tail. The p -value is the area in the right-tail of the distribution.
- If the alternative hypothesis is a “not equal to”, then the test is two-tail. The p -value is the sum of the area in the two-tails of the distribution. Each tail represents exactly half of the p -value.
- Think about the meaning of the p -value. A data analyst (and anyone else) should have more confidence that they made the correct decision to reject the null hypothesis with a smaller p -value (for example, 0.001 as opposed to 0.04) even if using a significance level of 0.05. Similarly, for a large p -value such as 0.4, as opposed to a p -value of 0.056 (a significance level of 0.05 is less than either number), a data analyst should have more confidence that they made the correct decision in not rejecting the null hypothesis. This makes the data analyst use judgment rather than mindlessly applying rules.
- The significance level must be identified before collecting the sample data and conducting the test. Generally, the significance level will be included in the question. If no significance level is given, a common standard is to use a significance level of 5%.
- An alternative approach for hypothesis testing is to use what is called the critical value approach . In this book, we will only use the p -value approach. Some of the videos below may mention the critical value approach, but this approach will not be used in this book.
Steps to Conduct a Hypothesis Test for a Population Mean with Unknown Population Standard Deviation
- Write down the null and alternative hypotheses in terms of the population mean [latex]\mu[/latex]. Include appropriate units with the values of the mean.
- Use the form of the alternative hypothesis to determine if the test is left-tailed, right-tailed, or two-tailed.
- Collect the sample information for the test and identify the significance level [latex]\alpha[/latex].
[latex]\begin{eqnarray*} t & = & \frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}} \\ \\ df & = & n-1 \\ \\ \end{eqnarray*}[/latex]
- The results of the sample data are significant. There is sufficient evidence to conclude that the null hypothesis [latex]H_0[/latex] is an incorrect belief and that the alternative hypothesis [latex]H_a[/latex] is most likely correct.
- The results of the sample data are not significant. There is not sufficient evidence to conclude that the alternative hypothesis [latex]H_a[/latex] may be correct.
- Write down a concluding sentence specific to the context of the question.
USING EXCEL TO CALCULE THE P -VALUE FOR A HYPOTHESIS TEST ON A POPULATION MEAN WITH UNKNOWN POPULATION STANDARD DEVIATION
The p -value for a hypothesis test on a population mean is the area in the tail(s) of the distribution of the sample mean. When the population standard deviation is unknown, use the [latex]t[/latex]-distribution to find the p -value.
If the p -value is the area in the left-tail:
- For t-score , enter the value of [latex]t[/latex] calculated from [latex]\displaystyle{t=\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}}[/latex].
- For degrees of freedom , enter the degrees of freedom for the [latex]t[/latex]-distribution [latex]n-1[/latex].
- For the logic operator , enter true . Note: Because we are calculating the area under the curve, we always enter true for the logic operator.
- The output from the t.dist function is the area under the [latex]t[/latex]-distribution to the left of the entered [latex]t[/latex]-score.
- Visit the Microsoft page for more information about the t.dist function.
If the p -value is the area in the right-tail:
- The output from the t.dist.rt function is the area under the [latex]t[/latex]-distribution to the right of the entered [latex]t[/latex]-score.
- Visit the Microsoft page for more information about the t.dist.rt function.
If the p -value is the sum of area in the tails:
- For t-score , enter the absolute value of [latex]t[/latex] calculated from [latex]\displaystyle{t=\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}}[/latex]. Note: In the t.dist.2t function, the value of the [latex]t[/latex]-score must be a positive number. If the [latex]t[/latex]-score is negative, enter the absolute value of the [latex]t[/latex]-score into the t.dist.2t function.
- The output from the t.dist.2t function is the sum of areas in the tails under the [latex]t[/latex]-distribution.
- Visit the Microsoft page for more information about the t.dist.2t function.
Statistics students believe that the mean score on the first statistics test is 65. A statistics instructor thinks the mean score is higher than 65. He samples ten statistics students and obtains the following scores:
| 65 | 67 | 66 | 68 | 72 |
| 65 | 70 | 63 | 63 | 71 |
The instructor performs a hypothesis test using a 1% level of significance. The test scores are assumed to be from a normal distribution.
Hypotheses:
[latex]\begin{eqnarray*} H_0: & & \mu=65 \\ H_a: & & \mu \gt 65 \end{eqnarray*}[/latex]
From the question, we have [latex]n=10[/latex], [latex]\overline{x}=67[/latex], [latex]s=3.1972...[/latex] and [latex]\alpha=0.01[/latex].
This is a test on a population mean where the population standard deviation is unknown (we only know the sample standard deviation [latex]s=3.1972...[/latex]). So we use a [latex]t[/latex]-distribution to calculate the p -value. Because the alternative hypothesis is a [latex]\gt[/latex], the p -value is the area in the right-tail of the distribution.

To use the t.dist.rt function, we need to calculate out the [latex]t[/latex]-score:
[latex]\begin{eqnarray*} t & = & \frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}} \\ & = & \frac{67-65}{\frac{3.1972...}{\sqrt{10}}} \\ & = & 1.9781... \end{eqnarray*}[/latex]
The degrees of freedom for the [latex]t[/latex]-distribution is [latex]n-1=10-1=9[/latex].
| t.dist.rt | ||
| 1.9781…. | 0.0396 | |
| 9 |
So the p -value[latex]=0.0396[/latex].
Conclusion:
Because p -value[latex]=0.0396 \gt 0.01=\alpha[/latex], we do not reject the null hypothesis. At the 1% significance level there is not enough evidence to suggest that mean score on the test is greater than 65.
- The null hypothesis [latex]\mu=65[/latex] is the claim that the mean test score is 65.
- The alternative hypothesis [latex]\mu \gt 65[/latex] is the claim that the mean test score is greater than 65.
- Keep all of the decimals throughout the calculation (i.e. in the sample standard deviation, the [latex]t[/latex]-score, etc.) to avoid any round-off error in the calculation of the p -value. This ensures that we get the most accurate value for the p -value.
- The p -value is the area in the right-tail of the [latex]t[/latex]-distribution, to the right of [latex]t=1.9781...[/latex].
- The p -value of 0.0396 tells us that under the assumption that the mean test score is 65 (the null hypothesis), there is a 3.96% chance that the mean test score is 65 or more. Compared to the 1% significance level, this is a large probability, and so is likely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis.
A company claims that the average change in the value of their stock is $3.50 per week. An investor believes this average is too high. The investor records the changes in the company’s stock price over 30 weeks and finds the average change in the stock price is $2.60 with a standard deviation of $1.80. At the 5% significance level, is the average change in the company’s stock price lower than the company claims?
[latex]\begin{eqnarray*} H_0: & & \mu=$3.50 \\ H_a: & & \mu \lt $3.50 \end{eqnarray*}[/latex]
From the question, we have [latex]n=30[/latex], [latex]\overline{x}=2.6[/latex], [latex]s=1.8[/latex] and [latex]\alpha=0.05[/latex].
This is a test on a population mean where the population standard deviation is unknown (we only know the sample standard deviation [latex]s=1.8.[/latex]). So we use a [latex]t[/latex]-distribution to calculate the p -value. Because the alternative hypothesis is a [latex]\lt[/latex], the p -value is the area in the left-tail of the distribution.
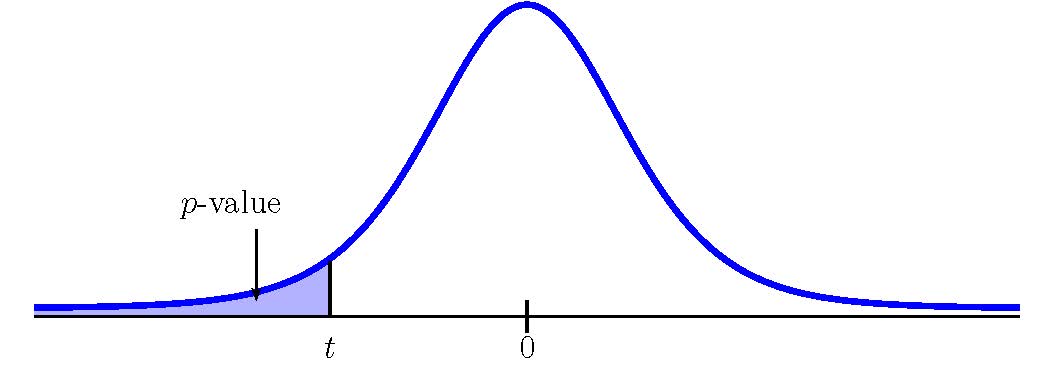
To use the t.dist function, we need to calculate out the [latex]t[/latex]-score:
[latex]\begin{eqnarray*} t & = & \frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}} \\ & = & \frac{2.6-3.5}{\frac{1.8}{\sqrt{30}}} \\ & = & -1.5699... \end{eqnarray*}[/latex]
The degrees of freedom for the [latex]t[/latex]-distribution is [latex]n-1=30-1=29[/latex].
| t.dist | ||
| -1.5699…. | 0.0636 | |
| 29 | ||
| true |
So the p -value[latex]=0.0636[/latex].
Because p -value[latex]=0.0636 \gt 0.05=\alpha[/latex], we do not reject the null hypothesis. At the 5% significance level there is not enough evidence to suggest that average change in the stock price is lower than $3.50.
- The null hypothesis [latex]\mu=$3.50[/latex] is the claim that the average change in the company’s stock is $3.50 per week.
- The alternative hypothesis [latex]\mu \lt $3.50[/latex] is the claim that the average change in the company’s stock is less than $3.50 per week.
- The p -value is the area in the left-tail of the [latex]t[/latex]-distribution, to the left of [latex]t=-1.5699...[/latex].
- The p -value of 0.0636 tells us that under the assumption that the average change in the stock is $3.50 (the null hypothesis), there is a 6.36% chance that the average change is $3.50 or less. Compared to the 5% significance level, this is a large probability, and so is likely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis. In other words, the company’s claim that the average change in their stock price is $3.50 per week is most likely correct.
A paint manufacturer has their production line set-up so that the average volume of paint in a can is 3.78 liters. The quality control manager at the plant believes that something has happened with the production and the average volume of paint in the cans has changed. The quality control department takes a sample of 100 cans and finds the average volume is 3.62 liters with a standard deviation of 0.7 liters. At the 5% significance level, has the volume of paint in a can changed?
[latex]\begin{eqnarray*} H_0: & & \mu=3.78 \mbox{ liters} \\ H_a: & & \mu \neq 3.78 \mbox{ liters} \end{eqnarray*}[/latex]
From the question, we have [latex]n=100[/latex], [latex]\overline{x}=3.62[/latex], [latex]s=0.7[/latex] and [latex]\alpha=0.05[/latex].
This is a test on a population mean where the population standard deviation is unknown (we only know the sample standard deviation [latex]s=0.7[/latex]). So we use a [latex]t[/latex]-distribution to calculate the p -value. Because the alternative hypothesis is a [latex]\neq[/latex], the p -value is the sum of area in the tails of the distribution.

To use the t.dist.2t function, we need to calculate out the [latex]t[/latex]-score:
[latex]\begin{eqnarray*} t & = & \frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}} \\ & = & \frac{3.62-3.78}{\frac{0.07}{\sqrt{100}}} \\ & = & -2.2857... \end{eqnarray*}[/latex]
The degrees of freedom for the [latex]t[/latex]-distribution is [latex]n-1=100-1=99[/latex].
| t.dist.2t | ||
| 2.2857…. | 0.0244 | |
| 99 |
So the p -value[latex]=0.0244[/latex].
Because p -value[latex]=0.0244 \lt 0.05=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis. At the 5% significance level there is enough evidence to suggest that average volume of paint in the cans has changed.
- The null hypothesis [latex]\mu=3.78[/latex] is the claim that the average volume of paint in the cans is 3.78.
- The alternative hypothesis [latex]\mu \neq 3.78[/latex] is the claim that the average volume of paint in the cans is not 3.78.
- Keep all of the decimals throughout the calculation (i.e. in the [latex]t[/latex]-score) to avoid any round-off error in the calculation of the p -value. This ensures that we get the most accurate value for the p -value.
- The p -value is the sum of the area in the two tails. The output from the t.dist.2t function is exactly the sum of the area in the two tails, and so is the p -value required for the test. No additional calculations are required.
- The t.dist.2t function requires that the value entered for the [latex]t[/latex]-score is positive . A negative [latex]t[/latex]-score entered into the t.dist.2t function generates an error in Excel. In this case, the value of the [latex]t[/latex]-score is negative, so we must enter the absolute value of this [latex]t[/latex]-score into field 1.
- The p -value of 0.0244 is a small probability compared to the significance level, and so is unlikely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis. In other words, the average volume of paint in the cans has most likely changed from 3.78 liters.
Watch this video: Hypothesis Testing: t -test, right tail by ExcelIsFun [11:02]
Watch this video: Hypothesis Testing: t -test, left tail by ExcelIsFun [7:48]
Watch this video: Hypothesis Testing: t -test, two tail by ExcelIsFun [8:54]
Concept Review
The hypothesis test for a population mean is a well established process:
- Collect the sample information for the test and identify the significance level.
- When the population standard deviation is unknown, find the p -value (the area in the corresponding tail) for the test using the [latex]t[/latex]-distribution with [latex]\displaystyle{t=\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}}[/latex] and [latex]df=n-1[/latex].
- Compare the p -value to the significance level and state the outcome of the test.
Attribution
“ 9.6 Hypothesis Testing of a Single Mean and Single Proportion “ in Introductory Statistics by OpenStax is licensed under a Creative Commons Attribution 4.0 International License.
Introduction to Statistics Copyright © 2022 by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Hypothesis Testing: Testing for a Population Variance
A hypothesis testing is a procedure in which a claim about a certain population parameter is tested. A population parameter is a numerical constant that represents o characterizes a distribution. Typically, a hypothesis test is about a population mean, typically notated as \(\mu\), but in reality it can be about any population parameter, such a population proportion \(p\), or a population standard deviation \(\sigma\).
In this case, we are going to analyze the case of a hypothesis test involving a population standard deviation \(\sigma\). As with any type of hypothesis testing , sample data is required to test a claim about \(\sigma\). Notice that sometimes the claim involves the population variance \({{\sigma }^{2}}\) instead, but it is essentially the same thing because, for example, making the claim about the population variance that \({{\sigma }^{2}}=16\) is absolutely equivalent to making the claim \(\sigma =4\) about the population standard deviation. So therefore, always keep in mind that making a claim about the population variance has always paired a claim about the population standard deviation, and vice versa.
The procedures for determining the null and alternative hypotheses and the type of tail for the test are applied all the same the steps used for testing a claim about the population mean (This is, we state the given claim(s) in mathematical form and examine the type of sign involved).
Assume that an official from the treasury claims that post-1983 pennies have weights with a standard deviation greater than 0.0230 g. Assume that a simple random sample of n = 25 pre-1983 pennies is collected, and that sample has a standard deviation of 0.03910 g. Use a 0.05 significance level to test the claim that pre-1983 pennies have weights with a standard deviation greater than 0.0230 g. Based on these sample results, does it appear that weights of pre-1983 pennies vary more than those of post-1983 pennies?
HOW DO WE SOLVE THIS?
We need to test
\[\begin{align}{H}_{0}: \sigma \le {0.0230} \\ {{H}_{A}}: \sigma > {0.0230} \\ \end{align}\]
The value of the Chi Square statistics is computed as
\[{{\chi }^{2}}=\frac{\left( n-1 \right){{s}^{2}}}{{{\sigma }^{2}}}=\frac{\left( 25-1 \right)\times {0.03910^2}}{0.0230^2}= {69.36}\]
The upper critical value for \(\alpha = 0.05\) and df = 24 is
\[\chi _{upper}^{2}= {36.415}\]
which means that we reject the null hypothesis.
This means that we have enough evidence to support the claim that weights of pre-1983 pennies vary more than those of post-1983 pennies, at the 0.05 significance level.
log in to your account
Reset password.
User Preferences
Content preview.
Arcu felis bibendum ut tristique et egestas quis:
- Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
- Duis aute irure dolor in reprehenderit in voluptate
- Excepteur sint occaecat cupidatat non proident
Keyboard Shortcuts
12.1 - one variance.
Yeehah again! The theoretical work for developing a hypothesis test for a population variance \(\sigma^2\) is already behind us. Recall that if you have a random sample of size n from a normal population with (unknown) mean \(\mu\) and variance \(\sigma^2\), then:
\(\chi^2=\dfrac{(n-1)S^2}{\sigma^2}\)
follows a chi-square distribution with n −1 degrees of freedom. Therefore, if we're interested in testing the null hypothesis:
\(H_0 \colon \sigma^2=\sigma^2_0\)
against any of the alternative hypotheses:
\(H_A \colon\sigma^2 \neq \sigma^2_0,\quad H_A \colon\sigma^2<\sigma^2_0,\text{ or }H_A \colon\sigma^2>\sigma^2_0\)
we can use the test statistic:
\(\chi^2=\dfrac{(n-1)S^2}{\sigma^2_0}\)
and follow the standard hypothesis testing procedures. Let's take a look at an example.
Example 12-1 Section

A manufacturer of hard safety hats for construction workers is concerned about the mean and the variation of the forces its helmets transmits to wearers when subjected to an external force. The manufacturer has designed the helmets so that the mean force transmitted by the helmets to the workers is 800 pounds (or less) with a standard deviation to be less than 40 pounds. Tests were run on a random sample of n = 40 helmets, and the sample mean and sample standard deviation were found to be 825 pounds and 48.5 pounds, respectively.
Do the data provide sufficient evidence, at the \(\alpha = 0.05\) level, to conclude that the population standard deviation exceeds 40 pounds?
We're interested in testing the null hypothesis:
\(H_0 \colon \sigma^2=40^2=1600\)
against the alternative hypothesis:
\(H_A \colon\sigma^2>1600\)
Therefore, the value of the test statistic is:
\(\chi^2=\dfrac{(40-1)48.5^2}{40^2}=57.336\)
Is the test statistic too large for the null hypothesis to be true? Well, the critical value approach would have us finding the threshold value such that the probability of rejecting the null hypothesis if it were true, that is, of committing a Type I error, is small... 0.05, in this case. Using Minitab (or a chi-square probability table), we see that the cutoff value is 54.572:
That is, we reject the null hypothesis in favor of the alternative hypothesis if the test statistic \(\chi^2\) is greater than 54.572. It is. That is, the test statistic falls in the rejection region:
Therefore, we conclude that there is sufficient evidence, at the 0.05 level, to conclude that the population standard deviation exceeds 40.
Of course, the P -value approach yields the same conclusion. In this case, the P -value is the probablity that we would observe a chi-square(39) random variable more extreme than 57.336:
As the drawing illustrates, the P -value is 0.029 (as determined using the chi-square probability calculator in Minitab). Because \(P = 0.029 ≤ 0.05\), we reject the null hypothesis in favor of the alternative hypothesis.
Do the data provide sufficient evidence, at the \(\alpha = 0.05\) level, to conclude that the population standard deviation differs from 40 pounds?
In this case, we're interested in testing the null hypothesis:
\(H_A \colon\sigma^2 \neq 1600\)
The value of the test statistic remains the same. It is again:
Now, is the test statistic either too large or too small for the null hypothesis to be true? Well, the critical value approach would have us dividing the significance level \(\alpha = 0.05\) into 2, to get 0.025, and putting one of the halves in the left tail, and the other half in the other tail. Doing so (and using Minitab to get the cutoff values), we get that the lower cutoff value is 23.654 and the upper cutoff value is 58.120:
That is, we reject the null hypothesis in favor of the two-sided alternative hypothesis if the test statistic \(\chi^2\) is either smaller than 23.654 or greater than 58.120. It is not. That is, the test statistic does not fall in the rejection region:
Therefore, we fail to reject the null hypothesis. There is insufficient evidence, at the 0.05 level, to conclude that the population standard deviation differs from 40.
Of course, the P -value approach again yields the same conclusion. In this case, we simply double the P -value we obtained for the one-tailed test yielding a P -value of 0.058:
\(P=2\times P\left(\chi^2_{39}>57.336\right)=2\times 0.029=0.058\)
Because \(P = 0.058 > 0.05\), we fail to reject the null hypothesis in favor of the two-sided alternative hypothesis.
The above example illustrates an important fact, namely, that the conclusion for the one-sided test does not always agree with the conclusion for the two-sided test. If you have reason to believe that the parameter will differ from the null value in a particular direction, then you should conduct the one-sided test.
Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
Hypothesis testing for the variance of a population
Someone is trying to introduce a new process in the production of a precision instrument for industrial use. The new process keeps the average weight but hopes to reduce the variability, which until now has been characterized by $\sigma^2 = 14.5$ . Because the complete introduction of the new process has costs, a test has been done and 16 instruments have been produced with this new method. For $\alpha = 0.05$ and knowing that the sample variance $s^2 > = 6.8$ , what is the decision to take? Suppose that the universe can be considered approximately normal.
I have the population variance, so I can use the normal distribution. My hypothesis is
$$H_0 : \sigma ^2 = 14.5$$
The test value:
$$X^2_0 = \frac{15*6.8^2}{14.5^2}) = 3.2989 $$
$$X^2_{\alpha,n-1} = X^2_{0.05,15} = 25.00$$
$X^2_0 > X^2_{\alpha,n-1}$ is false, so I fail to reject H_0?
- probability
- hypothesis-testing
- $\begingroup$ Some difficulties here, also mentioned in my Answer. (1) No alternative hypothesis is stated. Important to know if it's one-sided or two-sided. (2) And why do you write $6.8^2$ when $S^2 = 6.8$ is already a sample variance? (3) You need to clarify your notation for numbers associated with a chi-squared distribution. $\endgroup$ – BruceET Commented May 27, 2020 at 3:03
- $\begingroup$ @BruceET The OP may have failed to state an alternative hypothesis, but I think it is clear from the quoted question what it is supposed to be. $\endgroup$ – StubbornAtom Commented May 27, 2020 at 6:52
- 1 $\begingroup$ @StubbornAtom. You're probably right. But in my experience, if engineers can make a process better they can (often do) make it worse. But then I suppose the data would be hidden rather than analyzed. $\endgroup$ – BruceET Commented May 27, 2020 at 7:25
- $\begingroup$ @BruceET "But in my experience, if engineers can make a process better they can (often do) make it worse. " sounds like my statistics professor. He's an engineer. $\endgroup$ – Segmentation fault Commented May 28, 2020 at 12:33
2 Answers 2
"Suppose that the universe can be considered approximately normal."
If you are willing to make the assumption that the underlying data are IID normal then you can derive a confidence interval from the pivotal quantity $(n-1) S^2/\sigma^2 \sim \text{ChiSq}(n-1)$ . The other answer by BruceET shows you how to do this, and this will solve your immediate question.
However, if you want to learn sampling theory properly, I strongly recommend you go beyond the immediate question here, and think about what you would need to do if you are not willing to make the (ridiculous) assumption that "the universe is approximately normal". You can find a more general discussion of moment results in sampling theory, and a solution to this broader problem, in O'Neill (2014) . The main thing to note is that the variance of the sample variance depends on the kurtosis of the underlying population distribution. If you assume a normal distribution then you are assuming knowledge of the kurtosis of the population, without reference to the actual data. This means that you will often over or underestimate the variability of the sample variance and get bad results for confidence intervals for the true variance.
As a general rule, if you want to look at the true moments of sample moments, you need to add their orders to find out how many moments of the underlying population affect this. Thus, determination of the variance (second order) of the sample variance (second order) requires knowledge up to the fourth moment of the underlying population distribution. It is generally a bad idea to ignore the data and instead assume specific values for underlying moments that affect the problem at hand. Thus, when formulating a confidence interval for the true variance of the population, it is generally a bad idea to assume normality of the population, since that assumes a specific value for the kurtosis, which affects the variance of the sample variance.
- 1 $\begingroup$ Good to have this (+1). // I have just added some reminders of the normal assumption to my Answer. (Also fixed some typos.) $\endgroup$ – BruceET Commented May 27, 2020 at 2:58
Because $\frac{(n-1)S^2}{\sigma^2} \sim \mathsf{Chisq}(\nu=n-1),$ a 95% confidence interval (CI) for $\sigma^2$ based on a sample variance $S^2$ is of the form $\left(\frac{(n-1)S^2}{U},\, \frac{(n-1)S^2}{U}\right),$ where $L$ and $U$ cut probability $0.025$ from the lower and upper tails of $\mathsf{Chisq}(\nu=n-1),$ respectively. [This confidence interval is based on the assumption that weights are normal.]
Thus a 95% CI for $\sigma^2$ based on $S^2 = 6.8$ for a normal sample of size $n = 16$ is $(3.71, 16.29).$ This CI represents non-rejectable values of $\sigma_0^2.$ [The computation is done below using R statistical software, but you can verify it using printed tables of the chi-squared distribution.]
Because $\sigma_0^2 = 14.5$ lies in the CI so you cannot reject $H_0: \sigma^2 = 14.5$ against $H_a: \sigma^2 \ne 14.5$ at the 5% level.
Can you find critical values for the test statistic $Q = \frac{(n-1)S^2}{\sigma_0^2},$ beyond which the null hypothesis would be rejected (in either direction)?
Notes: There is some confusion in your question: (1) You do not state null and alternative hypotheses, so it is not clear whether you are doing a one- or two-sided test. (2) You seem to be mixing up sample standard deviation $S$ with $S^2$ ---you are squaring $S^2.$
If you want a one-sided test, you need a one-sided CI, which gives an upper bound $(-\infty, 14.05),$ which does not contain $14.5.$
In this case, can you find a critical value for the test statistic $Q =\frac{(n-1)S^2}{\sigma_0^2},$ below which the null hypothesis $H_0: \sigma^2 = 14.5$ would be rejected in favor of the one-sided alternative $H_a: \mu < 14.5?$
You must log in to answer this question.
Not the answer you're looking for browse other questions tagged probability statistics hypothesis-testing ..
- Upcoming Events
- 2024 Community Moderator Election ends in 3 days
- Featured on Meta
- We've made changes to our Terms of Service & Privacy Policy - July 2024
- Bringing clarity to status tag usage on meta sites
- Upcoming Moderator Election
- 2024 Community Moderator Election
Hot Network Questions
- Where exactly was this picture taken?
- Difference between "backpedal" and "change your tune"
- Advice needed: Team needs developers, but company isn't posting jobs
- What is the connection between a regular language's pumping number, and the number of states of an equivalent deterministic automaton?
- Is It Possible to Assign Meaningful Amplitudes to Properties in Quantum Mechanics?
- Word to classify what powers a god is associated with?
- Enigmatic Puzzle 4: Three Leaf Clover
- Terminal autocomplete (tab) not completing when changing directory up one level (cd ../)
- conflict of \counterwithin and cleveref package when sectioncounter is reset
- Did the United States have consent from Texas to cede a piece of land that was part of Texas?
- What does it mean to have a truth value of a 'nothing' type instance?
- How do you "stealth" a relativistic superweapon?
- How can I cover all my skin (face+neck+body) while swimming outside (sea or outdoor pool) to avoid UV radiations?
- Web App - Set a Max Width or Let it Expand Responsively?
- Function to find the most common numeric ordered pairings (value, count)
- Someone said 24-hour time for 0215 can be 零二么五小時 --- Why would 么 be used instead of 幺? Havent these 2 characters been different for nearly 70 years?
- How to read data from Philips P2000C over its serial port to a modern computer?
- 'best poster' and 'best talk' prizes - can we do better?
- How to handle stealth before combat starts?
- What is the legal status of the Avengers before Civil War and after Winter Soldier?
- Does the expansion of space imply anything about the dimensionality of the Universe?
- What is the meaning of these Greek words ἵπποπείρην and ἐπεμβάτην?
- Sulphur smell in Hot water only
- Does the Ghost achievement require no kills?
Pardon Our Interruption
As you were browsing something about your browser made us think you were a bot. There are a few reasons this might happen:
- You've disabled JavaScript in your web browser.
- You're a power user moving through this website with super-human speed.
- You've disabled cookies in your web browser.
- A third-party browser plugin, such as Ghostery or NoScript, is preventing JavaScript from running. Additional information is available in this support article .
To regain access, please make sure that cookies and JavaScript are enabled before reloading the page.

IMAGES
COMMENTS
Hypothesis Test about a Variance When people think of statistical inference, they usually think of inferences involving population means or proportions. However, the particular population parameter needed to answer an experimenter's practical questions varies from one situation to another, and sometimes a population's variability is more important than its mean. Thus, product quality is ...
Lesson 12: Tests for Variances. Continuing our development of hypothesis tests for various population parameters, in this lesson, we'll focus on hypothesis tests for population variances. Specifically, we'll develop: a hypothesis test for testing whether a single population variance σ 2 equals a particular value.
Lesson 12: Tests for Variances. Continuing our development of hypothesis tests for various population parameters, in this lesson, we'll focus on hypothesis tests for population variances. Specifically, we'll develop: a hypothesis test for testing whether a single population variance \ (\sigma^2\) equals a particular value.
A test of a single variance assumes that the underlying distribution is normal. The null and alternative hypotheses are stated in terms of the population variance (or population standard deviation). …
In a two-tailed hypothesis test for population variance, we will only have sample information relating to one of the two tails. We must determine which of the tails the sample information belongs to, and then calculate out the area in that tail.
This page explains how to perform hypothesis tests about the variance of a normal distribution, called Chi-square tests. We analyze two different situations: when it is unknown. Depending on the situation, the Chi-square statistic used in the test has a different distribution. At the end of the page, we propose some solved exercises.
The hypothesis is based on available information and the investigator's belief about the population parameters. The specific test considered here is called analysis of variance (ANOVA) and is a test of hypothesis that is appropriate to compare means of a continuous variable in two or more independent comparison groups.
Learn how to test the variance of a population using a chi-square distribution and a sample data set. OpenStax offers a clear and concise explanation with examples.
Chi-Square Test for the Variance. A chi-square test ( Snedecor and Cochran, 1983) can be used to test if the variance of a population is equal to a specified value. This test can be either a two-sided test or a one-sided test. The two-sided version tests against the alternative that the true variance is either less than or greater than the ...
10.1 - Z-Test: When Population Variance is Known Let's start by acknowledging that it is completely unrealistic to think that we'd find ourselves in the situation of knowing the population variance, but not the population mean. Therefore, the hypothesis testing method that we learn on this page has limited practical use.
Chi-squared distribution, showing χ 2 on the x-axis and p-value (right tail probability) on the y-axis.. A chi-squared test (also chi-square or χ 2 test) is a statistical hypothesis test used in the analysis of contingency tables when the sample sizes are large. In simpler terms, this test is primarily used to examine whether two categorical variables (two dimensions of the contingency table ...
Performing a Hypothesis Test Regarding σ. Step 1: State the null and alternative hypotheses. Step 2: Decide on a level of significance, α. Step 3: Compute the test statistic, . Step 4: Determine the P -value. Step 5: Reject the null hypothesis if the P -value is less than the level of significance, α.
I discuss hypothesis tests for a single population variance. The methods used here are based on the assumption of sampling from a normally distributed population (these methods involve the chi ...
Do you want to compare the variances or standard deviations of two populations? Learn how to use the F-test to perform this type of hypothesis testing in this chapter of Mostly Harmless Statistics. You will also find examples, formulas, and assumptions for the F-test.
Example: Hypothesis Test for Population Variance Helen is the Customer Service Assistant Manager who supervises the customer service reps (CSR). Last year, the variance for the time it takes a CSR to resolve customer inquires on the phone is 9 minutes.
12 In hypothesis testing, a common question is what is the population variance? My question is how can we ever know the population variance? If we knew the entire distribution, we might as well know the mean of the entire population. Then what is the point of hypothesis testing? hypothesis-testing variance t-test z-test Share Cite Improve this question edited May 25, 2016 at 13:20 rg255 892 3 ...
The test, as every other well formed hypothesis test, has two non-overlapping hypotheses, the null and the alternative hypothesis. The null hypothesis is a statement about the population variance which represents the assumption of no effect, and the alternative hypothesis is the complementary hypothesis to the null hypothesis.
Steps to Conduct a Hypothesis Test for a Population Mean with Unknown Population Standard Deviation Write down the null and alternative hypotheses in terms of the population mean μ μ . Include appropriate units with the values of the mean. Use the form of the alternative hypothesis to determine if the test is left-tailed, right-tailed, or two-tailed. Collect the sample information for the ...
A test of a single variance assumes that the underlying distribution is normal. The null and alternative hypotheses are stated in terms of the population variance (or population standard deviation). …
11.1 - When Population Variances Are Equal. Let's start with the good news, namely that we've already done the dirty theoretical work in developing a hypothesis test for the difference in two population means μ 1 − μ 2 when we developed a ( 1 − α) 100 % confidence interval for the difference in two population means.
A hypothesis testing is a procedure in which a claim about a certain population parameter is tested. A population parameter is a numerical constant that represents o characterizes a distribution. Typically, a hypothesis test is about a population mean, typically notated as \mu μ, but in reality it can be about any population parameter, such a ...
12.1 - One Variance. Yeehah again! The theoretical work for developing a hypothesis test for a population variance σ 2 is already behind us. Recall that if you have a random sample of size n from a normal population with (unknown) mean μ and variance σ 2, then: χ 2 = ( n − 1) S 2 σ 2. follows a chi-square distribution with n −1 degrees ...
F-Test for Comparing Two Population Variances One major application of a test for the equality of two population variances is for checking the validity of the equal variance assumption (σ21 = σ22) ( σ 1 2 = σ 2 2) for a two-sample t-test. First we hypothesize two populations of measurements that are normally distributed.
The main thing to note is that the variance of the sample variance depends on the kurtosis of the underlying population distribution. If you assume a normal distribution then you are assuming knowledge of the kurtosis of the population, without reference to the actual data.
3. The coefficient of determination (R^2) represents: a) The proportion of the dependent variable explained by the independent variable(s) b) The strength of the linear relationship between two variables c) The standard deviation of the residuals d) The slope of the regression line Ans: A 4. Which rank correlation coefficient is used when the variables are measured on an ordinal scale?