
Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
CHAPTER 5 Solving First Degree Equations in One Variable

5.7 Use a Problem-Solving Strategy
Learning Objectives
By the end of this section, you will be able to:
- Approach word problems with a positive attitude
- Use a problem-solving strategy for word problems
- Solve number problems
Approach Word Problems with a Positive Attitude
“If you think you can… or think you can’t… you’re right.”—Henry Ford
The world is full of word problems! Will my income qualify me to rent that apartment? How much punch do I need to make for the party? What size diamond can I afford to buy my girlfriend? Should I fly or drive to my family reunion?
How much money do I need to fill the car with gas? How much tip should I leave at a restaurant? How many socks should I pack for vacation? What size turkey do I need to buy for Thanksgiving dinner, and then what time do I need to put it in the oven? If my sister and I buy our mother a present, how much does each of us pay?
Now that we can solve equations, we are ready to apply our new skills to word problems. Do you know anyone who has had negative experiences in the past with word problems? Have you ever had thoughts like the student below?

When we feel we have no control, and continue repeating negative thoughts, we set up barriers to success. We need to calm our fears and change our negative feelings.
Start with a fresh slate and begin to think positive thoughts. If we take control and believe we can be successful, we will be able to master word problems! Read the positive thoughts in (Figure 2) and say them out loud.

Think of something, outside of school, that you can do now but couldn’t do 3 years ago. Is it driving a car? Snowboarding? Cooking a gourmet meal? Speaking a new language? Your past experiences with word problems happened when you were younger—now you’re older and ready to succeed!
Use a Problem-Solving Strategy for Word Problems
We have reviewed translating English phrases into algebraic expressions, using some basic mathematical vocabulary and symbols. We have also translated English sentences into algebraic equations and solved some word problems. The word problems applied math to everyday situations. We restated the situation in one sentence, assigned a variable, and then wrote an equation to solve the problem. This method works as long as the situation is familiar and the math is not too complicated.
Now, we’ll expand our strategy so we can use it to successfully solve any word problem. We’ll list the strategy here, and then we’ll use it to solve some problems. We summarize below an effective strategy for problem solving.
Use a Problem-Solving Strategy to Solve Word Problems.
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
- Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebraic equation.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
Pilar bought a purse on sale for $18, which is one-half of the original price. What was the original price of the purse?
Step 1. Read the problem. Read the problem two or more times if necessary. Look up any unfamiliar words in a dictionary or on the internet.
- In this problem, is it clear what is being discussed? Is every word familiar?
Step 2. Identify what you are looking for. Did you ever go into your bedroom to get something and then forget what you were looking for? It’s hard to find something if you are not sure what it is! Read the problem again and look for words that tell you what you are looking for!
- In this problem, the words “what was the original price of the purse” tell us what we need to find.
Step 3. Name what we are looking for. Choose a variable to represent that quantity. We can use any letter for the variable, but choose one that makes it easy to remember what it represents.
Step 4. Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Translate the English sentence into an algebraic equation.
Reread the problem carefully to see how the given information is related. Often, there is one sentence that gives this information, or it may help to write one sentence with all the important information. Look for clue words to help translate the sentence into algebra. Translate the sentence into an equation.
| Restate the problem in one sentence with all the important information. | |
| Translate into an equation. |
Step 5. Solve the equation using good algebraic techniques. Even if you know the solution right away, using good algebraic techniques here will better prepare you to solve problems that do not have obvious answers.
| Solve the equation. | |
| Multiply both sides by 2. | |
| Simplify. |
- Does $36 make sense in the problem? Yes, because 18 is one-half of 36, and the purse was on sale at half the original price.
Step 7. Answer the question with a complete sentence. The problem asked “What was the original price of the purse?”
- The answer to the question is: “The original price of the purse was $36.”
If this were a homework exercise, our work might look like this:
Pilar bought a purse on sale for $18, which is one-half the original price. What was the original price of the purse?
| Let | |
| 18 is one-half the original price. | |
| Multiply both sides by 2. | |
| Simplify. | |
| Check. Is $36 a reasonable price for a purse? | Yes. |
| Is 18 one half of 36? | |
| The original price of the purse was $36. |
Joaquin bought a bookcase on sale for $120, which was two-thirds of the original price. What was the original price of the bookcase?
Two-fifths of the songs in Mariel’s playlist are country. If there are 16 country songs, what is the total number of songs in the playlist?
Let’s try this approach with another example.
Ginny and her classmates formed a study group. The number of girls in the study group was three more than twice the number of boys. There were 11 girls in the study group. How many boys were in the study group?
| the problem. | |
| what we are looking for. | How many boys were in the study group? |
| Choose a variable to represent the number of boys. | Let |
| Restate the problem in one sentence with all the important information. | |
| Translate into an equation. | |
| the equation. | |
| Subtract 3 from each side. | |
| Simplify. | |
| Divide each side by 2. | |
| Simplify. | |
| First, is our answer reasonable? | Yes, having 4 boys in a study group seems OK. The problem says the number of girls was 3 more than twice the number of boys. If there are four boys, does that make eleven girls? Twice 4 boys is 8. Three more than 8 is 11. |
| the question. | There were 4 boys in the study group. |
Guillermo bought textbooks and notebooks at the bookstore. The number of textbooks was 3 more than twice the number of notebooks. He bought 7 textbooks. How many notebooks did he buy?
Gerry worked Sudoku puzzles and crossword puzzles this week. The number of Sudoku puzzles he completed is eight more than twice the number of crossword puzzles. He completed 22 Sudoku puzzles. How many crossword puzzles did he do?
Solve Number Problems
Now that we have a problem solving strategy, we will use it on several different types of word problems. The first type we will work on is “number problems.” Number problems give some clues about one or more numbers. We use these clues to write an equation. Number problems don’t usually arise on an everyday basis, but they provide a good introduction to practicing the problem solving strategy outlined above.
The difference of a number and six is 13. Find the number.
| the problem. Are all the words familiar? | |
| what we are looking for. | the number |
| Choose a variable to represent the number. | Let |
| Remember to look for clue words like “difference… of… and…” | |
| Restate the problem as one sentence. | |
| Translate into an equation. | |
| the equation. | |
| Simplify. | |
| The difference of 19 and 6 is 13. It checks! | |
| the question. | The number is 19. |
The difference of a number and eight is 17. Find the number.
The sum of twice a number and seven is 15. Find the number.
| the problem. | |
| what we are looking for. | the number |
| Choose a variable to represent the number. | Let |
| Restate the problem as one sentence. | |
| Translate into an equation. | |
| the equation. | |
| Subtract 7 from each side and simplify. | |
| Divide each side by 2 and simplify. | |
| Is the sum of twice 4 and 7 equal to 15? | |
| the question. | The number is 4. |
Did you notice that we left out some of the steps as we solved this equation? If you’re not yet ready to leave out these steps, write down as many as you need.
The sum of four times a number and two is 14. Find the number.
The sum of three times a number and seven is 25. Find the number.
Some number word problems ask us to find two or more numbers. It may be tempting to name them all with different variables, but so far we have only solved equations with one variable. In order to avoid using more than one variable, we will define the numbers in terms of the same variable. Be sure to read the problem carefully to discover how all the numbers relate to each other.
One number is five more than another. The sum of the numbers is 21. Find the numbers.
| the problem. | |
| what we are looking for. | We are looking for two numbers. |
| We have two numbers to name and need a name for each. | |
| Choose a variable to represent the first number. | Let |
| What do we know about the second number? | One number is five more than another. |
| Restate the problem as one sentence with all the important information. | The sum of the 1 number and the 2 number is 21. |
| Translate into an equation. | |
| Substitute the variable expressions. | |
| the equation. | |
| Combine like terms. | |
| Subtract 5 from both sides and simplify. | |
| Divide by 2 and simplify. | |
| Find the second number, too. | |
| Do these numbers check in the problem? | |
| Is one number 5 more than the other? | |
| Is thirteen 5 more than 8? Yes. | |
| Is the sum of the two numbers 21? | |
| the question. | The numbers are 8 and 13. |
One number is six more than another. The sum of the numbers is twenty-four. Find the numbers.
The sum of two numbers is fifty-eight. One number is four more than the other. Find the numbers.
The sum of two numbers is negative fourteen. One number is four less than the other. Find the numbers.
| the problem. | |
| what we are looking for. | We are looking for two numbers. |
| Choose a variable. | Let |
| One number is 4 less than the other. | |
| Write as one sentence. | The sum of the 2 numbers is negative 14. |
| Translate into an equation. | |
| the equation. | |
| Combine like terms. | |
| Add 4 to each side and simplify. | |
| Simplify. | |
| Is −9 four less than −5? | |
| Is their sum −14? | |
| the question. | The numbers are −5 and −9. |
The sum of two numbers is negative twenty-three. One number is seven less than the other. Find the numbers.
One number is ten more than twice another. Their sum is one. Find the numbers.
| the problem. | |
| what you are looking for. | We are looking for two numbers. |
| Choose a variable. | Let |
| One number is 10 more than twice another. | |
| Restate as one sentence. | Their sum is one. |
| The sum of the two numbers is 1. | |
| Translate into an equation. | |
| the equation. | |
| Combine like terms. | |
| Subtract 10 from each side. | |
| Divide each side by 3. | |
| Is ten more than twice −3 equal to 4? | |
| Is their sum 1? | |
| the question. | The numbers are −3 and −4. |
One number is eight more than twice another. Their sum is negative four. Find the numbers.
Some number problems involve consecutive integers. Consecutive integers are integers that immediately follow each other.
Examples of consecutive integers are:
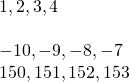
The sum of two consecutive integers is 47. Find the numbers.
| the problem. | |
| what you are looking for. | two consecutive integers |
| each number. | Let |
| Restate as one sentence. | The sum of the integers is 47. |
| Translate into an equation. | |
| the equation. | |
| Combine like terms. | |
| Subtract 1 from each side. | |
| Divide each side by 2. | |
| the question. | The two consecutive integers are 23 and 24. |
| the problem. | |
| what we are looking for. | three consecutive integers |
| each of the three numbers. | Let |
| consecutive integer | |
| consecutive integer | |
| Restate as one sentence. | The sum of the three integers is −42. |
| Translate into an equation. | |
| the equation. | |
| Combine like terms. | |
| Subtract 3 from each side. | |
| Divide each side by 3. | |
| the question. | The three consecutive integers are −13, −14, and −15. |
Now that we have worked with consecutive integers, we will expand our work to include consecutive even integers and consecutive odd integers. Consecutive even integers are even integers that immediately follow one another. Examples of consecutive even integers are:
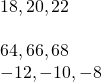
Consecutive odd integers are odd integers that immediately follow one another. Consider the consecutive odd integers 77, 79, and 81
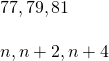
Does it seem strange to add 2 (an even number) to get from one odd integer to the next? Do you get an odd number or an even number when we add 2 to 3? to 11? to 47?
Whether the problem asks for consecutive even numbers or odd numbers, you don’t have to do anything different. The pattern is still the same—to get from one odd or one even integer to the next, add 2
Find three consecutive even integers whose sum is 84
| the problem. | |
| what we are looking for. | three consecutive even integers |
| the integers. | Let |
| Restate as one sentence. | The sume of the three even integers is 84. |
| Translate into an equation. | |
| the equation. | |
| Combine like terms. | |
| Subtract 6 from each side. | |
| Divide each side by 3. | |
| the question. | The three consecutive integers are 26, 28, and 30. |
TRY IT 10.1
Find three consecutive even integers whose sum is 102
TRY IT 10.2
A married couple together earns $110,000 a year. The wife earns $16,000 less than twice what her husband earns. What does the husband earn?
| the problem. | |
| what we are looking for. | How much does the husband earn? |
| . | |
| Choose a variable to represent the amount the husband earns. | Let |
| The wife earns $16,000 less than twice that. | |
| Together the husband and wife earn $110,000. | |
| Restate the problem in one sentence with all the important information. | |
| Translate into an equation. | |
| the equation. | h + 2h − 16,000 = 110,000 |
| Combine like terms. | |
| Add 16,000 to both sides and simplify. | |
| Divide each side by 3. | |
| If the wife earns $68,000 and the husband earns $42,000 is the total $110,000? Yes! | |
| the question. | The husband earns $42,000 a year. |
TRY IT 11.1
According to the National Automobile Dealers Association, the average cost of a car in 2014 was 28,500. This was 1,500 less than 6 times the cost in 1975. What was the average cost of a car in 1975?
TRY IT 11.2
The Canadian Real Estate Association (CREA) data shows that the median price of new home in the Canada in December 2018 was $470,000. This was $14,000 more than 19 times the price in December 1967. What was the median price of a new home in December 1967?
$24,000
Key Concepts
- Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.
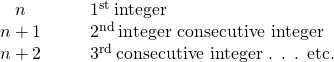
Consecutive even integers are even integers that immediately follow one another.
Consecutive odd integers are odd integers that immediately follow one another.
Practice Makes Perfect
Use the approach word problems with a positive attitude.
In the following exercises, prepare the lists described.
| 1. List five positive thoughts you can say to yourself that will help you approach word problems with a positive attitude. You may want to copy them on a sheet of paper and put it in the front of your notebook, where you can read them often. | 2. List five negative thoughts that you have said to yourself in the past that will hinder your progress on word problems. You may want to write each one on a small piece of paper and rip it up to symbolically destroy the negative thoughts. |
In the following exercises, solve using the problem solving strategy for word problems. Remember to write a complete sentence to answer each question.
| 3. Two-thirds of the children in the fourth-grade class are girls. If there are 20 girls, what is the total number of children in the class? | 4. Three-fifths of the members of the school choir are women. If there are 24 women, what is the total number of choir members? |
| 5. Zachary has 25 country music CDs, which is one-fifth of his CD collection. How many CDs does Zachary have? | 6. One-fourth of the candies in a bag of M&M’s are red. If there are 23 red candies, how many candies are in the bag? |
| 7. There are 16 girls in a school club. The number of girls is four more than twice the number of boys. Find the number of boys. | 8. There are 18 Cub Scouts in Pack 645. The number of scouts is three more than five times the number of adult leaders. Find the number of adult leaders. |
| 9. Huong is organizing paperback and hardback books for her club’s used book sale. The number of paperbacks is 12 less than three times the number of hardbacks. Huong had 162 paperbacks. How many hardback books were there? | 10. Jeff is lining up children’s and adult bicycles at the bike shop where he works. The number of children’s bicycles is nine less than three times the number of adult bicycles. There are 42 adult bicycles. How many children’s bicycles are there? |
| 11. Philip pays $1,620 in rent every month. This amount is $120 more than twice what his brother Paul pays for rent. How much does Paul pay for rent? | 12. Marc just bought an SUV for $54,000. This is $7,400 less than twice what his wife paid for her car last year. How much did his wife pay for her car? |
| 13. Laurie has $46,000 invested in stocks and bonds. The amount invested in stocks is $8,000 less than three times the amount invested in bonds. How much does Laurie have invested in bonds? | 14. Erica earned a total of $50,450 last year from her two jobs. The amount she earned from her job at the store was $1,250 more than three times the amount she earned from her job at the college. How much did she earn from her job at the college? |
In the following exercises, solve each number word problem.
| 15. The sum of a number and eight is 12. Find the number. | 16. The sum of a number and nine is 17. Find the number. |
| 17. The difference of a number and 12 is three. Find the number. | 18. The difference of a number and eight is four. Find the number. |
| 19. The sum of three times a number and eight is 23. Find the number. | 20. The sum of twice a number and six is 14. Find the number. |
| 21.The difference of twice a number and seven is 17. Find the number. | 22. The difference of four times a number and seven is 21. Find the number. |
| 23. Three times the sum of a number and nine is 12. Find the number. | 24. Six times the sum of a number and eight is 30. Find the number. |
| 25. One number is six more than the other. Their sum is 42. Find the numbers. | 26. One number is five more than the other. Their sum is 33. Find the numbers. |
| 27. The sum of two numbers is 20. One number is four less than the other. Find the numbers. | 28. The sum of two numbers is 27. One number is seven less than the other. Find the numbers. |
| 29. The sum of two numbers is | 30. The sum of two numbers is |
| 31. The sum of two numbers is | 32. The sum of two numbers is |
| 33. One number is 14 less than another. If their sum is increased by seven, the result is 85. Find the numbers. | 34. One number is 11 less than another. If their sum is increased by eight, the result is 71. Find the numbers. |
| 35. One number is five more than another. If their sum is increased by nine, the result is 60. Find the numbers. | 36. One number is eight more than another. If their sum is increased by 17, the result is 95. Find the numbers. |
| 37. One number is one more than twice another. Their sum is | 38. One number is six more than five times another. Their sum is six. Find the numbers. |
| 39. The sum of two numbers is 14. One number is two less than three times the other. Find the numbers. | 40. The sum of two numbers is zero. One number is nine less than twice the other. Find the numbers. |
| 41. The sum of two consecutive integers is 77. Find the integers. | 42. The sum of two consecutive integers is 89. Find the integers. |
| 43. The sum of two consecutive integers is | 44. The sum of two consecutive integers is |
| 45. The sum of three consecutive integers is 78. Find the integers. | 46. The sum of three consecutive integers is 60. Find the integers. |
| 47. Find three consecutive integers whose sum is | 48. Find three consecutive integers whose sum is |
| 49. Find three consecutive even integers whose sum is 258. | 50. Find three consecutive even integers whose sum is 222. |
| 51. Find three consecutive odd integers whose sum is 171. | 52. Find three consecutive odd integers whose sum is 291. |
| 53. Find three consecutive even integers whose sum is | 54. Find three consecutive even integers whose sum is |
| 55. Find three consecutive odd integers whose sum is | 56. Find three consecutive odd integers whose sum is |
Everyday Math
| 57. Patty paid $35 for a purse on sale for $10 off the original price. What was the original price of the purse? | 58. Travis bought a pair of boots on sale for $25 off the original price. He paid $60 for the boots. What was the original price of the boots? |
| 59. Minh spent $6.25 on five sticker books to give his nephews. Find the cost of each sticker book. | 60. Alicia bought a package of eight peaches for $3.20. Find the cost of each peach. |
| 61. Tom paid $1,166.40 for a new refrigerator, including $86.40 tax. What was the price of the refrigerator? | 62. Kenji paid $2,279 for a new living room set, including $129 tax. What was the price of the living room set? |
Writing Exercises
| 63. What has been your past experience solving word problems? | 64. When you start to solve a word problem, how do you decide what to let the variable represent? |
| 65. What are consecutive odd integers? Name three consecutive odd integers between 50 and 60. | 66. What are consecutive even integers? Name three consecutive even integers between |
| 1. Answers will vary | 3. 30 | 5. 125 |
| 7. 6 | 9. 58 | 11. $750 |
| 13. $13,500 | 15. 4 | 17. 15 |
| 19. 5 | 21. 12 | 23. |
| 25. 18, 24 | 27. 8, 12 | 29. |
| 31. | 33. 32, 46 | 35. 23, 28 |
| 37. | 39. 4, 10 | 41. 38, 39 |
| 43. | 45. 25, 26, 27 | 47. |
| 49. 84, 86, 88 | 51. 55, 57, 59 | 53. |
| 55. | 57. $45 | 59. $1.25 |
| 61. $1080 | 63. Answers will vary | 65. Consecutive odd integers are odd numbers that immediately follow each other. An example of three consecutive odd integers between 50 and 60 would be 51, 53, and 55. |
Attributions
This chapter has been adapted from “Use a Problem-Solving Strategy” in Elementary Algebra (OpenStax) by Lynn Marecek and MaryAnne Anthony-Smith, which is under a CC BY 4.0 Licence . Adapted by Izabela Mazur. See the Copyright page for more information.
Introductory Algebra Copyright © 2021 by Izabela Mazur is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.
Share This Book
Module 5: Multi-Step Linear Equations
Using a problem-solving strategy to solve number problems, learning outcomes.
- Apply the general problem-solving strategy to number problems
- Identify how many numbers you are solving for given a number problem
- Solve consecutive integer problems
Now we will translate and solve number problems. In number problems, you are given some clues about one or more numbers, and you use these clues to build an equation. Number problems don’t usually arise on an everyday basis, but they provide a good introduction to practicing the Problem-Solving Strategy. Remember to look for clue words such as difference , of , and and .
The difference of a number and six is [latex]13[/latex]. Find the number.
| Step 1. the problem. Do you understand all the words? | |
| Step 2. what you are looking for. | the number |
| Step 3. Choose a variable to represent the number. | Let [latex]n=\text{the number}[/latex] |
| Step 4. Restate as one sentence. Translate into an equation. | [latex]n-6\enspace\Rightarrow[/latex] The difference of a number and 6 [latex]=\enspace\Rightarrow[/latex] is [latex]13\enspace\Rightarrow[/latex] thirteen |
| Step 5. the equation. Add 6 to both sides. Simplify. | [latex]n-6=13[/latex] [latex]n-6\color{red}{+6}=13\color{red}{+6}[/latex] [latex]n=19[/latex] |
| Step 6. The difference of [latex]19[/latex] and [latex]6[/latex] is [latex]13[/latex]. It checks. | |
| Step 7. the question. | The number is [latex]19[/latex]. |
The sum of twice a number and seven is [latex]15[/latex]. Find the number.
Show Solution
| Step 1. the problem. | |
| Step 2. what you are looking for. | the number |
| Step 3. Choose a variable to represent the number. | Let [latex]n=\text{the number}[/latex] |
| Step 4. Restate the problem as one sentence. Translate into an equation. | [latex]2n\enspace\Rightarrow[/latex] The sum of twice a number [latex]+\enspace\Rightarrow[/latex] and [latex]7\enspace\Rightarrow[/latex] seven [latex]=\enspace\Rightarrow[/latex] is [latex]15\enspace\Rightarrow[/latex] fifteen |
| Step 5. the equation. | [latex]2n+7=15[/latex] |
| Subtract 7 from each side and simplify. | [latex]2n=8[/latex] |
| Divide each side by 2 and simplify. | [latex]n=4[/latex] |
| Step 6. is the sum of twice [latex]4[/latex] and [latex]7[/latex] equal to [latex]15[/latex]? [latex]2\cdot{4}+7=15[/latex] [latex]8+7=15[/latex] [latex]15=15\quad\checkmark[/latex] | |
| Step 7. the question. | The number is [latex]4[/latex]. |
Watch the following video to see another example of how to solve a number problem.
Solving for Two or More Numbers
Some number word problems ask you to find two or more numbers. It may be tempting to name them all with different variables, but so far we have only solved equations with one variable. We will define the numbers in terms of the same variable. Be sure to read the problem carefully to discover how all the numbers relate to each other.
One number is five more than another. The sum of the numbers is twenty-one. Find the numbers.
| Step 1. the problem. | ||
| Step 2. what you are looking for. | You are looking for two numbers. | |
| Step 3. Choose a variable to represent the first number. What do you know about the second number? Translate. | Let [latex]n=\text{1st number}[/latex] One number is five more than another. [latex]x+5={2}^{\text{nd}}\text{number}[/latex] | |
| Step 4. Restate the problem as one sentence with all the important information. Translate into an equation. Substitute the variable expressions. | The sum of the numbers is [latex]21[/latex]. The sum of the 1st number and the 2nd number is [latex]21[/latex]. [latex]n\enspace\Rightarrow[/latex] First number [latex]+\enspace\Rightarrow[/latex] + [latex]n+5\enspace\Rightarrow[/latex] Second number [latex]=\enspace\Rightarrow[/latex] = [latex]21\enspace\Rightarrow[/latex] 21 | |
| Step 5. the equation. | [latex]n+n+5=21[/latex] | |
| Combine like terms. | [latex]2n+5=21[/latex] | |
| Subtract five from both sides and simplify. | [latex]2n=16[/latex] | |
| Divide by two and simplify. | [latex]n=8[/latex] 1st number | |
| Find the second number too. | [latex]n+5[/latex] 2nd number | |
| Substitute [latex]n = 8[/latex] | [latex]\color{red}{8}+5[/latex] | |
| [latex]13[/latex] | ||
| Step 6. | ||
| Do these numbers check in the problem? Is one number 5 more than the other? Is thirteen, 5 more than 8? Yes. Is the sum of the two numbers 21? | [latex]13\stackrel{\text{?}}{=}8+5[/latex] [latex]13=13\quad\checkmark[/latex] [latex]8+13\stackrel{\text{?}}{=}21[/latex] [latex]21=21\quad\checkmark[/latex] | |
| Step 7. the question. | The numbers are [latex]8[/latex] and [latex]13[/latex]. |
Watch the following video to see another example of how to find two numbers given the relationship between the two.
The sum of two numbers is negative fourteen. One number is four less than the other. Find the numbers.
| Step 1. the problem. | ||
| Step 2. what you are looking for. | two numbers | |
| Step 3. Choose a variable. What do you know about the second number? Translate. | Let [latex]n=\text{1st number}[/latex] One number is [latex]4[/latex] less than the other. [latex]n-4={2}^{\text{nd}}\text{number}[/latex] | |
| Step 4. Write as one sentence. Translate into an equation. Substitute the variable expressions. | The sum of two numbers is negative fourteen. [latex]n\enspace\Rightarrow[/latex] First number [latex]+\enspace\Rightarrow[/latex] + [latex]n-4\enspace\Rightarrow[/latex] Second number [latex]=\enspace\Rightarrow[/latex] = [latex]-14\enspace\Rightarrow[/latex] -14 | |
| Step 5. the equation. | [latex]n+n-4=-14[/latex] | |
| Combine like terms. | [latex]2n-4=-14[/latex] | |
| Add 4 to each side and simplify. | [latex]2n=-10[/latex] | |
| Divide by 2. | [latex]n=-5[/latex] 1st number | |
| Substitute [latex]n=-5[/latex] to find the 2 number. | [latex]n-4[/latex] 2nd number | |
| [latex]\color{red}{-5}-4[/latex] | ||
| [latex]-9[/latex] | ||
| Step 6. | ||
| Is −9 four less than −5? Is their sum −14? | [latex]-5-4\stackrel{\text{?}}{=}-9[/latex] [latex]-9=-9\quad\checkmark[/latex] [latex]-5+(-9)\stackrel{\text{?}}{=}-14[/latex] [latex]-14=-14\quad\checkmark[/latex] | |
| Step 7. the question. | The numbers are [latex]−5[/latex] and [latex]−9[/latex]. |
One number is ten more than twice another. Their sum is one. Find the numbers.
| Step 1. the problem. | ||
| Step 2. what you are looking for. | two numbers | |
| Step 3. Choose a variable. One number is ten more than twice another. | Let [latex]x=\text{1st number}[/latex] [latex]2x+10={2}^{\text{nd}}\text{number}[/latex] | |
| Step 4. Restate as one sentence. | Their sum is one. | |
| Translate into an equation | [latex]x+(2x+10)\enspace\Rightarrow[/latex] The sum of the two numbers [latex]=\enspace\Rightarrow[/latex] is [latex]1\enspace\Rightarrow[/latex] 1 | |
| Step 5. the equation. | [latex]x+2x+10=1[/latex] | |
| Combine like terms. | [latex]3x+10=1[/latex] | |
| Subtract 10 from each side. | [latex]3x=-9[/latex] | |
| Divide each side by 3 to get the first number. | [latex]x=-3[/latex] | |
| Substitute to get the second number. | [latex]2x+10[/latex] | |
| [latex]2(\color{red}{-3})+10[/latex] | ||
| [latex]4[/latex] | ||
| Step 6. | ||
| Is 4 ten more than twice −3? Is their sum 1? | [latex]2(-3)+10\stackrel{\text{?}}{=}4[/latex] [latex]-6+10=4[/latex] [latex]4=4\quad\checkmark[/latex] [latex]-3+4\stackrel{\text{?}}{=}1[/latex] [latex]1=1\quad\checkmark[/latex] | |
| Step 7. the question. | The numbers are [latex]−3[/latex] and [latex]4[/latex]. |
Solving for Consecutive Integers
Consecutive integers are integers that immediately follow each other. Some examples of consecutive integers are:
[latex]\begin{array}{c}\phantom{\rule{0.2}{0ex}}\\ \phantom{\rule{0.2}{0ex}}\\ \phantom{\rule{0.2}{0ex}}\\ \phantom{\rule{0.2}{0ex}}\\ \hfill \text{…}1,2,3,4\text{,…}\hfill \end{array}[/latex] [latex]\text{…}-10,-9,-8,-7\text{,…}[/latex] [latex]\text{…}150,151,152,153\text{,…}[/latex]
Notice that each number is one more than the number preceding it. So if we define the first integer as [latex]n[/latex], the next consecutive integer is [latex]n+1[/latex]. The one after that is one more than [latex]n+1[/latex], so it is [latex]n+1+1[/latex], or [latex]n+2[/latex].
[latex]\begin{array}{cccc}n\hfill & & & \text{1st integer}\hfill \\ n+1\hfill & & & \text{2nd consecutive integer}\hfill \\ n+2\hfill & & & \text{3rd consecutive integer}\hfill \end{array}[/latex]
The sum of two consecutive integers is [latex]47[/latex]. Find the numbers.
| Step 1. the problem. | ||
| Step 2. what you are looking for. | two consecutive integers | |
| Step 3. | Let [latex]n=\text{1st integer}[/latex] [latex]n+1=\text{next consecutive integer}[/latex] | |
| Step 4. Restate as one sentence. Translate into an equation. | [latex]n+n+1\enspace\Rightarrow[/latex] The sum of the integers [latex]=\enspace\Rightarrow[/latex] is [latex]47\enspace\Rightarrow[/latex] 47 | |
| Step 5. the equation. | [latex]n+n+1=47[/latex] | |
| Combine like terms. | [latex]2n+1=47[/latex] | |
| Subtract 1 from each side. | [latex]2n=46[/latex] | |
| Divide each side by 2. | [latex]n=23[/latex] 1st integer | |
| Substitute to get the second number. | [latex]n+1[/latex] 2nd integer | |
| [latex]\color{red}{23}+1[/latex] | ||
| [latex]24[/latex] | ||
| Step 6. | [latex]23+24\stackrel{\text{?}}{=}47[/latex] [latex]47=47\quad\checkmark[/latex] | |
| Step 7. the question. | The two consecutive integers are [latex]23[/latex] and [latex]24[/latex]. |
Find three consecutive integers whose sum is [latex]42[/latex].
| Step 1. the problem. | ||
| Step 2. what you are looking for. | three consecutive integers | |
| Step 3. | Let [latex]n=\text{1st integer}[/latex] [latex]n+1=\text{2nd consecutive integer}[/latex] [latex]n+2=\text{3rd consecutive integer}[/latex]
| |
| Step 4. Restate as one sentence. Translate into an equation. | [latex]n\enspace +\enspace n+1\enspace +\enspace n+2\enspace\Rightarrow[/latex] The sum of the three integers [latex]=\enspace\Rightarrow[/latex] is [latex]42\enspace\Rightarrow[/latex] 42 | |
| Step 5. the equation. | [latex]n+n+1+n+2=42[/latex] | |
| Combine like terms. | [latex]3n+3=42[/latex] | |
| Subtract 3 from each side. | [latex]3n=39[/latex] | |
| Divide each side by 3. | [latex]n=13[/latex] 1st integer | |
| Substitute to get the second number. | [latex]n+1[/latex] 2nd integer | |
| [latex]\color{red}{13}+1[/latex] | ||
| [latex]24[/latex] | ||
| Substitute to get the third number. | [latex]n+2[/latex] 3rd integer | |
| [latex]\color{red}{13}+2[/latex] | ||
| [latex]15[/latex] | ||
| Step 6. | [latex]13+14+15\stackrel{\text{?}}{=}42[/latex] [latex]42=42\quad\checkmark[/latex] | |
| Step 7. the question. | The three consecutive integers are [latex]13[/latex], [latex]14[/latex], and [latex]15[/latex]. |
Watch this video for another example of how to find three consecutive integers given their sum.
- Ex: Linear Equation Application with One Variable - Number Problem. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/juslHscrh8s . License : CC BY: Attribution
- Ex: Write and Solve an Equation for Consecutive Natural Numbers with a Given Sum. Authored by : James Sousa (Mathispower4u.com). Located at : https://youtu.be/Bo67B0L9hGs . License : CC BY: Attribution
- Write and Solve a Linear Equations to Solve a Number Problem (1) Mathispower4u . Authored by : James Sousa (Mathispower4u.com) for Lumen Learning. Located at : https://youtu.be/izIIqOztUyI . License : CC BY: Attribution
- Question ID 142763, 142770, 142775, 142806, 142811, 142816, 142817. Authored by : Lumen Learning. License : CC BY: Attribution . License Terms : IMathAS Community License, CC-BY + GPL
- Prealgebra. Provided by : OpenStax. License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]

Our website uses cookies and thereby collects information about your visit to improve our website (by analyzing), show you Social Media content and relevant advertisements. Please see our page for furher details or agree by clicking the 'Accept' button.
Cookie settings
Below you can choose which kind of cookies you allow on this website. Click on the "Save cookie settings" button to apply your choice.
Functional Our website uses functional cookies. These cookies are necessary to let our website work.
Analytical Our website uses analytical cookies to make it possible to analyze our website and optimize for the purpose of a.o. the usability.
Social media Our website places social media cookies to show you 3rd party content like YouTube and FaceBook. These cookies may track your personal data.
Advertising Our website places advertising cookies to show you 3rd party advertisements based on your interests. These cookies may track your personal data.
Other Our website places 3rd party cookies from other 3rd party services which aren't Analytical, Social media or Advertising.
Default cookie settings Save cookie settings
This content is blocked. Accept cookies within the '%CC%' category to view this content. click to accept all cookies Accept %CC% cookies
2.1 Use a General Strategy to Solve Linear Equations
Learning objectives.
By the end of this section, you will be able to:
- Solve linear equations using a general strategy
- Classify equations
- Solve equations with fraction or decimal coefficients
Be Prepared 2.1
Before you get started, take this readiness quiz.
Simplify: 3 2 ( 12 x + 20 ) . 3 2 ( 12 x + 20 ) . If you missed this problem, review Example 1.51 .
Be Prepared 2.2
Simplify: 5 − 2 ( n + 1 ) . 5 − 2 ( n + 1 ) . If you missed this problem, review Example 1.55 .
Be Prepared 2.3
Find the LCD of 5 6 5 6 and 1 4 . 1 4 . If you missed this problem, review Example 1.28 .
Solve Linear Equations Using a General Strategy
Solving an equation is like discovering the answer to a puzzle. The purpose in solving an equation is to find the value or values of the variable that makes it a true statement. Any value of the variable that makes the equation true is called a solution to the equation. It is the answer to the puzzle!
Solution of an Equation
A solution of an equation is a value of a variable that makes a true statement when substituted into the equation.
To determine whether a number is a solution to an equation, we substitute the value for the variable in the equation. If the resulting equation is a true statement, then the number is a solution of the equation.
Determine Whether a Number is a Solution to an Equation.
- Step 1. Substitute the number for the variable in the equation.
- Step 2. Simplify the expressions on both sides of the equation.
- If it is true, the number is a solution.
- If it is not true, the number is not a solution.
Example 2.1
Determine whether the values are solutions to the equation: 5 y + 3 = 10 y − 4 . 5 y + 3 = 10 y − 4 .
ⓐ y = 3 5 y = 3 5 ⓑ y = 7 5 y = 7 5
Since a solution to an equation is a value of the variable that makes the equation true, begin by substituting the value of the solution for the variable.
| Multiply. | |
| Simplify. |
Since y = 3 5 y = 3 5 does not result in a true equation, y = 3 5 y = 3 5 is not a solution to the equation 5 y + 3 = 10 y − 4 . 5 y + 3 = 10 y − 4 .
| Multiply. | |
| Simplify. |
Since y = 7 5 y = 7 5 results in a true equation, y = 7 5 y = 7 5 is a solution to the equation 5 y + 3 = 10 y − 4 . 5 y + 3 = 10 y − 4 .
Determine whether the values are solutions to the equation: 9 y + 2 = 6 y + 3 . 9 y + 2 = 6 y + 3 .
ⓐ y = 4 3 y = 4 3 ⓑ y = 1 3 y = 1 3
Determine whether the values are solutions to the equation: 4 x − 2 = 2 x + 1 . 4 x − 2 = 2 x + 1 .
ⓐ x = 3 2 x = 3 2 ⓑ x = − 1 2 x = − 1 2
There are many types of equations that we will learn to solve. In this section we will focus on a linear equation .
Linear Equation
A linear equation is an equation in one variable that can be written, where a and b are real numbers and a ≠ 0 , a ≠ 0 , as:
To solve a linear equation it is a good idea to have an overall strategy that can be used to solve any linear equation. In the next example, we will give the steps of a general strategy for solving any linear equation. Simplifying each side of the equation as much as possible first makes the rest of the steps easier.
Example 2.2
How to solve a linear equation using a general strategy.
Solve: 7 ( n − 3 ) − 8 = −15 7 ( n − 3 ) − 8 = −15 .
Solve: 2 ( m − 4 ) + 3 = −1 . 2 ( m − 4 ) + 3 = −1 .
Solve: 5 ( a − 3 ) + 5 = −10 . 5 ( a − 3 ) + 5 = −10 .
These steps are summarized in the General Strategy for Solving Linear Equations below.
Solve linear equations using a general strategy.
- Step 1. Simplify each side of the equation as much as possible. Use the Distributive Property to remove any parentheses. Combine like terms.
- Step 2. Collect all the variable terms on one side of the equation. Use the Addition or Subtraction Property of Equality.
- Step 3. Collect all the constant terms on the other side of the equation. Use the Addition or Subtraction Property of Equality.
- Step 4. Make the coefficient of the variable term equal to 1. Use the Multiplication or Division Property of Equality. State the solution to the equation.
- Step 5. Check the solution. Substitute the solution into the original equation to make sure the result is a true statement.
Example 2.3
Solve: 2 3 ( 3 m − 6 ) = 5 − m . 2 3 ( 3 m − 6 ) = 5 − m .
| Distribute. | ||
| Add to both sides to get the variables only on the left. | ||
| Simplify. | ||
| Add 4 to both sides to get constants only on the right. | ||
| Simplify. | ||
| Divide both sides by three. | ||
| Simplify. | ||
| Check: | ||
| Let | ||
Solve: 1 3 ( 6 u + 3 ) = 7 − u . 1 3 ( 6 u + 3 ) = 7 − u .
Solve: 2 3 ( 9 x − 12 ) = 8 + 2 x . 2 3 ( 9 x − 12 ) = 8 + 2 x .
We can solve equations by getting all the variable terms to either side of the equal sign . By collecting the variable terms on the side where the coefficient of the variable is larger, we avoid working with some negatives. This will be a good strategy when we solve inequalities later in this chapter. It also helps us prevent errors with negatives.
Example 2.4
Solve: 4 ( x − 1 ) − 2 = 5 ( 2 x + 3 ) + 6 . 4 ( x − 1 ) − 2 = 5 ( 2 x + 3 ) + 6 .
| Distribute. | ||||
| Combine like terms. | ||||
| Subtract from each side to get the variables only on the right since | ||||
| Simplify. | ||||
| Subtract 21 from each side to get the constants on left. | ||||
| Simplify. | ||||
| Divide both sides by 6. | ||||
| Simplify. | ||||
| Check: | ||||
| Let | ||||
Solve: 6 ( p − 3 ) − 7 = 5 ( 4 p + 3 ) − 12 . 6 ( p − 3 ) − 7 = 5 ( 4 p + 3 ) − 12 .
Solve: 8 ( q + 1 ) − 5 = 3 ( 2 q − 4 ) − 1 . 8 ( q + 1 ) − 5 = 3 ( 2 q − 4 ) − 1 .
Example 2.5
Solve: 10 [ 3 − 8 ( 2 s − 5 ) ] = 15 ( 40 − 5 s ) . 10 [ 3 − 8 ( 2 s − 5 ) ] = 15 ( 40 − 5 s ) .
| Simplify from the innermost parentheses first. | ||
| Combine like terms in the brackets. | ||
| Distribute. | ||
| Add to both sides to get the variables to the right. | ||
| Simplify. | ||
| Subtract 600 from both sides to get the constants to the left. | ||
| Simplify. | ||
| Divide both sides by 85. | ||
| Simplify. | ||
| Check: | ||
| Let | ||
Solve: 6 [ 4 − 2 ( 7 y − 1 ) ] = 8 ( 13 − 8 y ) . 6 [ 4 − 2 ( 7 y − 1 ) ] = 8 ( 13 − 8 y ) .
Try It 2.10
Solve: 12 [ 1 − 5 ( 4 z − 1 ) ] = 3 ( 24 + 11 z ) . 12 [ 1 − 5 ( 4 z − 1 ) ] = 3 ( 24 + 11 z ) .
Classify Equations
Whether or not an equation is true depends on the value of the variable. The equation 7 x + 8 = −13 7 x + 8 = −13 is true when we replace the variable, x , with the value −3 , −3 , but not true when we replace x with any other value. An equation like this is called a conditional equation . All the equations we have solved so far are conditional equations.
Conditional Equation
An equation that is true for one or more values of the variable and false for all other values of the variable is a conditional equation .
Now let’s consider the equation 7 y + 14 = 7 ( y + 2 ) . 7 y + 14 = 7 ( y + 2 ) . Do you recognize that the left side and the right side are equivalent? Let’s see what happens when we solve for y .
| Distribute. | |
| Subtract to each side to get the to one side. | |
| Simplify—the ’s are eliminated. | |
| But is true. |
This means that the equation 7 y + 14 = 7 ( y + 2 ) 7 y + 14 = 7 ( y + 2 ) is true for any value of y . We say the solution to the equation is all of the real numbers. An equation that is true for any value of the variable is called an identity .
An equation that is true for any value of the variable is called an identity .
The solution of an identity is all real numbers.
What happens when we solve the equation −8 z = −8 z + 9 ? −8 z = −8 z + 9 ?
| Add to both sides to leave the constant alone on the right. | |
| Simplify—the are eliminated. | |
| But |
Solving the equation −8 z = −8 z + 9 −8 z = −8 z + 9 led to the false statement 0 = 9 . 0 = 9 . The equation −8 z = −8 z + 9 −8 z = −8 z + 9 will not be true for any value of z . It has no solution. An equation that has no solution, or that is false for all values of the variable, is called a contradiction .
Contradiction
An equation that is false for all values of the variable is called a contradiction .
A contradiction has no solution.
The next few examples will ask us to classify an equation as conditional, an identity, or as a contradiction.
Example 2.6
Classify the equation as a conditional equation, an identity, or a contradiction and then state the solution: 6 ( 2 n − 1 ) + 3 = 2 n − 8 + 5 ( 2 n + 1 ) . 6 ( 2 n − 1 ) + 3 = 2 n − 8 + 5 ( 2 n + 1 ) .
| Distribute. | |
| Combine like terms. | |
| Subtract from each side to get the ’s to one side. | |
| Simplify. | |
| This is a true statement. | The equation is an identity. |
| The solution is all real numbers. |
Try It 2.11
Classify the equation as a conditional equation, an identity, or a contradiction and then state the solution: 4 + 9 ( 3 x − 7 ) = −42 x − 13 + 23 ( 3 x − 2 ) . 4 + 9 ( 3 x − 7 ) = −42 x − 13 + 23 ( 3 x − 2 ) .
Try It 2.12
Classify the equation as a conditional equation, an identity, or a contradiction and then state the solution: 8 ( 1 − 3 x ) + 15 ( 2 x + 7 ) = 2 ( x + 50 ) + 4 ( x + 3 ) + 1 . 8 ( 1 − 3 x ) + 15 ( 2 x + 7 ) = 2 ( x + 50 ) + 4 ( x + 3 ) + 1 .
Example 2.7
Classify the equation as a conditional equation, an identity, or a contradiction and then state the solution: 8 + 3 ( a − 4 ) = 0 . 8 + 3 ( a − 4 ) = 0 .
| Distribute. | ||
| Combine like terms. | ||
| Add 4 to both sides. | ||
| Simplify. | ||
| Divide. | ||
| Simplify. | ||
| The equation is true when | This is a conditional equation. | |
| The solution is | ||
Try It 2.13
Classify the equation as a conditional equation, an identity, or a contradiction and then state the solution: 11 ( q + 3 ) − 5 = 19 . 11 ( q + 3 ) − 5 = 19 .
Try It 2.14
Classify the equation as a conditional equation, an identity, or a contradiction and then state the solution: 6+14 ( k − 8 ) = 95 . 6+14 ( k − 8 ) = 95 .
Example 2.8
Classify the equation as a conditional equation, an identity, or a contradiction and then state the solution: 5 m + 3 ( 9 + 3 m ) = 2 ( 7 m − 11 ) . 5 m + 3 ( 9 + 3 m ) = 2 ( 7 m − 11 ) .
| Distribute. | |
| Combine like terms. | |
| Subtract from both sides. | |
| Simplify. | |
| But | The equation is a contradiction. |
| It has no solution. |
Try It 2.15
Classify the equation as a conditional equation, an identity, or a contradiction and then state the solution: 12 c + 5 ( 5 + 3 c ) = 3 ( 9 c − 4 ) . 12 c + 5 ( 5 + 3 c ) = 3 ( 9 c − 4 ) .
Try It 2.16
Classify the equation as a conditional equation, an identity, or a contradiction and then state the solution: 4 ( 7 d + 18 ) = 13 ( 3 d − 2 ) − 11 d . 4 ( 7 d + 18 ) = 13 ( 3 d − 2 ) − 11 d .
We summarize the methods for classifying equations in the table.
| Type of equation | What happens when you solve it? | Solution |
|---|---|---|
| True for one or more values of the variables and false for all other values | One or more values | |
| True for any value of the variable | All real numbers | |
| False for all values of the variable | No solution |
Solve Equations with Fraction or Decimal Coefficients
We could use the General Strategy to solve the next example. This method would work fine, but many students do not feel very confident when they see all those fractions. So, we are going to show an alternate method to solve equations with fractions. This alternate method eliminates the fractions.
We will apply the Multiplication Property of Equality and multiply both sides of an equation by the least common denominator (LCD) of all the fractions in the equation. The result of this operation will be a new equation, equivalent to the first, but without fractions. This process is called clearing the equation of fractions.
To clear an equation of decimals, we think of all the decimals in their fraction form and then find the LCD of those denominators.
Example 2.9
How to solve equations with fraction or decimal coefficients.
Solve: 1 12 x + 5 6 = 3 4 . 1 12 x + 5 6 = 3 4 .
Try It 2.17
Solve: 1 4 x + 1 2 = 5 8 . 1 4 x + 1 2 = 5 8 .
Try It 2.18
Solve: 1 8 x + 1 2 = 1 4 . 1 8 x + 1 2 = 1 4 .
Notice in the previous example, once we cleared the equation of fractions, the equation was like those we solved earlier in this chapter. We changed the problem to one we already knew how to solve. We then used the General Strategy for Solving Linear Equations .
Solve Equations with Fraction or Decimal Coefficients.
- Step 1. Find the least common denominator (LCD) of all the fractions and decimals (in fraction form) in the equation.
- Step 2. Multiply both sides of the equation by that LCD. This clears the fractions and decimals.
- Step 3. Solve using the General Strategy for Solving Linear Equations.
Example 2.10
Solve: 5 = 1 2 y + 2 3 y − 3 4 y . 5 = 1 2 y + 2 3 y − 3 4 y .
We want to clear the fractions by multiplying both sides of the equation by the LCD of all the fractions in the equation.
| Find the LCD of all fractions in the equation. | ||
| The LCD is 12. | ||
| Multiply both sides of the equation by 12. | ||
| Distribute. | ||
| Simplify—notice, no more fractions. | ||
| Combine like terms. | ||
| Divide by five. | ||
| Simplify. | ||
| Check: | ||
| Let | ||
Try It 2.19
Solve: 7 = 1 2 x + 3 4 x − 2 3 x . 7 = 1 2 x + 3 4 x − 2 3 x .
Try It 2.20
Solve: −1 = 1 2 u + 1 4 u − 2 3 u . −1 = 1 2 u + 1 4 u − 2 3 u .
In the next example, we’ll distribute before we clear the fractions.
Example 2.11
Solve: 1 2 ( y − 5 ) = 1 4 ( y − 1 ) . 1 2 ( y − 5 ) = 1 4 ( y − 1 ) .
| Distribute. | ||
| Simplify. | ||
| Multiply by the LCD, four. | ||
| Distribute. | ||
| Simplify. | ||
| Collect the variables to the left. | ||
| Simplify. | ||
| Collect the constants to the right. | ||
| Simplify. | ||
| An alternate way to solve this equation is to clear the fractions without distributing first. If you multiply the factors correctly, this method will be easier. | ||
| Multiply by the LCD, 4. | ||
| Multiply four times the fractions. | ||
| Distribute. | ||
| Collect the variables to the left. | ||
| Simplify. | ||
| Collect the constants to the right. | ||
| Simplify. | ||
| Check: | ||
| Let | ||
| Finish the check on your own. | ||
Try It 2.21
Solve: 1 5 ( n + 3 ) = 1 4 ( n + 2 ) . 1 5 ( n + 3 ) = 1 4 ( n + 2 ) .
Try It 2.22
Solve: 1 2 ( m − 3 ) = 1 4 ( m − 7 ) . 1 2 ( m − 3 ) = 1 4 ( m − 7 ) .
When you multiply both sides of an equation by the LCD of the fractions, make sure you multiply each term by the LCD—even if it does not contain a fraction.
Example 2.12
Solve: 4 q + 3 2 + 6 = 3 q + 5 4 4 q + 3 2 + 6 = 3 q + 5 4
| Multiply both sides by the LCD, 4. | ||
| Distribute. | ||
| Simplify. | ||
| Collect the variables to the left. | ||
| Simplify. | ||
| Collect the constants to the right. | ||
| Simplify. | ||
| Divide both sides by five. | ||
| Simplify. | ||
| Check: | ||
| Let | ||
| Finish the check on your own. | ||
Try It 2.23
Solve: 3 r + 5 6 + 1 = 4 r + 3 3 . 3 r + 5 6 + 1 = 4 r + 3 3 .
Try It 2.24
Solve: 2 s + 3 2 + 1 = 3 s + 2 4 . 2 s + 3 2 + 1 = 3 s + 2 4 .
Some equations have decimals in them. This kind of equation may occur when we solve problems dealing with money or percentages. But decimals can also be expressed as fractions. For example, 0.7 = 7 10 0.7 = 7 10 and 0.29 = 29 100 . 0.29 = 29 100 . So, with an equation with decimals, we can use the same method we used to clear fractions—multiply both sides of the equation by the least common denominator .
The next example uses an equation that is typical of the ones we will see in the money applications in a later section. Notice that we will clear all decimals by multiplying by the LCD of their fraction form.
Example 2.13
Solve: 0.25 x + 0.05 ( x + 3 ) = 2.85 . 0.25 x + 0.05 ( x + 3 ) = 2.85 .
Look at the decimals and think of the equivalent fractions:
Notice, the LCD is 100. By multiplying by the LCD we will clear the decimals from the equation.
| Distribute first. | |
| Combine like terms. | |
| To clear decimals, multiply by 100. | |
| Distribute. | |
| Subtract 15 from both sides. | |
| Simplify. | |
| Divide by 30. | |
| Simplify. | |
| Check it yourself by substituting into the original equation. | |
Try It 2.25
Solve: 0.25 n + 0.05 ( n + 5 ) = 2.95 . 0.25 n + 0.05 ( n + 5 ) = 2.95 .
Try It 2.26
Solve: 0.10 d + 0.05 ( d − 5 ) = 2.15 . 0.10 d + 0.05 ( d − 5 ) = 2.15 .
Section 2.1 Exercises
Practice makes perfect.
Solve Equations Using the General Strategy
In the following exercises, determine whether the given values are solutions to the equation.
6 y + 10 = 12 y 6 y + 10 = 12 y
ⓐ y = 5 3 y = 5 3 ⓑ y = − 1 2 y = − 1 2
4 x + 9 = 8 x 4 x + 9 = 8 x
ⓐ x = − 7 8 x = − 7 8 ⓑ x = 9 4 x = 9 4
8 u − 1 = 6 u 8 u − 1 = 6 u
ⓐ u = − 1 2 u = − 1 2 ⓑ u = 1 2 u = 1 2
9 v − 2 = 3 v 9 v − 2 = 3 v
ⓐ v = − 1 3 v = − 1 3 ⓑ v = 1 3 v = 1 3
In the following exercises, solve each linear equation.
15 ( y − 9 ) = −60 15 ( y − 9 ) = −60
−16 ( 3 n + 4 ) = 32 −16 ( 3 n + 4 ) = 32
− ( w − 12 ) = 30 − ( w − 12 ) = 30
− ( t − 19 ) = 28 − ( t − 19 ) = 28
51 + 5 ( 4 − q ) = 56 51 + 5 ( 4 − q ) = 56
−6 + 6 ( 5 − k ) = 15 −6 + 6 ( 5 − k ) = 15
3 ( 10 − 2 x ) + 54 = 0 3 ( 10 − 2 x ) + 54 = 0
−2 ( 11 − 7 x ) + 54 = 4 −2 ( 11 − 7 x ) + 54 = 4
2 3 ( 9 c − 3 ) = 22 2 3 ( 9 c − 3 ) = 22
3 5 ( 10 x − 5 ) = 27 3 5 ( 10 x − 5 ) = 27
1 5 ( 15 c + 10 ) = c + 7 1 5 ( 15 c + 10 ) = c + 7
1 4 ( 20 d + 12 ) = d + 7 1 4 ( 20 d + 12 ) = d + 7
3 ( 4 n − 1 ) − 2 = 8 n + 3 3 ( 4 n − 1 ) − 2 = 8 n + 3
9 ( 2 m − 3 ) − 8 = 4 m + 7 9 ( 2 m − 3 ) − 8 = 4 m + 7
12 + 2 ( 5 − 3 y ) = −9 ( y − 1 ) − 2 12 + 2 ( 5 − 3 y ) = −9 ( y − 1 ) − 2
−15 + 4 ( 2 − 5 y ) = −7 ( y − 4 ) + 4 −15 + 4 ( 2 − 5 y ) = −7 ( y − 4 ) + 4
5 + 6 ( 3 s − 5 ) = −3 + 2 ( 8 s − 1 ) 5 + 6 ( 3 s − 5 ) = −3 + 2 ( 8 s − 1 )
−12 + 8 ( x − 5 ) = −4 + 3 ( 5 x − 2 ) −12 + 8 ( x − 5 ) = −4 + 3 ( 5 x − 2 )
4 ( p − 4 ) − ( p + 7 ) = 5 ( p − 3 ) 4 ( p − 4 ) − ( p + 7 ) = 5 ( p − 3 )
3 ( a − 2 ) − ( a + 6 ) = 4 ( a − 1 ) 3 ( a − 2 ) − ( a + 6 ) = 4 ( a − 1 )
4 [ 5 − 8 ( 4 c − 3 ) ] = 12 ( 1 − 13 c ) − 8 4 [ 5 − 8 ( 4 c − 3 ) ] = 12 ( 1 − 13 c ) − 8
5 [ 9 − 2 ( 6 d − 1 ) ] = 11 ( 4 − 10 d ) − 139 5 [ 9 − 2 ( 6 d − 1 ) ] = 11 ( 4 − 10 d ) − 139
3 [ −9 + 8 ( 4 h − 3 ) ] = 2 ( 5 − 12 h ) − 19 3 [ −9 + 8 ( 4 h − 3 ) ] = 2 ( 5 − 12 h ) − 19
3 [ −14 + 2 ( 15 k − 6 ) ] = 8 ( 3 − 5 k ) − 24 3 [ −14 + 2 ( 15 k − 6 ) ] = 8 ( 3 − 5 k ) − 24
5 [ 2 ( m + 4 ) + 8 ( m − 7 ) ] = 2 [ 3 ( 5 + m ) − ( 21 − 3 m ) ] 5 [ 2 ( m + 4 ) + 8 ( m − 7 ) ] = 2 [ 3 ( 5 + m ) − ( 21 − 3 m ) ]
10 [ 5 ( n + 1 ) + 4 ( n − 1 ) ] = 11 [ 7 ( 5 + n ) − ( 25 − 3 n ) ] 10 [ 5 ( n + 1 ) + 4 ( n − 1 ) ] = 11 [ 7 ( 5 + n ) − ( 25 − 3 n ) ]
In the following exercises, classify each equation as a conditional equation, an identity, or a contradiction and then state the solution.
23 z + 19 = 3 ( 5 z − 9 ) + 8 z + 46 23 z + 19 = 3 ( 5 z − 9 ) + 8 z + 46
15 y + 32 = 2 ( 10 y − 7 ) − 5 y + 46 15 y + 32 = 2 ( 10 y − 7 ) − 5 y + 46
18 ( 5 j − 1 ) + 29 = 47 18 ( 5 j − 1 ) + 29 = 47
24 ( 3 d − 4 ) + 100 = 52 24 ( 3 d − 4 ) + 100 = 52
22 ( 3 m − 4 ) = 8 ( 2 m + 9 ) 22 ( 3 m − 4 ) = 8 ( 2 m + 9 )
30 ( 2 n − 1 ) = 5 ( 10 n + 8 ) 30 ( 2 n − 1 ) = 5 ( 10 n + 8 )
7 v + 42 = 11 ( 3 v + 8 ) − 2 ( 13 v − 1 ) 7 v + 42 = 11 ( 3 v + 8 ) − 2 ( 13 v − 1 )
18 u − 51 = 9 ( 4 u + 5 ) − 6 ( 3 u − 10 ) 18 u − 51 = 9 ( 4 u + 5 ) − 6 ( 3 u − 10 )
45 ( 3 y − 2 ) = 9 ( 15 y − 6 ) 45 ( 3 y − 2 ) = 9 ( 15 y − 6 )
60 ( 2 x − 1 ) = 15 ( 8 x + 5 ) 60 ( 2 x − 1 ) = 15 ( 8 x + 5 )
9 ( 14 d + 9 ) + 4 d = 13 ( 10 d + 6 ) + 3 9 ( 14 d + 9 ) + 4 d = 13 ( 10 d + 6 ) + 3
11 ( 8 c + 5 ) − 8 c = 2 ( 40 c + 25 ) + 5 11 ( 8 c + 5 ) − 8 c = 2 ( 40 c + 25 ) + 5
In the following exercises, solve each equation with fraction coefficients.
1 4 x − 1 2 = − 3 4 1 4 x − 1 2 = − 3 4
3 4 x − 1 2 = 1 4 3 4 x − 1 2 = 1 4
5 6 y − 2 3 = − 3 2 5 6 y − 2 3 = − 3 2
5 6 y − 1 3 = − 7 6 5 6 y − 1 3 = − 7 6
1 2 a + 3 8 = 3 4 1 2 a + 3 8 = 3 4
5 8 b + 1 2 = − 3 4 5 8 b + 1 2 = − 3 4
2 = 1 3 x − 1 2 x + 2 3 x 2 = 1 3 x − 1 2 x + 2 3 x
2 = 3 5 x − 1 3 x + 2 5 x 2 = 3 5 x − 1 3 x + 2 5 x
1 3 w + 5 4 = w − 1 4 1 3 w + 5 4 = w − 1 4
1 2 a − 1 4 = 1 6 a + 1 12 1 2 a − 1 4 = 1 6 a + 1 12
1 3 b + 1 5 = 2 5 b − 3 5 1 3 b + 1 5 = 2 5 b − 3 5
1 3 x + 2 5 = 1 5 x − 2 5 1 3 x + 2 5 = 1 5 x − 2 5
1 4 ( p − 7 ) = 1 3 ( p + 5 ) 1 4 ( p − 7 ) = 1 3 ( p + 5 )
1 5 ( q + 3 ) = 1 2 ( q − 3 ) 1 5 ( q + 3 ) = 1 2 ( q − 3 )
1 2 ( x + 4 ) = 3 4 1 2 ( x + 4 ) = 3 4
1 3 ( x + 5 ) = 5 6 1 3 ( x + 5 ) = 5 6
4 n + 8 4 = n 3 4 n + 8 4 = n 3
3 p + 6 3 = p 2 3 p + 6 3 = p 2
3 x + 4 2 + 1 = 5 x + 10 8 3 x + 4 2 + 1 = 5 x + 10 8
10 y − 2 3 + 3 = 10 y + 1 9 10 y − 2 3 + 3 = 10 y + 1 9
7 u − 1 4 − 1 = 4 u + 8 5 7 u − 1 4 − 1 = 4 u + 8 5
3 v − 6 2 + 5 = 11 v − 4 5 3 v − 6 2 + 5 = 11 v − 4 5
In the following exercises, solve each equation with decimal coefficients.
0.4 x + 0.6 = 0.5 x − 1.2 0.4 x + 0.6 = 0.5 x − 1.2
0.7 x + 0.4 = 0.6 x + 2.4 0.7 x + 0.4 = 0.6 x + 2.4
0.9 x − 1.25 = 0.75 x + 1.75 0.9 x − 1.25 = 0.75 x + 1.75
1.2 x − 0.91 = 0.8 x + 2.29 1.2 x − 0.91 = 0.8 x + 2.29
0.05 n + 0.10 ( n + 8 ) = 2.15 0.05 n + 0.10 ( n + 8 ) = 2.15
0.05 n + 0.10 ( n + 7 ) = 3.55 0.05 n + 0.10 ( n + 7 ) = 3.55
0.10 d + 0.25 ( d + 5 ) = 4.05 0.10 d + 0.25 ( d + 5 ) = 4.05
0.10 d + 0.25 ( d + 7 ) = 5.25 0.10 d + 0.25 ( d + 7 ) = 5.25
Everyday Math
Fencing Micah has 74 feet of fencing to make a dog run in his yard. He wants the length to be 2.5 feet more than the width. Find the length, L , by solving the equation 2 L + 2 ( L − 2.5 ) = 74 . 2 L + 2 ( L − 2.5 ) = 74 .
Stamps Paula bought $22.82 worth of 49-cent stamps and 21-cent stamps. The number of 21-cent stamps was eight less than the number of 49-cent stamps. Solve the equation 0.49 s + 0.21 ( s − 8 ) = 22.82 0.49 s + 0.21 ( s − 8 ) = 22.82 for s , to find the number of 49-cent stamps Paula bought.
Writing Exercises
Using your own words, list the steps in the general strategy for solving linear equations.
Explain why you should simplify both sides of an equation as much as possible before collecting the variable terms to one side and the constant terms to the other side.
What is the first step you take when solving the equation 3 − 7 ( y − 4 ) = 38 ? 3 − 7 ( y − 4 ) = 38 ? Why is this your first step?
If an equation has several fractions, how does multiplying both sides by the LCD make it easier to solve?
If an equation has fractions only on one side, why do you have to multiply both sides of the equation by the LCD?
For the equation 0.35 x + 2.1 = 3.85 , 0.35 x + 2.1 = 3.85 , how do you clear the decimal?
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
ⓑ If most of your checks were:
…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.
…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Whom can you ask for help?Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?
…no - I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
- Authors: Lynn Marecek, Andrea Honeycutt Mathis
- Publisher/website: OpenStax
- Book title: Intermediate Algebra 2e
- Publication date: May 6, 2020
- Location: Houston, Texas
- Book URL: https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
- Section URL: https://openstax.org/books/intermediate-algebra-2e/pages/2-1-use-a-general-strategy-to-solve-linear-equations
© Jul 24, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
How to improve your problem solving skills and build effective problem solving strategies

Design your next session with SessionLab
Join the 150,000+ facilitators using SessionLab.
Recommended Articles
A step-by-step guide to planning a workshop, 54 great online tools for workshops and meetings, how to create an unforgettable training session in 8 simple steps.
- 18 Free Facilitation Resources We Think You’ll Love
Effective problem solving is all about using the right process and following a plan tailored to the issue at hand. Recognizing your team or organization has an issue isn’t enough to come up with effective problem solving strategies.
To truly understand a problem and develop appropriate solutions, you will want to follow a solid process, follow the necessary problem solving steps, and bring all of your problem solving skills to the table. We’ll forst look at what problem solving strategies you can employ with your team when looking for a way to approach the process. We’ll then discuss the problem solving skills you need to be more effective at solving problems, complete with an activity from the SessionLab library you can use to develop that skill in your team.
Let’s get to it!
Problem solving strategies
What skills do i need to be an effective problem solver, how can i improve my problem solving skills.
Problem solving strategies are methods of approaching and facilitating the process of problem-solving with a set of techniques , actions, and processes. Different strategies are more effective if you are trying to solve broad problems such as achieving higher growth versus more focused problems like, how do we improve our customer onboarding process?
Broadly, the problem solving steps outlined above should be included in any problem solving strategy though choosing where to focus your time and what approaches should be taken is where they begin to differ. You might find that some strategies ask for the problem identification to be done prior to the session or that everything happens in the course of a one day workshop.
The key similarity is that all good problem solving strategies are structured and designed. Four hours of open discussion is never going to be as productive as a four-hour workshop designed to lead a group through a problem solving process.
Good problem solving strategies are tailored to the team, organization and problem you will be attempting to solve. Here are some example problem solving strategies you can learn from or use to get started.
Use a workshop to lead a team through a group process
Often, the first step to solving problems or organizational challenges is bringing a group together effectively. Most teams have the tools, knowledge, and expertise necessary to solve their challenges – they just need some guidance in how to use leverage those skills and a structure and format that allows people to focus their energies.
Facilitated workshops are one of the most effective ways of solving problems of any scale. By designing and planning your workshop carefully, you can tailor the approach and scope to best fit the needs of your team and organization.
Problem solving workshop
- Creating a bespoke, tailored process
- Tackling problems of any size
- Building in-house workshop ability and encouraging their use
Workshops are an effective strategy for solving problems. By using tried and test facilitation techniques and methods, you can design and deliver a workshop that is perfectly suited to the unique variables of your organization. You may only have the capacity for a half-day workshop and so need a problem solving process to match.
By using our session planner tool and importing methods from our library of 700+ facilitation techniques, you can create the right problem solving workshop for your team. It might be that you want to encourage creative thinking or look at things from a new angle to unblock your groups approach to problem solving. By tailoring your workshop design to the purpose, you can help ensure great results.
One of the main benefits of a workshop is the structured approach to problem solving. Not only does this mean that the workshop itself will be successful, but many of the methods and techniques will help your team improve their working processes outside of the workshop.
We believe that workshops are one of the best tools you can use to improve the way your team works together. Start with a problem solving workshop and then see what team building, culture or design workshops can do for your organization!
Run a design sprint
Great for:
- aligning large, multi-discipline teams
- quickly designing and testing solutions
- tackling large, complex organizational challenges and breaking them down into smaller tasks
By using design thinking principles and methods, a design sprint is a great way of identifying, prioritizing and prototyping solutions to long term challenges that can help solve major organizational problems with quick action and measurable results.
Some familiarity with design thinking is useful, though not integral, and this strategy can really help a team align if there is some discussion around which problems should be approached first.
The stage-based structure of the design sprint is also very useful for teams new to design thinking. The inspiration phase, where you look to competitors that have solved your problem, and the rapid prototyping and testing phases are great for introducing new concepts that will benefit a team in all their future work.
It can be common for teams to look inward for solutions and so looking to the market for solutions you can iterate on can be very productive. Instilling an agile prototyping and testing mindset can also be great when helping teams move forwards – generating and testing solutions quickly can help save time in the long run and is also pretty exciting!
Break problems down into smaller issues
Organizational challenges and problems are often complicated and large scale in nature. Sometimes, trying to resolve such an issue in one swoop is simply unachievable or overwhelming. Try breaking down such problems into smaller issues that you can work on step by step. You may not be able to solve the problem of churning customers off the bat, but you can work with your team to identify smaller effort but high impact elements and work on those first.
This problem solving strategy can help a team generate momentum, prioritize and get some easy wins. It’s also a great strategy to employ with teams who are just beginning to learn how to approach the problem solving process. If you want some insight into a way to employ this strategy, we recommend looking at our design sprint template below!
Use guiding frameworks or try new methodologies
Some problems are best solved by introducing a major shift in perspective or by using new methodologies that encourage your team to think differently.
Props and tools such as Methodkit , which uses a card-based toolkit for facilitation, or Lego Serious Play can be great ways to engage your team and find an inclusive, democratic problem solving strategy. Remember that play and creativity are great tools for achieving change and whatever the challenge, engaging your participants can be very effective where other strategies may have failed.
LEGO Serious Play
- Improving core problem solving skills
- Thinking outside of the box
- Encouraging creative solutions
LEGO Serious Play is a problem solving methodology designed to get participants thinking differently by using 3D models and kinesthetic learning styles. By physically building LEGO models based on questions and exercises, participants are encouraged to think outside of the box and create their own responses.
Collaborate LEGO Serious Play exercises are also used to encourage communication and build problem solving skills in a group. By using this problem solving process, you can often help different kinds of learners and personality types contribute and unblock organizational problems with creative thinking.
Problem solving strategies like LEGO Serious Play are super effective at helping a team solve more skills-based problems such as communication between teams or a lack of creative thinking. Some problems are not suited to LEGO Serious Play and require a different problem solving strategy.

Card Decks and Method Kits
- New facilitators or non-facilitators
- Approaching difficult subjects with a simple, creative framework
- Engaging those with varied learning styles
Card decks and method kids are great tools for those new to facilitation or for whom facilitation is not the primary role. Card decks such as the emotional culture deck can be used for complete workshops and in many cases, can be used right out of the box. Methodkit has a variety of kits designed for scenarios ranging from personal development through to personas and global challenges so you can find the right deck for your particular needs.
Having an easy to use framework that encourages creativity or a new approach can take some of the friction or planning difficulties out of the workshop process and energize a team in any setting. Simplicity is the key with these methods. By ensuring everyone on your team can get involved and engage with the process as quickly as possible can really contribute to the success of your problem solving strategy.
Source external advice
Looking to peers, experts and external facilitators can be a great way of approaching the problem solving process. Your team may not have the necessary expertise, insights of experience to tackle some issues, or you might simply benefit from a fresh perspective. Some problems may require bringing together an entire team, and coaching managers or team members individually might be the right approach. Remember that not all problems are best resolved in the same manner.
If you’re a solo entrepreneur, peer groups, coaches and mentors can also be invaluable at not only solving specific business problems, but in providing a support network for resolving future challenges. One great approach is to join a Mastermind Group and link up with like-minded individuals and all grow together. Remember that however you approach the sourcing of external advice, do so thoughtfully, respectfully and honestly. Reciprocate where you can and prepare to be surprised by just how kind and helpful your peers can be!
Mastermind Group
- Solo entrepreneurs or small teams with low capacity
- Peer learning and gaining outside expertise
- Getting multiple external points of view quickly
Problem solving in large organizations with lots of skilled team members is one thing, but how about if you work for yourself or in a very small team without the capacity to get the most from a design sprint or LEGO Serious Play session?
A mastermind group – sometimes known as a peer advisory board – is where a group of people come together to support one another in their own goals, challenges, and businesses. Each participant comes to the group with their own purpose and the other members of the group will help them create solutions, brainstorm ideas, and support one another.
Mastermind groups are very effective in creating an energized, supportive atmosphere that can deliver meaningful results. Learning from peers from outside of your organization or industry can really help unlock new ways of thinking and drive growth. Access to the experience and skills of your peers can be invaluable in helping fill the gaps in your own ability, particularly in young companies.
A mastermind group is a great solution for solo entrepreneurs, small teams, or for organizations that feel that external expertise or fresh perspectives will be beneficial for them. It is worth noting that Mastermind groups are often only as good as the participants and what they can bring to the group. Participants need to be committed, engaged and understand how to work in this context.
Coaching and mentoring
- Focused learning and development
- Filling skills gaps
- Working on a range of challenges over time
Receiving advice from a business coach or building a mentor/mentee relationship can be an effective way of resolving certain challenges. The one-to-one format of most coaching and mentor relationships can really help solve the challenges those individuals are having and benefit the organization as a result.
A great mentor can be invaluable when it comes to spotting potential problems before they arise and coming to understand a mentee very well has a host of other business benefits. You might run an internal mentorship program to help develop your team’s problem solving skills and strategies or as part of a large learning and development program. External coaches can also be an important part of your problem solving strategy, filling skills gaps for your management team or helping with specific business issues.
Now we’ve explored the problem solving process and the steps you will want to go through in order to have an effective session, let’s look at the skills you and your team need to be more effective problem solvers.
Problem solving skills are highly sought after, whatever industry or team you work in. Organizations are keen to employ people who are able to approach problems thoughtfully and find strong, realistic solutions. Whether you are a facilitator , a team leader or a developer, being an effective problem solver is a skill you’ll want to develop.
Problem solving skills form a whole suite of techniques and approaches that an individual uses to not only identify problems but to discuss them productively before then developing appropriate solutions.
Here are some of the most important problem solving skills everyone from executives to junior staff members should learn. We’ve also included an activity or exercise from the SessionLab library that can help you and your team develop that skill.
If you’re running a workshop or training session to try and improve problem solving skills in your team, try using these methods to supercharge your process!
Active listening
Active listening is one of the most important skills anyone who works with people can possess. In short, active listening is a technique used to not only better understand what is being said by an individual, but also to be more aware of the underlying message the speaker is trying to convey. When it comes to problem solving, active listening is integral for understanding the position of every participant and to clarify the challenges, ideas and solutions they bring to the table.
Some active listening skills include:
- Paying complete attention to the speaker.
- Removing distractions.
- Avoid interruption.
- Taking the time to fully understand before preparing a rebuttal.
- Responding respectfully and appropriately.
- Demonstrate attentiveness and positivity with an open posture, making eye contact with the speaker, smiling and nodding if appropriate. Show that you are listening and encourage them to continue.
- Be aware of and respectful of feelings. Judge the situation and respond appropriately. You can disagree without being disrespectful.
- Observe body language.
- Paraphrase what was said in your own words, either mentally or verbally.
- Remain neutral.
- Reflect and take a moment before responding.
- Ask deeper questions based on what is said and clarify points where necessary.
Active Listening #hyperisland #skills #active listening #remote-friendly This activity supports participants to reflect on a question and generate their own solutions using simple principles of active listening and peer coaching. It’s an excellent introduction to active listening but can also be used with groups that are already familiar with it. Participants work in groups of three and take turns being: “the subject”, the listener, and the observer.
Analytical skills
All problem solving models require strong analytical skills, particularly during the beginning of the process and when it comes to analyzing how solutions have performed.
Analytical skills are primarily focused on performing an effective analysis by collecting, studying and parsing data related to a problem or opportunity.
It often involves spotting patterns, being able to see things from different perspectives and using observable facts and data to make suggestions or produce insight.
Analytical skills are also important at every stage of the problem solving process and by having these skills, you can ensure that any ideas or solutions you create or backed up analytically and have been sufficiently thought out.
Nine Whys #innovation #issue analysis #liberating structures With breathtaking simplicity, you can rapidly clarify for individuals and a group what is essentially important in their work. You can quickly reveal when a compelling purpose is missing in a gathering and avoid moving forward without clarity. When a group discovers an unambiguous shared purpose, more freedom and more responsibility are unleashed. You have laid the foundation for spreading and scaling innovations with fidelity.
Collaboration
Trying to solve problems on your own is difficult. Being able to collaborate effectively, with a free exchange of ideas, to delegate and be a productive member of a team is hugely important to all problem solving strategies.
Remember that whatever your role, collaboration is integral, and in a problem solving process, you are all working together to find the best solution for everyone.
Marshmallow challenge with debriefing #teamwork #team #leadership #collaboration In eighteen minutes, teams must build the tallest free-standing structure out of 20 sticks of spaghetti, one yard of tape, one yard of string, and one marshmallow. The marshmallow needs to be on top. The Marshmallow Challenge was developed by Tom Wujec, who has done the activity with hundreds of groups around the world. Visit the Marshmallow Challenge website for more information. This version has an extra debriefing question added with sample questions focusing on roles within the team.
Communication
Being an effective communicator means being empathetic, clear and succinct, asking the right questions, and demonstrating active listening skills throughout any discussion or meeting.
In a problem solving setting, you need to communicate well in order to progress through each stage of the process effectively. As a team leader, it may also fall to you to facilitate communication between parties who may not see eye to eye. Effective communication also means helping others to express themselves and be heard in a group.
Bus Trip #feedback #communication #appreciation #closing #thiagi #team This is one of my favourite feedback games. I use Bus Trip at the end of a training session or a meeting, and I use it all the time. The game creates a massive amount of energy with lots of smiles, laughs, and sometimes even a teardrop or two.
Creative problem solving skills can be some of the best tools in your arsenal. Thinking creatively, being able to generate lots of ideas and come up with out of the box solutions is useful at every step of the process.
The kinds of problems you will likely discuss in a problem solving workshop are often difficult to solve, and by approaching things in a fresh, creative manner, you can often create more innovative solutions.
Having practical creative skills is also a boon when it comes to problem solving. If you can help create quality design sketches and prototypes in record time, it can help bring a team to alignment more quickly or provide a base for further iteration.
The paper clip method #sharing #creativity #warm up #idea generation #brainstorming The power of brainstorming. A training for project leaders, creativity training, and to catalyse getting new solutions.
Critical thinking
Critical thinking is one of the fundamental problem solving skills you’ll want to develop when working on developing solutions. Critical thinking is the ability to analyze, rationalize and evaluate while being aware of personal bias, outlying factors and remaining open-minded.
Defining and analyzing problems without deploying critical thinking skills can mean you and your team go down the wrong path. Developing solutions to complex issues requires critical thinking too – ensuring your team considers all possibilities and rationally evaluating them.
Agreement-Certainty Matrix #issue analysis #liberating structures #problem solving You can help individuals or groups avoid the frequent mistake of trying to solve a problem with methods that are not adapted to the nature of their challenge. The combination of two questions makes it possible to easily sort challenges into four categories: simple, complicated, complex , and chaotic . A problem is simple when it can be solved reliably with practices that are easy to duplicate. It is complicated when experts are required to devise a sophisticated solution that will yield the desired results predictably. A problem is complex when there are several valid ways to proceed but outcomes are not predictable in detail. Chaotic is when the context is too turbulent to identify a path forward. A loose analogy may be used to describe these differences: simple is like following a recipe, complicated like sending a rocket to the moon, complex like raising a child, and chaotic is like the game “Pin the Tail on the Donkey.” The Liberating Structures Matching Matrix in Chapter 5 can be used as the first step to clarify the nature of a challenge and avoid the mismatches between problems and solutions that are frequently at the root of chronic, recurring problems.
Data analysis
Though it shares lots of space with general analytical skills, data analysis skills are something you want to cultivate in their own right in order to be an effective problem solver.
Being good at data analysis doesn’t just mean being able to find insights from data, but also selecting the appropriate data for a given issue, interpreting it effectively and knowing how to model and present that data. Depending on the problem at hand, it might also include a working knowledge of specific data analysis tools and procedures.
Having a solid grasp of data analysis techniques is useful if you’re leading a problem solving workshop but if you’re not an expert, don’t worry. Bring people into the group who has this skill set and help your team be more effective as a result.
Decision making
All problems need a solution and all solutions require that someone make the decision to implement them. Without strong decision making skills, teams can become bogged down in discussion and less effective as a result.
Making decisions is a key part of the problem solving process. It’s important to remember that decision making is not restricted to the leadership team. Every staff member makes decisions every day and developing these skills ensures that your team is able to solve problems at any scale. Remember that making decisions does not mean leaping to the first solution but weighing up the options and coming to an informed, well thought out solution to any given problem that works for the whole team.
Lightning Decision Jam (LDJ) #action #decision making #problem solving #issue analysis #innovation #design #remote-friendly The problem with anything that requires creative thinking is that it’s easy to get lost—lose focus and fall into the trap of having useless, open-ended, unstructured discussions. Here’s the most effective solution I’ve found: Replace all open, unstructured discussion with a clear process. What to use this exercise for: Anything which requires a group of people to make decisions, solve problems or discuss challenges. It’s always good to frame an LDJ session with a broad topic, here are some examples: The conversion flow of our checkout Our internal design process How we organise events Keeping up with our competition Improving sales flow
Dependability
Most complex organizational problems require multiple people to be involved in delivering the solution. Ensuring that the team and organization can depend on you to take the necessary actions and communicate where necessary is key to ensuring problems are solved effectively.
Being dependable also means working to deadlines and to brief. It is often a matter of creating trust in a team so that everyone can depend on one another to complete the agreed actions in the agreed time frame so that the team can move forward together. Being undependable can create problems of friction and can limit the effectiveness of your solutions so be sure to bear this in mind throughout a project.
Team Purpose & Culture #team #hyperisland #culture #remote-friendly This is an essential process designed to help teams define their purpose (why they exist) and their culture (how they work together to achieve that purpose). Defining these two things will help any team to be more focused and aligned. With support of tangible examples from other companies, the team members work as individuals and a group to codify the way they work together. The goal is a visual manifestation of both the purpose and culture that can be put up in the team’s work space.
Emotional intelligence
Emotional intelligence is an important skill for any successful team member, whether communicating internally or with clients or users. In the problem solving process, emotional intelligence means being attuned to how people are feeling and thinking, communicating effectively and being self-aware of what you bring to a room.
There are often differences of opinion when working through problem solving processes, and it can be easy to let things become impassioned or combative. Developing your emotional intelligence means being empathetic to your colleagues and managing your own emotions throughout the problem and solution process. Be kind, be thoughtful and put your points across care and attention.
Being emotionally intelligent is a skill for life and by deploying it at work, you can not only work efficiently but empathetically. Check out the emotional culture workshop template for more!
Facilitation
As we’ve clarified in our facilitation skills post, facilitation is the art of leading people through processes towards agreed-upon objectives in a manner that encourages participation, ownership, and creativity by all those involved. While facilitation is a set of interrelated skills in itself, the broad definition of facilitation can be invaluable when it comes to problem solving. Leading a team through a problem solving process is made more effective if you improve and utilize facilitation skills – whether you’re a manager, team leader or external stakeholder.
The Six Thinking Hats #creative thinking #meeting facilitation #problem solving #issue resolution #idea generation #conflict resolution The Six Thinking Hats are used by individuals and groups to separate out conflicting styles of thinking. They enable and encourage a group of people to think constructively together in exploring and implementing change, rather than using argument to fight over who is right and who is wrong.
Flexibility
Being flexible is a vital skill when it comes to problem solving. This does not mean immediately bowing to pressure or changing your opinion quickly: instead, being flexible is all about seeing things from new perspectives, receiving new information and factoring it into your thought process.
Flexibility is also important when it comes to rolling out solutions. It might be that other organizational projects have greater priority or require the same resources as your chosen solution. Being flexible means understanding needs and challenges across the team and being open to shifting or arranging your own schedule as necessary. Again, this does not mean immediately making way for other projects. It’s about articulating your own needs, understanding the needs of others and being able to come to a meaningful compromise.
The Creativity Dice #creativity #problem solving #thiagi #issue analysis Too much linear thinking is hazardous to creative problem solving. To be creative, you should approach the problem (or the opportunity) from different points of view. You should leave a thought hanging in mid-air and move to another. This skipping around prevents premature closure and lets your brain incubate one line of thought while you consciously pursue another.
Working in any group can lead to unconscious elements of groupthink or situations in which you may not wish to be entirely honest. Disagreeing with the opinions of the executive team or wishing to save the feelings of a coworker can be tricky to navigate, but being honest is absolutely vital when to comes to developing effective solutions and ensuring your voice is heard.
Remember that being honest does not mean being brutally candid. You can deliver your honest feedback and opinions thoughtfully and without creating friction by using other skills such as emotional intelligence.
Explore your Values #hyperisland #skills #values #remote-friendly Your Values is an exercise for participants to explore what their most important values are. It’s done in an intuitive and rapid way to encourage participants to follow their intuitive feeling rather than over-thinking and finding the “correct” values. It is a good exercise to use to initiate reflection and dialogue around personal values.
Initiative
The problem solving process is multi-faceted and requires different approaches at certain points of the process. Taking initiative to bring problems to the attention of the team, collect data or lead the solution creating process is always valuable. You might even roadtest your own small scale solutions or brainstorm before a session. Taking initiative is particularly effective if you have good deal of knowledge in that area or have ownership of a particular project and want to get things kickstarted.
That said, be sure to remember to honor the process and work in service of the team. If you are asked to own one part of the problem solving process and you don’t complete that task because your initiative leads you to work on something else, that’s not an effective method of solving business challenges.
15% Solutions #action #liberating structures #remote-friendly You can reveal the actions, however small, that everyone can do immediately. At a minimum, these will create momentum, and that may make a BIG difference. 15% Solutions show that there is no reason to wait around, feel powerless, or fearful. They help people pick it up a level. They get individuals and the group to focus on what is within their discretion instead of what they cannot change. With a very simple question, you can flip the conversation to what can be done and find solutions to big problems that are often distributed widely in places not known in advance. Shifting a few grains of sand may trigger a landslide and change the whole landscape.
Impartiality
A particularly useful problem solving skill for product owners or managers is the ability to remain impartial throughout much of the process. In practice, this means treating all points of view and ideas brought forward in a meeting equally and ensuring that your own areas of interest or ownership are not favored over others.
There may be a stage in the process where a decision maker has to weigh the cost and ROI of possible solutions against the company roadmap though even then, ensuring that the decision made is based on merit and not personal opinion.
Empathy map #frame insights #create #design #issue analysis An empathy map is a tool to help a design team to empathize with the people they are designing for. You can make an empathy map for a group of people or for a persona. To be used after doing personas when more insights are needed.
Being a good leader means getting a team aligned, energized and focused around a common goal. In the problem solving process, strong leadership helps ensure that the process is efficient, that any conflicts are resolved and that a team is managed in the direction of success.
It’s common for managers or executives to assume this role in a problem solving workshop, though it’s important that the leader maintains impartiality and does not bulldoze the group in a particular direction. Remember that good leadership means working in service of the purpose and team and ensuring the workshop is a safe space for employees of any level to contribute. Take a look at our leadership games and activities post for more exercises and methods to help improve leadership in your organization.
Leadership Pizza #leadership #team #remote-friendly This leadership development activity offers a self-assessment framework for people to first identify what skills, attributes and attitudes they find important for effective leadership, and then assess their own development and initiate goal setting.
In the context of problem solving, mediation is important in keeping a team engaged, happy and free of conflict. When leading or facilitating a problem solving workshop, you are likely to run into differences of opinion. Depending on the nature of the problem, certain issues may be brought up that are emotive in nature.
Being an effective mediator means helping those people on either side of such a divide are heard, listen to one another and encouraged to find common ground and a resolution. Mediating skills are useful for leaders and managers in many situations and the problem solving process is no different.
Conflict Responses #hyperisland #team #issue resolution A workshop for a team to reflect on past conflicts, and use them to generate guidelines for effective conflict handling. The workshop uses the Thomas-Killman model of conflict responses to frame a reflective discussion. Use it to open up a discussion around conflict with a team.
Planning
Solving organizational problems is much more effective when following a process or problem solving model. Planning skills are vital in order to structure, deliver and follow-through on a problem solving workshop and ensure your solutions are intelligently deployed.
Planning skills include the ability to organize tasks and a team, plan and design the process and take into account any potential challenges. Taking the time to plan carefully can save time and frustration later in the process and is valuable for ensuring a team is positioned for success.
3 Action Steps #hyperisland #action #remote-friendly This is a small-scale strategic planning session that helps groups and individuals to take action toward a desired change. It is often used at the end of a workshop or programme. The group discusses and agrees on a vision, then creates some action steps that will lead them towards that vision. The scope of the challenge is also defined, through discussion of the helpful and harmful factors influencing the group.
Prioritization
As organisations grow, the scale and variation of problems they face multiplies. Your team or is likely to face numerous challenges in different areas and so having the skills to analyze and prioritize becomes very important, particularly for those in leadership roles.
A thorough problem solving process is likely to deliver multiple solutions and you may have several different problems you wish to solve simultaneously. Prioritization is the ability to measure the importance, value, and effectiveness of those possible solutions and choose which to enact and in what order. The process of prioritization is integral in ensuring the biggest challenges are addressed with the most impactful solutions.
Impact and Effort Matrix #gamestorming #decision making #action #remote-friendly In this decision-making exercise, possible actions are mapped based on two factors: effort required to implement and potential impact. Categorizing ideas along these lines is a useful technique in decision making, as it obliges contributors to balance and evaluate suggested actions before committing to them.
Project management
Some problem solving skills are utilized in a workshop or ideation phases, while others come in useful when it comes to decision making. Overseeing an entire problem solving process and ensuring its success requires strong project management skills.
While project management incorporates many of the other skills listed here, it is important to note the distinction of considering all of the factors of a project and managing them successfully. Being able to negotiate with stakeholders, manage tasks, time and people, consider costs and ROI, and tie everything together is massively helpful when going through the problem solving process.
Record keeping
Working out meaningful solutions to organizational challenges is only one part of the process. Thoughtfully documenting and keeping records of each problem solving step for future consultation is important in ensuring efficiency and meaningful change.
For example, some problems may be lower priority than others but can be revisited in the future. If the team has ideated on solutions and found some are not up to the task, record those so you can rule them out and avoiding repeating work. Keeping records of the process also helps you improve and refine your problem solving model next time around!
Personal Kanban #gamestorming #action #agile #project planning Personal Kanban is a tool for organizing your work to be more efficient and productive. It is based on agile methods and principles.
Research skills
Conducting research to support both the identification of problems and the development of appropriate solutions is important for an effective process. Knowing where to go to collect research, how to conduct research efficiently, and identifying pieces of research are relevant are all things a good researcher can do well.
In larger groups, not everyone has to demonstrate this ability in order for a problem solving workshop to be effective. That said, having people with research skills involved in the process, particularly if they have existing area knowledge, can help ensure the solutions that are developed with data that supports their intention. Remember that being able to deliver the results of research efficiently and in a way the team can easily understand is also important. The best data in the world is only as effective as how it is delivered and interpreted.
Customer experience map #ideation #concepts #research #design #issue analysis #remote-friendly Customer experience mapping is a method of documenting and visualizing the experience a customer has as they use the product or service. It also maps out their responses to their experiences. To be used when there is a solution (even in a conceptual stage) that can be analyzed.
Risk management
Managing risk is an often overlooked part of the problem solving process. Solutions are often developed with the intention of reducing exposure to risk or solving issues that create risk but sometimes, great solutions are more experimental in nature and as such, deploying them needs to be carefully considered.
Managing risk means acknowledging that there may be risks associated with more out of the box solutions or trying new things, but that this must be measured against the possible benefits and other organizational factors.
Be informed, get the right data and stakeholders in the room and you can appropriately factor risk into your decision making process.
Decisions, Decisions… #communication #decision making #thiagi #action #issue analysis When it comes to decision-making, why are some of us more prone to take risks while others are risk-averse? One explanation might be the way the decision and options were presented. This exercise, based on Kahneman and Tversky’s classic study , illustrates how the framing effect influences our judgement and our ability to make decisions . The participants are divided into two groups. Both groups are presented with the same problem and two alternative programs for solving them. The two programs both have the same consequences but are presented differently. The debriefing discussion examines how the framing of the program impacted the participant’s decision.
Team-building
No single person is as good at problem solving as a team. Building an effective team and helping them come together around a common purpose is one of the most important problem solving skills, doubly so for leaders. By bringing a team together and helping them work efficiently, you pave the way for team ownership of a problem and the development of effective solutions.
In a problem solving workshop, it can be tempting to jump right into the deep end, though taking the time to break the ice, energize the team and align them with a game or exercise will pay off over the course of the day.
Remember that you will likely go through the problem solving process multiple times over an organization’s lifespan and building a strong team culture will make future problem solving more effective. It’s also great to work with people you know, trust and have fun with. Working on team building in and out of the problem solving process is a hallmark of successful teams that can work together to solve business problems.
9 Dimensions Team Building Activity #ice breaker #teambuilding #team #remote-friendly 9 Dimensions is a powerful activity designed to build relationships and trust among team members. There are 2 variations of this icebreaker. The first version is for teams who want to get to know each other better. The second version is for teams who want to explore how they are working together as a team.
Time management
The problem solving process is designed to lead a team from identifying a problem through to delivering a solution and evaluating its effectiveness. Without effective time management skills or timeboxing of tasks, it can be easy for a team to get bogged down or be inefficient.
By using a problem solving model and carefully designing your workshop, you can allocate time efficiently and trust that the process will deliver the results you need in a good timeframe.
Time management also comes into play when it comes to rolling out solutions, particularly those that are experimental in nature. Having a clear timeframe for implementing and evaluating solutions is vital for ensuring their success and being able to pivot if necessary.
Improving your skills at problem solving is often a career-long pursuit though there are methods you can use to make the learning process more efficient and to supercharge your problem solving skillset.
Remember that the skills you need to be a great problem solver have a large overlap with those skills you need to be effective in any role. Investing time and effort to develop your active listening or critical thinking skills is valuable in any context. Here are 7 ways to improve your problem solving skills.
Share best practices
Remember that your team is an excellent source of skills, wisdom, and techniques and that you should all take advantage of one another where possible. Best practices that one team has for solving problems, conducting research or making decisions should be shared across the organization. If you have in-house staff that have done active listening training or are data analysis pros, have them lead a training session.
Your team is one of your best resources. Create space and internal processes for the sharing of skills so that you can all grow together.
Ask for help and attend training
Once you’ve figured out you have a skills gap, the next step is to take action to fill that skills gap. That might be by asking your superior for training or coaching, or liaising with team members with that skill set. You might even attend specialized training for certain skills – active listening or critical thinking, for example, are business-critical skills that are regularly offered as part of a training scheme.
Whatever method you choose, remember that taking action of some description is necessary for growth. Whether that means practicing, getting help, attending training or doing some background reading, taking active steps to improve your skills is the way to go.
Learn a process
Problem solving can be complicated, particularly when attempting to solve large problems for the first time. Using a problem solving process helps give structure to your problem solving efforts and focus on creating outcomes, rather than worrying about the format.
Tools such as the seven-step problem solving process above are effective because not only do they feature steps that will help a team solve problems, they also develop skills along the way. Each step asks for people to engage with the process using different skills and in doing so, helps the team learn and grow together. Group processes of varying complexity and purpose can also be found in the SessionLab library of facilitation techniques . Using a tried and tested process and really help ease the learning curve for both those leading such a process, as well as those undergoing the purpose.
Effective teams make decisions about where they should and shouldn’t expend additional effort. By using a problem solving process, you can focus on the things that matter, rather than stumbling towards a solution haphazardly.
Create a feedback loop
Some skills gaps are more obvious than others. It’s possible that your perception of your active listening skills differs from those of your colleagues.
It’s valuable to create a system where team members can provide feedback in an ordered and friendly manner so they can all learn from one another. Only by identifying areas of improvement can you then work to improve them.
Remember that feedback systems require oversight and consideration so that they don’t turn into a place to complain about colleagues. Design the system intelligently so that you encourage the creation of learning opportunities, rather than encouraging people to list their pet peeves.
While practice might not make perfect, it does make the problem solving process easier. If you are having trouble with critical thinking, don’t shy away from doing it. Get involved where you can and stretch those muscles as regularly as possible.
Problem solving skills come more naturally to some than to others and that’s okay. Take opportunities to get involved and see where you can practice your skills in situations outside of a workshop context. Try collaborating in other circumstances at work or conduct data analysis on your own projects. You can often develop those skills you need for problem solving simply by doing them. Get involved!
Use expert exercises and methods
Learn from the best. Our library of 700+ facilitation techniques is full of activities and methods that help develop the skills you need to be an effective problem solver. Check out our templates to see how to approach problem solving and other organizational challenges in a structured and intelligent manner.
There is no single approach to improving problem solving skills, but by using the techniques employed by others you can learn from their example and develop processes that have seen proven results.
Try new ways of thinking and change your mindset
Using tried and tested exercises that you know well can help deliver results, but you do run the risk of missing out on the learning opportunities offered by new approaches. As with the problem solving process, changing your mindset can remove blockages and be used to develop your problem solving skills.
Most teams have members with mixed skill sets and specialties. Mix people from different teams and share skills and different points of view. Teach your customer support team how to use design thinking methods or help your developers with conflict resolution techniques. Try switching perspectives with facilitation techniques like Flip It! or by using new problem solving methodologies or models. Give design thinking, liberating structures or lego serious play a try if you want to try a new approach. You will find that framing problems in new ways and using existing skills in new contexts can be hugely useful for personal development and improving your skillset. It’s also a lot of fun to try new things. Give it a go!
Encountering business challenges and needing to find appropriate solutions is not unique to your organization. Lots of very smart people have developed methods, theories and approaches to help develop problem solving skills and create effective solutions. Learn from them!
Books like The Art of Thinking Clearly , Think Smarter, or Thinking Fast, Thinking Slow are great places to start, though it’s also worth looking at blogs related to organizations facing similar problems to yours, or browsing for success stories. Seeing how Dropbox massively increased growth and working backward can help you see the skills or approach you might be lacking to solve that same problem. Learning from others by reading their stories or approaches can be time-consuming but ultimately rewarding.
A tired, distracted mind is not in the best position to learn new skills. It can be tempted to burn the candle at both ends and develop problem solving skills outside of work. Absolutely use your time effectively and take opportunities for self-improvement, though remember that rest is hugely important and that without letting your brain rest, you cannot be at your most effective.
Creating distance between yourself and the problem you might be facing can also be useful. By letting an idea sit, you can find that a better one presents itself or you can develop it further. Take regular breaks when working and create a space for downtime. Remember that working smarter is preferable to working harder and that self-care is important for any effective learning or improvement process.
Want to design better group processes?
Over to you
Now we’ve explored some of the key problem solving skills and the problem solving steps necessary for an effective process, you’re ready to begin developing more effective solutions and leading problem solving workshops.
Need more inspiration? Check out our post on problem solving activities you can use when guiding a group towards a great solution in your next workshop or meeting. Have questions? Did you have a great problem solving technique you use with your team? Get in touch in the comments below. We’d love to chat!
James Smart is Head of Content at SessionLab. He’s also a creative facilitator who has run workshops and designed courses for establishments like the National Centre for Writing, UK. He especially enjoys working with young people and empowering others in their creative practice.
Leave a Comment Cancel reply
Your email address will not be published. Required fields are marked *
Going from a mere idea to a workshop that delivers results for your clients can feel like a daunting task. In this piece, we will shine a light on all the work behind the scenes and help you learn how to plan a workshop from start to finish. On a good day, facilitation can feel like effortless magic, but that is mostly the result of backstage work, foresight, and a lot of careful planning. Read on to learn a step-by-step approach to breaking the process of planning a workshop into small, manageable chunks. The flow starts with the first meeting with a client to define the purposes of a workshop.…

Effective online tools are a necessity for smooth and engaging virtual workshops and meetings. But how do you choose the right ones? Do you sometimes feel that the good old pen and paper or MS Office toolkit and email leaves you struggling to stay on top of managing and delivering your workshop? Fortunately, there are plenty of great workshop tools to make your life easier when you need to facilitate a meeting and lead workshops. In this post, we’ll share our favorite online tools you can use to make your life easier and run better workshops and meetings. In fact, there are plenty of free online workshop tools and meeting…

How does learning work? A clever 9-year-old once told me: “I know I am learning something new when I am surprised.” The science of adult learning tells us that, in order to learn new skills (which, unsurprisingly, is harder for adults to do than kids) grown-ups need to first get into a specific headspace. In a business, this approach is often employed in a training session where employees learn new skills or work on professional development. But how do you ensure your training is effective? In this guide, we'll explore how to create an effective training session plan and run engaging training sessions. As team leader, project manager, or consultant,…
Design your next workshop with SessionLab
Join the 150,000 facilitators using SessionLab
Sign up for free
Using Variable Equations as a Problem Solving Strategy
Renee Murphy
Problem solving using variable equations.
Loading ad...
- Google Classroom
- Microsoft Teams
- Download PDF

More From Forbes
Leveraging systems models: a strategic advantage for it professionals.
- Share to Facebook
- Share to Twitter
- Share to Linkedin
Thomas Lim is the Vice-Dean of Centre for Systems Leadership at SIM Academy. He is an AI+Web3 practitioner & author of Think.Coach.Thrive!
IT professionals increasingly need to navigate projects arising from greater business complexity. The integration of systems models with established methodologies, like design thinking, agile and lean, presents a unique opportunity for IT experts to enhance their capacity and expertise. This systemic integration not only enriches their problem-solving tool kits but also ensures the delivery of innovative, sustainable solutions that align with the strategic objectives of their organizations.
The landscape of IT projects has expanded beyond straightforward software development to include complex ecosystems involving artificial intelligence (AI), cloud computing, big data and more. This complexity necessitates a holistic view of project management and solution development, where understanding interdependencies and emergent behaviors becomes crucial. Systems models, with their focus on the interrelations within and among systems, offer a comprehensive framework for analyzing and addressing these complexities.
Enhancing Design Thinking With Systems Thinking
Within the Design Thinking phases, there are opportunities to embed systems thinking models. For example, during the Ideate phase, using causal loops would help clarify the Theory of Success.
Agile methodologies emphasize flexibility, rapid iteration and stakeholder collaboration. Integrating systems dynamics into agile practices allows IT professionals to model and simulate the behaviors of complex systems over time. This predictive capability can inform sprint planning, risk management and the prioritization of features based on their potential impact on the system. By understanding the feedback loops and causal relationships that drive system behavior, IT teams can anticipate challenges and opportunities, leading to more informed decision-making and effective agile implementation.
Diagnosing With The Levels Of Perspective Model
The Levels of Perspective Systems Model categorizes viewpoints from which a system can be analyzed, ranging from concrete events to deep-rooted structures and mental models. This hierarchical framework includes the Events level, Patterns of Behavior level, Structural level and, sometimes, the Mental Models level. Each level offers a unique lens through which IT developers can understand and address complex challenges.
Enhancing Design Thinking
Design thinking emphasizes empathy, collaboration and iterative learning to solve problems creatively. By applying the Levels of Perspective Model, IT developers can deepen their empathetic understanding by recognizing not only the immediate needs (Events level) but also the underlying patterns and behaviors of users (Patterns of Behavior level). This approach allows developers to design solutions that are more closely aligned with users' evolving behaviors and preferences. Additionally, considering the Structural and Mental Models levels enable developers to identify and challenge assumptions about what users need or value, leading to more innovative and user-centric solutions.
Complementing Agile Methodologies
The Levels of Perspective Model can enhance agile practices by encouraging developers to look beyond the immediate backlog of tasks (Events level) and consider the broader patterns of team dynamics and project progress (Patterns of Behavior level). This wider perspective can help in anticipating challenges and opportunities for improvement.
Stacking Systemic Choices Using The Hierarchy Of Choices
The Hierarchy of Choices model offers a structured approach to decision-making that can greatly enhance the effectiveness of IT developers. By delineating decisions across five levels—fundamental, primary, secondary, tertiary and other choices—this model provides a comprehensive framework that aligns closely with design thinking and agile and lean methodologies, enhancing developers' capacity to deliver impactful, user-centered solutions efficiently.
Fundamental Choice: The Purpose Behind Existence
At the core of every IT project is the fundamental question: Why does this project exist? This aligns with the empathetic core of design thinking, which starts with understanding the user's needs and challenges.
Primary Choice: Defining Desired Outcomes
What results does the project aim to achieve? Identifying primary choices involves setting clear, measurable goals, a principle that resonates with the outcome-focused nature of agile methodologies. For developers, defining these outcomes provides a clear direction for the project, facilitating prioritization and helping to maintain focus on delivering value to the end-users.
Secondary Choice: Crafting The Strategy
Deciding on the strategy—how the project will achieve its goals—ties into lean thinking, which emphasizes value streams and waste elimination. For IT developers, understanding the chosen strategy informs the selection of technologies, architectural patterns and development practices that align with project goals. This strategic alignment ensures that resources are optimized and efforts are directed toward activities that directly contribute to the project's objectives.
Tertiary Choice: Selecting Tactics
Tactical choices concern the specific actions taken to implement the strategy. This is where agile practices shine, offering a flexible framework for iterative development, continuous integration and regular feedback loops. Developers, by making informed tactical decisions, can adapt to changes quickly, experiment with solutions and refine their approach based on real-time feedback, all while ensuring alignment with the overarching strategy.
Finally, the model includes a broad category for other choices, encompassing the operational decisions related to the what, where, how and when of project execution.
The Road Ahead
As IT professionals strive to navigate the complexities of modern projects, the integration of systems models with traditional methodologies like design thinking, agile and lean offers a powerful synergy. This systemic integration enables a holistic understanding of complex environments, fosters innovative problem-solving and supports the agile adaptation to change. By embracing these integrated approaches, IT professionals can elevate their expertise, deliver impactful solutions and achieve strategic alignment in their projects, ensuring their role as key drivers of digital transformation.
In conclusion, the relevance of systems models in the IT domain cannot be overstated. As we advance into a future where projects become increasingly complex and interconnected, the ability to integrate and apply these models alongside established IT methodologies will be a defining skill for IT professionals. This systemic integration not only enhances their capacity to address current challenges but also positions them to lead the way in shaping the digital landscapes of tomorrow.
Forbes Coaches Council is an invitation-only community for leading business and career coaches. Do I qualify?

- Editorial Standards
- Reprints & Permissions

Case Interview Preparation
Perform at your best during your case interview., bcgers share their case study interview tips., follow these dos and don ’ ts to ace your case prep:, test your case interview skills with these interactive quizzes., set out a climate strategy for a client., restore client satisfaction at a digital bank..

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
3.7 Use a Problem-Solving Strategy
Learning Objectives
By the end of this section, you will be able to:
- Approach word problems with a positive attitude
- Use a problem-solving strategy for word problems
- Solve number problems
Approach Word Problems with a Positive Attitude
“If you think you can… or think you can’t… you’re right.”—Henry Ford
The world is full of word problems! Will my income qualify me to rent that apartment? How much punch do I need to make for the party? What size diamond can I afford to buy my girlfriend? Should I fly or drive to my family reunion?
How much money do I need to fill the car with gas? How much tip should I leave at a restaurant? How many socks should I pack for vacation? What size turkey do I need to buy for Thanksgiving dinner, and then what time do I need to put it in the oven? If my sister and I buy our mother a present, how much does each of us pay?
Now that we can solve equations, we are ready to apply our new skills to word problems. Do you know anyone who has had negative experiences in the past with word problems? Have you ever had thoughts like the student below?

When we feel we have no control, and continue repeating negative thoughts, we set up barriers to success. We need to calm our fears and change our negative feelings.
Start with a fresh slate and begin to think positive thoughts. If we take control and believe we can be successful, we will be able to master word problems! Read the positive thoughts in (Figure 2) and say them out loud.

Think of something, outside of school, that you can do now but couldn’t do 3 years ago. Is it driving a car? Snowboarding? Cooking a gourmet meal? Speaking a new language? Your past experiences with word problems happened when you were younger—now you’re older and ready to succeed!
Use a Problem-Solving Strategy for Word Problems
We have reviewed translating English phrases into algebraic expressions, using some basic mathematical vocabulary and symbols. We have also translated English sentences into algebraic equations and solved some word problems. The word problems applied math to everyday situations. We restated the situation in one sentence, assigned a variable, and then wrote an equation to solve the problem. This method works as long as the situation is familiar and the math is not too complicated.
Now, we’ll expand our strategy so we can use it to successfully solve any word problem. We’ll list the strategy here, and then we’ll use it to solve some problems. We summarize below an effective strategy for problem solving.
Use a Problem-Solving Strategy to Solve Word Problems.
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
- Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebraic equation.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
Pilar bought a purse on sale for $18, which is one-half of the original price. What was the original price of the purse?
Step 1. Read the problem. Read the problem two or more times if necessary. Look up any unfamiliar words in a dictionary or on the internet.
- In this problem, is it clear what is being discussed? Is every word familiar?
Step 2. Identify what you are looking for. Did you ever go into your bedroom to get something and then forget what you were looking for? It’s hard to find something if you are not sure what it is! Read the problem again and look for words that tell you what you are looking for!
- In this problem, the words “what was the original price of the purse” tell us what we need to find.
Step 3. Name what we are looking for. Choose a variable to represent that quantity. We can use any letter for the variable, but choose one that makes it easy to remember what it represents.
Step 4. Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Translate the English sentence into an algebraic equation.
Reread the problem carefully to see how the given information is related. Often, there is one sentence that gives this information, or it may help to write one sentence with all the important information. Look for clue words to help translate the sentence into algebra. Translate the sentence into an equation.
| Restate the problem in one sentence with all the important information. | |
| Translate into an equation. |
Step 5. Solve the equation using good algebraic techniques. Even if you know the solution right away, using good algebraic techniques here will better prepare you to solve problems that do not have obvious answers.
| Solve the equation. | |
| Multiply both sides by 2. | |
| Simplify. |
- Does $36 make sense in the problem? Yes, because 18 is one-half of 36, and the purse was on sale at half the original price.
Step 7. Answer the question with a complete sentence. The problem asked “What was the original price of the purse?”
- The answer to the question is: “The original price of the purse was $36.”
If this were a homework exercise, our work might look like this:
Pilar bought a purse on sale for $18, which is one-half the original price. What was the original price of the purse?
| Let | |
| 18 is one-half the original price. | |
| Multiply both sides by 2. | |
| Simplify. | |
| Check. Is $36 a reasonable price for a purse? | Yes. |
| Is 18 one half of 36? | |
| The original price of the purse was $36. |
Joaquin bought a bookcase on sale for $120, which was two-thirds of the original price. What was the original price of the bookcase?
Two-fifths of the songs in Mariel’s playlist are country. If there are 16 country songs, what is the total number of songs in the playlist?
Let’s try this approach with another example.
Ginny and her classmates formed a study group. The number of girls in the study group was three more than twice the number of boys. There were 11 girls in the study group. How many boys were in the study group?
| the problem. | |
| what we are looking for. | How many boys were in the study group? |
| Choose a variable to represent the number of boys. | Let |
| Restate the problem in one sentence with all the important information. |
|
| Translate into an equation. | |
| the equation. | |
| Subtract 3 from each side. | |
| Simplify. | |
| Divide each side by 2. | |
| Simplify. | |
| First, is our answer reasonable? | Yes, having 4 boys in a study group seems OK. The problem says the number of girls was 3 more than twice the number of boys. If there are four boys, does that make eleven girls? Twice 4 boys is 8. Three more than 8 is 11. |
| the question. | There were 4 boys in the study group. |
Guillermo bought textbooks and notebooks at the bookstore. The number of textbooks was 3 more than twice the number of notebooks. He bought 7 textbooks. How many notebooks did he buy?
Gerry worked Sudoku puzzles and crossword puzzles this week. The number of Sudoku puzzles he completed is eight more than twice the number of crossword puzzles. He completed 22 Sudoku puzzles. How many crossword puzzles did he do?
Solve Number Problems
Now that we have a problem solving strategy, we will use it on several different types of word problems. The first type we will work on is “number problems.” Number problems give some clues about one or more numbers. We use these clues to write an equation. Number problems don’t usually arise on an everyday basis, but they provide a good introduction to practicing the problem solving strategy outlined above.
The difference of a number and six is 13. Find the number.
| the problem. Are all the words familiar? | |
| what we are looking for. | the number |
| Choose a variable to represent the number. | Let |
| Remember to look for clue words like “difference… of… and…” | |
| Restate the problem as one sentence. | |
| Translate into an equation. | |
| the equation. | |
| Simplify. | |
| The difference of 19 and 6 is 13. It checks! | |
| the question. | The number is 19. |
The difference of a number and eight is 17. Find the number.
The sum of twice a number and seven is 15. Find the number.
| the problem. | |
| what we are looking for. | the number |
| Choose a variable to represent the number. | Let |
| Restate the problem as one sentence. |
|
| Translate into an equation. | |
| the equation. | |
| Subtract 7 from each side and simplify. | |
| Divide each side by 2 and simplify. | |
| Is the sum of twice 4 and 7 equal to 15? | |
| the question. | The number is 4. |
You may be now ready to skip some of the steps while solving such equations which is fine to do and just write down as many as you need but remember that if you write all the steps the chances of miscalculations is reduced.
The sum of four times a number and two is 14. Find the number.
The sum of three times a number and seven is 25. Find the number.
Some number word problems ask us to find two or more numbers. It may be tempting to name them all with different variables, but so far we have only solved equations with one variable. In order to avoid using more than one variable, we will define the numbers in terms of the same variable. Be sure to read the problem carefully to discover how all the numbers relate to each other.
One number is five more than another. The sum of the numbers is 21. Find the numbers.
| the problem. | |
| what we are looking for. | We are looking for two numbers. |
| We have two numbers to name and need a name for each. | |
| Choose a variable to represent the first number. | Let |
| What do we know about the second number? | One number is five more than another. |
| Restate the problem as one sentence with all the important information. | The sum of the 1 number and the 2 number is 21. |
| Translate into an equation. | |
| Substitute the variable expressions. | |
| the equation. | |
| Combine like terms. | |
| Subtract 5 from both sides and simplify. | |
| Divide by 2 and simplify. | number |
| Find the second number, too. | number |
| Do these numbers check in the problem? | |
| Is one number 5 more than the other? | |
| Is thirteen 5 more than 8? Yes. | |
| Is the sum of the two numbers 21? | |
| the question. | The numbers are 8 and 13. |
One number is six more than another. The sum of the numbers is twenty-four. Find the numbers.
The sum of two numbers is fifty-eight. One number is four more than the other. Find the numbers.
The sum of two numbers is negative fourteen. One number is four less than the other. Find the numbers.
| the problem. | |
| what we are looking for. | We are looking for two numbers. |
| Choose a variable. | Let |
| One number is 4 less than the other. | |
| Write as one sentence. | The sum of the 2 numbers is negative 14. |
| Translate into an equation. | |
| the equation. | |
| Combine like terms. | |
| Add 4 to each side and simplify. | |
| Simplify. | 1 number –> |
| 2 number–> | |
| Is −9 four less than −5? | |
| Is their sum −14? | |
| the question. | The numbers are −5 and −9. |
The sum of two numbers is negative twenty-three. One number is seven less than the other. Find the numbers.
One number is ten more than twice another. Their sum is one. Find the numbers.
| the problem. | |
| what you are looking for. | We are looking for two numbers. |
| Choose a variable. | Let |
| One number is 10 more than twice another. | |
| Restate as one sentence. | Their sum is one. |
| The sum of the two numbers is 1. | |
| Translate into an equation. | |
| the equation. | |
| Combine like terms. | |
| Subtract 10 from each side. | |
| Divide each side by 3. | 1 number –> |
| 2 number–> | |
| Is ten more than twice −3 equal to 4? | |
| Is their sum 1? | |
| the question. | The numbers are −3 and 4. |
One number is eight more than twice another. Their sum is negative four. Find the numbers.
Some number problems involve consecutive integers. Consecutive integers are integers that immediately follow each other.
Examples of consecutive integers are:

The sum of two consecutive integers is 47. Find the numbers.
| the problem. | |
| what you are looking for. | two consecutive integers |
| each number. | Let |
| Restate as one sentence. | The sum of the integers is 47. |
| Translate into an equation. | |
| the equation. | |
| Combine like terms. | |
| Subtract 1 from each side. | |
| Divide each side by 2. | 1 number –> |
| next number –> | |
| the question. | The two consecutive integers are 23 and 24. |
| the problem. | |
| what we are looking for. | three consecutive integers |
| each of the three numbers. | Let |
| consecutive integer | |
| consecutive integer | |
| Restate as one sentence. | The sum of the three integers is −42. |
| Translate into an equation. | |
| the equation. | |
| Combine like terms. Subtract 3 from each side. | |
| Divide each side by 3. | |
| 1 integer –> | |
| 2 integer–> | |
| 3rd integer–> | |
| the question. | The three consecutive integers are −13, −14, and −15. |
Now that we have worked with consecutive integers, we will expand our work to include consecutive even integers and consecutive odd integers. Consecutive even integers are even integers that immediately follow one another. Examples of consecutive even integers are:

Consecutive odd integers are odd integers that immediately follow one another. Consider the consecutive odd integers 77, 79, and 81

Does it seem strange to add 2 (an even number) to get from one odd integer to the next? Do you get an odd number or an even number when we add 2 to 3? to 11? to 47?
Whether the problem asks for consecutive even numbers or odd numbers, you don’t have to do anything different. The pattern is still the same—to get from one odd or one even integer to the next, add 2
Find three consecutive even integers whose sum is 84
| the problem. | |
| what we are looking for. | three consecutive even integers |
| the integers. | Let |
| Restate as one sentence. | The sum of the three even integers is 84. |
| Translate into an equation. | |
| the equation. | |
| Combine like terms. | |
| Subtract 6 from each side. | |
| Divide each side by 3. | |
| the question. | The three consecutive integers are 26, 28, and 30. |
TRY IT 10.1
Find three consecutive even integers whose sum is 102
TRY IT 10.2
A married couple together earns $110,000 a year. The wife earns $16,000 less than twice what her husband earns. What does the husband earn?
| the problem. | |
| what we are looking for. | How much does the husband earn? |
| . | |
| Choose a variable to represent the amount the husband earns. | Let |
| The wife earns $16,000 less than twice that. | |
| Together the husband and wife earn $110,000. | |
| Restate the problem in one sentence with all the important information. | |
| Translate into an equation. | |
| the equation. | |
| Combine like terms. | |
| Add 16,000 to both sides and simplify. | |
| Divide each side by 3. | |
| If the wife earns $68,000 and the husband earns $42,000 is the total $110,000? Yes! | |
| the question. | The husband earns $42,000 a year. |
TRY IT 11.1
According to the National Automobile Dealers Association, the average cost of a car in 2014 was 28,500. This was 1,500 less than 6 times the cost in 1975. What was the average cost of a car in 1975?
TRY IT 11.2
The Canadian Real Estate Association (CREA) data shows that the median price of new home in the Canada in December 2018 was $470,000. This was $14,000 more than 19 times the price in December 1967. What was the median price of a new home in December 1967?
$24,000
Key Concepts
- Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.

Consecutive even integers are even integers that immediately follow one another.

Consecutive odd integers are odd integers that immediately follow one another.
Practice Makes Perfect
Use the approach word problems with a positive attitude.
In the following exercises, prepare the lists described.
| 1. List five positive thoughts you can say to yourself that will help you approach word problems with a positive attitude. You may want to copy them on a sheet of paper and put it in the front of your notebook, where you can read them often. | 2. List five negative thoughts that you have said to yourself in the past that will hinder your progress on word problems. You may want to write each one on a small piece of paper and rip it up to symbolically destroy the negative thoughts. |
In the following exercises, solve using the problem solving strategy for word problems. Remember to write a complete sentence to answer each question.
| 3. Two-thirds of the children in the fourth-grade class are girls. If there are 20 girls, what is the total number of children in the class? | 4. Three-fifths of the members of the school choir are women. If there are 24 women, what is the total number of choir members? |
| 5. Zachary has 25 country music CDs, which is one-fifth of his CD collection. How many CDs does Zachary have? | 6. One-fourth of the candies in a bag of M&M’s are red. If there are 23 red candies, how many candies are in the bag? |
| 7. There are 16 girls in a school club. The number of girls is four more than twice the number of boys. Find the number of boys. | 8. There are 18 Cub Scouts in Pack 645. The number of scouts is three more than five times the number of adult leaders. Find the number of adult leaders. |
| 9. Huong is organizing paperback and hardback books for her club’s used book sale. The number of paperbacks is 12 less than three times the number of hardbacks. Huong had 162 paperbacks. How many hardback books were there? | 10. Jeff is lining up children’s and adult bicycles at the bike shop where he works. The number of children’s bicycles is nine less than three times the number of adult bicycles. There are 42 adult bicycles. How many children’s bicycles are there? |
| 11. Philip pays $1,620 in rent every month. This amount is $120 more than twice what his brother Paul pays for rent. How much does Paul pay for rent? | 12. Marc just bought an SUV for $54,000. This is $7,400 less than twice what his wife paid for her car last year. How much did his wife pay for her car? |
| 13. Laurie has $46,000 invested in stocks and bonds. The amount invested in stocks is $8,000 less than three times the amount invested in bonds. How much does Laurie have invested in bonds? | 14. Erica earned a total of $50,450 last year from her two jobs. The amount she earned from her job at the store was $1,250 more than three times the amount she earned from her job at the college. How much did she earn from her job at the college? |
In the following exercises, solve each number word problem.
| 15. The sum of a number and eight is 12. Find the number. | 16. The sum of a number and nine is 17. Find the number. |
| 17. The difference of a number and 12 is three. Find the number. | 18. The difference of a number and eight is four. Find the number. |
| 19. The sum of three times a number and eight is 23. Find the number. | 20. The sum of twice a number and six is 14. Find the number. |
| 21.The difference of twice a number and seven is 17. Find the number. | 22. The difference of four times a number and seven is 21. Find the number. |
| 23. Three times the sum of a number and nine is 12. Find the number. | 24. Six times the sum of a number and eight is 30. Find the number. |
| 25. One number is six more than the other. Their sum is 42. Find the numbers. | 26. One number is five more than the other. Their sum is 33. Find the numbers. |
| 27. The sum of two numbers is 20. One number is four less than the other. Find the numbers. | 28. The sum of two numbers is 27. One number is seven less than the other. Find the numbers. |
| 29. The sum of two numbers is | 30. The sum of two numbers is |
| 31. The sum of two numbers is | 32. The sum of two numbers is |
| 33. One number is 14 less than another. If their sum is increased by seven, the result is 85. Find the numbers. | 34. One number is 11 less than another. If their sum is increased by eight, the result is 71. Find the numbers. |
| 35. One number is five more than another. If their sum is increased by nine, the result is 60. Find the numbers. | 36. One number is eight more than another. If their sum is increased by 17, the result is 95. Find the numbers. |
| 37. One number is one more than twice another. Their sum is | 38. One number is six more than five times another. Their sum is six. Find the numbers. |
| 39. The sum of two numbers is 14. One number is two less than three times the other. Find the numbers. | 40. The sum of two numbers is zero. One number is nine less than twice the other. Find the numbers. |
| 41. The sum of two consecutive integers is 77. Find the integers. | 42. The sum of two consecutive integers is 89. Find the integers. |
| 43. The sum of two consecutive integers is | 44. The sum of two consecutive integers is |
| 45. The sum of three consecutive integers is 78. Find the integers. | 46. The sum of three consecutive integers is 60. Find the integers. |
| 47. Find three consecutive integers whose sum is | 48. Find three consecutive integers whose sum is |
| 49. Find three consecutive even integers whose sum is 258. | 50. Find three consecutive even integers whose sum is 222. |
| 51. Find three consecutive odd integers whose sum is 171. | 52. Find three consecutive odd integers whose sum is 291. |
| 53. Find three consecutive even integers whose sum is | 54. Find three consecutive even integers whose sum is |
| 55. Find three consecutive odd integers whose sum is | 56. Find three consecutive odd integers whose sum is |
Everyday Math
| 57. Patty paid $35 for a purse on sale for $10 off the original price. What was the original price of the purse? | 58. Travis bought a pair of boots on sale for $25 off the original price. He paid $60 for the boots. What was the original price of the boots? |
| 59. Minh spent $6.25 on five sticker books to give his nephews. Find the cost of each sticker book. | 60. Alicia bought a package of eight peaches for $3.20. Find the cost of each peach. |
| 61. Tom paid $1,166.40 for a new refrigerator, including $86.40 tax. What was the price of the refrigerator? | 62. Kenji paid $2,279 for a new living room set, including $129 tax. What was the price of the living room set? |
Writing Exercises
| 63. What has been your past experience solving word problems? | 64. When you start to solve a word problem, how do you decide what to let the variable represent? |
| 65. What are consecutive odd integers? Name three consecutive odd integers between 50 and 60. | 66. What are consecutive even integers? Name three consecutive even integers between |
| 1. Answers will vary | 3. 30 | 5. 125 |
| 7. 6 | 9. 58 | 11. $750 |
| 13. $13,500 | 15. 4 | 17. 15 |
| 19. 5 | 21. 12 | 23. |
| 25. 18, 24 | 27. 8, 12 | 29. |
| 31. | 33. 32, 46 | 35. 23, 28 |
| 37. | 39. 4, 10 | 41. 38, 39 |
| 43. | 45. 25, 26, 27 | 47. |
| 49. 84, 86, 88 | 51. 55, 57, 59 | 53. |
| 55. | 57. $45 | 59. $1.25 |
| 61. $1080 | 63. Answers will vary | 65. Consecutive odd integers are odd numbers that immediately follow each other. An example of three consecutive odd integers between 50 and 60 would be 51, 53, and 55. |
Attributions
This chapter has been adapted from “Use a Problem-Solving Strategy” in Elementary Algebra (OpenStax) by Lynn Marecek and MaryAnne Anthony-Smith, which is under a CC BY 4.0 Licence . Adapted by Izabela Mazur. See the Copyright page for more information.
Intermediate Algebra II Copyright © 2021 by Pooja Gupta is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.
Share This Book

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
Chapter 1.7: Use a Problem-Solving Strategy
Learning Objectives
By the end of this section, you will be able to:
- Approach word problems with a positive attitude
- Use a problem-solving strategy for word problems
- Solve number problems
Approach Word Problems with a Positive Attitude
“If you think you can… or think you can’t… you’re right.”—Henry Ford
The world is full of word problems! Will my income qualify me to rent that apartment? How much punch do I need to make for the party? What size diamond can I afford to buy my girlfriend? Should I fly or drive to my family reunion?
How much money do I need to fill the car with gas? How much tip should I leave at a restaurant? How many socks should I pack for vacation? What size turkey do I need to buy for Thanksgiving dinner, and then what time do I need to put it in the oven? If my sister and I buy our mother a present, how much does each of us pay?
Now that we can solve equations, we are ready to apply our new skills to word problems. Do you know anyone who has had negative experiences in the past with word problems? Have you ever had thoughts like the student below?

When we feel we have no control, and continue repeating negative thoughts, we set up barriers to success. We need to calm our fears and change our negative feelings.
Start with a fresh slate and begin to think positive thoughts. If we take control and believe we can be successful, we will be able to master word problems! Read the positive thoughts in (Figure 2) and say them out loud.

Think of something, outside of school, that you can do now but couldn’t do 3 years ago. Is it driving a car? Snowboarding? Cooking a gourmet meal? Speaking a new language? Your past experiences with word problems happened when you were younger—now you’re older and ready to succeed!
Use a Problem-Solving Strategy for Word Problems
We have reviewed translating English phrases into algebraic expressions, using some basic mathematical vocabulary and symbols. We have also translated English sentences into algebraic equations and solved some word problems. The word problems applied math to everyday situations. We restated the situation in one sentence, assigned a variable, and then wrote an equation to solve the problem. This method works as long as the situation is familiar and the math is not too complicated.
Now, we’ll expand our strategy so we can use it to successfully solve any word problem. We’ll list the strategy here, and then we’ll use it to solve some problems. We summarize below an effective strategy for problem solving.
Use a Problem-Solving Strategy to Solve Word Problems.
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
- Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebraic equation.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
Pilar bought a purse on sale for $18, which is one-half of the original price. What was the original price of the purse?
Step 1. Read the problem. Read the problem two or more times if necessary. Look up any unfamiliar words in a dictionary or on the internet.
- In this problem, is it clear what is being discussed? Is every word familiar?
Step 2. Identify what you are looking for. Did you ever go into your bedroom to get something and then forget what you were looking for? It’s hard to find something if you are not sure what it is! Read the problem again and look for words that tell you what you are looking for!
- In this problem, the words “what was the original price of the purse” tell us what we need to find.
Step 3. Name what we are looking for. Choose a variable to represent that quantity. We can use any letter for the variable, but choose one that makes it easy to remember what it represents.
Step 4. Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Translate the English sentence into an algebraic equation.
Reread the problem carefully to see how the given information is related. Often, there is one sentence that gives this information, or it may help to write one sentence with all the important information. Look for clue words to help translate the sentence into algebra. Translate the sentence into an equation.
| Restate the problem in one sentence with all the important information. | |
| Translate into an equation. |
Step 5. Solve the equation using good algebraic techniques. Even if you know the solution right away, using good algebraic techniques here will better prepare you to solve problems that do not have obvious answers.
| Solve the equation. | |
| Multiply both sides by 2. | |
| Simplify. |
- Does $36 make sense in the problem? Yes, because 18 is one-half of 36, and the purse was on sale at half the original price.
Step 7. Answer the question with a complete sentence. The problem asked “What was the original price of the purse?”
- The answer to the question is: “The original price of the purse was $36.”
If this were a homework exercise, our work might look like this:
Pilar bought a purse on sale for $18, which is one-half the original price. What was the original price of the purse?
| Let | |
| 18 is one-half the original price. | |
| Multiply both sides by 2. | |
| Simplify. | |
| Check. Is $36 a reasonable price for a purse? | Yes. |
| Is 18 one half of 36? | |
| The original price of the purse was $36. |
Joaquin bought a bookcase on sale for $120, which was two-thirds of the original price. What was the original price of the bookcase?
Two-fifths of the songs in Mariel’s playlist are country. If there are 16 country songs, what is the total number of songs in the playlist?
Let’s try this approach with another example.
Ginny and her classmates formed a study group. The number of girls in the study group was three more than twice the number of boys. There were 11 girls in the study group. How many boys were in the study group?
| the problem. | |
| what we are looking for. | How many boys were in the study group? |
| Choose a variable to represent the number of boys. | Let |
| Restate the problem in one sentence with all the important information. | |
| Translate into an equation. | |
| the equation. | |
| Subtract 3 from each side. | |
| Simplify. | |
| Divide each side by 2. | |
| Simplify. | |
| First, is our answer reasonable? | Yes, having 4 boys in a study group seems OK. The problem says the number of girls was 3 more than twice the number of boys. If there are four boys, does that make eleven girls? Twice 4 boys is 8. Three more than 8 is 11. |
| the question. | There were 4 boys in the study group. |
Guillermo bought textbooks and notebooks at the bookstore. The number of textbooks was 3 more than twice the number of notebooks. He bought 7 textbooks. How many notebooks did he buy?
Gerry worked Sudoku puzzles and crossword puzzles this week. The number of Sudoku puzzles he completed is eight more than twice the number of crossword puzzles. He completed 22 Sudoku puzzles. How many crossword puzzles did he do?
Solve Number Problems
Now that we have a problem solving strategy, we will use it on several different types of word problems. The first type we will work on is “number problems.” Number problems give some clues about one or more numbers. We use these clues to write an equation. Number problems don’t usually arise on an everyday basis, but they provide a good introduction to practicing the problem solving strategy outlined above.
The difference of a number and six is 13. Find the number.
| the problem. Are all the words familiar? | |
| what we are looking for. | the number |
| Choose a variable to represent the number. | Let |
| Remember to look for clue words like “difference… of… and…” | |
| Restate the problem as one sentence. | |
| Translate into an equation. | |
| the equation. | |
| Simplify. | |
| The difference of 19 and 6 is 13. It checks! | |
| the question. | The number is 19. |
The difference of a number and eight is 17. Find the number.
The sum of twice a number and seven is 15. Find the number.
| the problem. | |
| what we are looking for. | the number |
| Choose a variable to represent the number. | Let |
| Restate the problem as one sentence. | |
| Translate into an equation. | |
| the equation. | |
| Subtract 7 from each side and simplify. | |
| Divide each side by 2 and simplify. | |
| Is the sum of twice 4 and 7 equal to 15? | |
| the question. | The number is 4. |
Did you notice that we left out some of the steps as we solved this equation? If you’re not yet ready to leave out these steps, write down as many as you need.
The sum of four times a number and two is 14. Find the number.
The sum of three times a number and seven is 25. Find the number.
Some number word problems ask us to find two or more numbers. It may be tempting to name them all with different variables, but so far we have only solved equations with one variable. In order to avoid using more than one variable, we will define the numbers in terms of the same variable. Be sure to read the problem carefully to discover how all the numbers relate to each other.
One number is five more than another. The sum of the numbers is 21. Find the numbers.
| the problem. | |
| what we are looking for. | We are looking for two numbers. |
| We have two numbers to name and need a name for each. | |
| Choose a variable to represent the first number. | Let |
| What do we know about the second number? | One number is five more than another. |
| Restate the problem as one sentence with all the important information. | The sum of the 1 number and the 2 number is 21. |
| Translate into an equation. | |
| Substitute the variable expressions. | |
| the equation. | |
| Combine like terms. | |
| Subtract 5 from both sides and simplify. | |
| Divide by 2 and simplify. | |
| Find the second number, too. | |
| Do these numbers check in the problem? | |
| Is one number 5 more than the other? | |
| Is thirteen 5 more than 8? Yes. | |
| Is the sum of the two numbers 21? | |
| the question. | The numbers are 8 and 13. |
One number is six more than another. The sum of the numbers is twenty-four. Find the numbers.
The sum of two numbers is fifty-eight. One number is four more than the other. Find the numbers.
The sum of two numbers is negative fourteen. One number is four less than the other. Find the numbers.
| the problem. | |
| what we are looking for. | We are looking for two numbers. |
| Choose a variable. | Let |
| One number is 4 less than the other. | |
| Write as one sentence. | The sum of the 2 numbers is negative 14. |
| Translate into an equation. | |
| the equation. | |
| Combine like terms. | |
| Add 4 to each side and simplify. | |
| Simplify. | |
| Is −9 four less than −5? | |
| Is their sum −14? | |
| the question. | The numbers are −5 and −9. |
The sum of two numbers is negative twenty-three. One number is seven less than the other. Find the numbers.
One number is ten more than twice another. Their sum is one. Find the numbers.
| the problem. | |
| what you are looking for. | We are looking for two numbers. |
| Choose a variable. | Let |
| One number is 10 more than twice another. | |
| Restate as one sentence. | Their sum is one. |
| The sum of the two numbers is 1. | |
| Translate into an equation. | |
| the equation. | |
| Combine like terms. | |
| Subtract 10 from each side. | |
| Divide each side by 3. | |
| Is ten more than twice −3 equal to 4? | |
| Is their sum 1? | |
| the question. | The numbers are −3 and −4. |
One number is eight more than twice another. Their sum is negative four. Find the numbers.
Some number problems involve consecutive integers. Consecutive integers are integers that immediately follow each other.
Examples of consecutive integers are:
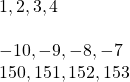
The sum of two consecutive integers is 47. Find the numbers.
| the problem. | |
| what you are looking for. | two consecutive integers |
| each number. | Let |
| Restate as one sentence. | The sum of the integers is 47. |
| Translate into an equation. | |
| the equation. | |
| Combine like terms. | |
| Subtract 1 from each side. | |
| Divide each side by 2. | |
| the question. | The two consecutive integers are 23 and 24. |
| the problem. | |
| what we are looking for. | three consecutive integers |
| each of the three numbers. | Let |
| consecutive integer | |
| consecutive integer | |
| Restate as one sentence. | The sum of the three integers is −42. |
| Translate into an equation. | |
| the equation. | |
| Combine like terms. | |
| Subtract 3 from each side. | |
| Divide each side by 3. | |
| the question. | The three consecutive integers are −13, −14, and −15. |
Now that we have worked with consecutive integers, we will expand our work to include consecutive even integers and consecutive odd integers. Consecutive even integers are even integers that immediately follow one another. Examples of consecutive even integers are:

Consecutive odd integers are odd integers that immediately follow one another. Consider the consecutive odd integers 77, 79, and 81
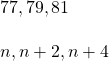
Does it seem strange to add 2 (an even number) to get from one odd integer to the next? Do you get an odd number or an even number when we add 2 to 3? to 11? to 47?
Whether the problem asks for consecutive even numbers or odd numbers, you don’t have to do anything different. The pattern is still the same—to get from one odd or one even integer to the next, add 2
Find three consecutive even integers whose sum is 84
| the problem. | |
| what we are looking for. | three consecutive even integers |
| the integers. | Let |
| Restate as one sentence. | The sume of the three even integers is 84. |
| Translate into an equation. | |
| the equation. | |
| Combine like terms. | |
| Subtract 6 from each side. | |
| Divide each side by 3. | |
| the question. | The three consecutive integers are 26, 28, and 30. |
TRY IT 10.1
Find three consecutive even integers whose sum is 102
TRY IT 10.2
A married couple together earns $110,000 a year. The wife earns $16,000 less than twice what her husband earns. What does the husband earn?
| the problem. | |
| what we are looking for. | How much does the husband earn? |
| . | |
| Choose a variable to represent the amount the husband earns. | Let |
| The wife earns $16,000 less than twice that. | |
| Together the husband and wife earn $110,000. | |
| Restate the problem in one sentence with all the important information. | |
| Translate into an equation. | |
| the equation. | h + 2h − 16,000 = 110,000 |
| Combine like terms. | |
| Add 16,000 to both sides and simplify. | |
| Divide each side by 3. | |
| If the wife earns $68,000 and the husband earns $42,000 is the total $110,000? Yes! | |
| the question. | The husband earns $42,000 a year. |
TRY IT 11.1
According to the National Automobile Dealers Association, the average cost of a car in 2014 was 28,500. This was 1,500 less than 6 times the cost in 1975. What was the average cost of a car in 1975?
TRY IT 11.2
The Canadian Real Estate Association (CREA) data shows that the median price of new home in the Canada in December 2018 was $470,000. This was $14,000 more than 19 times the price in December 1967. What was the median price of a new home in December 1967?
$24,000
Key Concepts
- Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.
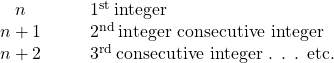
Consecutive even integers are even integers that immediately follow one another.
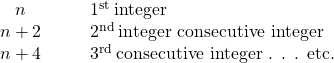
Consecutive odd integers are odd integers that immediately follow one another.
Practice Makes Perfect
Use the approach word problems with a positive attitude.
In the following exercises, prepare the lists described.
| 1. List five positive thoughts you can say to yourself that will help you approach word problems with a positive attitude. You may want to copy them on a sheet of paper and put it in the front of your notebook, where you can read them often. | 2. List five negative thoughts that you have said to yourself in the past that will hinder your progress on word problems. You may want to write each one on a small piece of paper and rip it up to symbolically destroy the negative thoughts. |
In the following exercises, solve using the problem solving strategy for word problems. Remember to write a complete sentence to answer each question.
| 3. Two-thirds of the children in the fourth-grade class are girls. If there are 20 girls, what is the total number of children in the class? | 4. Three-fifths of the members of the school choir are women. If there are 24 women, what is the total number of choir members? |
| 5. Zachary has 25 country music CDs, which is one-fifth of his CD collection. How many CDs does Zachary have? | 6. One-fourth of the candies in a bag of M&M’s are red. If there are 23 red candies, how many candies are in the bag? |
| 7. There are 16 girls in a school club. The number of girls is four more than twice the number of boys. Find the number of boys. | 8. There are 18 Cub Scouts in Pack 645. The number of scouts is three more than five times the number of adult leaders. Find the number of adult leaders. |
| 9. Huong is organizing paperback and hardback books for her club’s used book sale. The number of paperbacks is 12 less than three times the number of hardbacks. Huong had 162 paperbacks. How many hardback books were there? | 10. Jeff is lining up children’s and adult bicycles at the bike shop where he works. The number of children’s bicycles is nine less than three times the number of adult bicycles. There are 42 adult bicycles. How many children’s bicycles are there? |
| 11. Philip pays $1,620 in rent every month. This amount is $120 more than twice what his brother Paul pays for rent. How much does Paul pay for rent? | 12. Marc just bought an SUV for $54,000. This is $7,400 less than twice what his wife paid for her car last year. How much did his wife pay for her car? |
| 13. Laurie has $46,000 invested in stocks and bonds. The amount invested in stocks is $8,000 less than three times the amount invested in bonds. How much does Laurie have invested in bonds? | 14. Erica earned a total of $50,450 last year from her two jobs. The amount she earned from her job at the store was $1,250 more than three times the amount she earned from her job at the college. How much did she earn from her job at the college? |
In the following exercises, solve each number word problem.
| 15. The sum of a number and eight is 12. Find the number. | 16. The sum of a number and nine is 17. Find the number. |
| 17. The difference of a number and 12 is three. Find the number. | 18. The difference of a number and eight is four. Find the number. |
| 19. The sum of three times a number and eight is 23. Find the number. | 20. The sum of twice a number and six is 14. Find the number. |
| 21.The difference of twice a number and seven is 17. Find the number. | 22. The difference of four times a number and seven is 21. Find the number. |
| 23. Three times the sum of a number and nine is 12. Find the number. | 24. Six times the sum of a number and eight is 30. Find the number. |
| 25. One number is six more than the other. Their sum is 42. Find the numbers. | 26. One number is five more than the other. Their sum is 33. Find the numbers. |
| 27. The sum of two numbers is 20. One number is four less than the other. Find the numbers. | 28. The sum of two numbers is 27. One number is seven less than the other. Find the numbers. |
| 29. The sum of two numbers is | 30. The sum of two numbers is |
| 31. The sum of two numbers is | 32. The sum of two numbers is |
| 33. One number is 14 less than another. If their sum is increased by seven, the result is 85. Find the numbers. | 34. One number is 11 less than another. If their sum is increased by eight, the result is 71. Find the numbers. |
| 35. One number is five more than another. If their sum is increased by nine, the result is 60. Find the numbers. | 36. One number is eight more than another. If their sum is increased by 17, the result is 95. Find the numbers. |
| 37. One number is one more than twice another. Their sum is | 38. One number is six more than five times another. Their sum is six. Find the numbers. |
| 39. The sum of two numbers is 14. One number is two less than three times the other. Find the numbers. | 40. The sum of two numbers is zero. One number is nine less than twice the other. Find the numbers. |
| 41. The sum of two consecutive integers is 77. Find the integers. | 42. The sum of two consecutive integers is 89. Find the integers. |
| 43. The sum of two consecutive integers is | 44. The sum of two consecutive integers is |
| 45. The sum of three consecutive integers is 78. Find the integers. | 46. The sum of three consecutive integers is 60. Find the integers. |
| 47. Find three consecutive integers whose sum is | 48. Find three consecutive integers whose sum is |
| 49. Find three consecutive even integers whose sum is 258. | 50. Find three consecutive even integers whose sum is 222. |
| 51. Find three consecutive odd integers whose sum is 171. | 52. Find three consecutive odd integers whose sum is 291. |
| 53. Find three consecutive even integers whose sum is | 54. Find three consecutive even integers whose sum is |
| 55. Find three consecutive odd integers whose sum is | 56. Find three consecutive odd integers whose sum is |
Everyday Math
| 57. Patty paid $35 for a purse on sale for $10 off the original price. What was the original price of the purse? | 58. Travis bought a pair of boots on sale for $25 off the original price. He paid $60 for the boots. What was the original price of the boots? |
| 59. Minh spent $6.25 on five sticker books to give his nephews. Find the cost of each sticker book. | 60. Alicia bought a package of eight peaches for $3.20. Find the cost of each peach. |
| 61. Tom paid $1,166.40 for a new refrigerator, including $86.40 tax. What was the price of the refrigerator? | 62. Kenji paid $2,279 for a new living room set, including $129 tax. What was the price of the living room set? |
Writing Exercises
| 63. What has been your past experience solving word problems? | 64. When you start to solve a word problem, how do you decide what to let the variable represent? |
| 65. What are consecutive odd integers? Name three consecutive odd integers between 50 and 60. | 66. What are consecutive even integers? Name three consecutive even integers between |
| 1. Answers will vary | 3. 30 | 5. 125 |
| 7. 6 | 9. 58 | 11. $750 |
| 13. $13,500 | 15. 4 | 17. 15 |
| 19. 5 | 21. 12 | 23. |
| 25. 18, 24 | 27. 8, 12 | 29. |
| 31. | 33. 32, 46 | 35. 23, 28 |
| 37. | 39. 4, 10 | 41. 38, 39 |
| 43. | 45. 25, 26, 27 | 47. |
| 49. 84, 86, 88 | 51. 55, 57, 59 | 53. |
| 55. | 57. $45 | 59. $1.25 |
| 61. $1080 | 63. Answers will vary | 65. Consecutive odd integers are odd numbers that immediately follow each other. An example of three consecutive odd integers between 50 and 60 would be 51, 53, and 55. |
Attributions
This chapter has been adapted from “Use a Problem-Solving Strategy” in Elementary Algebra (OpenStax) by Lynn Marecek and MaryAnne Anthony-Smith, which is under a CC BY 4.0 Licence . Adapted by Izabela Mazur. See the Copyright page for more information.
Pre-Calculus Copyright © 2022 by St. Clair College is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book

IMAGES
COMMENTS
Problem Solving Strategy 3 (Using a variable to find the sum of a sequence.) Gauss's strategy for sequences. last term = fixed number (n-1) + first term. The fix number is the the amount each term is increasing or decreasing by. "n" is the number of terms you have. You can use this formula to find the last term in the sequence or the number of ...
Math in the Modern World Playlist:https://www.youtube.com/playlist?list=PLbZl6MGLeYnsoaxa2L-xouDPHcoe9z23xLearning Objective: Use variables to solve recreati...
Let p = p = the original price of the shirt. Step 4. Translate into an equation. It may help to first restate the problem in one sentence, with all the important information. Then translate the sentence into an equation. Step 5. Solve the equation using good algebra techniques.
Step 3. Name what we are looking for. Choose a variable to represent that quantity. We can use any letter for the variable, but choose one that makes it easy to remember what it represents. Step 4. Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information.
Use a Problem-Solving Strategy to Solve Word Problems. Step 1. Read the problem. Make sure all the words and ideas are understood. Step 2. Identify what we are looking for. Step 3. Name what we are looking for. Choose a variable to represent that quantity.
Use a Problem Solving Strategy for word problems. Step 1. Read the problem. Make sure all the words and ideas are understood. Step 2. Identify what you ... In order to avoid using more than one variable, we will define the numbers in terms of the same variable. Be sure to read the problem carefully to discover how all the numbers relate to each ...
Problem-Solving Strategy. Read the problem. Make sure all the words and ideas are understood. Identify what we are looking for. Name what we are looking for. Choose a variable to represent that quantity. Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information.
This method is often useful when your unkown is a numeric value. Although the problem below can be solved by using the "Guess And Test " strategy, I will solve this problem using the "Use A Variable" method, since it is more efficient in this case. Often, this method implies that there will be some degree of Algebra involved.
Use a Problem Solving Strategy for word problems. Step 1. Read the problem. Make sure all the words and ideas are understood. Step 2. Identify what you are looking for. Step 3. Name what you are looking for. Choose a variable to represent that quantity.
Apply the general problem-solving strategy to number problems; ... We will define the numbers in terms of the same variable. Be sure to read the problem carefully to discover how all the numbers relate to each other. example. One number is five more than another. The sum of the numbers is twenty-one. Find the numbers.
Problem Solving Strategy 2 (Using a variable to find the sum of a sequence.) Gauss's strategy for sequences: last term = (fixed number) (n -1) + first term. The fix number is the amount each term is increasing or decreasing by. "n" is the number of terms you have. You can use this formula to find the last term in the sequence or the number of ...
Solve Linear Equations Using a General Strategy. Solving an equation is like discovering the answer to a puzzle. The purpose in solving an equation is to find the value or values of the variable that makes it a true statement. Any value of the variable that makes the equation true is called a solution to the equation. It is the answer to the ...
2.2 Use a Solving Problem Strategy. Topics covered in this section are: Use a problem solving strategy for word problems; Solve number word problems; ... To use the formula we substitute in the values for variables that are given, and then solve for the unknown variable. It may be helpful to organize the information in a chart.
Choose a variable to represent that quantity. We can use any letter for the variable, but choose one that makes it easy to remember what it represents. Let the original price of the purse. Step 4. Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information.
5. Find a pattern. Finding a pattern is a strategy in which students look for patterns in the given information in order to solve the problem. When the problem consists of data like numbers or events that are repeated then it can be solved using the "find a pattern" problem-solving strategy.
Planning skills are vital in order to structure, deliver and follow-through on a problem solving workshop and ensure your solutions are intelligently deployed. Planning skills include the ability to organize tasks and a team, plan and design the process and take into account any potential challenges.
In general, effective problem-solving strategies include the following steps: Define the problem. Come up with alternative solutions. Decide on a solution. Implement the solution. Problem-solving ...
Use a Problem-solving Strategy for Word Problems. In earlier chapters, you translated word phrases into algebraic expressions, using some basic mathematical vocabulary and symbols. ... You can use any letter for the variable, but it may help to choose one that helps you remember what it represents. Let p = the original price of the shirt.
Live worksheets > English > Math > Algebra > Using Variable Equations as a Problem Solving Strategy. Using Variable Equations as a Problem Solving Strategy. Problem solving using variable equations. ID: 1898178. Language: English. School subject: Math. Grade/level: Grade 5. Age: 10-11. Main content: Algebra.
Enhancing Design Thinking. Design thinking emphasizes empathy, collaboration and iterative learning to solve problems creatively. By applying the Levels of Perspective Model, IT developers can ...
Case interviews help you experience the type of work we do and show off your problem-solving skills. Explore BCG's case interview preparation tools today.
If an amount of money, P, called the principal, is invested or borrowed for a period of t years at an annual interest rate r, the amount of interest, I, earned or paid is: I = interest I = Prt where P = principal r = rate t = time. 2.3: Use a Problem Solving Strategy CC BY 4.0 OpenStax source content. Now that we can solve equations, we are ...
We summarize below an effective strategy for problem solving. Use a Problem-Solving Strategy to Solve Word Problems. Read the problem. Make sure all the words and ideas are understood. Identify what we are looking for. Name what we are looking for. Choose a variable to represent that quantity.
Problem-Solving Strategy. Read the problem. Make sure all the words and ideas are understood. Identify what we are looking for. Name what we are looking for. Choose a variable to represent that quantity. Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information.
We will now apply the problem solving strategy to "number word problems." Number word problems give some clues about one or more numbers and we use these clues to write an equation. Number word problems provide good practice for using the Problem Solving Strategy.