applying free fall concepts to problem solving

• High School
• You don't have any recent items yet.
• You don't have any courses yet.
• You don't have any books yet.
• You don't have any Studylists yet.
• Information

Applying Free Fall Concepts to Problem 2

Physics basics, physical science, van nuys high school, recommended for you, students also viewed.

• Safety contract 2
• Chatper 12 - Section 3 (Working with Fluids) Notes
• 2CAEE1AA B788 4893 9174 A828CAF86A5A
• Edited - Joseth Borders - Copy of Free Fall SE
• Untitled design - It is an assignment I did for science
• Gizmos+Water+Cycle+Lab

Related documents

• Gizmos Student Exploration Worksheet
• Work - I like school
• Viusal Summary USH Explore America
• Density Lab SE - gismo
• اختلاطات التخدير
• Segment One Exam Study Guide

Preview text

Applying free fall concepts to problem-solving.

There are a few conceptual characteristics of free fall motion that will be of value when using the equations to analyze free fall motion. These concepts are described as follows:

An object in free fall experiences an acceleration of -9 m/s/s. (The - sign indicates a downward acceleration.) Whether explicitly stated or not, the value of the acceleration in the kinematic equations is -9 m/s/s for any freely falling object.

If an object is merely dropped (as opposed to being thrown) from an elevated height, then the initial velocity of the object is 0 m/s.

If an object is projected upwards in a perfectly vertical direction, then it will slow down as it rises upward. The instant at which it reaches the peak of its trajectory, its velocity is 0 m/s. This value can be used as one of the motion parameters in the kinematic equations; for example, the final velocity (vf) after traveling to the peak would be assigned a value of 0 m/s.

If an object is projected upwards in a perfectly vertical direction, then the velocity at which it is projected is equal in magnitude and opposite in sign to the velocity that it has when it returns to the same height. That is, a ball projected vertically with an upward velocity of +30 m/s will have a downward velocity of -30 m/s when it returns to the same height.

These four principles and the four kinematic equations can be combined to solve problems involving the motion of free falling objects. The two examples below illustrate application of free fall principles to kinematic problem-solving..

Example Problem A

Luke drops a pile of roof shingles from the top of a roof located 8 meters above the ground. Determine the time required for the shingles to reach the ground.

The solution to this problem begins by the construction of an informative diagram of the physical situation.

This is shown below.

The second step

involves the identification and listing of known information in variable form. You might note that in the statement of the problem, there is only one piece of numerical information explicitly stated: 8 meters. The displacement (d) of the shingles is -8. m. (The - sign indicates that the displacement is downward). The remaining information must be extracted from the problem statement based upon your understanding of the above principles. For example, the vi value can be inferred to be 0 m/s since the shingles are dropped (released from rest). And the acceleration (a) of the shingles can be inferred to be -9 m/s 2 since the shingles are free-falling). (Always pay careful attention to the + and - signs for the given quantities.)

The next step

of the solution involves the listing of the unknown (or desired) information in variable form. In this case, the problem requests information about the time of fall. So t is the unknown quantity. The results of the first three steps are shown in the table below.

Diagram: Given: Fi vi = 0 m/s d = -8 m

a = - 9 m/s 2

involves identifying a kinematic equation that allows you to determine the unknown quantity. There are four kinematic equations to choose from. In general, you will always choose the equation that contains the three known and the one unknown variable. In this specific case, the three known variables and the one unknown variable are d, vi, a, and t. Thus, you will look for an equation that has these four variables listed in it. An inspection of the four equations above reveals that the equation on the top left contains all four variables.

d = vi • t + ½ • a • t 2

Once the equation is identified and written down, the next step involves substituting known values into the equation and using proper algebraic steps to solve for the unknown information. This step is shown below.

height). So d is the unknown information. The results of the first three steps are shown in the table below.

Diagram: Given: Find:

vi = 26 m/s vf = 0 m/s

a = -9 m/s 2

The next step involves identifying a kinematic equation that would allow you to determine the unknown quantity. There are four kinematic equations to choose from. Again, you will always search for an equation that contains the three known variables and the one unknown variable. In this specific case, the three known variables and the one unknown variable are vi, vf, a, and d. An inspection of the four equations above reveals that the equation on the top right contains all four variables.

vf 2 = vi 2 + 2 • a • d

(0 m/s) 2 = (26 m/s) 2 + 2 •(-9/s 2 ) •d

0 m 2 /s 2 = 686 m 2 /s 2 + (-19 m/s 2 ) •d

(-19 m/s 2 ) • d = 0 m 2 /s 2 -686 m 2 /s 2

(-19 m/s 2 ) • d = -686 m 2 /s 2

d = (-686 m 2 /s 2 )/ (-19 m/s 2 )

d = 35. 0 m

The solution above reveals that the vase will travel upwards for a displacement of 35. meters before reaching its peak. (Note that this value is rounded to the third digit.)

The last step of the problem-solving strategy involves checking the answer to assure that it is both reasonable and accurate. The value seems reasonable enough. The vase

is thrown with a speed of approximately 50 mi/hr (merely approximate 1 m/s to be equivalent to 2 mi/hr). Such a throw will never make it further than one football field in height (approximately 100 m), yet will surely make it past the 10-yard line (approximately 10 meters). The calculated answer certainly falls within this range of reasonability. Checking for accuracy involves substituting the calculated value back into the equation for displacement and insuring that the left side of the equation is equal to the right side of the equation. Indeed it is!

Kinematic equations provide a useful means of determining the value of an unknown motion parameter if three motion parameters are known. In the case of a free-fall motion, the acceleration is often known. And in many cases, another motion parameter can be inferred through a solid knowledge of some basic kinematic principles.

• Multiple Choice

Topic : Physics Basics

Subject : physical science.

• More from: Physics Basics 52   Documents Go to topic
• More from: Physical Science Honors 975   Documents Go to course

Mechanical Engineering

Kinematic equations and free fall.

As mentioned in Lesson 5, a free-falling object is an object that is falling under the sole influence of gravity. That is to say that any object that is moving and being acted upon only be the force of gravity is said to be “in a state of  free fall .” Such an object will experience a downward acceleration of 9.8 m/s/s. Whether the object is falling downward or rising upward towards its peak, if it is under the sole influence of gravity, then its acceleration value is 9.8 m/s/s.

Like any moving object, the motion of an object in free fall can be described by four kinematic equations. The kinematic equations that describe any object’s motion are:

The symbols in the above equation have a specific meaning: the symbol  d  stands for the  displacement ; the symbol  t  stands for the  time ; the symbol  a  stands for the  acceleration  of the object; the symbol  v i  stands for the  initial velocity  value; and the symbol  v f  stands for the  final velocity .  

Applying Free Fall Concepts to Problem-Solving

There are a few conceptual characteristics of free fall motion that will be of value when using the equations to analyze free fall motion. These concepts are described as follows:

·         An object in free fall experiences an acceleration of -9.8 m/s/s. (The – sign indicates a downward acceleration.) Whether explicitly stated or not, the value of the acceleration in the kinematic equations is -9.8 m/s/s for any freely falling object.

·         If an object is merely dropped (as opposed to being thrown) from an elevated height, then the initial velocity of the object is 0 m/s.

·         If an object is projected upwards in a perfectly vertical direction, then it will slow down as it rises upward. The instant at which it reaches the peak of its trajectory, its velocity is 0 m/s. This value can be used as one of the motion parameters in the kinematic equations; for example, the final velocity ( v f ) after traveling to the peak would be assigned a value of 0 m/s.

·         If an object is projected upwards in a perfectly vertical direction, then the velocity at which it is projected is equal in magnitude and opposite in sign to the velocity that it has when it returns to the same height. That is, a ball projected vertically with an upward velocity of +30 m/s will have a downward velocity of -30 m/s when it returns to the same height.

These four principles and the four kinematic equations can be combined to solve problems involving the motion of free falling objects. The two examples below illustrate application of free fall principles to kinematic problem-solving. In each example, the problem solving strategy that was introduced earlier in this lesson will be utilized.  

Example Problem A

Luke Autbeloe drops a pile of roof shingles from the top of a roof located 8.52 meters above the ground. Determine the time required for the shingles to reach the ground.

The solution to this problem begins by the construction of an informative diagram of the physical situation. This is shown below. The second step involves the identification and listing of known information in variable form. You might note that in the statement of the problem, there is only one piece of numerical information explicitly stated: 8.52 meters. The displacement (d) of the shingles is -8.52 m. (The – sign indicates that the displacement is downward). The remaining information must be extracted from the problem statement based upon your understanding of the above principles. For example, the v i  value can be inferred to be 0 m/s since the shingles are dropped (released from rest; see note above). And the acceleration (a) of the shingles can be inferred to be -9.8 m/s 2  since the shingles are free-falling (see note above). (Always pay careful attention to the + and – signs for the given quantities.) The next step of the solution involves the listing of the unknown (or desired) information in variable form. In this case, the problem requests information about the time of fall. So t is the unknown quantity. The results of the first three steps are shown in the table below.

The next step involves identifying a kinematic equation that allows you to determine the unknown quantity. There are four kinematic equations to choose from. In general, you will always choose the equation that contains the three known and the one unknown variable. In this specific case, the three known variables and the one unknown variable are d, v i , a, and t. Thus, you will look for an equation that has these four variables listed in it. An inspection of the four equations above reveals that the equation on the top left contains all four variables.

d = v i   • t + ½ • a • t 2

Once the equation is identified and written down, the next step involves substituting known values into the equation and using proper algebraic steps to solve for the unknown information. This step is shown below.

-8.52 m = (0 m/s) • (t) + ½ • (-9.8 m/s 2 ) • (t) 2

-8.52 m = (0 m) *(t) + (-4.9 m/s 2 ) • (t) 2

-8.52 m = (-4.9 m/s 2 ) • (t) 2

(-8.52 m)/(-4.9 m/s 2 ) = t 2

1.739 s 2  = t 2

The solution above reveals that the shingles will fall for a time of 1.32 seconds before hitting the ground. (Note that this value is rounded to the third digit.)

The last step of the problem-solving strategy involves checking the answer to assure that it is both reasonable and accurate. The value seems reasonable enough. The shingles are falling a distance of approximately 10 yards (1 meter is pretty close to 1 yard); it seems that an answer between 1 and 2 seconds would be highly reasonable. The calculated time easily falls within this range of reasonability. Checking for accuracy involves substituting the calculated value back into the equation for time and insuring that the left side of the equation is equal to the right side of the equation. Indeed it is!  

Example Problem B

Rex Things throws his mother’s crystal vase vertically upwards with an initial velocity of 26.2 m/s. Determine the height to which the vase will rise above its initial height.

Once more, the solution to this problem begins by the construction of an informative diagram of the physical situation. This is shown below. The second step involves the identification and listing of known information in variable form. You might note that in the statement of the problem, there is only one piece of numerical information explicitly stated: 26.2 m/s. The initial velocity (v i ) of the vase is +26.2 m/s. (The + sign indicates that the initial velocity is an upwards velocity). The remaining information must be extracted from the problem statement based upon your understanding of the above principles. Note that the v f value can be inferred to be 0 m/s since the final state of the vase is the peak of its trajectory (see note above). The acceleration (a) of the vase is -9.8 m/s 2  (see note above). The next step involves the listing of the unknown (or desired) information in variable form. In this case, the problem requests information about the displacement of the vase (the height to which it rises above its starting height). So d is the unknown information. The results of the first three steps are shown in the table below.

The next step involves identifying a kinematic equation that would allow you to determine the unknown quantity. There are four kinematic equations to choose from. Again, you will always search for an equation that contains the three known variables and the one unknown variable. In this specific case, the three known variables and the one unknown variable are v i , v f , a, and d. An inspection of the four equations above reveals that the equation on the top right contains all four variables.

v f 2   = v i 2   + 2 • a • d

(0 m/s) 2  = (26.2 m/s) 2  + 2 •(-9.8m/s 2 ) •d

0 m 2 /s 2  = 686.44 m 2 /s 2  + (-19.6 m/s 2 ) •d

(-19.6 m/s 2 ) • d = 0 m 2 /s 2  -686.44 m 2 /s 2

(-19.6 m/s 2 ) • d = -686.44 m 2 /s 2

d = (-686.44 m 2 /s 2 )/ (-19.6 m/s 2 )

The solution above reveals that the vase will travel upwards for a displacement of 35.0 meters before reaching its peak. (Note that this value is rounded to the third digit.)

The last step of the problem-solving strategy involves checking the answer to assure that it is both reasonable and accurate. The value seems reasonable enough. The vase is thrown with a speed of approximately 50 mi/hr (merely approximate 1 m/s to be equivalent to 2 mi/hr). Such a throw will never make it further than one football field in height (approximately 100 m), yet will surely make it past the 10-yard line (approximately 10 meters). The calculated answer certainly falls within this range of reasonability. Checking for accuracy involves substituting the calculated value back into the equation for displacement and insuring that the left side of the equation is equal to the right side of the equation. Indeed it is!

Related Posts

Nearsightedness and its correction, farsightedness and its correction, the wonder of accommodation, image formation and detection, the mathematics of lenses.

Free Fall Motion: Explanation, Review, and Examples

• The Albert Team
• Last Updated On: February 16, 2023

Free fall and projectile motion describe objects that are moving through the air and acted on only by gravity. In this post, we will describe this type of motion using both graphs and kinematic equations. Since projectile motion involves two dimensions, these problems can be complex. We will explain many examples so you can see how to solve different types of projectile motion. 

What We Review

An object that is moving under only the influence of gravity is in free fall. In order for an object to be in free fall, wind and air resistance must be ignored. On Earth, all objects in free fall accelerate downward at the rate of gravity or 9.81\text{ m/s}^2 .

Applying Free Fall to Kinematic Equations

When analyzing free fall motion, we can apply the same kinematic equations as we did for motion on the ground. We can then use these equations to determine properties such as distance, time, and velocity. 

How to Find Distance Fallen for an Object in Free Fall

If an object is in free fall, we can use kinematic equations to find the distance it falls during a certain time. You will typically use the following kinematic equation to calculate the distance fallen:

In order to use this equation, you need to know the initial velocity of the object and the time of flight. Remember that the acceleration of a free falling object is always equal to the acceleration due to gravity, 9.81\text{ m/s}^2 . 

Many free fall physics problems will include scenarios where objects are dropped from rest. In this case, the initial velocity is zero and the first term of the kinematic equation above will cancel out. 

If the time is not known, another method for calculating the distance fallen is to use the following kinematic equation:

In this case, you must know the final velocity v_f of the object. Then, you can solve the equation for the distance d .

How to Find Time for an Object in Free Fall

The amount of time an object is in free fall will depend on its velocity and the distance it falls. Similar to distance, there are two equations you can use to find the time, depending on what you know. 

If you know the initial and final velocity of the object, then the simplest way to calculate time is using the kinematic equation:

This equation can be solved for time. Then, you’ll only need to substitute the values for the velocities and the acceleration due to gravity.

Another method to find time if you do not know the object’s final velocity is to use the equation:

Note that in this equation there are two terms that include the time t . Unless the initial velocity is zero, this can make it more challenging to solve this equation for time. If using this equation, you may need to use the quadratic formula to solve for time.

How to Find Final Velocity for an Object in Free Fall

The final velocity of an object in free fall depends on the amount of time it falls. Due to the acceleration of gravity, the velocity will increase every second by 9.81\text{ m/s} . The final velocity can be calculated using the equation:

If you do not know the amount of time the object is falling, another method for calculating the final velocity is using the kinematic equation: 

This equation requires that you instead know the distance that the object falls. If you are using this equation to find the final velocity, remember that the final velocity is squared in this equation. That means you will need to take a square root as your final step to solve for the final velocity. 

Examples of Free Fall

In this next section, we’ll apply the methods you just learned to solve some problems about free fall motion.

Example 1: How to Find the Distance for an Object Dropped from Rest

For example, an object is dropped from rest from the top of a tall building. It hits the ground 5\text{ s} after it is dropped. What is the height of the building? 

In this scenario, we know that the object’s initial velocity is zero because it was dropped from rest. We also know that the acceleration is 9.81\text{ m/s}^2 . This problem is asking us to find the distance the object falls. This will be equal to the height of the building.

Based on this information, we can use the following kinematic equation to find the distance:

Substituting the given values produces:

Therefore, the height of the building is about 123\text{ m} .

Example 2: How to Find the Final Velocity for an Object with Initial Velocity

In another example, an object in free fall has an initial, downward velocity of 2\text{ m/s} and falls a distance of 45\text{ m} . What is the object’s final velocity? 

In this scenario, we are given the object’s initial velocity, v_i and the distance d . We also know that the acceleration is 9.81\text{ m/s}^2 . Based on this information, we can use the following kinematic equation to find the final velocity:

Since the initial velocity is in the same direction as the acceleration (downward) we can use the same sign for both values.

Our last step is to eliminate the square by taking the square root:

Therefore, the final velocity of the object is about 30\text{ m/s} .

Motion Graphs for Objects in Free Fall

In addition to using physics equations, we can also represent free fall motion with motion graphs. Position-time graphs, velocity-time graphs, and acceleration-time graphs can tell us a lot about the object’s motion over time. Want a more in-depth review of motion graphs? Check out this blog post !

Position-Time Graph for an Object in Free Fall

In terms of position, many objects in free fall start at a high position, or height off the ground, and move downward. Objects in free fall accelerate due to gravity. Therefore, the position-time graph for free fall motion must be curved. This means that objects in free fall start with a slow velocity and gradually speed up which is represented by the steep downward curve of the graph. 

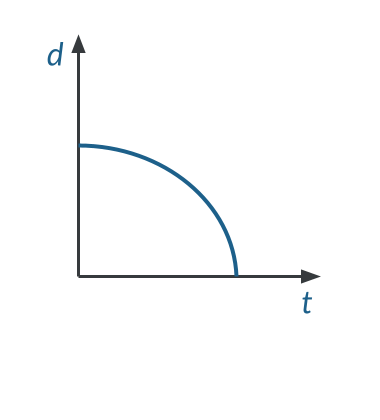
Velocity-Time Graph for an Object in Free Fall

As an object falls, its velocity increases due to the acceleration of gravity. This means that the velocity starts slow and steadily increases in the downward direction. The graph below shows the velocity-time for an object in free fall:

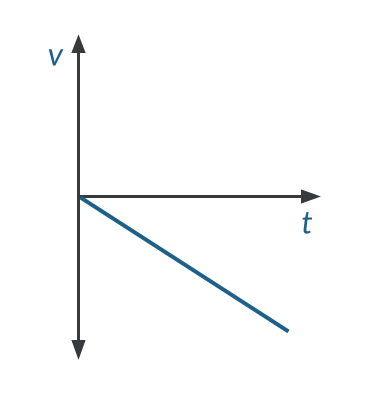
Note that the slope of this graph is constant and represents the acceleration due to gravity, or -9.81\text{ m/s}^2 .

Acceleration-Time Graph for an Object in Free Fall

Free fall acceleration is constant. Throughout the entire time that an object is falling, it is accelerating at a rate equal to the acceleration due to gravity, -9.81\text{ m/s}^2 . As shown in the graph below, the acceleration-time graph is a constant negative line. 

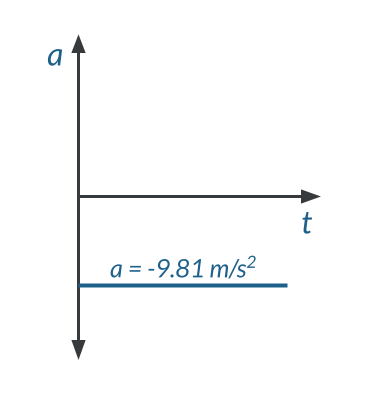
Projectile Motion

A projectile is an object that is launched or thrown into the air and then only influenced by gravity. Projectile motion has many similarities to free fall motion, however, projectiles may also travel a horizontal distance in addition to falling vertically down. 

Examples of Projectile Motion

The exact trajectory, or path, a projectile will take depends on how it is launched. However, all projectiles follow a curved trajectory such as in the image shown below:

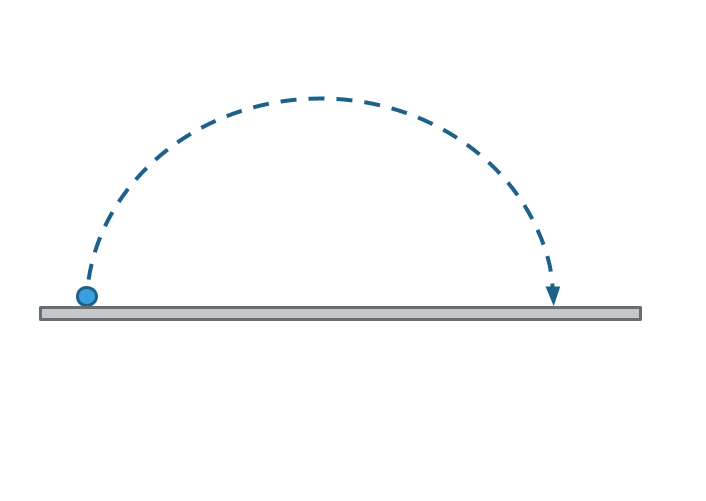
If you play or watch sports, you likely have already observed projectile motion. Projectile motion describes the arc of a basketball in a free throw, a fly ball in baseball, or a volleyball bumped over the net. 

Horizontal Component of Velocity

To analyze projectile motion, we must separate the motion into horizontal and vertical components. The horizontal component of a projectile’s velocity is independent of the vertical component of velocity. Since gravity acts vertically, there are no horizontal forces acting on projectiles. This means that the horizontal component of a projectile’s velocity remains constant throughout the entire flight. 

Example: Finding the Horizontal Component

For example, a projectile is launched from the ground with an initial speed of 8\text{ m/s} at a 60^{\circ} angle. What is the horizontal component of the projectile’s velocity?

We will need to use trig identities to determine the components of the velocity. We can visualize the components as a triangle where the hypotenuse is the initial velocity and the sides represent the horizontal, v_{ix} , and vertical, v_{iy} , components of the velocity.

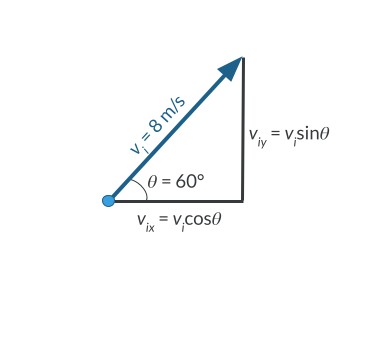
Cosine is defined as the adjacent side of the triangle divided by the hypotenuse. Since the horizontal component is adjacent to the angle, we can use cosine to find the horizontal component of velocity:

Therefore, the horizontal component of the initial velocity is 4\text{ m/s} .

Need to review your trig identities? Try out this resource from Khan Academy .

Vertical Component of Velocity

The vertical component of a projectile’s velocity will be influenced by gravity, which acts vertically on the object causing it to accelerate downward. Therefore, the vertical component of velocity will change throughout the projectile’s flight. We can calculate the vertical component of velocity at a particular time in a method similar to calculating the horizontal component. 

Example: Finding the Vertical Component

In the same example, a projectile is launched from the ground with an initial speed of 8\text{ m/s} at a 60^{\circ} angle. What is the vertical component of the projectile’s velocity?

As we visualize the velocity components, we are solving this time for the opposite side of the triangle. Sine is defined as the opposite side of the triangle divided by the hypotenuse. Therefore, the initial vertical velocity is:

Solving Projectile Motion Questions

Let’s apply what we’ve learned to some examples of projectile motion!

Example 1: Finding the Range of a Projectile

In this example, a projectile is fired horizontally with a speed of 5\text{ m/s} from a cliff with a height of 60\text{ m} . How far from the base of the cliff will the projectile land? 

In this scenario, we are given the initial horizontal velocity v_{ix}=5\text{ m/s} and the vertical change in position d_y=-60\text{ m} . Since the projectile is launched horizontally, the initial vertical velocity, v_{iy} , is zero. We also always know in projectile motion that the vertical acceleration is a_y=-9.81\text{ m/s}^2 and the horizontal acceleration, a_x , is zero.

This problem is asking us to find the horizontal displacement, or d_x . This is also referred to as the range . We can use the following kinematic equation to find the projectile’s final horizontal position:

Since the horizontal acceleration of a projectile is zero, this equation can be simplified to:

Before we can solve this equation, we must first determine the time of the projectile’s flight. We can actually use this same equation in the vertical direction to solve for time:

Since the initial vertical velocity is zero, this equation can be simplified to:

Solving for t :

Substituting the given values:

Now we can use this time to calculate the horizontal displacement of the projectile:

Therefore, the projectile will land about 17.5\text{ m} from the base of the cliff. 

Example 2: Finding the Maximum Height of a Projectile

As another example, a projectile is launched from the ground with an initial velocity of 25\text{ m/s} at an angle of 50^{\circ} . What is the projectile’s maximum height?

As a projectile travels upward, its vertical velocity becomes slower and slower due to the negative acceleration of gravity. At the maximum height of the trajectory, the projectile’s vertical velocity will momentarily be zero as the projectile stops and turns to move downward. Therefore, in this scenario, our final vertical velocity, v_{fy} , is zero.

We can use the following kinematic equation to solve for the maximum height, d_y :

Solving for d_y :

Before we can use this equation to calculate the height, we will need to use the sine trig identity to find the vertical component of the initial velocity:

Since the initial velocity is in the opposite direction as the acceleration, it’s really important to remember the sign here. If we define moving up as positive, then the initial velocity is positive and the acceleration is negative. Substituting this initial vertical velocity and the given values into the equation above gives:

Therefore, the projectile will reach a maximum height of about 18.7\text{ m} .

For more examples and an explanation of solving these types of projectile motion problems, check out this youtube video from Professor Dave . 

Understanding free fall and projectile motion allows you to solve some of the most complex problems you will encounter in introductory physics. All projectiles are acted on only by gravity, and the vertical and horizontal components of motion are independent of each other. This allows us to apply our kinematic equations to solve for a projectile’s time of flight, velocity, and displacement in each direction.  

Interested in a school license?​

Popular posts.

AP® Score Calculators

Simulate how different MCQ and FRQ scores translate into AP® scores

AP® Review Guides

The ultimate review guides for AP® subjects to help you plan and structure your prep.

Core Subject Review Guides

Review the most important topics in Physics and Algebra 1 .

SAT® Score Calculator

See how scores on each section impacts your overall SAT® score

ACT® Score Calculator

See how scores on each section impacts your overall ACT® score

Grammar Review Hub

Comprehensive review of grammar skills

AP® Posters

Download updated posters summarizing the main topics and structure for each AP® exam.

About me and why I created this physics website.

Free Fall Problems

• Search Website

Real World Applications — for high school level and above

• Amusement Parks
• Battle & Weapons
• Engineering
• Miscellaneous

Education & Theory — for high school level and above

• Useful Formulas
• Physics Questions
• Example Mechanics Problems
• Learn Physics Compendium

Kids Section

• Physics For Kids
• Science Experiments
• Science Fair Ideas
• Science Quiz
• Science Toys
• Teacher Resources
• Commercial Disclosure
• Privacy Policy

© Copyright 2009-2024 real-world-physics-problems.com

Questions to ponder

1. Describe the motion of a falling body.

2. What are the forces affecting the motion of a falling body?

3. In the absence of air friction , how would the acceleration of a large mass compare with the acceleration of a small mass?  

http://www.tompetty.com/

Video Instruction

showmethephysics.com

Fill in the Blank Notes

I. Motion of objects moving freely under the force of gravity.

Freefall - falling where the only force is gravity

Guy jumps from the 3rd floor onto a tree. Wild stuff

Galileo (1564 - 1642)

Credit : Original portrait by Justus Sustermans painted in 1636.

[Flash] Rutgers U.

Click on the Arrow

Free Fall - D vs. t Plot Rutgers U.

Distance and Time Rutgers U.

(Roll your mouse over this)

Show Me The Physics

Gravity/Moon - Feather & Hammer NASA

showmethphysics.com

g = - 9.8 m/s 2

Rounding off g we get -10 m/s 2

Ex) An object thrown upward at +40 m/s

An object is thrown up at a velocity of 30 m/s

About how long will it take to hit the ground?

Draw the V vs t Plot

A. Motion diagram for free fall on any planet or moon

Label the slope pictured above that could be Jupiter? Moon?

 Top Line: Jupiter

Bottom Line: Moon 

D vs t - free fall

A ball is thrown upward. What's the acceleration  due to gravity at the peak?

AP Question

Ex) Compare the displacement of an object dropped during its first second with its  displacement after 3 seconds.

 Δd = V i t + 1/2aΔt 2

 Δd = 1/2aΔt 2

9 times greater

Effect of Mass on Falling Bodies

Show Me The Physics YouTube Channel

©Tony Mangiacapre., - All Rights Reserved [ Home ] Established 1995 Use any material on this site (w/ attribution)

• TPC and eLearning
• What's NEW at TPC?
• Read Watch Interact
• Practice Review Test
• Teacher-Tools
• Request a Demo
• Get A Quote
• Subscription Selection
• Seat Calculator
• Ad Free Account
• Edit Profile Settings
• Metric Conversions Questions
• Metric System Questions
• Metric Estimation Questions
• Significant Digits Questions
• Proportional Reasoning
• Acceleration
• Distance-Displacement
• Dots and Graphs
• Graph That Motion
• Match That Graph
• Name That Motion
• Motion Diagrams
• Pos'n Time Graphs Numerical
• Pos'n Time Graphs Conceptual
• Up And Down - Questions
• Balanced vs. Unbalanced Forces
• Change of State
• Force and Motion
• Mass and Weight
• Match That Free-Body Diagram
• Net Force (and Acceleration) Ranking Tasks
• Newton's Second Law
• Normal Force Card Sort
• Recognizing Forces
• Air Resistance and Skydiving
• Solve It! with Newton's Second Law
• Which One Doesn't Belong?
• Component Addition Questions
• Head-to-Tail Vector Addition
• Projectile Mathematics
• Trajectory - Angle Launched Projectiles
• Trajectory - Horizontally Launched Projectiles
• Vector Addition
• Vector Direction
• Which One Doesn't Belong? Projectile Motion
• Forces in 2-Dimensions
• Being Impulsive About Momentum
• Explosions - Law Breakers
• Hit and Stick Collisions - Law Breakers
• Case Studies: Impulse and Force
• Impulse-Momentum Change Table
• Keeping Track of Momentum - Hit and Stick
• Keeping Track of Momentum - Hit and Bounce
• What's Up (and Down) with KE and PE?
• Energy Conservation Questions
• Energy Dissipation Questions
• Energy Ranking Tasks
• LOL Charts (a.k.a., Energy Bar Charts)
• Match That Bar Chart
• Words and Charts Questions
• Name That Energy
• Stepping Up with PE and KE Questions
• Case Studies - Circular Motion
• Circular Logic
• Forces and Free-Body Diagrams in Circular Motion
• Gravitational Field Strength
• Universal Gravitation
• Angular Position and Displacement
• Linear and Angular Velocity
• Angular Acceleration
• Rotational Inertia
• Balanced vs. Unbalanced Torques
• Getting a Handle on Torque
• Torque-ing About Rotation
• Properties of Matter
• Fluid Pressure
• Buoyant Force
• Sinking, Floating, and Hanging
• Pascal's Principle
• Flow Velocity
• Bernoulli's Principle
• Balloon Interactions
• Charge and Charging
• Charge Interactions
• Charging by Induction
• Conductors and Insulators
• Coulombs Law
• Electric Field
• Electric Field Intensity
• Polarization
• Case Studies: Electric Power
• Know Your Potential
• Light Bulb Anatomy
• I = ∆V/R Equations as a Guide to Thinking
• Parallel Circuits - ∆V = I•R Calculations
• Resistance Ranking Tasks
• Series Circuits - ∆V = I•R Calculations
• Series vs. Parallel Circuits
• Equivalent Resistance
• Period and Frequency of a Pendulum
• Pendulum Motion: Velocity and Force
• Energy of a Pendulum
• Period and Frequency of a Mass on a Spring
• Horizontal Springs: Velocity and Force
• Vertical Springs: Velocity and Force
• Energy of a Mass on a Spring
• Decibel Scale
• Frequency and Period
• Closed-End Air Columns
• Name That Harmonic: Strings
• Rocking the Boat
• Wave Basics
• Matching Pairs: Wave Characteristics
• Wave Interference
• Waves - Case Studies
• Color Addition and Subtraction
• Color Filters
• If This, Then That: Color Subtraction
• Light Intensity
• Color Pigments
• Converging Lenses
• Curved Mirror Images
• Law of Reflection
• Refraction and Lenses
• Total Internal Reflection
• Who Can See Who?
• Lab Equipment
• Lab Procedures
• Formulas and Atom Counting
• Atomic Models
• Bond Polarity
• Entropy Questions
• Cell Voltage Questions
• Heat of Formation Questions
• Reduction Potential Questions
• Oxidation States Questions
• Measuring the Quantity of Heat
• Hess's Law
• Oxidation-Reduction Questions
• Galvanic Cells Questions
• Thermal Stoichiometry
• Molecular Polarity
• Quantum Mechanics
• Balancing Chemical Equations
• Bronsted-Lowry Model of Acids and Bases
• Classification of Matter
• Collision Model of Reaction Rates
• Density Ranking Tasks
• Dissociation Reactions
• Complete Electron Configurations
• Elemental Measures
• Enthalpy Change Questions
• Equilibrium Concept
• Equilibrium Constant Expression
• Equilibrium Calculations - Questions
• Equilibrium ICE Table
• Intermolecular Forces Questions
• Ionic Bonding
• Lewis Electron Dot Structures
• Limiting Reactants
• Line Spectra Questions
• Mass Stoichiometry
• Measurement and Numbers
• Metals, Nonmetals, and Metalloids
• Metric Estimations
• Metric System
• Molarity Ranking Tasks
• Mole Conversions
• Name That Element
• Names to Formulas
• Names to Formulas 2
• Nuclear Decay
• Particles, Words, and Formulas
• Periodic Trends
• Precipitation Reactions and Net Ionic Equations
• Pressure Concepts
• Pressure-Temperature Gas Law
• Pressure-Volume Gas Law
• Chemical Reaction Types
• Significant Digits and Measurement
• States Of Matter Exercise
• Stoichiometry Law Breakers
• Stoichiometry - Math Relationships
• Subatomic Particles
• Spontaneity and Driving Forces
• Gibbs Free Energy
• Volume-Temperature Gas Law
• Acid-Base Properties
• Energy and Chemical Reactions
• Chemical and Physical Properties
• Valence Shell Electron Pair Repulsion Theory
• Writing Balanced Chemical Equations
• Mission CG1
• Mission CG10
• Mission CG2
• Mission CG3
• Mission CG4
• Mission CG5
• Mission CG6
• Mission CG7
• Mission CG8
• Mission CG9
• Mission EC1
• Mission EC10
• Mission EC11
• Mission EC12
• Mission EC2
• Mission EC3
• Mission EC4
• Mission EC5
• Mission EC6
• Mission EC7
• Mission EC8
• Mission EC9
• Mission RL1
• Mission RL2
• Mission RL3
• Mission RL4
• Mission RL5
• Mission RL6
• Mission KG7
• Mission RL8
• Mission KG9
• Mission RL10
• Mission RL11
• Mission RM1
• Mission RM2
• Mission RM3
• Mission RM4
• Mission RM5
• Mission RM6
• Mission RM8
• Mission RM10
• Mission LC1
• Mission RM11
• Mission LC2
• Mission LC3
• Mission LC4
• Mission LC5
• Mission LC6
• Mission LC8
• Mission SM1
• Mission SM2
• Mission SM3
• Mission SM4
• Mission SM5
• Mission SM6
• Mission SM8
• Mission SM10
• Mission KG10
• Mission SM11
• Mission KG2
• Mission KG3
• Mission KG4
• Mission KG5
• Mission KG6
• Mission KG8
• Mission KG11
• Mission F2D1
• Mission F2D2
• Mission F2D3
• Mission F2D4
• Mission F2D5
• Mission F2D6
• Mission KC1
• Mission KC2
• Mission KC3
• Mission KC4
• Mission KC5
• Mission KC6
• Mission KC7
• Mission KC8
• Mission AAA
• Mission SM9
• Mission LC7
• Mission LC9
• Mission NL1
• Mission NL2
• Mission NL3
• Mission NL4
• Mission NL5
• Mission NL6
• Mission NL7
• Mission NL8
• Mission NL9
• Mission NL10
• Mission NL11
• Mission NL12
• Mission MC1
• Mission MC10
• Mission MC2
• Mission MC3
• Mission MC4
• Mission MC5
• Mission MC6
• Mission MC7
• Mission MC8
• Mission MC9
• Mission RM7
• Mission RM9
• Mission RL7
• Mission RL9
• Mission SM7
• Mission SE1
• Mission SE10
• Mission SE11
• Mission SE12
• Mission SE2
• Mission SE3
• Mission SE4
• Mission SE5
• Mission SE6
• Mission SE7
• Mission SE8
• Mission SE9
• Mission VP1
• Mission VP10
• Mission VP2
• Mission VP3
• Mission VP4
• Mission VP5
• Mission VP6
• Mission VP7
• Mission VP8
• Mission VP9
• Mission WM1
• Mission WM2
• Mission WM3
• Mission WM4
• Mission WM5
• Mission WM6
• Mission WM7
• Mission WM8
• Mission WE1
• Mission WE10
• Mission WE2
• Mission WE3
• Mission WE4
• Mission WE5
• Mission WE6
• Mission WE7
• Mission WE8
• Mission WE9
• Vector Walk Interactive
• Name That Motion Interactive
• Kinematic Graphing 1 Concept Checker
• Kinematic Graphing 2 Concept Checker
• Graph That Motion Interactive
• Two Stage Rocket Interactive
• Rocket Sled Concept Checker
• Force Concept Checker
• Free-Body Diagrams Concept Checker
• Free-Body Diagrams The Sequel Concept Checker
• Skydiving Concept Checker
• Elevator Ride Concept Checker
• Vector Addition Concept Checker
• Vector Walk in Two Dimensions Interactive
• Name That Vector Interactive
• River Boat Simulator Concept Checker
• Projectile Simulator 2 Concept Checker
• Projectile Simulator 3 Concept Checker
• Hit the Target Interactive
• Turd the Target 1 Interactive
• Turd the Target 2 Interactive
• Balance It Interactive
• Go For The Gold Interactive
• Egg Drop Concept Checker
• Fish Catch Concept Checker
• Exploding Carts Concept Checker
• Collision Carts - Inelastic Collisions Concept Checker
• Its All Uphill Concept Checker
• Stopping Distance Concept Checker
• Chart That Motion Interactive
• Roller Coaster Model Concept Checker
• Uniform Circular Motion Concept Checker
• Horizontal Circle Simulation Concept Checker
• Vertical Circle Simulation Concept Checker
• Race Track Concept Checker
• Gravitational Fields Concept Checker
• Orbital Motion Concept Checker
• Angular Acceleration Concept Checker
• Balance Beam Concept Checker
• Torque Balancer Concept Checker
• Aluminum Can Polarization Concept Checker
• Charging Concept Checker
• Name That Charge Simulation
• Coulomb's Law Concept Checker
• Electric Field Lines Concept Checker
• Put the Charge in the Goal Concept Checker
• Circuit Builder Concept Checker (Series Circuits)
• Circuit Builder Concept Checker (Parallel Circuits)
• Circuit Builder Concept Checker (∆V-I-R)
• Circuit Builder Concept Checker (Voltage Drop)
• Equivalent Resistance Interactive
• Pendulum Motion Simulation Concept Checker
• Mass on a Spring Simulation Concept Checker
• Particle Wave Simulation Concept Checker
• Boundary Behavior Simulation Concept Checker
• Slinky Wave Simulator Concept Checker
• Simple Wave Simulator Concept Checker
• Wave Addition Simulation Concept Checker
• Standing Wave Maker Simulation Concept Checker
• Color Addition Concept Checker
• Painting With CMY Concept Checker
• Stage Lighting Concept Checker
• Filtering Away Concept Checker
• InterferencePatterns Concept Checker
• Young's Experiment Interactive
• Plane Mirror Images Interactive
• Who Can See Who Concept Checker
• Optics Bench (Mirrors) Concept Checker
• Name That Image (Mirrors) Interactive
• Refraction Concept Checker
• Total Internal Reflection Concept Checker
• Optics Bench (Lenses) Concept Checker
• Kinematics Preview
• Velocity Time Graphs Preview
• Moving Cart on an Inclined Plane Preview
• Stopping Distance Preview
• Cart, Bricks, and Bands Preview
• Fan Cart Study Preview
• Friction Preview
• Coffee Filter Lab Preview
• Friction, Speed, and Stopping Distance Preview
• Up and Down Preview
• Projectile Range Preview
• Ballistics Preview
• Juggling Preview
• Marshmallow Launcher Preview
• Air Bag Safety Preview
• Colliding Carts Preview
• Collisions Preview
• Engineering Safer Helmets Preview
• Push the Plow Preview
• Its All Uphill Preview
• Energy on an Incline Preview
• Modeling Roller Coasters Preview
• Hot Wheels Stopping Distance Preview
• Ball Bat Collision Preview
• Energy in Fields Preview
• Weightlessness Training Preview
• Roller Coaster Loops Preview
• Universal Gravitation Preview
• Keplers Laws Preview
• Kepler's Third Law Preview
• Charge Interactions Preview
• Sticky Tape Experiments Preview
• Wire Gauge Preview
• Voltage, Current, and Resistance Preview
• Light Bulb Resistance Preview
• Series and Parallel Circuits Preview
• Thermal Equilibrium Preview
• Linear Expansion Preview
• Heating Curves Preview
• Electricity and Magnetism - Part 1 Preview
• Electricity and Magnetism - Part 2 Preview
• Vibrating Mass on a Spring Preview
• Period of a Pendulum Preview
• Wave Speed Preview
• Slinky-Experiments Preview
• Standing Waves in a Rope Preview
• Sound as a Pressure Wave Preview
• DeciBel Scale Preview
• DeciBels, Phons, and Sones Preview
• Sound of Music Preview
• Shedding Light on Light Bulbs Preview
• Models of Light Preview
• Electromagnetic Radiation Preview
• Electromagnetic Spectrum Preview
• EM Wave Communication Preview
• Digitized Data Preview
• Light Intensity Preview
• Concave Mirrors Preview
• Object Image Relations Preview
• Snells Law Preview
• Reflection vs. Transmission Preview
• Magnification Lab Preview
• Reactivity Preview
• Ions and the Periodic Table Preview
• Periodic Trends Preview
• Chemical Reactions Preview
• Intermolecular Forces Preview
• Melting Points and Boiling Points Preview
• Bond Energy and Reactions Preview
• Reaction Rates Preview
• Ammonia Factory Preview
• Stoichiometry Preview
• Nuclear Chemistry Preview
• Gaining Teacher Access
• Task Tracker Directions
• Conceptual Physics Course
• On-Level Physics Course
• Honors Physics Course
• Chemistry Concept Builders
• All Chemistry Resources
• Users Voice
• Tasks and Classes
• Webinars and Trainings
• Subscription
• Subscription Locator
• 1-D Kinematics
• Newton's Laws
• Vectors - Motion and Forces in Two Dimensions
• Momentum and Its Conservation
• Work and Energy
• Circular Motion and Satellite Motion
• Thermal Physics
• Static Electricity
• Electric Circuits
• Vibrations and Waves
• Sound Waves and Music
• Light and Color
• Reflection and Mirrors
• Measurement and Calculations
• Elements, Atoms, and Ions
• Compounds,Names, and Formulas
• The Modern Atomic Model
• Chemical Bonding
• The Mole and its Applications
• Chemical Reactions
• About the Physics Interactives
• Task Tracker
• Usage Policy
• Newtons Laws
• Vectors and Projectiles
• Forces in 2D
• Momentum and Collisions
• Circular and Satellite Motion
• Balance and Rotation
• Electromagnetism
• Waves and Sound
• Atomic Physics
• Forces in Two Dimensions
• Work, Energy, and Power
• Circular Motion and Gravitation
• Sound Waves
• 1-Dimensional Kinematics
• Circular, Satellite, and Rotational Motion
• Einstein's Theory of Special Relativity
• Waves, Sound and Light
• QuickTime Movies
• About the Concept Builders
• Pricing For Schools
• Directions for Version 2
• Measurement and Units
• Relationships and Graphs
• Rotation and Balance
• Vibrational Motion
• Reflection and Refraction
• Teacher Accounts
• Kinematic Concepts
• Kinematic Graphing
• Wave Motion
• Sound and Music
• About CalcPad
• 1D Kinematics
• Vectors and Forces in 2D
• Simple Harmonic Motion
• Rotational Kinematics
• Rotation and Torque
• Rotational Dynamics
• Electric Fields, Potential, and Capacitance
• Transient RC Circuits
• Light Waves
• Units and Measurement
• Stoichiometry
• Molarity and Solutions
• Thermal Chemistry
• Acids and Bases
• Kinetics and Equilibrium
• Solution Equilibria
• Oxidation-Reduction
• Nuclear Chemistry
• Newton's Laws of Motion
• Work and Energy Packet
• Static Electricity Review
• NGSS Alignments
• 1D-Kinematics
• Projectiles
• Circular Motion
• Magnetism and Electromagnetism
• Graphing Practice
• About the ACT
• ACT Preparation
• For Teachers
• Other Resources
• Solutions Guide
• Solutions Guide Digital Download
• Solution Guide Corrections
• Motion in One Dimension
• Work, Energy and Power
• Chemistry of Matter
• Measurement and the Metric System
• Early Atomic Models
• Names and Formulas
• The Modern Model of the Atom
• Algebra Based On-Level Physics
• Honors Physics
• Conceptual Physics
• Other Tools
• Frequently Asked Questions
• Purchasing the Download
• Purchasing the Digital Download
• About the NGSS Corner
• NGSS Search
• Force and Motion DCIs - High School
• Energy DCIs - High School
• Wave Applications DCIs - High School
• Force and Motion PEs - High School
• Energy PEs - High School
• Wave Applications PEs - High School
• Crosscutting Concepts
• The Practices
• Physics Topics
• NGSS Corner: Activity List
• NGSS Corner: Infographics
• About the Toolkits
• Position-Velocity-Acceleration
• Position-Time Graphs
• Velocity-Time Graphs
• Newton's First Law
• Newton's Second Law
• Newton's Third Law
• Terminal Velocity
• Projectile Motion
• Forces in 2 Dimensions
• Impulse and Momentum Change
• Momentum Conservation
• Work-Energy Fundamentals
• Work-Energy Relationship
• Roller Coaster Physics
• Satellite Motion
• Electric Fields
• Circuit Concepts
• Series Circuits
• Parallel Circuits
• Describing-Waves
• Wave Behavior Toolkit
• Standing Wave Patterns
• Resonating Air Columns
• Wave Model of Light
• Plane Mirrors
• Curved Mirrors
• Teacher Guide
• Using Lab Notebooks
• Current Electricity
• Light Waves and Color
• Reflection and Ray Model of Light
• Refraction and Ray Model of Light
• Teacher Resources
• Subscriptions

• Newton's Laws
• Einstein's Theory of Special Relativity
• About Concept Checkers
• School Pricing
• Newton's Laws of Motion
• Newton's First Law
• Newton's Third Law

Free Fall - Complete Toolkit

• To know the meaning of free fall and the conditions under which it occurs.
• To know the value for the acceleration of gravity (g) and to relate this value to velocity-time information.
• o relate the motion of a free-falling object to the graphical descriptions of its motion.
• To use equations to calculate how fast and how far a free-falling object will move in a given amount of time.
• To understand that the acceleration of gravity is independent of the mass of the free-falling object.

Readings from The Physics Classroom Tutorial

• The Physics Classroom Tutorial, 1-D Kinematics Chapter, Lesson 5 http://www.physicsclassroom.com/class/1DKin/Lesson-5/Introduction

Interactive Simulations

Video and Animations

Labs and Investigations

• The Physics Classroom, The Laboratory, Free Fall Students use a motion detector to determine the acceleration of a falling object.  
• The Physics Classroom, The Laboratory, Dune Buggy Challenge This challenging lab project requires that students combine information about free falling motion and linear motion in order to calculate when a marble must be released in order for it to land is a toy car that is moving along the table below. Link:  http://www.physicsclassroom.com/lab#1dk

Minds On Physics Internet Modules:

• Newton's Laws, Ass’t NL10 -  Free Fall Acceleration

Concept Building Exercises:

• The Curriculum Corner, 1-D Kinematics, Free Fall

Problem-Solving Exercises:

• The Calculator Pad, 1-D Kinematics, Problems #25 - #28

Science Reasoning Activities:

• Science Reasoning Center, 1-D Kinematics, Kinematics

Real Life Connections:

Common Misconception:

• Acceleration of Gravity and Mass Many students believe that a more massive object will free fall faster than a less massive object. While this dependence upon mass is relevant to situations in which objects fall under the influence of air resistance, it does not apply to free-falling objects. All objects, regardless of mass, will free fall at a rate of 9.8 m/s/s.   

Elsewhere on the Web:

• HS-PS2-1 :     Analyze data to support the claim that Newton’s second law of motion describes the mathematical relationship among the new force on a macroscopic object, its mass, and its acceleration.  (Clarification statement:  Examples of data could include tables or graphs of position or velocity as a function of time for objects subject to a net unbalanced force, such as a falling object.)
• MS-PS2.B.iii      Forces that act at a distance (electric, magnetic, and gravitational) can be explained by fields that extend through space and can be mapped by their effect on a test object (a charged object or a ball, respectively).    Limited alignment
• HS-PS2.A.i        Newton’s second law accurately predicts changes in the motion of macroscopic objects.  
• Plan and conduct an investigation individually and collaboratively to produce data to serve as the basis for evidence … and consider limitations on the precision of the data  
• Create and/or revise a computational model or simulation of a phenomenon, designed device, process, or system.
• Use mathematical and/or algorithmic representations of phenomena or design solutions to describe and/or support claims and explanations.
• Use a computational representation of phenomena to describe and/or support claims and/or explanations
• MP.1     Make sense of problems and persevere in solving them.
• MP.2     Reason abstractly and quantitatively
• A-CED.4   Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations.
• F-IF.4      For a function that models a relationship between two quantities, interpret key features of graphs and tables in terms of the quantities, and sketch graphs showing key features given a verbal description of the relationship.
• F-IF.8.b      Use the properties of exponents to interpret expressions for exponential functions.
• N-VM.1      Recognize vector quantities as having both magnitude and direction. Represent vector quantities by directed line segments, and use appropriate symbols for vectors and their magnitudes.
• N-VM.3     Solve problems involving velocity and other quantities that can be represented by vectors.
• RST.11-12.2     Determine the central ideas or conclusions of a text; summarize complex concepts, processes, or information presented in a text by paraphrasing them in simpler but still accurate terms.
• RST.11-12.3     Follow precisely a complex multistep procedure when carrying out experiments, taking measurements, or performing technical tasks; analyze the specific results based on explanations in the text.
• RST.11-12.4     Determine the meaning of symbols, key terms, and other domain-specific words and phrases as they are used in a specific scientific or technical context relevant to grades 11—12 texts and topics.
• RST.11-12.9     Synthesize information from a range of sources (e.g., texts, experiments, simulations) into a coherent understanding of a process, phenomenon, or concept, resolving conflicting information when possible.
• RST.11-12.10   -- By the end of grade 12, read and comprehend science/technical texts in the grades 11-CCR text complexity band independently and proficiently.
• High School H.3.1.5     When the change in an object’s instantaneous velocity is the same in each successive unit time interval, the object has constant acceleration. For straight-line motion, constant acceleration can be represented by and calculated from a linear instantaneous velocity vs. time graph, a motion diagram, and the mathematical expression [a = (vf - vi)/(tf - ti)]. The sign (+ or -) of the constant acceleration indicates the direction of the change-of-velocity vector. A negative sign does not necessarily mean that the object is traveling in the negative direction or that it is slowing down. (Boundary: The term “deceleration” should be avoided because students tend to associate a negative sign of acceleration only with slowing down.)
• High School H.3.1.7       When the acceleration is constant, the magnitude of the average velocity during a time interval is one-half of the sum of the initial and final instantaneous velocities  [v = (vf + vi)/2].
• High School H.3.4.4      When people are in free fall, they feel “weightless” because people do not feel the extremely small gravitational force on each atom in their bodies. When standing, people feel the (normal) force of the ground pushing upwards on their feet, which produces the sensation of weight. 
• High School H.3.4.3      When an object’s distance from Earth’s surface is small compared to Earth’s radius, then a simplifying assumption is that the gravitational force on an object depends only on the mass of the object. In this case, objects fall with approximately the same acceleration: 9.8 m/sec/sec.  
• Explain what is “constant” when an object is moving with a constant acceleration, the two ways in which an object that has a positive constant acceleration can be moving (speeding up or slowing down) and the two ways in which an object that has a negative constant acceleration can be moving (speeding up or slowing down). Justify the explanations by constructing sketches of motion diagrams and using the shape of instantaneous velocity versus time graphs.
• Translate between different representations of the motion of objects: verbal and/or written descriptions, motion diagrams, data tables, graphical representations (position vs. time graphs and instantaneous velocity vs. time graphs) and mathematical representations.
• Evaluate the evidence for claims about the velocity or acceleration of objects in different experimental problems, using the criteria: (a) appropriate match of the evidence to the question or prediction; (b) adequate precision and accuracy; (c) correctness or data analysis and representation procedures (e.g., error bars on graphs for best estimate of slopes; and (d) the investigation was replicated (by other groups or classes).   Partial alignment
• Explain why all objects near Earth’s surface fall with approximately the same acceleration, despite having different masses and weights. Justify by using the universal law of gravitation and Newton’s Second Law.

• For educators
• English (US)
• English (India)
• English (UK)
• Greek Alphabet

Question: Applying Free Fall Concepts to Problem Solving There are a few conceptual characteristics of free fall motion that will be of value when using the equations to analyze free fall motion. These concepts are described as follows: • An object in free fall experiences an acceleration of -9.8 m/s/s. (The - sign indicates a downward acceleration.) Whether

Not the question you’re looking for?

Post any question and get expert help quickly.