assignment problem diagonal

Hungarian Method

The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term “Hungarian method” to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry. Let’s go through the steps of the Hungarian method with the help of a solved example.

Hungarian Method to Solve Assignment Problems

The Hungarian method is a simple way to solve assignment problems. Let us first discuss the assignment problems before moving on to learning the Hungarian method.

What is an Assignment Problem?

A transportation problem is a type of assignment problem. The goal is to allocate an equal amount of resources to the same number of activities. As a result, the overall cost of allocation is minimised or the total profit is maximised.

Because available resources such as workers, machines, and other resources have varying degrees of efficiency for executing different activities, and hence the cost, profit, or loss of conducting such activities varies.

Assume we have ‘n’ jobs to do on ‘m’ machines (i.e., one job to one machine). Our goal is to assign jobs to machines for the least amount of money possible (or maximum profit). Based on the notion that each machine can accomplish each task, but at variable levels of efficiency.

Hungarian Method Steps

Check to see if the number of rows and columns are equal; if they are, the assignment problem is considered to be balanced. Then go to step 1. If it is not balanced, it should be balanced before the algorithm is applied.

Step 1 – In the given cost matrix, subtract the least cost element of each row from all the entries in that row. Make sure that each row has at least one zero.

Step 2 – In the resultant cost matrix produced in step 1, subtract the least cost element in each column from all the components in that column, ensuring that each column contains at least one zero.

Step 3 – Assign zeros

• Analyse the rows one by one until you find a row with precisely one unmarked zero. Encircle this lonely unmarked zero and assign it a task. All other zeros in the column of this circular zero should be crossed out because they will not be used in any future assignments. Continue in this manner until you’ve gone through all of the rows.
• Examine the columns one by one until you find one with precisely one unmarked zero. Encircle this single unmarked zero and cross any other zero in its row to make an assignment to it. Continue until you’ve gone through all of the columns.

Step 4 – Perform the Optimal Test

• The present assignment is optimal if each row and column has exactly one encircled zero.
• The present assignment is not optimal if at least one row or column is missing an assignment (i.e., if at least one row or column is missing one encircled zero). Continue to step 5. Subtract the least cost element from all the entries in each column of the final cost matrix created in step 1 and ensure that each column has at least one zero.

Step 5 – Draw the least number of straight lines to cover all of the zeros as follows:

(a) Highlight the rows that aren’t assigned.

(b) Label the columns with zeros in marked rows (if they haven’t already been marked).

(c) Highlight the rows that have assignments in indicated columns (if they haven’t previously been marked).

(d) Continue with (b) and (c) until no further marking is needed.

(f) Simply draw the lines through all rows and columns that are not marked. If the number of these lines equals the order of the matrix, then the solution is optimal; otherwise, it is not.

Step 6 – Find the lowest cost factor that is not covered by the straight lines. Subtract this least-cost component from all the uncovered elements and add it to all the elements that are at the intersection of these straight lines, but leave the rest of the elements alone.

Step 7 – Continue with steps 1 – 6 until you’ve found the highest suitable assignment.

Hungarian Method Example

Use the Hungarian method to solve the given assignment problem stated in the table. The entries in the matrix represent each man’s processing time in hours.

\(\begin{array}{l}\begin{bmatrix} & I & II & III & IV & V \\1 & 20 & 15 & 18 & 20 & 25 \\2 & 18 & 20 & 12 & 14 & 15 \\3 & 21 & 23 & 25 & 27 & 25 \\4 & 17 & 18 & 21 & 23 & 20 \\5 & 18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)

With 5 jobs and 5 men, the stated problem is balanced.

\(\begin{array}{l}A = \begin{bmatrix}20 & 15 & 18 & 20 & 25 \\18 & 20 & 12 & 14 & 15 \\21 & 23 & 25 & 27 & 25 \\17 & 18 & 21 & 23 & 20 \\18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)

Subtract the lowest cost element in each row from all of the elements in the given cost matrix’s row. Make sure that each row has at least one zero.

\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 5 & 10 \\6 & 8 & 0 & 2 & 3 \\0 & 2 & 4 & 6 & 4 \\0 & 1 & 4 & 6 & 3 \\2 & 2 & 0 & 3 & 4 \\\end{bmatrix}\end{array} \)

Subtract the least cost element in each Column from all of the components in the given cost matrix’s Column. Check to see if each column has at least one zero.

\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 3 & 7 \\6 & 8 & 0 & 0 & 0 \\0 & 2 & 4 & 4 & 1 \\0 & 1 & 4 & 4 & 0 \\2 & 2 & 0 & 1 & 1 \\\end{bmatrix}\end{array} \)

When the zeros are assigned, we get the following:

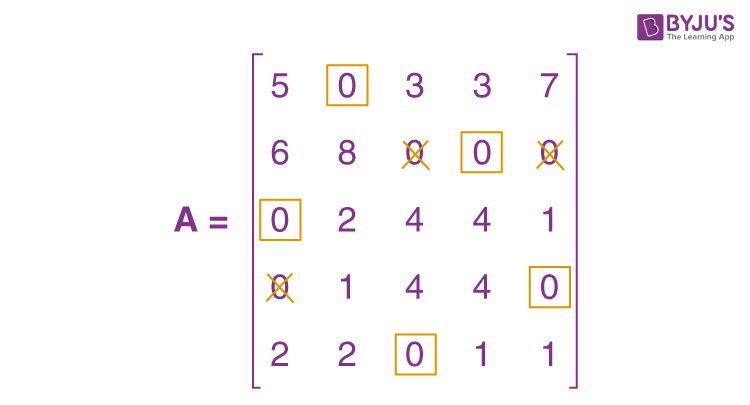
The present assignment is optimal because each row and column contain precisely one encircled zero.

Where 1 to II, 2 to IV, 3 to I, 4 to V, and 5 to III are the best assignments.

Hence, z = 15 + 14 + 21 + 20 + 16 = 86 hours is the optimal time.

Practice Question on Hungarian Method

Use the Hungarian method to solve the following assignment problem shown in table. The matrix entries represent the time it takes for each job to be processed by each machine in hours.

\(\begin{array}{l}\begin{bmatrix}J/M & I & II & III & IV & V \\1 & 9 & 22 & 58 & 11 & 19 \\2 & 43 & 78 & 72 & 50 & 63 \\3 & 41 & 28 & 91 & 37 & 45 \\4 & 74 & 42 & 27 & 49 & 39 \\5 & 36 & 11 & 57 & 22 & 25 \\\end{bmatrix}\end{array} \)

Stay tuned to BYJU’S – The Learning App and download the app to explore all Maths-related topics.

Frequently Asked Questions on Hungarian Method

What is hungarian method.

The Hungarian method is defined as a combinatorial optimization technique that solves the assignment problems in polynomial time and foreshadowed subsequent primal–dual approaches.

What are the steps involved in Hungarian method?

The following is a quick overview of the Hungarian method: Step 1: Subtract the row minima. Step 2: Subtract the column minimums. Step 3: Use a limited number of lines to cover all zeros. Step 4: Add some more zeros to the equation.

What is the purpose of the Hungarian method?

When workers are assigned to certain activities based on cost, the Hungarian method is beneficial for identifying minimum costs.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Assignment problem: Hungarian method 3

Assignment problem: Hungarian Method Nui Ruppert (Mtk_Nr.: 373224) David Lenh (Mtk_Nr.: 368343) Amir Farshchi Tabrizi (Mtk-Nr.: 372894)

In this OR-Wiki entry we're going to explain the Hungarian method with 3 examples. In the first example you'll find the optimal solution after a few steps with the help of the reduced matrix. The second example illustrates a complex case where you need to proceed all the steps of the algorithm to get to an optimal solution. Finally in the third example we will show how to solve a maximization problem with the Hungarian method.

Inhaltsverzeichnis

• 1 Introduction
• 2 Example 1 – Minimization problem
• 3 Example 2 – Minimazation problem
• 4 Example 3 – Maximization problem
• 6 References

Introduction

The Hungarian method is a combinatorial optimization algorithm which was developed and published by Harold Kuhn in 1955. This method was originally invented for the best assignment of a set of persons to a set of jobs. It is a special case of the transportation problem. The algorithm finds an optimal assignment for a given “n x n” cost matrix. “Assignment problems deal with the question how to assign n items (e.g. jobs) to n machines (or workers) in the best possible way. […] Mathematically an assignment is nothing else than a bijective mapping of a finite set into itself […]” [1]

The assignment constraints are mathematically defined as:

To make clear how to solve an assignment problem with the Hungarian algorithm we will show you the different cases with several examples which can occur .

Example 1 – Minimization problem

In this example we have to assign 4 workers to 4 machines. Each worker causes different costs for the machines. Your goal is to minimize the total cost to the condition that each machine goes to exactly 1 person and each person works at exactly 1 machine. For comprehension: Worker 1 causes a cost of 6 for machine 1 and so on …

To solve the problem we have to perform the following steps:

Step 1 – Subtract the row minimum from each row.

Step 2 – Subtract the column minimum from each column from the reduced matrix.

The idea behind these 2 steps is to simplify the matrix since the solution of the reduced matrix will be exactly the same as of the original matrix.

Step 3 – Assign one “0” to each row & column.

Now that we have simplified the matrix we can assign each worker with the minimal cost to each machine which is represented by a “0”.

- In the first row we have one assignable “0” therefore we assign it to worker 3 .

- In the second row we also only have one assignable “0” therefore we assign it to worker 4 .

- In the third row we have two assignable “0”. We leave it as it is for now.

- In the fourth row we have one assignable “0” therefore we assign it. Consider that we can only assign each worker to each machine hence we can’t allocate any other “0” in the first column.

- Now we go back to the third row which now only has one assignable “0” for worker 2 .

As soon as we can assign each worker to one machine, we have the optimal solution . In this case there is no need to proceed any further steps. Remember also, if we decide on an arbitrary order in which we start allocating the “0”s then we may get into a situation where we have 3 assignments as against the possible 4. If we assign a “0” in the third row to worker 1 we wouldn’t be able to allocate any “0”s in column one and row two.

The rule to assign the “0”:

- If there is an assignable “0”, only 1 assignable “0” in any row or any column, assign it.

- If there are more than 1, leave it and proceed.

This rule would try to give us as many assignments as possible.

Now there are also cases where you won’t get an optimal solution for a reduced matrix after one iteration. The following example will explain it.

Example 2 – Minimazation problem

In this example we have the fastest taxi company that has to assign each taxi to each passenger as fast as possible. The numbers in the matrix represent the time to reach the passenger.

We proceed as in the first example.

Iteration 1:

Now we have to assign the “0”s for every row respectively to the rule that we described earlier in example 1.

- In the first row we have one assignable “0” therefore we assign it and no other allocation in column 2 is possible.

- In the second row we have one assignable “0” therefore we assign it.

- In the third row we have several assignable “0”s. We leave it as it is for now and proceed.

- In the fourth and fifth row we have no assignable “0”s.

Now we proceed with the allocations of the “0”s for each column .

- In the first column we have one assignable “0” therefore we assign it. No other “0”s in row 3 are assignable anymore.

Now we are unable to proceed because all the “0”s either been assigned or crossed. The crosses indicate that they are not fit for assignments because assignments are already made.

We realize that we have 3 assignments for this 5x5 matrix. In the earlier example we were able to get 4 assignments for a 4x4 matrix. Now we have to follow another procedure to get the remaining 2 assignments (“0”).

Step 4 – Tick all unassigned rows.

Step 5 – If a row is ticked and has a “0”, then tick the corresponding column (if the column is not yet ticked).

Step 6 – If a column is ticked and has an assignment, then tick the corresponding row (if the row is not yet ticked).

Step 7 - Repeat step 5 and 6 till no more ticking is possible.

In this case there is no more ticking possible and we proceed with the next step.

Step 8 – Draw lines through unticked rows and ticked columns. The number of lines represents the maximum number of assignments possible.

Step 9 – Find out the smallest number which does not have any line passing through it. We call it Theta. Subtract theta from all the numbers that do not have any lines passing through them and add theta to all those numbers that have two lines passing through them. Keep the rest of them the same.

(With this step we create a new “0”)

With the new assignment matrix we start to assign the “0”s after the explained rules. Nevertheless we have 4 assignments against the required 5 for an optimal solution. Therefore we have to repeat step 4 – 9.

Iteration 2:

Step 4 – Tick all unassigned row.

Note: The indices of the ticks show you the order we added them.

Iteration 3:

Iteration 4:

After the fourth iteration we assign the “0”s again and now we have an optimal solution with 5 assignments.

The solution:

- Taxi1 => Passenger1 - duration 12

- Taxi2 => Passenger4 - duration 11

- Taxi3 => Passenger2 - duration 8

- Taxi4 => Passenger3 - duration 14

- Taxi5 => Passenger5 - duration 11

If we define the needed duration as costs, the minimal cost for this problem is 56.

Example 3 – Maximization problem

Furthermore the Hungarian algorithm can also be used for a maximization problem in which case we first have to transform the matrix. For example a company wants to assign different workers to different machines. Each worker is more or less efficient with each machine. The efficiency can be defined as profit. The higher the number, the higher the profit.

As you can see, the maximal profit of the matrix is 13. The simple twist that we do is rather than try to maximize the profit, we’re going to try to minimize the profit that you don’t get. If every value is taken away from 13, then we can minimize the amount of profit lost. We receive the following matrix:

From now on we proceed as usual with the steps to get to an optimal solution.

With the determined optimal solution we can compute the maximal profit:

- Worker1 => Machine2 - 9

- Worker2 => Machine4 - 11

- Worker3 => Machine3 - 13

- Worker4 => Machine1 - 7

Maximal profit is 40.

The optimal solution is found if there is one assigned “0” for each row and each column.

[1] Linear Assignment Problems and Extensions, Rainer E. Burkard, Eranda Cela

[2] Operations Research Skript TU Kaiserslautern, Prof. Dr. Oliver Wendt

[3] The Hungarian method for the assignment problem, H. W. Kuhn, Bryn Mawr College

Fundamental of Operations Research, Lec. 16, Prof. G. Srinivasan

Navigationsmenü

• Quelltext anzeigen
• Versionsgeschichte

Meine Werkzeuge

• Gemeinschaftsportal
• Operations Research
• Studentenbeiträge zum Thema Operations Research
• Wirtschaftsinformatik
• Aktuelle Ereignisse
• Letzte Änderungen
• Zufällige Seite
• Links auf diese Seite
• Änderungen an verlinkten Seiten
• Spezialseiten
• Druckversion
• Permanenter Link
• Seiten­informationen

• Diese Seite wurde zuletzt am 1. Juli 2013 um 11:03 Uhr geändert.
• Datenschutz
• Über Operations-Research-Wiki

8 16 15 91 64 83 42 93 75 27 76 95 75 81 50 20 42 96 90 24 38 28 2 15 81

15 16 64 8 91 93 42 27 83 75 75 95 50 76 81 96 42 24 20 90 2 28 81 38 15

15 + 42 + 50 + 20 + 15 = 142

Academia.edu no longer supports Internet Explorer.

To browse Academia.edu and the wider internet faster and more securely, please take a few seconds to  upgrade your browser .

Enter the email address you signed up with and we'll email you a reset link.

• We're Hiring!
• Help Center

A New Diagonal Optimal Approach for Assignment Problem

Different situations give rise to the assignment problem, where we must discover an optimal way to assign 'n' objects to 'm' in an bijective function. We have, in this research, propose the possibility of solving exactly the Linear Assignment Problem with a method that would be more efficient than the Hungarian method of exact solution. This method is based on applying a series of pairwise interchanges of assignments to a starting heuristically generated feasible solution, wherein each pairwise interchange is guaranteed to improve the objective function value of the feasible solution.It seems that our algorithm finds the optimal solution which is the same as one found by the Hungarian method, but in much simpler. 7980 M. Khalid et al.

Related Papers

IOP Publishing

Hussein Ali Hussein Al-Dallal Al-Saeedi

International Journal for Research in Applied Science & Engineering Technology (IJRASET)

IJRASET Publication

In this paper a new method is proposed for finding an optimal solution of a wide range of assignment problems, directly. A numerical illustration is established and the optimality of the result yielded by this method is also checked. The most attractive feature of this method is that it requires very simple arithmetical and logical calculations. The method is illustrated through an example.

archana pandey

Assignment problems arise in different situation where we have to find an optimal way to assign n-objects to mother objects in an injective fashion. The assignment problems are a well studied topic in combinatorial optimization. These problems find numerous application in production planning, telecommunication VLSI design, economic etc. The assignment problems is a special case of Transportation problem. Depending on the objective we want to optimize, we obtain the typical assignment problems. Assignment problem is an important subject discussed in real physical world we endeavor in this paper to introduce a new approach to assignment problem namely, matrix ones assignment method or MOA-method for solving wide range of problem. An example using matrix ones assignment methods and the existing Hungarian method have been solved and compared it graphically. Also some of the variations and some special cases in assignment problem and its applications have been discussed in the paper.

Sultana Rafi

The assignment problem is a particular type of linear programming problem. In this paper, we analyzed the standard and existing proposed methods. After studying these methods, we proposed a new alternative method for solving the assignment problem. We examined the newly proposed method by a couple of numerical examples and compare this result with the standard method. The main characteristic of this newly proposed method is that it constructed a very easy logical and arithmetical algorithm. Here we point out some advantages and limitations of the new proposed method. Programming code for the newly proposed method has been added in this paper.

Oksana Pichugina

The paper presents a new iterative approach to solving Linear Assignment problems (LAP) and finding a perfect matching in a weighted bipartite graph iteratively. For that, a new permutation-matrix model of optimal linear assignment is proposed, which allows recursively finding solutions on a set of augmenting paths built based on the current matching. The results can be combined with other methods for solving a LAP such as the Hungarian Algorithm and minimal cost method in order to find an optimum faster.

Ajit Pal Singh

YMER Digital

Assignment model comes under the class of linear programming model which is the most used techniques of operations research, which looks alike with transportation model with an objective function of minimizing the time or cost of manufacturing the products by allocating one job to one machine or one machine to one job or one destination to one origin or one origin to one destination only. In this paper, we represent linear mathematical formulation of Assignment problem and solved using Lingo Software. Keyword: Resource Allocation, Optimization Problem, Lingo Software, Assignment problem.

American Journal of Operations Research

Mr Ebenezer Quayson

Bhausaheb G Kore

In this paper I have proposed a new approach to solve an unbalanced assignment problem (UBAP). This approach includes two parts. First is to obtain an initial basic feasible solution (IBFS) and second part is to test optimality of an IBFS. I have proposed two new methods Row Penalty Assignment Method (RPAM) and Column Penalty Assignment Method (CPAM) to obtain an IBFS of an UBAP. Also I have proposed a new method Non-basic Smallest Effectiveness Method (NBSEM) to test optimality of an IBFS. We can solve an assignment problem of maximization type using this new approach in opposite sense. By this new approach, we achieve the goal with less number of computations and steps. Further we illustrate the new approach by suitable examples. INTRODUCTION The assignment problem is a special case of the transportation problem where the resources are being allocated to the activities on a one-to-one basis. Thus, each resource (e.g. an employee, machine or time slot) is to be assigned uniquely to a particular activity (e.g. a task, site or event). In assignment problems, supply in each row represents the availability of a resource such as a man, machine, vehicle, product, salesman, etc. and demand in each column represents different activities to be performed such as jobs, routes, factories, areas, etc. for each of which only one man or vehicle or product or salesman respectively is required. Entries in the square being costs, times or distances. The assignment method is a special linear programming technique for solving problems like choosing the right man for the right job when more than one choice is possible and when each man can perform all of the jobs. The ultimate objective is to assign a number of tasks to an equal number of facilities at minimum cost (or maximum profit) or some other specific goal. Let there be 'm' resources and 'n' activities. Let c ij be the effectiveness (in terms of cost, profit, time, etc.) of assigning resource i to activity j (i = 1, 2, …., m; j = 1, 2,…., n). Let x ij = 0, if resource i is not assigned to activity j and x ij = 1, if resource i is assigned to activity j. Then the objective is to determine x ij 's that will optimize the total effectiveness (Z) satisfying all the resource constraints and activity constraints. 1. Mathematical Formulation Let number of rows = m and number of columns = n. If m = n then an AP is said to be BAP otherwise it is said to be UBAP. A) Case 1: If m < n then mathematically the UBAP can be stated as follows:

Loading Preview

Sorry, preview is currently unavailable. You can download the paper by clicking the button above.

RELATED PAPERS

Michael Florian

Discrete Applied Mathematics

catherine roucairol

Industrial Engineering Journal

Shridhar Mhalsekar

AL-Rafidain Journal of Computer Sciences and Mathematics

Dr. Najla A Al-Saati

Trisna Darmawansyah

IJAR Indexing

Science Park Research Organization & Counselling

Eduardo Uchoa

Applied Mathematical Sciences

Anwar N Jasim

Lecture Notes in Economics and Mathematical Systems

Matthias Ehrgott

Computing Research Repository

Gregory Gutin

Jurnal Online Informatika

Ivanda Zevi Amalia

Journal of Heuristics

Philippe Fortemps

Mathematical Methods of Operations Research

Sergey Polyakovskiy , Frits Spieksma , Dries Goossens

Dr Avanish Kumar

IOSR Journals

Computational …

Laurent Herault

RELATED TOPICS

•   We're Hiring!
•   Help Center
• Find new research papers in:
• Health Sciences
• Earth Sciences
• Cognitive Science
• Mathematics
• Computer Science
• Academia ©2024