| LAPJV {TreeDist} | R Documentation |

Solve linear assignment problem using LAPJV
Description.
Use the algorithm of Jonker and Volgenant (1987) to solve the Linear Sum Assignment Problem (LSAP).
| Matrix of costs. |
The Linear Assignment Problem seeks to match each row of a matrix with a column, such that the cost of the matching is minimized.
The Jonker & Volgenant approach is a faster alternative to the Hungarian algorithm (Munkres 1957), which is implemented in clue::solve_LSAP() .
Note: the JV algorithm expects integers. In order to apply the function to a non-integer n , as in the tree distance calculations in this package, each n is multiplied by the largest available integer before applying the JV algorithm. If two values of n exhibit a trivial difference – e.g. due to floating point errors – then this can lead to interminable run times. (If numbers of the magnitude of billions differ only in their last significant digit, then the JV algorithm may undergo billions of iterations.) To avoid this, integers over 2^22 that differ by a value of 8 or less are treated as equal.
LAPJV() returns a list with two entries: score , the score of the optimal matching; and matching , the columns matched to each row of the matrix in turn.
C++ code by Roy Jonker, MagicLogic Optimization Inc. [email protected] , with contributions from Yong Yang [email protected] , after Yi Cao
Jonker R, Volgenant A (1987). “A shortest augmenting path algorithm for dense and sparse linear assignment problems.” Computing , 38 , 325–340. doi:10.1007/BF02278710 . Munkres J (1957). “Algorithms for the assignment and transportation problems.” Journal of the Society for Industrial and Applied Mathematics , 5 (1), 32–38. doi:10.1137/0105003 .
Implementations of the Hungarian algorithm exist in adagio , RcppHungarian , and clue and lpSolve ; for larger matrices, these are substantially slower. (See discussion at Stack Overflow .)
The JV algorithm is implemented for square matrices in the Bioconductor package GraphAlignment::LinearAssignment() .
Navigation Menu
Search code, repositories, users, issues, pull requests..., provide feedback.
We read every piece of feedback, and take your input very seriously.
Saved searches
Use saved searches to filter your results more quickly.
To see all available qualifiers, see our documentation .
- Notifications You must be signed in to change notification settings
Very simple implementation of the Hungarian Method for solving an asignation problem coded in R language.
sergioreyblanco/hungarian_method
Folders and files.
| Name | Name | |||
|---|---|---|---|---|
| 6 Commits | ||||
Repository files navigation
Implementation of the hungarian method in r language.
Here is a very simple implementation of the Hungarian Method in R language. It is used to solve assignment problems where a set of elements have to be asigned to an amount of other elements. The key of the problem is to find an optimal group of assignments of elements of the two set avoiding repetion. The word optimal is used because each assignment has a cost/profit. An example of this type of problem can be found in the following image (which corresponds to the example1 , in the terminology of the code developed):
The whole algorithm is implementated in the function assignmentSolver . It is divided in four well diferenced steps: caculation of the reduced matrix, the strikethrough crossed out of zeros, the update of the reduced matrix and the final gathering of the solution found. Moreover, this main function named assignmentSolver uses one auxiliary function called solutionChecking . Its usefulness is that of checking that the solution gathered is valid.
An instance of this function execution with example1 (using the terminology of the code) as input data is shown here:
As you can see, the cost/profit is given with its sign changed. The same happens with the values of each cell of the matrix used as input: the numbers have their sign changed. This is because the function minimizes a given matrix, but does not maximizes them.
The function takes as an input parameter a representation of a graph in the way of a matrix where each row is one element of the first set and each column represents one element of the second set. Thus, no assignment between elements of the same set or one with itself can be made. The introduced matrix must be a square one, so the method of the big M is used when there are less elements in the first set than in the second one, or viceversa. Each cell represents the profit (or cost) of assigning the corresponding element of the first set with other in the second one. Again, if one assingment between elements is not possible because of circumstances of the problem itself, an M is put in the corresponding cell. The function gives a return value consisting of a list with two components in which the first is the optimal assignment found and the other is the profit/cost of that assignment.
Example matrices are given (located in the last part of the code after the functions). Thus, you can test the function and create new ones. The first example matrix will result in a graph like this one:

The code does not need any additional libraries to run, besides the classical R environment.
- Stack Overflow for Teams Where developers & technologists share private knowledge with coworkers
- Advertising & Talent Reach devs & technologists worldwide about your product, service or employer brand
- OverflowAI GenAI features for Teams
- OverflowAPI Train & fine-tune LLMs
- Labs The future of collective knowledge sharing
- About the company Visit the blog
Collectives™ on Stack Overflow
Find centralized, trusted content and collaborate around the technologies you use most.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
Get early access and see previews of new features.
Matching algorithms in R (bipartite matching, Hungarian algorithm)
I wonder how to set up some example some fundamental matching procedures in R. There are many examples in various programming languages, but I have not yet found a good example for R.
Let’s say I want to match students to projects and I would consider 3 alternative approaches which I came across when googling on this issue:
1) Bipartite matching case: I ask each student to name 3 projects to work on (without stating any preference ranking among those 3).
2) Hungarian algorithm: I ask each student name 3 projects to work on WITH stating a preference ranking among those 3. As far as I understood the reasoning when applying the algorithm in this case would be something like: the better the rank the lower the “costs” to the student.
3) ??? approach: This should be pretty much related to (2). However, I think it is probably a better/ fairer approach (at least in the setting of the example). The students cannot pick projects, they even don’t know about the projects, but they have rate their qualifications (1 “not existent” to 10 “professional level”) with regards to a certain skillset. Further, the lecturer has rated the required skillset for every project. In addition to (2), a first step would be to calculate a similarity matrix and then to run the optimization routine from above.
I would appreciate any help in implementing those 3 approaches in R. Thank you.
UPDATE: The following questions seem to be related, but none show how to solve it in R: https://math.stackexchange.com/questions/132829/group-membership-assignment-by-preferences-optimization-problem https://superuser.com/questions/467577/using-optimization-to-assign-by-preference
- optimization
- linear-programming
- The R language is designed with statistical vector processing in mind. I would not expect it to be ideal for this sort of thing, or for many others. Because of this a quick google search will find you lots of information about calling other languages from R. A very simple way is to have R call other programs via system() as described for example in darrenjw.wordpress.com/2010/12/30/calling-c-code-from-r - although for the purposes of this method it doesn't matter much what the other program is written in so C could be almost anything. – mcdowella Commented May 23, 2013 at 4:11
- As those seem to be very fundamental techniques, I was wondering whether R does not also provide this functionality through e.g. the package optmatch or the package clue (i.e. solve_LSAP() ). – majom Commented May 23, 2013 at 20:17
- You can solve these using solve_LSAP(), you need to get the constraints and the cost functions right. You might even want to look at the package optimx. – jackStinger Commented Dec 9, 2013 at 5:44
Here are possible solutions using bipartite matching and the Hungarian algorithm.
My proposed solution using bipartite matching might not be what you have in mind. All the code below does is sample randomly for a specified number of iterations, after which at least one solution hopefully will have been identified. This might require a large number of iterations and a long time with large problems. The code below found three solutions to your example problem within 200 iterations.
Here is code for the Hungarian algorithm using package clue and solve_LSAP() as @jackStinger suggested. For this to work I had to replace the missing observations and I arbitrarily replaced them with 4. Person 5 did not get their first choice and Person 7 did not get any of their three choices.
Here is a link to a site showing how the Hungarian algorithm works: http://www.wikihow.com/Use-the-Hungarian-Algorithm
EDIT: June 5, 2014
Here is my first stab at optimizing the third scenario. I randomly assign each student to a project, then calculate the cost for that set of assignments. Cost is calculated by finding the difference between a student's skill set and the project's required skills. The absolute values of those differences are summed to give a total cost for the seven assignments.
Below I repeat the process 10,000 times and identify which of those 10,000 assignments results in the lowest cost.
An alternative approach would be to do an exhaustive search of all possible student-project assignments.
Neither the random search nor the exhaustive search is likely what you had in mind. However, the former will give an approximate optimal solution and the latter would give an exact optimal solution.
I might return to this problem later.
EDIT: June 6, 2014
Here is the exhaustive search. There are only 5040 possible ways to assign projects to the seven students. This search returns four optimal solutions:
- The third case perhaps can be solved with Munkres' Assignment Algorithm. I might look into that. However, Munkres' Assignment Algorithm looks like it might be a little complex to program and the exhaustive search approach I have already posted identifies the optimal solution quickly and easily. Although, the exhaustive search might not be feasible when the number of students and projects is large. – Mark Miller Commented Jun 6, 2014 at 17:10
Your Answer
Reminder: Answers generated by artificial intelligence tools are not allowed on Stack Overflow. Learn more
Sign up or log in
Post as a guest.
Required, but never shown
By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .
Not the answer you're looking for? Browse other questions tagged r optimization linear-programming or ask your own question .
- The Overflow Blog
- Mobile Observability: monitoring performance through cracked screens, old...
- Featured on Meta
- Announcing a change to the data-dump process
- Bringing clarity to status tag usage on meta sites
- What does a new user need in a homepage experience on Stack Overflow?
- Staging Ground Reviewer Motivation
- Feedback requested: How do you use tag hover descriptions for curating and do...
Hot Network Questions
- Coding exercise to represent an integer as words using python
- How specific does the GDPR require you to be when providing personal information to the police?
- Maximizing the common value of both sides of an equation
- magnetic boots inverted
- Who is the referent of "him" in Genesis 18:2?
- Can you give me an example of an implicit use of Godel's Completeness Theorem, say for example in group theory?
- Held Action Sneak attack after action surge
- Causal Reconciliation: Is this a viable way for my FTL system to preserve the course of History?
- Seinfeldisms in O.R
- Is there a way to define a function over the complex numbers, that satisfies a log property?
- How much new mathematics should we learn during the PhD? Are the courses we take during the PhD really important?
- How is it possible to know a proposed perpetual motion machine won't work without even looking at it?
- Can unlimited Duration spells be Dismissed?
- Does someone know when GPT5 will be publicly available?
- What unique phenomena would be observed in a system around a hypervelocity star?
- Is there a phrase for someone who's really bad at cooking?
- Whence “uniform distribution”?
- Is the ILIKE Operator in QGIS not working correctly?
- Is there a nonlinear resistor with a zero or infinite differential resistance?
- Is the spectrum of Hawking radiation identical to that of thermal radiation?
- Duties when bringing Canadian goods to US in luggage
- What is happening when a TV satellite stops broadcasting during an "eclipse"?
- How important is philosophy: does anyone delimit its importance?
- What does this translated phrase convey "The heart refuses to obey."?
Reset password New user? Sign up
Existing user? Log in
Hungarian Maximum Matching Algorithm
Already have an account? Log in here.
The Hungarian matching algorithm , also called the Kuhn-Munkres algorithm, is a \(O\big(|V|^3\big)\) algorithm that can be used to find maximum-weight matchings in bipartite graphs , which is sometimes called the assignment problem . A bipartite graph can easily be represented by an adjacency matrix , where the weights of edges are the entries. Thinking about the graph in terms of an adjacency matrix is useful for the Hungarian algorithm.
A matching corresponds to a choice of 1s in the adjacency matrix, with at most one 1 in each row and in each column.
The Hungarian algorithm solves the following problem:
In a complete bipartite graph \(G\), find the maximum-weight matching. (Recall that a maximum-weight matching is also a perfect matching.)
This can also be adapted to find the minimum-weight matching.
Say you are having a party and you want a musician to perform, a chef to prepare food, and a cleaning service to help clean up after the party. There are three companies that provide each of these three services, but one company can only provide one service at a time (i.e. Company B cannot provide both the cleaners and the chef). You are deciding which company you should purchase each service from in order to minimize the cost of the party. You realize that is an example of the assignment problem, and set out to make a graph out of the following information: \(\quad\) Company\(\quad\) \(\quad\) Cost for Musician\(\quad\) \(\quad\) Cost for Chef\(\quad\) \(\quad\) Cost for Cleaners\(\quad\) \(\quad\) Company A\(\quad\) \(\quad\) $108\(\quad\) \(\quad\) $125\(\quad\) \(\quad\) $150\(\quad\) \(\quad\) Company B\(\quad\) \(\quad\) $150\(\quad\) \(\quad\) $135\(\quad\) \(\quad\) $175\(\quad\) \(\quad\) Company C\(\quad\) \(\quad\) $122\(\quad\) \(\quad\) $148\(\quad\) \(\quad\) $250\(\quad\) Can you model this table as a graph? What are the nodes? What are the edges? Show Answer The nodes are the companies and the services. The edges are weighted by the price.
What are some ways to solve the problem above? Since the table above can be thought of as a \(3 \times 3\) matrix, one could certainly solve this problem using brute force, checking every combination and seeing what yields the lowest price. However, there are \(n!\) combinations to check, and for large \(n\), this method becomes very inefficient very quickly.
The Hungarian Algorithm Using an Adjacency Matrix
The hungarian algorithm using a graph.
With the cost matrix from the example above in mind, the Hungarian algorithm operates on this key idea: if a number is added to or subtracted from all of the entries of any one row or column of a cost matrix, then an optimal assignment for the resulting cost matrix is also an optimal assignment for the original cost matrix.
The Hungarian Method [1] Subtract the smallest entry in each row from all the other entries in the row. This will make the smallest entry in the row now equal to 0. Subtract the smallest entry in each column from all the other entries in the column. This will make the smallest entry in the column now equal to 0. Draw lines through the row and columns that have the 0 entries such that the fewest lines possible are drawn. If there are \(n\) lines drawn, an optimal assignment of zeros is possible and the algorithm is finished. If the number of lines is less than \(n\), then the optimal number of zeroes is not yet reached. Go to the next step. Find the smallest entry not covered by any line. Subtract this entry from each row that isn’t crossed out, and then add it to each column that is crossed out. Then, go back to Step 3.
Solve for the optimal solution for the example in the introduction using the Hungarian algorithm described above. Here is the initial adjacency matrix: Subtract the smallest value in each row from the other values in the row: Now, subtract the smallest value in each column from all other values in the column: Draw lines through the row and columns that have the 0 entries such that the fewest possible lines are drawn: There are 2 lines drawn, and 2 is less than 3, so there is not yet the optimal number of zeroes. Find the smallest entry not covered by any line. Subtract this entry from each row that isn’t crossed out, and then add it to each column that is crossed out. Then, go back to Step 3. 2 is the smallest entry. First, subtract from the uncovered rows: Now add to the covered columns: Now go back to step 3, drawing lines through the rows and columns that have 0 entries: There are 3 lines (which is \(n\)), so we are done. The assignment will be where the 0's are in the matrix such that only one 0 per row and column is part of the assignment. Replace the original values: The Hungarian algorithm tells us that it is cheapest to go with the musician from company C, the chef from company B, and the cleaners from company A. We can verify this by brute force. 108 + 135 + 250 = 493 108 + 148 + 175 = 431 150 + 125 + 250 = 525 150 + 148 + 150 = 448 122 + 125 + 175 = 422 122 + 135 + 150 = 407. We can see that 407 is the lowest price and matches the assignment the Hungarian algorithm determined. \(_\square\)
The Hungarian algorithm can also be executed by manipulating the weights of the bipartite graph in order to find a stable, maximum (or minimum) weight matching. This can be done by finding a feasible labeling of a graph that is perfectly matched, where a perfect matching is denoted as every vertex having exactly one edge of the matching.
How do we know that this creates a maximum-weight matching?
A feasible labeling on a perfect match returns a maximum-weighted matching. Suppose each edge \(e\) in the graph \(G\) connects two vertices, and every vertex \(v\) is covered exactly once. With this, we have the following inequality: \[w(M’) = \sum_{e\ \epsilon\ E} w(e) \leq \sum_{e\ \epsilon\ E } \big(l(e_x) + l(e_y)\big) = \sum_{v\ \epsilon\ V} l(v),\] where \(M’\) is any perfect matching in \(G\) created by a random assignment of vertices, and \(l(x)\) is a numeric label to node \(x\). This means that \(\sum_{v\ \epsilon\ V}\ l(v)\) is an upper bound on the cost of any perfect matching. Now let \(M\) be a perfect match in \(G\), then \[w(M) = \sum_{e\ \epsilon\ E} w(e) = \sum_{v\ \epsilon\ V}\ l(v).\] So \(w(M’) \leq w(M)\) and \(M\) is optimal. \(_\square\)
Start the algorithm by assigning any weight to each individual node in order to form a feasible labeling of the graph \(G\). This labeling will be improved upon by finding augmenting paths for the assignment until the optimal one is found.
A feasible labeling is a labeling such that
\(l(x) + l(y) \geq w(x,y)\ \forall x \in X, y \in Y\), where \(X\) is the set of nodes on one side of the bipartite graph, \(Y\) is the other set of nodes, \(l(x)\) is the label of \(x\), etc., and \(w(x,y)\) is the weight of the edge between \(x\) and \(y\).
A simple feasible labeling is just to label a node with the number of the largest weight from an edge going into the node. This is certain to be a feasible labeling because if \(A\) is a node connected to \(B\), the label of \(A\) plus the label of \(B\) is greater than or equal to the weight \(w(x,y)\) for all \(y\) and \(x\).
A feasible labeling of nodes, where labels are in red [2] .
Imagine there are four soccer players and each can play a few positions in the field. The team manager has quantified their skill level playing each position to make assignments easier.
How can players be assigned to positions in order to maximize the amount of skill points they provide?
The algorithm starts by labeling all nodes on one side of the graph with the maximum weight. This can be done by finding the maximum-weighted edge and labeling the adjacent node with it. Additionally, match the graph with those edges. If a node has two maximum edges, don’t connect them.
Although Eva is the best suited to play defense, she can't play defense and mid at the same time!
If the matching is perfect, the algorithm is done as there is a perfect matching of maximum weights. Otherwise, there will be two nodes that are not connected to any other node, like Tom and Defense. If this is the case, begin iterating.
Improve the labeling by finding the non-zero label vertex without a match, and try to find the best assignment for it. Formally, the Hungarian matching algorithm can be executed as defined below:
The Hungarian Algorithm for Graphs [3] Given: the labeling \(l\), an equality graph \(G_l = (V, E_l)\), an initial matching \(M\) in \(G_l\), and an unmatched vertex \(u \in V\) and \(u \notin M\) Augmenting the matching A path is augmenting for \(M\) in \(G_l\) if it alternates between edges in the matching and edges not in the matching, and the first and last vertices are free vertices , or unmatched, in \(M\). We will keep track of a candidate augmenting path starting at the vertex \(u\). If the algorithm finds an unmatched vertex \(v\), add on to the existing augmenting path \(p\) by adding the \(u\) to \(v\) segment. Flip the matching by replacing the edges in \(M\) with the edges in the augmenting path that are not in \(M\) \((\)in other words, the edges in \(E_l - M).\) Improving the labeling \(S \subseteq X\) and \(T \subseteq Y,\) where \(S\) and \(T\) represent the candidate augmenting alternating path between the matching and the edges not in the matching. Let \(N_l(S)\) be the neighbors to each node that is in \(S\) along edges in \(E_l\) such that \(N_l(S) = \{v|\forall u \in S: (u,v) \in E_l\}\). If \(N_l(S) = T\), then we cannot increase the size of the alternating path (and therefore can't further augment), so we need to improve the labeling. Let \(\delta_l\) be the minimum of \(l(u) + l(v) - w(u,v)\) over all of the \(u \in S\) and \(v \notin T\). Improve the labeling \(l\) to \(l'\): If \(r \in S,\) then \(l'(r) = l(r) - \delta_l,\) If \(r \in T,\) then \(l'(r) = l(r) + \delta_l.\) If \(r \notin S\) and \(r \notin T,\) then \(l'(r) = l(r).\) \(l'\) is a valid labeling and \(E_l \subset E_{l'}.\) Putting it all together: The Hungarian Algorithm Start with some matching \(M\), a valid labeling \(l\), where \(l\) is defined as the labelling \(\forall x \in X, y \in Y| l(y) = 0, l(x) = \text{ max}_{y \in Y}(w\big(x, y)\big)\). Do these steps until a perfect matching is found \((\)when \(M\) is perfect\():\) (a) Look for an augmenting path in \(M.\) (b) If an augmenting path does not exist, improve the labeling and then go back to step (a).
Each step will increase the size of the matching \(M\) or it will increase the size of the set of labeled edges, \(E_l\). This means that the process will eventually terminate since there are only so many edges in the graph \(G\). [4]
When the process terminates, \(M\) will be a perfect matching. By the Kuhn-Munkres theorem , this means that the matching is a maximum-weight matching.
The algorithm defined above can be implemented in the soccer scenario. First, the conflicting node is identified, implying that there is an alternating tree that must be reconfigured.
There is an alternating path between defense, Eva, mid, and Tom.
To find the best appropriate node, find the minimum \(\delta_l\), as defined in step 4 above, where \(l_u\) is the label for player \(u,\) \(l_v\) is the label for position \(v,\) and \(w_{u, v}\) is the weight on that edge.
The \(\delta_l\) of each unmatched node is computed, where the minimum is found to be a value of 2, between Tom playing mid \((8 + 0 – 6 = 2).\)
The labels are then augmented and the new edges are graphed in the example. Notice that defense and mid went down by 2 points, whereas Eva’s skillset got back two points. However, this is expected as Eva can't play in both positions at once.
Augmenting path leads to relabeling of nodes, which gives rise to the maximum-weighted path.
These new edges complete the perfect matching of the graph, which implies that a maximum-weighted graph has been found and the algorithm can terminate.
The complexity of the algorithm will be analyzed using the graph-based technique as a reference, yet the result is the same as for the matrix-based one.
Algorithm analysis [3] At each \(a\) or \(b\) step, the algorithm adds one edge to the matching and this happens \(O\big(|V|\big)\) times. It takes \(O\big(|V|\big)\) time to find the right vertex for the augmenting (if there is one at all), and it is \(O\big(|V|\big)\) time to flip the matching. Improving the labeling takes \(O\big(|V|\big)\) time to find \(\delta_l\) and to update the labelling accordingly. We might have to improve the labeling up to \(O\big(|V|\big)\) times if there is no augmenting path. This makes for a total of \(O\big(|V|^2\big)\) time. In all, there are \(O\big(|V|\big)\) iterations each taking \(O\big(|V|\big)\) work, leading to a total running time of \(O\big(|V|^3\big)\).
- Matching Algorithms
- Bruff, D. The Assignment Problem and the Hungarian Method . Retrieved June 26, 2016, from http://www.math.harvard.edu/archive/20_spring_05/handouts/assignment_overheads.pdf
- Golin, M. Bipartite Matching & the Hungarian Method . Retrieved Retrieved June 26th, 2016, from http://www.cse.ust.hk/~golin/COMP572/Notes/Matching.pdf
- Grinman, A. The Hungarian Algorithm for Weighted Bipartite Graphs . Retrieved June 26, 2016, from http://math.mit.edu/~rpeng/18434/hungarianAlgorithm.pdf
- Golin, M. Bipartite Matching & the Hungarian Method . Retrieved June 26, 2016, from http://www.cse.ust.hk/~golin/COMP572/Notes/Matching.pdf
Problem Loading...
Note Loading...
Set Loading...
Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
Constrained assignment problem (Linear Programming, Genetic Algorithm, etc...)
I'm looking for advice on how I should approach a specific problem. I have about 1000 shops that I have to assign to about 20 different supply centers out of a possible 28, and I'm trying to pick the best 20 (or less) centers that minimizes the overall distance between shops and supply centers.
I looked into the 'assignment problem' and how linear programming could help, but it seems this can only work if I have an equal number of shops and centers. I also looked into Genetic Algorithms and tried to code the algorithm to 1) ensure each shop is assigned to only one center and the center count must be no greater than 20, but results aren't that great (I can provide my R code if requested)
Should I continue trying to work with a Genetic Algorithm or can you folks suggest some other tool I should use or resource to look over? Thank you.
EDIT: Some nice user who's comment is now deleted suggested researching the Facility Location Problem . This seems more in line with what I'm looking for but most of the examples online cover single-facility problems, not multi-facility problems. Can anyone recommend a good resource for R or Python?
- optimization
- genetic-algorithms
- operations-research
EDIT: Apparently, I should have posted my original recommendation about the facility location problem as a reply to your question, not as an answer. I am new to the forum, but I get it now.
Any way, I believe your problem can be formulated as follows.
Let $y_i$ = 1 if supply center i is opened and 0 otherwise
$x_i,_j$ = 1 if supply center i feeds shop j and 0 otherwise
$c_i,_j$ = distance from supply center i to shop j
Then you want to solve the following linear programming problem.
minimize $\sum_i\sum_jc_i,_jx_i,_j$
subject to $\sum_ix_i,_j = 1$ j = 1,...,1000 (or the number of shops you have)
$\sum_jx_i,_j \le 1000y_i$ i = 1,...,28 (If you have a max capacity for each supply center, use that number instead of 1000; 1000 assumes there is no max capacity so one center could feasibly supply all shops)
$\sum_iy_i \le 20$ (max of 20 supply centers chosen)
$x_i,_j$ = 0 or 1 i=1,...,28; j =1,...,1000
$y_i$ = 0 or 1 i=1,...,14
The Rsymphony package in R can solve this problem for you. You will need a vector of the distances $c_i,_j$ and 0's for each $y_i$ as well as a matrix to take care of the constraints (the three summations starting after "subject to"). If you aren't familiar with the constraint matrix, each column contains the coefficients for that variable. The help file for the Rsymphony package has a couple examples that should help with that. Don't forget to include columns for the $y_i$ in the matrix as well. You will also need to set the $x_i,_j$ and $y_i$ to be binary by using
types = "B"
As an example, suppose we have 3 shops and 2 supply centers with distances between them as $x_1,_1$ = 2.8, $x_1,_2$ = 5.4, $x_1,_3$ = 1.4, $x_2,_1$ = 4.2, $x_2,_2$ = 3.0, $x_2,_3$ = 6.3. Then
tells us that we should open both supply centers and supply center 1 will supply shops 1 and 3 and supply center 2 will supply shop 2, for a total distance of 7.2.
I hope this helps.
- 1 $\begingroup$ Actually, this is a very direct answer to the question that suggests the use of the RSymphony package for integer linear programming to solve the problem. These types of integer programming problems are actually quite easy to solve exactly, so there's no need to use an heuristic approach such as genetic algorithms. $\endgroup$ – Brian Borchers Commented Feb 7, 2015 at 21:30
- $\begingroup$ @TAS thanks! Sorry for the late reply but I think this is exactly what I'm looking for! I'm going to test it out on my own data set and let you guys know soon. $\endgroup$ – gtnbz2nyt Commented Feb 11, 2015 at 15:12
- $\begingroup$ Glad to hear. I think the most difficult part will be coming up with your constraint matrix. $\endgroup$ – TAS Commented Feb 11, 2015 at 18:24
- $\begingroup$ @TAS Thanks a freaking million dude! It worked, and building the constraint matrix wasn't that hard once I took your example constraint matrix and broke it into different 'blocks' then binded them all together! $\endgroup$ – gtnbz2nyt Commented Feb 12, 2015 at 18:21
Your Answer
Sign up or log in, post as a guest.
Required, but never shown
By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .
Not the answer you're looking for? Browse other questions tagged r optimization linear genetic-algorithms operations-research or ask your own question .
- Featured on Meta
- Announcing a change to the data-dump process
- Bringing clarity to status tag usage on meta sites
Hot Network Questions
- Unable to update ubuntu 24.04 after incorrectly installing debian key
- Felt VR40 - 2020
- Is the ILIKE Operator in QGIS not working correctly?
- Writing an i with a line over it instead of an i with a dot and a line over it
- What does this translated phrase convey "The heart refuses to obey."?
- What happens when touching a piece which cannot make a legal move?
- How do eradicated diseases make a comeback?
- Is a company liable for "potential" harms?
- What unique phenomena would be observed in a system around a hypervelocity star?
- Can IRS make the taxpayer pay the costs of litigation if the latter loses the case?
- Overstayed Schengen but can I switch to US passport?
- Journal keeps messing with my proof
- Should you refactor when there are no tests?
- Cannot see my own router IP in VM machine in Kali Linux
- Causal Reconciliation: Is this a viable way for my FTL system to preserve the course of History?
- magnetic boots inverted
- What is the purpose of these 33-ohm series resistors on the RMII side of the LAN8742A?
- Whence “uniform distribution”?
- Does it pay to put effort in fixing this problem or better reinstall Ubuntu 24.04 from scratch?
- Why is simpler prose more popular these days?
- A short story about a boy who was the son of a "normal" woman and a vaguely human denizen of the deep
- How important is philosophy: does anyone delimit its importance?
- Why is there no article after 'by'?
- How to frame certain cells with tabluar?
- DSA Tutorial
- Data Structures
- Linked List
- Dynamic Programming
- Binary Tree
- Binary Search Tree
- Divide & Conquer
- Mathematical
- Backtracking
- Branch and Bound
- Pattern Searching
Hungarian Algorithm for Assignment Problem | Set 1 (Introduction)
- For each row of the matrix, find the smallest element and subtract it from every element in its row.
- Do the same (as step 1) for all columns.
- Cover all zeros in the matrix using minimum number of horizontal and vertical lines.
- Test for Optimality: If the minimum number of covering lines is n, an optimal assignment is possible and we are finished. Else if lines are lesser than n, we haven’t found the optimal assignment, and must proceed to step 5.
- Determine the smallest entry not covered by any line. Subtract this entry from each uncovered row, and then add it to each covered column. Return to step 3.
Try it before moving to see the solution
Explanation for above simple example:
An example that doesn’t lead to optimal value in first attempt: In the above example, the first check for optimality did give us solution. What if we the number covering lines is less than n.
Time complexity : O(n^3), where n is the number of workers and jobs. This is because the algorithm implements the Hungarian algorithm, which is known to have a time complexity of O(n^3).
Space complexity : O(n^2), where n is the number of workers and jobs. This is because the algorithm uses a 2D cost matrix of size n x n to store the costs of assigning each worker to a job, and additional arrays of size n to store the labels, matches, and auxiliary information needed for the algorithm.
In the next post, we will be discussing implementation of the above algorithm. The implementation requires more steps as we need to find minimum number of lines to cover all 0’s using a program. References: http://www.math.harvard.edu/archive/20_spring_05/handouts/assignment_overheads.pdf https://www.youtube.com/watch?v=dQDZNHwuuOY

Please Login to comment...
Similar reads.
- California Lawmakers Pass Bill to Limit AI Replicas
- Best 10 IPTV Service Providers in Germany
- Python 3.13 Releases | Enhanced REPL for Developers
- IPTV Anbieter in Deutschland - Top IPTV Anbieter Abonnements
- Content Improvement League 2024: From Good To A Great Article
Improve your Coding Skills with Practice
What kind of Experience do you want to share?
- Machine Learning Decision Tree – Solved Problem (ID3 algorithm)
- Poisson Distribution | Probability and Stochastic Process
- Conditional Probability | Joint Probability
- Solved assignment problems in communicaion |online Request
- while Loop in C++
EngineersTutor
Solved assignment problems – algorithms and flowcharts.
An algorithm is defined as sequence of steps to solve a problem (task) . The steps must be finite, well defined and unambiguous. Writing algorithm requires some thinking. Algorithm can also be defined as a plan to solve a problem and represents its logic. Note that an algorithm is of no use if it does not help us arrive at the desired solution
Algorithm characteristics
- It should have finite number of steps . No one can be expected to execute infinite number of steps.
- The steps must be in order and simple
- Each step should be defined clearly i.e. without un-ambiguity (without doubtfulness)
- Must include all required information
- Should exhibit at least one output
A flowchart is a pictorial (graphical) representation of an algorithm . A flowchart is drawn using different kinds of symbols. A symbol is used for a specific purpose. Each symbol has name.
| An algorithm is defined as . | . | Set of instructions. Instruction is a command to the computer to do some task. |
| Algorithm can also be defined as a plan to solve a problem and represents its logic. | A picture is worth of 1000 words. We can understand more from picture than words. | Implementation of Algorithm or flowchart |
Different algorithms have different performance characteristics to solve the same problem. Some algorithms are fast. Some are slow. Some occupy more memory space. Some occupy less memory space. Some are complex and some algorithms are simple.
Logically algorithm, flowchart and program are the same.
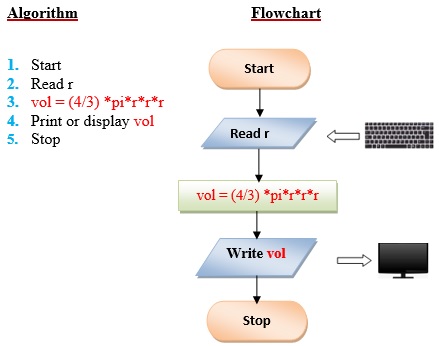
Q1 . Create a program to compute the volume of a sphere. Use the formula: V = (4/3) *pi*r 3 where pi is equal to 3.1416 approximately. The r is the radius of sphere. Display the result.
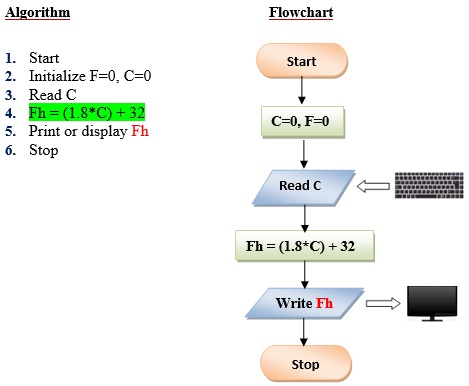
Q2 . Write a program the converts the input Celsius degree into its equivalent Fahrenheit degree. Use the formula: F = (9/5) *C+32.
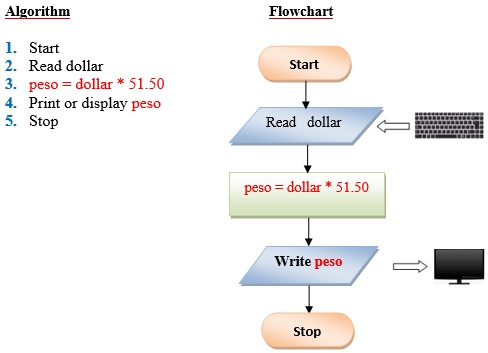
Q3 . Write a program that converts the input dollar to its peso exchange rate equivalent. Assume that the present exchange rate is 51.50 pesos against the dollar. Then display the peso equivalent exchange rate.
Q4 . Write a program that converts an input inch(es) into its equivalent centimeters. Take note that one inch is equivalent to 2.54cms.
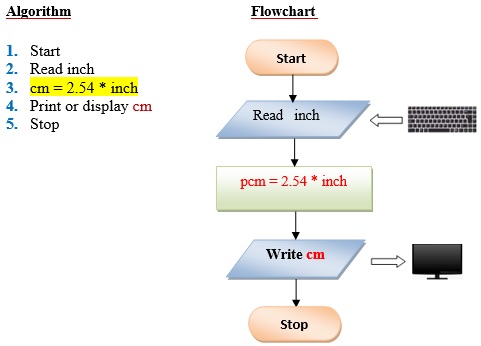
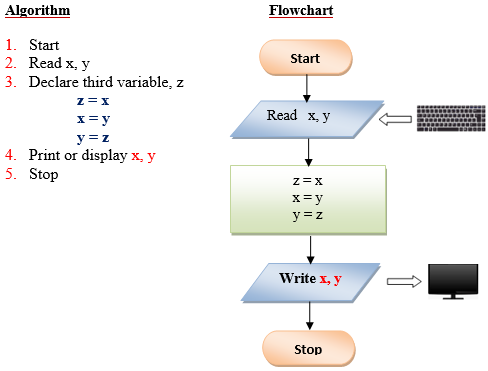
Q5 . Write a program that exchanges the value of two variables: x and y. The output must be: the value of variable y will become the value of variable x, and vice versa.
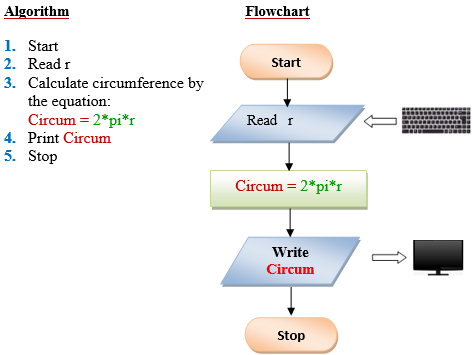
Q6 . Design a program to find the circumference of a circle. Use the formula: C=2πr, where π is approximately equivalent 3.1416.
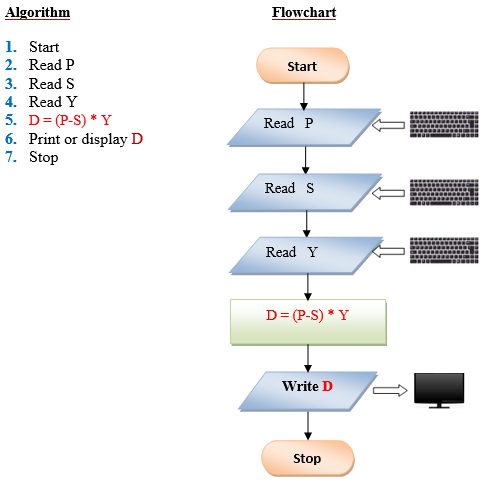
Q7 . Write a program that takes as input the purchase price of an item (P), its expected number of years of service (Y) and its expected salvage value (S). Then outputs the yearly depreciation for the item (D). Use the formula: D = (P – S) Y.
Q8 . Swapping of 2 variables without using temporary (or 3 rd variable).
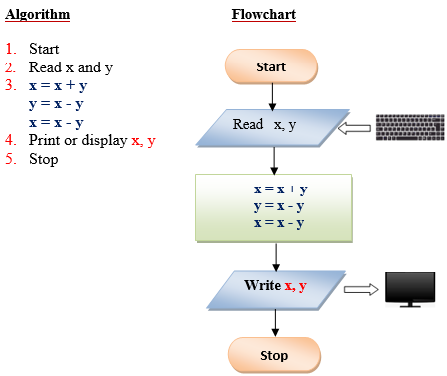
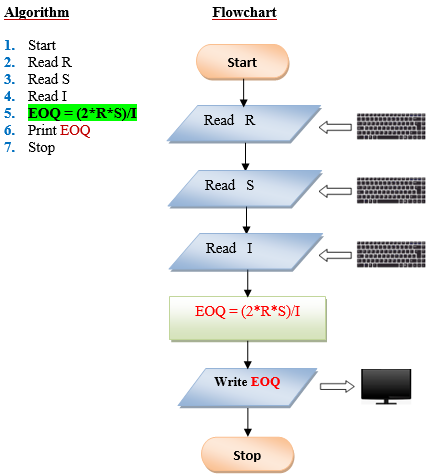
Q9 . Determine the most economical quantity to be stocked for each product that a manufacturing company has in its inventory: This quantity, called economic order quantity (EOQ) is calculated as follows: EOQ=2rs/1 where: R= total yearly production requirement S=set up cost per order I=inventory carrying cost per unit.
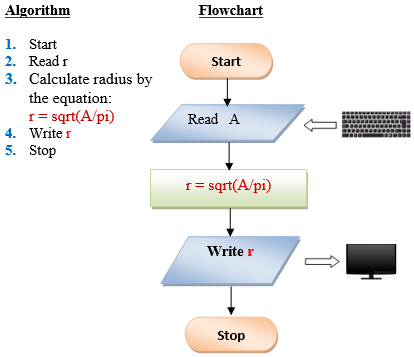
Q10 . Write a program to compute the radius of a circle. Derive your formula from the given equation: A=πr², then display the output.
- ← Solved Assignment Problems in Java (with Algorithm and Flowchart)
- Simple if statement in C →
Gopal Krishna
Hey Engineers, welcome to the award-winning blog,Engineers Tutor. I'm Gopal Krishna. a professional engineer & blogger from Andhra Pradesh, India. Notes and Video Materials for Engineering in Electronics, Communications and Computer Science subjects are added. "A blog to support Electronics, Electrical communication and computer students".
You May Also Like
Programming constructs, selection sort algorithm, examples of algorithms and flow charts – with java programs, leave a reply cancel reply.
Your email address will not be published. Required fields are marked *
Hungarian Method

The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term “Hungarian method” to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry. Let’s go through the steps of the Hungarian method with the help of a solved example.
Hungarian Method to Solve Assignment Problems
The Hungarian method is a simple way to solve assignment problems. Let us first discuss the assignment problems before moving on to learning the Hungarian method.
What is an Assignment Problem?
A transportation problem is a type of assignment problem. The goal is to allocate an equal amount of resources to the same number of activities. As a result, the overall cost of allocation is minimised or the total profit is maximised.
Because available resources such as workers, machines, and other resources have varying degrees of efficiency for executing different activities, and hence the cost, profit, or loss of conducting such activities varies.
Assume we have ‘n’ jobs to do on ‘m’ machines (i.e., one job to one machine). Our goal is to assign jobs to machines for the least amount of money possible (or maximum profit). Based on the notion that each machine can accomplish each task, but at variable levels of efficiency.
Hungarian Method Steps
Check to see if the number of rows and columns are equal; if they are, the assignment problem is considered to be balanced. Then go to step 1. If it is not balanced, it should be balanced before the algorithm is applied.
Step 1 – In the given cost matrix, subtract the least cost element of each row from all the entries in that row. Make sure that each row has at least one zero.
Step 2 – In the resultant cost matrix produced in step 1, subtract the least cost element in each column from all the components in that column, ensuring that each column contains at least one zero.
Step 3 – Assign zeros
- Analyse the rows one by one until you find a row with precisely one unmarked zero. Encircle this lonely unmarked zero and assign it a task. All other zeros in the column of this circular zero should be crossed out because they will not be used in any future assignments. Continue in this manner until you’ve gone through all of the rows.
- Examine the columns one by one until you find one with precisely one unmarked zero. Encircle this single unmarked zero and cross any other zero in its row to make an assignment to it. Continue until you’ve gone through all of the columns.
Step 4 – Perform the Optimal Test
- The present assignment is optimal if each row and column has exactly one encircled zero.
- The present assignment is not optimal if at least one row or column is missing an assignment (i.e., if at least one row or column is missing one encircled zero). Continue to step 5. Subtract the least cost element from all the entries in each column of the final cost matrix created in step 1 and ensure that each column has at least one zero.
Step 5 – Draw the least number of straight lines to cover all of the zeros as follows:
(a) Highlight the rows that aren’t assigned.
(b) Label the columns with zeros in marked rows (if they haven’t already been marked).
(c) Highlight the rows that have assignments in indicated columns (if they haven’t previously been marked).
(d) Continue with (b) and (c) until no further marking is needed.
(f) Simply draw the lines through all rows and columns that are not marked. If the number of these lines equals the order of the matrix, then the solution is optimal; otherwise, it is not.
Step 6 – Find the lowest cost factor that is not covered by the straight lines. Subtract this least-cost component from all the uncovered elements and add it to all the elements that are at the intersection of these straight lines, but leave the rest of the elements alone.
Step 7 – Continue with steps 1 – 6 until you’ve found the highest suitable assignment.
|
|
|---|
Hungarian Method Example
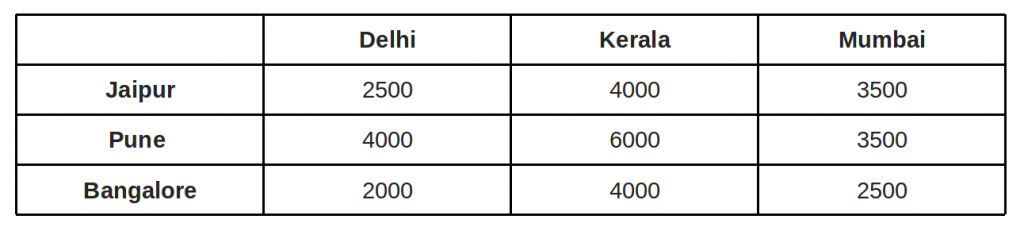
Use the Hungarian method to solve the given assignment problem stated in the table. The entries in the matrix represent each man’s processing time in hours.
\(\begin{array}{l}\begin{bmatrix} & I & II & III & IV & V \\1 & 20 & 15 & 18 & 20 & 25 \\2 & 18 & 20 & 12 & 14 & 15 \\3 & 21 & 23 & 25 & 27 & 25 \\4 & 17 & 18 & 21 & 23 & 20 \\5 & 18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)
With 5 jobs and 5 men, the stated problem is balanced.
\(\begin{array}{l}A = \begin{bmatrix}20 & 15 & 18 & 20 & 25 \\18 & 20 & 12 & 14 & 15 \\21 & 23 & 25 & 27 & 25 \\17 & 18 & 21 & 23 & 20 \\18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)
Subtract the lowest cost element in each row from all of the elements in the given cost matrix’s row. Make sure that each row has at least one zero.
\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 5 & 10 \\6 & 8 & 0 & 2 & 3 \\0 & 2 & 4 & 6 & 4 \\0 & 1 & 4 & 6 & 3 \\2 & 2 & 0 & 3 & 4 \\\end{bmatrix}\end{array} \)
Subtract the least cost element in each Column from all of the components in the given cost matrix’s Column. Check to see if each column has at least one zero.
\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 3 & 7 \\6 & 8 & 0 & 0 & 0 \\0 & 2 & 4 & 4 & 1 \\0 & 1 & 4 & 4 & 0 \\2 & 2 & 0 & 1 & 1 \\\end{bmatrix}\end{array} \)
When the zeros are assigned, we get the following:
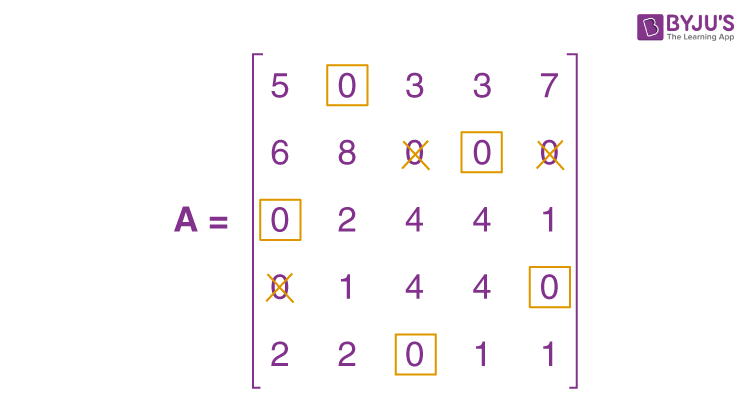
The present assignment is optimal because each row and column contain precisely one encircled zero.
Where 1 to II, 2 to IV, 3 to I, 4 to V, and 5 to III are the best assignments.
Hence, z = 15 + 14 + 21 + 20 + 16 = 86 hours is the optimal time.
Practice Question on Hungarian Method
Use the Hungarian method to solve the following assignment problem shown in table. The matrix entries represent the time it takes for each job to be processed by each machine in hours.
\(\begin{array}{l}\begin{bmatrix}J/M & I & II & III & IV & V \\1 & 9 & 22 & 58 & 11 & 19 \\2 & 43 & 78 & 72 & 50 & 63 \\3 & 41 & 28 & 91 & 37 & 45 \\4 & 74 & 42 & 27 & 49 & 39 \\5 & 36 & 11 & 57 & 22 & 25 \\\end{bmatrix}\end{array} \)
Stay tuned to BYJU’S – The Learning App and download the app to explore all Maths-related topics.
Frequently Asked Questions on Hungarian Method
What is hungarian method.
The Hungarian method is defined as a combinatorial optimization technique that solves the assignment problems in polynomial time and foreshadowed subsequent primal–dual approaches.
What are the steps involved in Hungarian method?
The following is a quick overview of the Hungarian method: Step 1: Subtract the row minima. Step 2: Subtract the column minimums. Step 3: Use a limited number of lines to cover all zeros. Step 4: Add some more zeros to the equation.
What is the purpose of the Hungarian method?
When workers are assigned to certain activities based on cost, the Hungarian method is beneficial for identifying minimum costs.
| MATHS Related Links | |
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.

COMMENTS
The Linear Assignment Problem seeks to match each row of a matrix with a column, such that the cost of the matching is minimized. The Jonker & Volgenant approach is a faster alternative to the Hungarian algorithm (Munkres 1957), which is implemented in clue::solve_LSAP() . Note: the JV algorithm expects integers.
The word optimal is used because each assignment has a cost/profit. An example of this type of problem can be found in the following image (which corresponds to the example1, in the terminology of the code developed): The whole algorithm is implementated in the function assignmentSolver. It is divided in four well diferenced steps: caculation ...
Hungarian algorithm steps for minimization problem. Step 1: For each row, subtract the minimum number in that row from all numbers in that row. Step 2: For each column, subtract the minimum number in that column from all numbers in that column. Step 3: Draw the minimum number of lines to cover all zeroes.
The formal definition of the assignment problem (or linear assignment problem) is . Given two sets, A and T, together with a weight function C : A × T → R.Find a bijection f : A → T such that the cost function: (, ())is minimized. Usually the weight function is viewed as a square real-valued matrix C, so that the cost function is written down as: , The problem is "linear" because the cost ...
Solution 2: Hungarian Algorithm The optimal assignment can be found using the Hungarian algorithm. The Hungarian algorithm has worst case run-time complexity of O(n^3). Solution 3: DFS/BFS on state space tree A state space tree is a N-ary tree with property that any path from root to leaf node holds one of many solutions to given problem.
The algorithm maintains a matching M and compatible prices p. Pf. Follows from Lemmas 2 and 3 and initial choice of prices. ! Theorem. The algorithm returns a min cost perfect matching. Pf. Upon termination M is a perfect matching, and p are compatible Optimality follows from Observation 2. ! Theorem. The algorithm can be implemented in O(n 3 ...
For purposes of an example in R assume matrix m below where each row is a student and each column is a job and 1 means the student's top choice, 2 means the second choice and so on. 9 means the student did not rank the job. There were 3 students and 4 tasks so we added a dummy student, U, of all 9s for the last row so that the number of students and tasks are the same.
Aringhieri et al. (2015) presented a two-stage heuristic algorithm for the assignment problem. The algorithm was tested using real data collected from a state hospital in Genova, Italy. The results show that the proposed method performs well in terms of both solution quality and computation time [11]. When the
4. Here are possible solutions using bipartite matching and the Hungarian algorithm. My proposed solution using bipartite matching might not be what you have in mind. All the code below does is sample randomly for a specified number of iterations, after which at least one solution hopefully will have been identified.
The Hungarian matching algorithm, also called the Kuhn-Munkres algorithm, is a \(O\big(|V|^3\big)\) algorithm that can be used to find maximum-weight matchings in bipartite graphs, which is sometimes called the assignment problem.A bipartite graph can easily be represented by an adjacency matrix, where the weights of edges are the entries.Thinking about the graph in terms of an adjacency ...
First, label each of your "bags" as a number between 0 and n − 1 n − 1, where n = 19 ∗ 20 = 380 n = 19 ∗ 20 = 380 (the total number of bags). Let P then be a vector of 380 integers, each getting a value between 2 and 20 inclusive. The interpretation is that P[i] = k P [ i] = k indicates bag ID i i goes into bin k k.
1. Actually, this is a very direct answer to the question that suggests the use of the RSymphony package for integer linear programming to solve the problem. These types of integer programming problems are actually quite easy to solve exactly, so there's no need to use an heuristic approach such as genetic algorithms. - Brian Borchers.
The Hungarian algorithm, aka Munkres assignment algorithm, utilizes the following theorem for polynomial runtime complexity (worst case O(n 3)) and guaranteed optimality: If a number is added to or subtracted from all of the entries of any one row or column of a cost matrix, then an optimal assignment for the resulting cost matrix is also an ...
The Hungarian Method for Solving the Assignment Problem We're ready to state the Hungarian method now that we've seen a couple of examples. Initialize the algorithm: { Subtract the lowest row value from each row. { For each column, subtract the lowest value. Steps 1 and 2 create zeros to start the algorithm o .
Assignment problems deal with the question of how to assign other items (machines, tasks). There are different ways in mathematics to describe an assignment: we can view an assignment as a bijective mapping φ between two finite sets . We can write a permutation φ as 12…nφ (1)φ (2)…φ (n), which means that 1 is mapped to φ (1), 2 is ...
THE HUNGARIAN METHOD FOR THE ASSIGNMENT. PROBLEM'. H. W. Kuhn. Bryn Y a w College. Assuming that numerical scores are available for the perform- ance of each of n persons on each of n jobs, the "assignment problem" is the quest for an assignment of persons to jobs so that the sum of the. n scores so obtained is as large as possible.
The Hungarian method is a combinatorial optimization algorithm that solves the assignment problem in polynomial time and which anticipated later primal-dual methods.It was developed and published in 1955 by Harold Kuhn, who gave it the name "Hungarian method" because the algorithm was largely based on the earlier works of two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry.
The assignment problem is a special case of the transportation problem, which in turn is a special case of the min-cost flow problem, so it can be solved using algorithms that solve the more general cases. Also, our problem is a special case of binary integer linear programming problem (which is NP-hard). But, due to the specifics of the ...
The Hungarian method is a combinatorial optimization algorithm which solves the assignment problem in polynomial time . Later it was discovered that it was a primal-dual Simplex method.. It was developed and published by Harold Kuhn in 1955, who gave the name "Hungarian method" because the algorithm was largely based on the earlier works of two Hungarian mathematicians: Denes Konig and Jeno ...
Program. An algorithm is defined as sequence of steps to solve a problem (task). A flowchart is pictorial (graphical) representation of an algorithm. Set of instructions. Instruction is a command to the computer to do some task. Algorithm can also be defined as a plan to solve a problem and represents its logic. A picture is worth of 1000 words.
The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term "Hungarian method" to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry. Let's go through the steps of the Hungarian method with the help of a solved example.